Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation
Abstract
:1. Introduction
2. Definitions and Preliminaries Concepts
3. Laplace Adomian Decomposition Method
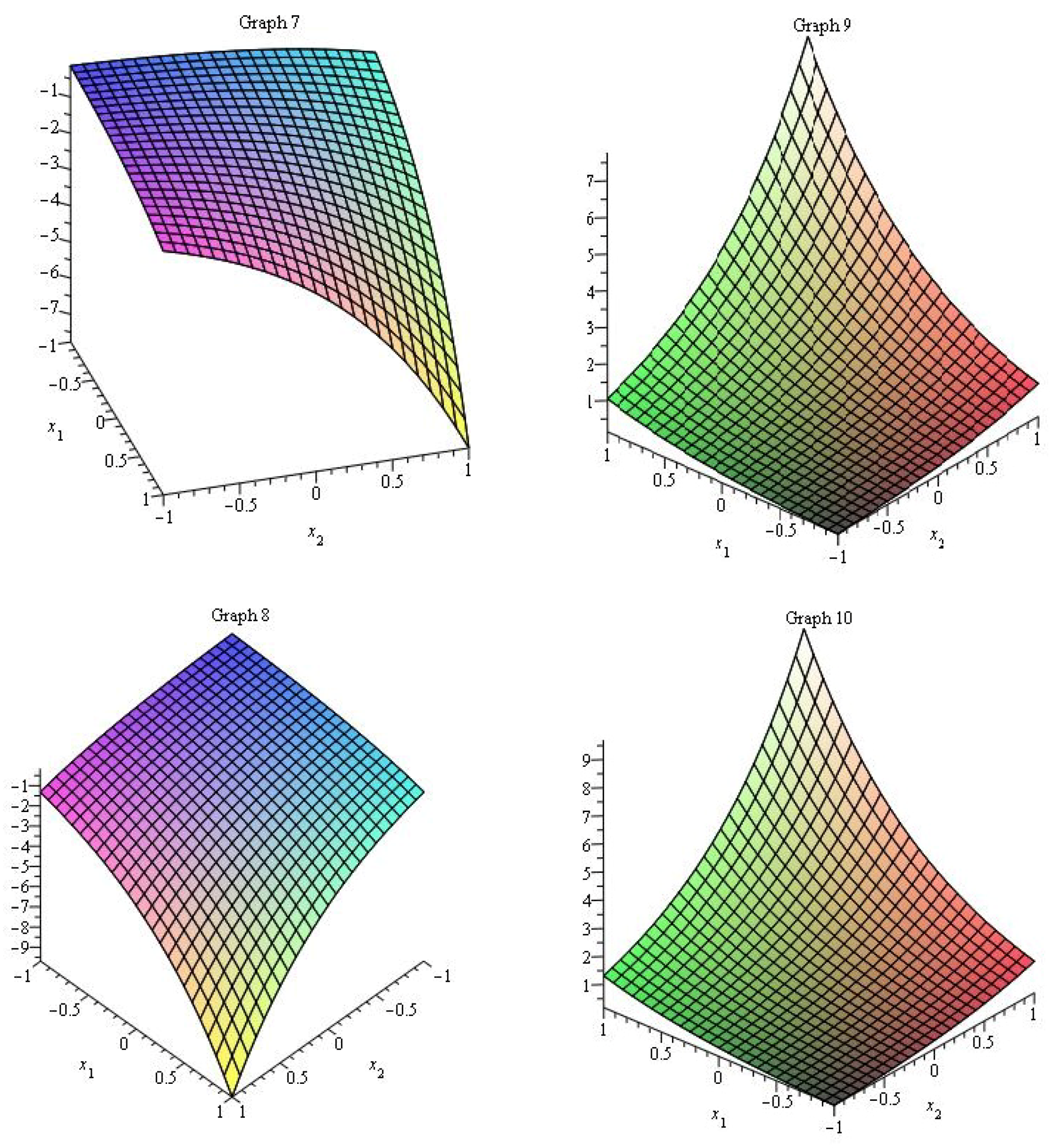
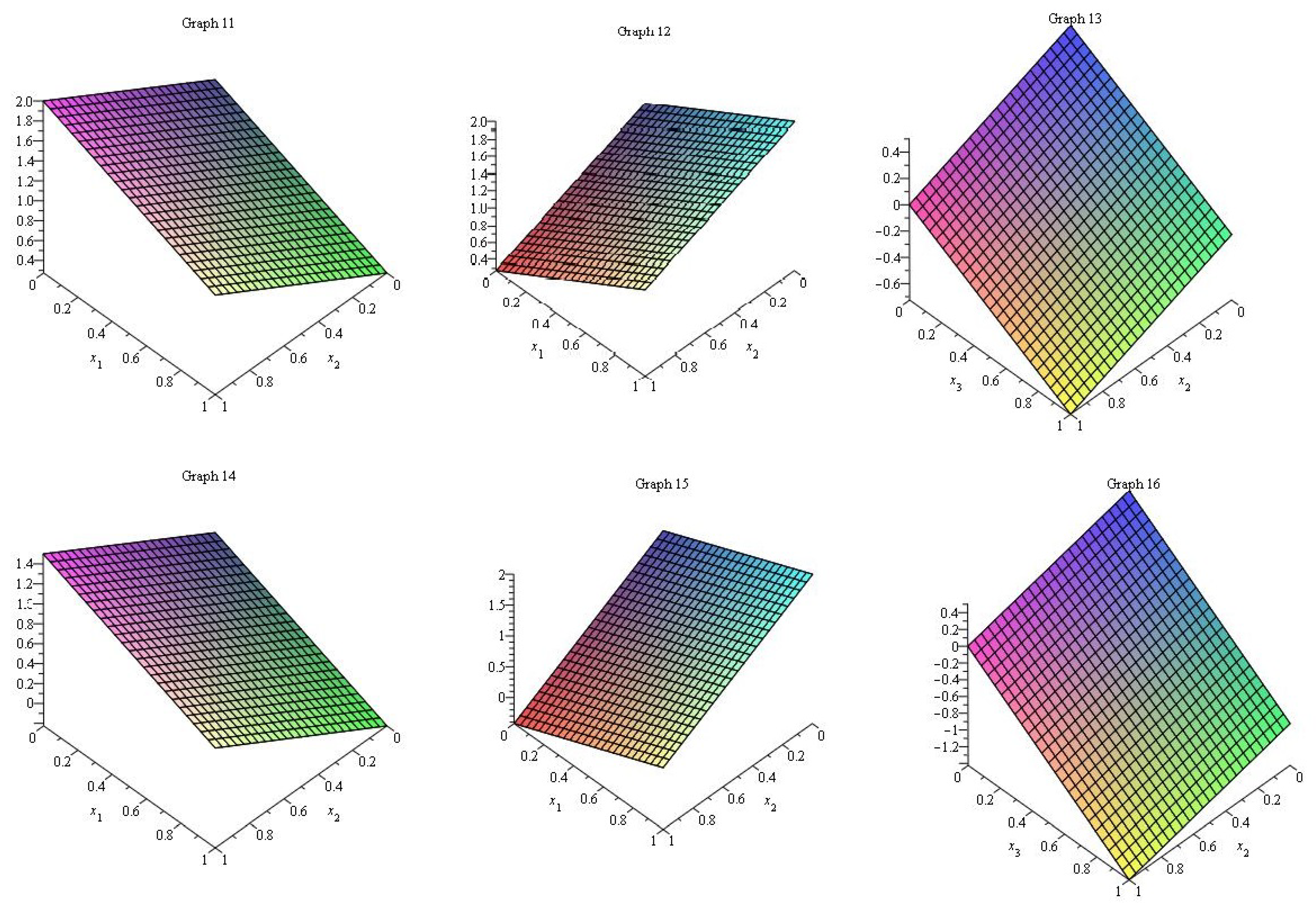
4. Description of Figures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khuri, S. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 2001, 1, 141–155. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; Bahgat, M.; Zaki, M. Numerical approaches to system of fractional partial differential equations. J. Egypt. Math. Soc. 2017, 25, 141–150. [Google Scholar] [CrossRef]
- Jafari, H.; Khalique, C.; Nazari, M. Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion wave equations. Appl. Math. Lett. 2011, 24, 1799–1805. [Google Scholar] [CrossRef]
- Ahmad Alhendi, F.; Alderremy, A. Numerical Solutions of Three-Dimensional Coupled Burgers’ Equations by Using Some Numerical Methods. J. Appl. Math. Phys. 2016, 4, 2011–2030. [Google Scholar] [CrossRef]
- Mishra, V.; Rani, D. Newton-Raphson based modified Laplace Adomian decomposition method for solving quadratic Riccati differential equations. In Proceedings of the 4th International Conference on Advancements in Engineering & Technology, Punjab, India, 18–19 March 2016; Volume 57. [Google Scholar]
- Haq, F.; Shah, K.; Khan, A.; Shahzad, M.; Rahman, G. Numerical Solution of Fractional Order Epidemic Model of a Vector Born Disease by Laplace Adomian Decomposition Method. Punjab Univ. J. Math. 2017, 49, 13–22. [Google Scholar]
- Qasim, A.F.; AL-Rawi, E.S. Adomian Decomposition Method with Modified Bernstein Polynomials for Solving Ordinary and Partial Differential Equations. J. Appl. Math. 2018. [Google Scholar] [CrossRef]
- Yousef, H.M.; Ismail, A.M. Application of the Laplace Adomian decomposition method for solution system of delay differential equations with initial value problem. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018; Volume 1974, p. 020038. [Google Scholar]
- Rani, D.; Mishra, V. Modification of Laplace Adomian decomposition method for solving nonlinear Volterra integral and integro-differential equations based on Newton Raphson formula. Eur. J. Pure Appl. Math. 2018, 11, 202–214. [Google Scholar] [CrossRef]
- Birajdar, G. Numerical Solution of Time Fractional Navier-Stokes Equation by Discrete Adomian decomposition method. Nonlinear Eng. 2014, 3, 21–26. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin, Germany, 2014; Volume 378. [Google Scholar]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, L. Weak solutions of the time-fractional Navier-Stokes equations and optimal control. Comput. Math. Appl. 2017, 73, 1016–1027. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M. Analytical solution of fractional Navier-Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef]
- Edeki, S.O.; Akinlabi, G.O. Coupled Method for Solving Time-Fractional Navier-Stokes Equation. Int. J. Circuits Syst. Signal Process. 2018, 12, 27–34. [Google Scholar]
- Singh, B.; Kumar, P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier-Stokes equation. Ain Shams Eng. J. 2016, 9, 827–834. [Google Scholar] [CrossRef]
- Ganji, Z.; Ganji, D.; Ganji, A.; Rostamian, M. Analytical solution of time-fractional Navier-Stokes equation in polar coordinate by homotopy perturbation method. Numer. Methods Part. Differ. Equ. 2010, 26, 117–124. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Science Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations. 1993. Available online: http://www.citeulike.org/group/14583/article/4204050 (accessed on 29 January 2019).
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, S.; Shah, R.; khan, H.; Arif, M. Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry 2019, 11, 149. https://doi.org/10.3390/sym11020149
Mahmood S, Shah R, khan H, Arif M. Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry. 2019; 11(2):149. https://doi.org/10.3390/sym11020149
Chicago/Turabian StyleMahmood, Shahid, Rasool Shah, Hassan khan, and Muhammad Arif. 2019. "Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation" Symmetry 11, no. 2: 149. https://doi.org/10.3390/sym11020149





