Parametric Robust Control of the Multivariable 2 × 2 Looper System in Steel Hot Rolling: A Comparison between Multivariable QFT and H∞
Abstract
:1. Introduction
2. FM Multivariable Model
3. Methodology
3.1. Multivariable Decentralized Robust QFT Controller
- for tracking specifications:where 0 ≤ |a(ω)|< |b(ω)| ∀ ω.
- and for disturbance rejection specifications:where S is the sensitivity function to output disturbances.
3.2. H∞ Robust Controller
4. Controller Designed
4.1. mvQFT Robust Controller Design for the Looper System
4.2. H∞ Robust Controller Design for the Looper System
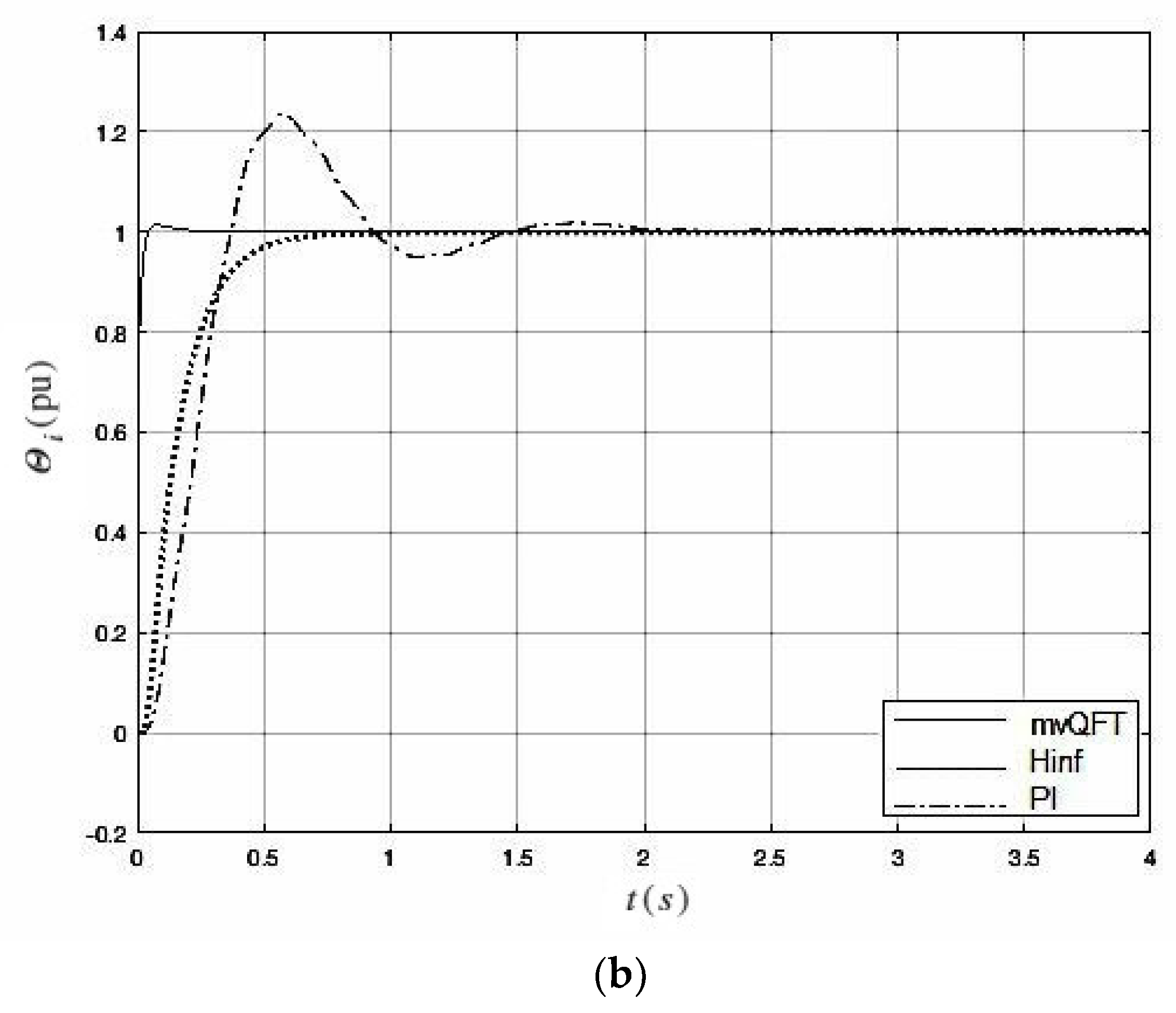
5. Simulation Results and Discussion
- Nominal Condition Test (N-test). Step responses of the nominal closed loop systems are obtained.
- Decupling Test (D-test). A step is applied on one reference input while the other remains zero, thus the impact of each reference input on the cross-coupling output is tested. The cross-coupling output response provides a measure of the column diagonal dominance of the closed loop system, i.e., the decoupling capabilities. Here, the value of such a response is referred to as “interaction level” (IL) and it is expected to be low. IL from θiref to σi is denoted as θi→σi, while σi→θi denotes that from σiref to θi. The nominal plant is used for this test. Although, in practice there are no standard limits for IL, in this work, an IL above 10% is considered to be undesirable.
- Parametric Uncertainty Test (U-test). Initially, each parameter takes a random value within its uncertainty region, changing randomly every 2s during the simulation time to allow the response to settle and confirm convergence. The methods used above to model the parametric uncertainties do not guarantee stability for the worst case; therefore, the parameters change randomly to test the system stability under the largest possible number of parameter value combinations (not under parameter variation, since the control techniques used here assume time-invariant uncertain parameters). During these tests, the perturbations inputs remain zero.
- Perturbation Test (P-test). This test is performed with the perturbation signals enabled, while the parameters remain constant on their operating values. Real signals of σi−1 and σi+1 were collected from the HSM and used for these tests. Hi and Vri+1 were not available, hence sinusoidal signals are used to simulate them, taking each one a random frequency value between 0 Hz and 7 Hz independently. Their frequencies remain constant during the simulation time.
- Uncertainty and Perturbation Test (P+U-test). The conditions of U-test and P-test are combined.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roberts, W.L. Flat Processing of Steel; Marcel Dekker: New York, NY, USA, 1988; pp. 1–196. [Google Scholar]
- Obregon, A.; Mendiola, P.; Evers, P.K.; Cavazos, A.; Leduc, L. Linear Multivariable Dynamic Model of a Hot Strip Finishing Mill. Proc. IMechE Part I J. Syst. Control Eng. 2010, 224, 1007–1021. [Google Scholar] [CrossRef]
- Okada, M.; Murayama, K.; Urano, A.; Iwasaki, Y.; Kawano, A.; Shiomi, H. Optimal Control System for hot strip finishing mill. Control Eng. Pract. 1996, 6, 1029–1034. [Google Scholar] [CrossRef]
- Cuzzola, F.A. A multivariable and multi-objective approach for control of hot-strip mills. J. Dyn. Syst. Meas. Contr. 2006, 128, 856–868. [Google Scholar] [CrossRef]
- Zhan, M.; Yang, W.; Wang, S. Dual perturbation AGC design based on QFT/μ controller in hot strip rolling process. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; TCCT: Beijing, China, 2010; pp. 5682–5686. [Google Scholar]
- Hyun-Hee, K.; Sung-Jin, K.; Min Cheol, L. The development of flying touch hot rolling control method based on SMCSPO. In Proceedings of the IEEE Conference on Advance Itelligent Mechatronics, Banf, AB, Canada, 12–15 July 2016; IEEE: New York, NY, USA, 2016; pp. 334–338. [Google Scholar]
- Peng, W.; Yafeng, J.; Chen, S.; Zhang, D. Rolling characteristics analysis and dynamic roll force locking strategy for hot strip mill. J. Cent. South Univ. Sci. Tech. 2017, 48, 1492–1498. [Google Scholar]
- Asano, K. Applications of model-driven control in steel processes. In Proceedings of the IFAC 18th World Congress, Milano, Italy, 28 August–2 September 2011; IFAC: Laxenburg, Austria, 2011; pp. 12096–12101. [Google Scholar]
- Hearns, G.; Grimble, M.J. Multivariable control of a hot strip finishing mill. In Proceedings of the IEEE American Control Conference, Albuquerque, Mexico, 4–6 June 1997; IEEE: New York, NY, USA, 1997; pp. 3775–3779. [Google Scholar]
- González Palacios, K.Y.; Cavazos González, A. Control robusto multivariable de espesor de cinta de acero y posición del formador de onda en un molino de laminación en caliente mediante H∞. In Proceedings of the IEEE Congreso Internacional sobre Innovación y Desarrollo Tecnológico, Cuernavaca, Mexico, 7–9 Septembre 2016; IEEE: Morelos, México, 2016; pp. 1–6. [Google Scholar]
- Yu, C.; Wang, H.; Jing, Y. Tension control in hot strip process based on LMI approach. In Proceedings of the 23rd Chinese Control and Decision Conference, Mianyang, China, 23–25 May 2011; IEEE: New York, NY, USA, 2011; pp. 1424–1427. [Google Scholar]
- Chen, J.X.; Yang, W.D.; Sun, Y.G. H∞ control of looper tension control systems based on a discrete time model. J. Iron Steel Res. Int. 2013, 20, 28–31. [Google Scholar] [CrossRef]
- Zhe, Y.; Ding, L.; Xiaoli, C.; Rui, W.; Fucai, Q.; Gang, Z. Decentralized robust decoupling control for looper tension and height system. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Hearns, G.; Grimble, J.M. Inferential control for rolling mills. IEEE Proc. Ctrl. Theory Appl. 2000, 147, 673–679. [Google Scholar] [CrossRef]
- Hearns, G.; Grimble, J.M. Quantitative Feedback Theory for Rolling Mills. In Proceedings of the IEEE International Conference on Control Applications, Glasgow, UK, 18–20 September 2002; IEEE: New York, NY, USA; pp. 367–372. [Google Scholar]
- Horowitz, I. Quantitative Feedback Theory. IEE Proc. Ctrl. Theory Appl. 1982, 129, 215–226. [Google Scholar] [CrossRef]
- Sidi, M.J. Design of Robust Control Systems: From Classical to Modern Practical Approach; Krieger Publishing Company: Malabar, FL, USA, 2001; pp. 149–247. [Google Scholar]
- Don Juan Ríos, O.A.; Rojas Lugo, E.A.; Cavazos González, A. Control robusto paramétrico QFT del sistema del formador de onda en un molino de laminación en caliente. Cienc. Ergo-Sum 2016, 23, 35–48. [Google Scholar]
- Pliego Reyes, N.L.; Cavazos González, A. Control robusto del espesor de la cinta de acero en un molino de laminación en caliente mediante teoría de retroalimentación cuantitativa. In Proceedings of the Congreso Nacional de Control Automático, Monterrey, Mexico, 4–6 October 2017; AMCA: Mexico City, Mexico, 2017; pp. 213–219. [Google Scholar]
- Choi, I.S.; Rossiter, J.A.; Fleming, P. An application of the model based predictive control in a hot strip mill. In Proceedings of the 11th IFAC Symposium on Automation in Mining, Mineral and Metal Processing, Nancy, France, 8–10 September 2004; IFAC: Laxenburg, Austria, 2004; pp. 131–136. [Google Scholar]
- Choi, I.S.; Rossiter, J.A.; Fleming, P. Looper and tension control in hot rolling mills: A survey. J. Process Control 2007, 17, 509–521. [Google Scholar] [CrossRef]
- Schuurmans, J.; Jones, T. Control of mass flow in a hot strip mill using model based predictive control. In Proceedings of the IEEE International Conference on Control Applications, Glasgow, UK, 18–20 September 2002; IEEE: New York, NY, USA, 2002; pp. 379–384. [Google Scholar]
- Yin, F.C.; Sun, J.; Peng, W.; Wang, H.Y. Dynimic matrix predictive control for hydraulic looper system in hot strip mills. J. Cent. South Univ. 2017, 24, 1369–1378. [Google Scholar] [CrossRef]
- Noh, I.; Won, S.; Jang, Y.J. Non-interactive looper and strip tension control for hot finishing mill using nonlinear disturbance observer. ISIJ Int. 2012, 6, 1092–1100. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, J.; Zhang, J.; Li, J. Looper tension sliding mode control for hot strip finishing mills. J. Iron Steel Res. Int. 2012, 19, 23–30. [Google Scholar] [CrossRef]
- Yaniv, O. Synthesis of uncertain MIMO feedback systems for gain and phase margin at different channel breaking points. Automatica 1992, 28, 1017–1020. [Google Scholar] [CrossRef]
- ASM. Metals Handbook: Vol. 1: Properties and Selection: Irons, Steels and High-Performance Alloys; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control, Analysis and Design, 2nd ed.; John Wiley and Sons: West Sussex, UK, 2001; pp. 301–303, 309. [Google Scholar]
- Hearns, G.; Grimble, J.M. Fault Tolerant Strip Tension Control. In Proceedings of the 1998 American Control Conference, Philadelphia, PA, USA, 24–26 June 1998; pp. 2992–2996. [Google Scholar]
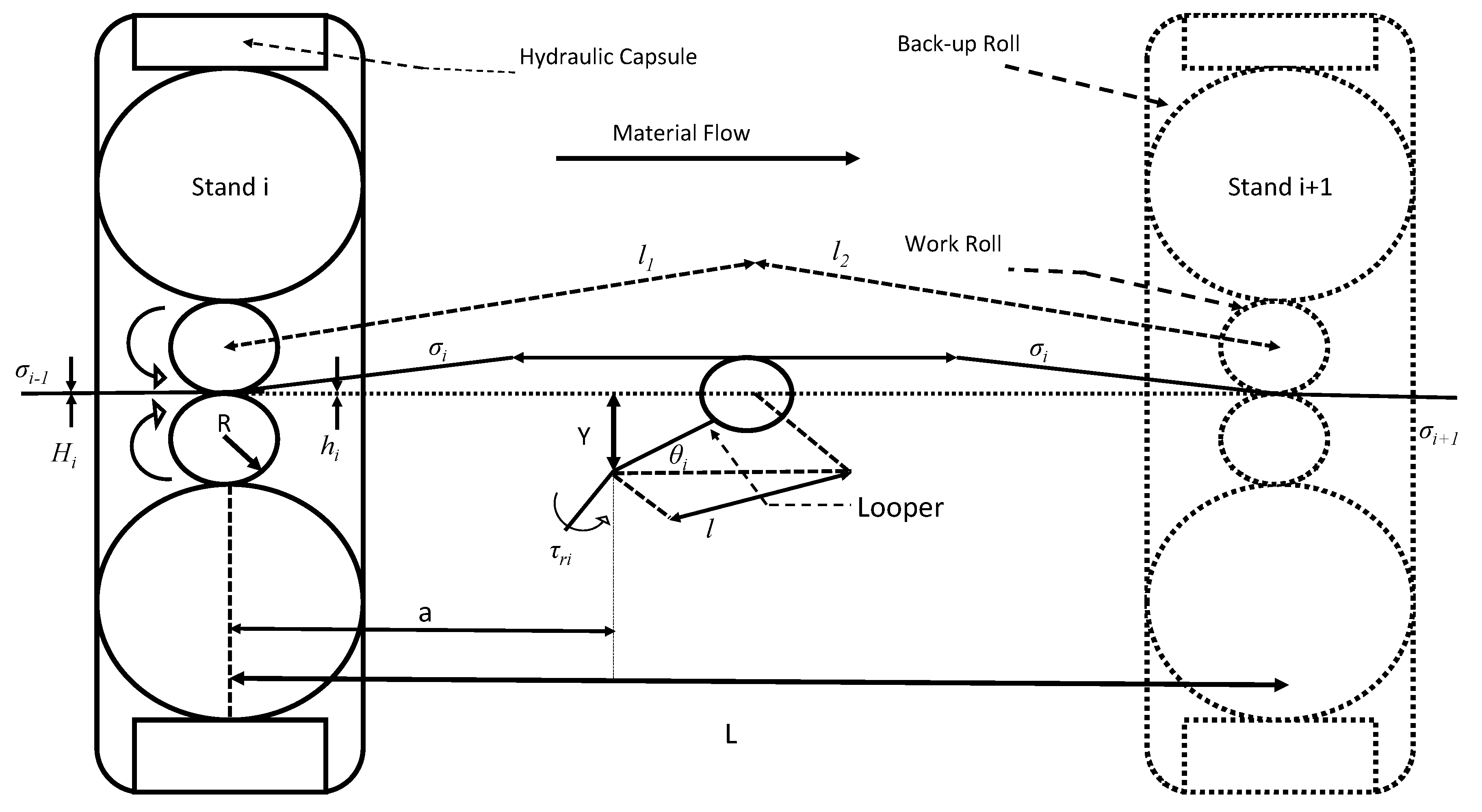
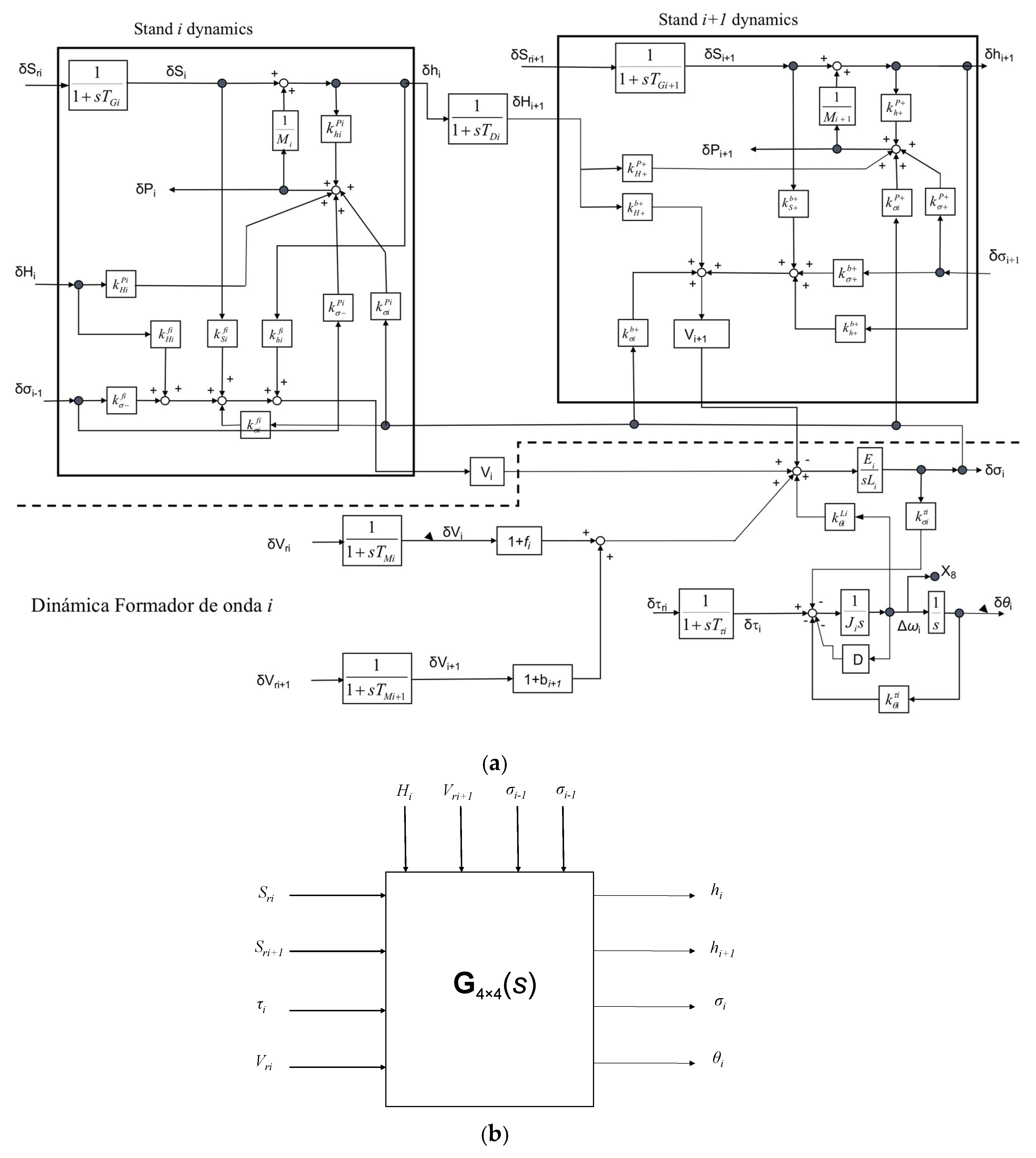


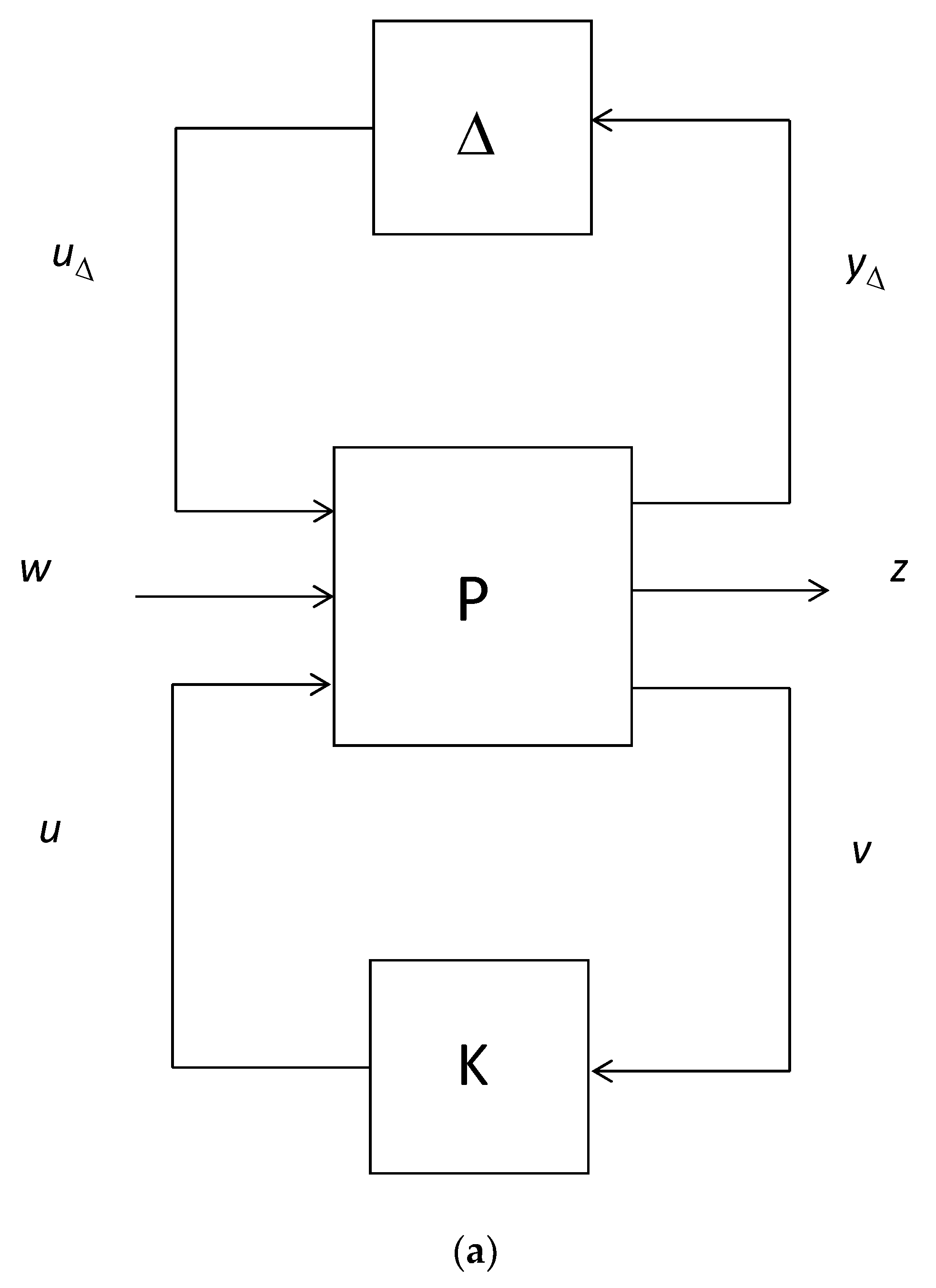
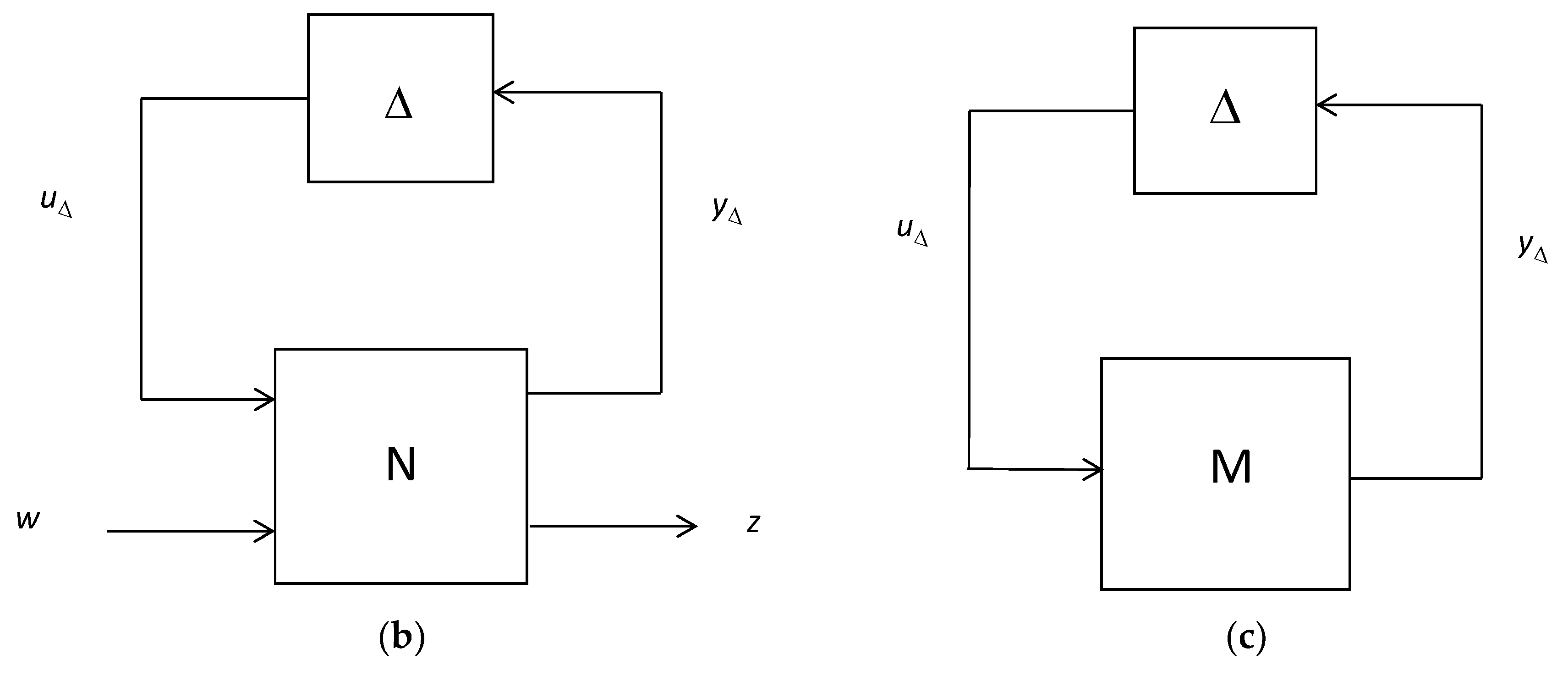







| Variable | Symbol | Units | Parameter | Symbol | Units |
|---|---|---|---|---|---|
| Stand i hydraulic cylinder position reference | Sri | m | Stand i mill modulus | Mi | N/m |
| Stand i + 1 hydraulic cylinder position reference | Sri+1 | m | Stand i + 1 mill modulus | Mi+1 | N/m |
| Stand i roll linear velocity reference | Vri | m/s | Steel Young’s modulus at operating temperature | Ei | N/m2 |
| Looper i torque reference | τi | Nm | Looper i roll radius | r | m |
| Stand i exit thickness | hi | m | Distance between stand i and i + 1 backup roll centers | Li | m |
| Stand i entry thickness | Hi | m | Steel density | ρ | Kg/m3 |
| Stand i + 1 exit thickness | hi+1 | m | Looper i momentum of inertia | Ji | Kgm2 |
| Stand i − 1 exit tension | σi−1 | N | Looper i friction | Di | Nm/rad/s |
| Stand i roll linear velocity | Vi | m/s | Stand i cylinder position regulator time constant | TGi | s |
| Stand i + 1 roll linear velocity reference | Vri+1 | m/s | Stand i + 1cylinder position regulator time constant | TGi+1 | s |
| Stand i exit tension | σi | N | Time constant of delay approximation between hi y Hi+1 | TDi | s |
| Stand i + 1 exit thickness | σi+1 | N | Stand i work roll speed regulator time constant | TMi | s |
| Looper i length | li | m | Stand i + 1 work roll speed regulator time constant | TMi+1 | s |
| Looper i angular position | θi | Radians | Looper i torque regulator time constant | Tτi | s |
| Stand i roll separation force | Pi | N | Stand i forward slip | fi | - |
| Stand i + 1 roll separation force stand i + 1 | Pi+1 | N | Stand i + 1 backward slip | bi+1 | - |
| Controller | σi | θi | ||||
|---|---|---|---|---|---|---|
| Mp | tp | ts | Mp | tp | ts | |
| PI | 43.4% | 0.52 s | 1.97 s | 23.5% | 0.56 s | 1.364 s |
| H∞ | null | null | 1.012 s | null | null | 0.55 s |
| mvQFT | 42% | 3.5 × 10−3 s | 0.23 s | 1.4% | 0.075 s | 0.32 s |
| Controller | σi→θi | θi→σi | ||
|---|---|---|---|---|
| Transient | Steady State | Transient | Steady State | |
| PI | −0.042 | 1.5 × 10−3 | 1.066 | −0.5 × 10−3 |
| H∞ | 0.8 × 10−3 | null | 0.24 | null |
| mvQFT | −0.051 | 0.83 × 10−3 | 0.33 | −0.03 |
| Controller | τri | Vri |
|---|---|---|
| PI | 4.5 × 10−12 | 3.6 × 10−9 |
| H∞ | 4.5 × 10−12 | 5.4 × 10−9 |
| mvQFT | 3.7 | 6.8 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cantú, L.F.; Mendiola, P.; Domínguez, Á.A.; Cavazos, A. Parametric Robust Control of the Multivariable 2 × 2 Looper System in Steel Hot Rolling: A Comparison between Multivariable QFT and H∞. Metals 2019, 9, 839. https://doi.org/10.3390/met9080839
Cantú LF, Mendiola P, Domínguez ÁA, Cavazos A. Parametric Robust Control of the Multivariable 2 × 2 Looper System in Steel Hot Rolling: A Comparison between Multivariable QFT and H∞. Metals. 2019; 9(8):839. https://doi.org/10.3390/met9080839
Chicago/Turabian StyleCantú, Luis F., Pedro Mendiola, Álvaro A. Domínguez, and Alberto Cavazos. 2019. "Parametric Robust Control of the Multivariable 2 × 2 Looper System in Steel Hot Rolling: A Comparison between Multivariable QFT and H∞" Metals 9, no. 8: 839. https://doi.org/10.3390/met9080839




