An Adaptive Controller Based on Interconnection and Damping Assignment Passivity-Based Control for Underactuated Mechanical Systems: Application to the Ball and Beam System
Abstract
:1. Introduction
2. Problem Statement
2.1. Review of IDA-PBC Design
2.2. Possible Uncertainties
3. Controller Design and Stability Analysis
4. Example: The Ball and Beam System
4.1. System Model
4.2. Controller Design
4.3. Stability Analysis
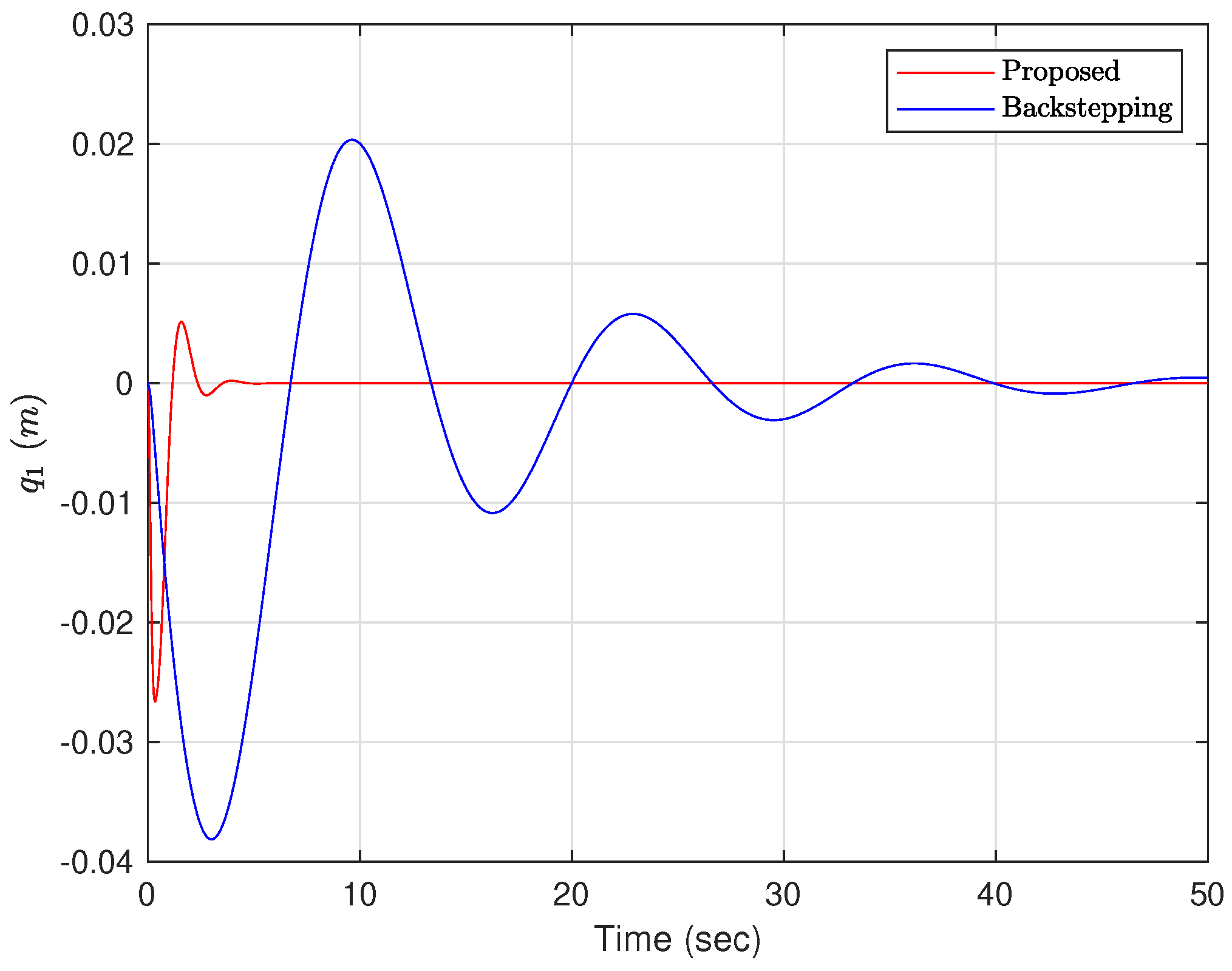
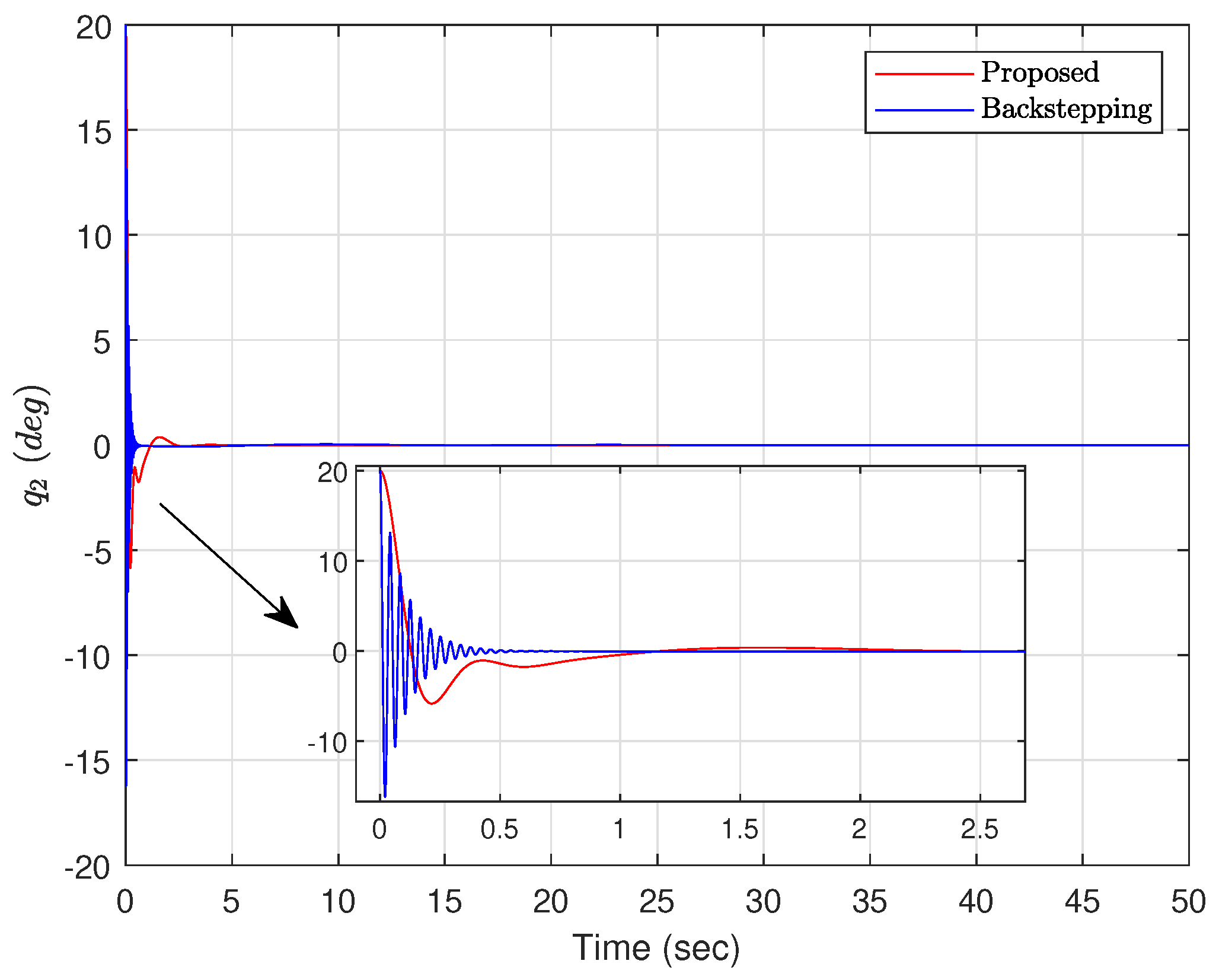
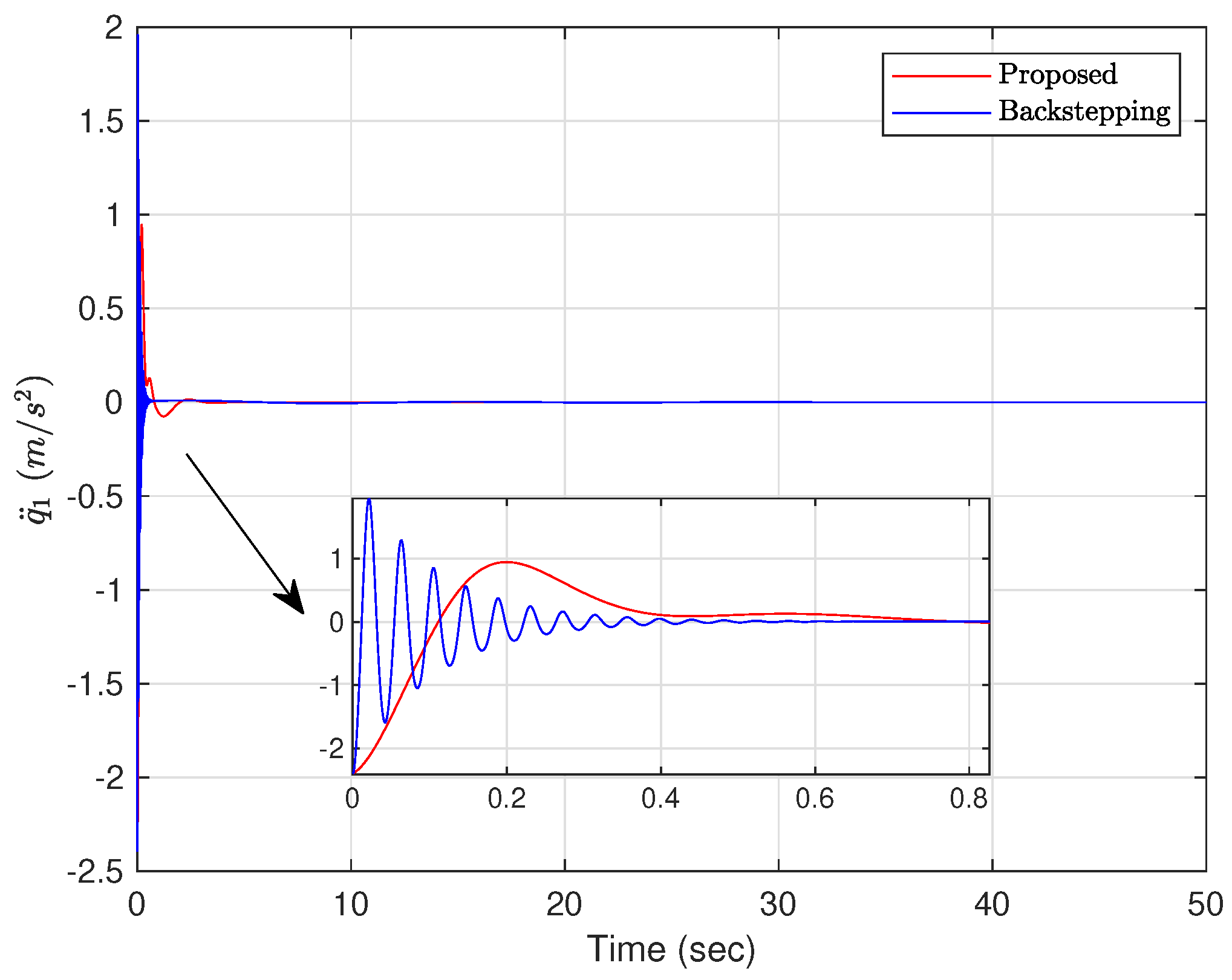
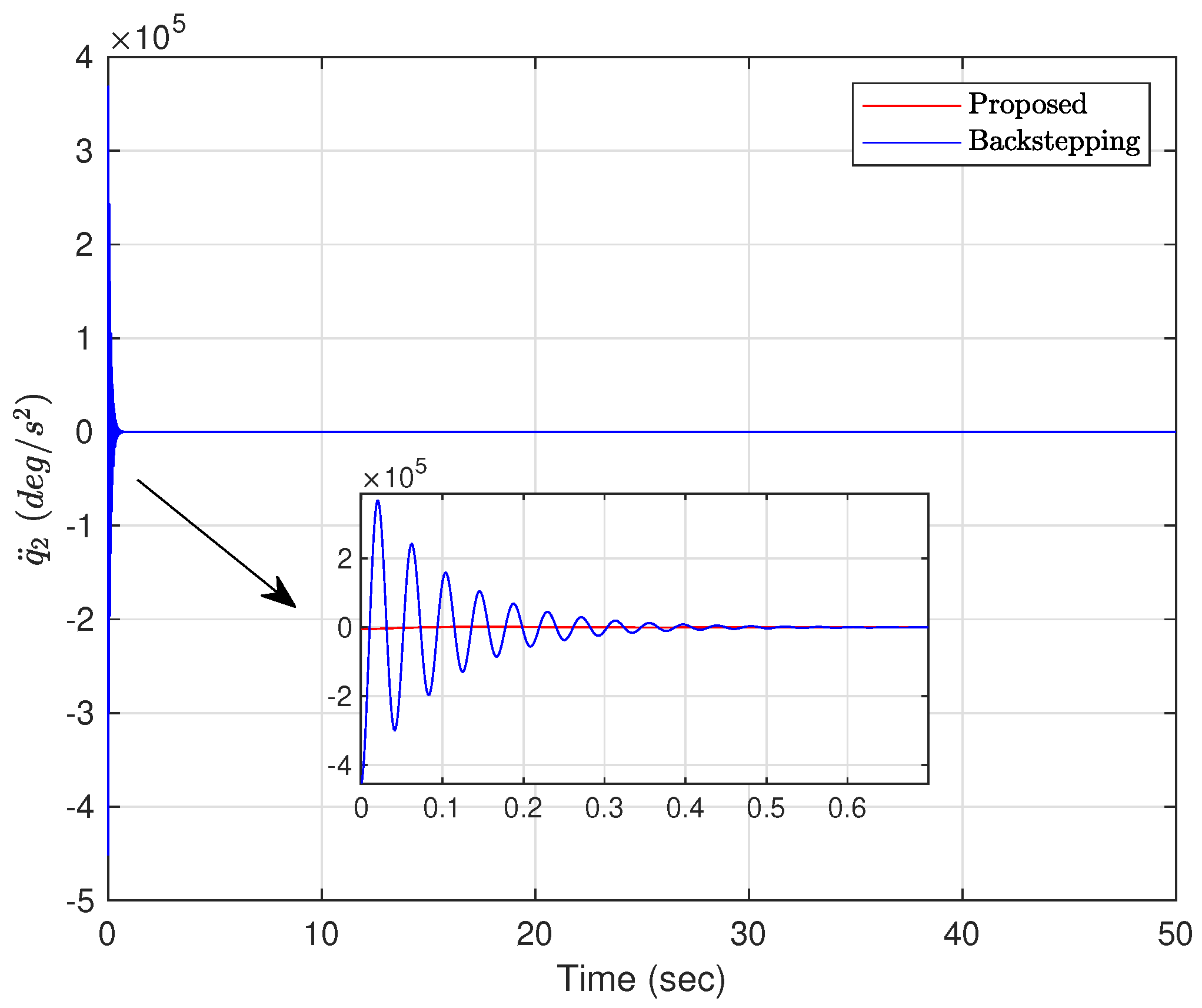
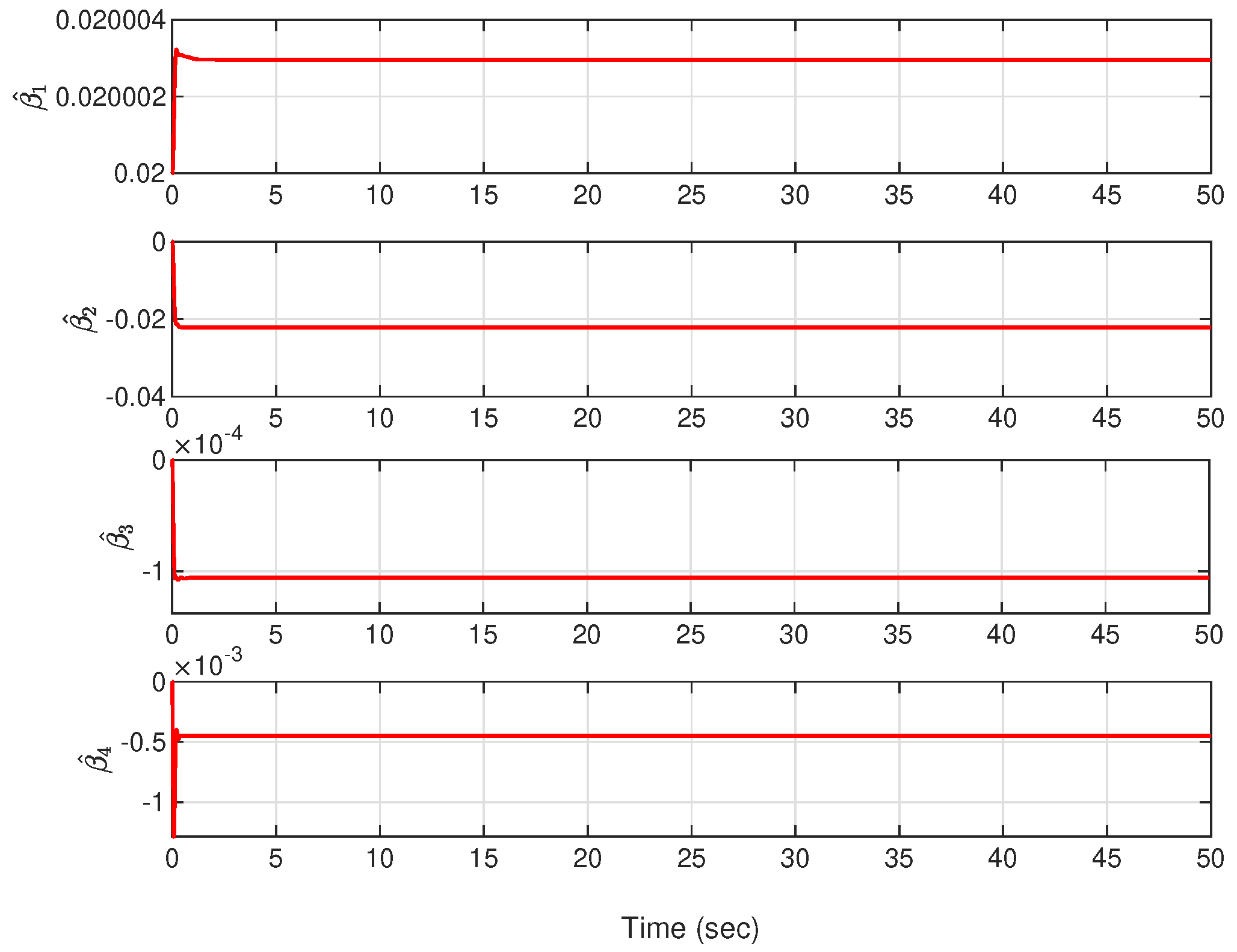
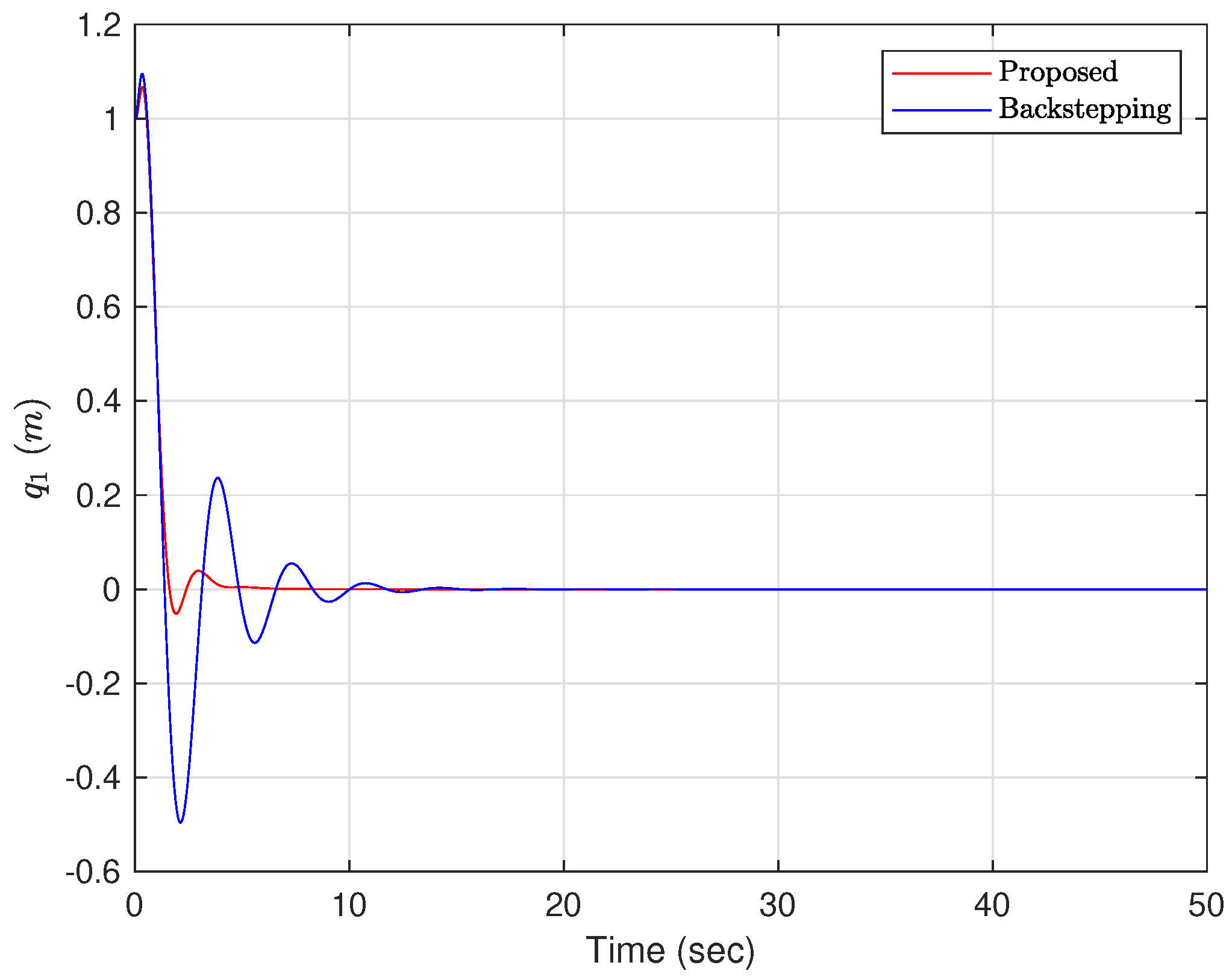
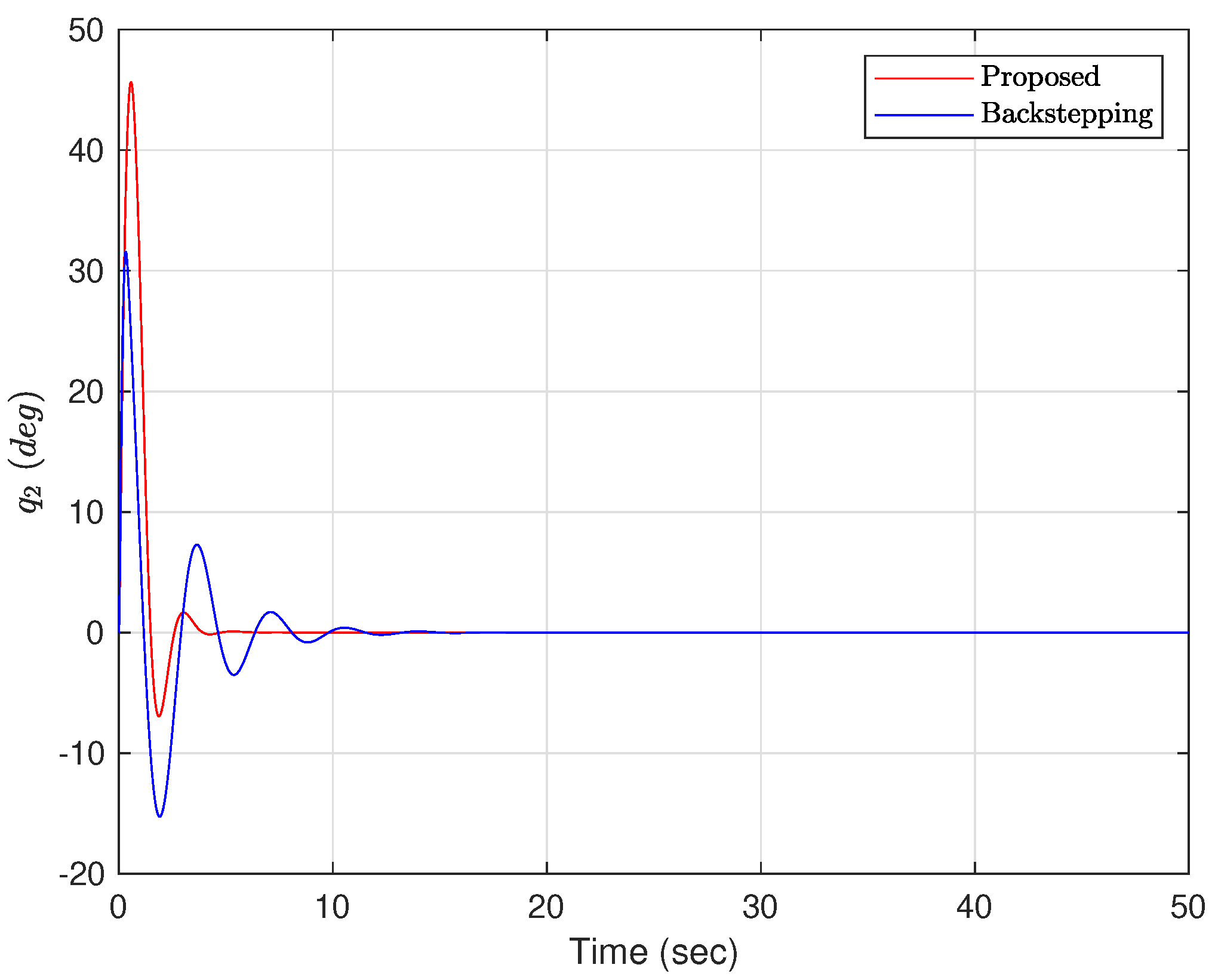
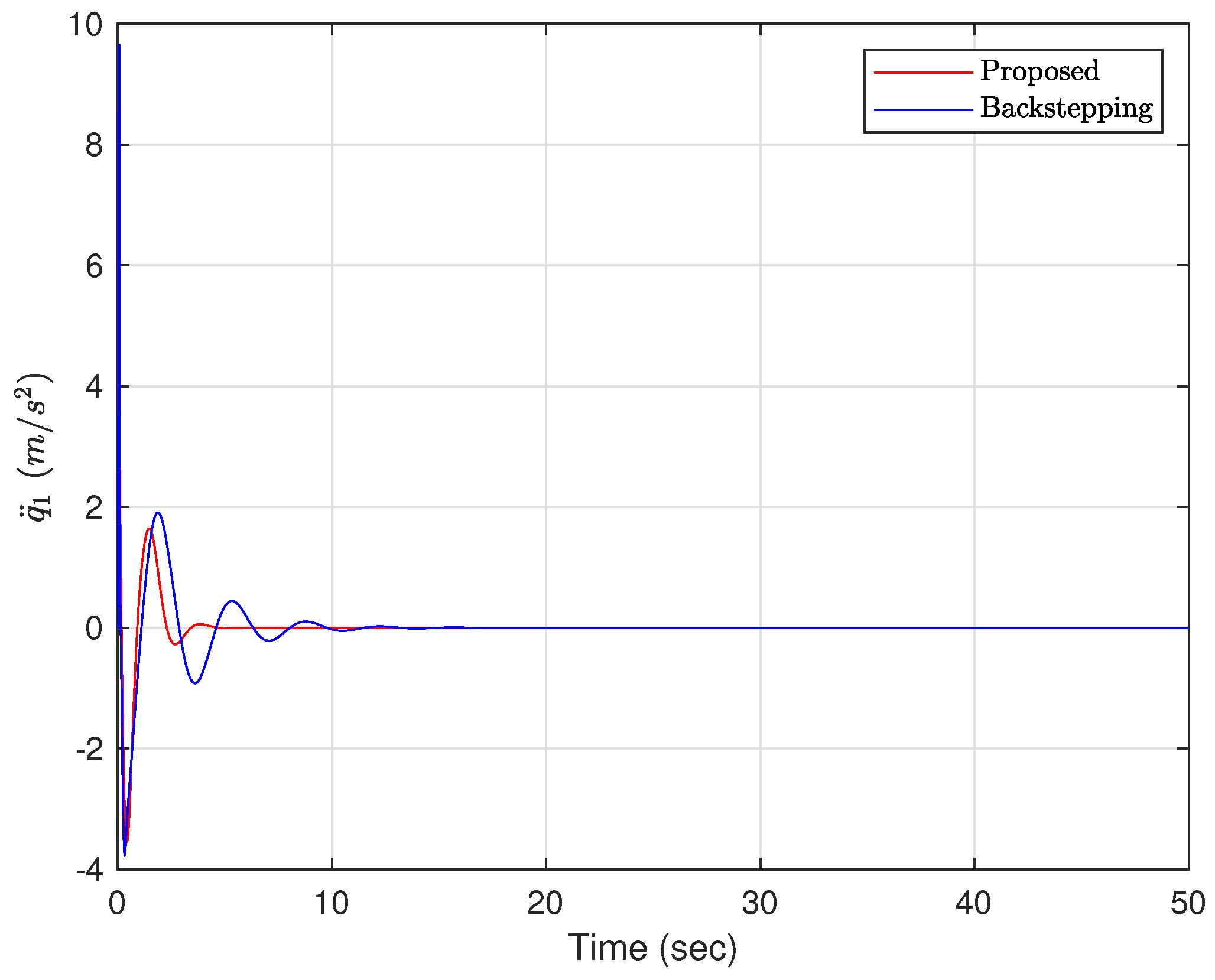
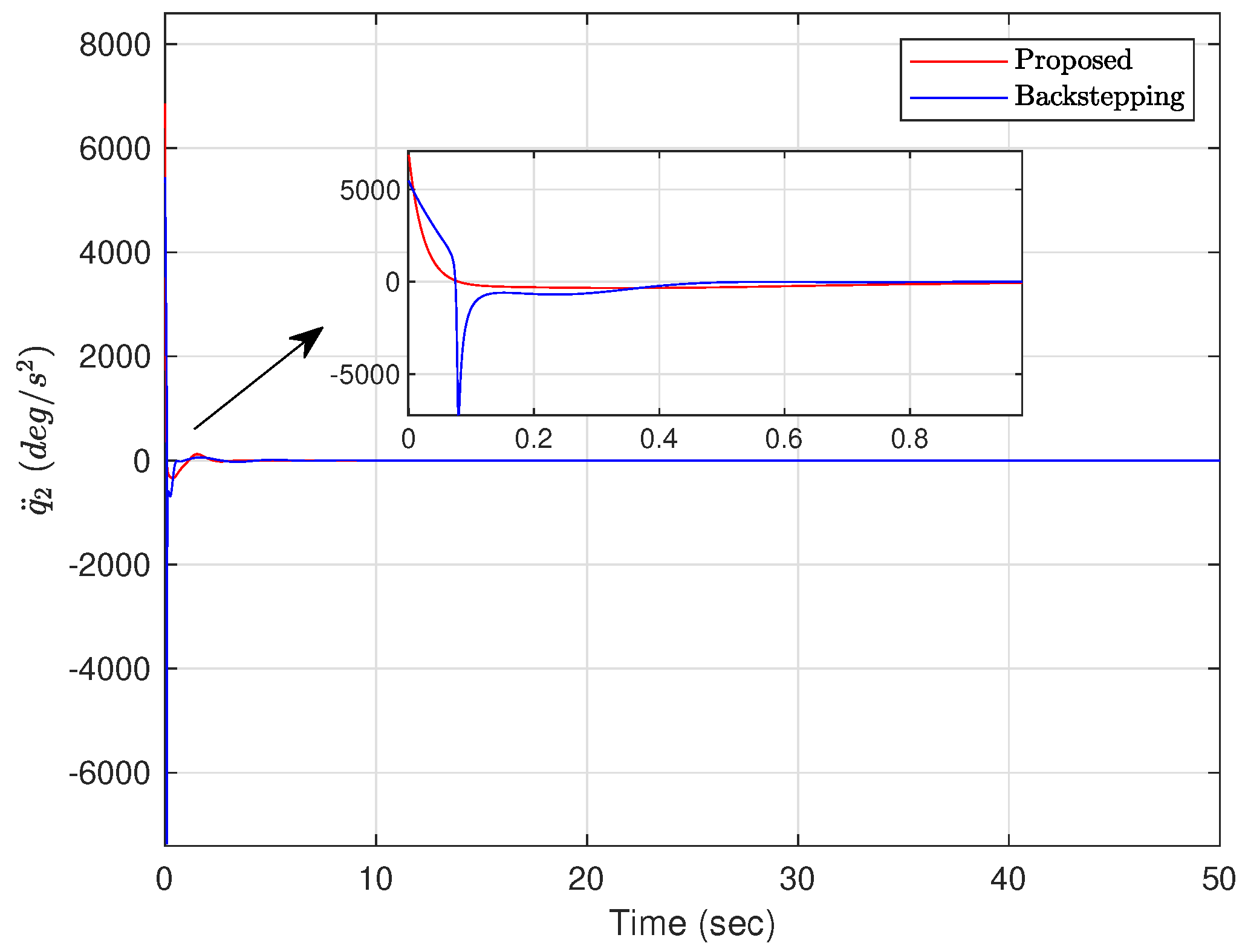
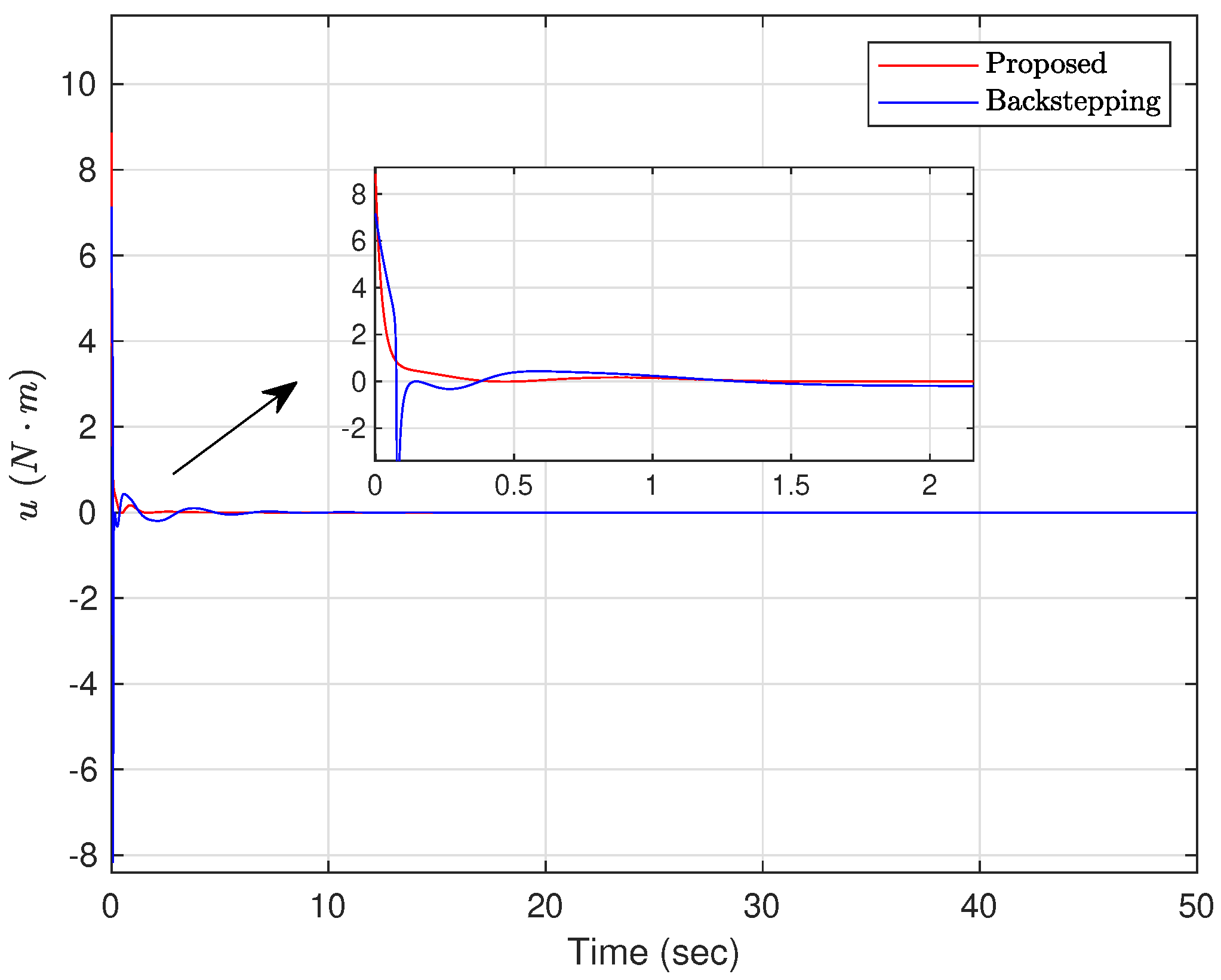
4.4. Numerical Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Yu, H. A survey of underactuated mechanical systems. IET Control Theory Appl. 2013, 7, 921–935. [Google Scholar]
- Ortega, R.; Spong, M.W.; Gomez-Estern, F.; Blankenstein, G. Stabilization of a class of underactuated mechanical systems via interconnection and damping assignment. IEEE Trans. Automat. Control 2002, 47, 1218–1233. [Google Scholar] [CrossRef]
- Mahindrakar, A.D.; Astolfi, A.; Ortega, R.; Viola, G. Further constructive results on interconnection and damping assignment control of mechanical systems: The Acrobot example. Int. J. Robust Robust Nonlinear Control 2010, 16, 671–685. [Google Scholar] [CrossRef]
- Rodriguez, H.; Ortega, R.; Escobar, G. A robustly stable output feedback saturated controller for the Boost DC-to-DC converter. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999. [Google Scholar]
- Aoues, S.; Matignon, D.; Alazard, D. Control of a flexible spacecraft using discrete IDA-PBC design. IFAC-PapersOnLine 2015, 48, 188–193. [Google Scholar] [CrossRef]
- Acosta, J.A.; Ortega, R.; Astolfi, A.; Mahindrakar, A.D. Interconnection and damping assignment passivity-based control of mechanical systems with underactuation degree one. IEEE Trans. Automat. Control 2005, 50, 1936–1955. [Google Scholar] [CrossRef]
- Ryalat, M.; Laila, D.S. A simplified IDA-PBC design for underactuated mechanical systems with applications. Eur. J. Control 2016, 27, 1–16. [Google Scholar] [CrossRef]
- Zhang, M.; Ortega, R.; Liu, Z.; Su, H. A new family of interconnection and damping assignment passivity-based controllers. Int. J. Robust Nonlinear Control 2016, 50, 50–65. [Google Scholar] [CrossRef]
- Blankenstein, G.; Ortega, R.; Van Der Schaft, A.J. The matching conditions of controlled Lagrangians and IDA-passivity based control. Int. J. Control 2002, 75, 645–665. [Google Scholar] [CrossRef]
- Gomez-Estern, F.; Ortega, R.; Rubio, F.R.; Aracil, J. Stabilization of a class of underactuated mechanical systems via total energy shaping. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001. [Google Scholar]
- Viola, G.; Ortega, R.; Banavar, R.; Acosta, J.A.; Astolfi, A. Total Energy Shaping Control of Mechanical Systems: Simplifying the Matching Equations Via Coordinate Changes. IEEE Trans. Automat. Control 2007, 52, 1093–1099. [Google Scholar] [CrossRef]
- Gomez-Estern, F.; Van Der Schaft, A.J. Physical damping in IDA-PBC controlled underactuated mechanical systems. Eur. J. Control 2004, 10, 451–468. [Google Scholar] [CrossRef]
- Tiefensee, F.; Monaco, S.; Normand-Cyrot, D. IDA-PBC under sampling for port-controlled hamiltonian systems. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010. [Google Scholar]
- Liu, Z.; Theilliol, D.; Yang, L.; He, Y.; Han, J. Interconnection and Damping Assignment Passivity-Based Control Design Under Loss of Actuator Effectiveness. J. Intell. Robot. Syst. 2020, 100, 29–45. [Google Scholar] [CrossRef]
- Donaire, A.; Romero, J.G.; Ortega, R.; Siciliano, B.; Crespo, M. Robust IDA-PBC for underactuated mechanical systems subject to matched disturbances. Int. J. Robust Nonlinear Control 2017, 27, 1000–1016. [Google Scholar] [CrossRef]
- Haddad, N.K.; Chemori, A.; Belghith, S. Robustness enhancement of IDA-PBC controller in stabilising the inertia wheel inverted pendulum: Theory and real-time experiments. Int. J. Control 2017, 91, 2657–2672. [Google Scholar] [CrossRef]
- Haddad, N.K.; Chemori, A.; Pena, J.J.; Belghith, S. Stabilization of inertia wheel inverted pendulum by model reference adaptive IDA-PBC: From simulation to real-time experiments. In Proceedings of the 2015 3rd International Conference on Control, Engineering and Information Technology, Tlemcen, Algeria, 25–27 May 2015. [Google Scholar]
- Ryalat, M.; Laila, D.S.; Torbati, M.M. Integral IDA-PBC and PID-like control for port-controlled Hamiltonian systems. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Ferguson, J.; Donaire, A.; Ortega, R.; Middleton, R.H. Robust integral action of port-Hamiltonian systems. IFAC-PapersOnLine 2018, 51, 181–186. [Google Scholar] [CrossRef]
- Ryalat, M.; Laila, D.S. A Robust IDA-PBC Approach for Handling Uncertainties in Underactuated Mechanical Systems. IEEE Trans. Automat. Control 2018, 63, 3495–3502. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernádez-González, O.; Valencia-Palomo, G.; López-Estrada, F.R.; Rodríguez-Mata, A.E.; Garrido, J. Filtered Observer-Based IDA-PBC Control for Trajectory Tracking of a Quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Haddad, N.K.; Chemori, A.; Belghith, S. External disturbance rejection in IDA-PBC controller for underactuated mechanical systems: From theory to real time experiments. In Proceedings of the 2014 IEEE Conference on Control Applications, Antibes, France, 8–10 October 2014. [Google Scholar]
- García-Beltrán, C.D.; Miranda-Araujo, E.M.; Guerrero-Sanchez, M.E.; Valencia-Palomo, G.; Hernández-González, O.; Gómez-Peñate, S. Passivity-based control laws for an unmanned powered parachute aircraft. Asian J. Control 2021, 23, 2087–2096. [Google Scholar] [CrossRef]
- Lv, C.; Yu, H.; Chen, J.; Zhao, N.; Chi, J. Trajectory tracking control for unmanned surface vessel with input saturation and disturbances via robust state error IDA-PBC approach. J. Frankl. Inst. 2022, 359, 1899–1924. [Google Scholar] [CrossRef]
- Guerrero-Sanchez, M.E.; Hernandez-Gonzalez, O.; Valencia-Palomo, G.; Mercado-Ravell, D.A.; Lopez-Estrada, F.R.; Hoyo-Montano, J.A. Robust IDA-PBC for under-actuated systems with inertia matrix dependent of the unactuated coordinates: Application to a UAV carrying a load. Nonlinear Dyn. 2021, 105, 3225–3238. [Google Scholar] [CrossRef]
- Chang, D.E. The Method of Controlled Lagrangians: Energy plus Force Shaping. SIAM J. Control Optim. 2010, 48, 4821–4845. [Google Scholar] [CrossRef]
- Delgado, S.; Kotyczka, P. Overcoming the Dissipation Condition in Passivity-based Control for a class of mechanical systems. IFAC Proc. Vol. 2014, 47, 11189–11194. [Google Scholar] [CrossRef]
- Hauser, J.; Sastry, S.; Kokotovic, P. Nonlinear control via approximate input-output linearization: The ball and beam example. IEEE Trans. Automat. Control 1992, 37, 392–398. [Google Scholar] [CrossRef]
- Gordillo, F.; Gómez-Estern, F.; Ortega, R.; Aracil, J. On the ball and beam problem: Regulation with guaranteed transient performance and tracking periodic orbits. In Proceedings of the 15th International Symposium on Mathematical Theory of Networks and Systems, Bayreuth, Germany, 12–16 August 2002. [Google Scholar]
- Howimanporn, S.; Chookaew, S.; Silawatchananai, C. Monitoring and Controlling of a Real-Time Ball Beam Fuzzy Predicting Based on PLC Network and Information Technologies. J. Adv. Inf. Technol. 2022, 13, 1–8. [Google Scholar] [CrossRef]
- Kharola, A.; Patil, P.P. Neural Fuzzy Control of Ball and Beam System. Int. J. Energy Optim. 2017, 6, 64–78. [Google Scholar] [CrossRef]
- Ali, S.S. Position Control of Ball and Beam System Using Robust H∞ Loop Shaping Controller. Indones. J. Electr. Eng. Comput. Sci. 2020, 19, 91–98. [Google Scholar] [CrossRef]
- Jiang, J.; Astolfi, A. Stabilization of a class of underactuated nonlinear systems via underactuated back-stepping. IEEE Trans. Automat. Control 2021, 66, 5429–5435. [Google Scholar] [CrossRef]
- Gembalczyk, G.; Domogala, P.; Leśniowski, K. Modeling of underactuated ball and beam system—A comparative study. Actuators 2023, 12, 59. [Google Scholar] [CrossRef]
- Andreeva, F.; Aucklyb, D.; Gosavic, S.; Kapitanskib, L.; Kelkard, A.; Whitec, W. Matching, linear systems, and the ball and beam. Automatica 2002, 38, 2147–2152. [Google Scholar] [CrossRef]
- Ravichandran, M.T.; Mahindrakar, A. Robust stabilization of a class of underactuated mechanical systems using time scaling and Lyapunov redesign. IEEE Trans. Ind. Electron. 2011, 58, 4299–4313. [Google Scholar] [CrossRef]
- Popayan, J.A.; Cieza, O.B.; Reger, J. Adaptive IDA-PBC for a class of UMSs: The IWIP analysis. IFAC-PapersOnLine 2019, 52, 478–483. [Google Scholar] [CrossRef]
- Franco, E. IDA-PBC with adaptive friction compensation for underactuated mechanical systems. Int. J. Control 2021, 94, 860–870. [Google Scholar] [CrossRef]
- Ryalat, M.; Laila, D.S.; ElMoaqet, H. Adaptive interconnection and damping assignment passivity based control for underactuated mechanical systems. Int. J. Control Autom. Syst. 2021, 19, 864–877. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Shao, H.; Liu, C.; Li, N.; Guo, X.; Zheng, F.; Sun, L. An Adaptive Controller Based on Interconnection and Damping Assignment Passivity-Based Control for Underactuated Mechanical Systems: Application to the Ball and Beam System. Actuators 2023, 12, 408. https://doi.org/10.3390/act12110408
Liu X, Shao H, Liu C, Li N, Guo X, Zheng F, Sun L. An Adaptive Controller Based on Interconnection and Damping Assignment Passivity-Based Control for Underactuated Mechanical Systems: Application to the Ball and Beam System. Actuators. 2023; 12(11):408. https://doi.org/10.3390/act12110408
Chicago/Turabian StyleLiu, Xiaoping, Huaizhi Shao, Cungen Liu, Ning Li, Xinpeng Guo, Fei Zheng, and Lijun Sun. 2023. "An Adaptive Controller Based on Interconnection and Damping Assignment Passivity-Based Control for Underactuated Mechanical Systems: Application to the Ball and Beam System" Actuators 12, no. 11: 408. https://doi.org/10.3390/act12110408





