What Is an Artificial Muscle? A Systemic Approach.
Abstract
:1. Introduction
2. The Actuator as a Stable System


3. Concept of Linear Artificial Muscle


4. Biomimetic Artificial Muscle for Antagonist Actuators
4.1. Biomimetic Artificial Muscle Combining a Non-Linear Static Characteristic with a Linear Viscosity

4.2. Constant Moment Arm Antagonist Artificial Muscle Actuator

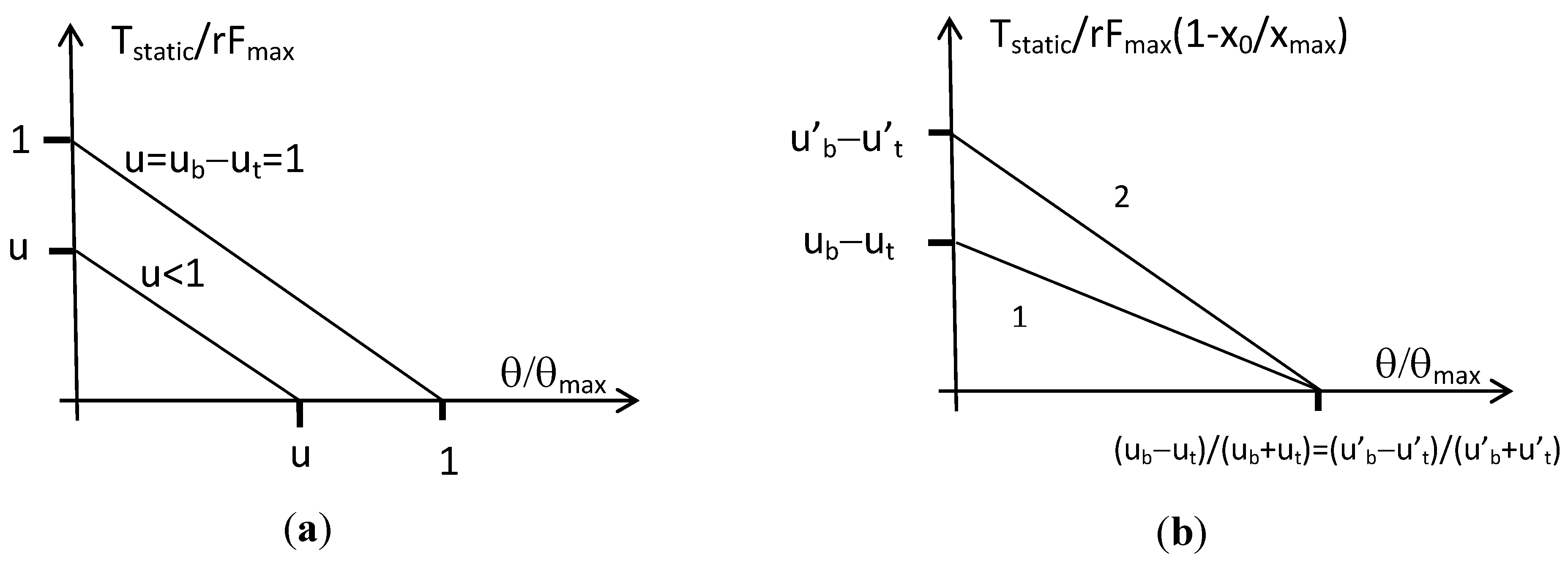
4.3. Elbow-Type Antagonist Artificial Muscle Actuator

5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Madden, J.D.W.; Vandesteeg, N.A.; Anquetil, A.; Madden, P.G.A.; Takshi, A.; Pytel, R.Z.; Lafontaine, S.R.; Wieringa, P.A.; Hunter, I.W. Artificial muscle technology: Physical principles and naval prospects. IEEE J. Ocean. Eng. 2004, 29, 706–728. [Google Scholar] [CrossRef]
- Shahinpoor, M. Ionic polymer-conductor composites as biomimetic sensors, robotic actuators and artificial muscles—A review. Electrochim. Acta 2003, 48, 2343–2353. [Google Scholar] [CrossRef]
- Bar-Cohen, Y. Biomimetics using electroactive polymers (EAP) as artificial muscles—A review. J. Adv. Mater. 2006, 38, 3–9. [Google Scholar]
- O’Halloran, A.; O’Malley, F.; McHugh, P. A review on dielectric elastomer actuators, technology, applications, and challenges. J. Appl. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Tondu, B. Artificial muscles for humanoid robots. In Humanoid Robots: Human-like Machines; Hackel, M., Ed.; Itech: Vienna, Austria, 2007; Chapter 5; pp. 642–677. [Google Scholar]
- Kuribayashi, K. Criteria for the evaluation of new actuators as energy converters. Adv. Robot. 1993, 7, 289–307. [Google Scholar] [CrossRef]
- Huber, J.E.; Fleck, N.A.; Ashby, M.F. The selection of mechanical actuators based on performances indices. Proc. R. Soc. London A 1997, 453, 2185–2205. [Google Scholar] [CrossRef]
- Hunter, I.W.; Lafontaine, S. A comparison of muscle with artificial actuators. In Proceedings of the 5th Technical Digest of the IEEE Solid-State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, 22–25 June 1992; pp. 178–185.
- Hannaford, B.; Winters, J. Actuator properties and movement control: Biological and technological models. In Multiple Muscle Systems: Biomechanics and Movement Organization; Winters, J.M., Woo, S.L.-Y., Eds.; Springer-Verlag: New York, NY, USA, 1990; Chapter 7; pp. 101–196. [Google Scholar]
- Paynter, H.M. Analysis and Design of Engineering Systems; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Holmes, R. The Characteristics of Mechanical Engineering Systems; Pergamon: Oxford, UK, 1977. [Google Scholar]
- On/Off or Closed-Loop Control? Hydraulics & Pneumatics. Available online: http://hydraulicspneumatics.com/200/TechZone/SystemIntrumen/Article/False/12850/TechZone-SystemInstrumen (accessed on 1 December 2015).
- Kuhn, W.; Hargitay, B.; Katchalsky, A.; Eisenberg, H. Reversible dilatation and contraction by changing the state of ionization of high-polymer acid networks. Nature 1950, 165, 514–516. [Google Scholar] [CrossRef]
- Katchalsky, A. Rapid swelling and deswelling of reversible gels of polymeric acids by ionization. Experientia 1949, 5, 319–320. [Google Scholar] [CrossRef] [PubMed]
- Treloar, L.G.R. The Physics of Rubber Technology; Oxford University Press: Oxford, UK, 1958. [Google Scholar]
- Johnson, W.; Soden, P.D. The discharge characteristics of confined rubber cylinders. Int. J. Mech. Sci. 1966, 8, 213–225. [Google Scholar] [CrossRef]
- Tondu, B. Theory of an artificial pneumatic muscle and application to the modelling of McKibben artificial muscle. CRAS série II 1995, 320, 105–114, (in French with an abridged English version). [Google Scholar]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model. IEEE/ASME Trans. Mechatron. 2010, 16, 177–186. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.; Park, J.-H. Design and fabrication of a locomotive mechanism for capsule-type endoscope using shape memory Alloys (SMAs). IEEE/ASME Trans. Mechatron. 2005, 10, 77–86. [Google Scholar] [CrossRef]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Part B 1938, 126, 136–195l. [Google Scholar] [CrossRef]
- Hogan, N. Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans. Autom. Control 1984, AC-29, 681–690. [Google Scholar] [CrossRef]
- Klute, G.K.; Czerniecki, J.M.; Hannaford, B. Artificial muscles: Actuators for biorobotic systems. Int. J. Robot. Res. 2002, 21, 295–309. [Google Scholar] [CrossRef]
- Ralston, H.J.; Polissar, M.J.; Inman, V.T.; Close, J.R.; Feinstein, B. Dynamic features of human isolated voluntary muscle in isometric and free contractions. J. Appl. Physiol. 1949, 1, 526–533. [Google Scholar] [PubMed]
- Caldwell, D.G. Natural and artificial muscle elements as robot actuators. Mechatronics 1993, 3, 269–283. [Google Scholar] [CrossRef]
- Nakamura, T.; Saga, N.; Yaegashi, K. Develoment of a pneumatic artificial muscle based on biomechanical characteristics. In Proceedings of the 2003 IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; pp. 729–734.
- Tondu, B. McKibben artificial muscle can be adapted to be in accordance with the Hill skeletal muscle model. In Proceedings of the 1st IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Pisa, Italy, 20–22 February 2006; pp. 714–720.
- Fenn, W.O.; Marsh, B.S. Muscular force at different speeds of shortening. J. Physiol. 1935, 85, 277–297. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tondu, B. What Is an Artificial Muscle? A Systemic Approach. Actuators 2015, 4, 336-352. https://doi.org/10.3390/act4040336
Tondu B. What Is an Artificial Muscle? A Systemic Approach. Actuators. 2015; 4(4):336-352. https://doi.org/10.3390/act4040336
Chicago/Turabian StyleTondu, Bertrand. 2015. "What Is an Artificial Muscle? A Systemic Approach." Actuators 4, no. 4: 336-352. https://doi.org/10.3390/act4040336




