PHD and CPHD Algorithms Based on a Novel Detection Probability Applied in an Active Sonar Tracking System
Abstract
:1. Introduction
2. Background
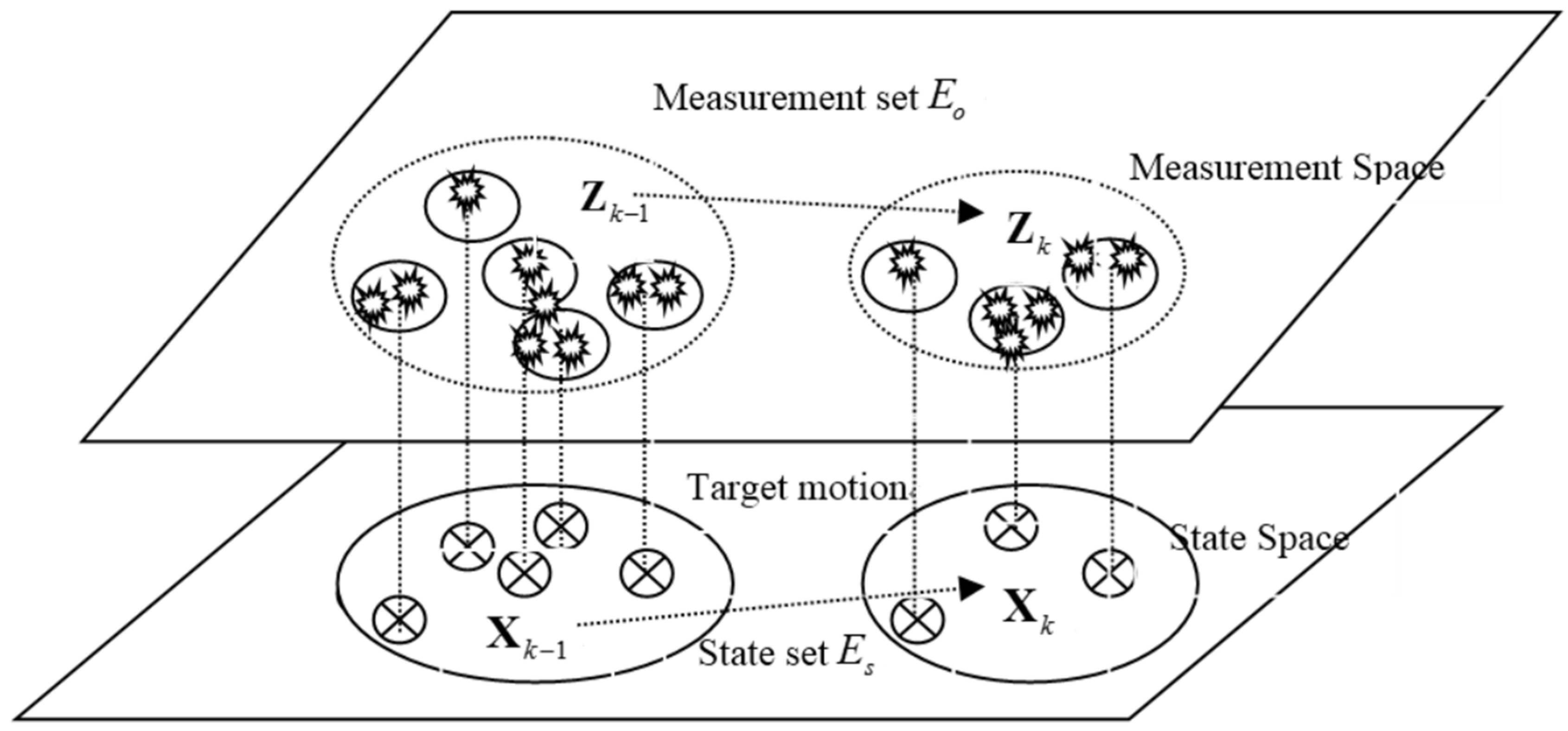
2.1. The Foundation of Multi-Targetstracking Using RFS
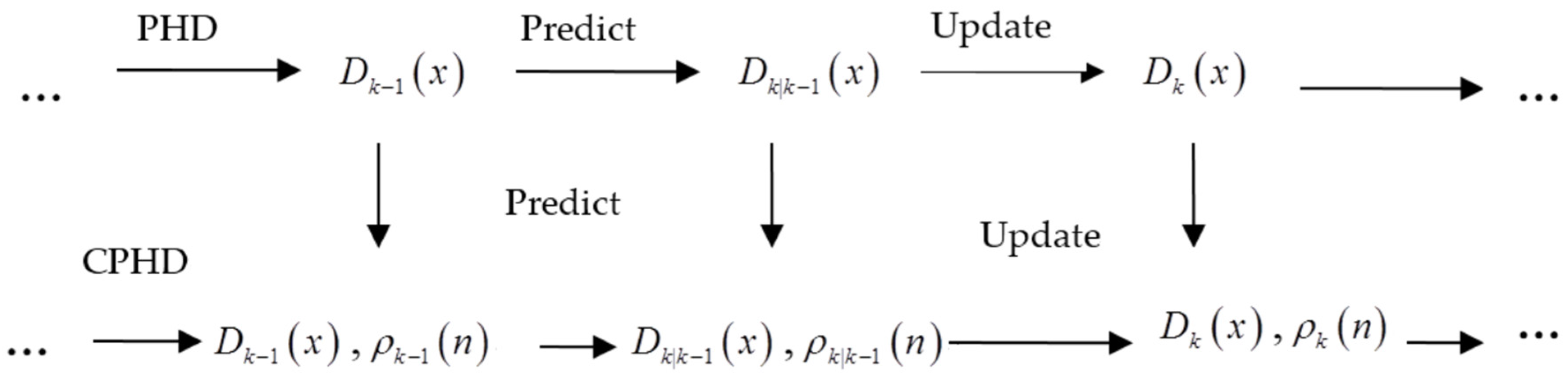
2.2. GM-PHD Algorithm
- A.1.
- The motion model and sensor measurement model are all linear Gaussian.where is the state transition matrix, is the measurement matrix, and and are the process noise covariance and measurement noise covariance respectively.
- A.2.
- The survival and detection probabilities for targets are state independent.
- A.3.
- The target birth RFS is also a Gaussian mixture of the form.where, , , , , are given parameters that determine the intensity of target birth; and , are calculated using Kalman filter [24], which are used in many parts in the paper.
2.3. GM-CPHD Algorithm
3. The Proposed Algorithm Based on Novel Detection Probability
3.1. Gating Technical Strategy
3.2. An Novel Detection Probability Model
3.3. The Proposed Algorithm with Novel Detection Probability
4. Simulation and Analysis
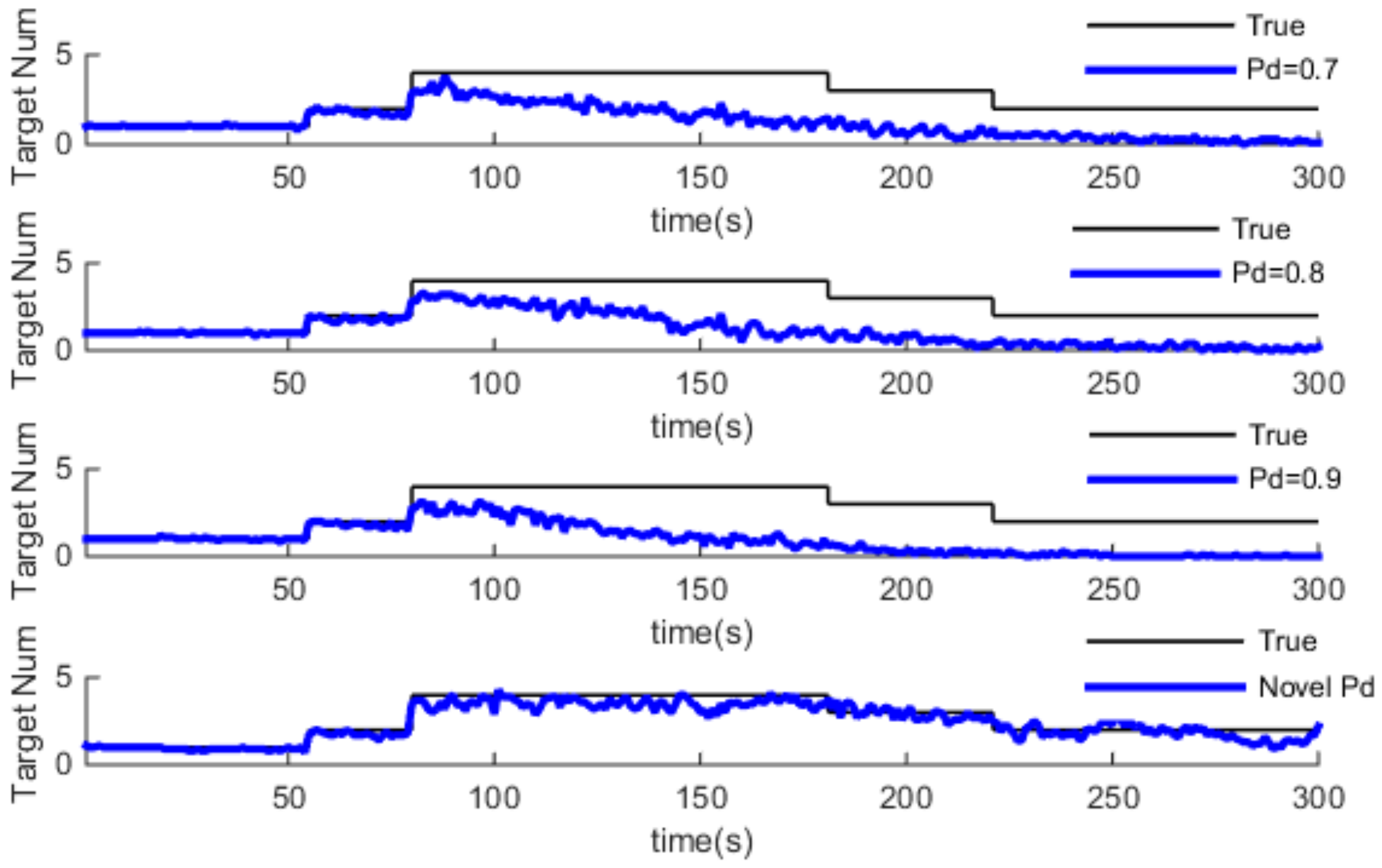
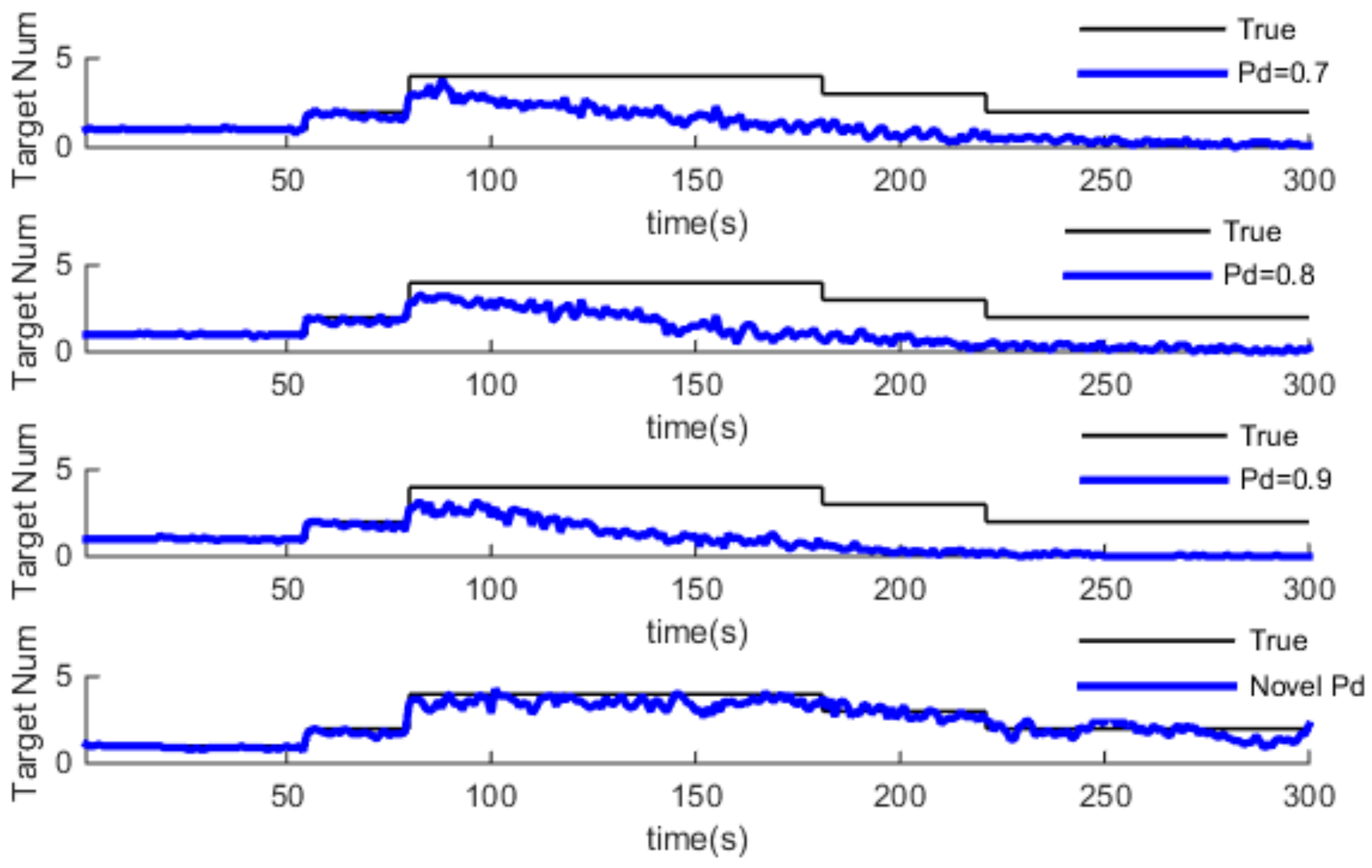
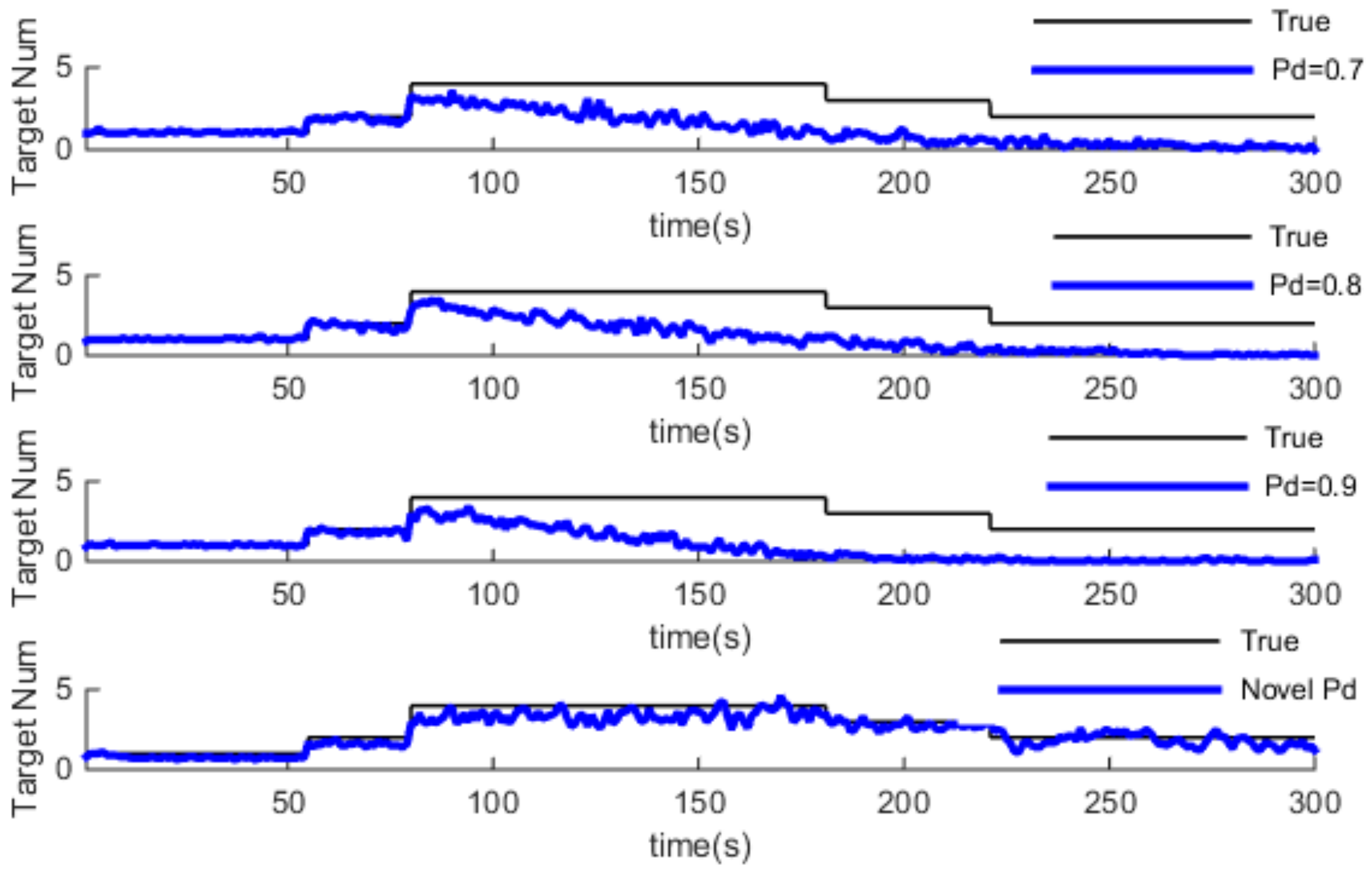
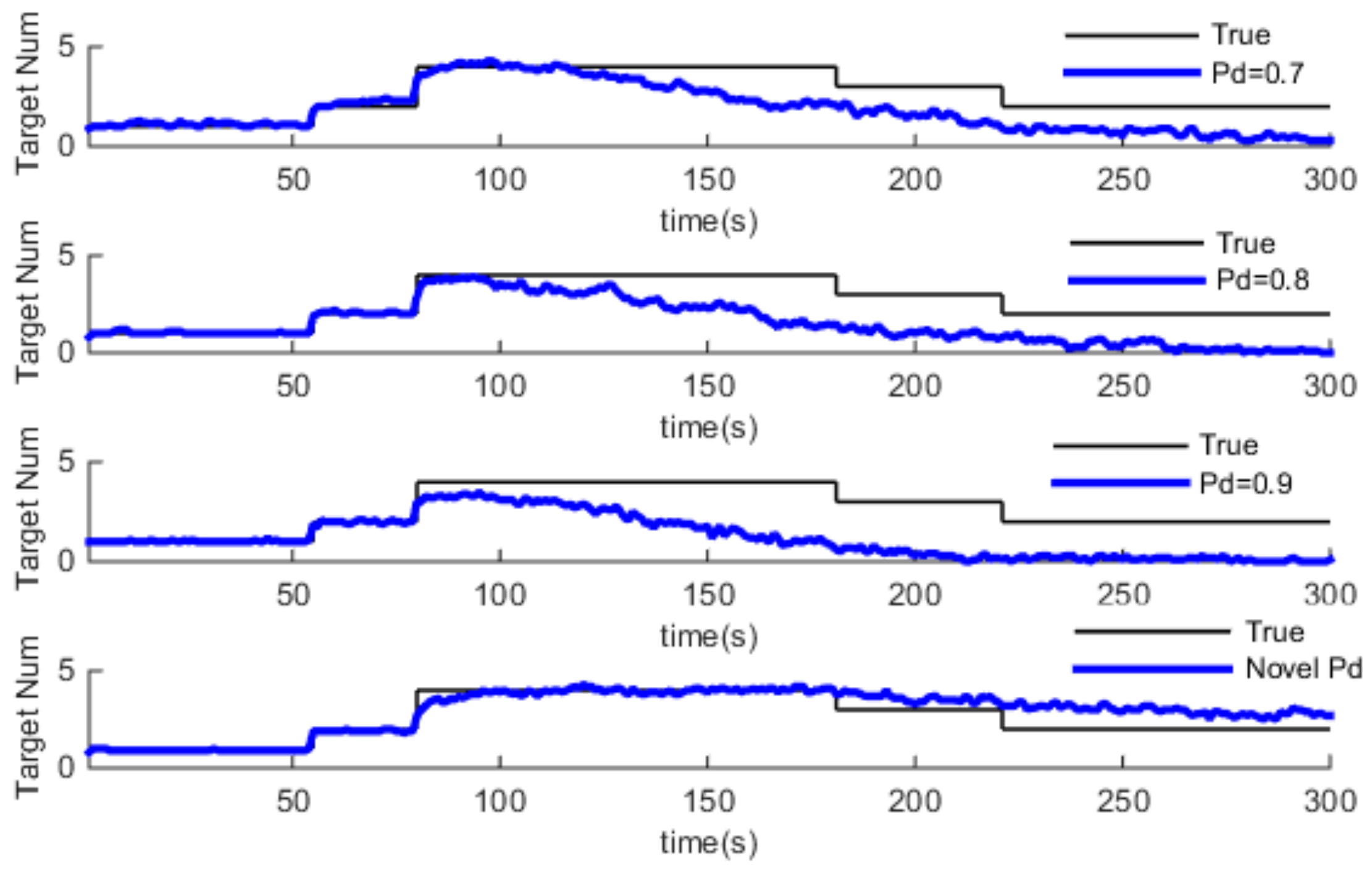
4.1. Simulation and Analysis of GM-PHD and Pd-GM-PHD
4.2. Simulation and Analysis of GM-CPHD and Pd-GM-CPHD
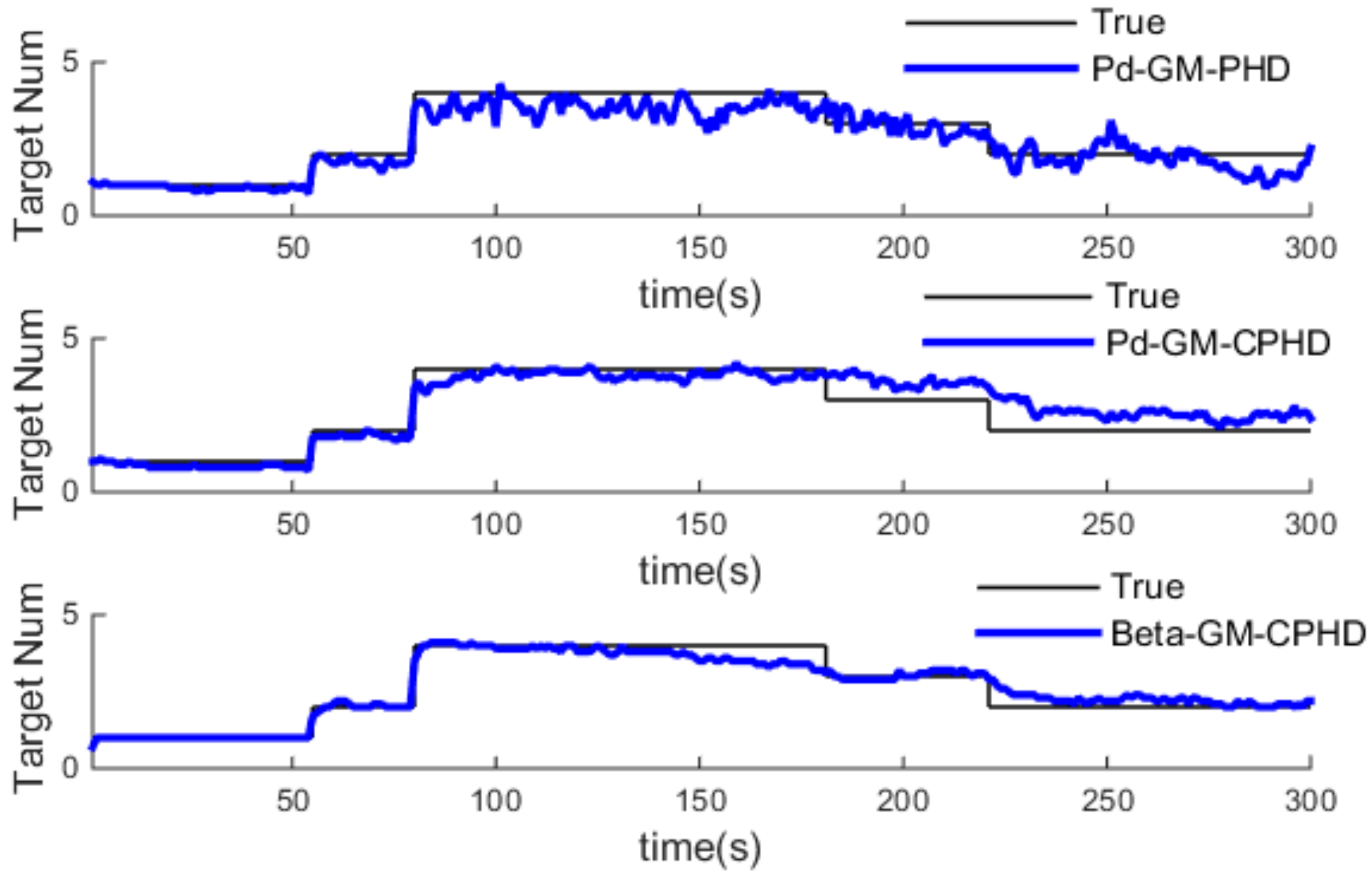
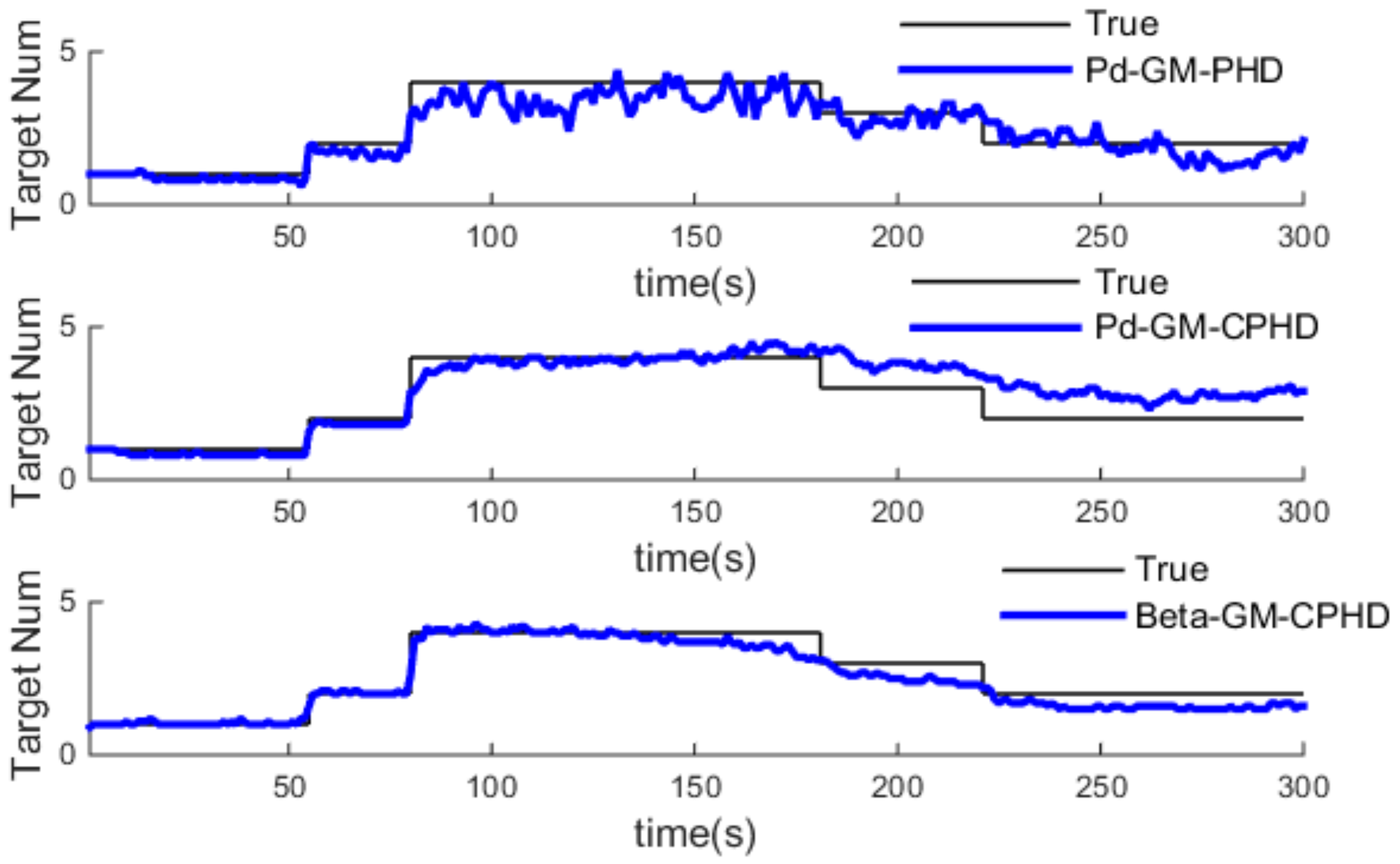
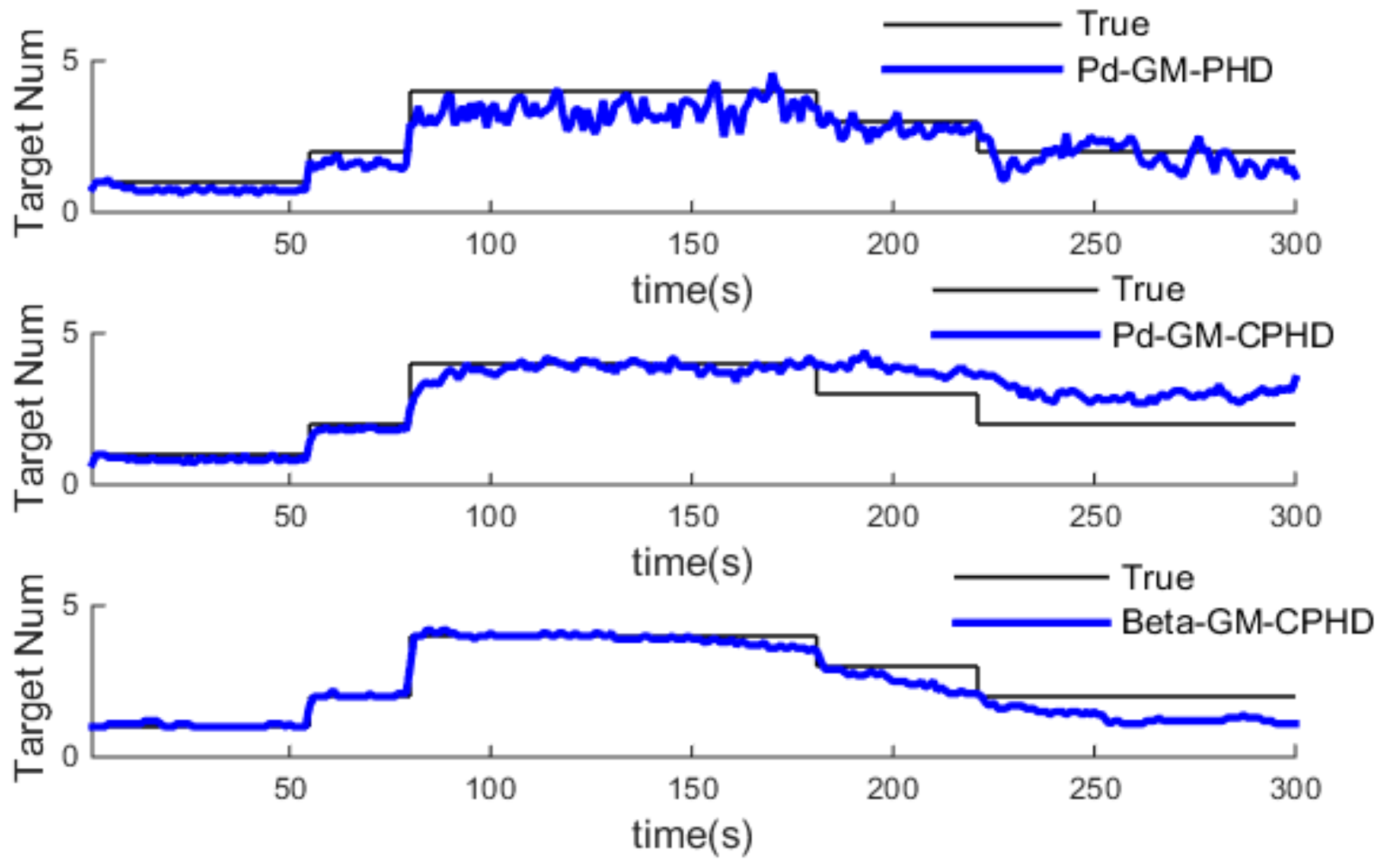
4.3. Simulation and Analysis of Different Three Algorithm
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mallick, M.; Vo, B.-N.; Kirubarajan, T.; Arulampalam, S. Introduction to the Issue on Multitarget Tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 373–375. [Google Scholar] [CrossRef]
- Li, X.R.; Bar-Shalom, Y. Tracking in clutter with nearest neighbor filters: Analysis and performance. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 995–1010. [Google Scholar]
- Chen, X.; Li, Y.; Li, Y.; Yu, J.; Li, X. A Novel Probability Data Association for Target Tracking in a Clutter Environment. Sensors 2016, 16, 2180. [Google Scholar] [CrossRef] [PubMed]
- Habtemariam, B.; Tharmarasa, R.; Thayaparan, T.; Mallick, M.; Kirubarajan, T. A Multiple-Detection Joint Probabilistic Data Association Filter. IEEE J. Sel. Top. Signal Process. 2013, 7, 461–471. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Lee, E.H.; Zhang, Q.; Song, T.L. Markov Chain Realization of Joint Integrated Probabilistic Data Association. Sensors 2017, 17, 2865. [Google Scholar] [CrossRef] [PubMed]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. Bayesian Filtering with Random Finite Set Observations. IEEE Trans. Signal Process. 2008, 56, 1313–1326. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget Bayes Filtering via First-order Multitarget Moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.-N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for Multitarget Filtering with Random Finite Sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Vo, B.-N.; Ma, W.-K. The Gaussian Mixture Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Beard, M.; Reuter, S.; Granström, K.; Vo, B.-T.; Vo, B.-N.; Scheel, A. Multiple Extended Target Tracking with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2016, 64, 1638–1653. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M. Hybrid multi-Bernoulli and CPHD filters for superpositional sensors. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2847–2863. [Google Scholar] [CrossRef]
- Schlangen, I.; Delande, E.D.; Houssineau, J.; Clark, D.E. A Second-Order PHD Filter with Mean and Variance in Target Number. IEEE Trans. Signal Process. 2018, 66, 48–63. [Google Scholar] [CrossRef]
- Tobias, M.; Lanterman, A.D. Probability Hypothesis Density-based Multitarget Tracking with Multiple Bistatic Range and Doppler Observations. IEE Proc. Radar Sonar Navig. 2005, 152, 195–205. [Google Scholar] [CrossRef]
- Clark, D.E.; Bell, J. Bayesian multiple target tracking in forward scan sonar images using the PHD filter. IEE Proc. Radar Sonar Navig. 2005, 152, 327–334. [Google Scholar] [CrossRef]
- Kalyan, B.; Balasuriya, A.; Wijesoma, S. Multiple target tracking in underwater sonar images using Particle-PHD filter. In Proceedings of the OCEANS 2006—Asia Pacific, Singapore, 16–19 May 2007. [Google Scholar]
- Hendeby, G.; Karlsson, R. Gaussian mixture PHD filtering with variable probability of detection. In Proceedings of the 2014 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Mahler, R.; Vo, B.-T.; Vo, B.-N. CPHD filtering with unknown clutter rate and detection profile. IEEE Trans. Signal Process. 2011, 59, 3497–3513. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, Z.; Hu, S. Gaussian Mixture CPHD filter with Gating technique. Signal Process. 2009, 89, 1521–1530. [Google Scholar] [CrossRef]
- Macagnano, D.; De Abreu, G.T.F. Adaptive Gating for Multitarget Tracking with Gaussian Mixture filter. IEEE Trans. Signal Process. 2012, 60, 1533–1538. [Google Scholar] [CrossRef]
- Wang, X.; Fu, M.; Zhang, H. Target Tracking in Wireless Sensor Networks Based on the Combination of KF and MLE Using Distance Measurements. IEEE Trans. Mob. Comput. 2012, 11, 567–576. [Google Scholar] [CrossRef]
- El-Fallah, A.; Perloff, M. Multisensor-multitarget sensor management with target preference. Proc. SPIE 2004, 5429, 222–232. [Google Scholar]
- Tan, T. Sonar Technology; Harbin Engineering University Press: Harbin, China, 2009. [Google Scholar]
- Schonhoff, T.; Giordano, A. Detection and Estimation Theory and Its Application; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Schumacher, D.; Vo, B.-T.; Vo, B.-N. A Consistent Metric for Performance Evaluation of Multi-Object Filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]





| State | Initial State | Start Time (s) | End Time (s) | |
|---|---|---|---|---|
| Target | ||||
| target 1 | (300 m, 10 m/s, 400 m, 8 m/s) | |||
| target 2 | (630 m, 2 m/s, 800 m, 10 m/s) | |||
| target 3 | (500 m, 8 m/s, 1700 m, −5 m/s) | |||
| target 4 | (1200 m, 4 m/s, 200 m, 10 m/s) | |||
| Time Average OSPA-Distance (m) | GM-PHD | Pd-GM-PHD | ||
|---|---|---|---|---|
| 53.4 | 55.19 | 61.57 | 35.26 | |
| 54.96 | 56.58 | 62.33 | 37.34 | |
| 55.54 | 57.66 | 63.25 | 41.51 | |
| Time Average OSPA-Distance (m) | GM-CPHD | Pd-GM-CPHD | ||
|---|---|---|---|---|
| 34.04 | 43.34 | 52.04 | 25.22 | |
| 39.29 | 46.61 | 55.63 | 26.54 | |
| 40.29 | 47.63 | 56.18 | 30.05 | |
| Time Average OSPA-Distance (m) | Pd-GM-PHD | Pd-GM-CPHD | Beta-GM-CPHD |
|---|---|---|---|
| 35.26 | 25.22 | 30.94 | |
| 37.34 | 26.54 | 34.7 | |
| 41.51 | 30.05 | 35.18 |
| Clutter Intensity | Pd-GM-PHD | Pd-GM-CPHD | Beta-GM-CPHD |
|---|---|---|---|
| 2.86 | 5.76 | 44.32 | |
| 3.17 | 6.57 | 51.15 | |
| 4.48 | 10.55 | 69.35 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, Y.; Li, Y.; Yu, J. PHD and CPHD Algorithms Based on a Novel Detection Probability Applied in an Active Sonar Tracking System. Appl. Sci. 2018, 8, 36. https://doi.org/10.3390/app8010036
Chen X, Li Y, Li Y, Yu J. PHD and CPHD Algorithms Based on a Novel Detection Probability Applied in an Active Sonar Tracking System. Applied Sciences. 2018; 8(1):36. https://doi.org/10.3390/app8010036
Chicago/Turabian StyleChen, Xiao, Yaan Li, Yuxing Li, and Jing Yu. 2018. "PHD and CPHD Algorithms Based on a Novel Detection Probability Applied in an Active Sonar Tracking System" Applied Sciences 8, no. 1: 36. https://doi.org/10.3390/app8010036






