1. Introduction
In this paper, we demonstrate how the partial-wave method, as first introduced by Solie and Auld [
1], can be used to gain a new perspective on guided waves. This new perspective adds to our understanding of the structure of guided waves, and provides valuable insight into the leaky characteristics of Lamb waves (which are not to be confused with the study of leaky Lamb waves and their corresponding dispersion curve solutions).
At present, our understanding of guided waves is primarily informed by the derivation of characteristic equations and dispersion curve solutions. The dispersion curve solutions in particular have become significantly more accessible with the widespread use of the semi-analytical finite element (SAFE) method. However, the SAFE method does not provide the same level of understanding that would be possible by analyzing a characteristic equation. The most well-known example of this is that the two-part Lamb wave characteristic equation shows that all of the Lamb waves can be divided into two types: symmetric and anti-symmetric. Hence, the importance of the present work. However, this paper will not cover the calculation of dispersion curves, attenuation, energy loss, or anisotropic materials. Neither will it cover the derivation of characteristic equations for various guided waves.
For the purpose of clarity, in this paper, bulk waves are plane waves that travel through the bulk of a media, and surface waves are plane waves that travel along the surface of a media. It is emphasized that all of the waves are considered to have a planar wavefront.
Section 2 and
Section 3 will provide a brief history and the fundamentals of the partial-wave method and the Christoffel equation, respectively. These sections give special attention to the diction used and the assumptions made, as they are pertinent to how the interpretation presented in this paper deviates from the literature.
Section 4 describes this new method of interpretation. It discusses in detail how the slowness curve solutions of the Christoffel equation can be used to interpret the characteristics of most guided waves, and the Lamb wave solutions in particular.
Section 5 and
Section 6 apply the new method of interpretation to a variety of guided waves, which include Rayleigh waves, Stoneley waves, Lamb waves, and shear horizontal waves.
Section 7 focuses on Lamb waves, and a method developed in
Section 6 is used to investigate the contributions of each partial wave to Lamb waves from 50 kHz to 20 MHz for a 1-mm thick aluminum plate. This section also identifies characteristics of Lamb waves that have not been formally discussed in the literature.
Section 8 uses the results from the previous sections to develop an understanding of the leaky characteristics of Lamb waves. Various characteristics of the acoustic leakage from the waveguide can be easily determined, including the angle of propagation and the amplitude of emission based on the interface conditions. A correlation between the amount of acoustic leakage and the refraction qualities of obliquely travelling bulk waves in the guided wave is also identified.
4. Reinterpreting the Dispersion Curves
As mentioned previously, the Christoffel equation is only dependent upon the material properties of the elastic solid in which the plane waves propagate. The BCs are not used until the partial-wave method is applied. Not only that, but the boundary conditions are not limited to the conventional traction-free BCs (e.g., Lamb waves). As a result, the partial-wave method is not limited to any specific type of waveguide. In fact, most types of guided waves should be representable using slowness curves. For some, such as the shear horizontal guided waves, this approach is more cumbersome than the standard derivation. However, its value lies in how it provides a fundamental foundation for all of the guided waves, and a common method for interpreting and comparing each one. When considering reflection/transmission, mode conversion, or multi-mode propagation, this perspective is quite beneficial.
In modern literature, perhaps the most commonly used dispersion curves are of Lamb waves in an aluminum plate in terms of phase velocity versus the frequency–thickness product. Using the three regions depicted in
Figure 1, we can divide the phase velocity dispersion curves into three regions, as shown in
Figure 2. By doing this, it is possible to view how the dispersion curve solutions match up with the partial waves’ characteristics. For example, this is a good way to dispel the potential misconception that guided waves are composed of multiple reflecting bulk waves. That is, the original assumption of plane wave propagation (Equation (4)), which is fundamental to the Christoffel equation, does not exclude the surface wave solution (i.e., imaginary-valued
) as
increases. It would be more accurate to say that guided waves are a superposition of reflecting bulk waves and surface waves with elliptical particle motion (this will be shown in the later calculations and examples).
In fact, guided waves composed solely of reflecting bulk waves exist only in Region 3 (c), where they are highly dispersive. However, there is one exception to this rule: there exists a range of phase velocities in Region 2 (
Figure 1b), where only bulk waves propagate, which will be discussed in a later section.
The A0 mode and Rayleigh waves exist in Region 1 (
Figure 1a), where each guided wave can be represented in terms of six surface waves. The low-frequency S0 mode is in Region 2 (b), and is composed of two surface waves and two bulk waves (as will be shown later in the paper), excluding the two shear horizontal partial waves.
The line separating Region 1 (
Figure 1a) and Region 2 (
Figure 1b) has great significance, since many Lamb wave modes appear nearly non-dispersive near it. That is, the higher-order Lamb waves approach the shear wave speed, and the A0 and S0 modes approach the Rayleigh wave speed for large
values. The shear horizontal modes also converge to this line for large
values. The line separating Region 2 (
Figure 1b) and Region 3 (
Figure 1c) has many higher-order Lamb modes, which appear nearly non-dispersive close to it as well.
The A0 and S0 Lamb wave modes’ tendency to approach the Rayleigh wave phase velocity can also be explained using this reinterpretation, since increasing
will increase the magnitude of the imaginary-valued
(see
Figure 1a). Once
increases sufficiently, the surface waves decay with the depth from the surface before interacting with the opposite traction-free boundary, thereby imitating a Rayleigh wave. This also explains why quasi-Rayleigh waves [
9] have similar wave structures to Rayleigh waves. That is, the quasi-Rayleigh wave and the Rayleigh wave are both composed of partial waves (with slight differences in amplitude and exponential decay).
Many higher-order Lamb modes have wave structures that are sinusoidal through the thickness, but have slightly larger or smaller amplitudes near the traction-free boundaries. In Region 2 (
Figure 1b), this could be explained by surface waves affecting the wave structure near the traction-free boundaries, while the reflecting bulk waves create the sinusoidal appearance.
This reinterpretation of guided waves provides for the relatively simple calculation of wave structures based on the superposition of the partial-wave eigensolutions. Based on the preceding concepts and with wave propagation in the
-direction,
. Solving Equations (15) and (16) for
results in:
and:
respectively. Equations (9), (10) and (17) can then be substituted into Equation (11) to get matrix
as a function of
and
:
And Equations (9), (10) and (18) can be substituted into Equation (11) to get matrix
as a function of and
and
:
Finding the reduced row echelon form of
and
gives the solution to the eigenvectors, which contain, at most, two free variables (i.e.,
and
). Considering
and
, and also the “
” terms in them, which correspond with the sign of
, results in four possible eigenvectors (not including the multiplicity). For the positive
eigenvalue of the longitudinal wave, the eigenvector is:
While for the negative
eigenvalue of the longitudinal wave, the eigenvector is:
For the positive
eigenvalue of the shear wave, the eigenvector is:
While for the shear wave’s negative
eigenvalue, the eigenvector is:
The superscripts and correspond to the longitudinal and the shear waves, respectively. The can be made more specific by using and to denote the shear vertical and shear horizontal polarizations.
Examining Equations (21) and (22), it is clear that for
, the square root becomes imaginary-valued, and for
, the square-root becomes real-valued. These two scenarios correspond with the surface wave and bulk wave solutions, respectively. The same holds true for Equations (23) and (24) with
instead of
, with
p = 0. For
or
and positive
, the corresponding eigenvector is:
and for negative
it is:
Hence, for very large
values (relative to their respective wave speeds), the eigenvectors become circularly polarized, regardless of whether it is a shear wave or longitudinal wave. Lastly, for a given
and
, the
values of the four partial waves (not including the multiplicity of the shear waves) can be calculated using Equations (15) and (16):
As implied previously, since the solution of the Christoffel equation does not depend on the boundary/interface conditions, a linear combination of the partial waves should be able to represent most elastodynamic guided waves, regardless of the boundary/interface conditions. We demonstrate this in the following sections. The material properties shown in
Table 1 will be used. For each partial-wave eigenvector calculated in the following examples, the free variable is set equal to unity; then, the resulting eigenvector is normalized into a unit vector by dividing by its magnitude.
8. Leaky Characteristics of Lamb Waves
Lamb waves travel through a traction-free plate. Leaky Lamb waves are the waves that propagate through the same waveguide when the traction-free boundaries are replaced with fluid half-spaces. The theoretical literature on leaky Lamb waves focuses on the calculation of dispersion curves and determining how these curves differ from the conventional Lamb wave dispersion curves [
15,
16]. The focus of this section is not this, but rather the leaky characteristics of Lamb waves, assuming there is no change in the dispersion curves. That is, the dispersion curves of a plate surrounded by a vacuum will be used as an approximation for the dispersion curves of a plate surrounded by air. This is a universal standard practice. The goal will be to use the partial-wave method to determine the characteristics of the acoustic leakage into the fluid from the Lamb wave travelling in the plate waveguide.
Before continuing, it should be stated that for fluids, the Eulerian form of the balance of linear momentum for acoustics is:
This complicates the velocity–pressure relationship of the acoustic fluid. To simplify this, it is assumed that the displacement is time-harmonic, which makes the particle velocity:
It is also assumed that the displacement is spatially harmonic and longitudinal in polarization such that:
where
is the unit vector denoting the direction of wave propagation. Using Equations (52) and (53) in Equation (51) results in:
The Eulerian form can approximate the Lagrangian form with these assumptions if:
Equation (55) can be rearranged to:
If it is assumed that the phase velocity is around
m/s and that displacements are about
m, then for frequencies much less than
rad/s, the Eulerian form should approximate the Lagrangian form. As a result, the simpler pressure–velocity relationship:
which was derived from the Lagrangian form of the balance of linear momentum for fluids assuming a time-harmonic displacement, can be used for the following example.
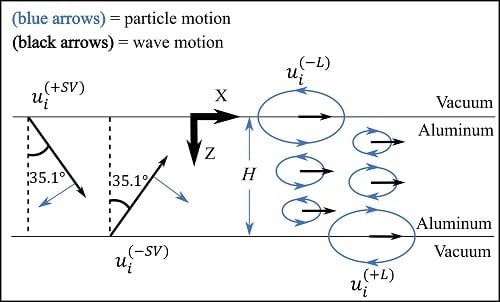
As an acoustic wave in a fluid, the slowness curve can be plotted as a circle with a radius equal to
. Plotted with respect to aluminum’s slowness curve, the order of magnitude difference in radii makes all but the very dispersive part of the A0 mode, at very low frequencies, emit acoustic bulk waves (see
Figure 10). At these low frequencies, the A0 mode is highly dispersive, and has a phase velocity lower than the acoustic wave speed in air.
The comparison of slowness curves from various media, which are shown in
Figure 10, is similar to an example in Auld [
2], but that example discussed the electromagnetic emission from a piezoelectric waveguide. The approach relies on Snell’s law, dictating that the wavenumber (i.e.,
) should be equal at the interface between media. However, if Snell’s law were to be used directly, complex-valued angles (i.e.,
) would need to be used.
Based on this slowness curve representation, it can be concluded that the acoustic leakage will be an obliquely travelling bulk wave. The angle of incidence of the acoustic leakage would be between 0° and 20° for most Lamb waves. If these findings are applied to air-coupled transducers, it would suggest that there is an optimum angle of reception for the air-coupled transducers.
The partial waves for air can be represented as an obliquely traveling longitudinal wave:
and the partial waves of a Lamb wave in an aluminum plate (see Equations (38) and (43)) can be used with five of the six available interface conditions:
where an expression for
can be found by using Equations (57) and (58) to find that:
Although stress components are expressly used in the boundary conditions detailed in this paper, it is understood that they describe traction continuity. Equations (59)–(64) represent the traction and displacement continuity conditions indicative of a fluid–solid interface. We assume that
,
,
,
,
, and
can be calculated as before by using the continuity conditions in Equations (59)−(64).
and
in this case would correspond with the amplitudes of the longitudinal waves at the top and bottom of the plate. All of the amplitudes were normalized by dividing each by:
Equations (38) and (58) can then be used to plot the wave structure, and verify that the interface conditions are satisfied.
Since it is now possible to calculate the amplitude of the acoustic leakage, every point of the Lamb wave dispersion curve can be input to determine the ideal guided wave mode for maximum (or minimum) acoustic leakage.
Figure 11 shows sample calculations for a 1-mm aluminum plate. The color axis of
Figure 11 is the average amplitude of acoustic leakage from Lamb waves:
Assuming there is a direct correlation between the strength of acoustic leakage and the amplitude of the acoustic wave coupled to the Lamb wave,
Figure 11 suggests several things:
Perhaps most interesting is that the maximum acoustic leakage is concentrated in Region 2 (
Figure 1b) of the dispersion curves, while Region 1 (
Figure 1a) has noticeably less acoustic leakage. A possible explanation for why this would be is that the guided wave modes in Region 1 (
Figure 1a) are composed of surface partial waves, which are inherently coupled to the interface.
In Region 2 (b), bulk shear vertical partial waves propagate through the thickness of the plate. Incident upon the aluminum–air interface, this can be modeled as an oblique incidence problem to determine the reflection and transmission characteristics, as shown in
Figure 12 where
is the incident angle of a shear vertical bulk wave.
Displacement terms for each bulk wave are constructed according to particle polarization and wave propagation direction. The same BCs that are detailed in Equations (59)−(64) are applied to this problem. Along with Snell’s law, these BCs are used to calculate the displacement amplitude ratios as a function of incidence angle,
, as shown in
Figure 13:
is the particle displacement amplitude ratio between the reflected longitudinal wave in the aluminum and the incident shear wave in the aluminum.
is the particle displacement amplitude ratio between the reflected shear wave in the aluminum and the incident shear wave in the aluminum.
is the particle displacement amplitude ratio between the transmitted longitudinal wave in the air and the incident shear wave in the aluminum.
It is noted that in place of , the ratio of wavenumbers were used, e.g., .
By setting up Snell’s law to be an equivalence between a bulk wave and an arbitrary wave in the same plate, the relation is:
Considering that
is defined with respect to the
z-axis, Snell’s law becomes:
The black vertical line in
Figure 13 corresponds with an incidence angle of about 45.45°, which translates to a phase velocity of 4350 m/s by Snell’s law. For reference, a phase velocity at the shear wave speed, 3100 m/s, corresponds with an incidence angle of 90°, and a phase velocity at the longitudinal wave speed, 6350 m/s, corresponds with an incidence angle of 29°. The angles in the vicinity of 45.45° are associated with very little mode conversion to longitudinal modes, but most importantly to a large transmission of acoustic longitudinal waves to the air half-space. The behavior of the waves within the plate is consistent with what is Region 2 of
Figure 8b.
Region 3 (c) would correspond to smaller angles of incidence as the phase velocity increases. For angles of incidence that are less than the first critical angle (i.e.,
), the mode conversion to longitudinal waves is significant with progressively less transmission of acoustic leakage as the angle of incidence decreases. At the larger phase velocities in Region 3 (
Figure 1c) (i.e.,
), the longitudinal bulk waves traveling through the plate would then begin to contribute significantly to any acoustic leakage.
In many studies of leaky Lamb waves, the fluid medium in which the wave leaks is water; thus, it is worth mentioning that the dispersion curves do not change significantly when water coupling is included [
15,
16]. As a result, many of the conclusions made in this example calculation pertaining to the form of the acoustic leakage can be found to agree, to some degree, with the findings in Hayashi and Inoue’s paper [
15]. Specifically, the findings that the oblique propagation of the longitudinal acoustic wave in the water and the evanescent propagation of it at a phase velocity less than the longitudinal wave speed in water agree. We reiterate that Hayashi and Inoue [
15] and Gravenkamp et al. [
16] focus on the study of the dispersion curves of leaky Lamb waves, which is different from what was done in this example calculation.
9. Conclusions
This paper exploits the Christoffel equation, slowness curves, and the partial-wave method to establish a foundation on which guided waves can be analyzed, compared, and explained. The approach was used to calculate the wave structures of many types of guided waves, once the frequency–wavenumber pairs were known. It is, of course, possible to calculate the wave structures using the well-known methods for dispersion curve calculation, but those methods can often be calculation-intensive. There are analytical expressions, but those leave little room for conceptual interpretation. Thus, the approach detailed in this paper is seen as a relatively easy, general, and informative method for calculating wave structures of specific modes of interest. Indicative of that are the Lamb wave characteristics observed in the paper, which relate to the phase difference between the top and bottom partial waves, and the amount by which each partial wave contributes to each Lamb wave. It was shown, among other things, that in Region 2 (
Figure 1b), there is a phase velocity range in which the Lamb waves consist of partial shear vertical bulk waves traveling at ±45°. These are known as Lame waves, and they exhibit the most leakage into the fluid half-spaces surrounding the plate. Likewise, there is a similar band where all of the modes are dominated by longitudinal surface waves. It was also shown that the symmetric and anti-symmetric modes can be characterized by the phase difference between the partial waves associated with the top surface and those associated with the bottom surface.
The example calculation of the leaky characteristics of Lamb waves is applicable to air-coupled transducers. The optimum angle calculation is merely Snell’s law, but the calculation of the amplitude of acoustic leakage provides us with a potentially simple methodology to compare the amount of acoustic leakage from various Lamb waves. Also, the potential relationship between the acoustic leakage from Lamb waves and the well-known oblique incidence problems could help to explain some of the acoustic leakage phenomenon using familiar and relatively simple theories. Beyond Lamb waves, a similar approach can be used for Rayleigh waves.
For other guided waves such as the Lamb-like waves in a plate on a half-space, the method detailed in this paper should still apply. That is, there will be six partial waves (i.e., four in the plate and two in the half-space) and six BCs (i.e., two traction-free at the top of the plate, and two traction continuity and two displacement continuity at the interface).
Lastly, the partial-wave method is not at all restricted to isotropic materials; it can also be used with anisotropic materials. If a similar approach is attempted for anisotropic materials, the immediately discernable differences would be that there are four regions instead of three in the dispersion curves, and three slowness curves instead of two. Some symmetry in the eigensolutions of the Christoffel equation may also disappear as a result of the anisotropy. That being said, the general approach is still expected to hold true, although further analysis is needed to confirm this.