Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery
Abstract
:Featured application
Abstract
1. Introduction
2. Theory
2.1. EEMD
2.2. Correlation Coefficient
2.3. SVD
2.4. KICA
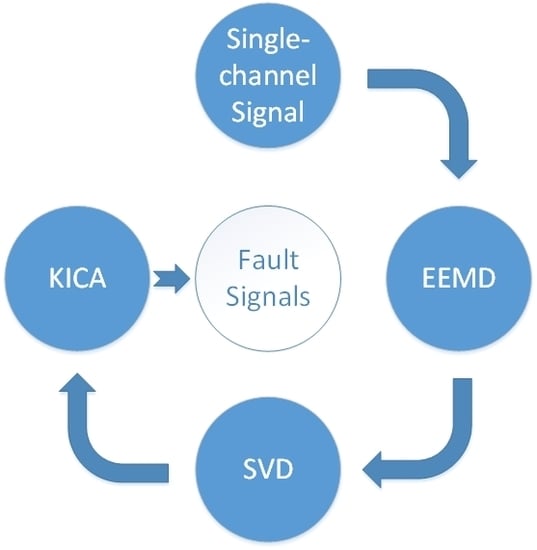
3. The Proposed Method
4. Application and Validation
4.1. Experimental Analysis of Faulty Gear
4.1.1. Wavelets
4.1.2. EMD
4.1.3. VMD
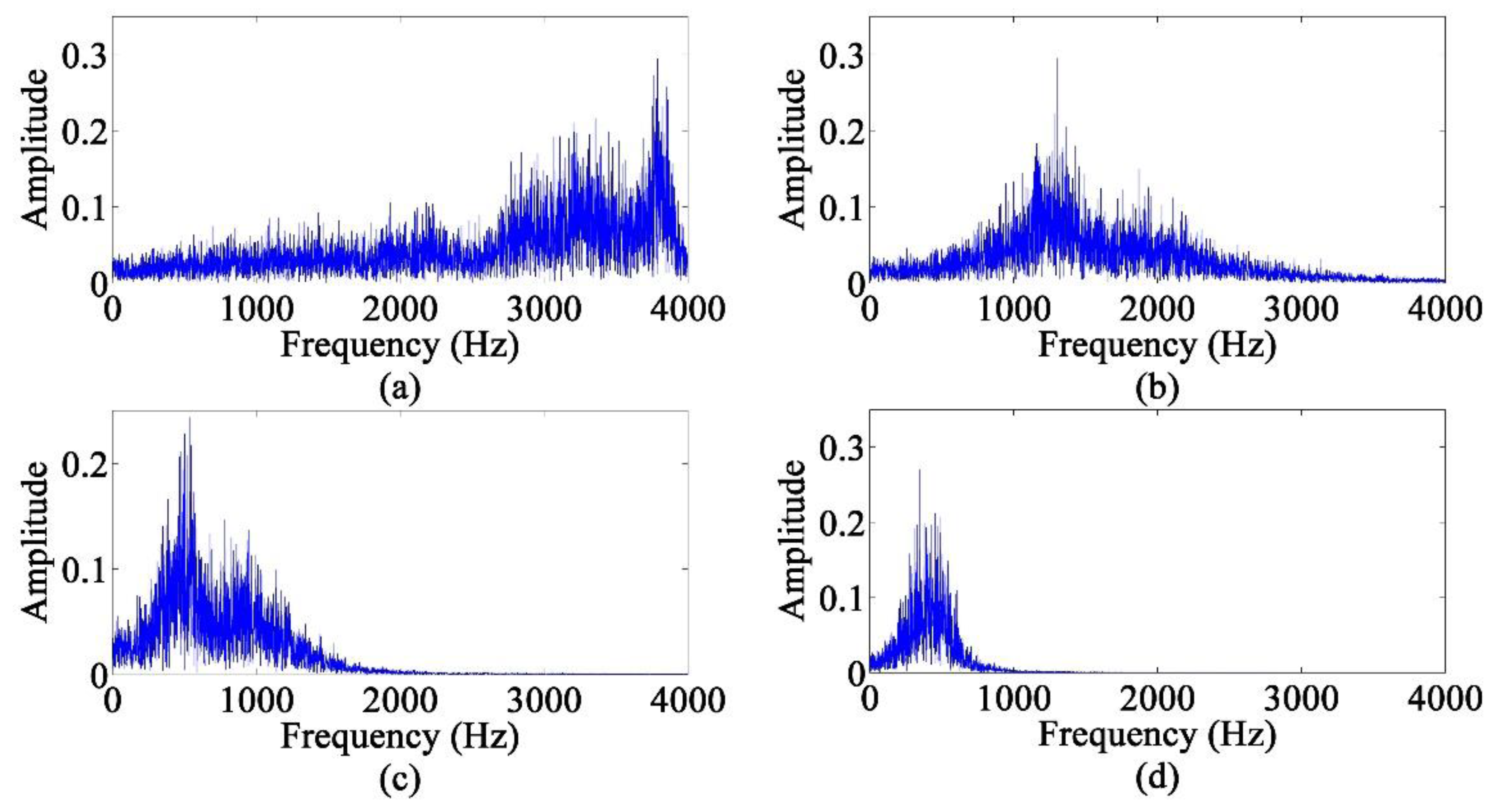
4.1.4. EEMD
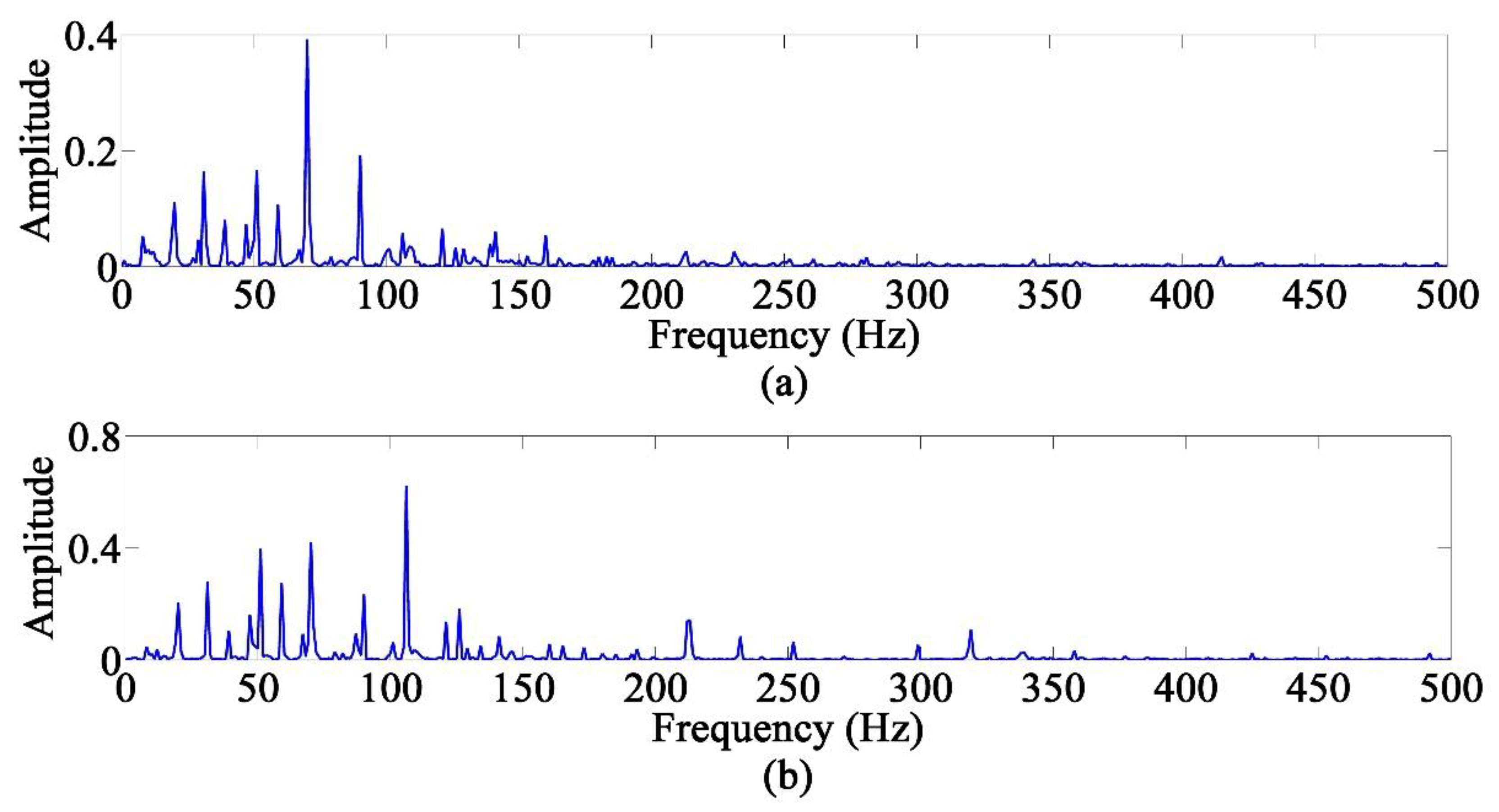
4.1.5. The Proposed Method
4.1.6. Results and Discussions
4.2. Experimental Analysis of Faulty Rolling Bearing
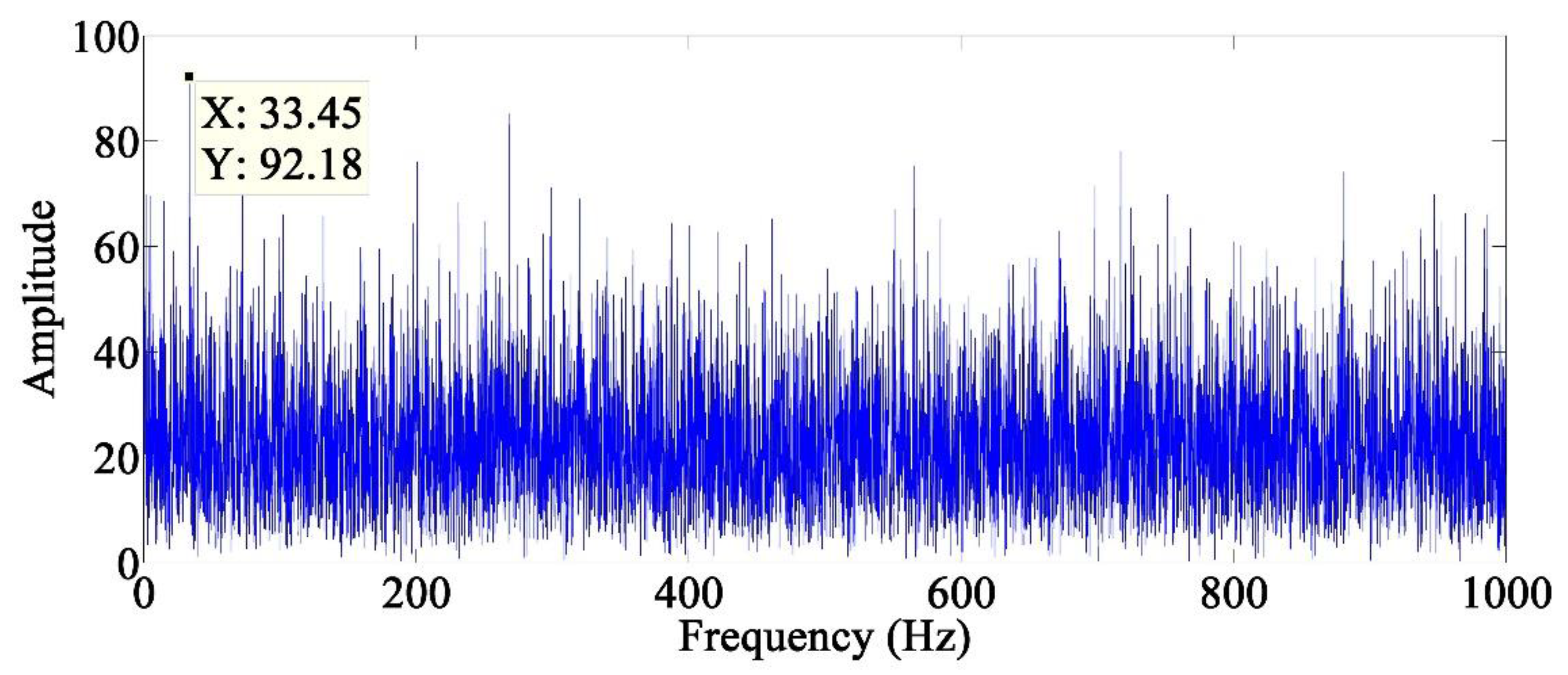
4.2.1. Wavelets
4.2.2. EMD
4.2.3. VMD
4.2.4. EEMD
4.2.5. The Proposed Method
4.2.6. Results and Discussions
4.3. Experimental Analysis of a Faulty Shaft
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cheng, J.; Yang, Y.; Yang, Y. A rotating machinery fault diagnosis method based on local mean decomposition. Digit. Signal Process. 2012, 22, 356–366. [Google Scholar] [CrossRef]
- Xu, T.; Yin, Z.; Cai, D.; Zheng, D. Fault diagnosis for rotating machinery based on Local Mean Decomposition morphology filtering and Least Square Support Vector Machine. J. Intell. Fuzzy Syst. 2017, 32, 2061–2070. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Ferracuti, F.; Freddi, A.; Monteriù, A. Statistical Spectral Analysis for Fault Diagnosis of Rotating Machines. IEEE Trans. Ind. Electron. 2017, 65, 4301–4310. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, A. Fault feature separation using wavelet-ICA filter. NDT E Int. 2005, 38, 421–427. [Google Scholar] [CrossRef]
- Keshtan, M.N.; Khajavi, M. Bearings fault diagnosis using vibrational signal analysis by EMD method. Res. Nondestruct. Eval. 2015, 27, 155–174. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, D.; Zuo, M.J. Adaptive Mode Decomposition Methods and Their Applications in Signal Analysis for Machinery Fault Diagnosis: A Review with Examples. IEEE Access 2017, 5, 24301–24331. [Google Scholar] [CrossRef]
- Tabrizi, A.; Garibaldi, L.; Fasana, A.; Marchesiello, S. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica 2015, 50, 865–874. [Google Scholar] [CrossRef]
- Cheng, G.; Chen, X.; Li, H.; Li, P.; Liu, H. Study on planetary gear fault diagnosis based on entropy feature fusion of ensemble empirical mode decomposition. Measurement 2016, 91, 140–154. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, K.; Su, L.; Wu, J.; Wang, H.; Chen, P. A Rolling Bearing Fault Diagnosis Method Based on Variational Mode Decomposition and an Improved Kernel Extreme Learning Machine. Appl. Sci. 2017, 7, 1004. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Wang, X.; Peng, Z. Multi-mode separation and nonlinear feature extraction of hybrid gear failures in coal cutters using adaptive nonstationary vibration analysis. Nonlinear Dyn. 2016, 84, 295–310. [Google Scholar] [CrossRef]
- Yang, Z.X.; Zhong, J.H. A Hybrid EEMD-Based SampEn and SVD for Acoustic Signal Processing and Fault Diagnosis. Entropy 2016, 18, 112. [Google Scholar] [CrossRef]
- Shen, H.; Jegelka, S.; Gretton, A. Fast kernel-based independent component analysis. IEEE Trans. Signal Process. 2009, 57, 3498–3511. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, W.; Li, X. Observation and Detection for a Class of Industrial Systems. IEEE Trans. Ind. Electron. 2017, 64, 6724–6731. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, R. On the explanation of spatial smoothing in MUSIC algorithm for coherent sources. Int. Conf. Inf. Sci. Technol. 2011, 699–702. [Google Scholar] [CrossRef]
- Yuan, X. Coherent Source Direction-Finding using a Sparsely-Distributed Acoustic Vector-Sensor Array. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2710–2715. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, Z.; He, Z. Information criterion-based source number estimation methods with comparison. Hsi-An Chiao Tung Ta Hsueh/J. Xi’an Jiaotong Univ. 2015, 49, 38–44. [Google Scholar]
- Ridder, F.D.; Pintelon, R.; Schoukens, J.; Gilikin, D.P. Modified AIC and MDL model selection criteria for short data records. IEEE Trans. Instrum. Meas. 2005, 54, 144–150. [Google Scholar] [CrossRef]
- Hill, E.R.; Xia, W.; Clarkson, M.J.; Desiardins, A.E. Identification and removal of laser-induced noise in photoacoustic imaging using singular value decomposition. Biomed. Opt. Express 2017, 8, 68–77. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Guo, J.; Fang, L. Improved singular value decomposition (TopSVD) for source number estimation of low SNR in blind source separation. IEEE Access 2017, 5, 26460–26465. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Salih, A.L.; Gaeid, K.S.; Ping, H.W.; Khalid, M. Fault Diagnosis of Induction Motor Using MCSA and FFT. Electr. Electron. Eng. 2011, 60, 39–48. [Google Scholar]
- Pan, M.C.; Tsao, W.C. Using appropriate IMFs for envelope analysis in multiple fault diagnosis of ball bearings. Int. J. Mech. Sci. 2013, 69, 114–124. [Google Scholar] [CrossRef]

















| Sequence Number | NSVR |
|---|---|
| 1 | 6.254 |
| 2 | 2.561 |
| 3 | 2.033 |
| 4 | 1.875 |
| 5 | 1.262 |
| 6 | 0.801 |
| Sequence Number | NSVR |
|---|---|
| 1 | 1.524 |
| 2 | 36.810 |
| 3 | 6.884 |
| 4 | 3.922 |
| 5 | 5.516 |
| 6 | 0.981 |
| Sequence Number | NSVR |
|---|---|
| 1 | 1.926 |
| 2 | 22.568 |
| 3 | 3.448 |
| 4 | 2.962 |
| 5 | 1.979 |
| 6 | 1.038 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, L.; Sun, H. Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery. Appl. Sci. 2018, 8, 1441. https://doi.org/10.3390/app8091441
Fang L, Sun H. Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery. Applied Sciences. 2018; 8(9):1441. https://doi.org/10.3390/app8091441
Chicago/Turabian StyleFang, Liang, and Hongchun Sun. 2018. "Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery" Applied Sciences 8, no. 9: 1441. https://doi.org/10.3390/app8091441
APA StyleFang, L., & Sun, H. (2018). Study on EEMD-Based KICA and Its Application in Fault-Feature Extraction of Rotating Machinery. Applied Sciences, 8(9), 1441. https://doi.org/10.3390/app8091441