A Mathematical Model of the Plane-Parallel Movement of an Asymmetric Machine-and-Tractor Aggregate
Abstract
:1. Introduction
2. Materials and Methods
- ○
- The surface of the field across which the particular harvesting aggregate moves is strictly horizontal, and therefore its inclination is neglected;
- ○
- The wheeled aggregating tractor is a solid body that has a longitudinal plane of symmetry passing through its center of mass;
- ○
- Fluctuations of the tractive resistance of the trailed windrower have no significant effect on the speed of the forward movement of this aggregate, which is then considered constant in first approximation;
- ○
- Interaction of the pneumatic tires of the aggregating tractor wheels and the supporting wheels of the trailed windrower with the surface of the soil (in the lateral directions) does not go beyond the limits of the well-known hypothesis of the “lateral drift” of tires;
- ○
- Because of the small values, the gyroscopic and stabilizing moments of the pneumatic tires of the tractor and windrower wheels are not considered;
- ○
- The slip angles of the pneumatic tires of the travelling wheels of the aggregating tractor, located on the same geometric axis, as well as the lateral forces acting on them, will be considered sufficiently small;
- ○
- The turning angles of the left-side and the right-side driven wheels of the aggregating tractor are considered small and equal, taking into account that the basic movement of this harvesting machine-and-tractor aggregate is close to rectilinear, when performing the technological process of cutting grain crops.
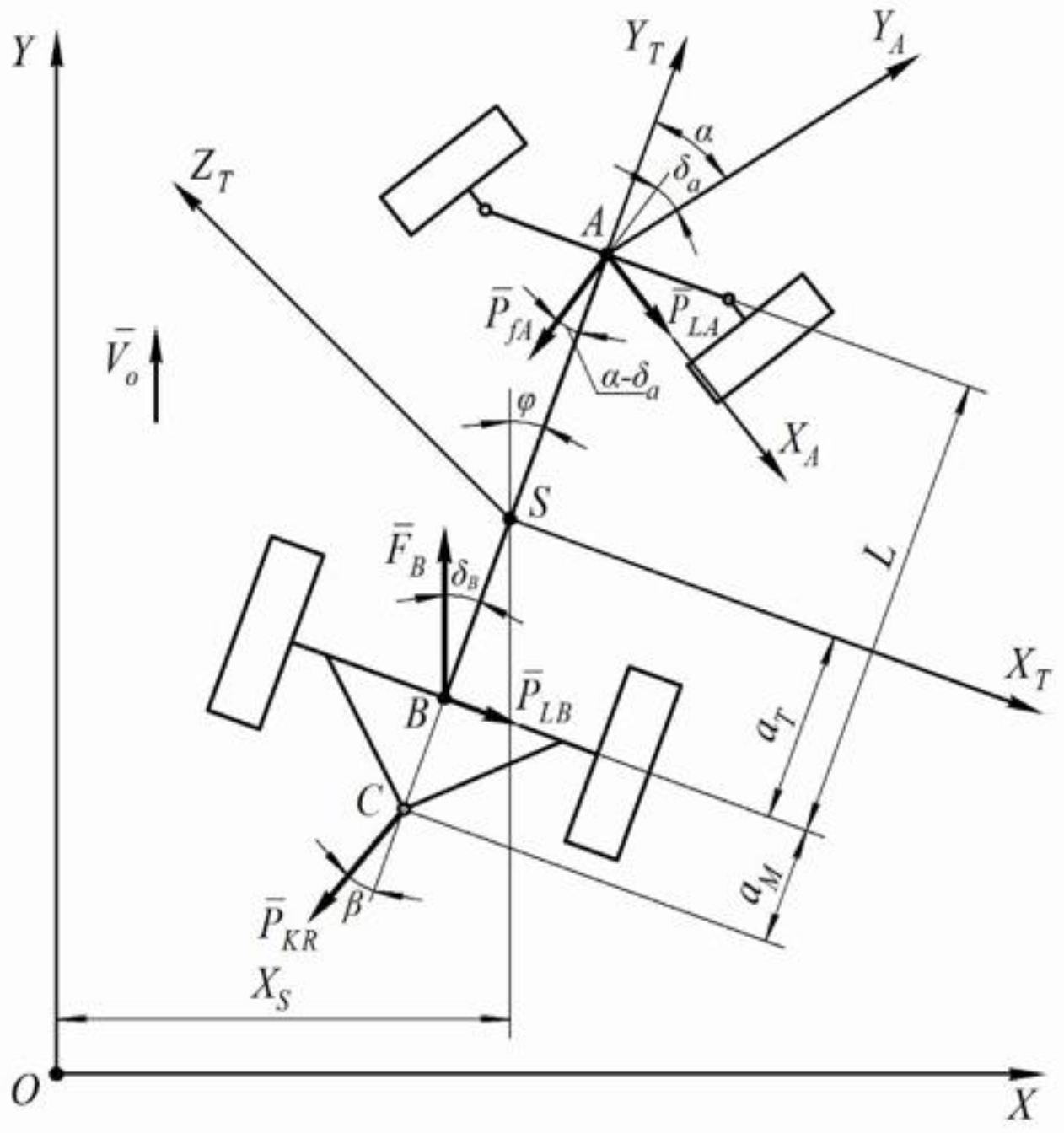
2.1. Mathematical Model of the Aggregating Wheeled Tractor
- (a)
- the driving force of the rear wheels summing up from the two driving wheels of the tractor is applied at point and forms a drift angle with the longitudinal axis of symmetry of the tractor;
- (b)
- the rolling resistance force of the front wheels of the tractor, which also sums up from the two wheels, is applied at the intersection point of their axis with the longitudinal axis (point ) and deviated from the direction of the movement of its propellers by the drift angle ;
- (c)
- lateral forces, respectively, from two wheels: and , applied at points and , respectively;
- (d)
- the traction resistance force of the windrower movement, applied at point and deviated from the longitudinal axis of the aggregating tractor, i.e., from axis , by angle .
2.2. Mathematical Model of the Trailed Windrower
- (a)
- the longitudinal and the transverse components of the resistance forces of the harvested stubble mass that are applied to the windrower at point ;
- (b)
- the rolling resistance force of the left-side wheel of the windrower applied at point and deviated from the plane of the wheel by the drift angle ;
- (c)
- the rolling resistance force of the two right-side wheels of the windrower (in the diagram they are represented as one equivalent wheel), which is applied at point and is deviated from the plane of the wheel by the drift angle ;
- (d)
- lateral forces and , applied respectively to the left-side and the right-side wheel of the windrower at points and .
3. Results and Discussion
3.1. Mathematical Model of the Entire Asymmetric Machine-and-Tractor Aggregate
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;;
- ;
- ;
3.2. Experimental Verification of the Adequacy of the Mathematical Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pascuzzi, S. A multibody approach applied to the study of driver injuries due to a narrow-track wheeled tractor rollover. J. Agric. Eng. 2015, 46, 105–114. [Google Scholar] [CrossRef]
- Pascuzzi, S.; Santoro, F. Exposure of farm workers to electromagnetic radiation from cellular network radio base stations situated on rural agricultural land. Int. J. Occup. Saf. Ergon. 2015, 21, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Cole, H.P.; Myers, M.L.; Westneat, S.C. Frequency and severity of injuries to operators during overturns of farm tractors. J. Agric. Saf. Health 2006, 12, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Hunter, A.G.M.; Owen, G.M. Tractor overturning accidents on slopes. J. Occup. Accid. 1983, 5, 195–210. [Google Scholar] [CrossRef]
- Bevly, D.M.; Gerdes, J.C.; Parkinson, B.W. A new yaw dynamic model for improved high speed control of a farm tractor. J. Dyn. Syst. Meas. Control 2002, 124, 659–667. [Google Scholar] [CrossRef]
- Deng, W.K.; Kang, X. Parametric Study on Vehicle-Trailer Dynamics for Stability Control (No. 2003-01-1321); SAE Technical Paper; SAE International: Troy, MI, USA, 2003. [Google Scholar]
- Hac, A.; Fulk, D.; Chen, H. Stability and control considerations of vehicle-trailer combination. SAE Int. J. Passeng. Cars Mech. Syst. 2008, 1, 925–937. [Google Scholar] [CrossRef]
- Wu, D.H. A theoretical study of the yaw/roll motions of a multiple steering articulated vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2001, 215, 1257–1265. [Google Scholar] [CrossRef]
- Bhatia, N.P.; Szegő, G.P. Stability Theory of Dynamical Systems; Springer: Heidelberg, Germany, 2002; ISBN 978-3-540-42748-3. [Google Scholar]
- Bulgakov, V.; Ivanovs, S.; Adamchuk, V. Estimated mathematical model of plane-parallel motion of trailed hemp harvesting aggregate. In Proceedings of the 14th International Scientific Conference: “Engineering for Rural Development”, Jelgava, Latvia, 20–22 May 2015; pp. 33–40. [Google Scholar]
- Bulgakov, V.; Ivanovs, S.; Adamchuk, V.; Nowak, J. Theoretical investigation of steering ability of movement of asymmetric swath header-and-tractor aggregate. In Proceedings of the 17th International Scientific Conference: “Engineering for Rural Development”, Jelgava, Latvia, 23–25 May 2018; pp. 301–308. [Google Scholar] [CrossRef]
- Bulgakov, V.; Ivanovs, S.; Adamchuk, V.; Nadykto, V. Theoretical investigation of turning ability of machine and tractor aggregate on basis of ploughing and intertilling wheeled tractor. In Proceedings of the 15th International Scientific Conference: “Engineering for Rural Development”, Jelgava, Latvia, 25–27 May 2016; pp. 1077–1084. [Google Scholar]
- Kang, X.; Deng, W. Vehicle-Trailer Handling Dynamics and Stability Control—An Engineering Review (No. 2007-01-0822); SAE Technical Paper; SAE International: Troy, MI, USA, 2007. [Google Scholar]
- Kyurchev, V.M. Mechanical and Technological Foundations of Aggregating Ploughing and Intertilling Tractors; Monograph, Institute for Agricultural Engineering and Electrification Press: Glevaha, Ukraine, 2015. [Google Scholar]
- Merkin, D. Introduction to the Stability Theory of Movement; Science: Moscow, Russia, 1976. [Google Scholar]
- Dreizler, R.M.; Ludde, C.S. Theoretical Mechanics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Rangavajhula, K.; Tsao, H.J. Effect of multi-axle steering on off-tracking and dynamic lateral response of articulated tractor-trailer combinations. Int. J. Heavy Veh. Syst. 2007, 14, 376–401. [Google Scholar] [CrossRef]
- Smith, M.J.; Wisten, M.B. A continuous day-to-day traffic assignment model and the existence of a continuous dynamic user equilibrium. Ann. Oper. Res. 1995, 60, 59–79. [Google Scholar] [CrossRef]
- Vasilenko, P. Introduction to Agricultural Mechanics; Agricultural Education: Kiev, Ukraine, 1996. [Google Scholar]
- Bulgakov, V.; Zaryshnyak, A.; Beloev, H.; Ivanovs, S. Investigation of amplitude-frequency response of disturbing and control impacts of asymmetric swath header machine-and-tractor aggregate. In Proceedings of the 17th International Scientific Conference: “Engineering for Rural Development”, Jelgava, Latvia, 23–25 May 2018; pp. 221–226. [Google Scholar] [CrossRef]
- Bulgakov, V.; Pascuzzi, S.; Ivanovs, S.; Kaletnik, G.; Yanovich, V. Angular oscillation model to predict the performance of a vibratory ball mill for the fine grinding of grain. Biosyst. Eng. 2018, 171, 155–164. [Google Scholar] [CrossRef]
- Bulgakov, V.; Grinik, I.; Lezhekin, A. Dynamics of the Grain Harvesting Aggregates; Agrarian Science: Kiev, Ukraine, 2010. [Google Scholar]
- Gyachev, L. Stability of the Movement of Agricultural Machines and Aggregates; Mechanical Engineering: Moscow, Russia, 1981. [Google Scholar]
- Nadykto, V. Analysis of the Turning Ability of the Machine and Tractor Aggregates on the Basis of Modular Means of Energy. Sci. Bull. Tavria Univ. Agric. Melitop. 2005, 29, 28–34. [Google Scholar]
- Gusjkov, V. Tractors: Theory; Mechanical Engineering: Moskow, Russia, 1988. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Springer: New York, NY, USA, 2003; ISBN 0-387-00177-8. [Google Scholar]
- Piskunov, N. Differential and Integral Calculation; Mechanical Engineering: Moskow, Russia, 1970; Volume 2. [Google Scholar]
- Pascuzzi, S.; Anifantis, A.S.; Blanco, I.; Scarascia Mugnozza, G. Electrolyzer performance analysis of an integrated hydrogen power system for greenhouse heating a case study. Sustainability 2016, 8, 629. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulgakov, V.; Pascuzzi, S.; Nadykto, V.; Ivanovs, S. A Mathematical Model of the Plane-Parallel Movement of an Asymmetric Machine-and-Tractor Aggregate. Agriculture 2018, 8, 151. https://doi.org/10.3390/agriculture8100151
Bulgakov V, Pascuzzi S, Nadykto V, Ivanovs S. A Mathematical Model of the Plane-Parallel Movement of an Asymmetric Machine-and-Tractor Aggregate. Agriculture. 2018; 8(10):151. https://doi.org/10.3390/agriculture8100151
Chicago/Turabian StyleBulgakov, Volodymyr, Simone Pascuzzi, Volodymyr Nadykto, and Semjons Ivanovs. 2018. "A Mathematical Model of the Plane-Parallel Movement of an Asymmetric Machine-and-Tractor Aggregate" Agriculture 8, no. 10: 151. https://doi.org/10.3390/agriculture8100151
APA StyleBulgakov, V., Pascuzzi, S., Nadykto, V., & Ivanovs, S. (2018). A Mathematical Model of the Plane-Parallel Movement of an Asymmetric Machine-and-Tractor Aggregate. Agriculture, 8(10), 151. https://doi.org/10.3390/agriculture8100151






