Tidal Datums with Spatially Varying Uncertainty in North-East Gulf of Mexico for VDatum Application
Abstract
:1. Introduction
- (1)
- First use the bathymetric and coastline data to develop a grid to be used by the hydrodynamic model.
- (2)
- Next calibrate a hydrodynamic model to best simulate the observed tidal datum characteristics for the region.
- (3)
- Then correct the model-data errors using a spatial interpolation technique.
- (4)
- Finally provide the corrected modeled datums (i.e., datum products) on a structured grid of points to be used by the VDatum software.
2. Method
3. Data and Grid Development
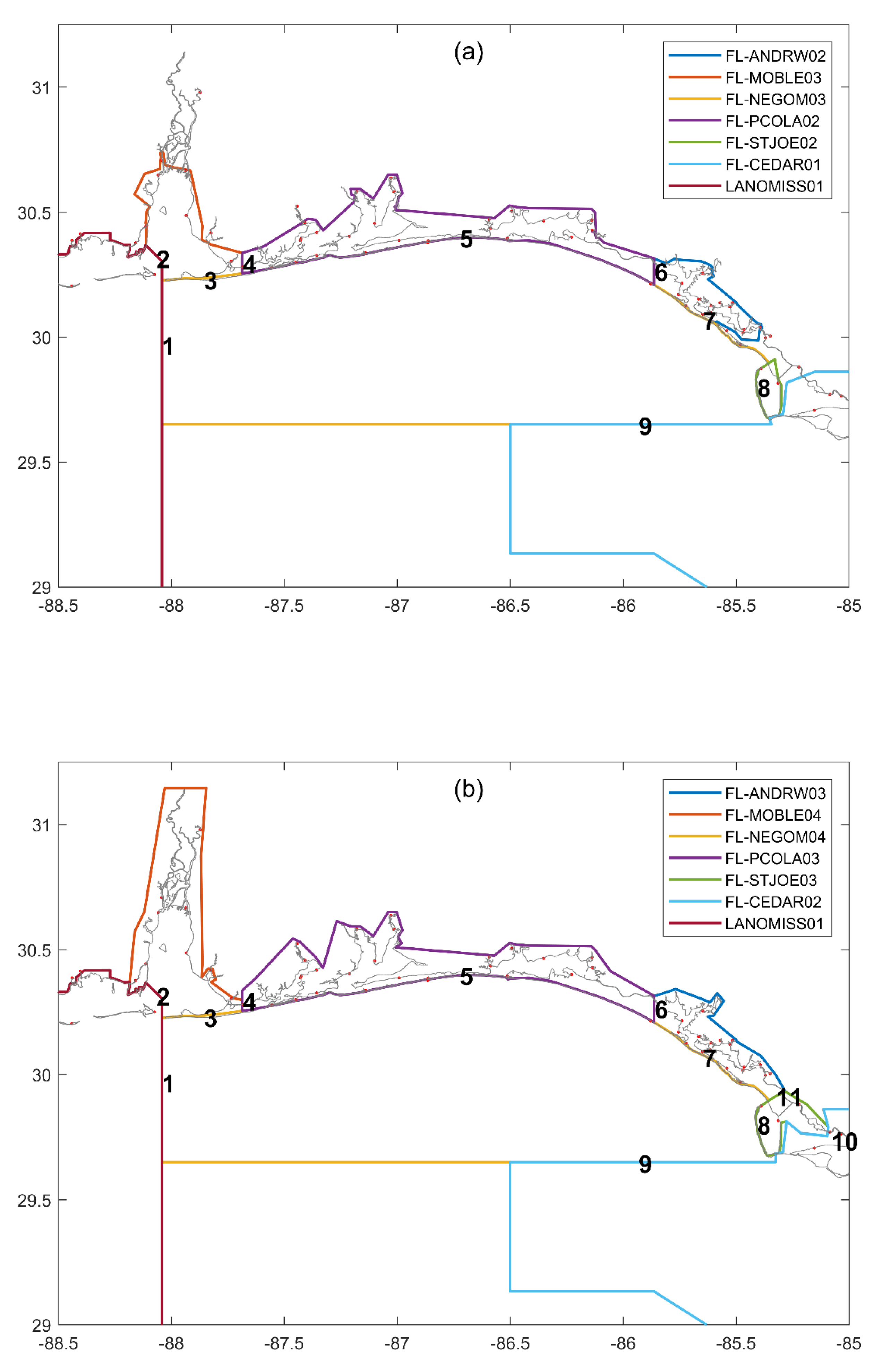
3.1. Study Area and Tidal Datum Data
3.2. Shoreline and Bathymetry Data
- (1)
- NOAA’s NOS bathymetry survey and Electronic Navigational Chars (ENC) data;
- (2)
- National Centers for Environmental Information’s (NCEI) Digital Elevation Models (DEMs);
- (3)
- The U.S. Army Corps of Engineers (USACE) survey data;
- (4)
- USGS DEMs.
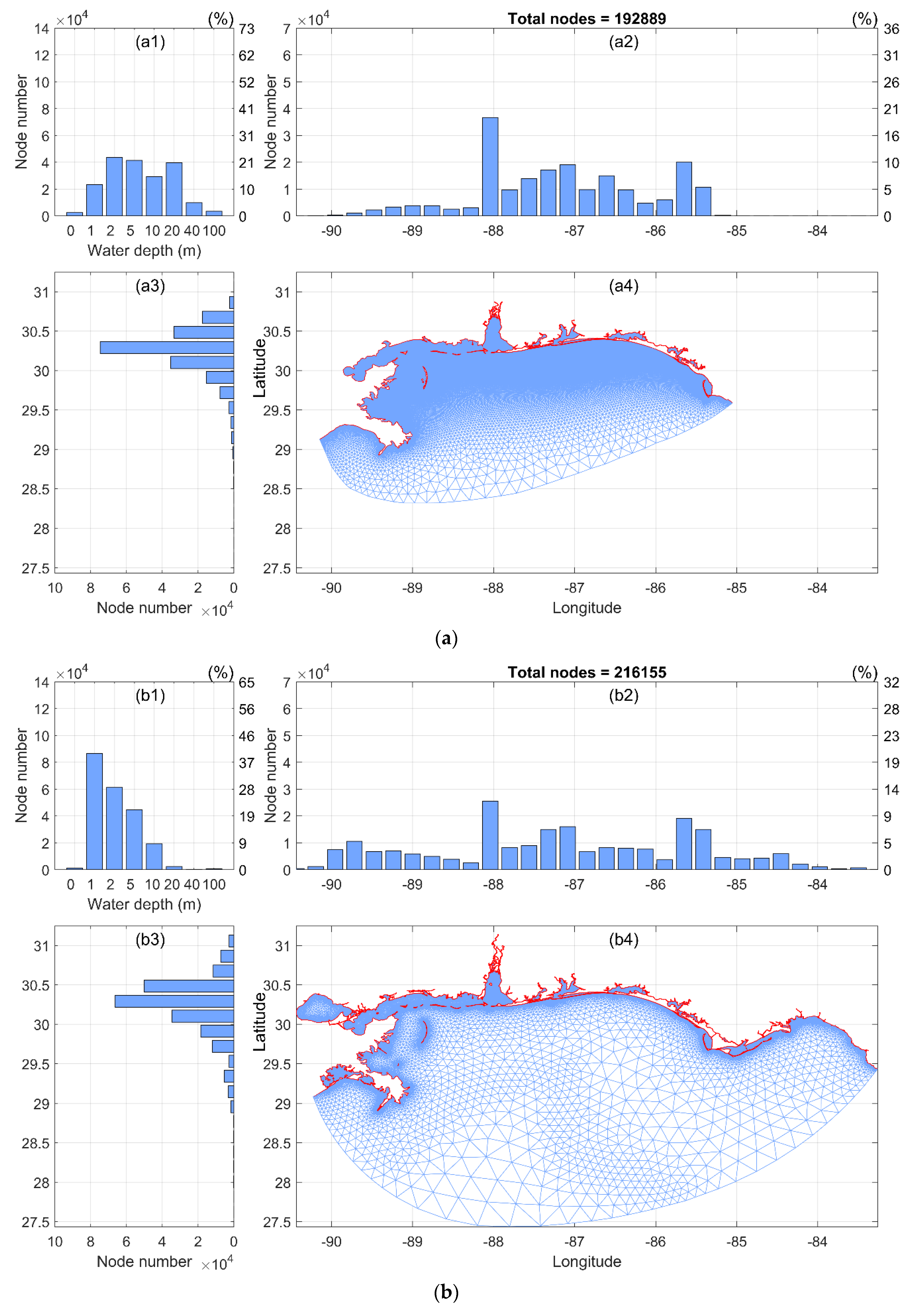
3.3. Grid Development
3.4. Model Setup
4. Results and Discussion
4.1. Validation and Error Analyses
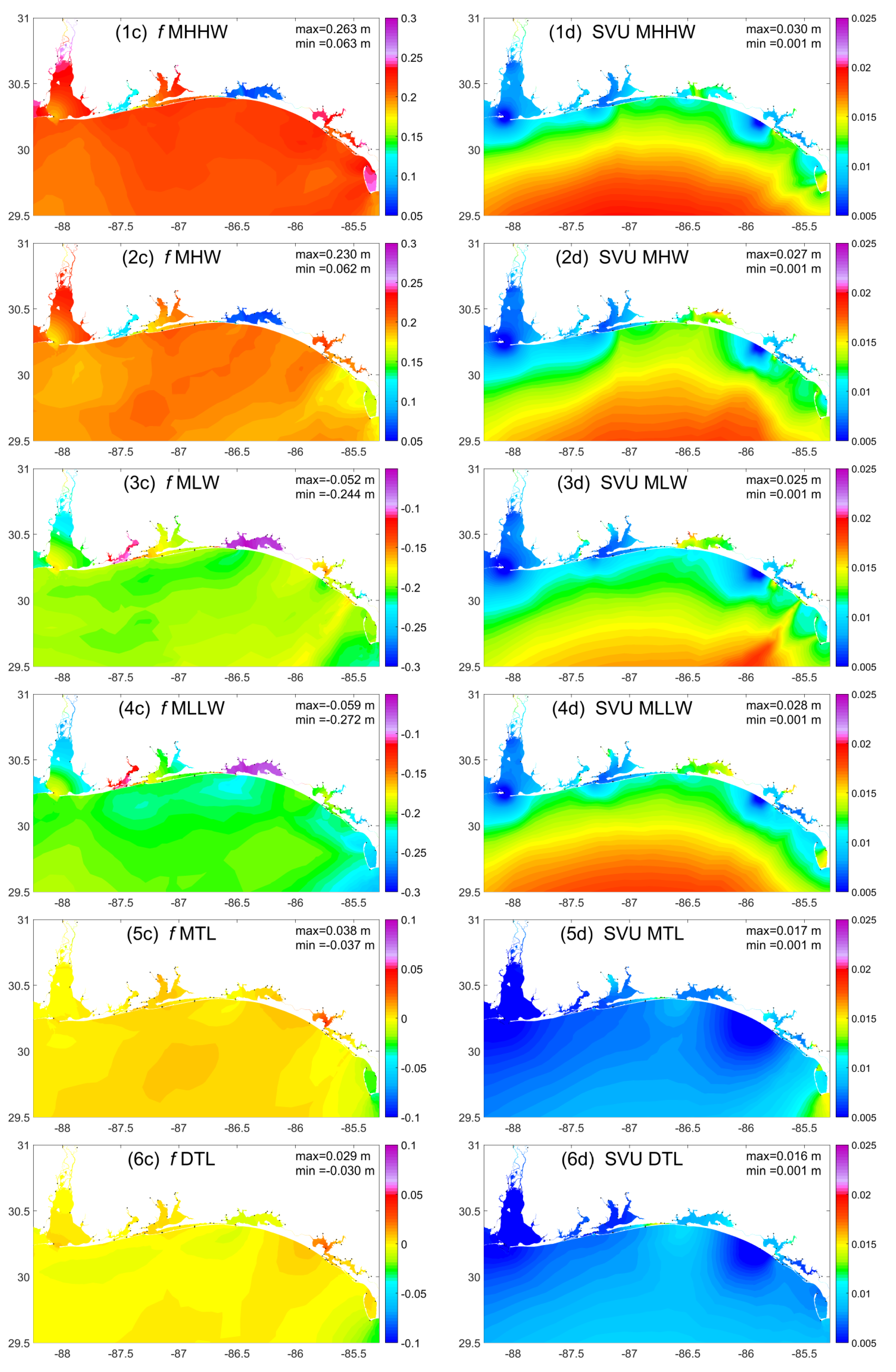
4.2. Datum Products and Spatially Varying Uncertainty
4.3. Lessons Learned
4.3.1. Sensitivity of Modeled Datums to Breakwaters
4.3.2. Sensitivity of Modeled Datums to Offshore Boundary Conditions
4.3.3. Sensitivity of Modeled Datums to Water Depth
4.3.4. Sensitivity of Spatially Varying Uncertainty to Model Error
4.3.5. Model Error at Intracoastal Waterway Station 8761678
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parker, B. The integration of bathymetry, topography, and shoreline and the vertical datum transformations behind it. Int. Hydrogr. Rev. 2002, 3, 35–47. [Google Scholar]
- Myers, E.P.; Wong, A.; Hess, K.; White, S.; Spargo, E.; Feyen, J.; Yang, Z.; Richardson, P.; Auer, C.; Sellars, J.; et al. Development of a national VDatum, and its application to sea level rise in North Carolina. In Proceedings of the U. S. Hydrographic Conference, San Diego, CA, USA, 29–31 March 2005. [Google Scholar]
- USGS. National Elevation Dataset (NED)—The Long Term Archive. Available online: https://lta.cr.usgs.gov/NED (accessed on 9 October 2018).
- Umbach, M.J. Hyrographic Manual, 4th ed.; NOAA Natioinal Ocean Service: Rockville, Maryland, 1976. [Google Scholar]
- NOAA. NOAA/NOS’ VDatum 3.9: Vertical Datums Transformation. Available online: https://vdatum.noaa.gov/ (accessed on 9 October 2018).
- University Colloge London. Vertical Offshore Reference Frames. Available online: https://www.ucl.ac.uk/vorf (accessed on 9 October 2018).
- SHOM. Data.Shom.Fr. Available online: https://data.shom.fr/ (accessed on 9 October 2018).
- Keysers, J.H.; Quadros, N.D.; Collier, P.A. Vertical Datum Transformations across the Littoral Zone; Department of Climate Change and Energy Efficiency: Canberra, Australia, 2013; p. 110. [Google Scholar]
- NOS. Standard Procedures to Develop and Support NOAA’s Vertical Datum Transformation Tool, VDatum; Version 2010.08.03; National Ocean Service: Silver Spring, MD, USA, 2010. [Google Scholar]
- Milbert, D.G.; Hess, K.W. Combination of topography and bathymetry through application of calibrated vertical datum transformations in the Tampa bay region. In Proceedings of the Second Biennial Coastal GeoTools Conference, Charleston, SC, USA, 8–11 January 2001. [Google Scholar]
- CO-OPS. Computational Techniques for Tidal Datum Handbook; NOAA Special Publication NOS-OPS 2: Silver Spring, MD, USA, 2003; p. 98. [Google Scholar]
- Dhingra, E.A.; Hess, K.W.; White, S.A. VDatum for the Northeast Gulf of Mexico from Mobile Bay, Alabama, to Cap San Blas, Florida: Tidal Datum Modeling and Population of the Marine Grids; NOAA Technical Memorandum NOS CS 14; Department of Commerce, National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2008; p. 64. [Google Scholar]
- Yang, Z.; Myers, E.P.; White, S.A. VDatum for Eastern Louisiana and Mississippi Coastal Waters: Tidal Datums, Marine Grids, and Sea Surface Topography; NOAA Technical Memorandum NOS CS 19; National Oceanic and Atmospheric Administration, National Ocean Service, Office of Coast Survey, Coast Survey Development Laboratory: Silver Spring, MD, USA, 2010; p. 56. [Google Scholar]
- Xu, J.; Myers, E.P.; Jeong, I.; White, S.A. VDatum for the Coastal Waters of Texas and Western Louisiana: Tidal Datums and Topography of the Sea Surface; NOAA Technical Memorandum NOS CS 22; National Oceanic and Atmospheric Administration, National Ocean Service, Office of Coast Survey, Coast Survey Development Laboratory: Silver Spring, MD, USA, 2010. [Google Scholar]
- Hess, K.W. Spatial interpolation of tidal data in irregularly-shaped coastal regions by numerical solution of Laplace’s equation. Estuar. Coast. Shelf Sci. 2002, 54, 175–192. [Google Scholar] [CrossRef]
- Hess, K.W.; Schmalz, R.A.; Zervas, C.; Collier, W.C. Tidal Constituent and Residual Interpolation (TCARI): A New Method for the Tidal Correction of Bathymetric Data; NOAA Technical Report NOS CS 4; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1999; p. 99. [Google Scholar]
- Hess, K.W.; Spargo, E.A.; Wong, A.M.; White, S.A.; Gill, S.K. VDatum for Central Coastal North Carolina: Tidal Datums, Marine Grids, and Sea Surface Topography; Coast Survey Development Laboratory, National Ocean Services: Silver Spring, MD, USA, 2005. [Google Scholar]
- NOAA. NOAA/NOS’ VDatum: Estimation of Vertical Uncertainties in VDatum. Available online: https://vdatum.noaa.gov/docs/est_uncertainties.html (accessed on 9 October 2018).
- Shi, L.; Myers, E.P. Statistical interpolation of tidal datums and computation of its associated spatially varying uncertainty. J. Mar. Sci. Eng. 2016, 4, 64. [Google Scholar] [CrossRef]
- Fearnley, S.M.; Miner, M.D.; Kulp, M.; Bohling, C.; Penland, S. Hurricane impact and recovery shoreline change analysis of the Chandeleur Islands, Louisiana, USA: 1855 to 2005. Geo-Mar. Lett. 2009, 29, 455–466. [Google Scholar] [CrossRef]
- Gill, S.K.; Schultz, J.R. Tidal Datums and Their Applications; NOAA Special Publication NOS CO-OPS 1; National Oceanic and Atmospheric Administration, Center for Operational Oceanographic Products and Services: Silver Spring, MD, USA, 2001; p. 111. [Google Scholar]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. Adcirc: An Advanced Three-Dimensional Circulation Model of Shelves, Coasts, and Estuaries, Report 1: Theory and Methodology of Adcirc-2ddi and Adcirc-3dl.; Technical Report DRP-92-6; U.S. Department of the Army: Arlington County, VA, USA, 1992. [Google Scholar]
- Luettich, R.A.; Westerink, J.J. Formulation and Numerical Implementation of the 2D/3D ADCIRC Finite Element Model Version 44.XX. 2004, p. 74. Available online: http://www.unc.edu/ims/adcirc/adcirc_theory_2004_12_08.pdf (accessed on 8 October 2018).
- Mukai, A.Y.; Westerink, J.J.; Luettich R.A., Jr.; Mark, D. Eastcoast 2001: A Tidal Constituent Database for the Western North Atlantic, Gulf of Mexico and Caribbean Sea; Technical Report, ERDC/CHL TR-02-24; Coastal and Hydraulics Laboratory, US Army Engineer Research and Development Center: Vicksburg, MI, USA, 2002; p. 201. [Google Scholar]
- Luettich, R.A.J.; Westerink, J.J. Continental Shelf Scale Convergence Studies with a Barotropic Tidal Model; American Geophysical Union Press: Washington, DC, USA, 1995; Volume 48, pp. 349–371. [Google Scholar]
- Spargo, E.; Westerink, J.J.; Luettich, R.A.; Mark, D. Developing a tidal constituent database for the eastern north pacific ocean. In Estuarine and Coastal Modeling VIII, Proceedings of the Eighth International Conference, Monterey, CA, USA, 3–5 November 2003; American Society of Civil Engineers: Reston, VA, USA, 2004; pp. 217–235. [Google Scholar]
- Hess, K.W.; White, S.A. VDatum for Puget Sound: Generation of the Grid and Population with Tidal Datums and Sea Surface Topography; NOAA Technical Memorandum NOS CS 4; National Oceanic and Atmospheric Administration, Coastal Survey Development Laboratory: Silver Spring, MD, USA, 2004; p. 27. [Google Scholar]
- Michalski, M. Tide station, Tidal Datum and Geodetic Datum Assessment for VDatum Project; National Oceanic and Atmospheric Administration, Center for Operational Oceanographic Products and Services: Silver Spring, MD, USA, 2011. [Google Scholar]
- Bodnar, A.N. Estimating Accuracies of Tidal Datums from Short Term Observations; Technical Report NOS CO-OPS 0074; National Oceanic and Atmospheric Administration, Center for Operational Oceanographic Products and Services: Silver Spring, MD, USA, 1981; p. 32. [Google Scholar]
- National Geodetic Survey. National Geodetic Survey—NOAA Shoreline Data Explorer. Available online: https://www.ngs.noaa.gov/CUSP/ (accessed on 9 October 2018).
- National Geodetic Survey. National Geodetic Survey Shoreline Products. Available online: https://geodesy.noaa.gov/RSD/shoredata/NGS_Shoreline_Products.htm (accessed on 9 October 2018).
- Taylor, L.A.; Eakins, B.W.; Carignan, K.S.; Warneken, R.R.; Sazonova, T.S.; Schoollcraft, D.C.; Sharman, G.F. Digital Elevation Model of Biloxi, Mississippi, 2008b: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-9; National Oceanic and Atmospheric Administration, National Geophysical Data Center: Boulder, CO, USA, 2008. [Google Scholar]
- Taylor, L.A.; Eakins, B.W.; Carignan, K.S.; Warneken, R.R.; Sazonova, T.; Schoollcraft, D.C.; Sharman, G.F. Digital Elevation Model of Panama City, Florida, 2008: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-8; National Oceanic and Atmospheric Administration, National Geophysical Data Center: Boulder, CO, USA, 2008; p. 27. [Google Scholar]
- Love, M.R.; Amante, C.J.; Taylor, L.A.; Eakins, B.W. Digital Elevation Models of New Orleans, Louisiana: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-49; National Oceanic and Atmospheric Administration, National Geophysical Data Center: Boulder, CO, USA, 2011; p. 46. [Google Scholar]
- Love, M.R.; Caldwell, R.J.; Carignan, K.S.; Eakins, B.W.; Taylor, L.A. Digital Elevation Models of Southern Louisiana: Procedures, Data Sources and Analysis; National Oceanic and Atmospheric Administration, National Geophysical Data Center: Boulder, CO, USA, 2010; p. 22. [Google Scholar]
- Love, M.R.; Amante, C.J.; Carignan, K.S.; Eakins, B.W.; Taylor, L.A. Digital Elevation Models of the Northern Gulf of Coast: Procedures, Data Sources and Analysis; National Oceanic and Atmospheric Administration, National Geophysical Data Center: Boulder, CO, USA, 2010. [Google Scholar]
- DeWitt, N.C.; Stalk, C.A.; Smith, C.G.; Locker, S.D.; Fredericks, J.J.; McCloskey, T.A.; Wheaton, C. Single Beam Bathymetry Data Collected in 2015 from Grand Bay, Mississippi/Alabama; United States Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- The Howard, T. Odum Florida Springs Institute. Wakulla Springs Baseline Ecosystem Assessment; Florida Springs Institute: High Springs, FL, USA, 2016; p. 101. [Google Scholar]
- AQUAVEO. Aquaveo: Water Resources Software and Engineering Consulting Services for Modeling Groundwater, Surface-Water, and Watershed Hydraulics & Hydrology. Available online: https://www.aquaveo.com/ (accessed on 9 October 2018).
- Tang, L.; Myers, E.P.; Shi, L.; Hess, K.; Carisio, A.; Michalski, M.; White, S.A.; Hoang, C. VDatum with Spatially Varying Uncertainty in the Northeast Gulf of Mexico from Mobile Bay, Alabama, to Cape San Blas, Florida; NOAA Technical Report NOS CS; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2018; p. 79. [Google Scholar]
- Szpilka, C.; Dresback, K.; Kolar, R.; Feyen, J.; Wang, J. Improvements for the western north atlantic, caribbean and gulf of mexico adcirc tidal database (EC2015). J. Mar. Sci. Eng. 2016. [Google Scholar] [CrossRef]
- Hess, K.W. Revised VDatum for the northeast gulf of Mexico. Unpublished work. 2012; 7. [Google Scholar]

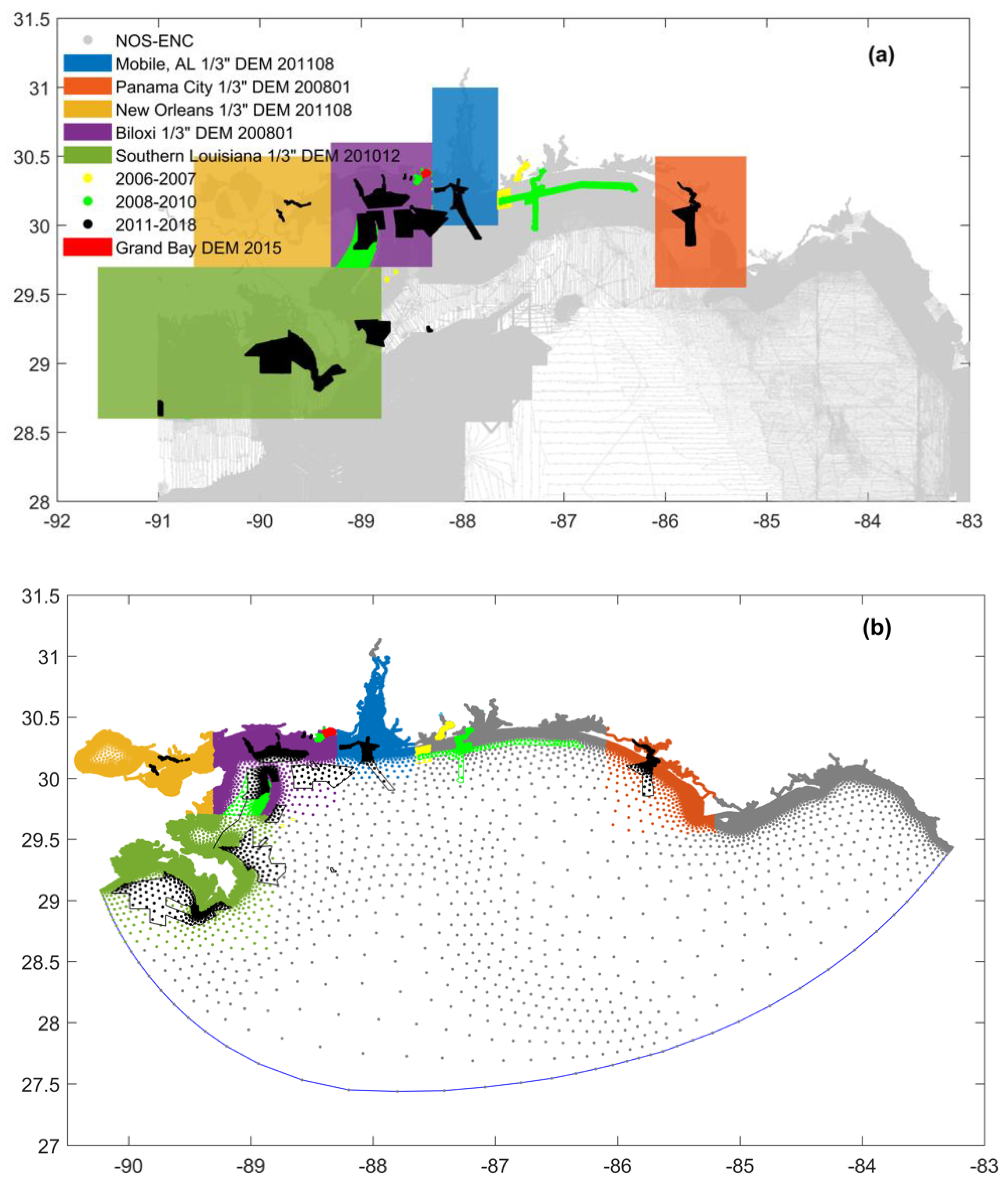











| Data Sources | Year | Datum Vertical | Horizontal |
|---|---|---|---|
| NOS Bathymetry Survey | 1872–2016 | MLLW/MLW | NAD83 |
| ENC | 2005 | MLLW | NAD83 |
| NCEI Mobile Bay 1/3″ DEM | 2011 | MHW | NAD83 |
| NCEI New Orleans 1/3″ DEM | 2011 | MHW | NAD83 |
| NCEI Southern Louisiana 1/3″ DEM | 2010 | MHW | NAD83 |
| NCEI Biloxi 1/3″ DEM | 2008 | MHW | WGS84 |
| NCEI Panama City 1/3″ DEM | 2008 | MHW | WGS84 |
| USGS Grand Bay 10 m DEM | 2015 | MLLW | NAD83 |
| NCEI Northern Gulf 1″ DEM | MHW | NAD83 | |
| USACE Escambia River Survey | 2015 | MLLW | FL State Plane |
| 1 Aucilla River Survey | 2014 | NAVD88 | NAD83 903 North |
| 1 Econfina River Survey | 2014 | NAVD88 | NAD83 903 North |
| 2 Wakulla River Segment Survey | 2015 | Unknown | WGS84 |
| Mesh Properties | 2008 | New Mesh | Increase in % |
|---|---|---|---|
| Shoreline length (km) | 3979 | 7482 | 88% |
| Area (km2) | 79,474 | 137,751 | 73% |
| Element number | 367,019 | 374,318 | 2% |
| Node number | 192,889 | 216,155 | 12% |
| Node number w/depth >20 m (percentage to total nodes) | 40,545 (21%) | 1777 (0.8%) | −96% |
| Node number w/depth 10–20 m | 28,312 | 9721 | −66% |
| Node number w/depth <10 m (percentage to total nodes) | 124,091 (64%) | 205,095 (95%) | 65% |
| Tide Stations | Error | MHHW (m) | MHW (m) | MLW (m) | MLLW (m) | Four Datums (m) |
|---|---|---|---|---|---|---|
| 83 stations in VDatum region | avg. error | 0.010 6.0% | 0.014 9.3% | 0.013 8.9% | 0.013 7.2% | 0.012 7.9% |
| RMSE | 0.013 | 0.017 | 0.017 | 0.016 | 0.016 | |
| 99 stations outside | avg. error | 0.028 14.0% | 0.020 12.6% | 0.020 12.8% | 0.032 14.2% | 0.025 13.4% |
| RMSE | 0.035 | 0.029 | 0.025 | 0.038 | 0.032 | |
| All 182 tide stations | avg. error | 0.020 10.4% | 0.017 11.1% | 0.017 11.0% | 0.023 11.0% | 0.019 10.9% |
| RMSE | 0.028 | 0.024 | 0.022 | 0.030 | 0.026 |
| REGION | No. of Tide Stations | MHHW | MHW | DTL | MTL | MLW | MLLW |
|---|---|---|---|---|---|---|---|
| FL_andrw03 | 26 | 0.61 | 0.67 | 0.46 | 0.69 | 0.67 | 0.66 |
| FL_moble04 | 7 | 0.60 | 0.43 | 0.31 | 0.39 | 0.83 | 0.61 |
| FL_negom04 | 4 | 0.42 | 0.57 | 0.36 | 0.5 | 0.75 | 0.65 |
| FL_pcola03 | 43 | 0.65 | 0.65 | 0.44 | 0.55 | 0.68 | 0.62 |
| FL_stjoe03 | 3 | 0.76 | 0.39 | 0.07 | 0.83 | 0.59 | 0.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Myers, E.; Shi, L.; Hess, K.; Carisio, A.; Michalski, M.; White, S.; Hoang, C. Tidal Datums with Spatially Varying Uncertainty in North-East Gulf of Mexico for VDatum Application. J. Mar. Sci. Eng. 2018, 6, 114. https://doi.org/10.3390/jmse6040114
Tang L, Myers E, Shi L, Hess K, Carisio A, Michalski M, White S, Hoang C. Tidal Datums with Spatially Varying Uncertainty in North-East Gulf of Mexico for VDatum Application. Journal of Marine Science and Engineering. 2018; 6(4):114. https://doi.org/10.3390/jmse6040114
Chicago/Turabian StyleTang, Liujuan, Edward Myers, Lei Shi, Kurt Hess, Alison Carisio, Michael Michalski, Stephen White, and Cuong Hoang. 2018. "Tidal Datums with Spatially Varying Uncertainty in North-East Gulf of Mexico for VDatum Application" Journal of Marine Science and Engineering 6, no. 4: 114. https://doi.org/10.3390/jmse6040114
APA StyleTang, L., Myers, E., Shi, L., Hess, K., Carisio, A., Michalski, M., White, S., & Hoang, C. (2018). Tidal Datums with Spatially Varying Uncertainty in North-East Gulf of Mexico for VDatum Application. Journal of Marine Science and Engineering, 6(4), 114. https://doi.org/10.3390/jmse6040114




