A DC-DC Converter Efficiency Model for System Level Analysis in Ultra Low Power Applications
Abstract
:1. Introduction
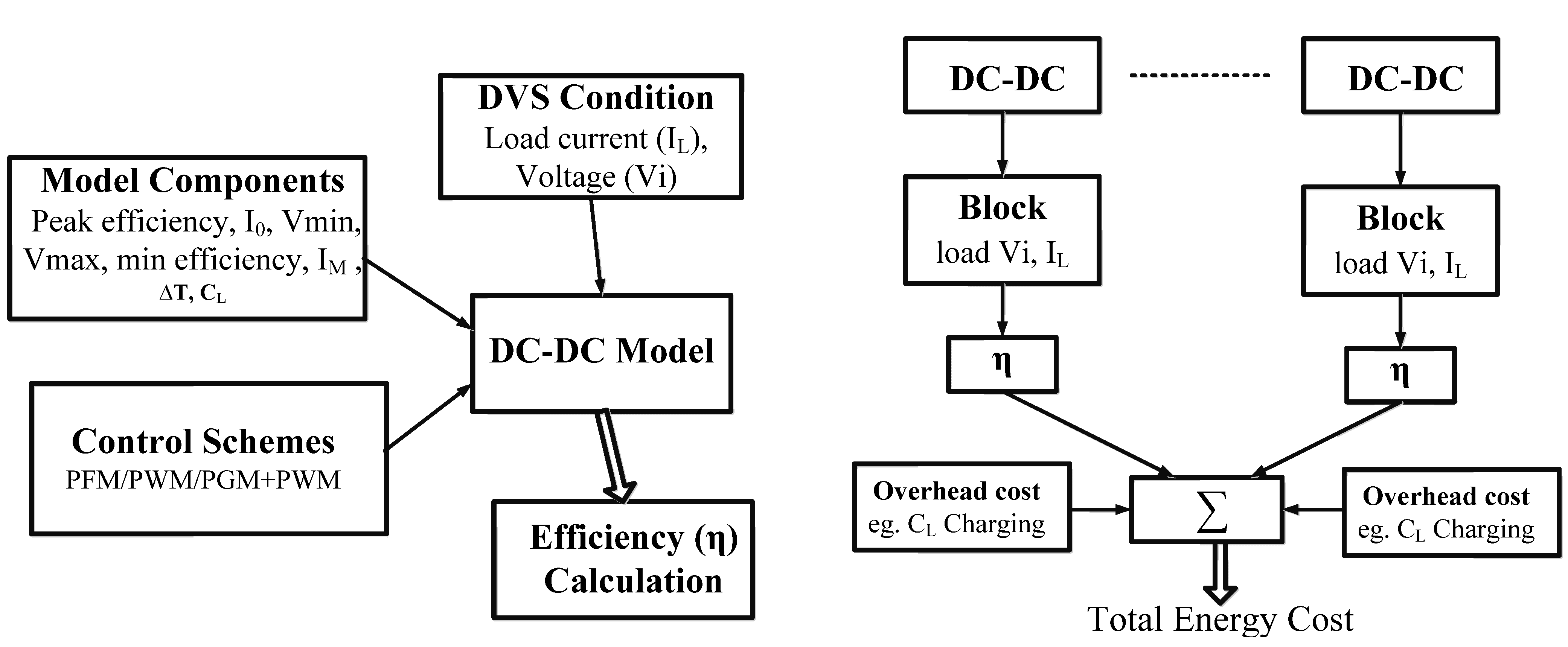
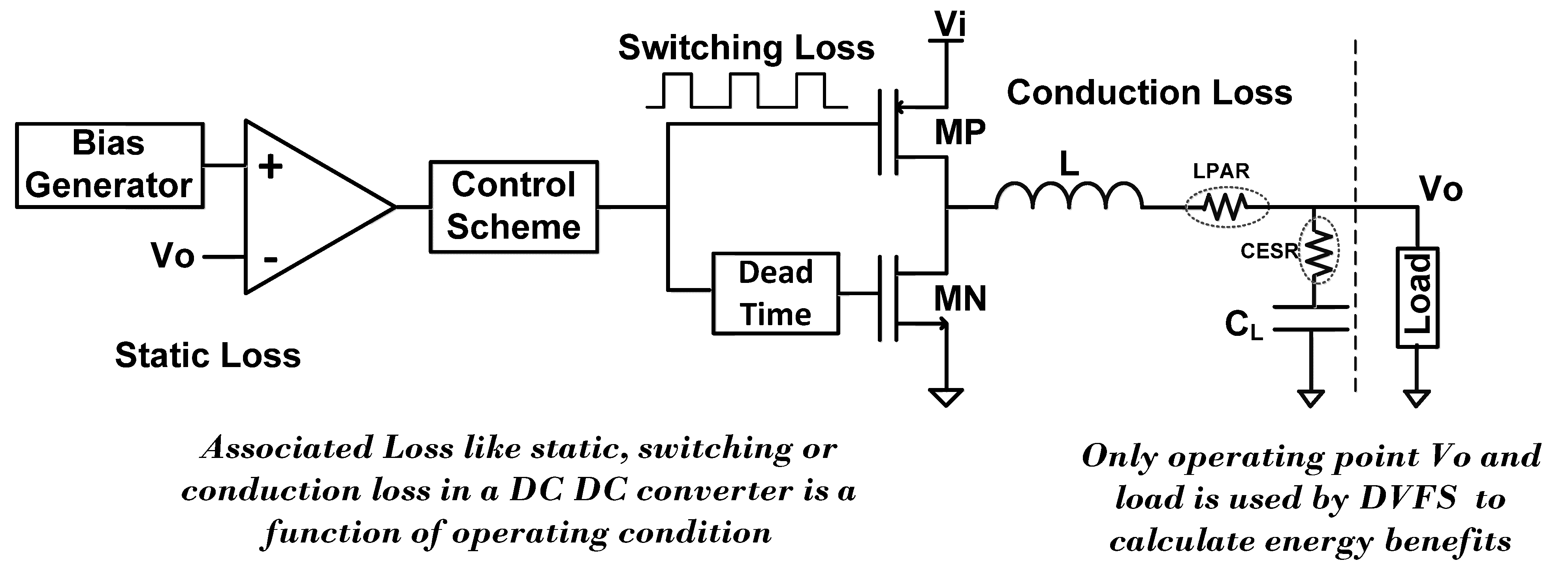
2. DC-DC Converter Model
2.1. DC-DC Efficiency with Load Current
2.1.1. Model for PWM Control Scheme
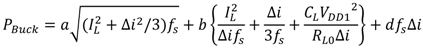
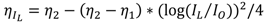
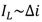
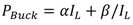
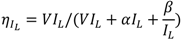
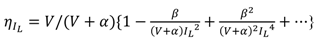
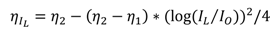
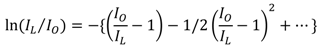
 and converting natural logarithm into logarithm of base 10 we get:
and converting natural logarithm into logarithm of base 10 we get:
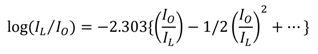
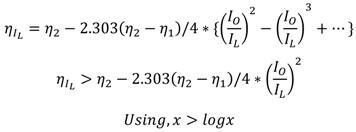
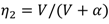
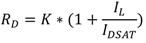
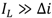
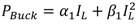
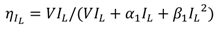
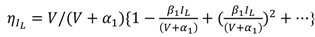
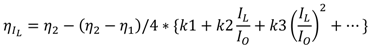
2.1.2. Model for PFM Control Scheme
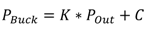
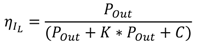
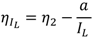
2.3. Verification of the Model


2.4. Efficiency with Output Voltage
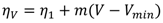
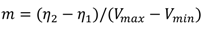 . This approximate linear behavior is reported in both [3] and [4]. Plugging Equation (2) for PWM or Equation (14) for PFM and using Equation (15) lets us write the combined voltage and load efficiency as:
. This approximate linear behavior is reported in both [3] and [4]. Plugging Equation (2) for PWM or Equation (14) for PFM and using Equation (15) lets us write the combined voltage and load efficiency as:
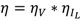
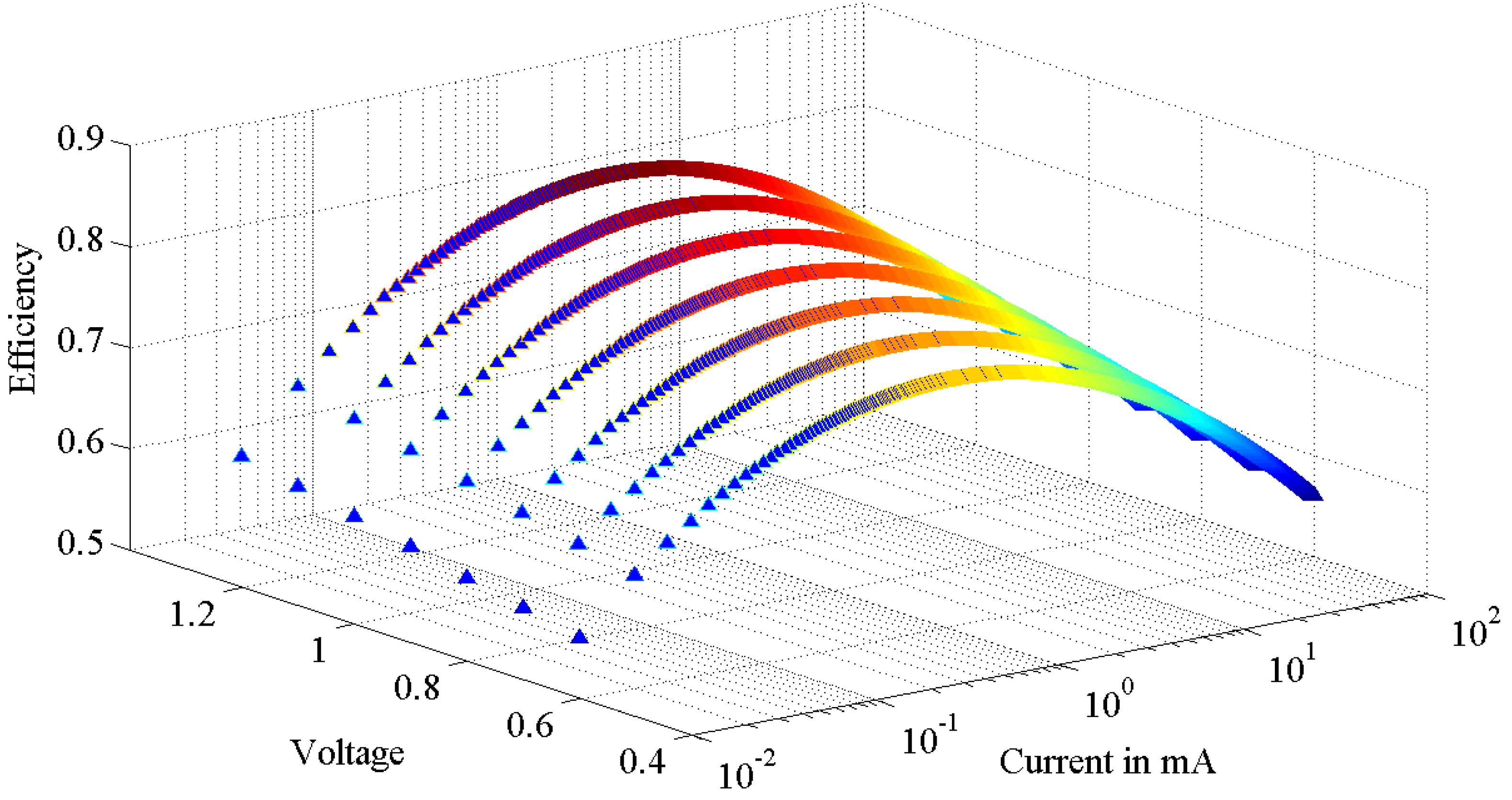
2.5. Settling Time
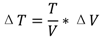
2.6. Supply Rail Switching Energy
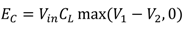
3. Evaluation of DVS Techniques Using the Proposed Model
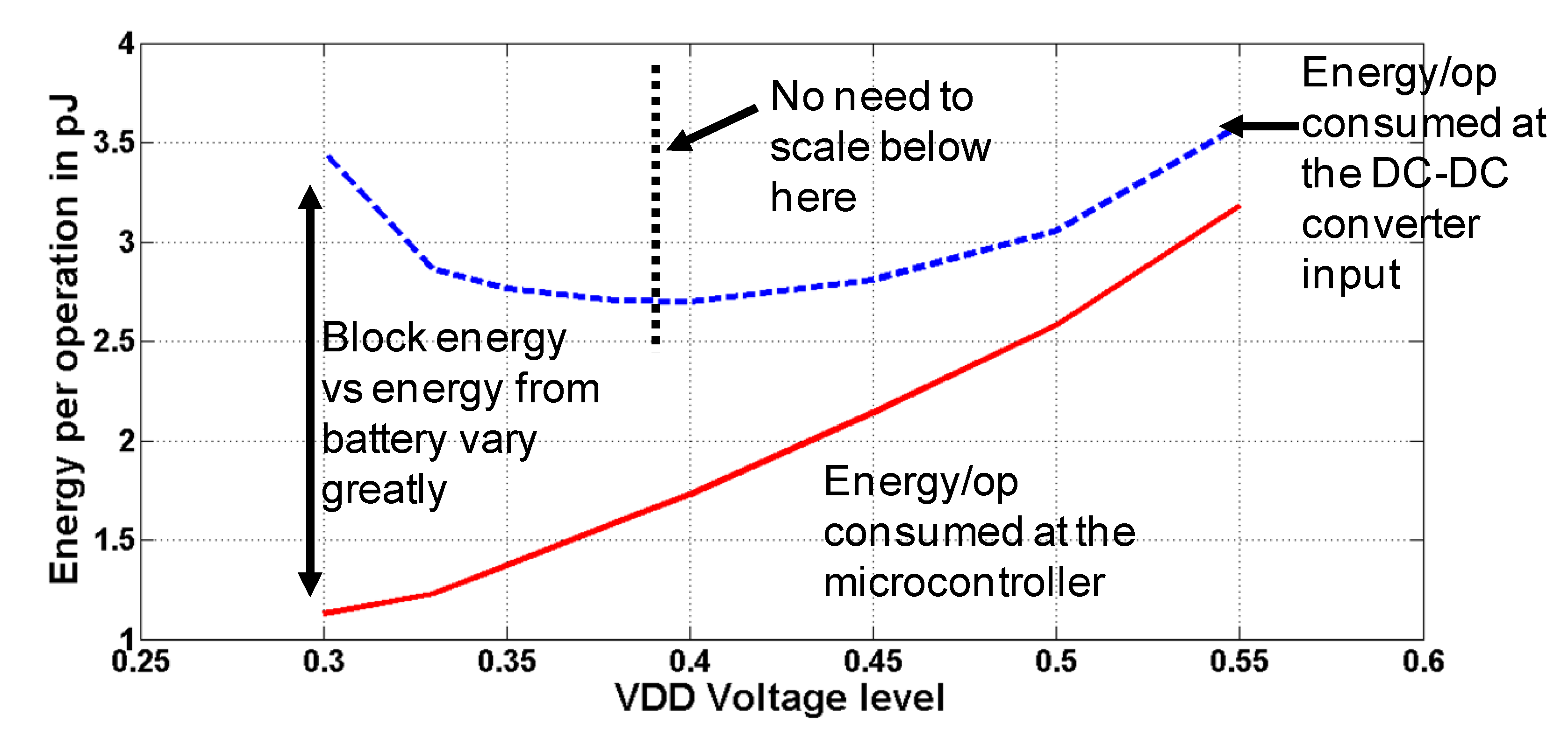
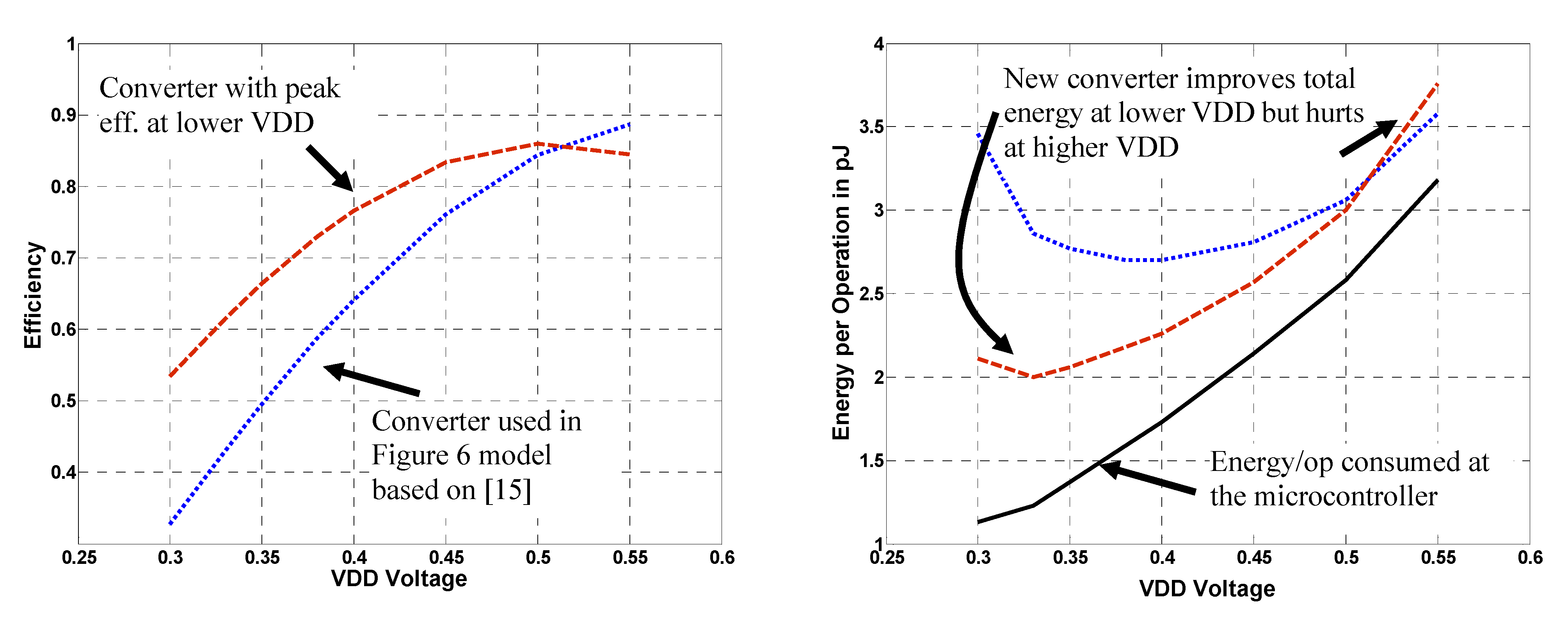
3.1. Framework for Energy Calculation in DVFS
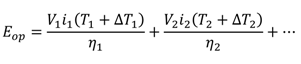
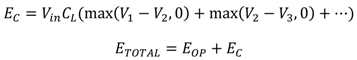
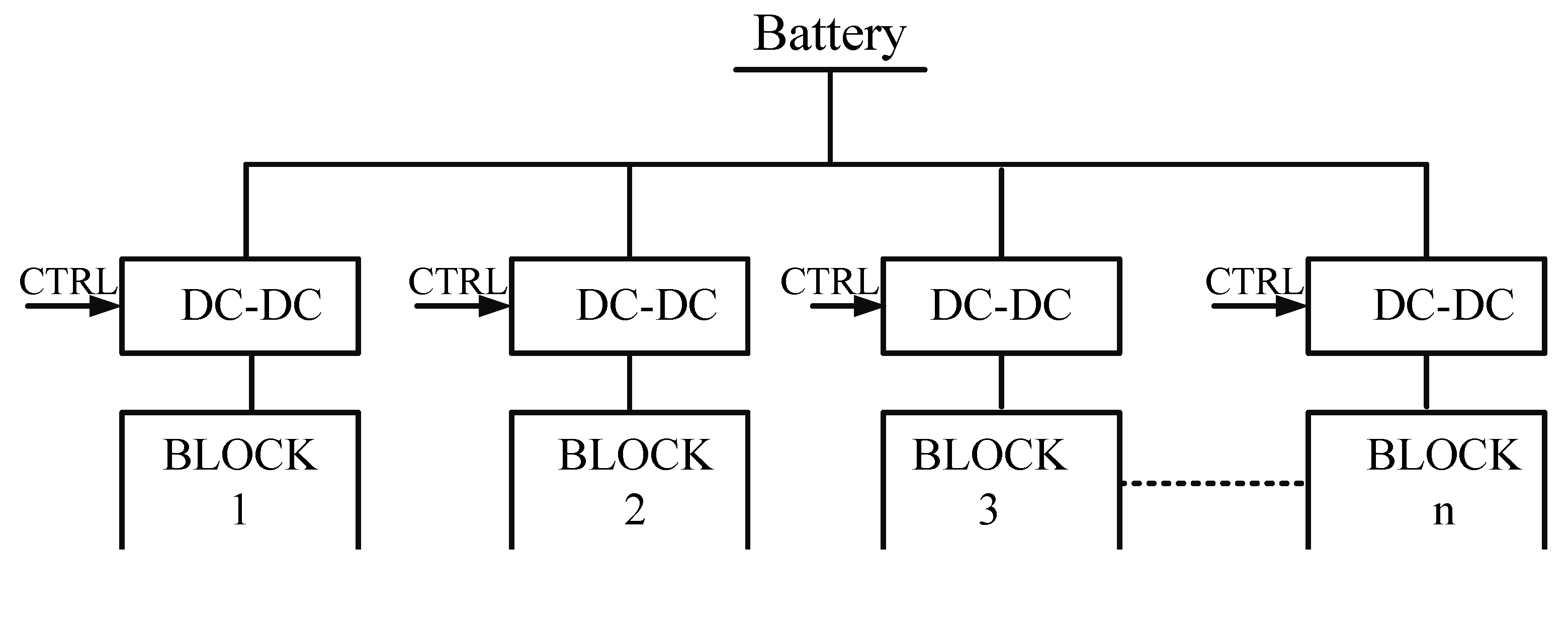
2.3. Panoptic Dynamic Voltage Scaling (PDVS)
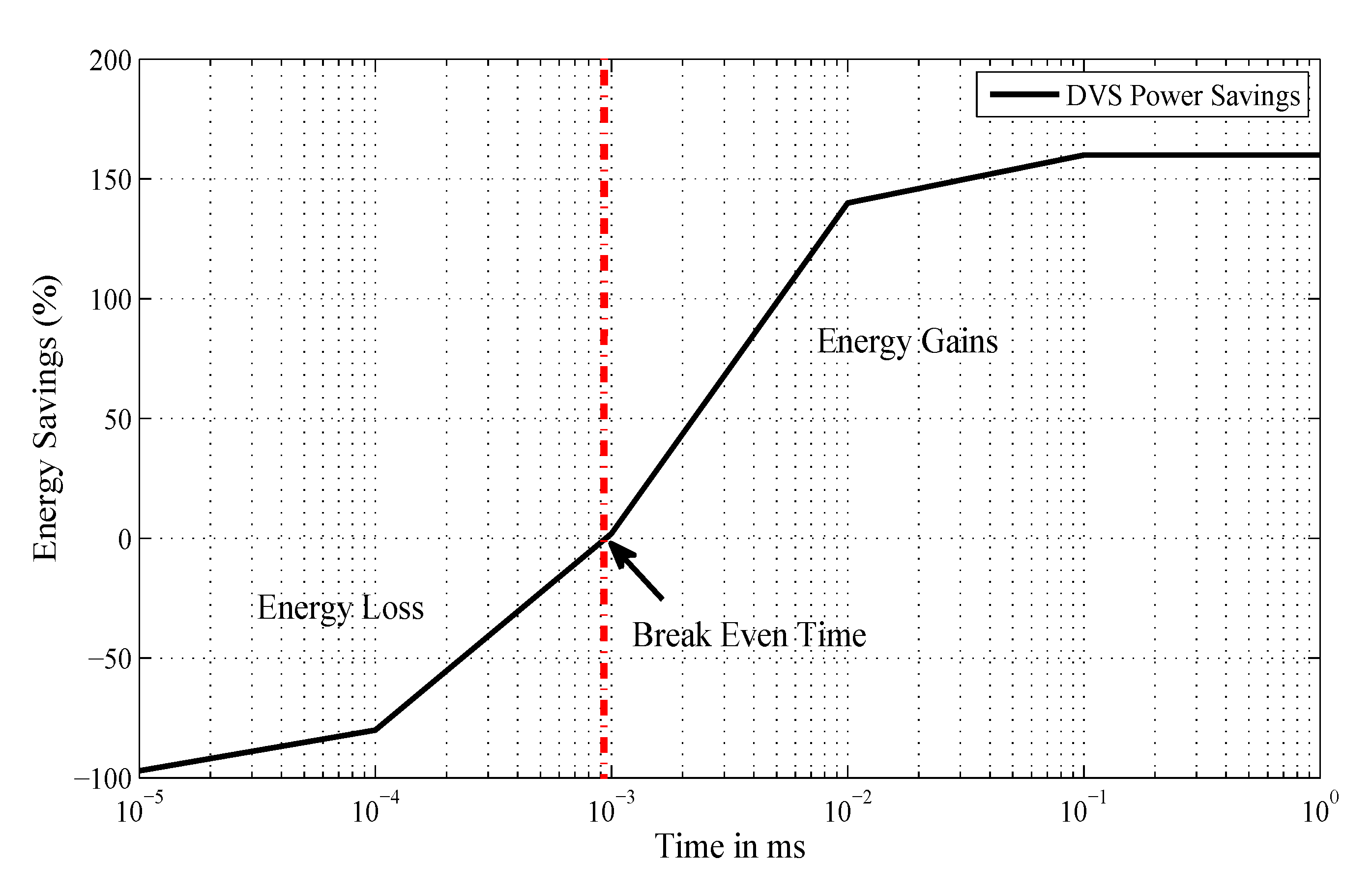

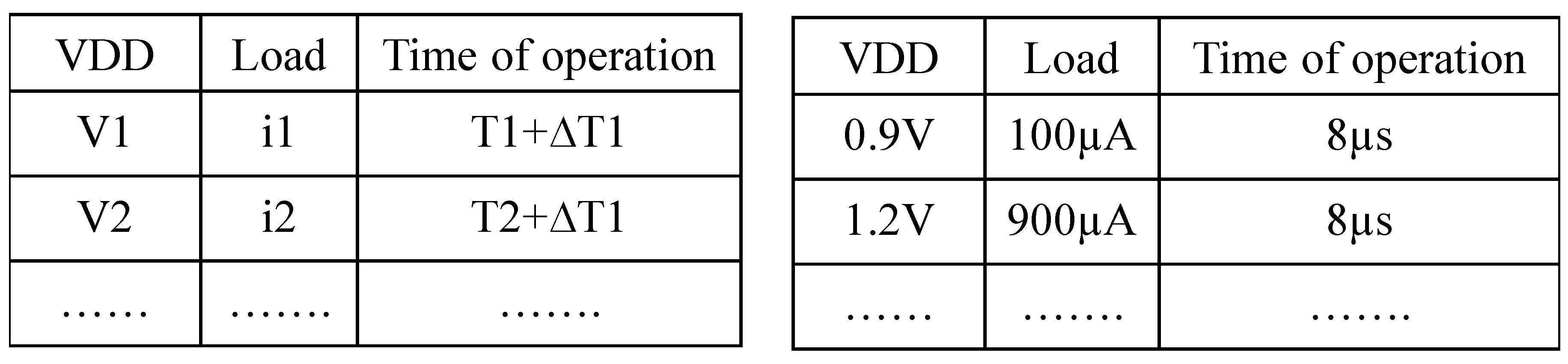
2.4. Framework for Energy Calculation in PDVS

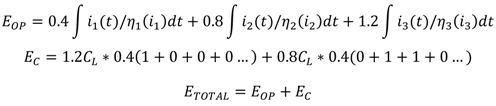
4. Comparison of DVFS and PDVS using the Proposed Model
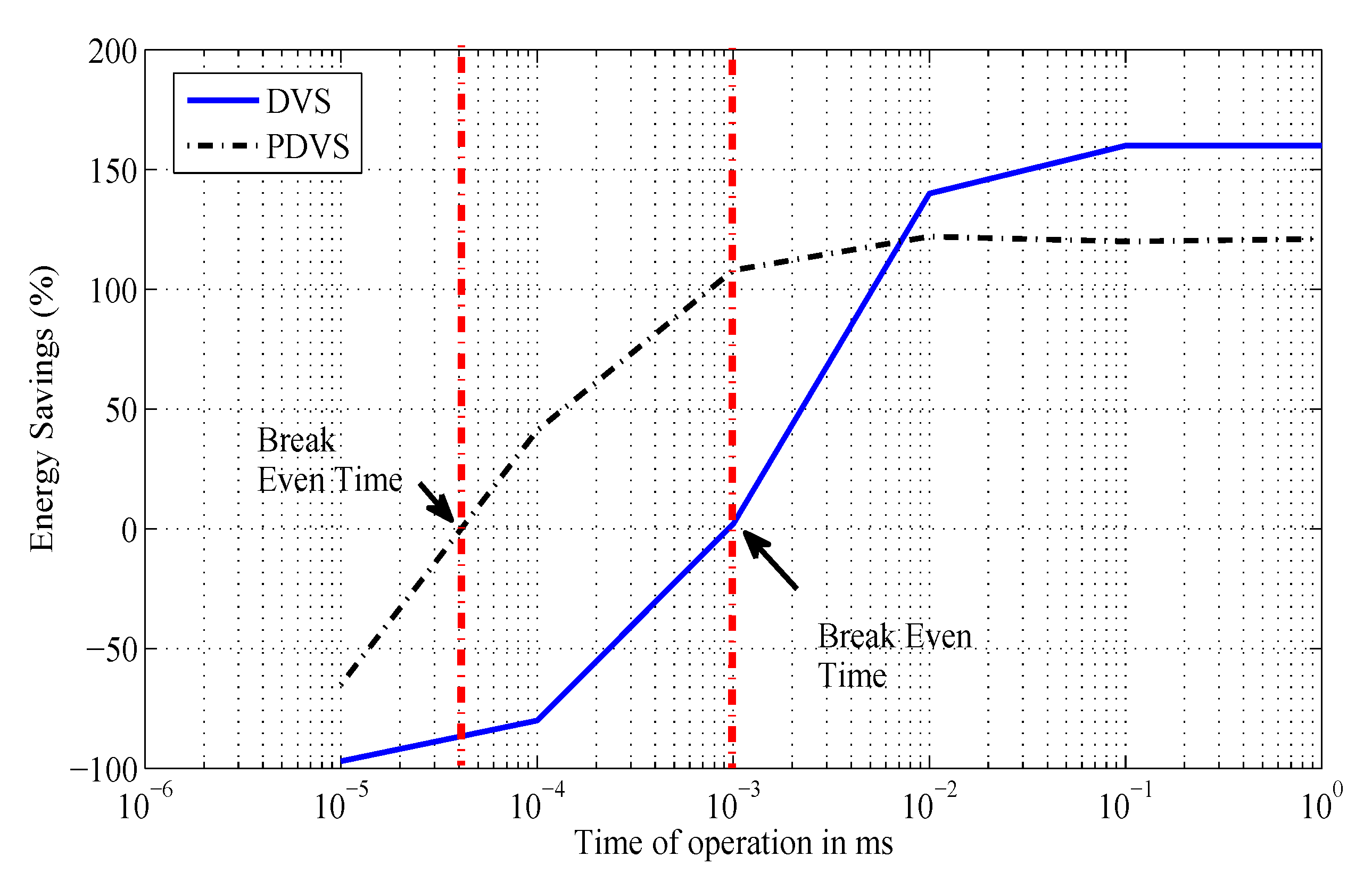
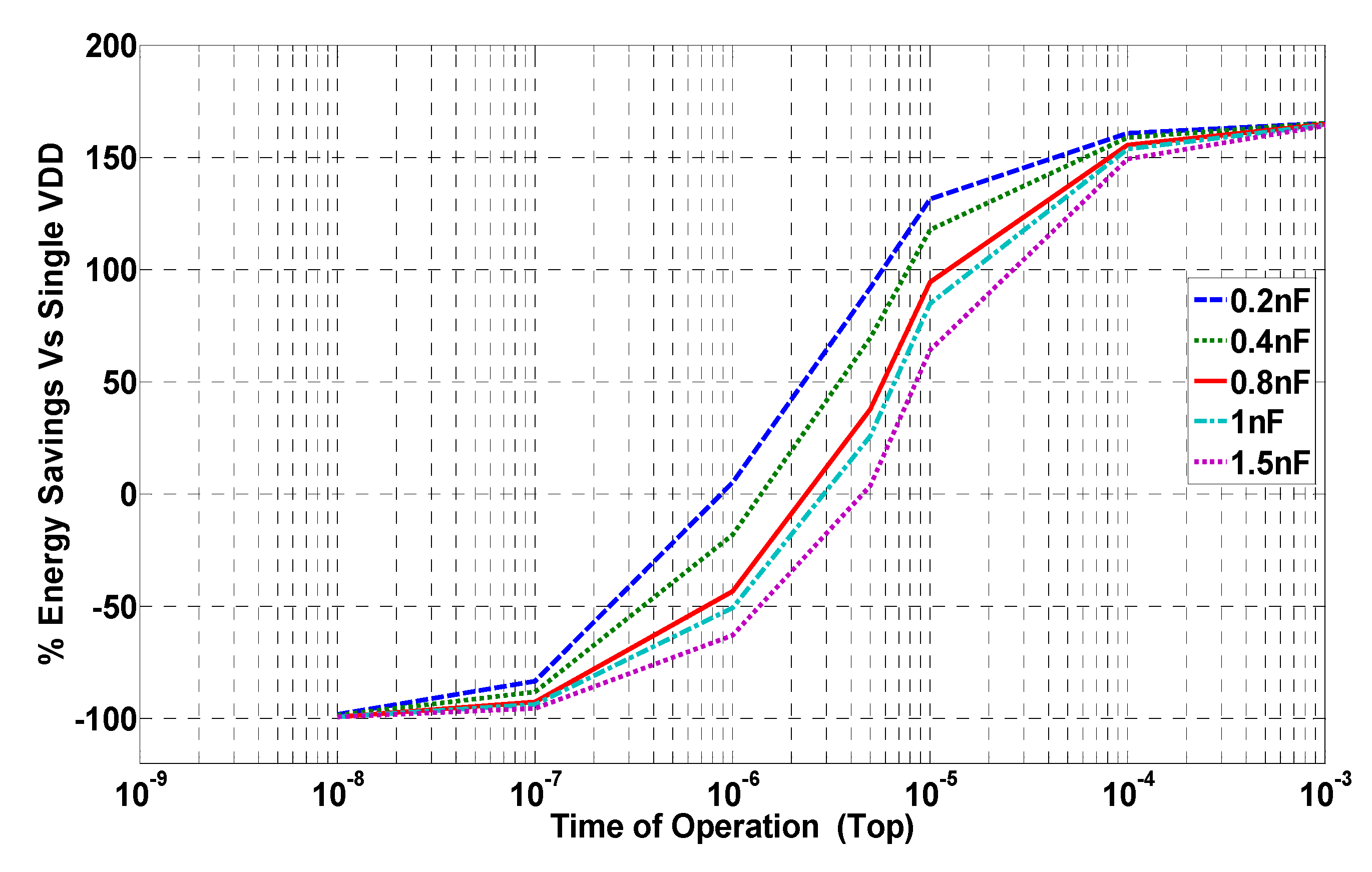
5. Conclusions
Acknowledgement
References
- Shrivastava, A.; Calhoun, B.H. Modeling DC-DC Converter Efficiency and Power Management in Ultra Low Power Systems. In Proceedings of the Sub-threshold Microelectronics Conference, Waltham, USA, 9–10 October 2012.
- Martin, S.M.; Flautner, K.; Mudge, T.; Blaauw, D. Combined dynamic voltage scaling and adaptive body biasing for lower power microprocessors under dynamic workloads. In Proceedings of the International Conference on Computer Aided Design, San Jose, USA, 10–14 November 2002.
- Kursun, V.; Narendra, S.G.; de, K.V.; Friedman, E.G. Efficiency Analysis of a High Frequency Buck Converter for On-Chip Integration with a Dual-VDD Microprocessor. In Proceedings of the IEEE European Solid State Circuits Conference, Firenze, Italy, 24–26 September 2002.
- Choi, Y.; Chang, N.; Kim, T. DC–DC converter-aware power management for low-power embedded systems. IEEE Trans. Comput. Aided Des. Integr. Circ. Syst. 2007, 26, 8. [Google Scholar]
- Yao, K.; Ye, M.; Xu, M.; Lee, F.C. Tapped-inductor buck converter for high-step-down DC-DC conversion. IEE Trans. Power Electron. 2005, 20, 775–780. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Ramadass, Y.K.; Chandrakasan, A.P. 20 µA to 100 mA DC–DC converter with 2.8-4.2 V battery supply for portable applications in 45 nm CMOS. IEEE J. Solid-State Circ 2011, 12, 2807–2820. [Google Scholar] [CrossRef]
- Li, W.; Xiao, J.; Zhao, Y.; He, X. PWM plus phase angle shift (PPAS) control scheme for combined multiport DC/DC converters. IEEE Trans. Power Electron. 2012, 27, 1479–1489. [Google Scholar] [CrossRef]
- Xiao, J.; Peterchev, A.V.; Zhang, J.; Sanders, S.R. A 4µA quiescent-current dual-mode digitally controlled buck converter IC for cellular phone applications. IEEE J. Solid-State Circ. 2004, 12, 2342–2348. [Google Scholar]
- Kuroda, T.; Suzuki, K.; Mita, S.; Fujita, T.; Yamane, F.; Sano, F.; Chiba, A.; Watanabe, Y.; Matsuda, K.; Maeda, T.; Sakurai, T.; Furuyama, T. Variable supply-voltage scheme for low-power high-speed CMOS digital design. IEEE J. Solid-State Circ. 1998, 33, 454–462. [Google Scholar] [CrossRef]
- Ramadass, Y.K.; Fayed, A.A.; Chandrakasan, A.P. A Fully-Integrated Switched-Capacitor Step-down DC-DC converter with digital capacitance modulation in 45nm CMOS. IEEE J. Solid-State Circ 2010, 45, 2557–2565. [Google Scholar] [CrossRef]
- Patounakis, G.; Li, Y.W.; Shepard, K.L. A fully integrated on-chip DC-DC conversion and power management system. IEEE J. Solid-State Circ. 2004, 39, 443–451. [Google Scholar] [CrossRef]
- Lee, C.F.; Mok, P.K.T. A monolithic current-mode CMOS DC-DC converter with on-chip current-sensing technique. IEEE J. Solid-State Circ. 2004, 39, 3–14. [Google Scholar]
- Zhang, Y.; Zhang, F.; Shakhsheer, Y.; Silver, J.; Klinefelter, A.; Nagaraju, M.; Boley, J.; Pandey, J.; Shrivastava, A.; Carlson, E.; et al. A battery-less 19μW MICS/ISM-band energy harvesting body sensor node SoC for ExG applications. IEEE J. Solid-State Circ. 2013, 48, 199–213. [Google Scholar] [CrossRef]
- Ramadass, Y.; Chandrakasan, A.P. Minimum energy tracking loop with embedded DC-DC converter enabling ultra-low-voltage operation down to 250 mV in 65 nm CMOS. IEEE J. Solid-State Circ. 2008, 43, 256–265. [Google Scholar] [CrossRef]
- Shaksheer, Y.; Khanna, S.; Craig, K.; Arrabi, S.; Lach, J.; Calhoun, B.H. A 90nm Data Flow Processor Demonstrating fine Grained DVS for Energy Efficient Operation from 0.25V to 1.2V. In Proceedings of the Custom Integrated Circuits Conference, San Jose, USA, 19–21 September 2011.
- Richelli, A.; Comensoli, S.; Kovacs-Vajna, Z.M. A DC/DC boosting technique and power management for ultralow-voltage energy harvesting applications. IEEE Trans. Industr. Electron. 2012, 59, 2701–2708. [Google Scholar]
- Bassi, G.; Colalongo, L.; Richelli, A.; Kovacs-Vajna, Z. A 150 Mv–1.2 V fully-integrated DC-DC converter for Thermal Energy Harvesting. In Proceedings of the 2012 International Symposium on Power ElectronicsElectrical DrivesAutomation and Motion (SPEEDAM), Sorrento, Italy, 20–22 June 2012; pp. 331–334.
- Richelli, A.; Colalongo, L.; Tonoli, S.; Kovacs-Vajna, Z.M. 2 V DC/DC boost converter for power harvesting applications. IEEE Trans. Power Electron. 2009, 24, 1541–1546. [Google Scholar] [CrossRef]
- Calhoun, B.H.; Wang, A.; Chandraksan, A.P. Modeling and sizing for minimum energy operation in subthreshold circuits. IEEE J. Solid-State Circ. 2005, 40, 1778–1786. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shrivastava, A.; Calhoun, B.H. A DC-DC Converter Efficiency Model for System Level Analysis in Ultra Low Power Applications. J. Low Power Electron. Appl. 2013, 3, 215-232. https://doi.org/10.3390/jlpea3030215
Shrivastava A, Calhoun BH. A DC-DC Converter Efficiency Model for System Level Analysis in Ultra Low Power Applications. Journal of Low Power Electronics and Applications. 2013; 3(3):215-232. https://doi.org/10.3390/jlpea3030215
Chicago/Turabian StyleShrivastava, Aatmesh, and Benton H. Calhoun. 2013. "A DC-DC Converter Efficiency Model for System Level Analysis in Ultra Low Power Applications" Journal of Low Power Electronics and Applications 3, no. 3: 215-232. https://doi.org/10.3390/jlpea3030215



