The Kernel Based Multiple Instances Learning Algorithm for Object Tracking
Abstract
:1. Introduction
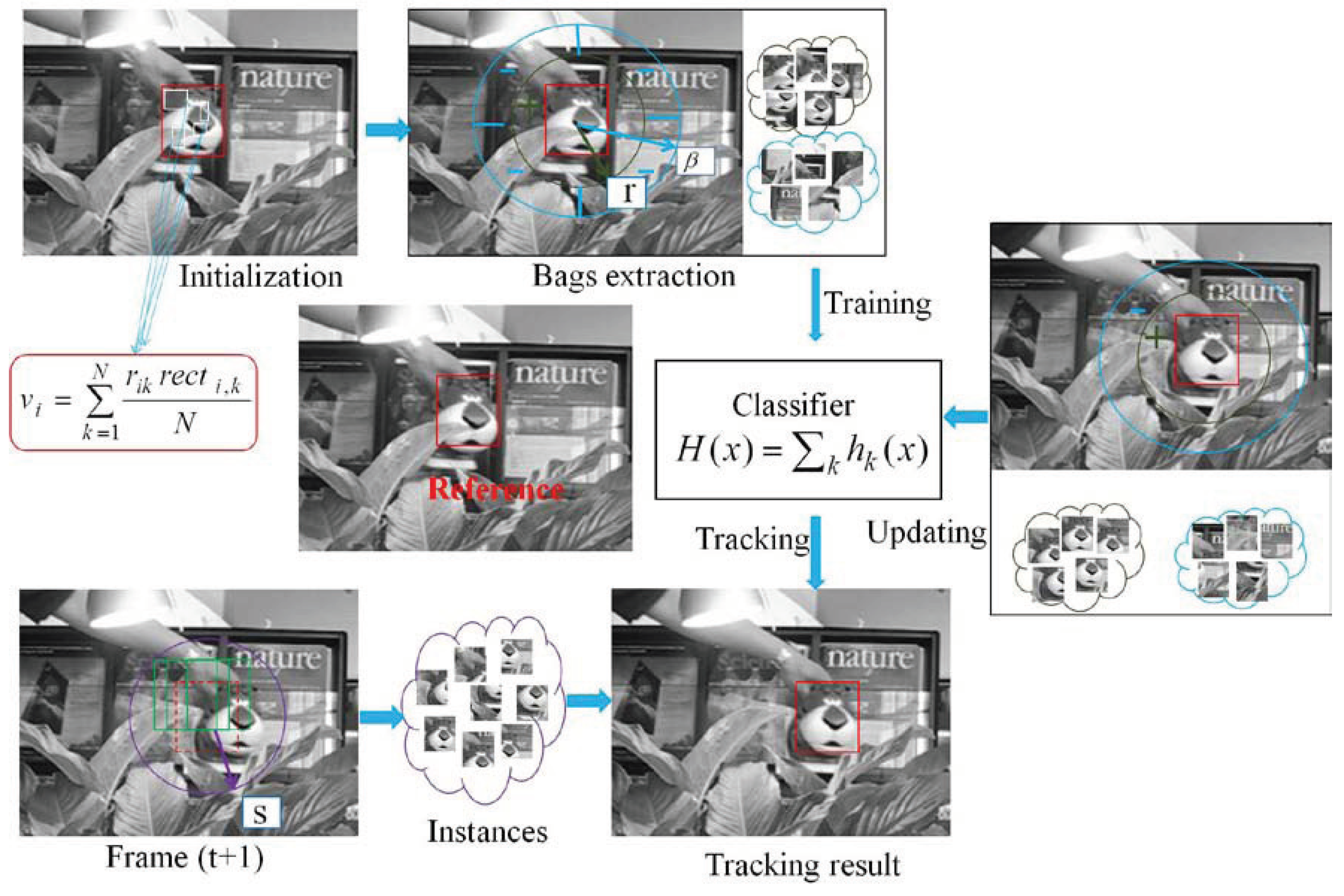
2. The WMIL Tracker
3. The KMIL Object Tracking System
3.1. The Kernel Based MIL Tracker
3.2. The Classifiers Update Strategy
4. Experiments
4.1. Parameters Setting
4.2. Tracking Object Location
4.3. Quantitative Analysis
4.4. Computational Cost
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MS | Mean Shift |
| IVT | Incremental Visual Tracking |
| VTD | Visual Tracking Decomposition |
| MOSSE | Minimum Output Sum of Squared Errors |
| CSK | Circulant Structure with Kernels |
| CN | Color Names |
| DCF | Discriminative Correlation Filter |
| DAT | Distractor Aware Tracking |
| C-COT | Continuous Convolution Operator |
| DeepSRDCF | Deep Spatially Regularized Discriminative Correlation Filter |
| DLSSVM | Dual Linear Structure Support Vector Machine |
| ECO | Efficient Convolution Operators |
| CT | Compressive Tracking |
| WMIL | Weighted Multiple Instance Learning |
| KMIL | Kernel based Weighted Multiple Instances Learning |
| KCF | Kernelized Correlation Filter |
| DSST | Discriminative Scale Space Tracking |
References
- Yilmaz, A. Object tracking: A survey. ACM Comput. Surv. 2006, 38, 13. [Google Scholar] [CrossRef]
- Gao, J.; Ling, H.; Hu, W.; Xing, J. Transfer Learning Based Visual Tracking with Gaussian Processes Regression. In Proceedings of the 13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 188–203. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, L.; Yang, M.H. Real-time compressive tracking. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 864–877. [Google Scholar] [CrossRef]
- Dadgostar, F.; Sarrafzadeh, A.; Overmyer, S.P. Face Tracking Using Mean-Shift Algorithm: A Fuzzy Approach for Boundary Detection. In Proceedings of the Affective Computing and Intelligent Interaction, First International Conference, (ACII 2005), Beijing, China, 22–24 October 2005; pp. 56–63. [Google Scholar] [CrossRef]
- Ross, D A.; Lim, J.; Lin, R.S. Incremental Learning for Robust Visual Tracking. Int. J. Comput. Vis. 2008, 77, 125–141. [Google Scholar] [CrossRef]
- Kwon, J.; Lee, K.M. Visual tracking decomposition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1269–1276. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.H.; Belongie, S. Robust Object Tracking with Online Multiple Instance Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1619–1632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hare, S.; Saffari, A.; Torr, P.H.S. Struck: Structured output tracking with kernels. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 263–270. [Google Scholar] [CrossRef]
- Avidan, S. Support Vector Tracking. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; pp. 1184–1191. [Google Scholar] [CrossRef]
- Grabner, H.; Grabner, M.; Bischof, H. Real-Time Tracking via On-line Boosting. In Proceedings of the British Machine Vision Conference 2006, Edinburgh, UK, 4–7 September 2006; pp. 47–56. [Google Scholar] [CrossRef]
- Grabner, H.; Leistner, C.; Bischof, H. Semi-supervised On-Line Boosting for Robust Tracking. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 234–247. [Google Scholar] [CrossRef]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar] [CrossRef]
- Rui, C.; Martins, P.; Batista, J. Exploiting the circulant structure of tracking-by-detection with kernels. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar] [CrossRef]
- Henriques, J.F.; Rui, C.; Martins, P. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Hager, G.; Khan, F.S. Learning Spatially Regularized Correlation Filters for Visual Tracking. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 Decenber 2015; pp. 4310–4318. [Google Scholar] [CrossRef]
- Danelljan, M.; Khan, F.S.; Felsberg, M. Adaptive Color Attributes for Real-Time Visual Tracking. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1090–1097. [Google Scholar] [CrossRef]
- Possegger, H.; Mauthner, T.; Bischof, H. In defense of color-based model-free tracking. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2113–2120. [Google Scholar] [CrossRef]
- Bertinetto, L.; Valmadre, J.; Golodetz, S. Staple: Complementary Learners for Real-Time Tracking. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Volume 38, pp. 1401–1409. [Google Scholar] [CrossRef]
- Danelljan, M.; Hager, G.; Khan, F.S. Discriminative Scale Space Tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danelljan, M.; Hager, G.; Khan, F.S. Convolutional Features for Correlation filter-based Visual Tracking. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015; pp. 621–629. [Google Scholar] [CrossRef]
- Held, D.; Thrun, S.; Savarese, S. Learning to Track at 100 FPS with Deep Regression Networks. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 749–765. [Google Scholar] [CrossRef]
- Danelljan, M.; Robinson, A.; Khan, F.S. Beyond Correlation Filters: Learning Continuous Convolution Operators for Visual Tracking. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 472–488. [Google Scholar] [CrossRef]
- Danelljan, M.; Bhat, G.; Khan, F. ECO: Efficient Convolution Operators for Tracking. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6931–6939. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.-H.; Belongi, S. Robust Object Tracking with Online Multiple Instance Learning. IEEE Transa. Pattern Anal. Mach. Intell. 2011, 33, 1619–1632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Song, H. Real-time visual tracking via online weighted multiple instance learning. Pattern Recognit. 2013, 46, 397–411. [Google Scholar] [CrossRef]
- Ning, J.; Yang, J.; Jiang, S.; Zhang, L.; Yang, M.-H. Object Tracking via Dual Linear Structured SVM and Explicit Feature Map. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4266–4274. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.-H. Online Object Tracking: A Benchmark. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2411–2418. [Google Scholar] [CrossRef]



| Parameters | r | s | K | M | |||
|---|---|---|---|---|---|---|---|
| CT | 4 | 8 | 30 | 20 | / | / | 0.85 |
| MIL | 4 | / | 50 | 35 | 250 | 50 | 0.85 |
| WMIL | 4 | 25 | 150 | 15 | 0.85 | ||
| KMIL(big object) | 4 | 25 | 150 | 15 | 0.25/0.85 | ||
| KMIL(small object) | 4 | r | 35 | 150 | 50 | 0.25/0.85 |
| Video Clip | MIL | CT | WMIL | KCF | KMIL | DSST |
|---|---|---|---|---|---|---|
| Tiger2 | 3.52 | 10.14 | 7.34 | 54.33 | 9.96 | 260 |
| Lemming | 3.13 | 9.41 | 8.96 | 35.73 | 9.98 | 103 |
| Shaking | 3.38 | 13.03 | 14.69 | 30.12 | 18.14 | 279 |
| Animal | 3.52 | 11.40 | 8.87 | 28.76 | 10.25 | 479 |
| Sylvester | 3.65 | 13.32 | 7.98 | 42.31 | 14.37 | 137 |
| Faceocc2 | 3.46 | 13.21 | 13.85 | 38.28 | 17.70 | 260 |
| Tiger1 | 3.02 | 10.4 | 7.93 | 10.94 | 9.22 | 265 |
| Football1 | 3.73 | 13.59 | 8.77 | 224 | 13.04 | 500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Wang, L.; Wen, B. The Kernel Based Multiple Instances Learning Algorithm for Object Tracking. Electronics 2018, 7, 97. https://doi.org/10.3390/electronics7060097
Han T, Wang L, Wen B. The Kernel Based Multiple Instances Learning Algorithm for Object Tracking. Electronics. 2018; 7(6):97. https://doi.org/10.3390/electronics7060097
Chicago/Turabian StyleHan, Tiwen, Lijia Wang, and Binbin Wen. 2018. "The Kernel Based Multiple Instances Learning Algorithm for Object Tracking" Electronics 7, no. 6: 97. https://doi.org/10.3390/electronics7060097
APA StyleHan, T., Wang, L., & Wen, B. (2018). The Kernel Based Multiple Instances Learning Algorithm for Object Tracking. Electronics, 7(6), 97. https://doi.org/10.3390/electronics7060097





