Small Signal Stability of a Balanced Three-Phase AC Microgrid Using Harmonic Linearization: Parametric-Based Analysis
Abstract
:1. Introduction
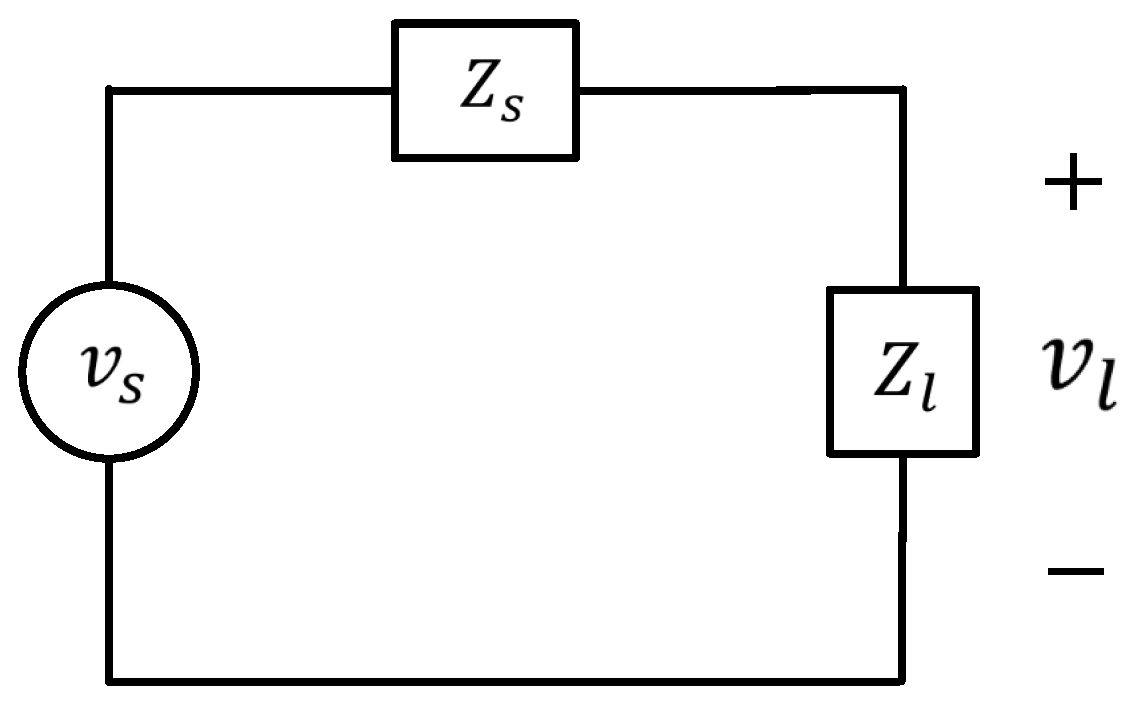
2. System Modeling Using HL
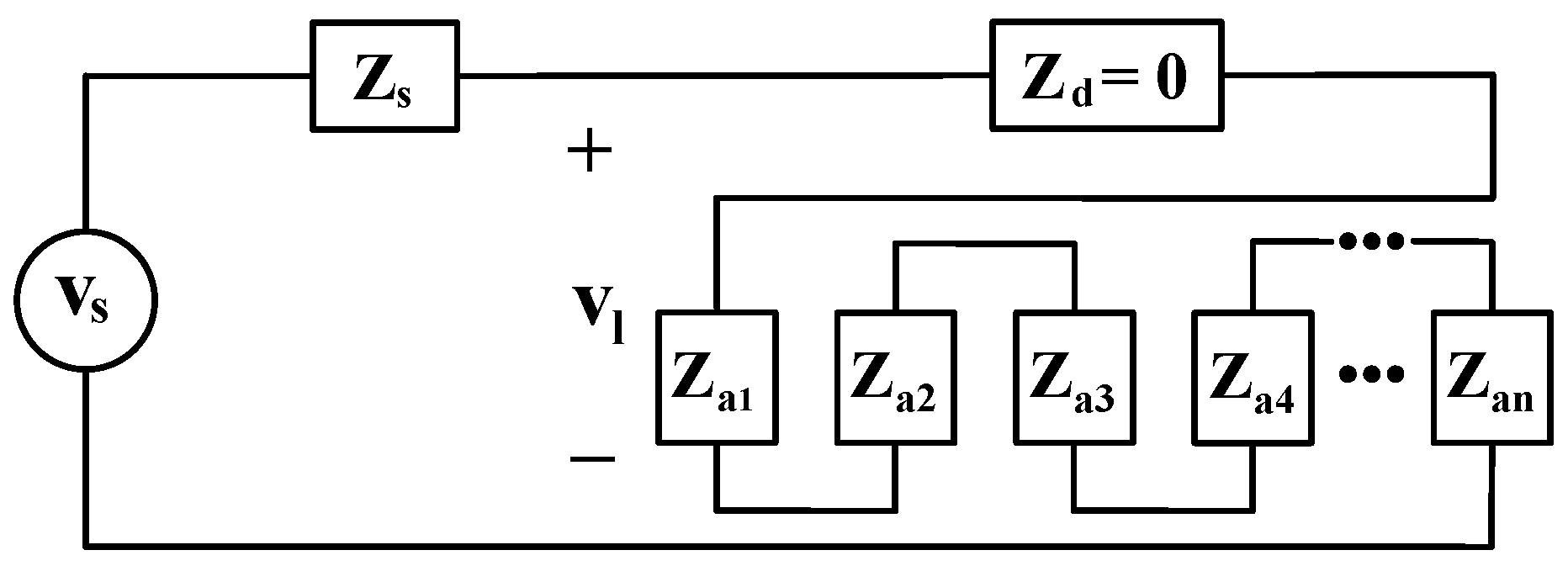
3. Mathematical Modeling of the Impedances at the PCC
4. Simulation Results
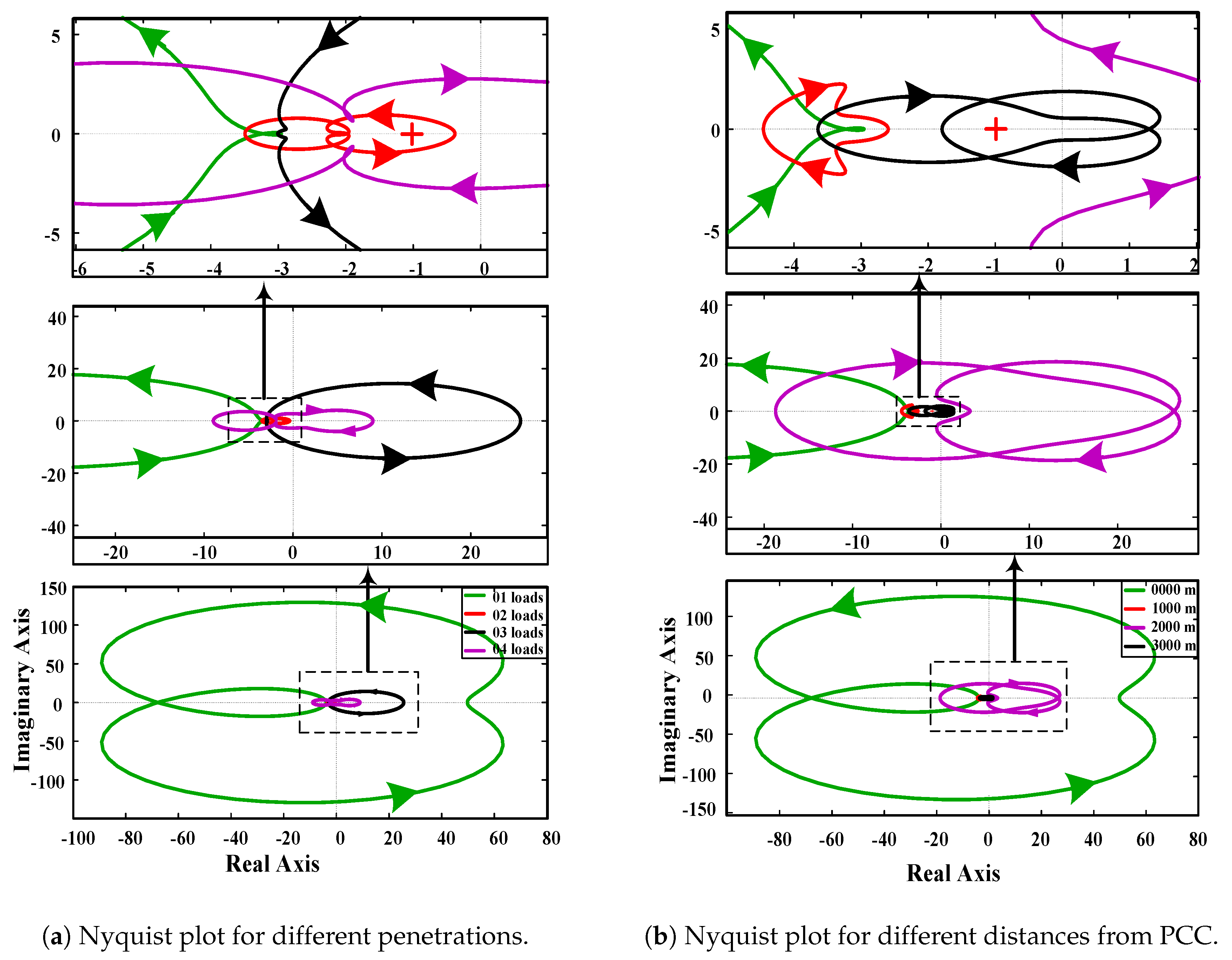
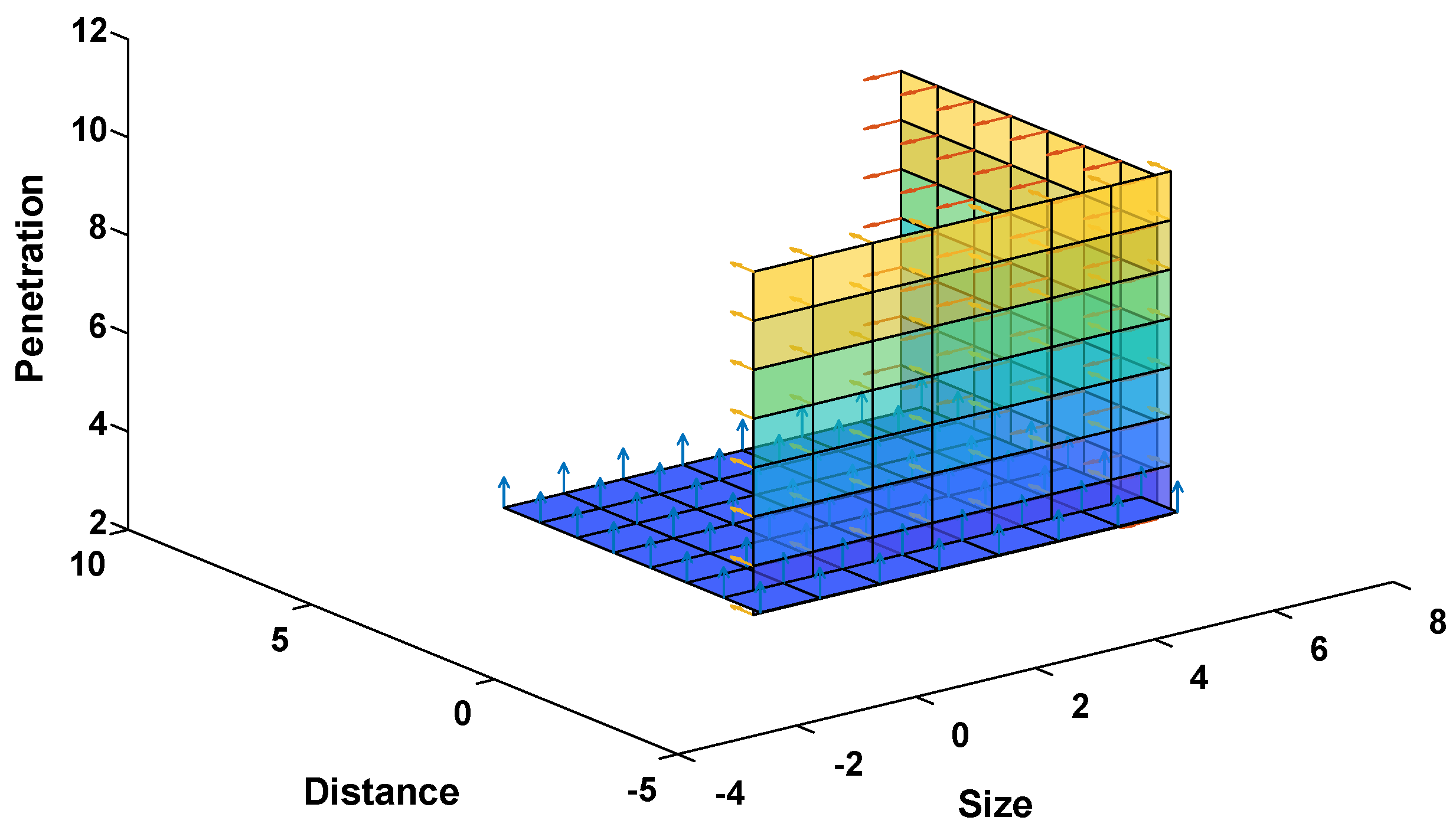
- First, stability was assessed by changing the parallel clustering (penetration) of grid-connected active loads.
- Then, the stability was evaluated by changing the distance of active loads from the PCC.
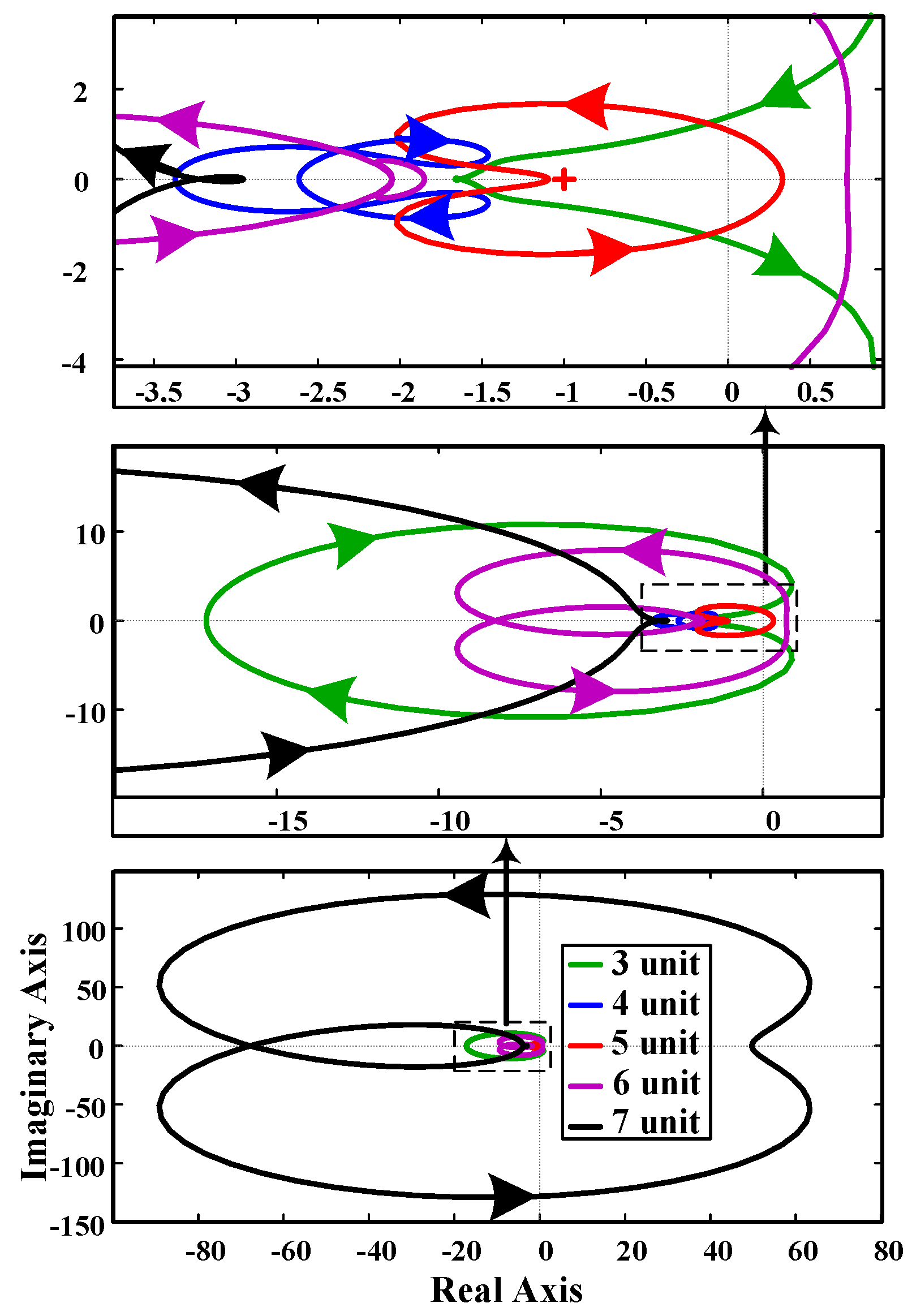
- Afterwards, the stability at the PCC was assessed by changing the serial clustering (size) of active loads.
4.1. Effect of Penetration
4.2. Effect of Distance from PCC
4.3. Effect of the Sizes of Active Loads
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siddique, M.N.; Ahmad, A.; Nawaz, M.K.; Bukhari, S.B.A. Optimal integration of hybrid (wind-solar) system with diesel power plant using HOMER. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1547–1557. [Google Scholar] [CrossRef]
- Matos, E.O.D.; Soares, T.M.; Bezerra, U.H.; De Tostes, L.M.E.; Rodrigo, A.; Manito, A.; Cordeiro, B.C., Jr. Using linear and non-parametric regression models to describe the contribution of non-linear loads on the voltage harmonic distortions in the electrical grid. IET Gener. Transm. Distrib. 2016, 10, 1825–1832. [Google Scholar] [CrossRef]
- Li, Y.W.; He, J. Distribution System Harmonic Compensation Methods: An Overview of DG-Interfacing Inverters. IEEE Ind. Electron. Mag. 2014, 8, 18–31. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Cobben, S.; Ribeiro, P.; Kling, W. Harmonic emission limits and responsibilities at a point of connection. IET Gener. Transm. Distrib. 2012, 6, 256–264. [Google Scholar] [CrossRef]
- Wildrick, C.; Lee, F.; Cho, B.; Choi, B. A method of defining the load impedance specification for a stable distributed power system. In Proceedings of the IEEE Power Electronics Specialist Conference PESC ’93, Seattle, WA, USA, 20–24 June 1993; pp. 826–832. [Google Scholar]
- Khaligh, A.; Rahimi, A.; Emadi, A. Negative Impedance Stabilizing Pulse Adjustment Control Technique for DC/DC Converters Operating in Discontinuous Conduction Mode and Driving Constant Power Loads. IEEE Trans. Veh. Technol. 2007, 56, 2005–2016. [Google Scholar] [CrossRef]
- Emadi, A.; Ehsani, M. Negative impedance stabilizing controls for pwm Dc-Dc converters using feedback linearization techniques. In Proceedings of the 35th Intersociety Energy Conversion Engineering Conference and Exhibit (Cat. No.00CH37022), Las Vegas, NV, USA, 24–28 July 2000; Volume 1, pp. 613–620. [Google Scholar]
- Preda, T.; Uhlen, K.; Nordgård, D.E. An overview of the present grid codes for integration of distributed generation. In Proceedings of the CIRED 2012 Workshop: Integration of Renewables into the Distribution Grid, Lisbon, Portugal, 29–30 May 2012; pp. 1–4. [Google Scholar]
- Sudhoff, S.; Corzine, K.; Glover, S.; Hegner, H.; Robey, H. DC link stabilized field oriented control of electric propulsion systems. IEEE Trans. Energy Convers. 1998, 13, 27–33. [Google Scholar] [CrossRef]
- Emadi, A.; Khaligh, A.; Rivetta, C.; Williamson, G. Constant Power Loads and Negative Impedance Instability in Automotive Systems: Definition, Modeling, Stability, and Control of Power Electronic Converters and Motor Drives. IEEE Trans. Veh. Technol. 2006, 55, 1112–1125. [Google Scholar] [CrossRef]
- Feng, X.; Liu, J.; Lee, F. Impedance Specifications for Stable DC Distributed Power Systems. IEEE Trans. Power Electron. 2002, 17, 157–162. [Google Scholar] [CrossRef]
- Belkhayat, M.; Cooley, R.; Witulski, A. Large Signal Stability Criteria For Distributed Systems with Constant Power Loads. In Proceedings of the PESC ’95 - Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; pp. 1333–1338. [Google Scholar]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Liu, J.; Feng, X.; Lee, F.; Borojevich, D. Stability margin monitoring for DC distributed power systems via current/voltage perturbation. In Proceedings of the Sixteenth Annual IEEE Applied Power Electronics Conference and Exposition APEC 2001 (Cat. No.01CH37181), Anaheim, CA, USA, 4–8 March 2001; Volume 2, pp. 745–751. [Google Scholar]
- Grigore, V.; Hatonen, J.; Kyyra, J.; Suntio, T. Dynamics of a buck converter with a constant power load. In Proceedings of the PESC 98 Record. 29th Annual IEEE Power Electronics Specialists Conference (Cat. No.98CH36196), Fukuoka, Japan, 22 May 1998; Volume 1, pp. 72–78. [Google Scholar]
- Chen, M.; Sun, J. Low-Frequency Input Impedance Modeling of Boost Single-Phase PFC Converters. IEEE Trans. Power Electron. 2007, 22, 1402–1409. [Google Scholar] [CrossRef]
- Prodic, A. Compensator Design and Stability Assessment for Fast Voltage Loops of Power Factor Correction Rectifiers. IEEE Trans. Power Electron. 2007, 22, 1719–1730. [Google Scholar] [CrossRef]
- Mithulananthan, N.; Kumar Saha, T.; Chidurala, A. Harmonic impact of high penetration photovoltaic system on unbalanced distribution networks—Learning from an urban photovoltaic network. IET Renew. Power Gener. 2016, 10, 485–494. [Google Scholar]
- He, J.; Li, Y.W.; Munir, M.S. A Flexible Harmonic Control Approach Through Voltage-Controlled DG-Grid Interfacing Converters. IEEE Trans. Ind. Electron. 2012, 59, 444–455. [Google Scholar] [CrossRef]
- Sun, J. Small-signal methods for AC distributed power systems—A review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Cespedes, M.; Sun, J. Adaptive Control of Grid-Connected Inverters Based on Online Grid Impedance Measurements. IEEE Trans. Sustain. Energy 2014, 5, 516–523. [Google Scholar] [CrossRef]
- Roinila, T.; Vilkko, M.; Sun, J. Online Grid Impedance Measurement Using Discrete-Interval Binary Sequence Injection. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 985–993. [Google Scholar] [CrossRef]
- Belkhayat, M. Stability Criteria for AC Power Systems with Regulated Loads. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1997. [Google Scholar]
- Francis, G.; Burgos, R.; Boroyevich, D.; Wang, F.; Karimi, K. An Algorithm and Implementation System for Measuring Impedance in the D-Q Domain. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 3221–3228. [Google Scholar]
- Wen, B.; Dong, D.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Impedance-Based Analysis of Grid-Synchronization Stability for Three-Phase Paralleled Converters. IEEE Trans. Power Electron. 2016, 31, 26–38. [Google Scholar] [CrossRef]
- Valdivia, V.; Lazaro, A.; Barrado, A.; Zumel, P.; Fernandez, C.; Sanz, M. Black-Box Modeling of Three-Phase Voltage Source Inverters for System-Level Analysis. IEEE Trans. Ind. Electron. 2012, 59, 3648–3662. [Google Scholar] [CrossRef]
- Rygg, A.; Molinas, M.; Zhang, C.; Cai, X. A Modified Sequence-Domain Impedance Definition and Its Equivalence to the dq-Domain Impedance Definition for the Stability Analysis of AC Power Electronic Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1383–1396. [Google Scholar] [CrossRef] [Green Version]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Yao, Z.; Therond, P.G.; Davat, B. Stability analysis of power systems by the generalised nyquist criterion. In Proceedings of the 1994 International Conference on Control Control ’94, Coventry, UK, 21–24 March 1994; pp. 739–744. [Google Scholar]
- Guanrong, C.; Moiola, J.L. Hopf Bifurcation Analysis: A Frequency Domain Approach; World Scientific: Singapore, 1996. [Google Scholar]
- Sanchez, S. Stability Investigation of Power Electronics Systems: A Microgrid Case. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Xu, Q.; Member, S.; Ma, F.; Luo, A.; Member, S. Analysis and Control of M3C based UPQC for Power Quality Improvement in Medium/High Voltage Power Grid. IEEE Trans. Power Electron. 2016, 31, 8182–8194. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics based Power Systems: A Discussion of Impedance and Eigenvalue-based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Familiant, Y.A.; Huang, J.; Corzine, K.A.; Belkhayat, M. New Techniques for Measuring Impedance Characteristics of Three-Phase AC Power Systems. IEEE Trans. Power Electron. 2009, 24, 1802–1810. [Google Scholar] [CrossRef]
- Valdivia, V.; Lázaro, A.; Barrado, A.; Zumel, P.; Fernández, C.; Sanz, M. Impedance Identification Procedure of Three-Phase Balanced Voltage Source Inverters Based on Transient Response Measurements. IEEE Trans. Power Electron. 2011, 26, 3810–3816. [Google Scholar] [CrossRef]
- Shen, Z.; Jaksic, M.; Mattavelli, P.; Boroyevich, D.; Verhulst, J.; Belkhayat, M. Design and implementation of three-phase AC impedance measurement unit (IMU) with series and shunt injection. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2674–2681. [Google Scholar]
- Shen, Z.; Jaksic, M.; Mattavelli, P.; Boroyevich, D.; Verhulst, J. Three-phase AC system impedance measurement unit (IMU) using chirp signal injection. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2666–2673. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Small-Signal Stability Analysis of Three-Phase AC Systems in the Presence of Constant Power Loads Based on Measured D-Q Frame Impedances. IEEE Trans. Power Electron. 2015, 30, 5952–5963. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of Phase-Locked Loop Low-Frequency Stability in Three-Phase Grid-Connected Power Converters Considering Impedance Interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Hoffmann, N.; Fuchs, F.W. Minimal Invasive Equivalent Grid Impedance Estimation in Inductive-Resistive Power Networks Using Extended Kalman Filter. IEEE Trans. Power Electron. 2014, 29, 631–641. [Google Scholar] [CrossRef]
- Xiao, P.; Venayagamoorthy, G.K.; Corzine, K.A.; Huang, J. Recurrent Neural Networks Based Impedance Measurement Technique for Power Electronic Systems. IEEE Trans. Power Electron. 2010, 25, 382–390. [Google Scholar] [CrossRef]
- Gelb, A.; Velde, W.E.V. Multiple-Input Describing Functions and Nonlinear System Design; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Shen, Z.; Jaksic, M.; Zhou, B.; Mattavelli, P.; Boroyevich, D.; Verhulst, J.; Belkhayat, M. Analysis of Phase Locked Loop (PLL) influence on dq impedance measurement in three-phase AC systems. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 939–945. [Google Scholar]






| Model | Disadvantages | Reference |
|---|---|---|
| Lyapunov Methods (Time Domain) | A detailed system modeling is required for this method, so it does not work well for complex large systems. Its converter model is unable to capture the harmonic effect. | [28,29,31,33] |
| Probabilistic Methods (Time Domain) | It requires huge computational effort, so this method is very time consuming. Inaccurate first approximation may lead to faulty conclusions. Not all applied schemes work for complex large systems. | [32] |
| Phasor Model | It is often not differentiable due to significantly higher dimensions. | [20] |
| Bifurcation Theory | It is slow in the time domain and more complicated in the frequency domain for a higher order system. | [30] |
| SRF Method | Limited to only balanced three-phase systems. | [20,33] |
| Parameter | Symbol | Value | Symbol | Value |
|---|---|---|---|---|
| Power Source | P | 2500 MVA | V | 120 kV |
| Line Section | [0.1153] | |||
| Line Section | [0.413] | |||
| Industrial Load | P | 30 MW | Q | 2 MVar |
| Residential Load 1 | P | 2 MW | Q | 0 |
| Residential Load 2 | P | 100 kW | Q | 0 |
| Penetration | Distance at PCC | Size | Effect on Stability |
|---|---|---|---|
| Increasing | Constant | Constant | Improve |
| Constant | Increasing | Constant | Improve |
| Constant | Constant | Increasing | Deteriorate |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.U.; Syed, I.; Ullah, M. Small Signal Stability of a Balanced Three-Phase AC Microgrid Using Harmonic Linearization: Parametric-Based Analysis. Electronics 2019, 8, 12. https://doi.org/10.3390/electronics8010012
Rahman AU, Syed I, Ullah M. Small Signal Stability of a Balanced Three-Phase AC Microgrid Using Harmonic Linearization: Parametric-Based Analysis. Electronics. 2019; 8(1):12. https://doi.org/10.3390/electronics8010012
Chicago/Turabian StyleRahman, Atta Ur, Irtaza Syed, and Mukhtar Ullah. 2019. "Small Signal Stability of a Balanced Three-Phase AC Microgrid Using Harmonic Linearization: Parametric-Based Analysis" Electronics 8, no. 1: 12. https://doi.org/10.3390/electronics8010012





