Determination of Complex Conductivity of Thin Strips with a Transmission Method
Abstract
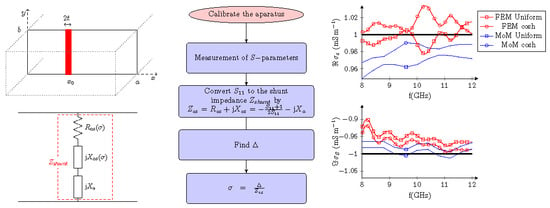
:1. Introduction
2. Theory
3. Current Distribution on the Strip
3.1. Uniform Current
3.2. Hyperbolic Cosine Distribution
4. Field on the Conductive Strip
5. Numerical Results
5.1. Reflection and Transmission Coefficients
5.2. Fields on the Aperture
5.3. Conductivity Estimation
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Simplification of Series in Equation (21)
References
- Baker-Jarvis, J. Transmission/Reflection and Short-Circuit Line Permittivity Measurements; Technical Report, NIST Technical Note 1341; National Institute of Standards and Technology: Boulder, CO, USA, 1990.
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kobayashi, Y.; Katoh, M. Microwave Measurement of Dielectric Properties of Low-Loss Materials by the Dielectric Rod Resonator Method. IEEE Trans. Microw. Theory Tech. 1985, 33, 586–592. [Google Scholar] [CrossRef]
- Champlin, K.S.; Krongard, R.R. The Measurement of Conductivity and Permittivity of Semiconductor Spheres by an Extension of the Cavity Perturbation Method. IRE Trans. Microw. Theory Tech. 1961, MTT-9, 545–551. [Google Scholar] [CrossRef]
- Courtney, W. Analysis and Evaluation of a Method of Measuring the Complex Permittivity and Permeability Microwave Insulators. IEEE Trans. Microw. Theory Tech. 1970, 18, 476–485. [Google Scholar] [CrossRef]
- Krupka, J.; Judek, J.; Jastrzȩbski, C.; Ciuk, T.; Wosik, J.; Zdrojek, M. Microwave complex conductivity of the YBCO thin films as a function of static external magnetic field. Appl. Phys. Lett. 2014, 104, 102603. [Google Scholar] [CrossRef]
- Le Floch, J.M.; Fan, Y.; Humbert, G.; Shan, Q.; Férachou, D.; Bara-Maillet, R.; Aubourg, M.; Hartnett, J.G.; Madrangeas, V.; Cros, D.; et al. Invited article: Dielectric material characterization techniques and designs of high-Q resonators for applications from micro to millimeter-waves frequencies applicable at room and cryogenic temperatures. Rev. Sci. Instrum. 2014, 85, 031301. [Google Scholar] [CrossRef] [PubMed]
- Krupka, J.; Strupinski, W.; Kwietniewski, N. Microwave Conductivity of Very Thin Graphene and Metal Films. J. Nanosci. Nanotechnol. 2011, 11, 3358–3362. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Gallop, J.; Goniszewski, S.; Shaforost, O.; Klein, N.; Yakimova, R. Non-contact method for measurement of the microwave conductivity of graphene. Appl. Phys. Lett. 2013, 103, 123103. [Google Scholar] [CrossRef] [Green Version]
- Ilić, A.Ž.; Budimir, D. Electromagnetic analysis of graphene based tunable waveguide resonators. Microw. Opt. Technol. Lett. 2014, 56, 2385–2388. [Google Scholar] [CrossRef]
- Obrzut, J.; Emiroglu, C.; Kirillov, O.; Yang, Y.; Elmquist, R.E. Surface conductance of graphene from non-contact resonant cavity. Measurement 2016, 87, 146–151. [Google Scholar] [CrossRef] [Green Version]
- Kato, Y.; Horibe, M. New Permittivity Measurement Methods Using Resonant Phenomena for High-Permittivity Materials. IEEE Trans. Instrum. Meas. 2017, 66, 1191–1200. [Google Scholar] [CrossRef]
- Nozaki, R.; Bose, T. Broadband complex permittivity measurements by time-domain spectroscopy. IEEE Trans. Instrum. Meas. 1990, 39, 945–951. [Google Scholar] [CrossRef]
- Booth, J.C.; Wu, D.H.; Anlage, S.M. A broadband method for the measurement of the surface impedance of thin films at microwave frequencies. Rev. Sci. Instrum. 1994, 65, 2082–2090. [Google Scholar] [CrossRef]
- Rzepecka, M.A.; Stuchly, S.S. A Lumped Capacitance Method for the Measurement of the Permittivity and Conductivity in the Frequency and Time Domain-A Further Analysis. IEEE Trans. Instrum. Meas. 1975, 24, 27–32. [Google Scholar] [CrossRef]
- Nag, B.; Roy, S.; Chatterji, C. Microwave measurement of conductivity and dielectric constant of semiconductors. Proc. IEEE 1963, 51, 962. [Google Scholar] [CrossRef]
- Abdulnour, J.; Akyel, C.; Wu, K. A generic approach for permittivity measurement of dielectric materials using a discontinuity in a rectangular waveguide or a microstrip line. IEEE Trans. Microw. Theory Tech. 1995, 43, 1060–1066. [Google Scholar] [CrossRef]
- Hong, Y.K.; Lee, C.Y.; Jeong, C.K.; Lee, D.E.; Kim, K.; Joo, J. Method and apparatus to measure electromagnetic interference shielding efficiency and its shielding characteristics in broadband frequency ranges. Rev. Sci. Instrum. 2003, 74, 1098–1102. [Google Scholar] [CrossRef]
- Wei, X.C.; Xu, Y.L.; Meng, N.; Xu, Y.; Hakro, A.; Dai, G.L.; Hao, R.; Li, E.P. A non-contact graphene surface scattering rate characterization method at microwave frequency by combining Raman spectroscopy and coaxial connectors measurement. Carbon N. Y. 2014, 77, 53–58. [Google Scholar] [CrossRef]
- Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Sharma, P.; Ionescu, A. Non-contact characterization of graphene surface impedance at micro and millimeter waves. J. Appl. Phys. 2012, 111, 114908. [Google Scholar] [CrossRef]
- Rostamnejadi, A. Microwave properties of La0.8Ag0.2MnO3 nanoparticles. Appl. Phys. A 2016, 122, 966. [Google Scholar] [CrossRef]
- Hassan, A.M.; Obrzut, J.; Garboczi, E.J. A Q-Band Free-Space Characterization of Carbon Nanotube Composites. IEEE Trans. Microw. Theory Tech. 2016, 64, 3807–3819. [Google Scholar] [CrossRef]
- Han, J.; Geyi, W. A New Method for Measuring the Properties of Dielectric Materials. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 425–428. [Google Scholar] [CrossRef]
- Jiang, J.; Geyi, W. Development of a new prototype system for measuring the permittivity of dielectric materials. J. Eng. 2014, 2014, 302–304. [Google Scholar] [CrossRef]
- Wang, X.; Geyi, W. Design of a Wideband System for Measuring Dielectric Properties. IEEE Trans. Instrum. Meas. 2017, 66, 69–76. [Google Scholar] [CrossRef]
- Bogle, A.; Havrilla, M.; Nyquis, D.; Kempel, L.; Rothwell, E. Electromagnetic Material Characterization using a Partially-Filled Rectangular Waveguide. J. Electromagn. Waves Appl. 2005, 19, 1291–1306. [Google Scholar] [CrossRef]
- Thiel, D.V.; Li, Q.; Li, X.; Gu, M. Laser induced carbon nano-structures for planar antenna fabrication at microwave frequencies. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; Volume 3, pp. 898–899. [Google Scholar]
- Wang, W.; Chakrabarti, S.; Chen, Z.; Yan, Z.; Tade, M.O.; Zou, J.; Li, Q. A novel bottom-up solvothermal synthesis of carbon nanosheets. J. Mater. Chem. A 2014, 2, 2390. [Google Scholar] [CrossRef]
- Collin, R.E. Field Theory of Guided Waves, 2nd ed.; IEEE-Press: Piscataway, NJ, USA, 1991. [Google Scholar]
- Senior, T.B.A.; Volakis, J.L. Approximate Boundary Conditions in Electromagnetics; No. 41; IET: London, UK, 1995. [Google Scholar]
- Bird, T.; Antengenuity, Eastwood NSW, Australia. Personal communication, 2017.
- Mathworks Inc. Available online: www.MATHWORKS.com (accessed on 6 December 2018).
- CST Microwave Studio. Available online: www.cst.com (accessed on 6 December 2018).
- FEKO. EM Software & Systems. Available online: www.feko.info (accessed on 6 December 2018).
- Kline, M. Euler and Infinite Series. Math. Mag. 1983, 56, 307–314. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products, 7th ed.; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
Sample Availability: Matlab codes to reproduce the figures are accessible via the Code Oceans®, https://doi.org/10.24433/CO.742c3ef5-4861-4d48-92a2-b2c45c669d3d; Simulation models to verify the modelling results are available via FigShare®, https://figshare.com/s/1116824ed2b8477319d2. |











© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahpari, M. Determination of Complex Conductivity of Thin Strips with a Transmission Method. Electronics 2019, 8, 21. https://doi.org/10.3390/electronics8010021
Shahpari M. Determination of Complex Conductivity of Thin Strips with a Transmission Method. Electronics. 2019; 8(1):21. https://doi.org/10.3390/electronics8010021
Chicago/Turabian StyleShahpari, Morteza. 2019. "Determination of Complex Conductivity of Thin Strips with a Transmission Method" Electronics 8, no. 1: 21. https://doi.org/10.3390/electronics8010021