A Novel Approach to Semantic Similarity Measurement Based on a Weighted Concept Lattice: Exemplifying Geo-Information
Abstract
:1. Introduction
2. Background
3. Weighted Concept Lattice
3.1. Knowledge Representation of the Feature Model
3.2. Combined Weight of Attribute
3.2.1. Inclusion Degree Importance of a Property
3.2.2. Formal Context
3.2.3. Information Entropy of Attributes
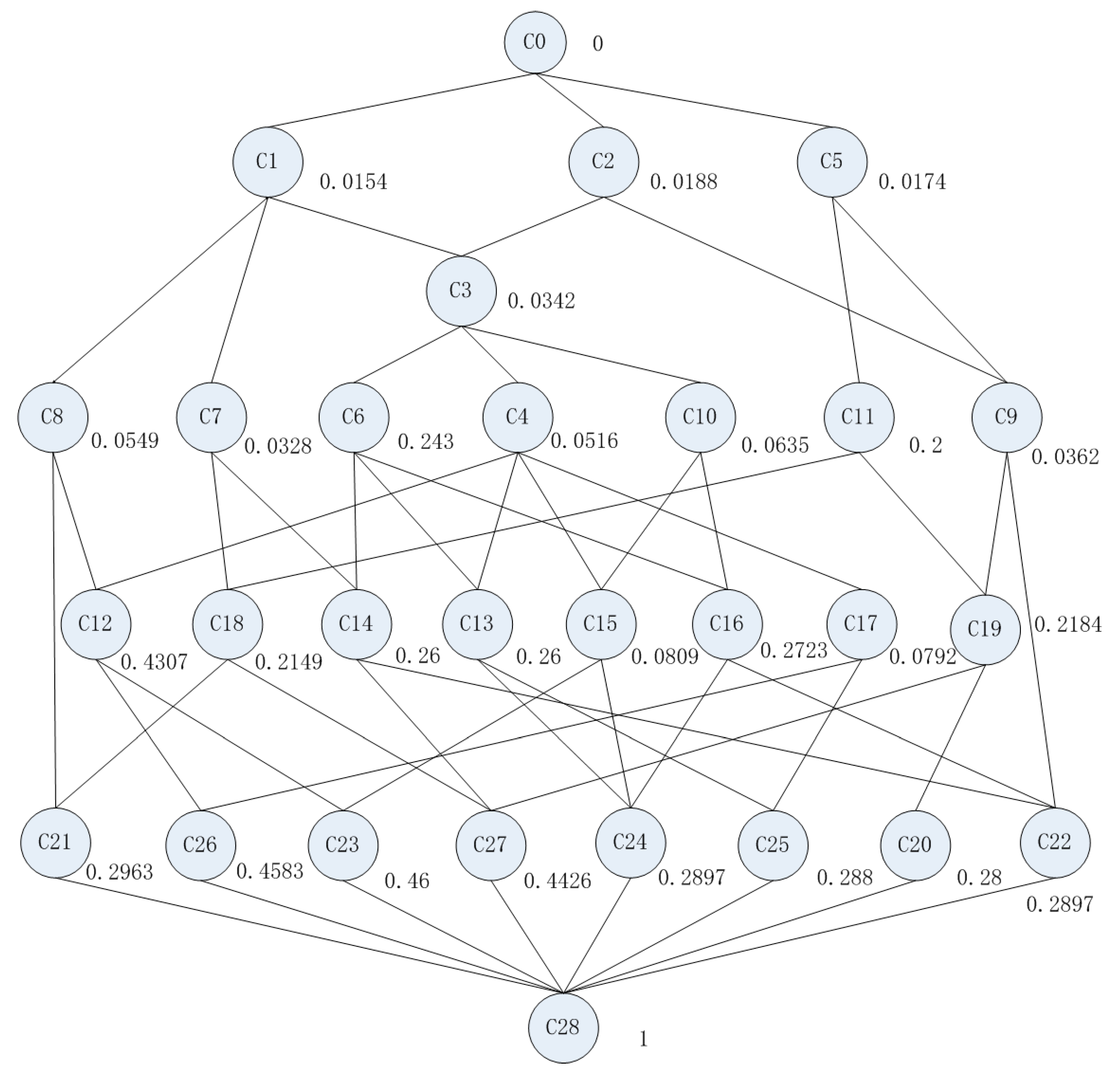
3.3. Construction of the Weighted Concept Lattice
4. Semantic Similarity Measurement
4.1. Relative Hierarchical Depth
4.2. Semantic Similarity Model
5. Case Study and Discussion
6. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Varelas, G.; Voutsakis, E.; Raftopoulou, P.; Petrakis, E.G.; Milios, E.E. Semantic similarity methods in wordNet and their application to information retrieval on the web. In Proceedings of the 7th Annual ACM International Workshop on Web Information and Data Management, Bremen, Germany, 31 October–5 November 2005; ACM: New York, NY, USA, 2005; pp. 10–16. [Google Scholar]
- Rodríguez, M.A.; Rodríguez, M.J. Determining semantic similarity among entity classes from different ontologies. IEEE Trans. Knowl. Data Eng. 2003, 15, 442–456. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Schwering, A. Approaches to Semantic Similarity Measurement for Geo-Spatial Data: A Survey. Trans. GIS 2008, 12, 5–29. [Google Scholar] [CrossRef]
- Resnik, P. Semantic similarity in a taxonomy: An information-based measure and its application to problems of ambiguity in natural language. J. Artif. Intell. Res. 1999, 11, 95–130. [Google Scholar]
- Pedersen, T.; Patwardhan, S.; Michelizzi, J. WordNet:: Similarity: Measuring the relatedness of concepts. In Proceedings of the Demonstration Papers at HLT-NAACL 2004, Boston, MA, USA, 2–7 May 2004; Association for Computational Linguistics: Stroudsburg, PA, USA, 2004; pp. 38–41. [Google Scholar]
- Ballatore, A.; Bertolotto, M.D.; Wilson, C. Geographic knowledge extraction and semantic similarity in OpenStreetMap. Knowl. Inf. Syst. 2013, 37, 61–81. [Google Scholar] [CrossRef]
- Rodríguez, M.A.; Egenhofer, M.J. Comparing geospatial entity classes: An asymmetric and context-dependent similarity measure. Int. J. Geogr. Inf. Sci. 2004, 18, 229–256. [Google Scholar] [CrossRef]
- Tversky, A.; Gati, I. Similarity, separability, and the triangle inequality. Psychol. Rev. 1982, 89, 123. [Google Scholar] [CrossRef] [PubMed]
- Luger, G.F. Artificial Intelligence: Structures and Strategies for Complex Problem Solving; Pearson: Boston, MA, USA, 2005. [Google Scholar]
- Gentner, D.; Arthur, A.B. Structure mapping in analogy and similarity. Am. Psychol. 1997, 52, 45. [Google Scholar] [CrossRef]
- Schwering, A. Hybrid model for semantic similarity measurement. In Proceedings of the OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”, Rhodes, Greece, 23–27 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1449–1465. [Google Scholar]
- Goldstone, R.L.; Son, J.Y. The transfer of scientific principles using concrete and idealized simulations. J. Learn. Sci. 2005, 14, 69–110. [Google Scholar] [CrossRef]
- Torgerson, W.S. Multidimensional scaling of similarity. Psychometrika 1965, 30, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Gärdenfors, P. Conceptual Spaces: The Geometry of Thought; MIT Press: London, UK, 2004. [Google Scholar]
- Schwering, A.; Raubal, M. Spatial relations for semantic similarity measurement. In Proceedings of the International Conference on Conceptual Modeling, Klagenfurt, Austria, 24–28 October 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 259–269. [Google Scholar]
- Janowicz, K.; Wilkes, M. Sim-dla: A novel semantic similarity measure for description logics reducing inter-concept to inter-instance similarity. In Proceedings of the European Semantic Web Conference, Crete, Greece, 31 May–4 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 353–367. [Google Scholar]
- Janowicz, K. Sim-DL: Towards a Semantic Similarity Measurement Theory for the Description Logic ALCNR in Geographic Information Retrieval. In Proceedings of the OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”, Montpellier, France, 29 October–3 November 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1681–1692. [Google Scholar]
- Janowicz, K.; Raubal, M.; Kuhn, W. The semantics of similarity in geographic information retrieval. J. Spat. Inf. Sci. 2011, 29–57. [Google Scholar] [CrossRef]
- Kim, J.; Vasardani, M.; Winter, S. Similarity matching for integrating spatial information extracted from place descriptions. J. Spat. Inf. Sci. 2017, 31, 56–80. [Google Scholar] [CrossRef]
- Francis-Landau, M.; Durrett, G.; Klein, D. Capturing semantic similarity for entity linking with convolutional neural networks. arXiv, 2016; arXiv:1604.00734. [Google Scholar]
- Mihalcea, R.; Wiebe, J. Simcompass: Using deep learning word embeddings to assess cross-level similarity. In Proceedings of the 8th International Workshop on Semantic Evaluation (SemEval 2014), Dublin, Ireland, 23–24 August 2014; Volume 2014, p. 560. [Google Scholar]
- Harispe, S.; Ranwez, S.; Janaqi, S.; Montmain, J. Semantic Similarity from Natural Language and Ontology Analysis; Morgan & Claypool Publishers: San Rafael, CA, USA, 2015; pp. 85–86. [Google Scholar]
- Bulskov, H.; Knappe, R.; Andreasen, T. On measuring similarity for conceptual querying. In Proceedings of the 5th International Conference on Flexible Query Answering Systems, Copenhagen, Denmark, 27–29 October 2002; Springer: London, UK, 2002; pp. 100–111. [Google Scholar]
- Alvarez, M.; Yan, C. A graph-based semantic similarity measure for the gene ontology. J. Bioinform. Comput. Biol. 2011, 9, 681–695. [Google Scholar] [CrossRef]
- Olsson, C.; Petrov, P.; Sherman, J.; Perez-Lopez, A. Finding and explaining similarities in Linked Data. In Proceedings of the Semantic Technology for Intelligence, Defense, and Security (STIDS 2011), Fairfax, VA, USA, 16–17 November 2011; pp. 52–59. [Google Scholar]
- Sánchez, D.; Batet, M.; Isern, D.; Valls, A. Ontology-based semantic similarity: A new feature-based approach. Expert Syst. Appl. 2012, 39, 7718–7728. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cross, V.; Yu, X. A fuzzy set framework for ontological similarity measures. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Mazandu, G.K.; Mulder, N.J. Information content-based Gene Ontology semantic similarity approaches: Toward a unified framework theory. BioMed Res. Int. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Saini, M.; Siddiqi, S. Graph-based computational model for computing semantic similarity. In Proceedings of the Emerging Research in Computing, Information, Communication and Applications (ERCICA2013), Bangalore, India, 2–3 August 2013; Elsevier: New Delhi, India, 2013; pp. 501–507. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer: Berlin, Germany, 1999. [Google Scholar]
- Stumme, G.; Adche, M.A. FCA-Merge: Bottom-up merging of ontologies. In Proceedings of the Seventeenth International Conference on Artificial Intelligence (IJCAI’01), Seattle, WA, USA, 4–10 August 2001; pp. 225–230. [Google Scholar]
- Kokla, M.; Kavouras, M. Fusion of top-level and geographical domain ontologies based on context formation and complementarity. Int. J. Geogr. Inf. Sci. 2001, 15, 679–687. [Google Scholar] [CrossRef]
- Xiao, J.; He, Z. A Concept Lattice for Semantic Integration of Geo-Ontologies Based on Weight of Inclusion Degree Importance and Information Entropy. Entropy 2016, 18, 399. [Google Scholar] [CrossRef]
- Borst, P.; Akkermans, H.; Top, J. Engineering ontologies. Int. J. Hum.-Comput. Stud. 1997, 46, 365–406. [Google Scholar] [CrossRef]
- Sowa, J.F. Knowledge Representation: Logical, Philosophical, and Computational Foundations; Brooks/Cole: Pacific Grove, CA, USA, 2000; Volume 13. [Google Scholar]
- Bechhofer, S. OWL: Web ontology language. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; pp. 2008–2009. [Google Scholar]
- Guarino, N.; Welty, C. A formal ontology of properties. In Proceedings of the International Conference on Knowledge Engineering and Knowledge Management, Juan-les-Pins, France, 2–6 October 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 97–112. [Google Scholar]
- Kavouras, M.; Kokla, M.; Tomai, E. Comparing categories among geographic ontologies. Comput. Geosci. 2005, 31, 145–154. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Ji, J.; Wu, G.X.; Li, W. Significance of attribute based on inclusion degree. J. Jiangxi Norm. Univ. (Nat. Sci.) 2009, 33, 656–660. (In Chinese) [Google Scholar]
- Hahn, U.; Chater, N.; Richardson, L.B. Similarity as transformation. Cognition 2003, 87, 1–32. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X. A new model of evaluating concept similarity. Knowl.-Based Syst. 2008, 21, 842–846. [Google Scholar] [CrossRef]
- Formica, A. Concept Similarity in Formal Concept Analysis: An Information Content Approach; Elsevier Science Publishers B.V.: New York, NY, UK, 2008. [Google Scholar]
- Ballatore, A.; Bertolotto, M.D.; Wilson, C. An evaluative baseline for geo-semantic relatedness and similarity. GeoInformatica 2014, 18, 747–767. [Google Scholar] [CrossRef]

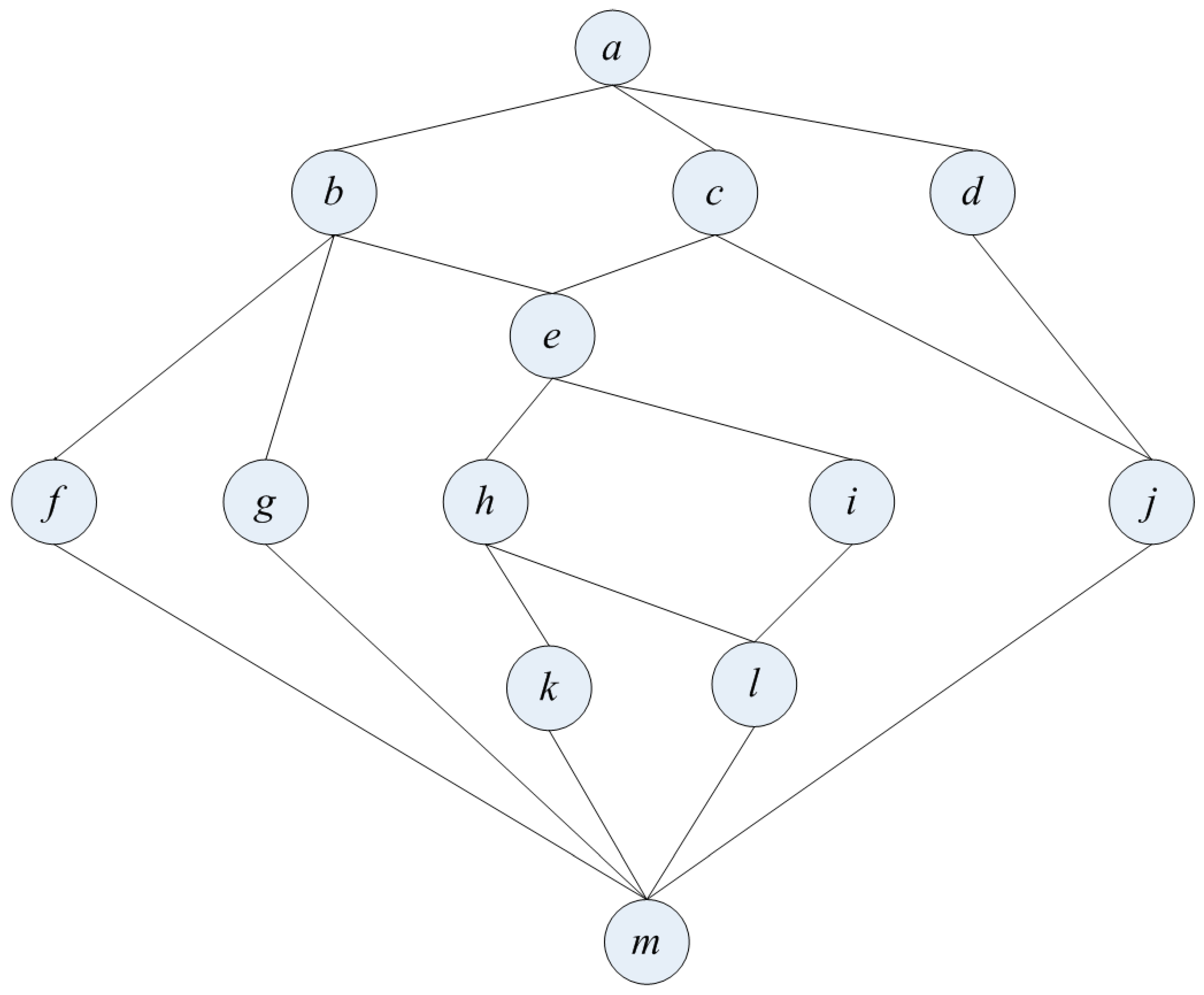
| Concept | Material | Cause | Spatial Morphology | Spatial Location | Time | Material State | Function |
|---|---|---|---|---|---|---|---|
| lake | a | c | f | h | j | o | |
| pond | a | d | f | h | j | o | |
| seasonal lake | a | c | f | h | k | o | |
| ground river | a | c | e | h | j | l | m |
| seasonal river | a | c | e | h | k | l | m |
| reservoir | a | d | f | h | (n, o) | ||
| spillway | a | d | e | i | n | ||
| dike | b | d | g | h | n |
| Identifier | a | b | c | d | e | f |
| Attribute | material/ | material/ | cause/ | cause/ | spatial morphology/ | spatial morphology/ |
| water | soil or stone | nature | artificial | long strip slot | depressions | |
| Identifier | g | h | i | j | k | l |
| Attribute | spatial morphology/ | spatial location/ | spatial location/ | time/ | time/ | material state/ |
| buildings | on the earth | underground | perennial | seasonal | flow | |
| Identifier | m | n | o | |||
| Attribute | function/ | function/ | function/ | |||
| shipping | prevent flood | store water |
| Concept | Material | Cause | Spatial Morphology | Spatial Location | Time | Material State | Function | Category |
|---|---|---|---|---|---|---|---|---|
| lake | a | c | f | h | j | o | 230,000 | |
| pond | a | d | f | h | j | o | 230,000 | |
| seasonal lake | a | c | f | h | k | o | 230,000 | |
| ground river | a | c | e | h | j | l | m | 210,000 |
| seasonal river | a | c | e | h | k | l | m | 210,000 |
| reservoir | a | d | f | h | (n, o) | 240,000 | ||
| spillway | a | d | e | i | n | 240,000 | ||
| dike | b | d | g | h | n | 270,000 |
| SN | Object | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lake | * | * | * | * | * | * | ||||||||||
| pond | * | * | * | * | * | * | ||||||||||
| seasonal lake | * | * | * | * | * | * | ||||||||||
| ground river | * | * | * | * | * | * | * | |||||||||
| seasonal river | * | * | * | * | * | * | * | |||||||||
| reservoir | * | * | * | * | * | * | ||||||||||
| spillway | * | * | * | * | * | |||||||||||
| dike | * | * | * | * | * |
| Inclusion Degree | Material | Cause | Spatial Morphology | Spatial Location | Time | Material State | Function |
|---|---|---|---|---|---|---|---|
| SIG (property) | 0.0145 | 0.0055 | 0.0177 | 0.0177 | 0.0875 | 0.0266 | 0.0816 |
| Attribute | p (x) | E (x) | SIG (x) | w (x) |
|---|---|---|---|---|
| a | 0.875 | 0.169 | 0.0072 | 0.0153 |
| b | 0.125 | 0.375 | 0.0072 | 0.0342 |
| c | 0.500 | 0.500 | 0.0028 | 0.0174 |
| d | 0.500 | 0.500 | 0.0028 | 0.0174 |
| e | 0.375 | 0.531 | 0.0059 | 0.0395 |
| f | 0.500 | 0.500 | 0.0059 | 0.0372 |
| g | 0.125 | 0.375 | 0.0059 | 0.0279 |
| h | 0.875 | 0.169 | 0.0089 | 0.0188 |
| i | 0.125 | 0.375 | 0.0089 | 0.0419 |
| j | 0.375 | 0.531 | 0.0044 | 0.0293 |
| k | 0.250 | 0.500 | 0.0044 | 0.0276 |
| l | 0.250 | 0.500 | 0.0266 | 0.168 |
| m | 0.250 | 0.500 | 0.0272 | 0.1716 |
| n | 0.375 | 0.531 | 0.0272 | 0.1821 |
| o | 0.500 | 0.500 | 0.0272 | 0.1716 |
| 1 | 0.943 | 0.907 | 0.458 | 0.305 | 0.707 | 0.196 | 0.195 | |
| 0.943 | 1 | 0.819 | 0.321 | 0.205 | 0.822 | 0.29 | 0.333 | |
| 0.911 | 0.822 | 1 | 0.304 | 0.343 | 0.709 | 0.196 | 0.194 | |
| 0.473 | 0.378 | 0.366 | 1 | 0.937 | 0.248 | 0.355 | 0.225 | |
| 0.366 | 0.284 | 0.395 | 0.939 | 1 | 0.247 | 0.355 | 0.225 | |
| 0.627 | 0.692 | 0.628 | 0.241 | 0.241 | 1 | 0.62 | 0.629 | |
| 0.2 | 0.294 | 0.201 | 0.293 | 0.294 | 0.69 | 1 | 0.648 | |
| 0.188 | 0.328 | 0.189 | 0.135 | 0.135 | 0.719 | 0.658 | 1 |
| 1 | 0.83 | 0.83 | 0.62 | 0.46 | 0.67 | 0.18 | 0.18 | |
| 0.83 | 1 | 0.67 | 0.46 | 0.31 | 0.83 | 0.36 | 0.36 | |
| 0.83 | 0.67 | 1 | 0.46 | 0.62 | 0.67 | 0.18 | 0.18 | |
| 0.62 | 0.46 | 0.46 | 1 | 0.86 | 0.31 | 0.33 | 0.17 | |
| 0.46 | 0.31 | 0.62 | 0.86 | 1 | 0.31 | 0.33 | 0.17 | |
| 0.67 | 0.83 | 0.67 | 0.31 | 0.31 | 1 | 0.55 | 0.55 | |
| 0.18 | 0.36 | 0.18 | 0.33 | 0.33 | 0.55 | 1 | 0.40 | |
| 0.18 | 0.36 | 0.18 | 0.17 | 0.17 | 0.55 | 0.40 | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; He, Z. A Novel Approach to Semantic Similarity Measurement Based on a Weighted Concept Lattice: Exemplifying Geo-Information. ISPRS Int. J. Geo-Inf. 2017, 6, 348. https://doi.org/10.3390/ijgi6110348
Xiao J, He Z. A Novel Approach to Semantic Similarity Measurement Based on a Weighted Concept Lattice: Exemplifying Geo-Information. ISPRS International Journal of Geo-Information. 2017; 6(11):348. https://doi.org/10.3390/ijgi6110348
Chicago/Turabian StyleXiao, Jia, and Zongyi He. 2017. "A Novel Approach to Semantic Similarity Measurement Based on a Weighted Concept Lattice: Exemplifying Geo-Information" ISPRS International Journal of Geo-Information 6, no. 11: 348. https://doi.org/10.3390/ijgi6110348
APA StyleXiao, J., & He, Z. (2017). A Novel Approach to Semantic Similarity Measurement Based on a Weighted Concept Lattice: Exemplifying Geo-Information. ISPRS International Journal of Geo-Information, 6(11), 348. https://doi.org/10.3390/ijgi6110348





