Free and Forced Vibration of Laminated and Sandwich Plates by Zig-Zag Theories Differently Accounting for Transverse Shear and Normal Deformability

Abstract

A number of mixed and displacement-based zig-zag theories are derived from the zig-zag adaptive theory (ZZA). As a consequence of their different assumptions on displacement, strain, and stress fields, and layerwise functions, these theories account for the transverse shear and normal deformability in different ways, but their unknowns are independent of the number of layers. Some have features that are reminiscent of ones that have been published in the literature for the sake of comparison. Benchmarks with different length-to-thickness ratios, lay-ups, material properties, and simply supported or clamped edges are studied with the intended aim of contributing toward better understanding the influence of transverse anisotropy on free vibration and the response of blast-loaded, multilayered, and sandwich plates, as well as enhancing the existing database. The results show that only theories whose layerwise contributions identically satisfy interfacial stress constrains and whose displacement fields are redefined for each layer provide results that are in agreement with elasticity solutions and three-dimensional (3D) finite element analysis (FEA) (mixed solid elements with displacements and out-of-plane stresses as nodal degrees of freedom (d.o.f.)) with a low expansion order of polynomials in the in-plane and out-of-plane directions. The choice of their layerwise functions is shown to be immaterial, while theories with fixed kinematics are shown to be strongly case-sensitive and often inadequate (even for slender components).

1. Introduction

Fibre-reinforced laminated and sandwich composites are fundamental to obtain a faster speed, longer range, larger payloads, less engine power, and a better operating economy of land, sea, and aerospace vehicles. Indeed, they possess excellent specific strength and stiffness properties along with many other advantages. However, their behaviour may be strongly influenced by local effects in their multi-phase structure, which can cause a relevant loss of strength and stiffness, and even lead to a possible catastrophic failure in service. To avert this, a three-dimensional description of their displacement and stress fields is required in the computer simulations. Displacements are no longer C¹-continuous as in homogeneous non-layered materials, but instead they should be C⁰-continuous (zig-zag effect), this being the only way to guarantee the continuity of transverse shear and normal stresses and of the transverse normal stress gradient that is necessary to satisfy the fulfillment of local equilibrium equations in layered materials.

A multitude of theories is currently available for laminated and sandwich composites, which account for layerwise effects at varying degrees of accuracy and computational costs. The papers by Carrera et al. [1,2] and by Demasi [3] are cited wherein a broad discussion of this matter can be found. Theories can be summarily categorized into equivalent single-layer (ESL), discrete-layer (DL), and zig-zag (ZZ) formulations, and further into displacement-based and mixed theories, because displacements, strains, and stress fields can be chosen separately from one another.

Given the limited accuracy offered by ESL even to predict overall response quantities for certain loading, material properties, and stack-up [4,5], they still remain widespread by virtue of their low computational cost (see Burlayenko et al. [6] and by Jun et al. [7]), but nowadays, DL and ZZ are becoming more and more widespread in their applications. Indeed, they have the merit of accurately predicting the displacement and stress fields irrespective of lay-up, layer properties, and loading or boundary conditions. However, DL could overwhelm the computational capacity when structures of industrial interest are analysed (unless their use is limited to critical areas) due to having too many variables. Instead, ZZ having intermediate characteristics between ESL and DL can strike the right balance between accuracy and cost-saving, allowing designers’ demand of theories to be met in a simple, already accurate form. In particular, ZZ accounting for the transverse normal deformability effect has been proven to be suitable for carrying out ply-level stress analyses at a lower cost than DL.

Relevant examples of dynamic studies carried out by DL and ZZ that highlight their superior performance include the papers by [1,2,3,6,7] Boscolo and Banerjee [8], Khdeir and Aldraihem [9], Sayyad and Ghugal [10], Kazanci [11], Lin and Zhang [12], Vescovini et al. [13], and in addition to the previous ones, [14,15,16,17,18,19] are also cited. Moreover, papers [1,2,3,4,5,8,13,20] are examples that prove the limitations of ESL and the importance of the transverse normal deformability under static localised loading for certain boundary conditions and lay-ups [21] and even for accurately predicting the first free-vibration mode frequencies. Although ZZ theories are ultimately finding an ever-increasing number of applications thanks to their accuracy at an affordable cost, the literature shows that undeservedly Di Sciuva’s zig-zag-like fuction DZZ is less used than Murakami’s zig-zag-like fuction MZZ (for a definition of acronyms, see

Table 1. Acronyms.

Acronym	Meaning	Acronym	Meaning
3D FEA	Mixed solid 3D elements (Ref. [48]).	MHR	HR mixed theory with Murakami’s zig-zag function (see Section 4.1, Ref. [47]).
DL	Discrete-layer theories.	MHR±	MHR with slope defined on a physical basis (see Section 4.1).
DZZ	Di Sciuva’s zig-zag theory (Ref. [22]).	MHR4	MHR with fourth-order polynomial transverse displacement (see Section 4.2, Ref. [47]).
EFSDT	Theory from Ref. [49].	MHR4±	MHR4 with slope defined on a physical basis (see Section 4.2).
EHSDT	Theory from Ref. [49].	MHWZZA	Modified HWZZ theory, type A (see Section 4.2, Ref. [47]).
ESL	Equivalent single-layer.	MHWZZA4	Modified MHWZZA theory, with fourth-order piecewise polynomial transverse displacement (see Section 4.2, Ref. [47]).
FSDT	First-order shear deformation theory.	MZZ	Murakami’s like zig-zag theory (Ref. [23]).
HR	Hellinger–Reissner variational theorem.	PVW	Principle of virtual work.
HRZZ	HR zig-zag theory (see Section 4.3, Ref. [47]).	RFSDT	Theory from Ref. [50].
HRZZ PP	Post-processed HRZZ (see Section 4.3).	RHQ40	Finite element from Ref. [50].
HRZZ4	HRZZ with fourth-order polynomial transverse displacement (see Section 4.3, Ref. [47]).	RHSDT	Theory from Ref. [50].
HSDT	Higher-order shear deformation theory.	RZT	Theory from Ref. [42].
HW	Hu–Washizu variational theorem.	SEUPT	Strain energy update technique (Ref. [29]).
HWg	Hu–Washizu canonical functional (see Section 2.1).	TOT	Theory from Ref. [5].
HWZZ	HW zig-zag mixed theory (see Section 3.2, Ref. [47]).	ZIGT	Theory from Ref. [5].
HWZZM	Modified HWZZ theory, type M, (see Section 3.3.1).	ZZ	Plate theories with zig-zag contributions.
HWZZM*	Modified HWZZ theory, type M*, (see Section 3.3.2).	ZZA	Zig-zag adaptive theory (see Section 3.1, Ref. [29]).
HWZZM(†)	Modified HWZZM theories, type † (see Section 3.3.2.2).	ZZA*	Modified ZZA theory (see Section 3.1.1).

† = A, B, B2, C, C2, 0 (variants of theory).

), despite their better accuracy with a low order of expansion of analytical solutions, as also demonstrated by the numerical results of this paper.

To contribute to the dissemination of DZZs and their further development, hereafter the typologies and specific characteristics of available ZZs are briefly reviewed. The intended aim is to explain the different behaviour of DZZ and MZZ as a consequence of their different layerwise contributions, namely Di Sciuva’s [22] (DZZ) or Murakami’s [23] (MZZ) zig-zag functions.

DZZ incorporates layerwise contributions as the product of assumed zig-zag functions and zig-zag amplitudes, the latter being computed to a priori satisfy the interfacial compatibility of out-of-plane stresses (for this reason, they are referred in literature as physically-based ZZ). Instead, MZZ assumes zig-zag functions that a priori feature a periodic change of the slope of displacements at interfaces, irrespective of the stack-up. As a consequence, stresses are assumed apart from the kinematics within the framework of Hellinger–Reissner variational theorem. For this reason, they are called kinematic-based ZZ. So, the development of MZZ is easier, and an efficient C⁰ formulation can more easily be generated, but they could not appropriately represent the displacement fields when the orientation angle of layers is aperiodic, as shown in the literature. According to findings by [1,2,5,24,25,26], it can be stated in general that MZZ are accurate only with a rather high expansion order of variables across the thickness and in the in-plane directions. As shown in [27,28,29,30,31,32,33], instead, DZZ accurately predict displacements and (very often but not in all cases) stresses with a lower expansion order.

As shown in the papers by Carrera et al. [1,2,24,25,26], Demasi [3], Mattei and Bardella [27], Icardi et al. [28,29], Li and Liu [30], Zhen and Wanji [31,32], and Shariyat [33], the transverse normal deformability, which is usually neglected because it is erroneously considered of little importance, on the contrary should be accounted for. Indeed, his contribution becomes of primary importance when boundary conditions other than simply-supported edges are considered, under a strong variation of mechanical properties across the thickness and for localised loading. However, a rather complex formulation of theories, i.e., with a sufficient number of parameters that can be defined in order to satisfy all of the relevant physical constraints, is required for these cases. Although very often power and Taylor’s series expansions are used across the thickness, hierarchic polynomials, and trigonometric and exponential functions, a combination of both or radial basis functions could be required to more efficiently represent variables [34,35,36,37,38,39].

The idea of separately hiring kinematics and stresses, so as to account for the transverse normal deformation without having to represent in a piecewise way the transverse displacement, was applied by Barut et al. to DZZ [40]. Other mixed DZZ that are based on a similar idea have a rather simple kinematics, but yet, the capability to quite accurately predict stresses has been formerly developed in HR form by Kim and Cho [41] and Tessler et al. [42]

Despite the notable contributions mentioned up to now, further research is required on ZZ because recent studies by Zhen and Wanji [43], Gherlone [44], and Groh and Weaver [45] have shown that MZZ could be less accurate than RZT [42], assuming the same degree of representation across the thickness, while [43] shows just the opposite for different cases. So, it is necessary to ascertain even whether three-dimensional (3D) DZZ can be as accurate as MZZ with a minor computational burden, so as to be effectively suitable for industrial purposes, considering also other theories in addition to those already examined in [44,45], especially those with a piecewise representation of the transverse displacement.

A massive amount of free vibration studies is currently found in the literature for cross-ply laminates, but other boundary conditions and lay-up that are equally interesting for practical applications need to be considered when testing the accuracy of theories (see, e.g., Li et al. [46]). It should be noted that for clamped edges, an incorrect vanishing transverse shear force resultant is predicted by ESL plate models; therefore, it is necessary to check on an adequate number of cases as to whether DZZ are immune from such mistakes. Also, lay-ups with a quite large variation of properties of layers, and in particular soft-core sandwiches, should be investigated to enhance the existing database. Another subject that needs further studies is what happens when zig-zag functions that are different from those commonly used [22,23] are assumed. It is also necessary to better clarify what effects have an a priori assumption of certain zig-zag amplitudes at certain interfaces, or even to all of the interfaces such as in MZZ, in order to save costs.

To contribute to this matter, in this paper, zig-zag theories in displacement-based and mixed form are particularized from the ZZA 3D zig-zag theory [29], assuming different layerwise functions. Consider that ZZA, here schematically defined as the adaptive zig-zag theory, assumes a variable kinematics with fixed degrees of freedom (d.o.f.) that consist of in-plane and transverse displacements $u_{\alpha }{}^0$, $w^0$ and transverse shear rotations ${\mathsf{\Gamma }}_{\alpha }^0$ at a middle reference plane. Moreover, it should be noticed that ZZA is capable of great accuracy, even with strong anisotropy at a cost that is still comparable to that of ESL.

The purpose of this paper is to test the accuracy of theories derived from ZZA under simplified hypotheses on displacement, deformations, and stress fields, so as to further reduce the computational cost, in order to assess whether and when the accuracy of ZZA can be preserved. The accuracy and the efficiency of these theories, which for the most part allow a redefinition of the coefficients layer-by-layer so as to satisfy all of the physical constraints and account for the normal transverse deformability effect (although in different ways), are assessed considering the free vibration and the response behaviour of blast-loaded multilayered and sandwich plates.

A new theory referred to as ZZA* is developed from ZZA in order to prove that once the coefficients of displacements are redefined across the thickness, the same accuracy degree can be achieved irrespective of the layerwise functions that are chosen. It will also be shown that as the coefficient is redefined, the same results are obtained even when zig-zag contributions do not explicitly appear. Other theories have been previously developed by the authors [47] in displacement-based and mixed form, either with Di Sciuva’s or Murakami’s zig-zag-like functions, and which also have characteristics similar to other theories that are already known in the literature, are considered for comparison.

Numerical applications aim to show the superiority of ZZA* over ZZA, including its lower computational costs with the same accuracy, for the quite large range of variation of lay-ups and boundary conditions that are considered. Benchmarks that are either retaken from the literature or new are considered, the former in order to enable a comparison of available theories, and the latter in order to enhance the existing database. The results by the present theories are compared to exact solutions whenever available or to 3D finite element analysis (FEA) [48]. The findings can be categorized as the new results of known benchmarks provided by the new theories and entirely new results for the new benchmarks, which could serve as test beds for future analytical and finite element models.

This study also aims to show the superiority of ZZA* over all of the other theories considered for most of the cases, since the use of simplified assumptions implies a loss of accuracy. It will be shown that the accuracy of the simplified theories, in particular those of Murakami, is strongly case-sensitive; therefore, they cannot be used interchangeably. Studies are carried out in closed form considering the free and forced vibrations of laminated and sandwich beams and plates, simply-supported and clamped edges, different lay-ups, and distinctly different material properties of constituent layers, so as to give rise to relevant 3D effects.

2. Preliminaries and Notations

Constituent layers are assumed to have a uniform arbitrary thickness $h^k$ and linear elastic properties. They are assumed to be perfectly bonded to each other and, as usual when the global-scale response is examined, the existing bonding resin interlayer is disregarded. For the same reason, sandwiches are described in homogenised form as multilayered structures with one or more thick soft intermediate layers as the cores, with the cell-scale effects being disregarded.

A rectangular, right-handed Cartesian coordinate reference system ($x,y,z$) is assumed as the reference frame, having ($x,y$) on the middle reference plane $\mathsf{\Omega }$ of the laminated plate (origin in the lower left edge) and $z$ as the thickness coordinate ($z\in [-0.5h,0.5h]$, with $h$ being the overall thickness). Lx and Ly symbolise the plate side-length in the x and y-directions, while ${}^{(k)}{z}^{+}$ and ${}^{(k)}{z}^{-}$ represent the upper and lower positions of the layer interfaces, respectively. Subscripts _k and superscripts ^k are used to indicate that a quantity belongs to the layer $k$, while ^u and _l mark the upper and lower faces of the laminate, and a comma is used to indicate spatial derivatives, e.g., ${(.)}_{,x}=\partial /\partial x$, ${(.)}_{,z}=\partial /\partial z$. The elastic in-plane and transverse displacement components are indicated as $u_{\alpha }$ and $u_{\varsigma }$, respectively. Strains are assumed to be infinitesimal and, to distinguish their origin, they are specified as ${\epsilon }_{ij}^u=1/2(u_{i,j}+u_{j,i})$, ${\epsilon }_{ij}^{\sigma }={(E_{ijkl})}^{-1}{\sigma }_{kl}$, respectively when they come from kinematic ${[.]}^u$ or stress-strain ${[.]}^{\sigma }$ relations. Once assumed as primary variables, they are indicated as ${\epsilon }_{ij}$, ${\epsilon }_{\alpha \varsigma }$, ${\epsilon }_{\varsigma \varsigma }$ ($i,j\equiv 1,2$; $\alpha \equiv x$, $\beta \equiv y$; $3\equiv \varsigma \equiv z$; ${\gamma }_{\alpha \beta }=2{\epsilon }_{\alpha \beta }$). Stresses from stress–strain constitutive relations are indicated as ${\sigma }_{ij}^{\epsilon }=E_{ijkl}{\epsilon }_{kl}$ $(C_{ijkl}=E_{ijkl}{}^{-1})$, while when they are assumed as primary variables, they are indicated as ${\sigma }_{ij}$, ${\sigma }_{\alpha \varsigma }$, ${\sigma }_{\varsigma \varsigma }$.

2.1. Recalls on Mixed Variational Theorems

Here a generalized version of Hu-Washizu theorem is used, whose primary displacement boundary condition link is weakened as ${\displaystyle {\int }_{S_u}(u_i}-{\tilde{u}}_i)n_j\partial {\sigma }_{ij}dS=0$ and which generates the following variational statement:

$$\begin{array}{l}\partial {\mathsf{\Pi }}_{HW}^g={\displaystyle \underset{V}{\int }[(}{\epsilon }_{ij}^u-{\epsilon }_{ij})\partial {\sigma }_{ij}+({\sigma }_{ij}^{\epsilon }-{\sigma }_{ij})\partial {\epsilon }_{ij}+{\sigma }_{ij}\partial {\epsilon }_{ij}^u-b_i\partial u_i]dv-{\displaystyle \underset{S_t}{\int }{\tilde{t}}_i\partial }{u}_{i}ds-\\ {\displaystyle \underset{S_u}{\int }[(u_i}-{\tilde{u}}_i)n_j\partial {\sigma }_{ij}+{\sigma }_{ij}{n}_j\partial u_i]ds=0\end{array}$$

(1)

Here $H{W}^g$ represents the canonical functional, $n_j$ are the components of the external unit normal to the volume bounding surface, $b_i$ are the components of body forces (they will contain inertial forces, as explained in (4)) and ${\displaystyle \underset{V}{\int }(}{\epsilon }_{ij}^u-{\epsilon }_{ij})\partial {\sigma }_{ij}dv$, ${\displaystyle \underset{V}{\int }({\sigma }_{ij}^{\epsilon }-{\sigma }_{ij})\partial {\epsilon }_{ij}}dv$ ensure the consistency of assumed strain and stress fields with their counterparts obtained from stress-strain and strain-displacement relations. As usual, the prismatic volume $V$ of the laminated plates is assumed to be bounded by a surface $S$ that is split into a surface $S_t$ on which surface tractions are prescribed and a surface $S_u$ on which surface displacements are prescribed. Body forces $b_i$ on $V$, prescribed surface tractions ${\tilde{t}}_i$ on $S_t$ and prescribed displacements ${\tilde{u}}_i$ on $S_u$ are assumed to act.

Theories with displacements and out of plane stresses assumed separately are developed from the HR variational theorem:

$$\begin{array}{l}\partial {\mathsf{\Pi }}_{HR}={\displaystyle \underset{V}{\int }[}{\sigma }_{ij}^{}\partial {\epsilon }_{ij}^u+({\gamma }_{i3}^u-{\gamma }_{i3}^{\sigma })\partial {\sigma }_{i3}+({\epsilon }_{33}^u-{\widehat{\epsilon }}_{33}^{\sigma })\partial {\sigma }_{33}-b_i\partial u_i]dv-{\displaystyle \underset{S_t}{\int }{\tilde{t}}_i\partial }{u}_{i}ds-\\ {\displaystyle \underset{S_u}{\int }[(u_i}-{\tilde{u}}_i)n_j\partial {\sigma }_{ij}+{\sigma }_{ij}{n}_j\partial u_i]ds=0\end{array}$$

(2)

where $\delta {\mathsf{\Pi }}_{HR}$ is the first variation of the HR canonical functional, and the following assumptions are made: ${\gamma }_{ij(i3)(33)}=2{\epsilon }_{ij(i3)(33)}$; ${\widehat{\epsilon }}_{33}^{\sigma }=1/C_{3333}({\sigma }_{33}-C_{33ij}{\epsilon }_{ij}^u)$, being $i,j=1,2\equiv x,y$; $3\equiv z$.

Dynamic governing equations are obtained from the previous variational statements (1), (2), or from the principle of virtual work (PVW), for theories in displacement-based form, accounting for the work of inertial forces.

2.2. Construction of Analytical Solutions

Closed-form solutions to dynamic governing equations are obtained, irrespective of the theory examined, expressing functional d.o.f. as a truncated series expansion of unknown amplitudes $A_{\Delta }^i$ and trial functions ${\Re }^i(x,y)$ that individually satisfy the prescribed boundary conditions:

$$\Delta ={\displaystyle \sum _{i=1}^{m_{\Delta }}{A}_{\Delta }^i}{\Re }^i(x,y)$$

(3)

Then, we substitute these expressions within PVW, HR, or HW functionals and operating as specified immediately below. Here, $\Delta$ symbolises in turns $u^0$, $v^0$, $w^0$, ${\theta }_x$, ${\theta }_y$, because middle plane displacements and rotations of the normal are assumed as the only functional d.o.f. for each theory of this paper. Mechanical boundary conditions are accounted for by determining a number of unknown amplitudes $A_{\Delta }^i$, in proportion to the number of boundary conditions enforced, using the Lagrange multipliers method to account for the relationships resulting from each mechanical condition. The remaining amplitudes are determined deriving the governing functional with respect to still unknown amplitudes and equating to zero, having considered the work of inertial forces:

$${\displaystyle \underset{V}{\int }[}-b_i\partial u_i]dv={\displaystyle \underset{V}{\int }[}-\rho {\ddot{u}}_i\partial u_i]dv$$

(4)

within the functionals. In this way, an algebraic system is obtained whose solution provides the numerical value of each amplitude; then, the displacement, strain, and stress fields can be computed.

Since symbolic calculus being used to construct the theories, the applied distributed loading can be conveniently defined as a continuous or discontinuous general function $\chi (x,y)$ acting on upper and/or lower faces (or just on a part of them), so that energy contributions can be constructed in exact closed form. In this way, a series expansion representation with a large number of components is not necessary to represent discontinuous or otherwise complex loading distributions; then, the construction of the structural model in the numerical applications can be simplified, and at the same time made more accurate.

The trial functions have been adopted in individual applications are explicitly defined below and in

Table 2. Trial functions.

Case	Expansion Order	Mesh (xa·yb·zh) (+)	Trial Function
b1	1	16·2·60	$u^0(x,y)={\displaystyle \sum _{m=1}^M{A}_m}\cos \left(\frac{m\pi x}{L_x}\right);w^0(x,y)={\displaystyle \sum _{m=1}^M{C}_m}\sin \left(\frac{m\pi x}{L_x}\right);{\gamma }_x^0(x,y)={\displaystyle \sum _{m=1}^M{D}_m}\cos \left(\frac{m\pi x}{L_x}\right);$
b2	1	16·2·60
b3	1	16·2·60
e1	5	16·2·60
g	3	16·2·60
c1	1	10·10·28	$u^0(x,y)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{A}_{mn}\cos \left(\frac{m\pi }{L_x}x\right)}}\sin \left(\frac{n\pi }{L_y}y\right);v^0(x,y)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{B}_{mn}\sin \left(\frac{m\pi }{L_x}x\right)}}\cos \left(\frac{n\pi }{L_y}y\right);$ $w^0(x,y)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{C}_{mn}\sin \left(\frac{m\pi }{L_x}x\right)}}\sin \left(\frac{n\pi }{L_y}y\right);$ ${\gamma }_x{}^0(x,y)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{D}_{mn}\cos \left(\frac{m\pi }{L_x}x\right)}}\sin \left(\frac{n\pi }{L_y}y\right);{\gamma }_y{}^0(x,y)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{E}_{mn}\sin \left(\frac{m\pi }{L_x}x\right)}}\cos \left(\frac{n\pi }{L_y}y\right);$
c2	1	10·10·28
d1	1	10·10·28
d2	1	10·10·28
e3	6	10·10·28
h	5	10·10·28
i1	11	10·10·28
i2	11	10·10·28
i3	11	10·10·28
a1	9	16·2·60	$u^0(x,y)={\displaystyle \sum _{i=1}^I{A}_i}{\left(\frac{x}{L}\right)}^i;w^0(x,y)={\displaystyle \sum _{i=1}^I{C}_i}{\left(\frac{x}{L}\right)}^i;{\gamma }_x^0(x,y)={\displaystyle \sum _{i=1}^I{D}_i}{\left(\frac{x}{L}\right)}^i$
a2	9	16·2·60
d2	4	10·10·28	$u_{\alpha }{}^0(x,y)={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{i=1}^I{A}_{\alpha i}}{\left(\frac{x}{L_x}\right)}^i{\left(\frac{y}{L_y}\right)}^j};{\gamma }_{\alpha }^0(x,y)={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{i=1}^I{D}_{\alpha i}}{\left(\frac{x}{L_x}\right)}^i{\left(\frac{y}{L_y}\right)}^j};$
e2	10	10·10·28
f	6	10·10·28

⁽⁺⁾ A uniform mesh is used; x_a and y_b represent the number of elements in x and y directions, respectively, z_h is the number of elements across the thickness.

along with the expansion order used in each case. Note that although it is different for each benchmark, the order of expansion used is the same for all theories when a specific one is examined being equal to the minimum one that makes ZZA accurate. This is done to homogenise results and in order to compare theories under the same conditions.

At the clamped edge of cantilever beams, hereafter assumed at $x=0$ by way of example, the following conditions are enforced

$$u^0(0,0)=0;w^0(0,0)=0;w^0{(0,0)}_{,x}=0;{\mathsf{\Gamma }}_x^0(0,0)=0;$$

(5)

the following further conditions are enforced:

$$u_{\alpha }{(0,z)}_{,z}=0;u_{\varsigma }{(0,z)}_{,z}=0;u_{\varsigma }{(0,z)}_{,xz}=0$$

(6)

to simulate that (5) holds identically across the thickness. To ensure that the transverse shear stress resultant force equals the constraint force, the following additional constraint

$${\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{xz}}(0,z)dz=T$$

(7)

is enforced, while at the free edge x = L such resultant force is enforced to vanish

$${\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{xz}}(L,z)dz=0$$

(8)

It should be noted that the boundary conditions in Equations (6) to (8) are enforced using Lagrange multipliers methods; no further conditions are enforced on bending moments, but if necessary, they could be coerced choosing the sufficient expansion order in Equation (3).

At the supported edge of the propped cantilever beams at x = L, the following support condition:

$$w^0(L,-h/2)=0$$

(9)

is enforced at the lower face $z=-h/2$, while the condition in Equation (8) is reformulated as:

$${\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{xz}}(L,z)dz=T_L$$

(10)

At the simply supported edges, the following boundary conditions are enforced

$$\begin{array}{llll}{w}^0(0,y)=0;& w^0(L_x,y)=0;& w^0{(0,y)}_{,xx}=0;& w^0{(L_x,y)}_{,xx}=0\\ w^0(x,0)=0;& w^0(x,L_y)=0;& w^0{(x,0)}_{,yy}=0;& w^0{(x,L_y)}_{,yy}=0\end{array}$$

(11)

on the reference mid-plane of plates at $x=0$, $x=L_x$, and $y=0$, $y=L_y$. Appropriate changes corresponding to the ones for simply supported beams are obtained. Table 2 provides the trial functions and expansion order that is assumed for each benchmark.

Any other boundary condition could be enforced in the same way, namely by choosing the trial functions that individually satisfy the prescribed boundary conditions. In the event of this not being possible and in order to satisfy the mechanical conditions, Lagrange multipliers method should be applied. In the numerical applications for cases g and h, the boundary condition to be further enforced is $u_{\varsigma }(x,h/2)=-u_{\varsigma }(x,-h/2)$, because some of their first free vibration modes exhibit anti-symmetric displacements in the transverse direction. In this way, a closed-form solution can be obtained with a reduced computational effort, instead of resorting to FEA, as is often done for such cases.

3. Higher-Order Theories

The laminated plate theories that are used as structural models are thoroughly examined below. Here, they are grouped into higher-order and lower-order ones. The latter represent simplified versions of the former, having mostly features that are similar to those of the theories that have been previously proposed in the literature. In the following section, it will be specified which are new and which have been previously developed by the authors. Governing equations will not be reported in explicit form, as they can be obtained in a straightforward way using standard techniques.

3.1. Features of the ZZA Theory and the Higher Order Theories Derived from It

As it forms the basis of all theories considered in this paper, the theoretical framework of ZZA below is expounded first. The through-thickness displacement field is postulated as [29]:

$$\begin{array}{cc}{u}_{\alpha }(x,y,z)& =[u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[F_{\alpha }^u(z){]}_i\\ & [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Phi }}_{\alpha }^k(x,y)(z-z_k)H_k(z)+{\displaystyle \sum _{j=1}^{n_{\Im }}{}_{\alpha }{C}_u^j(x,y)H_j(z)}{]}_c}\end{array}$$

(12)

$$\begin{array}{cc}{u}_{\varsigma }(x,y,z)& =[w^0(x,y){]}_0+[F^{\zeta }(z){]}_i+[{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Psi }}^k(x,y)(z-z_k)H_k(z)}+\\ & {\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Omega }}^k(x,y){(z-z_k)}^2{H}_k(z)+{\displaystyle \sum _{j=1}^{n_{\Im }}{C}_{\varsigma }^j(x,y)H_j(z){]}_c}}\end{array}$$

(13)

Three kinds of contributions that are distinctly separated into lower-${[\dots ]}_{}{}_0$, higher-${[\dots ]}_i$ and layerwise $[\dots ]{}_c$ are incorporated, whose specific purpose is described below.

• ${[\dots ]}_0$ is a linear contribution and contains the five functional degrees of freedom of the theory.
• ${[\dots ]}_i$ contains higher-order terms. Any combination of independent functions could be assumed to represent $[F_{\alpha }^u(z){]}_i$ and $[F^{\zeta }(z){]}_i$; however to include theory [28] as a particularization of ZZA [29], the following form is chosen:

  $$[F_{\alpha }^u(z){]}_i=[C_{\alpha }^i(x,y)z^2+D_{\alpha }^i(x,y)z^3+(O{z}^4\dots ){]}_i={[}_3{(.\widetilde{)}}_{\alpha }{]}_i+[(O{z}^4\dots ){]}_i$$

  (14)

  $$[F^{\zeta }(z){]}_i=[b^i(x,y)z+c^i(x,y)z^2+d^i(x,y)z^3+e^i(x,y)z^4+(O{z}^5\dots ){]}_i={[}_4{(.\widetilde{)}}_{\zeta }{]}_i+[(O{z}^5\dots ){]}_i$$

  (15)
  Higher-order contributions $[(O{z}^4\dots ){]}_i,$ are characteristic of ZZA, while the terms ${[}_3{(.\widetilde{)}}_{\alpha }{]}_i$, ${[}_4{(.\widetilde{)}}_{\zeta }{]}_i$ are the same as in the previous theory [28]. The closed-form expressions of coefficients $C_{\alpha }^i$, $D_{\alpha }^i$, $b^i$ to $e^i$ are obtained using symbolic calculus from enforcing the fulfilment of stress boundary conditions

  $${\sigma }_{\alpha \varsigma }={\sigma }_{\varsigma \varsigma ,\varsigma }=0;{\sigma }_{\varsigma \varsigma }=p^0{}_{(\pm )}$$

  (16)
  Here, $p^0{}_{(\pm )}$ represents the distributed transverse loading acting on the upper $p^0{}_{(+)}$ and lower $p^0{}_{(-)}$ faces. Of course, also, non-homogeneous conditions ${\sigma }_{\alpha \varsigma };{\sigma }_{\beta \varsigma }\ne 0$ could be enforced without any additional difficulty. For clarity, contributions ${[\dots ]}_i$ from Equations (14) and (15) are rearranged in the following way:

  $$\begin{array}{l}{U}_{\alpha }^i(x,y,z)=[A_{\alpha 2}{z}^2+A_{\alpha 3}{z}^3]+A_{\alpha 4}{z}^4+\dots +A_{\alpha n}{z}^n\\ U_{\zeta }^i(x,y,z)=[A_{\varsigma 1}z+A_{\varsigma 2}{z}^2+A_{\varsigma 3}{z}^3+A_{\varsigma 4}{z}^4]+A_{\varsigma 5}{z}^5+\dots +A_{\varsigma n}{z}^n\end{array}$$

  (17)
  The lower-order contributions under the square brackets in Equation (17) are determined by enforcing the fulfilment of the boundary conditions in Equation (16) and the local equilibrium equations:

  $${\sigma }_{\alpha \alpha ,\alpha }+{\sigma }_{\alpha \beta ,\beta }+{\sigma }_{\alpha z,z}=b_{\alpha };{\sigma }_{\alpha \varsigma ,\alpha }+{\sigma }_{\beta \varsigma ,\varsigma }+{\sigma }_{\varsigma \varsigma ,\varsigma }=b_{\varsigma }$$

  (18)

  at selected points across the thickness. Higher-order contributions $A_{\alpha 4}{z}^4+\dots +A_{\alpha n}{z}^n$, $A_{\varsigma 5}{z}^5+\dots +A_{\varsigma n}{z}^n$, which enable a variable-kinematics representation across the thickness, are computed for each fictitious computational layer $i$ in which the laminate is subdivided by imposing the fulfilment of Equation (18). However, except otherwise stated, a third/fourth-order representation that embraces the whole laminate is used in the applications which is adequate to obtain accurate results. Indeed, as shown in [21], this choice is a valuable combination of accuracy and cost-saving also when extreme variations of material properties give rise to very strong layerwise effects. A single computational layer is used for laminates, while two or three layers are used for sandwiches. Note that the in-plane position of equilibrium points can be chosen appropriately for each case.
• ${[\dots ]}_c$ represents the layerwise contributions; the expressions of zig-zag amplitudes ${\mathsf{\Phi }}_{\alpha }^k$, ${\mathsf{\Psi }}^k$ and ${\mathsf{\Omega }}^k$ are determined so that the continuity of out-of-plane stresses and the transverse normal stress gradient ${\sigma }_{\varsigma \varsigma ,\varsigma }$ at the layer interfaces is satisfied, as prescribed by the elasticity theory through the following stress compatibility conditions:

  $${\sigma }_{\alpha \varsigma }({}^{(k)}z^{+})={\sigma }_{\alpha \varsigma }({}^{(k)}z^{-});{\sigma }_{\varsigma \varsigma }({}^{(k)}z^{+})={\sigma }_{\varsigma \varsigma }({}^{(k)}z^{-});{\sigma }_{\varsigma \varsigma ,\varsigma }({}^{(k)}z^{+})={\sigma }_{\varsigma \varsigma ,\varsigma }({}^{(k)}z^{-})$$

  (19)

  at the physical and mathematical layer interfaces. Layerwise contributions ${}_{\alpha }c_u^j$ and $C_{\varsigma }^j$ restore the continuity of displacements at the mathematical layer interfaces. The symbols $n_i$ and $n_{\Im }$ in the summation of Equations (12) and (13) are used to distinguish the number of physical interfaces from that of the mathematical layer interfaces, respectively. In detail, ${\mathsf{\Phi }}_{\alpha }^k$ enables the continuity of transverse shear stresses, while ${\mathsf{\Psi }}^k$, ${\mathsf{\Omega }}^k$ enable the continuity of the transverse normal stress and of its gradient at physical and mathematical layer interfaces. All together, these provide the right slope changes of displacements at the interfaces of layers with different material properties and/or orientations.

Elsewhere in this paper, the symbols − and + indicate the position just before and just after the interface, respectively. The term $(z-z_k)H_k$ appearing in in Equations (12) and (13) is Di Sciuva’s zig-zag function [22], while ${(z-z_k)}^2{H}_k$ is Icardi’s parabolic zig-zag function [28], with H_k being the Heaviside unit step function (H_k = 0 for z < z_k, while H_k = 1 for z ≥ z_k).

The enforcement of the equilibrium and stress compatibility conditions in Equations (18) and (19) yields to a system of algebraic equations at each interface that is solved in closed form once and for all using a symbolic calculus tool. Notice that if just the material properties and/or the orientation of layers change, but not their number, symbolic expressions representing the solution will remain the same.

It will be shown forward that $(z-z_k)H_k$ and ${(z-z_k)}^2{H}_k$ can be replaced with any other layerwise function keeping the results unchanged, provided that coefficients inside ${[\dots ]}_i$ are re-computed for each computational layer, as outlined above. Layerwise functions can even be omitted if a sufficient number of coefficients are incorporated in ${[\dots ]}_i$ whose expressions are determined by enforcing the fulfilment of the interfacial stress compatibility conditions in Equation (19). To show this, a new theory ZZA* is developed in Section 3.1.1, which is devoid of ${[\dots ]}_c$, but incorporates new unknown coefficients within ${[\dots ]}_i$, which will be indicated as ${[\dots ]}_{i+c}$. Since this choice speeds up the computations of the coefficients of each layer, it turns into a computational advantage that grows with the number of computational layers, so it is worth taking into consideration.

The expressions of ${}_{\alpha }C_u^j$ and $C_w^j$ are determined in a straightforward way by enforcing the continuity of displacements at the mathematical layer interfaces

$$u_{\alpha }({}^{(k)}z^{+})=u_{\alpha }({}^{(k)}z^{-});u_{\varsigma }({}^{(k)}z^{+})=u_{\varsigma }({}^{(k)}z^{-})$$

(20)

Notice that as no d.o.f. derivatives are involved, the computation of ${}_{\alpha }C_u^j$ and $C_w^j$ is much easier and faster than those of ${\mathsf{\Phi }}_{\alpha }^k$, ${\mathsf{\Psi }}^k$, and ${\mathsf{\Omega }}^k$, which instead involve such derivatives. However, it must be considered that the computation of all of the above indicated zig-zag terms takes only an infinitesimal fraction of the overall calculation cost, and so remains compatible with that of ESL.

The strain energy updating technique (SEUPT) [29] can be used to obtain a C⁰ formulation of the ZZA theory, since derivatives of the d.o.f. are involved in the displacement field as a consequence of the enforcement of Equations (18) and (19).

3.1.1. ZZA* Displacement-Based Theory

This theory, which represents the new theoretical contribution brought by this paper, is developed with the intended aim to demonstrate that the choice of zig-zag functions is immaterial, provided that the coefficients of displacements ${[\dots ]}_i$ are recomputed as indicated above.

For this purpose the displacement field of ZZA* is assumed to be similar to that of ZZA except for the layerwise functions. In numerical applications it will be shown that the same accuracy of ZZA can be achieved without explicitly incorporating contributions ${[\dots ]}_c$, and consequently obtaining a reduction of the computational burden.

It will be shown by the numerical results that the choice of zig-zag functions is immaterial if the coefficients ${[\dots ]}_i$ are redefined layer-by-layer, so these functions do not even need to be explicitly incorporated in the displacement field. The same result wouldn’t be achieved by keeping the coefficients fixed across the thickness, in which case the accuracy depends on the choice of zig-zag functions.

The displacement field of ZZA* is conceived in the following way:

$$\begin{array}{ll}{u}_{\alpha }(x,y,z)=& [u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+\{{\displaystyle \sum _{k=1}^{n_{\Im }}}{}_k\tilde{B}_{\alpha }^i(x,y)z+\\ & +[C_{\alpha }^i(x,y)z^2]+[D_{\alpha }^i(x,y)z^3]+{\displaystyle \sum _{k=1}^{n_i}}{}_k\tilde{C}_{\alpha }^i(x,y){\}}_{i+c}\end{array}$$

(21)

$$\begin{array}{ll}{u}_{\varsigma }(x,y,z)=& [w^0(x,y){]}_0+\{[b^i(x,y)z+{\displaystyle \sum _{k=1}^{n_{\Im }}}{}_k\tilde{b}^i(x,y)z]+[c^i(x,y)z^2\\ & +{\displaystyle \sum _{k=1}^{n_i}}{}_k\tilde{c}^i(x,y)z_{}^2]+[d^i(x,y)z^3]+e^i(x,y)z^4+{\displaystyle \sum _{k=1}^{n_i}}{}_k\tilde{d}^i(x,y){\}}_{i+c}\end{array}$$

(22)

wherein the terms ${}_k\tilde{B}_{\alpha }^i$ and ${}_k\tilde{C}_{\alpha }^i$ serve the same purpose as ${\mathsf{\Phi }}_{\alpha }^k$ and ${}_{\alpha }{C}_u^j$ in Equation (12) inside ZZA, while ${}_k\tilde{b}^i$ and ${}_k\tilde{c}^i$ have the same function of ${\mathsf{\Omega }}^k$ and ${\mathsf{\Psi }}^k$, and ${}_k\tilde{d}^i$ has the function of $C_{\varsigma }^k$ in Equation (13). In the same way of ZZA, $C_{\alpha }^i$, $D_{\alpha }^i$, $b^i$, $c^i$, $d^i$ and $e^i$ allow the stress boundary conditions in Equation (16) and the local equilibrium equations in Equation (18) to be met. More specifically, $b^i$ and $c^i$ enable the fulfillment of the stress boundary conditions concerning ${\sigma }_{\varsigma \varsigma }$ and ${\sigma }_{\varsigma \varsigma ,\varsigma }$ over the lower bounding face, while they are cancelled in subsequent layers. Instead, $C_{\alpha }^i$, $D_{\alpha }^i$, $d^i$, and $e^i$ allow satisfying the three equilibria (18) at two points for each intermediate layer. In the lower layer, such coefficients enable the two boundary conditions on ${\sigma }_{\alpha \varsigma }$ to be enforced along with the three equilibrium equations at a single point. In this way, free variables still remain that allow meeting three equilibrium equations at a single point across the upper layer and the boundary conditions at the upper bounding surface. When more equilibrium points are desired, each layer can be subdivided into two or more computational layers. However, this doesn’t mean an increased expansion order or number of variables, since coefficients can be recomputed using the same order of representation for each computational layer, and the d.o.f. remain fixed. As for ZZA, closed-form expressions of all of the coefficients of ZZA* within contributions ${[\dots ]}_{i+c}$ are determined once and for all for a specific lay-up using a symbolic calculus tool.

3.2. HWZZ Mixed Theory

Such a theory was developed in [47] in order to reduce the computational effort of ZZA by keeping only the essential contributions to the displacement, strain, and stress fields, and hopefully preserving its accuracy. Developed within the framework of the Hu–Washizu theorem, HWZZ forms the basis of another mixed theory here used and called HWZZM, which considers a different zig-zag layerwise function.

3.2.1. Master Displacements

The displacements of HWZZ are derived from those of ZZA neglecting the contributions of ${\mathsf{\Omega }}^k$, because they are supposed to give imperceptible slope variations compared to those by ${\mathsf{\Phi }}_{\alpha }^k$, ${\mathsf{\Psi }}^k$. Also higher-order and adaptive contributions $A_{\alpha 4}{z}^4+\dots +A_{\alpha n}{z}^n$ and $A_{\varsigma 5}{z}^5+\dots +A_{\varsigma n}{z}^n$ are neglected and no decomposition into mathematical layers is allowed. As a consequence, contributions by ${}_{\alpha }{C}_u^j$ and $C_{\varsigma }^j$ are omitted. So, the displacement field of HWZZ is written:

$$\begin{array}{l}{u}_{\alpha }(x,y,z)=[u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[C_{\alpha }^i(x,y)z^2+D_{\alpha }^i(x,y)z^3{]}_i+\\ [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Phi }}_{\alpha }^k(x,y)(z-z_k)H_k(z){]}_c}\\ u_{\varsigma }(x,y,z)=[w^0(x,y){]}_0+[b^i(x,y)z+c^i(x,y)z^2+d^i(x,y)z^3+e^i(x,y)z^4{]}_i+\\ [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Psi }}^k(x,y)(z-z_k)H_k(z)}{]}_c\end{array}$$

(23)

3.2.2. Master Strains

Out-of-plane strains ${\epsilon }_{zz}$, ${\gamma }_{xz}$, ${\gamma }_{yz}$ are constructed on the basis of the ZZA layer-by-layer representation of displacements as:

$$\begin{array}{ll}\hfill {}_{\Im }u_{\alpha }(x,y,z)& =[u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[C_{\alpha }^i(x,y)z^2+D_{\alpha }^i(x,y)z^3{]}_i+\hfill \\ & [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Phi }}_{\alpha }^k(x,y)(z-z_k)H_k(z)+{\displaystyle \sum _{j=1}^{\Im }{}^{\alpha }C_u^j(x,y)H_j}{]}_c}\hfill \\ \hfill {}_{\Im }w_{\varsigma }(x,y,z)=& [w^0(x,y){]}_0+[b^i(x,y)z+c^i(x,y)z^2+d^i(x,y)z^3+e^i(x,y)z^4{]}_i+\hfill \\ & [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Psi }}^k(x,y)(z-z_k)H_k(z)}+{\displaystyle \sum _{j=1}^{\Im }{C}_{\varsigma }^j(x,y)H_j}{]}_c\hfill \end{array}$$

(24)

The symbol ${}^{\Im }(.)$ states that they refer to the computational layer $\Im$. On the contrary, no decomposition into mathematical layers is allowed for the in-plane strains:

$$\begin{array}{l}{\epsilon }_{xx}(x,y,z)=\stackrel{⌣}{\tilde{U}}{(x,y,z)}_{,x}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_{x,x}^k}(z-z_k)H_k\hfill \\ {\epsilon }_{yy}^{}(x,y,z)=\stackrel{⌣}{\tilde{V}}{(x,y,z)}_{,y}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_{y,y}^k}(z-z_k)H_k\hfill \\ {}^{\Im }\epsilon _{zz}(x,y,z)=\stackrel{⌣}{\tilde{W}}{(x,y,z)}_{,z}+{\displaystyle \sum _{k=1}^s{\mathsf{\Psi }}_{}^k}{H}_k\hfill \\ {}^{\Im }\gamma _{xz}(x,y,z)=[\stackrel{⌣}{\tilde{U}}{(x,y,z)}_{,z}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_x^k}{H}_k+\stackrel{⌣}{\tilde{W}}{(x,y,z)}_{,x}+{\displaystyle \sum _{k=1}^s{\mathsf{\Psi }}_{,x}^k}(z-z_k)H_k]\hfill \\ {}^{\Im }\gamma _{yz}(x,y,z)=[\stackrel{⌣}{\tilde{V}}{(x,y,z)}_{,z}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_y^k}{H}_k+\stackrel{⌣}{\tilde{W}}{(x,y,z)}_{,y}+{\displaystyle \sum _{k=1}^s{\mathsf{\Psi }}_{,y}^k}(z-z_k)H_k]\hfill \\ {\gamma }_{xy}(x,y,z)=[\stackrel{⌣}{\tilde{U}}{(x,y,z)}_{,y}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_{x,y}^k}(z-z_k)H_k+\stackrel{⌣}{\tilde{V}}{(x,y,z)}_{,x}+{\displaystyle \sum _{k=1}^s{\mathsf{\Phi }}_{y,x}^k}(z-z_k)H_k]\hfill \end{array}$$

(25)

The expressions of membrane stresses ${\sigma }_{xx}$, ${\sigma }_{yy}$, and ${\sigma }_{xy}$ are obtained in a straightforward way from stress–strain relations and previous strains, while those of the out-of-plane counterparts are assumed as specified next.

3.2.3. Master Stresses

Out-of-plane stresses are obtained from membrane stresses by integrating local equilibrium equations:

$${\sigma }_{xz}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}(b_x}-{\sigma }_{xx,x}-{\sigma }_{xy,y})dz;{\sigma }_{yz}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}(b_y}-{\sigma }_{xy,x}-{\sigma }_{yy,y})dz;{\sigma }_{zz}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}(b_z}-{\sigma }_{xz,x}-{\sigma }_{yz,y})dz$$

(26)

and then

$${\sigma }_{zz}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}\{b_z}-[{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}(b_{x,x}}-{\sigma }_{xx,xx}-{\sigma }_{xy,xy})dz]-[{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}(b_{y,y}}-{\sigma }_{xy,xy}-{\sigma }_{yy,yy})dz]\}dz$$

(27)

In this way, stress jumps resulting from the omission of contributions by ${\mathsf{\Omega }}^k$ are recovered. As a consequence of simplifying the assumptions that are made, HWZZ needs to be post-processed by ZZA in order to accurately represent displacements when very strong layerwise effects rise.

3.3. Other Mixed Theories

3.3.1. HWZZM Theory

Murakami’s zig-zag contributions are assumed [51], which are variations of the canonical form

$$M^k(z)={(-1)}^k{\zeta }^k$$

(28a)

where:

$${\zeta }^k=a^{k}z-b^k,a^k=\frac{2}{z_{k+1}-z_k},b^k=\frac{z_{k+1}+z_k}{z_{k+1}-z_k}$$

(28b)

In fact, the displacement field of HWZZM is assumed as:

$$\begin{array}{l}{}^{\Im }u_{\alpha }(x,y,z)=[u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[F_{\alpha }^u(z){]}_i+\\ [A_k^{u_{\alpha }}(z)[\frac{2z}{z_{k+1}-z_k}-\frac{z_{k+1}+z_k}{z_{k+1}-z_k}]+C_{\alpha }^k(x,y){]}_c\end{array}$$

(29)

$$\begin{array}{l}{}^{\Im }u_{\varsigma }(x,y,z)=[w^0(x,y){]}_0+[F^{\zeta }(z){]}_i+\hfill \\ [A_k^{u_{\varsigma }}(z)[\frac{2z}{z_{k+1}-z_k}-\frac{z_{k+1}+z_k}{z_{k+1}-z_k}]+B_k^{u_{\varsigma }}(z)[\frac{{(2z)}^2}{z_{k+1}-z_k}]+C_{\varsigma }^k(x,y)]c\hfill \end{array}$$

(30)

Differently to Murakami’s theories proposed in the literature, here, multiplier coefficients $A_k^{u_{\epsilon }}$, $A_k^{u_{\varsigma }}$, and $B_k^{u_{\varsigma }}$ are incorporated, which can be defined differently across the thickness to improve the accuracy. As has been done previously, their expressions are a priori determined by enforcing the continuity of the transverse shear and normal stress, and of the transverse normal stress gradient at layer interfaces, so that they are no longer uniform across the thickness. As before, $C_{\alpha }^k$ and $C_{\varsigma }^k$ restore the continuity of displacements at interfaces of mathematical layers.

HWZZM is developed starting from the displacement field in Equations (29) and (30) in the same way as HWZZ; namely, the decomposition into fictitious computational layers is not allowed for the displacement and in-plane strain fields, while it is allowed for out-of-plane strains. Contributions to in-plane displacements over the third-order and to the transverse displacement over the fourth-order are neglected. Stress–boundary conditions are enforced at the top and bottom laminate faces, while local equilibrium equations are enforced at the inner layers. Membrane stresses ${\sigma }_{xx}$, ${\sigma }_{yy}$, and ${\sigma }_{xy}$ come from stress–strain relations, while out-of-plane master stresses are derived integrating local equilibrium equations. The numerical findings will show that although different zig-zag functions contradistinguish ZZA, HWZZ, and HWZZM, their results are indistinguishable, so there will be evidence that the choice of such functions is immaterial, provided that ${[\dots ]}_i$ and ${[\dots ]}_c$ are recomputed at each interface.

3.3.2. HWZZM* New Theory and Theories Derived from It

In order to assess the effect of the choice of different zig-zag functions, a new theory called HWZZM* is derived from ZZA*, similar to how HWZZ was derived from ZZA. Then, other theories are particularized from HWZZM, assuming $A_k^{u_{\alpha }}(z)$, $A_k^{u_{\varsigma }}(z)$, and $B_k^{u_{\varsigma }}(z)$ are equal to those at a specific interface, which differ from one another.

3.3.2.1. HWZZM* Theory

The displacement field of HWZZM* is assumed in the following form

$$\begin{array}{ll}{u}_{\alpha }(x,y,z)=& [u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+\{{\displaystyle \sum _{k=1}^{n_{\Im }}}{}_k\tilde{B}_{\alpha }^i(x,y)z+\\ & +[C_{\alpha }^i(x,y)z^2]+[D_{\alpha }^i(x,y)z^3]{\}}_{i+c}\end{array}$$

(31)

$$\begin{array}{ll}{u}_{\varsigma }(x,y,z)=& [w^0(x,y){]}_0+\{[b^i(x,y)z+{\displaystyle \sum _{k=1}^{n_{\Im }}}{}_k\tilde{b}^i(x,y)z]+[c^i(x,y)z^2]+\\ & +[d^i(x,y)z^3]+e^i(x,y)z^4{\}}_{i+c}\end{array}$$

(32)

whose amplitudes are computed at each interface from the enforcement of the stress compatibility conditions in Equation (19). In this case, terms ${[\dots ]}_i$ only serve to satisfy the stress–boundary conditions and local equilibrium equations, while the satisfaction of stress compatibility conditions is demanded to ${[\dots ]}_c$.

It should be noted that Equations (31) and (32) imply a little reduction of the processing time, which is equal to 10% per each layer with respect to ZZA and to a somewhat lesser extent equal to 6% with respect to HWZZ. Of course, such an advantage will become more consistent as soon as the number of computational/constituent layers increase.

3.3.2.2. Theories with a Priori Chosen Zig-Zag Amplitudes

Several theories are particularized assuming a priori zig-zag amplitudes as the ones by HWZZM competing at a specific interface and then keeping them unchanged across the thickness, which is something similar to what is done using Murakami’s zig-zag functions, whose amplitudes are assumed a priori.

The amplitudes of HWZZMA are assumed to be coincident with those of HWZZM at the first interface from below, while the $A_k^{u_{\varsigma }}(z)$ and $B_k^{u_{\varsigma }}(z)$ of HWZZMB are assumed to be the same as those of HWZZMA at the first interface from below, but instead, $A_k^{u_{\alpha }}(z)$ is calculated as in HWZZM theory. In HWZZMC, only $B_k^{u_{\varsigma }}(z)$ is assumed to be uniform across the thickness and coincident with that of HWZZM at the first interface from below, while the remaining are computed at each interface. $B_k^{u_{\varsigma }}(z)$ are neglected in HWZZM0 theory, while $A_k^{u_{\alpha }}(z)$ and $A_k^{u_{\varsigma }}(z)$ are assumed in the same way as HWZZMB.

The HWZZMB2 and HWZZMC2 theories are the same as those of HWZZMB and HWZZMC, respectively, but currently, the amplitudes are assumed to be coincident with those of HWZZM at the first interface from above. Since zig-zag amplitudes are assumed, discontinuous out-of-plane stress may result; hence, the integration of local equilibrium equations is required to obviate this discontinuity, with a corresponding increase in costs by 0.9%. However, it must be considered that zig-zag amplitudes are not being computed at each interface, so a processing time saving of 10% is obtained, and in the end, a positive balance is achieved. However, applications will show a loss of accuracy, making it vain.

4. Lower-Order Theories

Lower-order theories are particularized from ZZA through limiting assumptions that take features that are reminiscent to those of the theories in the literature.

4.1. MHR Theory

MHR considers piecewise cubic in-plane displacements, wherein Murakami’s zig-zag function in Equation (28) is incorporated as the layerwise function, alongside a fourth-order polynomial transverse displacement [47]:

$$\begin{array}{l}{u}_{\alpha }(x,y,z)=[u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[C_{\alpha }^{}(x,y)z^2+D_{\alpha }(x,y)z^3{]}_i+u_{\alpha z}(x,y)M^k(z)\\ u_{\varsigma }(x,y,z)=[w^0(x,y){]}_0+[a(x,y)z+b(x,y)z^2+c(x,y)z^3+d(x,y)z^4{]}_i\end{array}$$

(33)

Coefficients $C_{\alpha }$, $D_{\alpha }$, $a$, $b$, $c$ and $d$ are still calculated by enforcing the fulfilment of the stress boundaries conditions in Equation (16), while $u_{\alpha z}$ is calculated by enforcing the fulfilment of the first and second equilibrium in Equation (18) at the middle plane of the laminate. Since out-of-plane stresses may be still discontinuous at layer interfaces, and since $u_{\alpha z}$ is assumed to be uniform across the thickness, the expressions of out-of-plane stresses are derived integrating local equilibrium equations within the framework of an HR variational theorem (2). A refined version that is referred as MHR±, is obtained by determining the right sign of Murakami’s zig-zag function (28) on a physical basis, instead of being forced to reverse at interfaces by the coefficient ${(-1)}^k$. The right slope is determined at each interface without a cost burden evaluating what sign ${(\pm 1)}^k$ attain the lowest residual force norm from three local equilibrium equations.

4.2. MHR4, MHWZZA and MHWZZA4 Theories

A refined variant MHR4 of MHR is obtained assuming the in-plane displacement field $u_{\alpha }$ by Equation (31), and a fourth-order piecewise variation of the transverse displacement [47]:

$$u_{\varsigma }(x,y,z)=[w^0(x,y){]}_0+[a(x,y)z+b(x,y)z^2+c(x,y)z^3+d(x,y)z^4{]}_i+w_z(x,y)M^k(z)$$

(34)

Coefficients $a$ to $d$ are determined by enforcing the fulfillment of the stress boundary conditions in Equation (16), whereas $w_z$ is calculated by enforcing the fulfilment of the third local equilibrium equation at the middle plane.

MHWZZA is developed assuming the same master displacement field as that of MHR in Equation (33) and the same master strain and stress fields as those of the HWZZ model, in Equations (25) and (26), respectively. To improve the accuracy, the displacement, strain, and stress fields of MHWZZA are recovered using ZZA as the post-processor.

Similarly to MHR±, a refined theory MHR4± is obtained from MHR4 determining the sign of Murakami’s zig-zag functions on a physical basis.

A further theory MHWZZA4 is derived assuming the in-plane displacement field in Equation (31) by MHR, the transverse displacement in Equation (13) by ZZA, and as the master strain and stress fields those by HWZZ in Equations (25) and (26), respectively. The only substantial difference of MHWZZA4 with respect to HWZZ and ZZA is a different zig-zag function; the just-mentioned theories along with ZZA* and HWZZM* make it possible to verify whether the accuracy is sensitive to the choice of zig-zag functions.

4.3. HRZZ and HRZZ4

HRZZ theory is developed postulating a uniform transverse displacement and a third-order zig-zag representation of in-plane displacements [47]:

$$\begin{array}{ll}{u}_{\alpha }(x,y,z)=& [u_{\alpha }{}^0(x,y)+z({\mathsf{\Gamma }}_{\alpha }^0(x,y)-w^0{(x,y)}_{,\alpha }){]}_0+[C_{\alpha }^i(x,y)z^2+D_{\alpha }^i(x,y)z^3{]}_i+\\ & [{\displaystyle \sum _{k=1}^{n_i}{\mathsf{\Phi }}_{\alpha }^k(x,y)(z-z_k)H_k(z)+{\displaystyle \sum _{k=1}^{\Im }{}_{\alpha }C_u^k(x,y)H_k}{]}_c}\\ u_{\varsigma }(x,y,z)=& w^0(x,y)\end{array}$$

(35)

Within the framework of the HR theorem, the transverse normal stress ${\sigma }_{33}$ is assumed to be the same as that of the ZZA model, while the transverse shear stresses ${\sigma }_{i3}$ are derived from the equilibrium equations assuming kinematic relations in Equation (25) to define membrane stresses. However, currently, second and higher-order derivatives of the d.o.f. are neglected, and a unique computational layer is assumed. Since a uniform transverse displacement is chosen and transformed, reduced stiffness properties are assumed. Then, ${\epsilon }_{ij}^{\sigma }=C_{ijkl}{\sigma }_{kl}$, $C_{ijkl}$ is the inverse of $E_{ijkl}$; $i,j=1,2\equiv x,y$; $3\equiv z$; ${\epsilon }_{ij}^u=1/2(u_{i,j}+u_{j,i})$; ${\gamma }_{ij(i3)(33)}=2{\epsilon }_{ij(i3)(33)}$, and ${\widehat{\epsilon }}_{33}^{\sigma }=1/C_{3333}({\sigma }_{33}-C_{33ij}{\epsilon }_{ij}^u)$.

In order to increase the accuracy of HRZZ, the ZZA theory will be used as the post-processor and the results obtained in this way will be indicated as HRZZ PP in the figures.

HRZZ4 assumes the same in-plane representation of HRZZ, the following fourth-order polynomial approximation of the transverse displacement [47]:

$$u_{\varsigma }(x,y,z)=[w^0(x,y){]}_0+[b(x,y)z+c(x,y)z^2+d(x,y)z^3+e(x,y)z^4{]}_i$$

(36)

and the same stress fields of HRZZ. In this case, ${\epsilon }_{33}^u$ being no longer null, it is unnecessary to use transformed, reduced stiffness properties. Similar to in the previous theories, coefficients b to e of Equation (36) are determined by enforcing the stress boundary conditions at the upper ${}^{+}$ and lower ${}^{-}$ faces (16). The out-of-plane master shear stresses ${\sigma }_{i3}$ are obtained through integrating local equilibrium equations, while the $\partial {\sigma }_{33}$ appearing in Equation (2) is assumed to be the same as that of ZZA.

5. Numerical Assessments and Discussion

The accuracy of previous theories is assessed, analysing free vibration modes and the transient dynamic behaviour under impulsive loading of simply supported and clamped, laminated, and sandwich beams and plates.

The lay-up, geometric, and material properties of each case are grouped in

Table 3. Data of cases.

Case	Lay-Up	Layer Thickness	Material	BCS	Lx/h	Ly/Lx
a1 [27]	[0/0/0]	[(2h/7)/(4h/7)/(h/7)]	[n/n/n]	CS	5.714	-
a2	[0/0/0]	[(2h/7)/(4h/7)/(h/7)]	[n/n/n]	CS	20	-
b1 [49]	[0/90/0]	[h/3]3	[p]3	SS	10	-
b2 [49]	[0/90/0/90]	[0.25h]4	[p]4	SS	10	-
b3 [49] (†)	[0/0/0]	[0.1h/0.8h/0.1h]	[p/mc/p]	SS	4, 10, 20	-
c1 [4]	[0/90/0/90]	[0.25h]4	[a]4	SSSS	5	1
c2 [4]	[90/0/90/0]	[0.25h]4	[b]4	SSSS	10/3	1
d1 [5]	[0/90/0]	[h/3]3	[c]3	SSSS	4, 10, 20, 30, 50, 100	1
d2 [50]	[0/90/0]	[h/3]3	[c]3	SSSS, CCCC, CSCS	10	1
e1 [5]	[0/90/0]	[0.25h/0.5h/0.25h]	[d]3	SFSF	5, 10, 20	-
e2 [52]	[0/90/0]	[h/3]3	[e]3	CCCC	10	1
e3 [4]	[0/90/0/0/90]	[(h/24)2/(5h/12)]S	[f2/g]S	SSSS	10	1
f [53]	[0/90]	[h/2]2	[h]2	SS	10	0.1
g (*†)	[0]8	[0.025h/0.05h/0.125h/0.3h]S	[m2/m1/m2/m3]S	SS	5	-
h (*†)	[0/90/0/0/90]	[(h/24)2/(5h/12)]S	[l1/l2/g/l1/l2]	SSSS	5	1
i1 [54]	[(45/−45)2/45/0]S	[(0.381mm)5/(12.7mm)]S	[o15/o2]S	SSSS	20.8696	1
i2 [55]	[0/90/0]	[(h/4)/(h/2)/(h/4)]	[q]3	SSSS	14.941	1
i3 (*†)	[(0/90)2/02]S	[(0.381mm)5/(12.7mm)]S	[o15/o2/o3/o15]	SSSS	10	1

* Transverse anisotropy; ^† Strong layerwise effects; (BCS: boundary conditions name; SS simply supported, C clamped).

and

Table 4. Mechanical Properties.

Material Name	a	b	c	d	e	f	g	h	l1	l2	m1	m2	m3	mc	n [iso]	o1	o2	o3	p	q
E1 [GPa]	M1	30E2	25E2	181	40E2	131	6.89 × 10−3	25E2	33.5	139	1	33	0.05	0.1	-	206.84	0.138	0.0138	172.4	132.4
E2 [GPa]	-	-	-	10.3	-	10.34	6.89 × 10−3	-	8	3.475	1	1	0.05	0.1	-	5.171	0.138	0.0138	6.9	10.8
E3 [GPa]	E2	E2	E2	10.3	E2	10.34	6.89 × 10−3	E2	8	3.475	1	1	0.02	0.1	M2	5.171	0. 138	0. 0138	6.9	10.8
G12 [GPa]	0.6E2	0.6E2	0.5E2	7.17	0.6E2	6.205	3.45 × 10−3	0.5E2	2.26	1.7375	0.02	8	0.0217	0.04	-	2.551	0.1027	0.01027	3.45	5.6
G13 [GPa]	0.6E2	0.6E2	0.5E2	7.17	0.6E2	6.895	3.45 × 10−3	0.2E2	2.26	1.7375	0.02	8	0.0217	0.04	-	2.551	0.1027	0.01027	3.45	5.6
G23 [GPa]	0.5E2	0.5E2	0.2E2	2.87	0.5E2	6.895	3.45 × 10−3	0.2E2	3	0.695	0.02	8	0.0217	0.04	-	2.551	0.06205	0.006205	1.38	5.6
υ12	0.25	0.25	0.25	0.25	0.25	0.22	0	0.25	0.35	0.25	0.25	0.25	0.15	0.25	0.33	0.25	0.35	0.35	0.25	0.24
υ13	0.25	0.25	0.25	0.25	0.25	0.22	0	0.25	0.35	0.25	0.25	0.25	0.15	0.25	0.33	0.25	0.35	0.35	0.25	0.24
υ23	0.25	0.25	0.25	0.33	0.25	0.49	0	0.25	0.33	0.25	0.25	0.25	0.15	0.25	0.33	0.25	0.02	0.02	0.25	0.24
Density [kg/m3]	ρ	ρ	ρ	1587	ρ	1627	97	ρ	1627	1627	1558.35	1558.35	16.3136	ρ	ρ	1558.35	16.3136	16.3136	ρ	1443

M1 E₁/E₂ = 3, 10, 20, 30, 40; M2 E_u/E_l = 1.6, E_u/E_c = 166.66; [iso] = isotropic E₁ = E₂ = E₃ G₁₂ = G₁₃ = G₂₃.

; the trial functions and the expansion order that are used in each study are reported in Table 2; the normalization of quantities is brought in

Table 5. Normalization of displacements, stresses and frequencies.

Case	Normalization
a1	$\overline{u_{\alpha }}=\frac{u\left(L_x,z\right)}{h{p}^0}\overline{u_{\varsigma }}=\frac{u_{\varsigma }\left(L_x,z\right)}{h{p}^0}\overline{{\sigma }_{\alpha \alpha }}=\frac{{\sigma }_{\alpha \alpha }\left(L_x,z\right)}{p^0{\left(L_x/h\right)}^2}\overline{{\sigma }_{\alpha \varsigma }}=\frac{A{\sigma }_{\alpha \varsigma }(L_x,z)}{P^0{L}_x}\overline{{\sigma }_{\varsigma \varsigma }}=\frac{{\sigma }_{\varsigma \varsigma }\left(L_x,z\right)}{p^0}$
a2	$\overline{u_{\alpha }}=\frac{u\left(L_x,z\right)}{h{p}^0}\overline{u_{\varsigma }}=\frac{u_{\varsigma }\left(L_x,z\right)}{h{p}^0}\overline{{\sigma }_{\alpha \alpha }}=\frac{{\sigma }_{\alpha \alpha }\left(L_x,z\right)}{p^0{\left(L_x/h\right)}^2}\overline{{\sigma }_{\alpha \varsigma }}=\frac{A{\sigma }_{\alpha \varsigma }(L_x,z)}{P^0{L}_x}\overline{{\sigma }_{\varsigma \varsigma }}=\frac{{\sigma }_{\varsigma \varsigma }\left(L_x,z\right)}{p^0}$
b1 b2 b3	$\overline{\omega }=\omega h\sqrt{\frac{{\rho }_{\_MATp}}{G_{12\_MATp}}}\overline{u_i}=\frac{u_i}{{\left|u_i\right|}_{\max }}\overline{{\sigma }_{ij}}=\frac{{\sigma }_{ij}}{{\left|{\sigma }_{ij}\right|}_{\max }}$
c1	$\overline{\omega }=10\omega h\sqrt{\frac{{\rho }_{\_MATa}}{E_{2\_MATa}}}\overline{u_i}=\frac{u_i}{{\left|u_i\right|}_{\max }}\overline{{\sigma }_{ij}}=\frac{{\sigma }_{ij}}{{\left|{\sigma }_{ij}\right|}_{\max }}$
c2	$\overline{\omega }=10\omega h\sqrt{\frac{{\rho }_{\_MATb}}{E_{2\_MATb}}}\overline{u_i}=\frac{u_i}{{\left|u_i\right|}_{\max }}\overline{{\sigma }_{ij}}=\frac{{\sigma }_{ij}}{{\left|{\sigma }_{ij}\right|}_{\max }}$
d1 d2	$\overline{\omega }=\omega \frac{L_x}{h}\sqrt{\frac{L_x^2{\rho }_{\_MATc}}{E_{2\_MATc}}}$
e1	$\overline{\omega }=\omega \frac{L_x^2}{h}\sqrt{\frac{{\rho }_{\_MATd}}{E_{2\_MATd}}}$
e2	$\overline{\omega }=\omega \frac{L_y^2}{{\pi }^2}\sqrt{\frac{{\rho }_{\_MATe}}{h{D}_0}}{D}_0=\frac{E_{2\_MATe}{h}^3}{12(1-{\nu }_{21\_MATe}{\nu }_{12\_MATe})}{\nu }_{21\_MATe}=0.00625$
e3	$\overline{\omega }=\omega \frac{L_x^2}{h}\sqrt{\frac{{\rho }_{\_MATf}}{E_{2\_MATf}}}$
f	$\overline{\omega }=\omega \frac{L_x^2}{L_y}\sqrt{\frac{{\rho }_{\_MATh}}{E_{2\_MATh}}}$
g	$\overline{\omega }=\omega \frac{L_x^2}{h}\sqrt{\frac{{\rho }_{\_MATm2}}{E_{2\_MATm2}}}\overline{u_i}=\frac{u_i}{{\left|u_i\right|}_{\max }}\overline{{\sigma }_{ij}}=\frac{{\sigma }_{ij}}{{\left|{\sigma }_{ij}\right|}_{\max }}$
h	$\overline{\omega }=\omega \frac{L_x^2}{h}\sqrt{\frac{{\rho }_{\_MATl2}}{E_{2\_MATl2}}}$
i1 i2	$\overline{u_{\varsigma }}=\frac{u_{\varsigma }}{h}$
i3	$\overline{u_{\varsigma }}=\frac{u_{\varsigma }}{w}$, $w\mathrm{static}\mathrm{response}$

; while the results are carried in

Table 6. Normalized fundamental frequencies, cases b1 and b2.

Theory	0/90/0 (b1)	0/90/0/90 (b2)	Theory	0/90/0 (b1)	0/90/0/90 (b2)
3D [49]	0.1462	0.1095	HWZZMC	0.1463	0.1095
EFSDT [49]	0.1448	0.1125	HWZZMC2	0.1465	0.1095
EHSDT [49]	0.1460	0.1090	HWZZM0	0.1550	0.1220
HSDT [49]	0.1505	0.1139	HRZZ	0.1462	0.1094
FSDT [49]	0.1616	0.1186	HRZZ4	0.1462	0.1095
3D FEA [48]	0.1464	0.1096	MHWZZA	0.1460	0.1095
ZZA	0.1463	0.1095	MHWZZA4	0.1461	0.1094
ZZA*	0.1463	0.1095	MHR	0.1463	0.1115
HWZZ	0.1463	0.1095	MHR4	0.1463	0.1162
HWZZM	0.1463	0.1095	MHR±	0.1463	0.1115
HWZZM*	0.1463	0.1095	MHR4±	0.1463	0.1162
HWZZMA	0.2499	0.1130	HSDT	0.1511	0.1157
HWZZMB	0.2199	0.1095	FSDT	0.1565	0.1162
HWZZMB2	0.1518	0.1124

,

Table 7. Normalized fundamental frequencies, case b3.

Lx/h	4	10	20	Lx/h	4	10	20
3D [49]	0.1011	0.0343	0.0155	HWZZMC	0.1017	0.0343	0.0156
EFSDT [49]	0.0848	0.0332	0.0153	HWZZMC2	0.1017	0.0343	0.0155
EHSDT [49]	0.0972	0.0341	0.0155	HWZZM0	0.1016	0.0343	0.0155
FSDT [49]	0.3325	0.1005	0.0316	HRZZ	0.0992	0.0342	0.0155
3D FEA [48]	0.1011	0.0343	0.0155	HRZZ4	0.0995	0.0342	0.0155
ZZA	0.1015	0.0343	0.0155	MHWZZA	0.1107	0.0373	0.0170
ZZA*	0.1015	0.0343	0.0155	MHWZZA4	0.1083	0.0374	0.0170
HWZZ	0.1015	0.0343	0.0155	MHR	0.1015	0.0343	0.0155
HWZZM	0.1015	0.0343	0.0155	MHR4	0.1015	0.0343	0.0155
HWZZM*	0.1015	0.0343	0.0155	MHR±	0.1015	0.0343	0.0155
HWZZMA	0.1250	0.0357	0.0159	MHR4±	0.1015	0.0343	0.0155
HWZZMB	0.1019	0.0343	0.0155	HSDT	0.1384	0.0503	0.0213
HWZZMB2	0.1016	0.0343	0.0155	FSDT	0.3055	0.0956	0.0310

,

Table 8. Normalized fundamental frequencies, case c1.

Theory	E1/E2 = 3	10	20	30	40
Exact [4]	2.6182	3.2578	3.7622	4.0660	4.2719
Zhen and Wanji [4]	2.6127	3.2513	3.7523	4.0532	4.2568
Matsunaga [56]	2.6021	3.2380	3.7400	4.0425	4.2477
3D FEA [48]	2.6118	3.2492	3.7500	4.0509	4.2546
ZZA	2.6026	3.2387	3.7406	4.0430	4.2481
ZZA*	2.6026	3.2387	3.7406	4.0430	4.2481
HWZZ	2.6026	3.2387	3.7406	4.0430	4.2481
HWZZM	2.6026	3.2387	3.7406	4.0430	4.2481
HWZZM*	2.6026	3.2387	3.7406	4.0430	4.2481
HWZZMA	2.6158	3.2591	3.7664	4.0716	4.2783
HWZZMB	2.6121	3.2529	3.7572	4.0603	4.2653
HWZZMB2	3.1157	4.3980	5.7265	6.7186	7.4660
HWZZMC	2.6064	3.2468	3.7537	4.0601	4.2681
HWZZMC2	2.6277	3.3004	3.8541	4.1970	4.4252
HWZZM0	2.8890	3.4550	3.9188	4.2047	4.4024
HRZZ	2.5977	3.2289	3.7250	4.0230	4.2247
HRZZ4	2.5980	3.2293	3.7255	4.0238	4.2256
MHWZZA	2.0844	4.0468	3.3020	3.1347	2.9820
MHWZZA4	2.0639	4.0052	3.2626	3.1124	2.9785
MHR	2.6101	3.3696	4.1243	4.6940	5.1627
MHR4	2.6265	3.3970	4.1616	4.7389	5.2142
MHR±	2.6038	3.2915	3.9165	4.3440	4.6645
MHR4±	2.6312	3.3774	4.0187	4.4254	4.7118
HSDT	2.6003	3.2781	3.8505	4.2139	4.4686
FSDT	2.5986	3.2836	3.8651	4.2342	4.4919

,

Table 9. Normalized fundamental frequencies (NFQ), case c2.

c2	NFQ	Theory	NFQ	Theory	NFQ
3D FEA [48]	0.7041	HWZZMB2	0.7268	MHWZZA4	0.7652
ZZA	0.7044	HWZZMC	0.7043	MHR	0.9394
ZZA*	0.7044	HWZZMC2	0.7199	MHR4	0.7596
HWZZ	0.7044	HWZZM0	0.7047	MHR±	0.7609
HWZZM	0.7044	HRZZ	0.6860	MHR4±	0.7674
HWZZM*	0.7044	HRZZ4	0.6855	HSDT	0.7432
HWZZMA	0.7094	MHWZZA	0.7505	FSDT	0.7451
HWZZMB	0.7084

,

Table 10. Normalized fundamental frequencies, case d1.

Lx/h	4	10	20	30	50	100
RFSDT [50]	7.1630	11.7000	14.0120	14.6450	15.0090	15.1720
RHSDT [50]	7.0270	11.4620	13.8880	14.5790	14.9830	15.1650
3D FEA [48]	6.8436	11.4306	13.9231	14.6593	15.0696	15.2550
ZZA	6.9254	11.4583	13.8889	14.5800	14.9833	15.1654
ZZA*	6.9254	11.4583	13.8889	14.5800	14.9833	15.1654
HWZZ	6.9254	11.4583	13.8889	14.5800	14.9833	15.1654
HWZZM	6.9254	11.4583	13.8889	14.5800	14.9833	15.1654
HWZZM*	6.9254	11.4583	13.8889	14.5800	14.9833	15.1654
HWZZMA	9.0597	14.2814	15.0815	15.0371	15.0748	15.1730
HWZZMB	8.3007	15.9403	18.0802	15.8433	15.1554	15.1760
HWZZMB2	7.6251	12.6836	13.9248	14.5871	14.9843	15.1655
HWZZMC	6.9999	11.4660	13.8897	14.5802	14.9834	15.1654
HWZZMC2	7.1409	11.4823	13.8915	14.5806	14.9834	15.1654
HWZZM0	7.2859	12.5356	17.7326	21.7236	27.4298	33.3973
HRZZ	6.3896	11.4502	13.8862	14.5787	14.9828	15.1653
HRZZ4	6.9104	11.4569	13.8888	14.5799	14.9833	15.1654
MHWZZA	9.9632	9.1000	12.3099	13.8952	14.7385	15.1043
MHWZZA4	9.9815	9.1054	12.3100	13.8952	14.7385	15.1043
MHR	6.9913	11.4647	13.8896	14.5802	14.9834	15.1654
MHR4	7.4725	11.6644	14.0961	14.7437	15.0712	15.1924
MHR±	6.9913	11.4647	13.8896	14.5802	14.9834	15.1654
MHR4±	7.4725	11.6644	14.0961	14.7437	15.0712	15.1924
HSDT	7.1160	11.7900	14.0600	14.6700	15.0190	15.1750
FSDT	7.4130	12.1630	14.2300	14.7570	15.0530	15.1830

,

Table 11. Normalized fundamental frequencies, case d2.

Theory	SSSS	CSCS	CCCC	Theory	SSSS	CSCS	CCCC
RHQ40 [50]	11.4000	15.9550	17.4810	HWZZM0	12.5356	17.1426	18.2727
3D FEA [48]	11.4306	15.3895	16.6658	HRZZ	11.4502	16.1304	17.5659
ZZA	11.4583	15.1875	16.4575	HRZZ4	11.4569	16.1481	17.6134
ZZA*	11.4583	15.1875	16.4575	MHWZZA	9.1000	6.0313	20.8865
HWZZ	11.4583	15.1875	16.4575	MHWZZA4	9.1054	6.3368	21.0304
HWZZM	11.4583	15.1875	16.4575	MHR	11.4647	16.6145	18.0505
HWZZM*	11.4583	15.1875	16.4575	MHR4	11.6644	16.9713	18.4802
HWZZMA	14.2814	17.4395	19.2037	MHR±	11.4647	16.6145	18.0505
HWZZMB	15.9403	20.8031	20.9520	MHR4±	11.6644	16.9713	18.4802
HWZZMB2	12.6836	16.8409	17.8968	HSDT	11.7900	17.4157	18.5237
HWZZMC	11.4660	14.5666	14.7679	FSDT	12.1630	16.4436	17.5603
HWZZMC2	11.4823	16.5033	18.0240

,

Table 12. Normalized fundamental frequencies, case e1.

Lx/h = 5	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5
Exact [5]	6.8060	16.5150	26.6880	37.2550	48.0350
Zhen and Wanji [4]	6.8161	16.6154	27.4212	39.8230	54.1984
ZIGT [5]	6.8128	16.7297	27.8623	40.9060	56.1529
TOT [5]	6.9762	16.8783	27.1417	38.1864	50.3407
FSDT [5]	7.4458	18.2491	28.7697	41.1668	49.2839
3D FEA [48]	6.8115	16.5343	26.7475	37.3746	48.3752
ZZA	6.8116	16.5253	26.7123	37.2801	49.1224
ZZA*	6.8116	16.5253	26.7123	37.2801	49.1224
HWZZ	6.8116	16.5253	26.7123	37.2801	49.1224
HWZZM	6.8116	16.5253	26.7123	37.2801	49.1224
HWZZM*	6.8116	16.5253	26.7123	37.2801	49.1224
HWZZMA	6.8351	17.5435	27.2260	39.0876	55.4790
HWZZMB	6.8136	16.5504	26.8150	37.5666	49.9111
HWZZMB2	6.8165	16.5876	26.9680	37.9747	50.6078
HWZZMC	6.8153	16.5795	26.9446	37.9232	50.5189
HWZZMC2	6.8150	16.5769	26.9400	37.9217	50.5219
HWZZM0	6.8136	16.6907	27.1274	38.0196	50.2967
HRZZ	6.8140	16.5026	26.6062	37.0322	48.7296
HRZZ4	6.8080	16.4870	26.6057	37.1091	48.9903
MHWZZA	6.4175	15.5732	25.2021	35.8711	46.9424
MHWZZA4	6.8271	16.5673	26.8199	37.4702	49.4131
MHR	6.8198	16.6463	27.2066	38.5180	51.6381
MHR4	6.8202	16.6614	27.2706	38.6497	51.8742
MHR±	6.8198	16.6463	27.2066	38.5180	51.6381
MHR4±	6.8202	16.6614	27.2706	38.6497	51.8742
HSDT	6.9828	16.8828	27.1485	38.1713	51.2504
FSDT	7.4237	18.1565	28.5888	38.7856	50.1428

,

Table 13. Normalized fundamental frequencies, case e1.

Lx/h = 10	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5
Exact [5]	9.3434	27.2240	46.4190	66.0580	86.1690
Zhen and Wanji [4]	9.3748	27.3267	46.6609	66.6898	87.7990
ZIGT [5]	9.3434	27.2512	46.6511	66.9168	88.4094
TOT [5]	9.4742	27.9046	47.6259	67.5113	87.7200
FSDT [5]	9.7639	29.7831	51.4787	72.9941	94.1827
3D FEA [48]	9.3534	27.1962	46.4747	66.3024	86.8487
ZZA	9.3556	27.2463	46.4492	66.0544	87.6999
ZZA*	9.3556	27.2463	46.4492	66.0544	87.6999
HWZZ	9.3556	27.2463	46.4492	66.0544	87.6999
HWZZM	9.3556	27.2463	46.4492	66.0544	87.6999
HWZZM*	9.3556	27.2463	46.4492	66.0544	87.6999
HWZZMA	9.3634	27.3403	46.9501	70.1202	89.1944
HWZZMB	9.3561	27.2544	46.4856	66.1550	88.2045
HWZZMB2	9.3568	27.2661	46.5389	66.3042	88.5122
HWZZMC	9.3561	27.2612	46.5239	66.2718	88.4563
HWZZMC2	9.3560	27.2598	46.5189	66.2615	88.4411
HWZZM0	9.3562	27.4362	46.8354	66.7382	89.0772
HRZZ	9.3589	27.2560	46.4346	65.9635	87.7726
HRZZ4	9.3549	27.2320	46.3866	65.9012	87.7148
MHWZZA	7.4987	20.7918	42.6638	65.0068	87.5899
MHWZZA4	9.3733	27.3067	46.5481	66.2214	88.3184
MHR	9.3577	27.2792	46.6134	66.5364	89.1480
MHR4	9.3577	27.2808	46.6293	66.5962	89.3332
MHR±	9.3577	27.2792	46.6134	66.5364	89.1480
MHR4±	9.3577	27.2808	46.6293	66.5962	89.3332
HSDT	9.4832	27.9312	47.6368	67.4822	89.5987
FSDT	9.7608	29.6950	51.2648	72.5723	95.7078

,

Table 14. Normalized fundamental frequencies, case e1.

Lx/h = 20	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5
Exact [5]	10.6400	37.3740	71.7440	108.8900	147.0400
Zhen and Wanji [4]	10.6897	37.6810	72.6193	110.5376	149.6296
ZIGT [5]	10.6400	37.3740	71.7440	108.9989	147.4811
TOT [5]	10.6932	37.8972	73.2506	111.6123	150.8630
FSDT [5]	10.7890	39.0558	77.0531	119.1257	162.4792
3D FEA [48]	10.6527	37.3755	71.5020	108.9389	147.0909
ZZA	10.6575	37.4222	71.8164	108.9263	149.6777
ZZA*	10.6575	37.4222	71.8164	108.9263	149.6777
HWZZ	10.6575	37.4222	71.8164	108.9263	149.6777
HWZZM	10.6575	37.4222	71.8164	108.9263	149.6777
HWZZM*	10.6575	37.4222	71.8164	108.9263	149.6777
HWZZMA	10.6601	37.4536	71.9498	109.2996	150.7192
HWZZMB	10.6577	37.4243	71.8267	108.9586	149.7543
HWZZMB2	10.6580	37.4272	71.8418	109.0057	149.8559
HWZZMC	10.6575	37.4246	71.8334	108.9862	149.8207
HWZZMC2	10.6575	37.4242	71.8312	108.9804	149.8098
HWZZM0	10.6583	37.6355	72.2589	109.6109	150.6415
HRZZ	10.6589	37.4357	71.8491	108.9650	149.2023
HRZZ4	10.6574	37.4197	71.7993	108.8690	149.2281
MHWZZA	10.5652	37.1202	71.2611	108.0743	146.5888
MHWZZA4	10.6719	37.4952	71.9809	109.1660	148.0695
MHR	10.6581	37.4306	71.8579	109.0565	150.0877
MHR4	10.6581	37.4307	71.8588	109.0624	150.1300
MHR±	10.6581	37.4306	71.8579	109.0565	150.0877
MHR4±	10.6581	37.4307	71.8588	109.0624	150.1300
HSDT	10.7061	37.9327	73.3318	111.6654	153.6012
FSDT	10.8047	39.0433	76.9153	118.7217	164.5034

,

Table 15. Normalized fundamental frequencies, case e2.

Theory	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5	Mode 6	Mode 7	Mode 8
Liew [54]	4.4470	6.6420	7.7000	9.1850	9.7380	11.3990	11.6440	12.4660
Zhen and Wanji [4]	4.5400	6.5240	8.1780	9.4730	9.4920	11.7690	12.3950	12.9040
3D FEA [48]	4.4815	6.4637	7.9938	9.3025	9.3507	11.3722	11.5329	12.3221
ZZA	4.4682	6.5561	8.1065	9.3271	9.3371	11.1756	11.7574	12.1556
ZZA*	4.4682	6.5561	8.1065	9.3271	9.3371	11.1756	11.7574	12.1556
HWZZ	4.4682	6.5561	8.1065	9.3271	9.3371	11.1756	11.7574	12.1556
HWZZM	4.4682	6.5561	8.1065	9.3271	9.3371	11.1756	11.7574	12.1556
HWZZM*	4.4682	6.5561	8.1065	9.3271	9.3371	11.1756	11.7574	12.1556
HWZZMA	5.8520	7.5208	8.1724	10.4894	11.1722	11.2569	12.0353	13.1691
HWZZMB	4.9570	6.9202	8.1959	9.6129	10.7028	11.1675	11.9800	13.0014
HWZZMB2	6.0808	7.7635	8.8739	10.0492	10.8949	11.2114	12.6851	13.2650
HWZZMC	4.4859	6.6243	8.1606	9.6488	9.8538	11.1884	11.8340	13.2442
HWZZMC2	4.5001	6.6668	8.0939	9.6464	10.3489	11.1834	11.8285	13.6387
HWZZM0	4.4380	6.4692	8.6268	9.6356	10.2157	11.1670	11.9858	12.6024
HRZZ	4.4780	6.5756	8.6593	9.0735	9.5258	10.9819	11.6335	12.1995
HRZZ4	4.4923	6.5622	8.6120	9.4418	9.4418	10.9114	11.6410	12.2389
MHWZZA	5.7704	12.5575	12.8292	14.2568	15.3680	18.8049	21.7441	28.1598
MHWZZA4	5.8917	11.1227	12.9126	14.1157	15.2158	18.6187	21.5288	27.8810
MHR	4.6236	6.4996	9.0278	9.5643	9.7380	12.2893	12.3381	14.5644
MHR4	5.7578	10.8328	12.8328	14.3956	14.4156	19.1566	19.9439	20.5045
MHR±	4.6236	6.4996	9.0278	9.5643	9.7380	12.2893	12.3381	14.5644
MHR4±	5.7578	10.8328	12.8328	14.3956	14.4156	19.1566	19.9439	20.5045
HSDT	4.2424	6.4851	9.0818	9.6084	10.3515	11.5880	14.3931	13.3191
FSDT	4.1816	6.5979	8.5147	9.3171	10.2948	11.3770	11.5306	13.1945

,

Table 16. Normalized fundamental frequencies, case e3.

Theory	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5	Mode 6
Zhen and Wanji [4]	1.9445	3.3796	4.5914	5.5268	6.5128	8.4311
3D FEA [48]	1.8497	3.2308	4.3091	5.2810	6.1583	7.7796
ZZA	1.8566	3.2341	4.3215	5.2778	6.1782	7.8258
ZZA*	1.8566	3.2341	4.3215	5.2778	6.1782	7.8258
HWZZ	1.8566	3.2341	4.3215	5.2778	6.1782	7.8258
HWZZM	1.8566	3.2341	4.3215	5.2778	6.1782	7.8258
HWZZM*	1.8566	3.2341	4.3215	5.2778	6.1782	7.8258
HWZZMA	2.9945	8.2464	13.0020	23.1893	27.6448	29.3959
HWZZMB	1.8699	3.2238	4.4780	6.4664	7.0973	8.4051
HWZZMB2	2.5594	3.3902	4.4765	6.7477	7.1172	19.0397
HWZZMC	4.3268	3.2572	4.3669	5.3203	6.2311	7.8900
HWZZMC2	1.8603	3.3297	4.4768	5.4447	6.3394	8.0418
HWZZM0	3.0133	7.4920	10.3910	11.3215	15.1346	21.7804
HRZZ	1.8359	3.1546	4.1342	4.9488	5.6326	6.5177
HRZZ4	1.8375	3.1628	4.1541	4.9832	5.6931	6.6864
MHWZZA	4.5991	6.3956	2.5602	2.9859	55.0032	35.4337
MHWZZA4	4.5536	6.3323	2.5349	2.9563	54.4586	35.0828
MHR	13.9456	29.5039	41.6109	68.7426	65.8617	71.6472
MHR4	13.9456	29.5039	41.6109	68.7426	65.8617	71.6472
MHR±	1.8542	3.2453	4.3281	5.2674	6.1564	7.7888
MHR4±	11.0690	14.1130	14.9723	15.2744	16.5324	18.4374
HSDT	6.5797	12.7968	14.5661	22.9323	26.7542	30.9263
FSDT	13.9752	31.0136	42.0946	51.7209	59.2477	72.5151

,

Table 17. Normalized fundamental frequencies, case f.

Theory	Mode 1	Mode 2	Mode 3	Mode 4
3D FEA [53]	5.7720	8.7220	17.8210	95.3190
N = 3 (30 DOFS) [53]	5.7976	8.8428	19.5380	98.1640
3D FEA [48]	5.7769	8.7914	17.8705	95.3828
ZZA	5.7770	8.8424	17.7962	97.1215
ZZA*	5.7770	8.8424	17.7962	97.1215
HWZZ	5.7770	8.8424	17.7962	97.1215
HWZZM	5.7770	8.8424	17.7962	97.1215
HWZZM*	5.7770	8.8424	17.7962	97.1215
HWZZMA	5.7770	8.8424	17.7962	97.1215
HWZZMB	5.7770	8.8424	17.7962	97.1215
HWZZMB2	5.7770	8.8424	17.7962	97.1215
HWZZMC	5.7770	8.8424	17.7962	97.1215
HWZZMC2	5.7770	8.8424	17.7962	97.1215
HWZZM0	5.7791	8.8522	17.7800	101.5429
HRZZ	5.7722	8.8389	18.4970	101.6298
HRZZ4	5,7767	8,8087	18,4986	101,6402
MHWZZA	6.1101	9.8335	22.2173	99.8945
MHWZZA4	5.8063	9.8330	22.2071	99.2816
MHR	5.8766	9.6492	20.5639	97.0202
MHR4	5.8955	9.6492	20.2339	105.1698
MHR±	5.8766	9.6492	20.5639	97.0202
MHR4±	5.8955	9.6492	20.2339	105.1698

,

Table 18. Normalized fundamental frequencies, case g.

Theory	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5
3D FEA [48]	4.1785	10.4238	14.6587	16.4979	19.0105
ZZA	4.1788	10.4263	14.6864	16.5272	19.0239
ZZA*	4.1788	10.4263	14.6864	16.5272	19.0239
HWZZ	4.1788	10.4263	14.6864	16.5272	19.0239
HWZZM	4.1788	10.4263	14.6864	16.5272	19.0239
HWZZM*	4.1788	10.4263	14.6864	16.5272	19.0239
HWZZMA	14.6663	51.8295	82.2952	171.8208	89.6849
HWZZMB	4.2350	33.5909	91.3964	157.6279	68.3833
HWZZMB2	4.3790	24.8306	91.5540	159.3091	58.0426
HWZZMC	4.1790	10.4292	14.6857	16.5275	19.1303
HWZZMC2	4.1790	10.4288	14.6860	16.5276	19.0365
HWZZM0	4.2300	11.5140	91.2793	157.4339	41.1479
HRZZ	4.1373	9.9206	88.7309	151.5792	16.6322
HRZZ4	4.1380	9.9266	88.6647	151.2531	16.6531
MHWZZA	3.0776	5.0099	20.3131	29.1520	6.3628
MHWZZA4	4.1977	11.3344	21.3343	24.6261	21.2708
MHR	15.2050	42.4682	77.9566	154.7082	70.0325
MHR4	15.2011	42.2872	65.2275	65.4027	66.8219
MHR±	15.2050	42.4682	77.9566	154.7082	70.0325
MHR4±	15.0620	32.3678	17.9254	26.7157	57.4925
HSDT	14.1892	37.7022	***	***	61.7475
FSDT	16.3886	49.9499	***	***	87.0203

*** Not provided by the theory.

,

Table 19. Normalized fundamental frequencies, case h.

Theory	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5	Mode 6
3D FEA [48]	1.6882	2.8796	3.4723	4.3033	4.6899	5.7441
ZZA	1.6898	2.8855	3.4777	4.3171	4.7030	5.7500
ZZA*	1.6898	2.8855	3.4777	4.3171	4.7030	5.7500
HWZZ	1.6898	2.8855	3.4777	4.3171	4.7030	5.7500
HWZZM	1.6898	2.8855	3.4777	4.3171	4.7030	5.7500
HWZZM*	1.6898	2.8855	3.4777	4.3171	4.7030	5.7500
HWZZMA	5.3141	7.2110	11.3333	19.3264	21.7117	46.2461
HWZZMB	1.7010	2.8913	3.5605	4.3693	4.7101	34.1888
HWZZMB2	1.7651	4.7210	3.5473	5.0578	10.6544	34.7002
HWZZMC	1.6898	2.8855	3.4778	4.3171	4.7030	5.7500
HWZZMC2	1.6898	2.8855	3.4778	4.3171	4.7030	5.7500
HWZZM0	2.5169	5.6364	5.9019	8.8827	11.3106	34.3120
HRZZ	1.6823	2.8517	3.3940	4.1648	4.5907	34.3046
HRZZ4	1.6821	2.8525	3.3965	4.1720	4.5948	34.1832
MHWZZA	11.7654	2.7153	2.7264	3.7526	6.8737	1.4635
MHWZZA4	1.1776	3.9325	4.3165	4.3950	4.5656	5.6519
MHR	12.7147	15.1380	16.4288	27.1626	27.6009	64.6322
MHR4	12.7626	16.6121	22.2689	27.7771	27.8687	75.2673
MHR±	1.6959	2.9097	3.4919	4.3405	4.7643	61.7387
MHR4±	5.1510	5.8356	6.7704	7.2618	7.2672	66.5689
HSDT	16.5610	28.7206	37.7283	44.0301	44.2319	***
FSDT	11.0783	17.6361	20.9784	25.0619	25.3697	***

*** Not provided by the theory.

and

Table 20. Normalized fundamental frequencies, cases i1 and i2.

Case	i1					i2
t [s]	0.0009	0.0045	0.0056	0.0065	0.0074	0.0039	0.0080	0.01996	0.02408
3D FEA [48]	2.0268	2.0165	−1.3291	1.3278	−1.3174	0.4064	-0.0467	0.3316	−0.1147
ZZA	2.0399	2.0179	−1.3298	1.3286	−1.3181	0.4079	−0.0468	0.3319	−0.1147
ZZA*	2.0399	2.0179	−1.3298	1.3286	−1.3181	0.4079	−0.0468	0.3319	−0.1147
HWZZ	2.0399	2.0179	−1.3298	1.3286	−1.3181	0.4079	−0.0468	0.3319	−0.1147
HWZZM	2.0399	2.0179	−1.3298	1.3286	−1.3181	0.4079	−0.0468	0.3319	−0.1147
HWZZM*	2.0399	2.0179	−1.3298	1.3286	−1.3181	0.4079	−0.0468	0.3319	−0.1147
HWZZMA	1.5226	1.2548	−0.2519	0.2502	−0.1867	0.4774	−0.0963	0.3901	−0.1635
HWZZMB	0.8607	0.8663	−0.5765	0.5915	−0.5914	0.3870	−0.0420	0.3162	−0.0798
HWZZMB2	0.0000	0.0001	−0.0001	−0.0001	−0.0001	0.3097	−0.0357	0.2522	−0.0870
HWZZMC	0.6718	0.5765	−0.4677	0.1563	−0.2202	0.4080	−0.0468	0.3320	−0.1147
HWZZMC2	1.0741	0.9654	−0.5935	0.9727	−1.0830	0.4064	−0.0466	0.3308	−0.1142
HWZZM0	0.8562	0.8598	−0.5746	0.5855	−0.5822	0.2912	0.0232	−0.0443	0.2659
HRZZ	2.0219	1.9176	−1.6341	1.4543	−1.5171	0.4079	−0.0468	0.3320	−0.1147
HRZZ4	2.0212	1.9175	−1.6332	1.4540	−1.5169	0.4076	−0.0468	0.3317	−0.1146
MHWZZA	1.6544	1.1687	−0.0994	0.1028	−0.0331	0.4080	−0.0468	0.3320	−0.1147
MHWZZA4	1.7847	1.7135	−0.8618	0.8970	−0.8344	0.4600	−0.0362	0.2485	0.0311
MHR	0.7774	0.9828	−0.4954	−0.0765	0.7464	0.4077	−0.0466	0.3319	−0.1146
MHR4	0.7320	1.0386	−0.2750	−0.2267	0.5604	0.3737	0.0019	0.1197	0.1580
MHR±	1.9734	1.9659	−1.2595	1.2568	−1.2586	0.4077	−0.0466	0.3319	−0.1146
MHR4±	1.2527	0.0008	−0.6226	0.8942	−1.0796	0.3737	0.0019	0.1197	0.1580

and the computational cost is reported in

Table 21. Processing time[s].

Case	a1	a2	b1	b2	b3	c1	c2	d1	d2
ZZA	15.0671	15.9719	5.3866	6.8790	5.1194	29.6992	30.6735	26.4457	27.3202
HRZZ	18.2312	18.2261	4.6117	6.1888	4.8988	27.7977	28.4370	24.2019	25.0022
HRZZ4	18.2237	18.4891	5.0138	5.0387	5.0302	34.1087	36.4426	26.3526	27.2240
HWZZ	12.4271	12.8490	4.9640	6.2761	4.8679	27.3591	28.5739	24.5286	25.3396
MHR	6.9574	6.6258	2.8107	4.8288	2.7918	22.1087	23.6429	17.3712	17.9456
MHR4	6.4946	6.9702	2.9093	5.1452	2.6853	23.0599	24.0987	17.8493	18.4395
MHWZZA	7.2359	7.6952	3.7606	5.2613	3.6640	25.6959	25.6960	20.5304	21.2093
MHWZZA4	7.8365	7.5861	3.7602	5.2608	3.6636	25.7012	25.8412	20.5553	21.2350
HWZZM	11.5344	11.7059	4.1887	5.5954	4.0014	27.2368	27.1604	22.0831	22.8133
HWZZMA	11.5265	11.6018	4.1595	5.4061	3.9401	26.7922	26.4161	21.6381	22.3536
HWZZMB	11.5307	11.6289	4.1817	5.5216	3.9819	26.5349	26.8692	21.8242	22.5459
HWZZMC	11.5314	11.6457	4.1869	5.5926	3.9198	26.5605	26.8951	21.8288	22.5506
HWZZMB2	11.5310	11.6389	4.1659	5.5490	3.9905	26.5797	26.9146	21.8544	22.5770
HWZZMC2	11.5317	11.6401	4.1849	5.5951	3.8996	26.5905	26.9255	21.8184	22.5399
HWZZM0	11.4287	11.5912	4.1554	5.5079	3.7994	26.2617	26.3411	21.4596	22.1692
MHR±	6.9574	6.6258	3.0388	4.8770	2.8197	22.1087	23.6429	17.4648	18.0423
MHR4±	6.4946	6.9702	3.0384	5.1967	2.7122	23.0599	24.0987	17.9451	18.5385
ZZA*	11.4951	11.6125	3.8722	5.1722	3.8378	25.3302	25.2592	20.7581	21.6727
HWZZM*	10.9577	11.0035	3.9374	5.3156	3.8013	24.0637	24.5123	19.5104	20.3723
FSDT	-	-	3.0397	3.8151	2.6100	8.7624	8.8968	11.7092	12.0963
HSDT	-	-	3.2507	4.1839	2.6134	11.5608	11.6764	13.1811	13.6169

Processing time of 3D FEA is always about 12 times longer than that of ZZA, excluding meshing preparation.

and

Table 22. Processing time[s].

Case	e1	e2	e3	f	g	h	i1	i2	i3
ZZA	15.2146	49.8998	52.3788	20.9916	20.4415	57.4363	147.6859	76.1909	143.1814
HRZZ	13.9237	45.6660	57.0334	19.2106	18.7072	52.5631	135.1555	69.7264	130.4250
HRZZ4	15.1610	49.7241	53.0857	20.9177	20.3696	57.2341	147.1661	75.9227	150.2565
HWZZ	14.1116	46.2823	37.5954	19.4698	18.9596	53.2725	136.9795	70.6674	138.1438
MHR	9.9939	32.7772	38.6301	13.7886	13.4273	37.7277	97.0092	50.0468	93.0318
MHR4	10.2689	33.6793	44.4327	14.1681	13.7968	38.7660	99.6791	51.4242	100.9251
MHWZZA	11.8114	38.7383	44.4865	16.2963	15.8692	44.5891	114.6519	59.1487	117.1169
MHWZZA4	11.8257	38.7852	47.7931	16.3160	15.8884	44.6430	114.7906	59.2202	116.9716
HWZZM	12.7047	41.6680	46.8301	17.5287	17.0694	47.9613	123.3228	63.6220	119.6847
HWZZMA	12.4487	40.8284	47.2328	17.1755	16.7254	46.9949	120.8379	62.3400	117.8773
HWZZMB	12.5558	41.1795	47.2427	17.3232	16.8693	47.3990	121.8770	62.8761	122.6692
HWZZMC	12.5584	41.1881	47.2981	17.3269	16.8728	47.4089	121.9025	62.8892	121.4148
HWZZMB2	12.5731	41.2365	47.2202	17.3472	16.8926	47.4645	122.0455	62.9630	125.2797
HWZZMC2	12.5524	41.1686	46.4436	17.3186	16.8648	47.3864	121.8446	62.8594	125.6217
HWZZM0	12.3460	40.4915	37.7979	17.0338	16.5874	46.6071	119.8407	61.8256	114.0284
MHR±	10.0477	32.9538	38.8376	13.8629	13.4996	37.9309	97.5317	50.3164	93.58166
MHR4±	10.3241	33.8602	47.7931	14.2442	13.8709	38.9742	100.2145	51.7004	98.46074
ZZA*	12.0695	38.7513	44.4886	16.4770	16.2159	44.6040	114.6902	59.8047	112.7978
HWZZM*	11.2246	37.2096	41.8193	15.4866	14.7633	42.3786	106.6619	56.2164	106.5141
FSDT	6.7364	22.0938	25.3415	-	9.0508	25.4307	65.3900	33.7345	64.1452
HSDT	7.5832	24.8711	28.5271	-	10.1885	28.6275	73.6099	37.9752	75.5128

Processing time reported include symbolic computation. For calculation, a laptop computer with quad-core CPU@2.60 GHz. 64-bit operating system and 8.00 GB RAM was used.

.

5.1. Propped Cantilever Sandwich Plate in Cylindrical Bending under Uniform Static Loading

Firstly, a static analysis of two propped cantilever sandwich plates in cylindrical bending under a uniform load $p^0{}_{(+)}$ on the top face are considered, in order to preliminary assess the accuracy of the theories in predicting the displacement and stress fields. The structure is clamped at x = 0 and restrained on the lower face at x = L_x; the elastic moduli of faces and core are assumed to be E_u/E_l = 1.6 and E_u/E_c = 166.6, respectively, and with a Poisson’s ratio $\upsilon =0.3$; the lower _(l) and upper ^(u) faces are t_l = c/2 and t_u = c/4 thick, respectively, where c is the core thickness. The results of the theories are compared to the ones by 3D FEA [48], whose elements are formulated in order to fulfil Equations (16) and (18), and the displacements and out-of-plane stresses are assumed as nodal d.o.f. The length-to-thickness ratios L_x/h = 5.714 (case a1) and 20 (case a2) are considered.

Regarding case a1, according to Mattei and Bardella [27] and Icardi and Sola [21], its through-thickness displacement and stress fields are very challenging, and require a very accurate description of the transverse shear force resultant at the clamped (7) and at the simply supported edges (10), and a very accurate description of the transverse normal stress; otherwise, incorrect stress predictions are obtained. Moreover, what makes this a tough case is the opposite sign that is assumed at the upper and lower faces by the transverse shear stress at the supported edge. 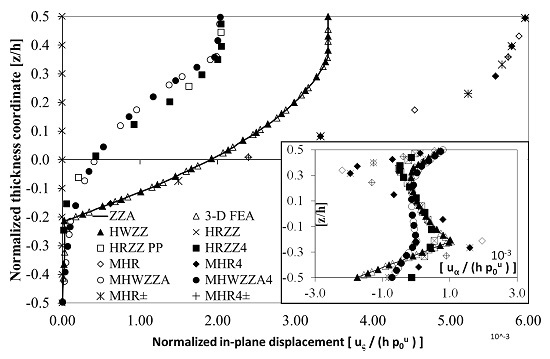Figure 1 shows the results for the thickest case (L_x/h = 5.714). It can be seen that, contrary to what was postulated by Murakami’s zig-zag function, at the supported edge, the slope of $u_{\varsigma }$ never reverses, while $u_{\alpha }$ doesn’t reverse near the upper interface, so MHR and MHR4 obtain inaccurate results. Even MHR± and MHR4±, whose interfacial displacement slope is determined on a physical basis, are not adequate, because their kinematics are too poor. MHWZZA4 and MHWZZA, incorporating strain and stress fields from HWZZ, obtain better results than MHR and MHR4, while HRZZ calculates an incorrect null transverse displacement at the supported edge. Summarizing, all of the lower-order theories obtain inaccurate results. Since the results of HWZZM are in good agreement with those of the adaptive theories ZZA, ZZA*, HWZZ, and 3D FEA, it is proven that the choice of layerwise functions is immaterial as long as higher-order coefficients are defined as in Section 3.1 and Section 3.3. HWZZMB, HWZZMB2, and HWZZM0 assuming arbitrarily zig-zag amplitudes can accurately predict the axial displacement but not the transverse one, while HWZZMC and HWZZMC2 calculate precise displacements, whereas HWZZMA always provides wrong results (so they are not reported in the figures). It should be noticed that the behaviour of theories arbitrarily assuming zig-zag amplitudes is very case-dependent, and only some are quite accurate.

The results for the slender case L_x/h = 20 are reported in Figure 2; the calculations show that a still significant difference between the predictions of theories exists, and ${\sigma }_{\alpha \varsigma }$ differs from that which is expected for the rather thin sandwich structures. Again, only higher-order theories obtain a good degree of accuracy, and HWZZMA is so inaccurate that results cannot be reported. The obvious conclusion is that even for a length-to-thickness ratio of 20, an accurate description of kinematics is of primary importance in the present case.

On the basis of the processing time required (see Table 21 and Table 22 and Section 5.10), it can be concluded that the adaptive theories ZZA, ZZA*, HWZZ, HWZZM, and HWZZM* are the most efficient ones, as they combine accuracy and low cost. It should be remembered that the same representation with the same low expansion order (Section 2.2) dictated by industrial needs is used for all of the theories. Since the results in the literature for MZZ have shown that greatly increasing the expansion order along with that of the representation across the thickness obviously produces more accurate results, prior statements are valid only for the conditions that are examined here. Below, dynamic tests are carried out that consider progressively more challenging benchmarks that highlight the need for sophisticated theories.

5.2. Free Vibration Modes of Simply Supported Laminated and Sandwich Plates in Cylindrical Bending

First, the analysis of simply supported cross-ply [0/90/0] (case b1) and [0/90]₂ (case b2) plates in cylindrical bending is presented, which primarily serves as a preliminary test of the accuracy of 3D FEA [48] in solving dynamics problems, this having yet been tested. Then, a [0/core/0] simply supported sandwich plate in cylindrical bending (cases b3) is studied, which has more marked layerwise effects.

The first fundamental frequency predicted by the present theories for case b1 is given in Table 6 considering a length-to-thickness ratio of 10. Comparisons are carried out with the exact solution and the results of EFSDT and EHSDT theories by Kim [49].

It can be seen that only ZZA, HWZZ, HWZZM, ZZA*, and HWZZM* higher-order theories provide very accurate results, but a sufficient accuracy is obtained by the HRZZ, HRZZ4, MHWZZA, MHWZZA4, MHR, MHR4, MHR±, MHR4±, and HWZZMC simplified theories. Instead, HWZZMA, HWZZMB, HWZZMB2, and HWZZM0 give an inaccurate prediction of it. However, case b1 does not appear to be severe, as many theories prove adequate. Although they have dissimilar characteristics, it is noted that HSDT and FSDT (shear correction factor of 5/6 chosen to minimize the error) calculate even the fundamental frequency inaccurately. The same considerations apply for case b2, with the same length-to-thickness ratio of 10, as shown in Table 6; therefore, the previous considerations are not repeated.

The fundamental frequency for a [0/core/0] simply supported sandwich plate constituting case b3 [49] is reported in Table 7 for three different length-to-thickness ratios (four, 10 and 20). Contrary to what one would expect, errors don’t dramatically decrease as Lx/h increases, and the behaviour of theories remains quite diversified. In particular, MHWZZA, MHWZZA4, and HWZZMA, HSDT, and FSDT (shear correction factor is 5/6) prove to be inaccurate irrespective of the length-to-thickness ratio.

Modal displacements and stresses are reported In Figure 3, Figure 4 and Figure 5, where the results are normalized as shown in Table 5, and show that the axial displacement $u_{\alpha }$ and the in-plane stress ${\sigma }_{\alpha \alpha }$ are accurately calculated except by MHWZZA and MHWZZA4, while the transverse shear stress ${\sigma }_{\alpha \varsigma }$ is inaccurately calculated by MHR, MHR4, MHR±, MHR4±, MHWZZA, and MHWZZA4 for the thickest case. An even bigger scattering is shown for $u_{\varsigma }$, which is accurately calculated only by ZZA, HWZZ, HWZZM, ZZA*, and HWZZM*, while on the contrary, the transverse normal stress ${\sigma }_{\varsigma \varsigma }$ is accurately calculated by all of the theories. Note that the results by HWZZMA are never reported in Figure 3 and Figure 4 as being too wrong. For the same reason, the stress and displacement distributions are not reported for FSDT and HSDT. Such big errors highlight the inapplicability of the most simplified theories even for slender cases, which is contrary to what is often claimed in the literature.

5.3. Fundamental Frequency and Modal Displacements and Stresses of a Simply Supported, Anti-Symmetric Cross-Ply Plate

The fundamental frequency of [0/90/0/90], simply supported, cross-ply square plates with a length-to-thickness ratio of five [4], is examined in Table 8 for increasing the values of the degree of orthotropy E₁/E₂ ranging from three to 40 (case c1).

Comparisons are given with the results by a global–local higher-order theory [4] and by Matsunaga [56], which were obtained using a higher-order ESL. It can be seen that all of the theories of this paper provide fairly accurate predictions of the fundamental frequency in correspondence with the lowest orthotropy ratios, while quite dispersed results are shown as this ratio reaches the value of 20. In particular, very incorrect results are given by ESL, FSDT (shear correction factor ${\pi }^2/12$), and HSDT for E₁/E₂ values greater than 30 and by theories MHR, MHR4, MHWZZA, MHWZZA4, HWZZM0, HWZZMB2, and HWZZMC2. Adaptive theories ZZA, ZZA*, HWZZ, HWZZM, and HWZZM* instead always provide results that are in very well agreement with the exact solution, irrespective of the orthotropy ratio.

The through-thickness variation of modal displacement $u_{\varsigma }$, transverse shear ${\sigma }_{\alpha \varsigma }$, and transverse normal ${\sigma }_{\varsigma \varsigma }$ modal stresses are reported in Figure 6 and Figure 7 for ratios E₁/E₂ of 3 and 40, respectively. Note that $u_{\alpha }$ is correctly captured by all of the theories only for E₁/E₂ = 3, so just the results for this highest ratio are reported. The results by HWZZMB2 and by HWZZM0 are only reported for E₁/E₂ = 40, as they are inaccurate for all of the other cases. All of the other theories provide a quite accurate prediction of the in-plane displacement as well as of ${\sigma }_{\alpha \varsigma }$, with the only exceptions being MHR and MHR4, while there is a bigger scattering of results regarding ${\sigma }_{\varsigma \varsigma }$.

The fundamental frequencies for case c2 with an orthotropy ratio E₁/E₂ of 30 and a length-to-thickness ratio of 10/3 are reported in Table 9. Modal displacements and modal in-plane and transverse shear and normal stresses for this case are shown in Figure 8, along with the results by 3D FEA, Zhen and Wanji [4], and Matsunaga [56]. These results show that MHWZZA, MHWZZA4, MHR, and MHR4 overestimate the fundamental frequency, while MHWZZA, MHWZZA4, MHR, and MHR4 incorrectly predict the in-plane displacement and stress, while MHR± and MHR4±, whose slope is defined on a physical basis, obtain better results than their counterparts MHR and MHR4 with the slope assumed a priori.

A rather large dispersion of results is shown for $u_{\varsigma }$ and for the transverse normal stress, while the transverse shear stress is erroneously provided by HRZZ, HRZZ4, MHWZZA, MHWZZA4, MHR, and MHR4 only across the first layer. Again, in this case, with the slope being defined on a physical basis, HSDT and FSDT (the latter uses π²/12 as the shear correction factor in order to improve the accuracy of the results) appear inadequate to perform the analysis.

5.4. Fundamental Frequency of a Cross-Ply Plate with Different Thickness Ratios and Boundary Conditions

The fundamental frequency of a [0/90/0] cross-ply square plate with a thickness ratio ranging from 4 to 100 and simply supported (case d1), all clamped, or simply supported edges and clamped on opposite sides (case d2), are reported in Table 10 and Table 11, respectively. The results are compared to those by Di Sciuva and Icardi [50] (RFSDT, RHSDT, theories and RHQ40 elements) and to 3D FEA [48], as well as to those by FSDT and HSDT.

The results of case d1 show a very well agreement among the theories each other, as well as with 3D FEA reference solutions when the length-to-thickness ratio increases, because the layerwise effects become less important, while remarkable differences are shown for the thickest cases. All of the theories appear to be accurate except for HWZZM0, MHWZZA, and MHWZZA4 (even for moderately thin plates), FSDT (shear correction factor 5/6), and HSDT (the latter two are accurate only for the lengths-to-thickness greater than 10).

The results for the different boundary conditions considered (case d2), namely clamped and simply supported edges (CSCS) and all-clamped edges (CCCC), are reported in Table 11 for a length-to-thickness ratio Lx/h = 10, along with the results for simply supported edges (SSSS).

It is noted that only ZZA, ZZA*, HWZZ, HWZZM and HWZZM* give predictions of the fundamental frequency that are always very well in agreement with 3D FEA, while all of the other theories are less accurate.

It is also noted that the errors are greater for CSCS and CCCC, which therefore prove more problematic than SSSS because the mechanical boundary constraints are more difficult to satisfy identically for clamped edges. In this case, FSDT (shear correction factor 5/6) and HSDT do not provide valid results for any boundary condition. Therefore, it is deduced that for cases d1 and d2 FSDT and HSDT are unsuitable, similarly to other theories with a fixed representation.

So, it is confirmed also in this case that only adaptive theories whose coefficients can be redefined across the thicknesses (ZZA, ZZA*, HWZZ, HWZZM, and HWZZM*) obtain always accurate results with low computational cost (see Section 5.10), and then, they should be preferred in the applications.

5.5. First and Higher-Order Free Vibration Frequencies of Potpourri Cases

Here, the vibration behaviour of plates made of different materials and with different boundary conditions is discussed. Table 12, Table 13 and Table 14 report the first five frequencies for a [0/90/0] square plate (the intermediate layer has a thickness of h/2, while the outer ones have a thickness of h/4) here referred to as case e1, which is retaken from Kapuria et al. [5] (ZIGT and TOT theories). This plate is simply supported along the edges parallel to the y-axis and free at the other two edges (SFSF). Length-to-thickness ratios of 5, 10 and 20 are considered.

Again, adaptive theories ZZA, HWZZ, ZZA*, HWZZM, ZZA*, and HWZZM* appear as the most accurate among those considered, irrespective of the mode examined. On the contrary, the other theories exhibit errors that grow with the frequency order and with the increasing thickness. Only ZZA, HWZZ, ZZA*, HWZZM, ZZA*, HWZZM*, HRZZ, HRZZ4, and MHWZZA4 obtain quite accurate results for length-to-thickness ratios of 5, while MHR, MHR4, MHR±, MHR4±, HWZZMA, and HWZZM0 can’t get the fourth and the fifth frequencies for the intermediate length-to-thickness ratio of 10. Instead, for L_x/h = 20, all of the theories except FSDT (shear correction factor ${\pi }^2/12$) and HSDT give accurate predictions of frequencies, as the layerwise effects tend to wears off, even if contrary to what is claimed in the literature, this does not always occur in all of the examined cases.

The first eight frequencies for a [0/90/0] square plate with clamped edges (CCCC), which is retaken from Zhen and Wanji [4] and Liew [52], and is here referred to as case e2, are reported in Table 15. In this case, in addition to 3D FEA, comparisons can be carried out with results obtained assuming a linear in-plane displacement across the thickness and a uniform transverse displacement. Errors less than 2% are shown by adaptive theories ZZA, ZZA*, HWZZ, HWZZM, and HWZZM* with respect to 3D FEA, whereas the other theories exhibit larger errors that increase with the order of frequency that is considered. However, guessing the shear correction factor, accurate results can be achieved by FSDT (in the current case with a shear correction factor of 5/6), as also shown in [56], despite the very simple kinematics. This gives a reason at least for the case that is currently examined, to those who consider ESL suitable for dynamic analysis. However, it could be argued that an appropriate shear correction factor could not easily be chosen in the industrial applications.

Table 16 reports the first six frequencies of case e3, which concerns a simply supported (SSSS) [0/90/core/0/90] soft-core sandwich plate with a length-to-thickness ratio of 10. It should be noted that for this case, it is necessary to enforce two additional conditions across the upper layer in the adaptive theories, which means the first two local equilibrium equations; otherwise, the accuracy drops. Having done this, again, all of the higher-order adaptive theories obtain accurate results for all of the frequencies.

Also HRZZ, HRZZ4, HWZZMB, HWZZMC, and HWZZMC2 provide quite accurate results, while other lower-order theories are inaccurate. As in many other cases, MHR and MHR4 are not adequate, because Murakami’s rule is not respected, so MHR± and MHR4±, whose slope sign is determined on a physical basis, obtain better results. Also, in this case, FSDT (shear correction factor 5/6) and HSDT (no need of shear correction factor) obtain inaccurate results.

5.6. Through-Thickness Mode of a Simply Supported, Cross-Ply Plate in Cylindrical Bending

A simply supported cylindrically bent [0/90] plate (case f) is now studied, which is retaken from Pagani et al. [53], who analysed it via finite elements. The interesting aspect of this case is that great cross-section deformations are already involved by the first four frequencies, which could undermine the concept of the plate on which the theories that are considered in this paper are based. Indeed, deformations from the first to the fourth frequency are respectively: a bending mode, a bending/torsional mode, a torsional mode, and finally an axial/shear mode.

The structure is 200-mm thick, while its length-to-thickness and length-to-side ratios are 10. In this case, a suited choice of even and odd trial functions should be made to obtain accurate results by the present theories, and a sufficiently high expansion order of the representation must also be considered, as indicated in Table 2.

The results for this case, which are reported in Table 17, where they are compared to the present FEA results and the ones from [53], show that adaptive ZZA, ZZA*, HWZZ, HWZZM, and HWZZM* theories only commit an error of the order of 2% or less, albeit their representation order across the thickness and their number of unknowns are lower of those of the theory that was used to construct finite elements in [53]. Since there is only one interface, HWZZMA, HWZZMB, HWZZMB2, HWZZMC, and HWZZMC2 achieve the same accuracy of HWZZM, whereas all of the other lower-order theories predict wrong frequencies, which is a sign that a refined kinematics is required. In this case, the results by FSDT and HSDT aren’t reported as being totally wrong.

5.7. First Five Free Vibration Frequencies of a Soft-Core Sandwich with Strong Transverse Normal and Shear Deformability Effects

For the purpose of checking which theory is able to effectively capture strong 3D effects related to transverse normal and shear deformability, case g is examined. It concerns a simply supported cylindrically bent sandwich plate with stiff faces and a compliant core that has not yet been considered in the literature. Each face has a thickness of 0.2 h, and is made of three layers having different thickness and properties, as indicated in Table 3, while the core is 0.6-h thick. The first and the third face layers proceeding from the outside toward the inside are made of the same very stiff material (m2), while the interposed layer is made of a more compliant material in tension, compression, and shear (m1); finally, the core is made of the most compliant material (m3), as indicated in Table 4. A length-to-thickness ratio of five is considered.

Table 18 reports the first five free vibration frequencies for this case, as predicted by the theories of this paper and by 3D FEA. The results indicate that the first, second, and fifth frequencies represent the bending modes, while the third and fourth ones represent more interesting motions that occur across the thickness in a symmetrical manner with respect to the mid-plane. So, specific boundary conditions should be enforced to get rid of these modes.

Moreover, the fulfillment of local equilibrium equations should be enforced near the core interfaces in the adaptive theories, the only ones where it is possible to do it; otherwise, poor results similar to those of other theories are obtained. The results demonstrate the superior accuracy of the adaptive theories ZZA, ZZA*, HWZZA, HWZZM, and HWZZM*, which were obtained thanks to the imposition of these constraints, irrespective of whether they directly considered a piecewise transverse displacement or recovered the effects of the normal transverse deformation differently. Naturally, in this case, the gap with other theories is much more marked than in the previous cases because of the greater importance assumed by the transverse normal deformation, it being the one that was less accurately reproduced. In this case, HWZZMC and HWZZMC2 obtain inaccurate results, with their errors increasing with the frequency order, i.e., the third and fourth frequencies are progressively more inaccurate.

From Figure 9, which reports the in-plane modal displacement, in-plane and transverse shear modal stresses for the first mode, and a minor subject to errors, it can be seen that all of the theories except HWZZMA, MHR, MHR4, MHR±, and MHR4± obtain quite accurate results, which is a sign that Murakami’s theories are inappropriate for this case. However, it is noted that the greatest errors occur on the transverse modal displacement and the normal modal stress. Figure 10 reports the modal stresses and displacements for the third frequency by ZZA, ZZA*, HWZZA, HWZZM, HWZZM*, HWZZMC, and HWZZMC2, while the results by other theories are not reported as being too wrong.

5.8. Free Vibration of a Thick Simply Supported [0/90/Core/0/90] Sandwich Plate

The first six free vibration modes of a simply supported sandwich plate having the same thickness of faces and core of case e3 and the same orientation is studied assuming a thicker length-to-thickness ratio of five. With the same purpose, stiffer faces are considered, as indicated in Table 3, while the core has the same properties as case e3. These choices, which are distinctive of a benchmark that has never been investigated before, here called case h, enhance the layerwise effects, and consequently they should highlight the quite different behaviours of the theories.

Table 19 reports the first six free vibration frequencies predicted by the present theories and by 3D FEA for this new case. Similar to the previous case g, the first five frequencies are bending modes, while the sixth represents a motion that occurs in a symmetrical manner in the thickness direction. So, the same considerations about the constraints that must be imposed apply again, and consequently, it is still demonstrated that the material properties and thickness of constituent layers constitutes a strong discriminatory effect on the accuracy of the theories.

Considerations that are similar to those of the previous case g apply, because only adaptive theories are always in well agreement with 3D FEA results. All of the other theories, except HWZZMC and HWZZMC2, which obtain results accurate enough, give inaccurate predictions, especially for the sixth mode.

5.9. Blast Pulse Loading

In this section, two square plates with a different lay-up and subject to step and exponential blast pulse loadings are analysed. The first is a sandwich plate that is subject to a step pulse (case i1), which has a length Lx of 609.6 mm, its core is 25.4-mm thick, and its two faces, each one being a five-layer laminate, have a total thickness of 1.905 mm. The second is a laminated [0/90/0] square plate whose central layer is two times thicker than the outer ones, whose length is 2540 mm and whose overall thickness is 170 mm (case i2), which is subject to an exponential blast pulse. Such case studies are retaken respectively from Hause and Librescu [54], where the step blast pulse overpressure loading is described as:

$$p=\{\begin{array}{l}{p}^0{}_{(+)}ift<5\mathrm{ms}\\ 0ift\ge 5\mathrm{ms}\end{array}$$

(37)

and from Librescu and Noisier [55], where the exponential blast pulse overpressure is considered as:

$$p=p^0{}_{(+)}(1-t/t_p)e^{-2t/t_p}$$

(38)

where t_p is 0.1 s.

The results for the first case i1 are reported in Figure 11 as the central plate deflection at the mid-plane normalized to the plate thickness. It can be seen that also in this case, only theories ZZA, ZZA*, HRZZ, HRZZ4, and HRZZ4* provide a correct time-variation of the deflection, which is in good agreement with 3D FEA. Notice that the results by [54] differ from the FEM results because of the lower-order model used therein. However, we see a similar behaviour where errors tend to disappear with respect to the present theories if a single half-wave in the x and y directions is considered instead of the expansion order that is reported in Table 2.

As for the other cases considered previously, again, MHR and MHR4 appear to be inadequate because Murakami’s rule is not respected, while their counterparts MHR± and MHR4±, whose slopes are computed on a physical basis, appear to be more accurate.

The results for the case i2 are reported in Figure 12, where again the transverse displacement is reported at z = 0 and at the center of the plate, and is still normalized to the plate thickness. Since now the layer has the same material properties and a symmetric stack-up, the layerwise effects fade, so the discrepancies between the results by theories also fade.

Anyway, MHWZZA4, MHR4, MHR4±, HWZZMA, and HWZZM0 still appear inaccurate, whereas the adaptive theories once again obtain results that are in very good agreement with 3D FEA. Table 20, which reports results for specific instants (0.9 ms, 4.5 ms, 5.6 ms, 6.5 ms, and 7.4 ms for i1 and 3.9 ms, 8.0 ms, 19.96 ms, and 24.08 ms for i2) show that the erroneous predictions (both frequency and amplitude of response are wrong) given by HRZZ, HRZZ4, HWZZMB, HWZZMB2, and HWZZMC2 are erroneous, which had not been noticed for the initial instant (0.9 ms for i1 and 3.9 ms for i2, which corresponded to the occurrence of the first peak of ZZA in each of the two cases) considered in Figure 11 and Figure 12).

It is worth noting that in both cases i1 and i2, there is no detectable difference when the transverse displacement is evaluated in points across the thickness other than at the middle plane as reported in the tables and figures, because both structures are thin. However, splitting the core into two halves whose upper half is much more compliant than the lower one (case i3), similar as to when a face is damaged, and assuming Lx/h = 10 and a different orientation of layers of faces, the results of Figure 13 are obtained, which show visible differences between the results of the theories. Those assuming a uniform or a polynomial transverse displacement in this case don’t account properly for this effect, so less accurate results are obtained, see e.g., MHR±, MHWZZA, MHWZZA4, HRZZ, HRZZ4, FSDT, and HSDT.

It is specified that a Newmark implicit time integration scheme was adopted for solving transient dynamic equations, since alternative explicit time integration schemes need extremely small time steps to be stable. However, for reasons of the stability of the algorithm, small time-steps are still required (30 $\mathsf{\mu }\mathrm{s}$) to limit the convergence and rounding errors. Since geometrical and material non-linearity are disregarded, the system to solve is a linear system, and the computational burden isn’t adversely affected by such a small time step.

5.10. Computational Effort of Theories

Table 21 and Table 22 reports the calculation times that are necessary to solve each of the benchmarks considered by the examined theories, which being based on the same five d.o.f., therefore have a memory storage occupation that is practically indistinguishable from one another. As closed-form solutions are considered even when other researchers recoursed to FEA due to the complexity of the solutions in the cases examined, calculation times are very short for all of the theories; that is, they remain comparable to those of FSDT and HSDT.

This testifies to the efficiency of the present adaptive and higher-order, because they require just a reduced expansion order, both with regard to the in-plane and through-thickness representation to achieve accurate results for all of the challenging benchmarks examined. So, it can be said that a level of accuracy that is comparable to that of the FEA has been obtained with a lower computational burden. However, FEA remains indispensable for solving the problems of industrial complexity, while the preliminary parametric studies can be performed as in this paper.

It appears that the MHR and MRH4 theories have the lowest processing time out of all of the theories, but this advantage is totally negated because they provide inaccurate results whenever strong layerwise effects rise, because in these cases, the slope varies differently from what is expected by Murakami’s rule. Although slightly more expensive, MHR± and MHR4± obtain often rather accurate results, since their slope sign of displacements is decided on a physical basis. HRZZ and HRZZ4 result in slower processing times than the adaptive theories for static cases whenever stresses must be computed through time-consuming procedures, but if this is not required, that is only global quantities are required, they result in faster processing times than the adaptive theories. However, this advantage nullified the results of HRZZ and HRZZ4, which were inaccurate in almost all of the cases that were considered.

Higher-order theories HWZZ, HWZZM, ZZA*, and HWZZM* provided rather more accurate results in all of the cases examined, and required a little longer processing time than HRZZ and HRZZ4. However, it is noted that HWZZM* with a priori assumed zig-zag amplitudes requires 20% less processing time than HWZZ, but they don’t appear to be the most accurate theories. In particular, HWZZMA, HWZZMB, HWZZMB2, HWZZMC, and HWZZMC2 appear to be inadequate in many cases. ZZA, HWZZ, HWZZM, ZZM*, and HWZZM* don’t qualify for the lowest calculation time between all of the theories, appear to be the most efficient theories, and thus are preferred in the applications, which are always very accurate and still have affordable costs. However, the best of such adaptive theories from this point of view turns out to be ZZA*, which has a slightly lower calculation cost.

6. Concluding Remarks

Various displacement-based and mixed zig-zag theories, which differ in the layerwise functions and in the scheme of the through-thickness representation of the displacements that are used, have been applied to investigate the free vibration behaviour and the response of blast-loaded laminated and sandwich plates with different length-to-thickness ratios, lay-ups, constituent materials, and boundary conditions. To homogenise the results, they are compared using the same type and order of representation as closed-form solutions, with the appropriate trial functions being selected for each benchmark to minimize the expansion order. The intended aim is to evaluate the merits and drawbacks of theories in order to establish which are significantly much more accurate and efficient.

The numerical applications show the importance of very accurately accounting for the transverse normal deformability whenever the layers have non-uniform mechanical properties and a different thickness. Indeed, adaptive zig-zag theories whose layerwise contributions identically satisfy interfacial stress constrains and whose displacement fields are redefined for each layer prove superiority. ZZA* theory shows that the choice of zig-zag functions is immaterial whenever the coefficients of displacements are recomputed across the computational layers. In this context, zig-zag functions can even be omitted, as the stress continuity constraints can be enforced in order to define the coefficients of displacement fields in a more computationally efficient way.

The accuracy of results is shown to be independent of the choice of zig-zag functions for ZZA*, but this result is extensible to all of the theories that in the same way provide a redefinition of the coefficients of displacements across the thickness, so as to satisfy the physical constraints. Vice versa, the theories whose coefficients of displacements are fixed fail to be accurate whenever strong layerwise effects rise or there is a strong transverse anisotropy, since finding a kind of fixed representation that is always suitable is impossible, unless a very high order of representation is used. That is the opposite of what this paper sets out, which is wanting to find accurate solutions at a low cost. Indeed, the accuracy of theories with a fixed representation appears to be largely case-dependent. Mixed theories such as MHWZZA and MHWZZA4 based on Murakami’s zig-zag function (as well as all those for which zig-zag amplitudes are a priori assumed) are often proven inaccurate, although not in all cases, even though they benefit from strain and stress fields by adaptive theories. The same happens even when the slope sign of displacements at interfaces is established on a physical basis, at least for the low orders of the in-plane and through-thickness representation that are considered in this paper, which however allow the adaptive theories to be already very accurate. Anyhow, it is not easy to discern for which cases the limiting assumptions of such theories do not have weight. Therefore, it is not possible to establish a general rule, although the results undoubtedly show that the theories accounting for layerwise effects without the determination of zig-zag amplitudes on a physical basis cannot provide an adequate level of accuracy with the low expansion orders that are considered in this paper.

A simplified uniform or polynomial representation of the transverse displacement is shown to be ineffective even when the strain and stress fields are retaken from other more accurate structural models, such as for MHWZZA. In particular, FSDT and HSDT theories are proven to be inaccurate in the majority of the examined cases.

Although the adaptive theories whose coefficients of displacements are redefined across the thickness do not get the lowest processing time, they were proven to be the efficient ones, since they always achieve the best accuracy with a processing time that is still short, while the other theories have lower calculation times, but also a much lower accuracy.