On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study
Abstract
:1. Introduction
Active Span Extension and Passive Pitch (ASAPP) Wing
2. Modeling and Validation
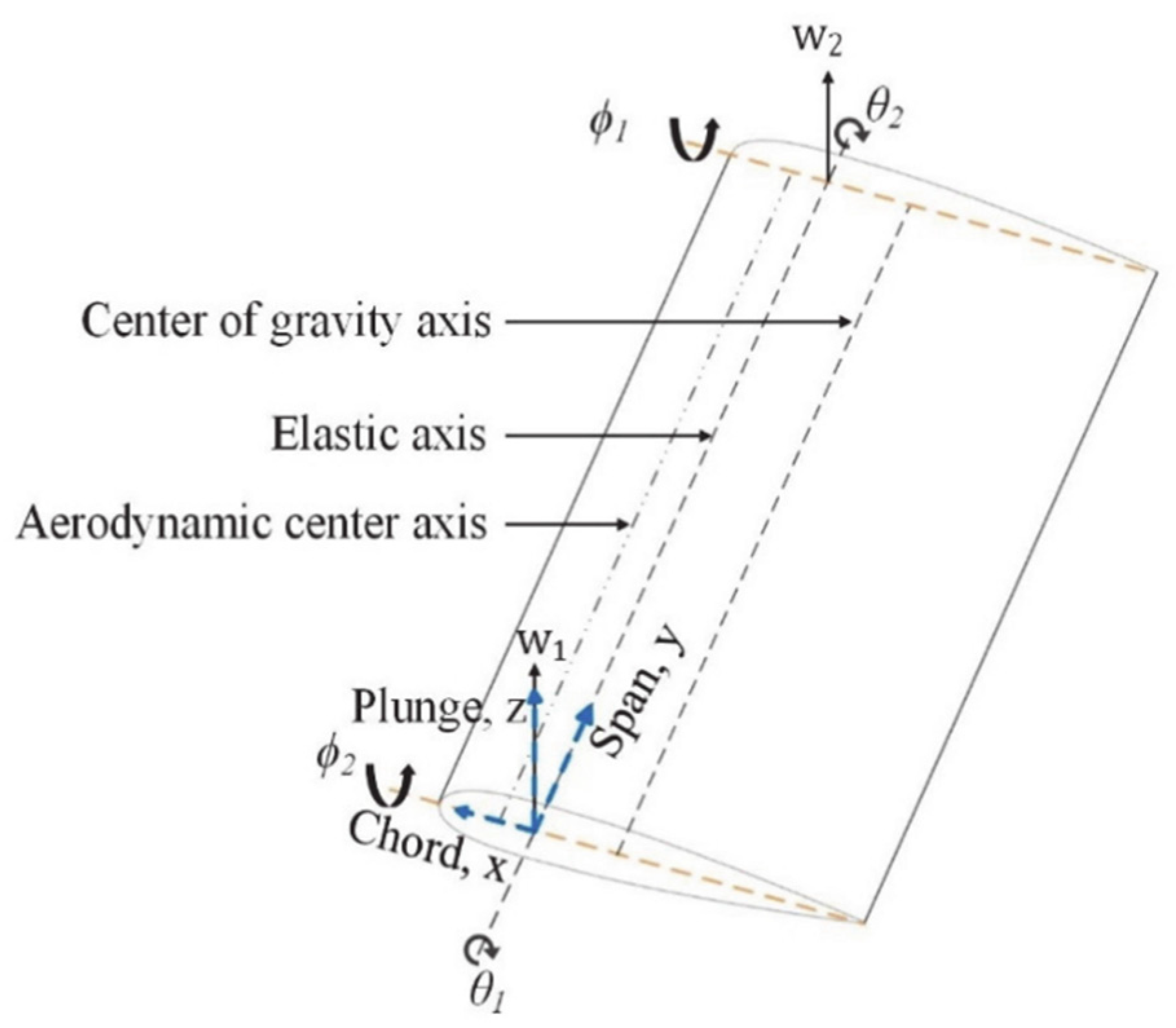
2.1. Structural Dynamics Model
2.2. Aerodynamic Model
2.3. Aeroelastic Model
2.4. Gust Load Modelling
2.5. Model Validation
3. Parametric Study
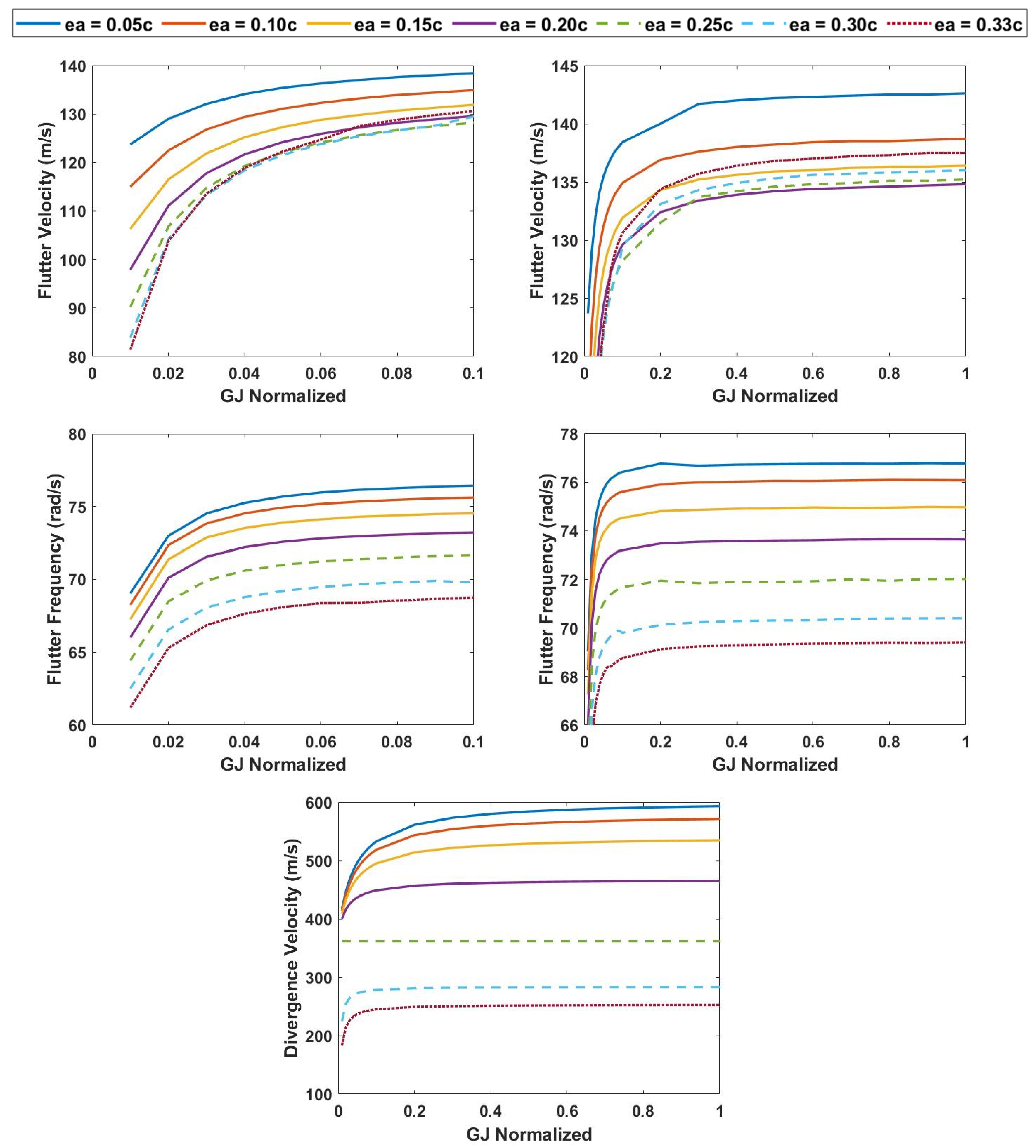
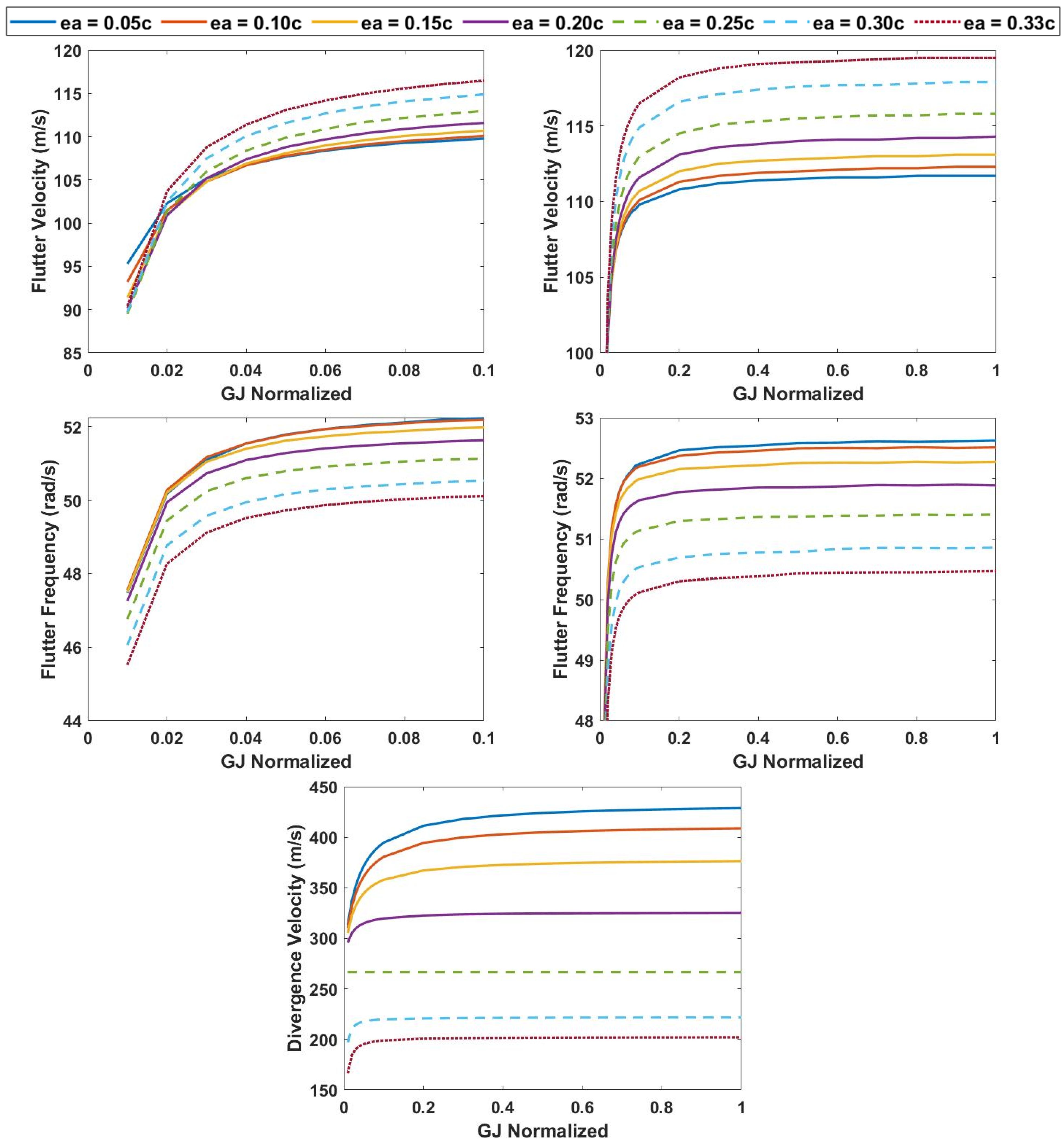
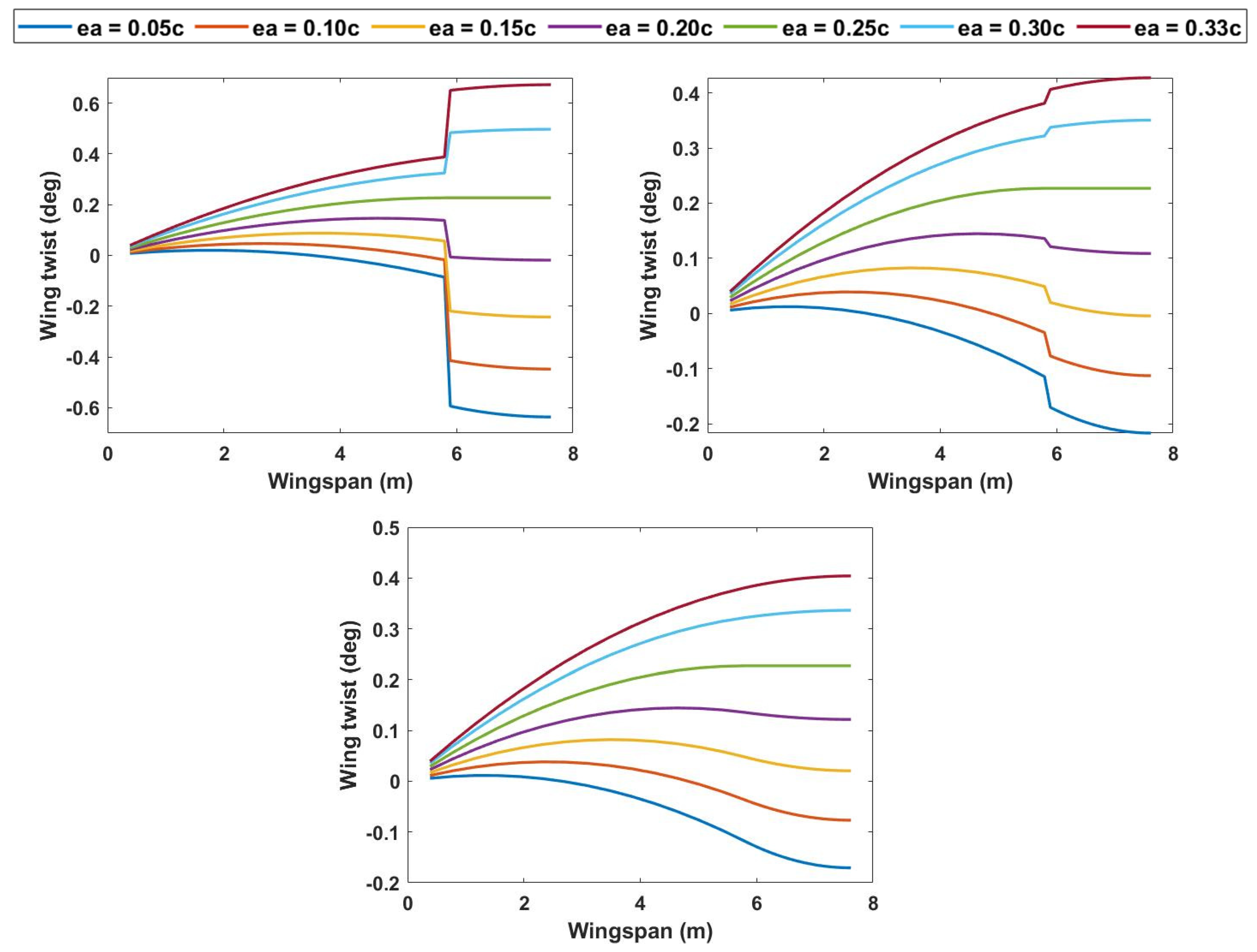
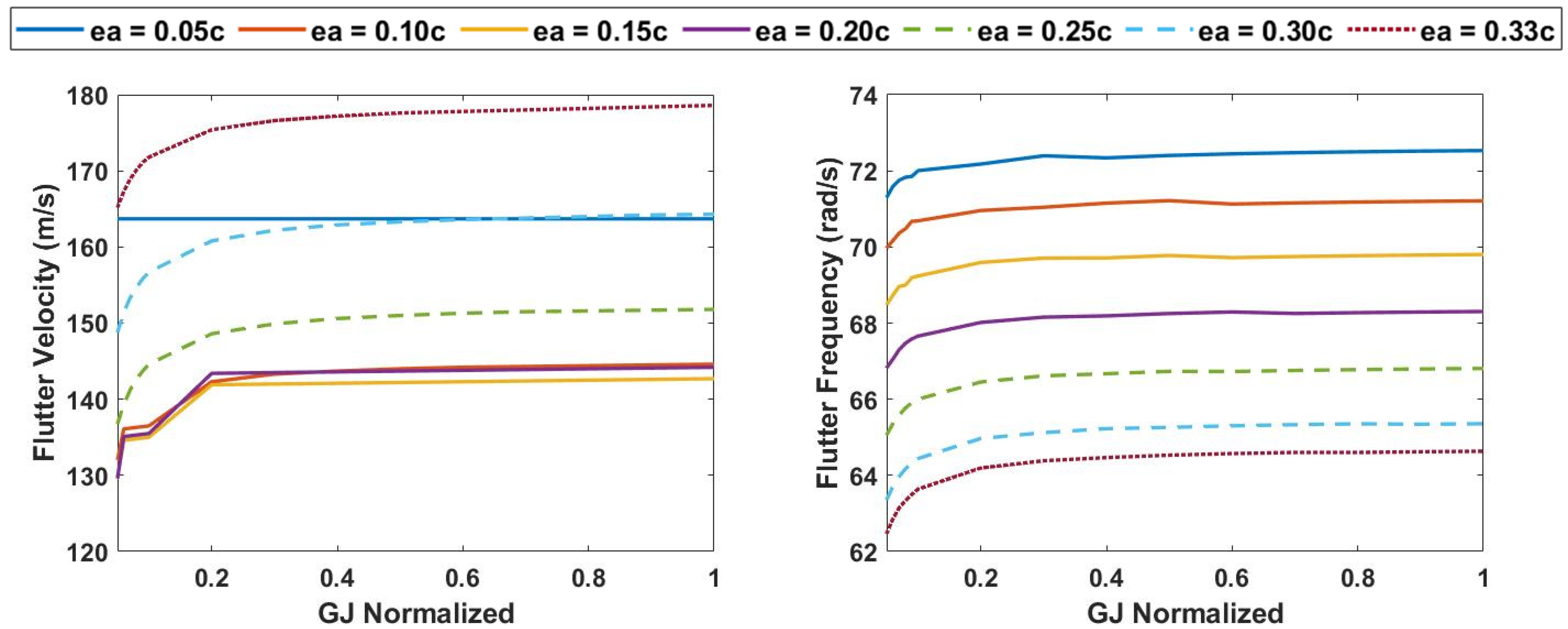
3.1. Variation in Elastic Axis and Torsional Rigidity at 0% Span Extension
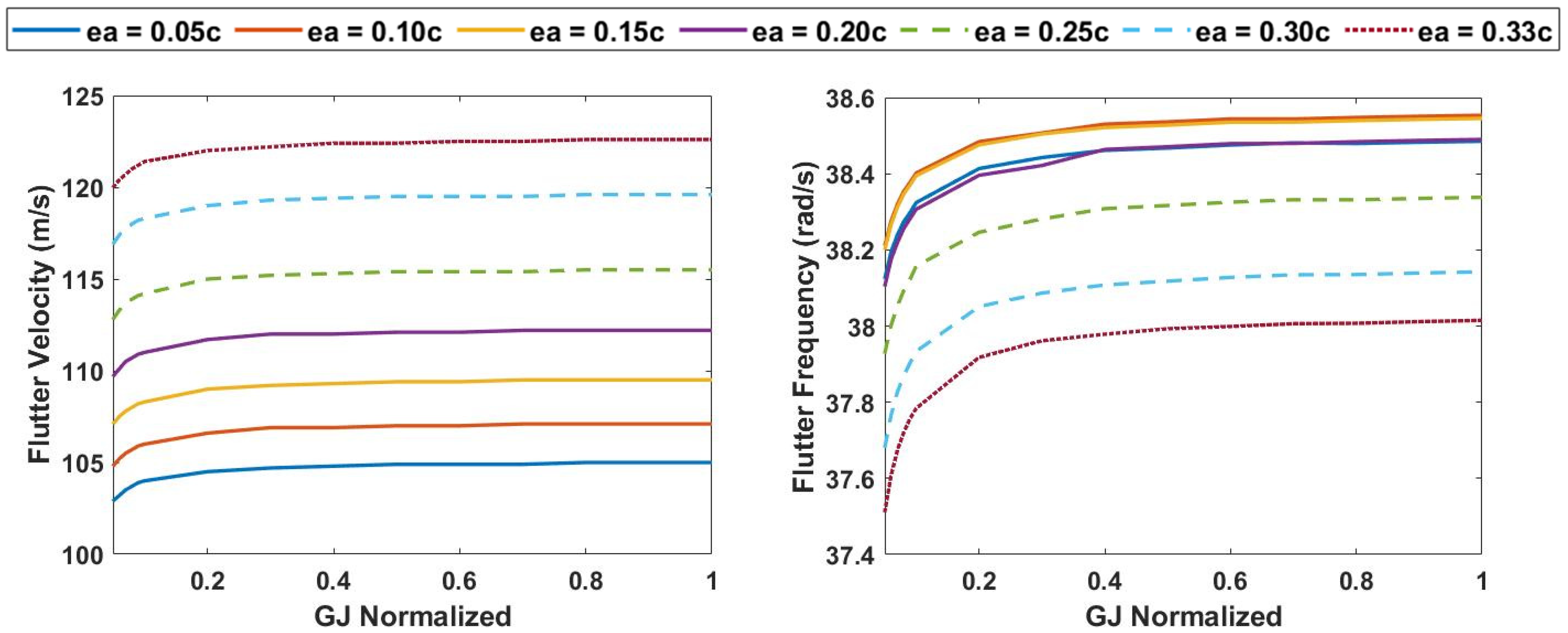
3.2. Variation in Elastic Axis and Torsional Rigidity at 25% Span Extension
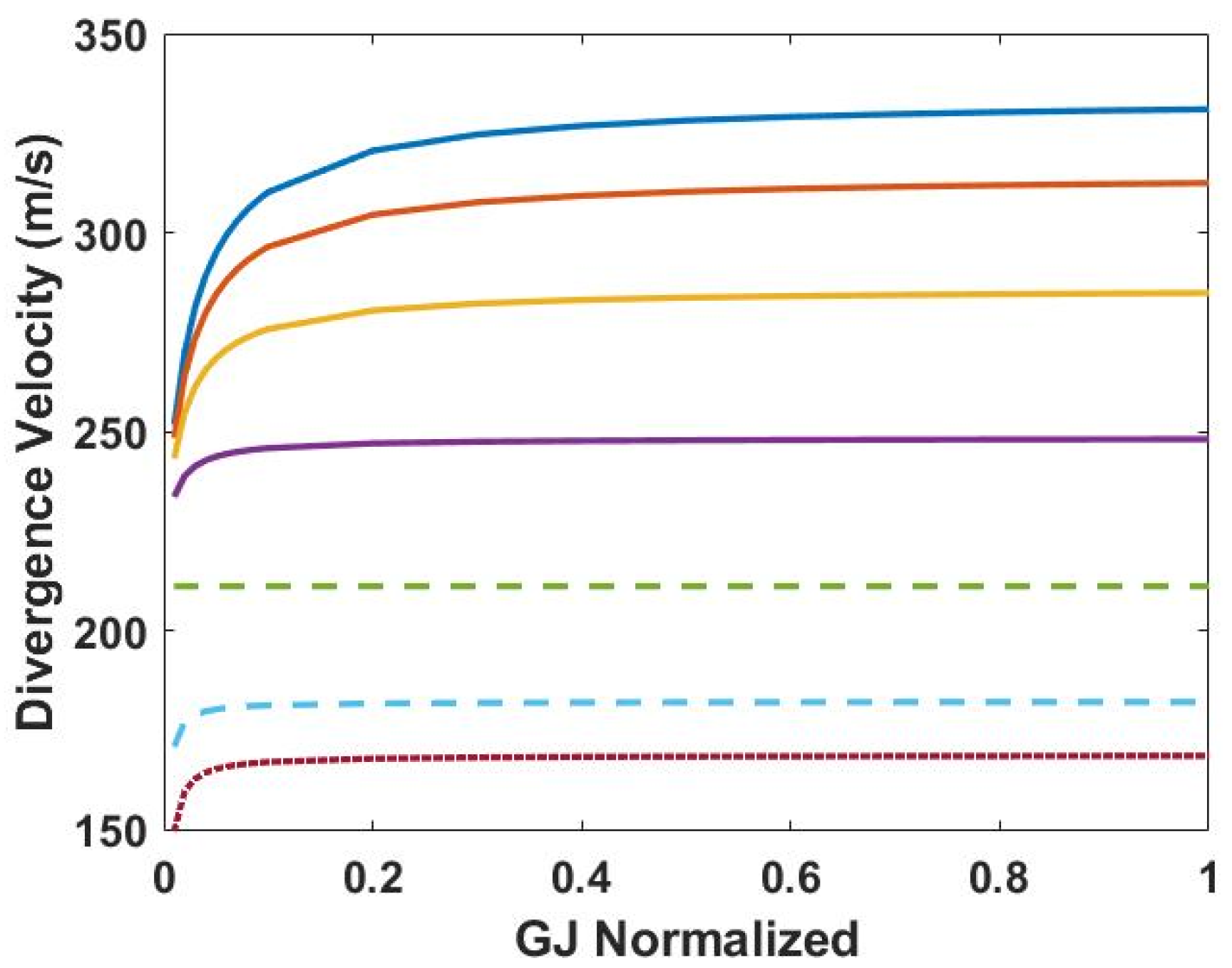
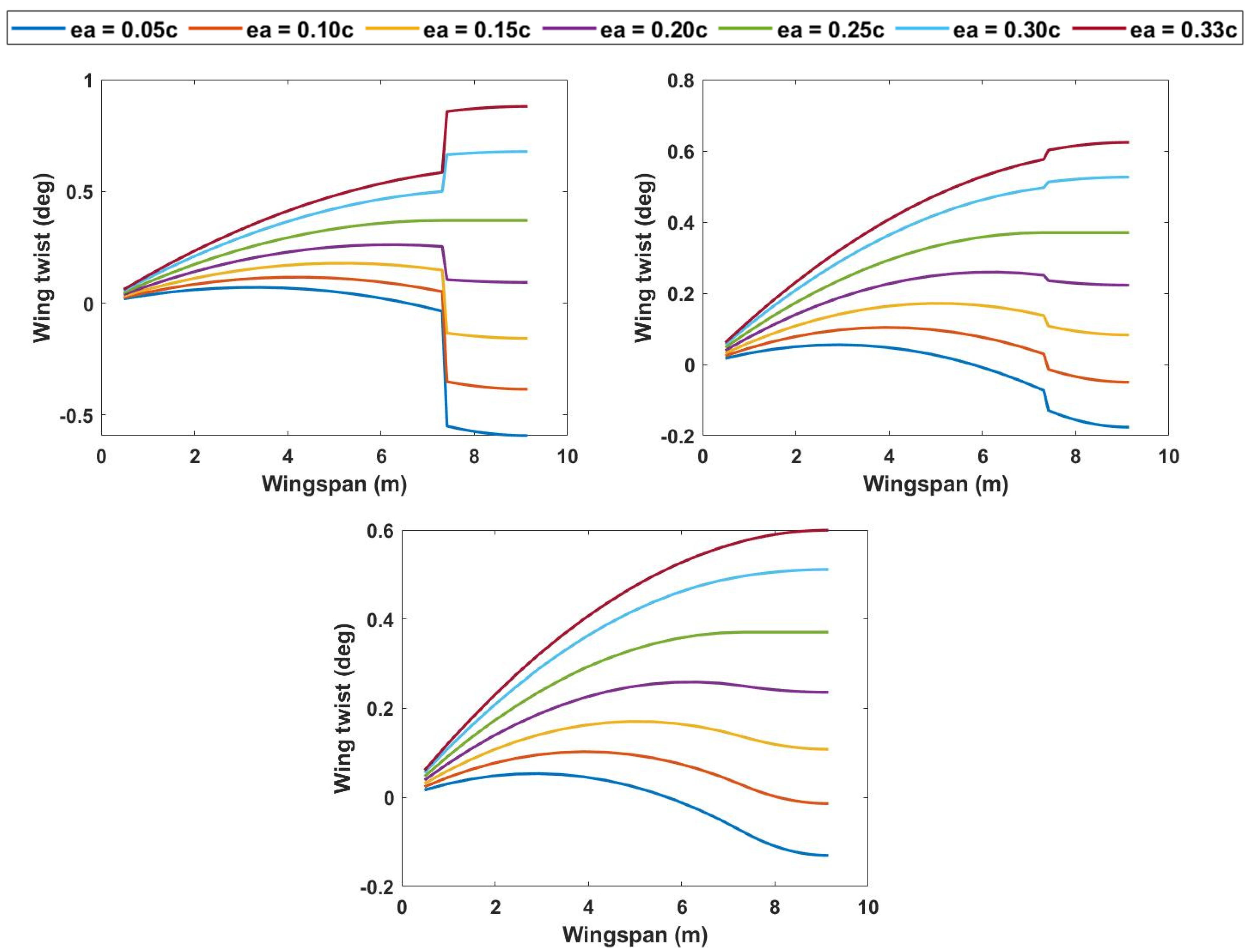
3.3. Variation in Elastic Axis and Torsional Rigidity at 50% Span Extension
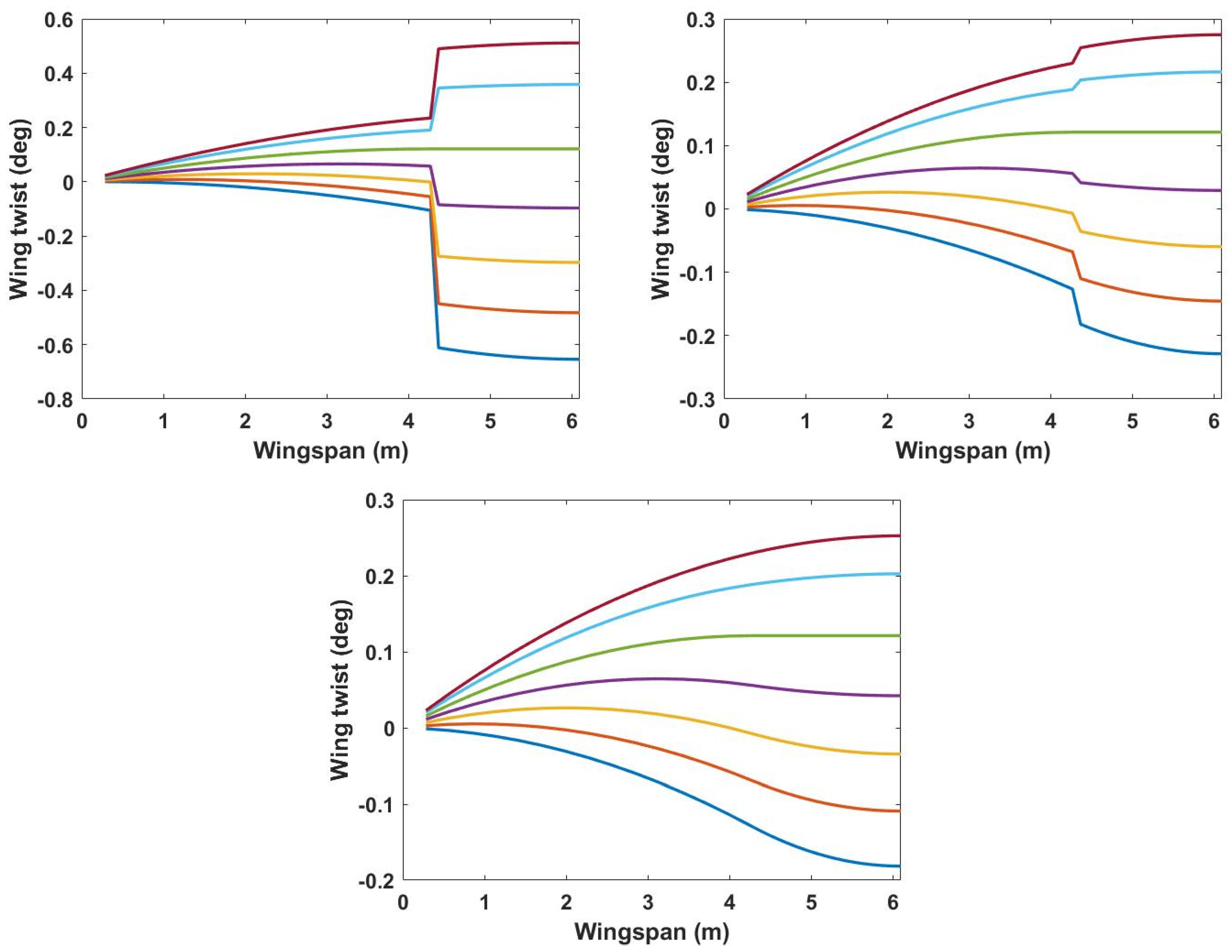
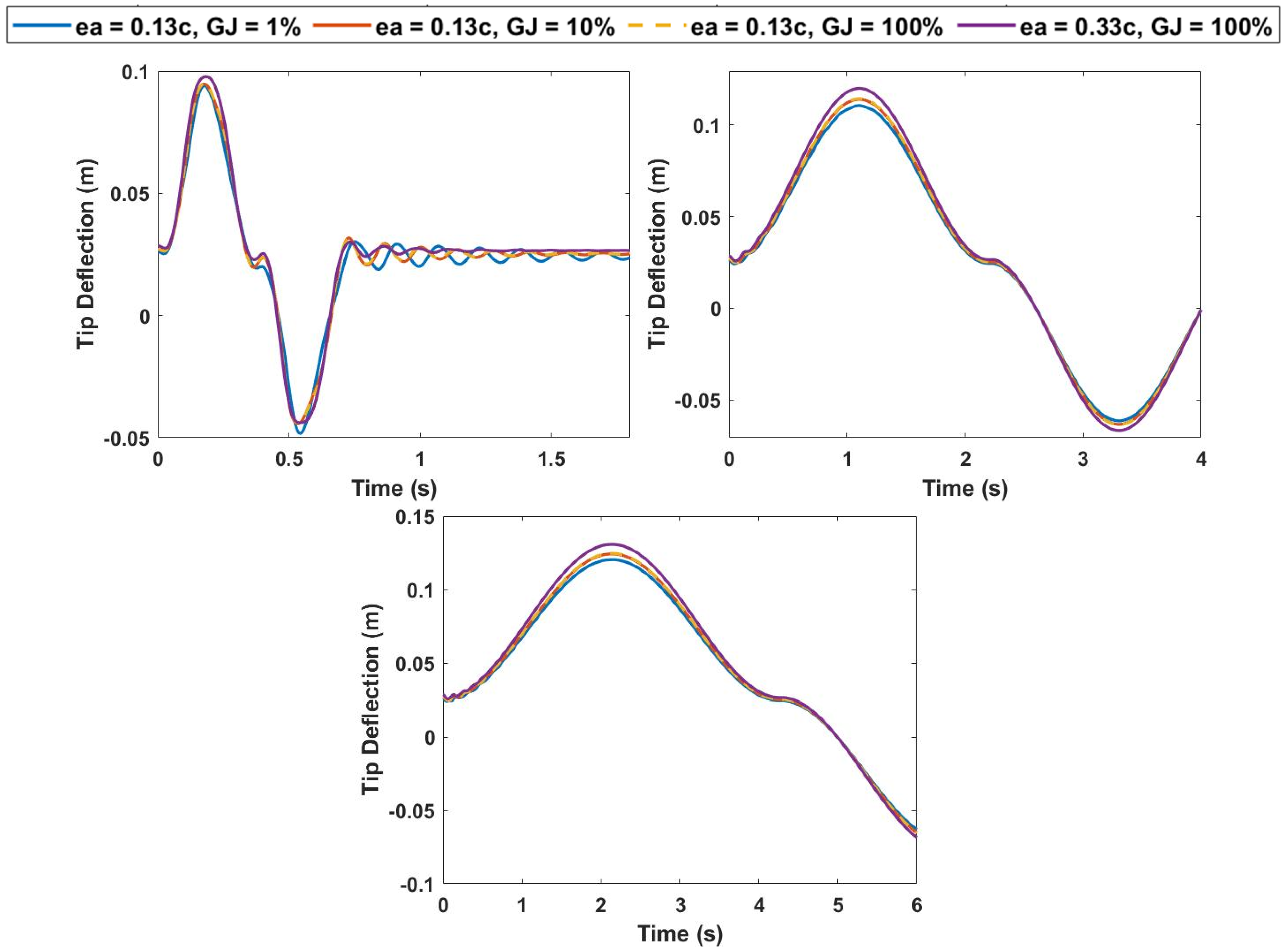
3.4. Aeroelastic Effect of Varying Outboard Wing Center of Gravity to 33% Chordwise Position
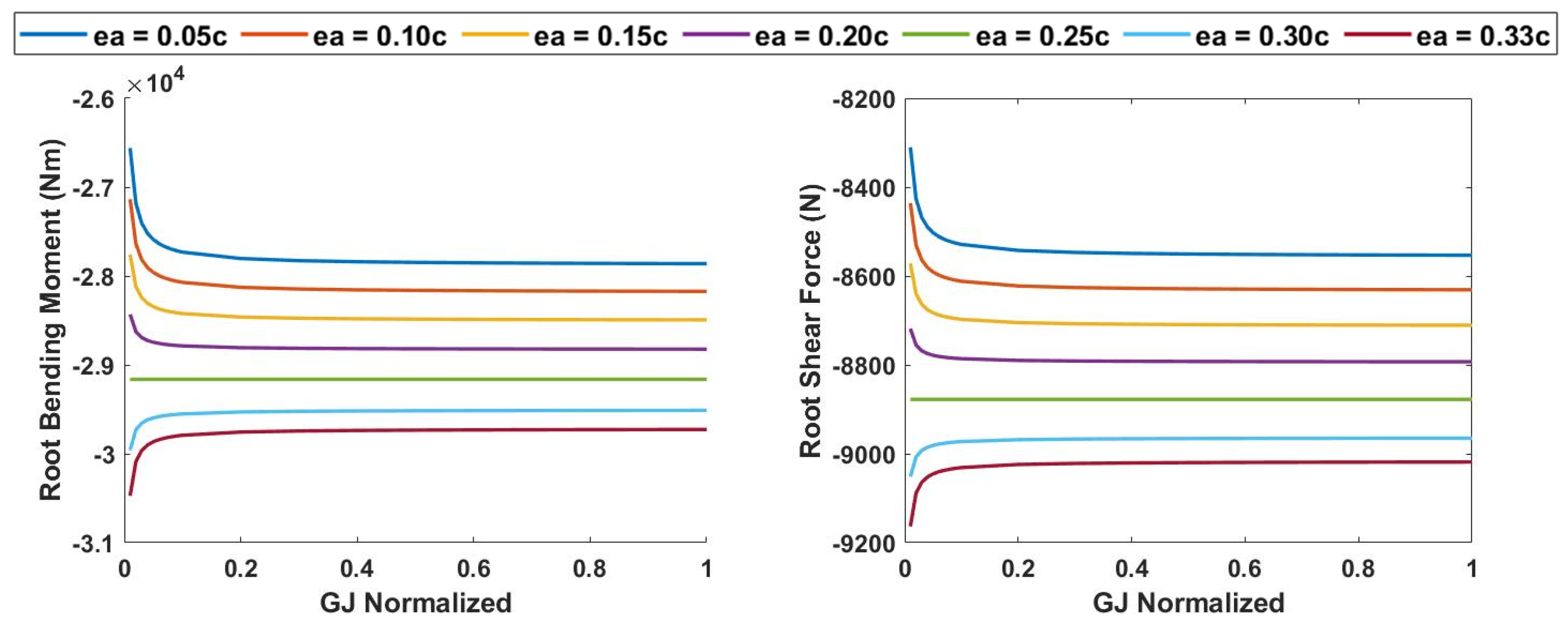
3.5. Gust Load Analysis
Quasi-Steady Analysis
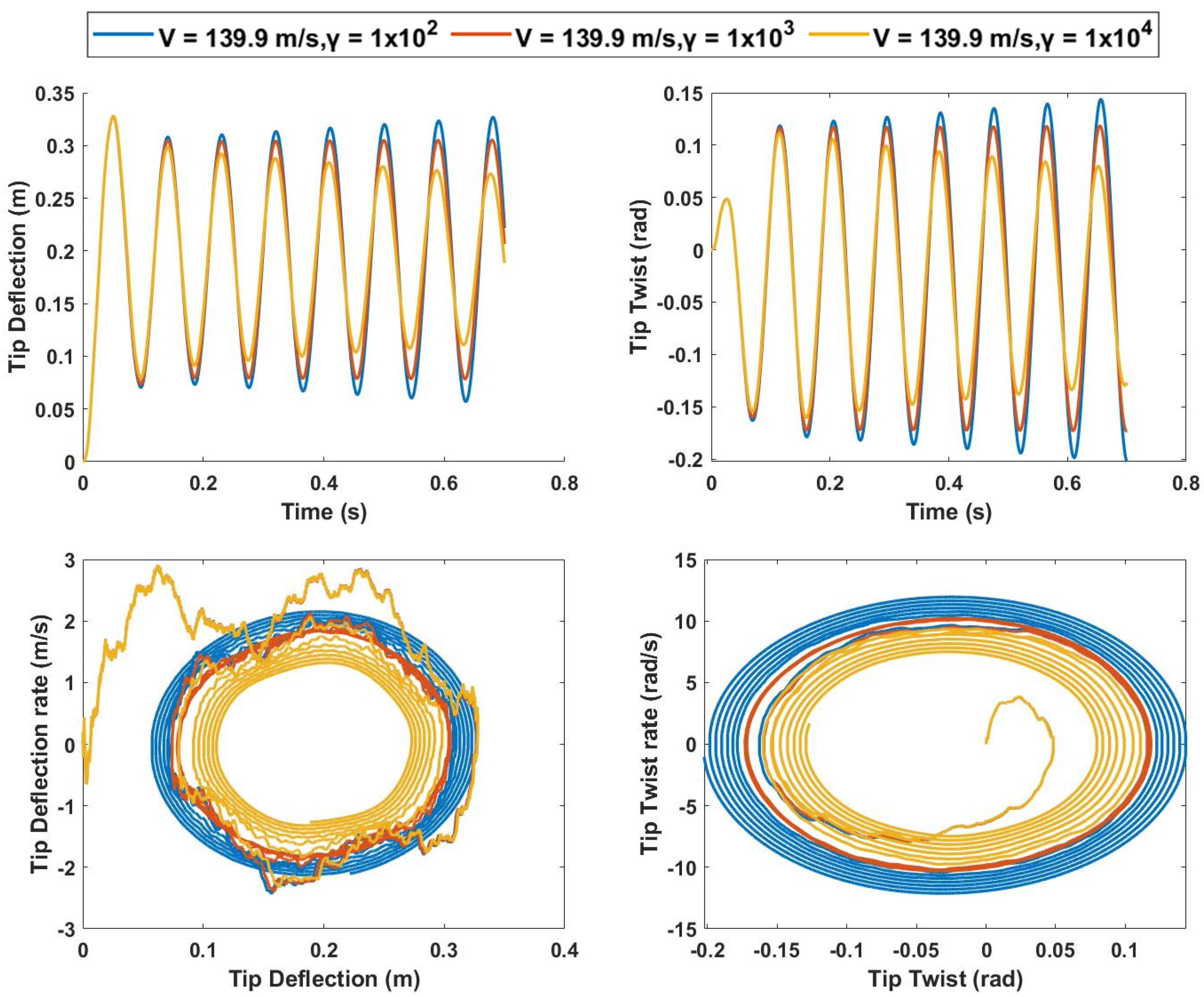
4. Cubic Nonlinearities
4.1. Hardening Spring
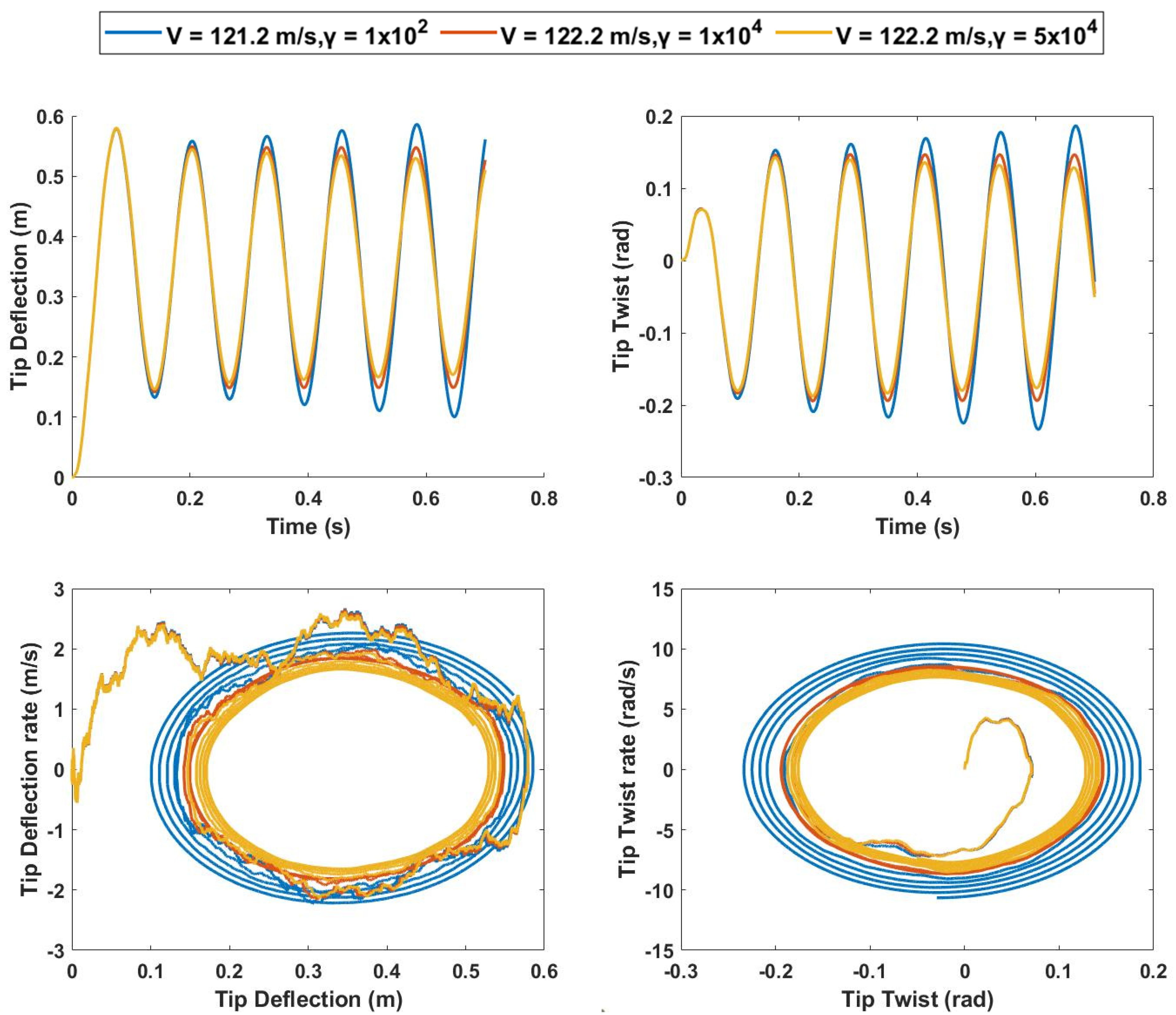
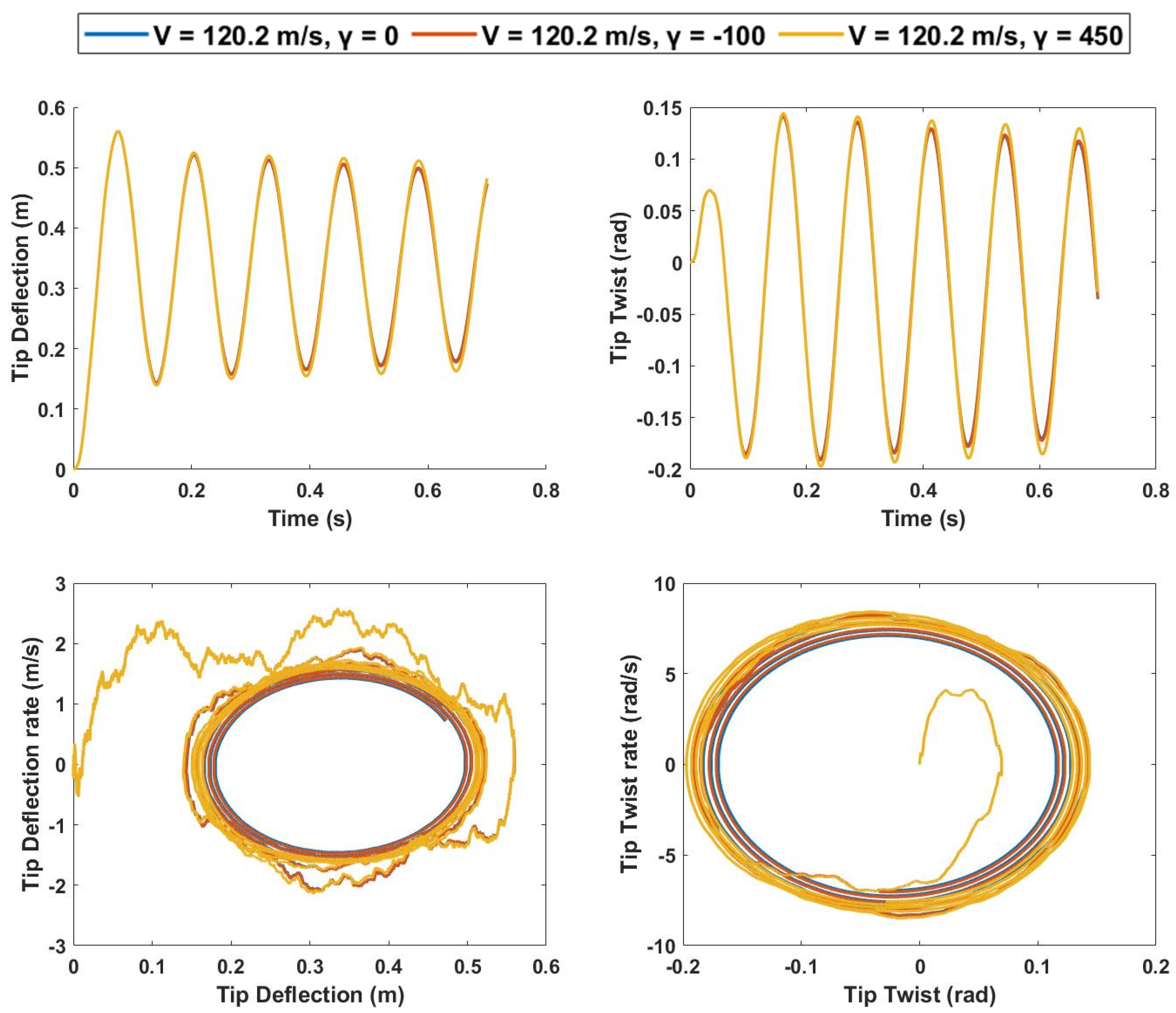
4.1.1. Spring Hardening Response for 0% Span Extension
4.1.2. Spring Hardening Response for 25% Span Extension
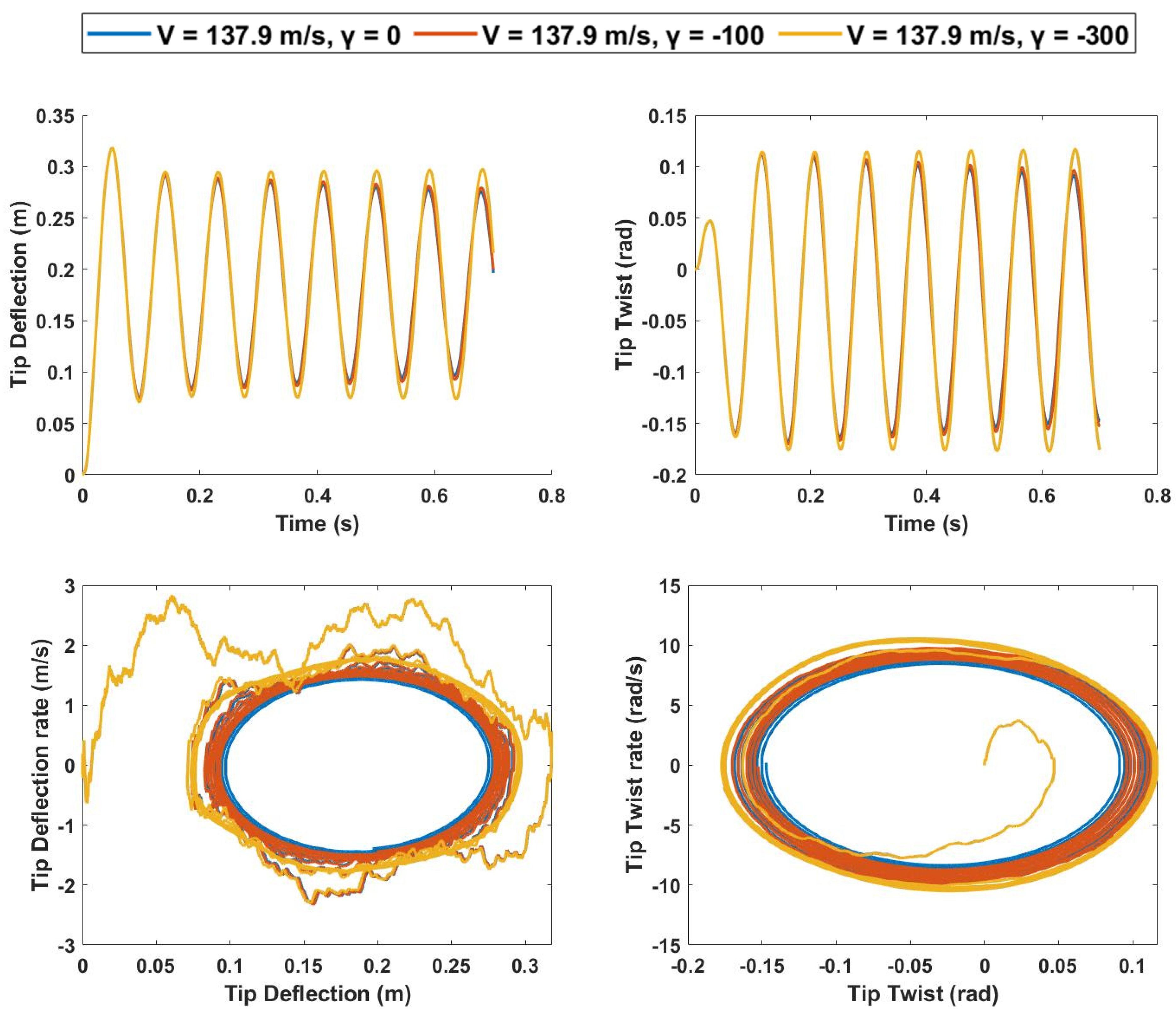
4.2. Softening Spring
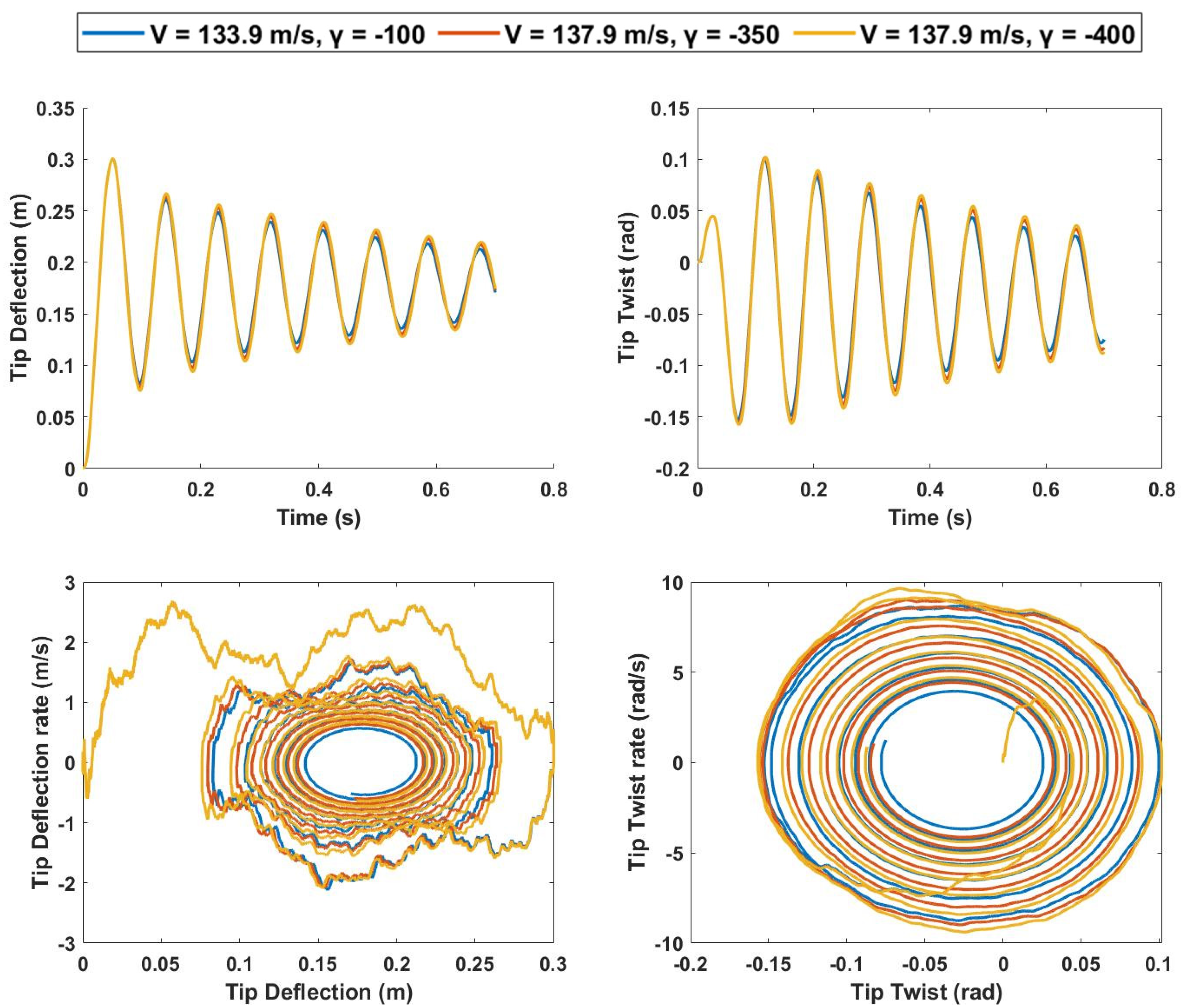
4.2.1. Spring Softening Response for 0% Span Extension
4.2.2. Spring Softening Response for 25% Span Extension
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| m’ | Mass per unit length |
| ρ | Density |
| ea | Elastic axis |
| cg | Center of gravity |
| w | Bending deflection |
| ϕ | Bending slope |
| t | Time |
| EI | Bending rigidity |
| GJ | Torsional rigidity |
| E | Young’s modulus |
| J | Torsional constant |
| l | Half span length of the wing |
| rα | Radius of gyration |
| θ | Angle of twist |
| Cw | Warping constant |
| Hb | Hermite’s cubic bending shape functions |
| Tt | Torsional shape functions |
| K | Stiffness matrix |
| M | Mass matrix |
| CL | Lift coefficient |
| C(k) | Theodorsen’s transfer function |
| Aerodynamic damping matrix | |
| Aerodynamic stiffness matrix | |
| A | Structural inertia matrix |
| D | Structural damping matrix |
| E | Structural stiffness matrix |
| B | Aerodynamic damping matrix |
| C | Aerodynamic stiffness matrix |
| q | Generalized coordinate |
Appendix A
| Derivative | Expression |
|---|---|
References
- Concilio, A.; Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Directorate-General for Mobility and Transport; Directorate-General for Research and Innovation. Flightpath 2050—Publications Office of the EU. EU Publications. pp. 1–32. Available online: https://op.europa.eu/en/publication-detail/-/publication/296a9bd7-fef9-4ae8-82c4-a21ff48be673 (accessed on 10 March 2022).
- Weisshaar, T. Morphing Aircraft Technology-New Shapes for Aircraft Design. Multifunct. Struct. Integr. Sens. Antennas 2006, O1-1–O1-20. [Google Scholar]
- Rodrigue, H.; Cho, S.; Han, M.W.; Bhandari, B.; Shim, J.E.; Ahn, S.H. Effect of Twist Morphing Wing Segment on Aerodynamic Performance of UAV. J. Mech. Sci. Technol. 2016, 30, 229–236. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M. Asapp: A Polymorphing Wing Capable of Active Span Extension and Passive Pitch. AIAA Scitech 2021, 2021, 0621. [Google Scholar]
- Okonkwo, P.; Smith, H. Review of Evolving Trends in Blended Wing Body Aircraft Design. Prog. Aerosp. Sci. 2016, 82, 1–23. [Google Scholar] [CrossRef]
- Bishop, W. The Development of Tailless Aircraft and Flying Wings. J. R. Aeronaut. Soc. 1961, 65, 799–806. [Google Scholar] [CrossRef]
- Aero-Isoclinic Wing and All-Moving Wing-Tips. Aircr. Eng. Aerosp. Technol. 1954, 26, 18. [CrossRef]
- Taylor, A.S. Manoeuvre Point Properties of the Aero-Isoclinic Wing. Aircr. Eng. Aerosp. Technol. 1952, 24, 257–262. [Google Scholar] [CrossRef]
- Andersen, G.R.; Cowan, D.L.; Piatak, D.J. Aeroelastic Modeling, Analysis and Testing of a Morphing Wing Structure. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Muhammed, S.P.; Ajaj, R.M.; Khan, K.A. A Compliant Polymorphing Wing for Small UAVs. Chin. J. Aeronaut. 2020, 33, 2575–2588. [Google Scholar] [CrossRef]
- Alsulami, A.; Akbar, M.; Joe, W.Y. A Comparative Study: Aerodynamics of Morphed Airfoils Using CFD Techniques and Analytical Tools. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; Volume 1, pp. 1–10. [Google Scholar] [CrossRef]
- Parancheerivilakkathil, M.S.; Haider, Z.; Ajaj, R.M.; Amoozgar, M. A polymorphing wing capable of span extension and variable pitch. Aerospace 2022, 9, 205. [Google Scholar] [CrossRef]
- Bae, J.S.; Seigler, T.M.; Inman, D.J. Aerodynamic and Static Aeroelastic Characteristics of a Variable-Span Morphing Wing. J. Aircr. 2005, 42, 528–534. [Google Scholar] [CrossRef]
- Neal, D.A.; Good, M.G.; Johnston, C.O.; Robertshaw, H.H.; Mason, W.H.; Inman, D.J. Design and Wind-Tunnel Analysis of a Fully Adaptive Aircraft Configuration. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar]
- Cooper, J.E.; Chekkal, I.; Cheung, R.C.M.; Wales, C.; Allen, N.J.; Lawson, S.; Peace, A.J.; Cook, R.; Standen, P.; Hancock, S.D.; et al. Design of a Morphing Wingtip. J. Aircr. 2015, 52, 1394–1403. [Google Scholar] [CrossRef]
- Miller, S.; Vio, G.A.; Cooper, J.E.; Vale, J.; Da Luz, L.; Gomes, A.; Lau, F.; Suleman, A.; Cavagna, L.; De Gaspari, A.; et al. SMorph–Smart Aircraft Morphing Technologies Project. In Proceedings of the 51th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Orlando, FL, USA, 12–15 April 2010. [Google Scholar] [CrossRef]
- Mei, C. Coupled vibrations of thin-walled beams of open section using the Finite Element Method. Int. J. Mech. Sci. 1970, 12, 883–891. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Flores, E.I.S.; Amoozgar, M.; Cooper, J.E. A parametric study on the aeroelasticity of flared hinge folding wingtips. Aerospace 2021, 8, 221. [Google Scholar] [CrossRef]
- Bennamia, I.; Badereddine, A.; Zebbiche, T. Measurement of Vibrations of Composite Wings Using High-Order Finite Element Beam. J. Meas. Eng. 2018, 6, 143–154. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter, NACA Report 496. Annu. Rep. Natl. Advis. Comm. Aeronaut. 1935, 268, 413. [Google Scholar]
- Brunton, S.L.; Rowley, C.W. Empirical state-space representations for Theodorsen’s lift model. J. Fluids Struct. 2013, 38, 174–186. [Google Scholar] [CrossRef]
- Fung, Y.C. An Introduction to the Theory of Aeroelasticity; Dover: New York, NY, USA, 2002. [Google Scholar]
- Hassig, H.J. An Approximate True Damping Solution of the Flutter Equation by Determinant Iteration. J. Aircr. 1971, 8, 885–889. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Friswell, M.I. Aeroelasticity of Compliant Span Morphing Wings. Smart Mater. Struct. 2018, 27, 105052. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H.; Cesnik, C.E.S. Nonlinear Aeroelastic Analysis of Complete Aircraft in Subsonic Flow. J. Aircr. 2000, 37, 753–760. [Google Scholar] [CrossRef]
- Raghavan, B.; Patil, M.J. Flight Dynamics of High-Aspect-Ratio Flying Wings: Effect of Large Trim Deformation. J. Aircr. 2009, 46, 1808–1812. [Google Scholar] [CrossRef] [Green Version]
- Dowell, E.H.; Clark, R.; Cox, D.; Curtiss, H.C.; Edwards, J.W.; Hall, K.C.; Peters, D.A.; Scanlan, R.; Simiu, E.; Sisto, F.; et al. A Modern Course in Aeroelasticity; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Woolston, D.S.; Runyan, H.L.; Andrews, R.E. An Investigation of Effects of Certain Types of Structural NonHnearities on Wing and Control Surface Flutter. J. Aeronaut. Sci. 1957, 24, 57–63. [Google Scholar] [CrossRef]
- Woolston, D.S.; Runyan, H.L.; Byrdsong, T.A. Some Effects of System Nonlinearities in the Problem of Aircraft Flutter; National Advisory Committee for Aeronautics: Washington, DC, USA, 1955.
- Lee, B.H.K.; Jiang, L.Y.; Wong, Y.S. Flutter of an Airfoil with a Cubic Nonlinear Restoring Force. In Proceedings of the 39th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Long Beach, CA, USA, 20–23 April 1998; Volume 1, pp. 237–257. [Google Scholar] [CrossRef]
- Lee, B.H.K.; LeBlanc, P. Flutter Analysis of a Two-Dimensional Airfoil with Cubic Non-Linear Restoring Force; BMT Limited: London, UK, 1986. [Google Scholar]
- Kim, D.H.; Lee, I. Transonic and Low-Supersonic Aeroelastic Analysis of a Two-Degree-of-Freedom Airfoil with a Freeplay Non-Linearity. J. Sound Vib. 2000, 234, 859–880. [Google Scholar] [CrossRef]
- O’Neil, T.; Gilliatt, H.; Strganac, T.W. Investigations of Aeroelastic Response for a System with Continuous Structural Nonlinearities. In Proceedings of the 37th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Salt Lake City, UT, USA, 15–17 April 1996. [Google Scholar] [CrossRef] [Green Version]















| Specifications | Goland Wing |
|---|---|
| Half span (m) | 6.096 |
| Chord (m) | 1.8288 |
| Mass per unit length (m’) (kg/m) | 35.71 |
| Air density (ρ) (kg/m3) | 1.225 |
| Moment of inertia per unit length (kgm) around ea | 8.64 |
| Center of gravity (from leading edge) | 43% of chord |
| Elastic axis location (from leading edge) | 33% of chord |
| Flexural rigidity (EI) (Nm2) | 9.77 × 106 |
| Torsional rigidity (GJ) (Nm2) | 9.87 × 105 |
| Method | |||||
|---|---|---|---|---|---|
| Present Work | Ref. [20] | Ref. [26] | Ref. [27] | Ref. [28] | |
| Flutter Velocity (m/s) | 137.4 | 136.99 | 137.11 | 135.60 | 136.22 |
| Flutter Frequency (rad/s) | 69.351 | 69.97 | 69.90 | 70.20 | 70.06 |
| Divergence Speed (m/s) | 252.31 | 252.47 | 252.80 | - | 250.82 |
| ASAPP Wing | Inboard Length (m) | Outboard Length (m) |
|---|---|---|
| Without span extension | 4.267 | 1.8288 |
| 25% span extension | 4.633 | 1.8288 |
| 50% span extension | 4.877 | 1.8288 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, Z.; Ajaj, R.M.; Seneviratne, L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study. Aerospace 2022, 9, 483. https://doi.org/10.3390/aerospace9090483
Haider Z, Ajaj RM, Seneviratne L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study. Aerospace. 2022; 9(9):483. https://doi.org/10.3390/aerospace9090483
Chicago/Turabian StyleHaider, Zawar, Rafic M. Ajaj, and Lakmal Seneviratne. 2022. "On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study" Aerospace 9, no. 9: 483. https://doi.org/10.3390/aerospace9090483






