Semi-Analytical Closed-Form Solutions for Dynamical Rössler-Type System
Abstract
:1. Introduction
2. Preliminary
2.1. Bratu’s Problem
2.2. The Rsller-Type System
3. The Optimal Parametric Iteration Method
3.1. Preliminary
3.2. Semi-Analytical Solutions Using OPIM Technique
4. Numerical Results and Validation
OPIM Solutions versus Iterative Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bratu, G. Sur les equation integrals non-lineaires. Bull. Math. Soc. Fr. 1914, 42, 113–142. [Google Scholar] [CrossRef]
- Lazureanu, C.; Binzar, T. Some symmetries of a Rössler type system. Sci. Bull. Math.-Phys. 2013, 58, 1–6. [Google Scholar]
- Raja, M.A.Z.; Samar, R.; Alaidarous, E.S.; Shivanian, E. Bio-inspired computing platform for reliable solution of Bratu-type equations arising in the modeling of electrically conducting solids. Appl. Math. Model. 2016, 40, 5964–5977. [Google Scholar] [CrossRef]
- Caglar, H.; Caglar, N.; Özer, M.; Valaristos, A.; Miliou, A.N.; Anagnostopoulos, A.N. Dynamics of the solution of Bratu’s equation. Nonlinear Anal. 2009, 71, e672–e678. [Google Scholar] [CrossRef]
- Jalilian, R. Non-polynomial spline method for solving Bratu’s problem. Comput. Phys. Commun. 2010, 181, 1868–1872. [Google Scholar] [CrossRef]
- Kafri, H.Q.; Khuri, S.A. Bratu’s problem: A novel approach using fixed-point iterations and Green’s functions. Comput. Phys. Commun. 2016, 198, 97–104. [Google Scholar] [CrossRef]
- Hichar, S.; Guerfi, A.; Douis, S.; Meftah, M.T. Application of nonlinear Bratu’s equation in two and three dimensions to electrostatics. Rep. Math. Phys. 2015, 76, 283–290. [Google Scholar] [CrossRef]
- Mohsen, A. A simple solution of the Bratu problem. Comput. Math. Appl. 2014, 67, 26–33. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 2005, 166, 652–663. [Google Scholar] [CrossRef]
- Syam, M.I.; Hamdan, A. An efficient method for solving Bratu equations. Appl. Math. Comput. 2006, 176, 704–713. [Google Scholar] [CrossRef]
- Boyd, J.P. One-point pseudospectral collocation for the one-dimensional Bratu equation. Appl. Math. Comput. 2011, 217, 5553–5565. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B.; Abdelrazek, A.; Ghazy, M.; Gamal, G. A modified perturbation solution to the one-dimensional Bratu problem. Appl. Math. Comput. 2019, 354, 296–304. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hashemi, M.S.; Liu, C.-S. The Lie-group shooting method for solving the Bratu equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4238–4249. [Google Scholar] [CrossRef]
- Deniz, S.; Bildik, N. Optimal perturbation iteration method for Bratu-type problems. J. King Saud Univ.-Sci. 2018, 30, 91–99. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. The Taylor wavelets method for solving the initial and boundary value problems of Bratu-type equations. Appl. Numer. Math. 2018, 128, 205–216. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Youssri, Y.H. Two spectral Legendre’s derivative algorithms for Lane-Emden, Bratu equations, and singular perturbed problems. Appl. Numer. Math. 2021, 169, 243–255. [Google Scholar] [CrossRef]
- Singh, S.M.; Singh, K. An advancement approach of Haar wavelet method and Bratu-type equations. Appl. Numer. Math. 2021, 170, 74–82. [Google Scholar]
- Mohsen, A. On the integral solution of the one-dimensional Bratu problem. J. Comput. Appl. Math. 2013, 251, 61–66. [Google Scholar] [CrossRef]
- Temimi, H.; Ben-Romdhane, M. An iterative finite difference method for solving Bratu’s problem. J. Comput. Appl. Math. 2016, 292, 76–82. [Google Scholar] [CrossRef]
- Jator, S.N.; Manathunga, V. Block Nyström type integrator for Bratu’s equation. J. Comput. Appl. Math. 2018, 327, 341–349. [Google Scholar] [CrossRef]
- Behl, R.; Sarría, Í.; González, R.; Magreñán, Á.A. Highly efficient family of iterative methods for solving nonlinear models. J. Comput. Appl. Math. 2019, 346, 110–132. [Google Scholar] [CrossRef]
- Tomar, S.; Pandey, R.K. An efficient iterative method for solving Bratu-type equations. J. Comput. Appl. Math. 2019, 357, 71–84. [Google Scholar] [CrossRef]
- Karamollahi, N.; Loghmani, G.B.; Heydari, M. A computational method to find dual solutions of the one-dimensional Bratu problem. J. Comput. Appl. Math. 2021, 388, 113309. [Google Scholar] [CrossRef]
- Jator, S.N.; Mayo, D.C.; Omojola, M.T. Block Hybrid Third Derivative Nyström type Method for Bratu’s equation. Math. Comput. Simul. 2021, 185, 256–271. [Google Scholar] [CrossRef]
- Jyoti; Singh, M. An iterative technique based on HPM for a class of one dimensional Bratu’s type problem. Math. Comput.Simul. 2022, 200, 50–64. [Google Scholar] [CrossRef]
- Aydinlik, S.; Kiris, A.; Roul, P. An effective approach based on Smooth Composite Chebyshev Finite Difference Method and its applications to Bratu–type and higher order Lane–Emden problems. Math. Comput. Simul. 2022, 202, 193–205. [Google Scholar] [CrossRef]
- Aksoy, Y.; Pakdemirli, M. New perturbation-iteration solutions for Bratu–type equations. Comput. Math. Appl. 2010, 59, 2802–2808. [Google Scholar] [CrossRef]
- Venkatesh, S.G.; Ayyaswamy, S.K.; Balachandar, S.R. The Legendre wavelet method for solving initial value problems of Bratu–type. Comput. Math. Appl. 2012, 63, 1287–1295. [Google Scholar] [CrossRef]
- Ragb, O.; Seddek, L.F.; Matbuly, M.S. Iterative differential quadrature solutions for Bratu problem. Comput. Math. Appl. 2017, 74, 249–257. [Google Scholar] [CrossRef]
- Masood, Z.; Majeed, K.; Samar, R.; Zahoor Raja, M.A. Design of Mexican Hat Wavelet neural networks for solving Bratu type nonlinear systems. Neurocomputing 2017, 221, 1–14. [Google Scholar] [CrossRef]
- Ahmad, A.; Sulaiman, M.; Aljohani, A.J.; Alhindi, A.; Alrabaiah, H. Design of an efficient algorithm for solution of Bratu differential equations. Ain Shams Eng. J. 2021, 12, 2211–2225. [Google Scholar] [CrossRef]
- Karimov, A.I.; Rybin, V.G.; Kopets, E.E.; Karimov, T.I.; Nepomuceno, E.; Butusov, D. Identifying empirical equations of chaotic circuit from data. Nonlinear Dynam. 2023, 111, 871–886. [Google Scholar] [CrossRef]
- Karimov, A.; Tutueva, A.; Karimov, T.; Druzhina, O.; Butusov, D. Adaptive generalized synchronization between circuit and computer implementations of the Rössler system. Appl. Sci. 2021, 11, 81. [Google Scholar] [CrossRef]
- Ding, Y.; Zheng, L. Existence of homoclinic orbit of Shilnikov type and the application in Rössler system. Math. Comput. Simul. 2023, 206, 770–779. [Google Scholar] [CrossRef]
- Zhou, H. Dynamical behavior of almost periodically forced neutral delayed equation and its applications. Proc. Am. Math. Soc. 2022, 150, 5293–5309. [Google Scholar] [CrossRef]
- Zhou, H. Analysis of a mathematical model arising from stage-structured predator-prey in a chemostat. Nonlinear Anal.-Real World Appl. 2024, 77, 104031. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, Y. Critical behavior of a semilinear time fractional diffusion equation with forcing term depending on time and space. Chaos Solitons Fract. 2024, 178, 114309. [Google Scholar] [CrossRef]
- Li, X.-L.; Guo, R. Interactions of Localized Wave Structures on Periodic Backgrounds for the Coupled Lakshmanan-Porsezian-Daniel Equations in Birefringent Optical Fibers. Ann. Phys. 2023, 535, 2200472. [Google Scholar] [CrossRef]
- Ascher, U.M.; Mattheij, R.M.M.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Lima, M.F.S.; Llibre, J. Global dynamics of the Rössler system with conserved quantities. J. Phys. A Math. Theor. 2011, 44, 365201. [Google Scholar] [CrossRef]
- Llibre, J.; Zhang, X. Darboux integrability for the Rössler system. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2002, 12, 421–428. [Google Scholar] [CrossRef]
- Tudoran, R.M.; Girban, A. On some asymptotic properties of the Rössler dynamical system. Stud. Univ. Babes-Bolyai Math. 2013, 58, 503–509. [Google Scholar]
- Marinca, V.; Draganescu, G.E. Construction of approximate periodic solutions to a modified van der Pol oscillator. Nonlinear Anal.-Real World Appl. 2010, 11, 4355–4362. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 60, 1607–1615. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. The Optimal Homotopy Asymptotic Method—Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Marinca, V.; Herisanu, N. An application of the optimal homotopy asymptotic method to Blasius problem. Rom. J. Tech. Sci. Appl. Mech. 2015, 60, 206–215. [Google Scholar]
- Marinca, V.; Herisanu, N. Nonlinear dynamic analysis of an electrical machine rotor-bearing system by the optimal homotopy perturbation method. Comput. Math. Appl. 2011, 61, 2019–2024. [Google Scholar] [CrossRef]
- Marinca, V.; Ene, R.D.; Marinca, B. Optimal Homotopy Perturbation Method for nonlinear problems with applications. Appl. Comput. Math. 2022, 21, 123–136. [Google Scholar]
- Ene, R.D.; Pop, N. Semi-Analytical Closed-Form Solutions for the Rikitake-Type System through the Optimal Homotopy Perturbation Method. Mathematics 2023, 11, 3078. [Google Scholar] [CrossRef]
- Ene, R.D.; Pop, N. Approximate Closed-Form Solutions for a Class of Dynamical Systems involving a Hamilton-Poisson Part. Mathematics 2023, 11, 4811. [Google Scholar] [CrossRef]
- Mickens, R.E. Iteration procedure for determining approximate solutions to nonlinear oscillation equations. J. Sound Vib. 1987, 116, 185–188. [Google Scholar] [CrossRef]
- Mickens, R.E. A generalized iteration procedure for calculating approximations to periodic solutions of “truly nonlinear oscillators”. J. Sound Vib. 2005, 287, 1045–1051. [Google Scholar] [CrossRef]
- Lim, C.W.; Wu, B.S. A modified procedure for certain non-linear oscillators. J. Sound Vib. 2002, 257, 202–226. [Google Scholar] [CrossRef]
- Hu, H. Solutions of a quadratic nonlinear oscillator: Iteration procedure. J. Sound Vib. 2006, 298, 1159–1165. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, J.K. A modified Mickens iteration procedure for nonlinear oscillators. J. Sound Vib. 2008, 314, 465–473. [Google Scholar] [CrossRef]
- Ene, R.D.; Pop, N.; Lapadat, M.; Dungan, L. Approximate closed-form solutions for the Maxwell-Bloch equations via the Optimal Homotopy Asymptotic Method. Mathematics 2022, 10, 4118. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Nonlinear Dynamical Systems in Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]

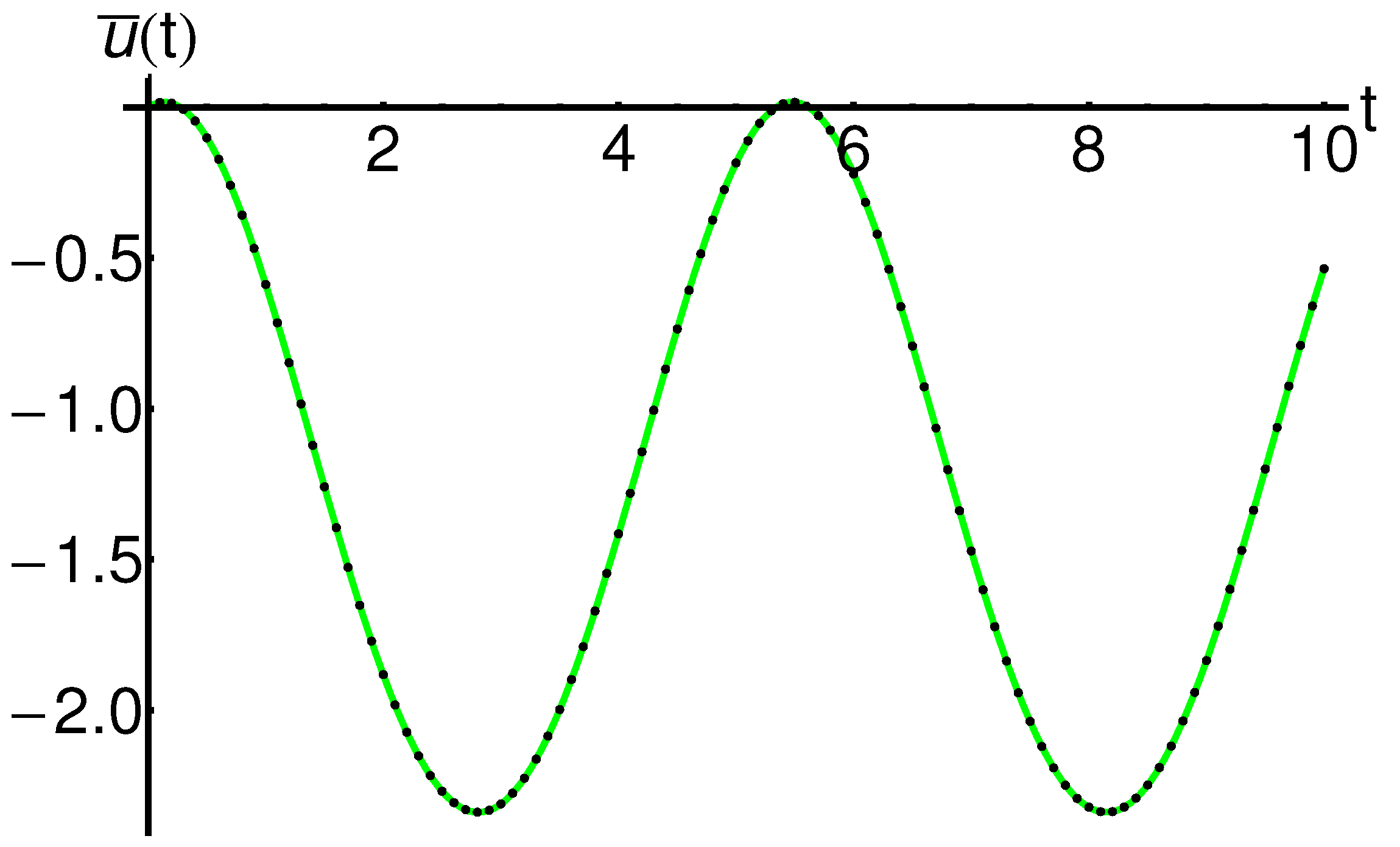
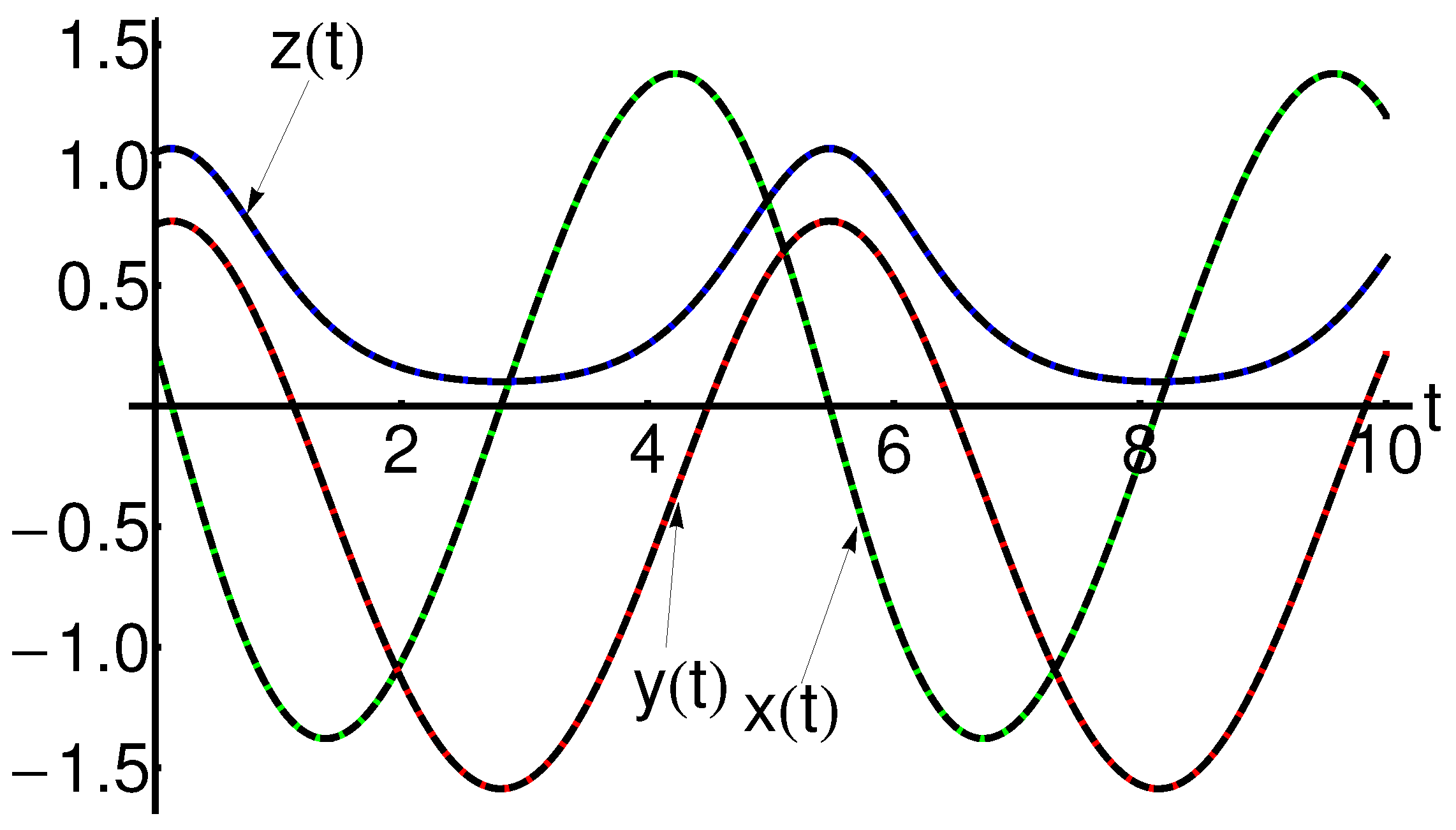
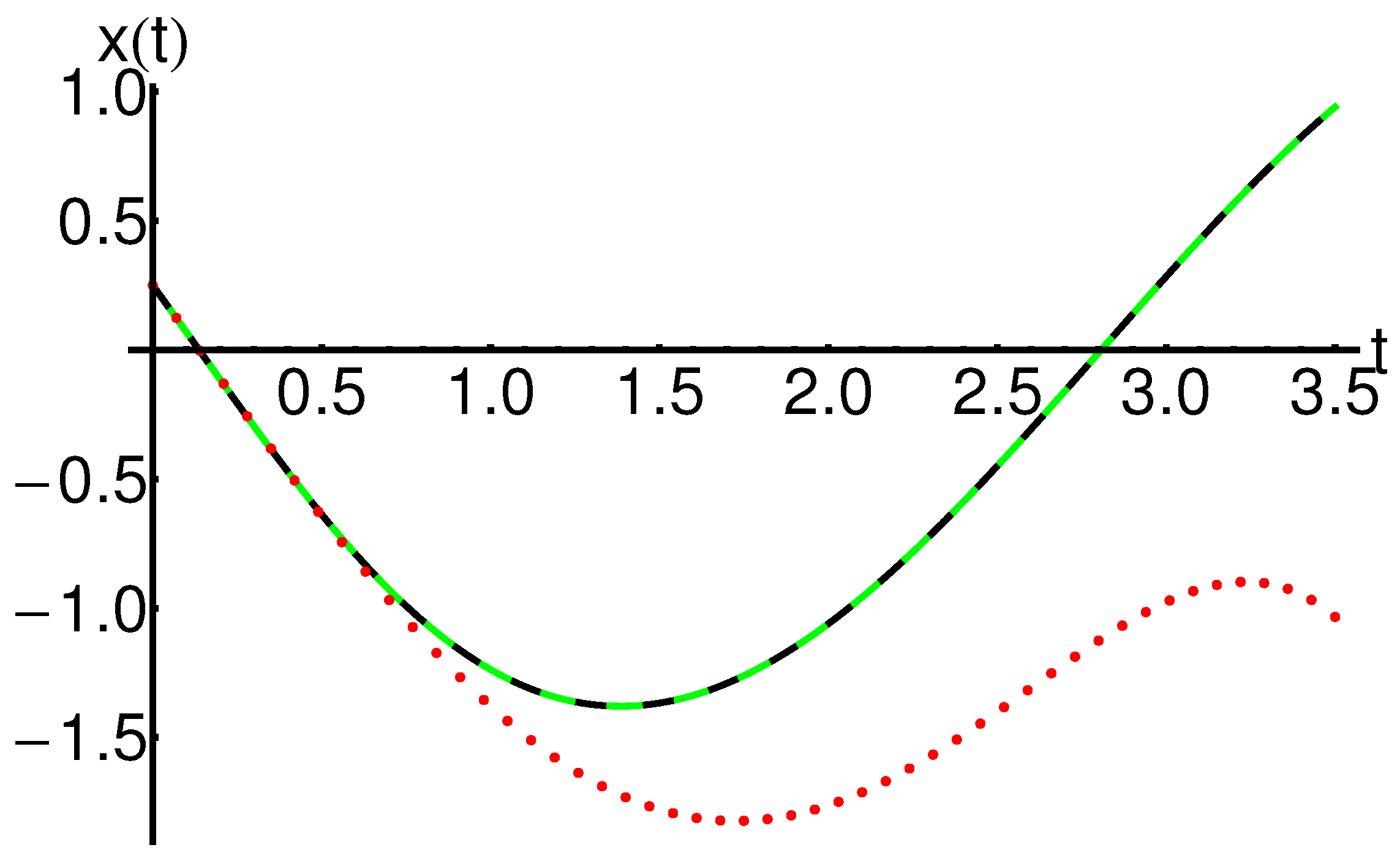
| t | ||||
|---|---|---|---|---|
| 0 | 5.68434 × | 8.12291 | 4.54747 | 7.10543 |
| 1/2 | 1.56141 | 8.68649 | 2.21405 | 4.85037 |
| 1 | 1.48405 | 1.41248 | 2.6783 | 5.0592 |
| 3/2 | 6.04191 | 3.44 | 1.44322 | 6.4853 |
| 2 | 3.3371 | 9.82754 | 3.82636 | 5.22813 |
| 5/2 | 6.32447 | 3.4972 | 3.48186 | 2.96143 |
| 3 | 3.62685 | 1.43278 | 7.30771 | 7.67939 |
| 7/2 | 4.35175 | 4.90013 | 7.79294 | 7.20673 |
| 4 | 4.14164 | 1.68089 | 1.48269 | 4.27381 |
| 9/2 | 3.19588 | 1.68538 | 2.11227 | 1.03521 |
| 5 | 1.32596 | 1.90962 | 2.91648 | 9.71333 |
| 11/2 | 1.90914 | 3.46814 | 1.51662 | 4.52946 |
| 6 | 1.3966 | 2.01006 | 3.01251 | 8.10717 |
| 13/2 | 3.33686 | 8.48484 | 4.2035 | 9.86731 |
| 7 | 1.15607 | 1.38123 | 8.79764 | 7.25709 |
| 15/2 | 3.18879 | 9.57228 | 2.69659 | 1.10401 |
| 8 | 5.01597 | 1.00957 | 5.19338 | 1.25896 |
| 17/2 | 6.856 | 5.66887 | 2.75871 | 9.05699 |
| 9 | 3.01073 | 5.25215 | 5.99213 | 1.1485 |
| 19/2 | 6.08924 | 1.05709 | 6.60261 | 1.42172 |
| 10 | 4.58559 | 2.81366 | 1.80462 | 1.40391 |
| t | |||
|---|---|---|---|
| 0 | −8.12291 | −7.10542 | 7.10542 |
| 1/2 | −0.1009833721 | −0.1009828870 | 4.85037 |
| 1 | −0.5875537666 | −0.5875532607 | 5.05920 |
| 3/2 | −1.2588228636 | −1.2588222150 | 6.48530 |
| 2 | −1.8816621245 | −1.8816616017 | 5.22813 |
| 5/2 | −2.2683521270 | −2.2683518309 | 2.96142 |
| 3 | −2.3108289294 | −2.3108281614 | 7.67938 |
| 7/2 | −1.9975070462 | −1.9975063255 | 7.20673 |
| 4 | −1.4151229407 | −1.4151225133 | 4.27380 |
| 9/2 | −0.7351867600 | −0.7351857248 | 1.03520 |
| 5 | −0.1849885987 | −0.1849876273 | 9.71333 |
| t | |||
|---|---|---|---|
| 0 | 0.25 | 0.2499999249 | 7.50267 |
| 1/2 | −0.6367781227 | −0.6367801438 | 2.02113 |
| 1 | −1.2376076804 | −1.2376093968 | 1.71634 |
| 3/2 | −1.3673785582 | −1.3673786474 | 8.91577 |
| 2 | −1.0603932046 | −1.0603910929 | 2.11171 |
| 5/2 | −0.4497705143 | −0.4497711768 | 6.62540 |
| 3 | 0.2837908478 | 0.2837896153 | 1.23259 |
| 7/2 | 0.9401129558 | 0.9401146702 | 1.71439 |
| 4 | 1.3313637430 | 1.3313651699 | 1.42692 |
| 9/2 | 1.3107276683 | 1.3107251137 | 2.55464 |
| 5 | 0.8126645233 | 0.8126672218 | 2.69845 |
| t | |||
|---|---|---|---|
| 0 | 0.25 | 0.2499999249 | 0.25 |
| 0.35 | −0.3847286943 | −0.3847266999 | −0.3823724677 |
| 0.7 | −0.9282966040 | −0.9282953550 | −0.9683700083 |
| 1.05 | −1.2724487484 | −1.2724506529 | −1.4370077000 |
| 1.4 | −1.3794335466 | −1.3794320704 | −1.7324569333 |
| 1.75 | −1.2616050449 | −1.2616062739 | −1.8234993489 |
| 2.1 | −0.9572932068 | −0.9572918609 | −1.7129807750 |
| 2.45 | −0.5195989669 | −0.5196005038 | −1.4472651645 |
| 2.8 | −0.0116471526 | −0.0116453617 | −1.1256885333 |
| 3.15 | 0.4978649029 | 0.4978635857 | −0.9100128968 |
| 3.5 | 0.9401129558 | 0.9401146702 | −1.0338802083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ene, R.-D.; Pop, N. Semi-Analytical Closed-Form Solutions for Dynamical Rössler-Type System. Mathematics 2024, 12, 1308. https://doi.org/10.3390/math12091308
Ene R-D, Pop N. Semi-Analytical Closed-Form Solutions for Dynamical Rössler-Type System. Mathematics. 2024; 12(9):1308. https://doi.org/10.3390/math12091308
Chicago/Turabian StyleEne, Remus-Daniel, and Nicolina Pop. 2024. "Semi-Analytical Closed-Form Solutions for Dynamical Rössler-Type System" Mathematics 12, no. 9: 1308. https://doi.org/10.3390/math12091308





