Global Stabilizing Control of a Continuous Ethanol Fermentation Process Starting from Batch Mode Production
Abstract
:1. Introduction
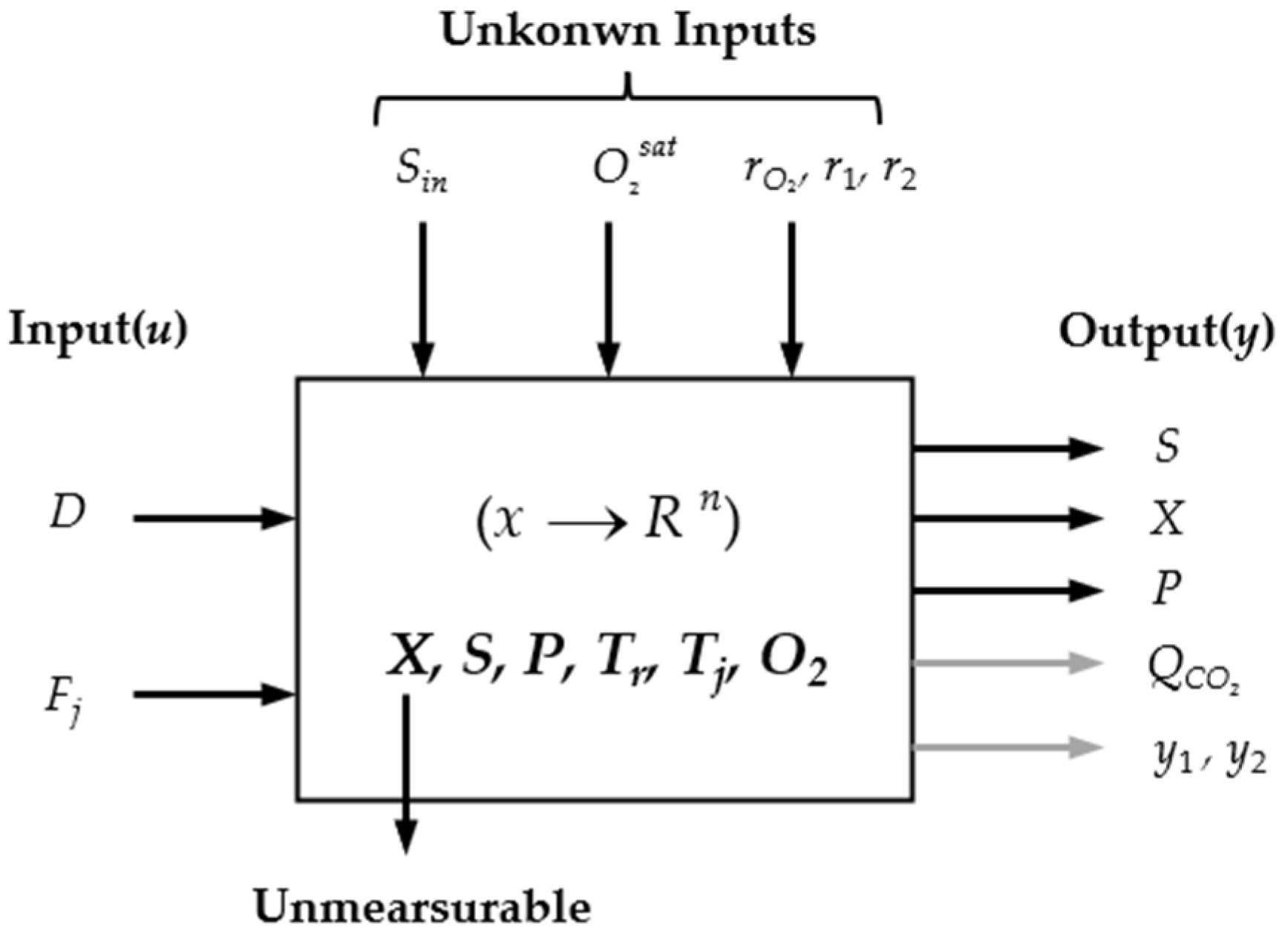
2. Problem Formulation
- Monitoring Information: The quantity r2(·) is available on-line from the plant, and for a large part of bioprocesses, the production (or consumption) of gaseous components, as peculiar to ethanol fermentation by S. cerevisiae, CO2 is monitored and is directly related to r2(·), and the accumulation of CO2 evolution rate (CER) is proportional to P when D is fixed.
- Dynamic Heat Balance of the Jacketed Fermenter: In order to assure a hospitable environment, fermentation temperature is regulated to maintain at an optimum. The aerobiotic respiration effect might cause exothermic reactions and a jacket cooler is integrated to remove redundant heat, and heat transfer between the broth and coolant is rendered as perfect convection,where ΔHr is the mole enthalpy change in the oxidation reaction; KTAT is the heat transfer coefficient multiples area of heat exchange. Note that O2 from the sterilized air is dissolved into the broth and transported by input effluents, and the aerobiotic effect of yeast leads to exothermic reactions. Dissolved oxygen (DO) content in the electrolyte solution is influenced by pH, Tr, and the global effect of ionic strength ∑HkIk,where ∑HkIk is accounted as [28,29] follows,
- 3.
- Temperature influence on the kinetics: The maximum specific growth rate μm is correlated with the broth temperature which is provided in the form of the Arrhenius formula,where Ea1 and Ea2 are the activation energy, and A1 and A2 are the preexponential factors.
3. Controller and Estimator Design
3.1. Global Stabilizing Control
3.2. Observer-Based Estimation
3.2.1. Estimation of the Input Substrate Concentration
3.2.2. Estimation of the Un-Measurable Biomass Concentration
3.2.3. Estimation of the Fermentation Kinetics
4. Results and Discussion
4.1. Fermentation Modeling Issues
4.2. Analysis of the Open-Loop System
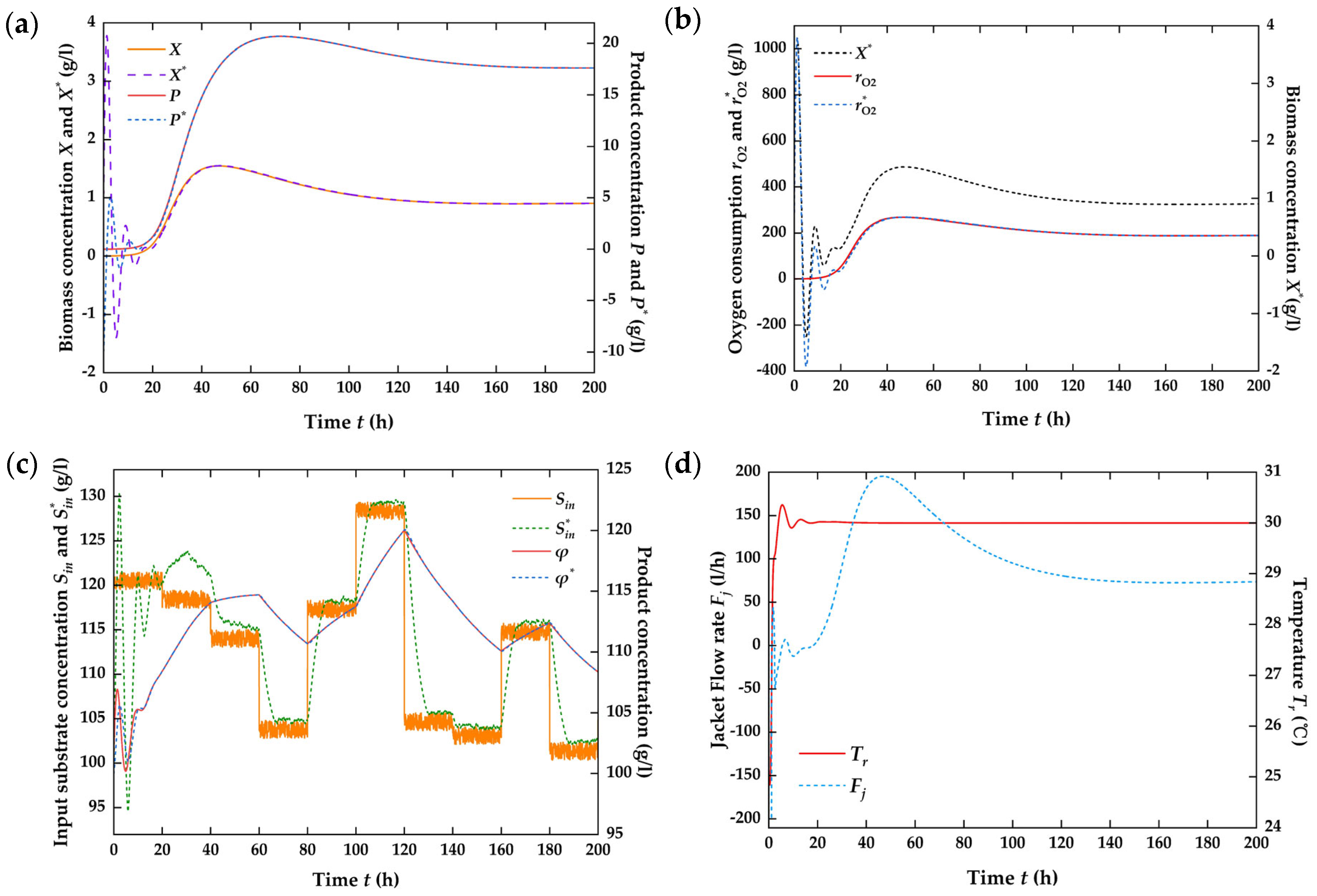
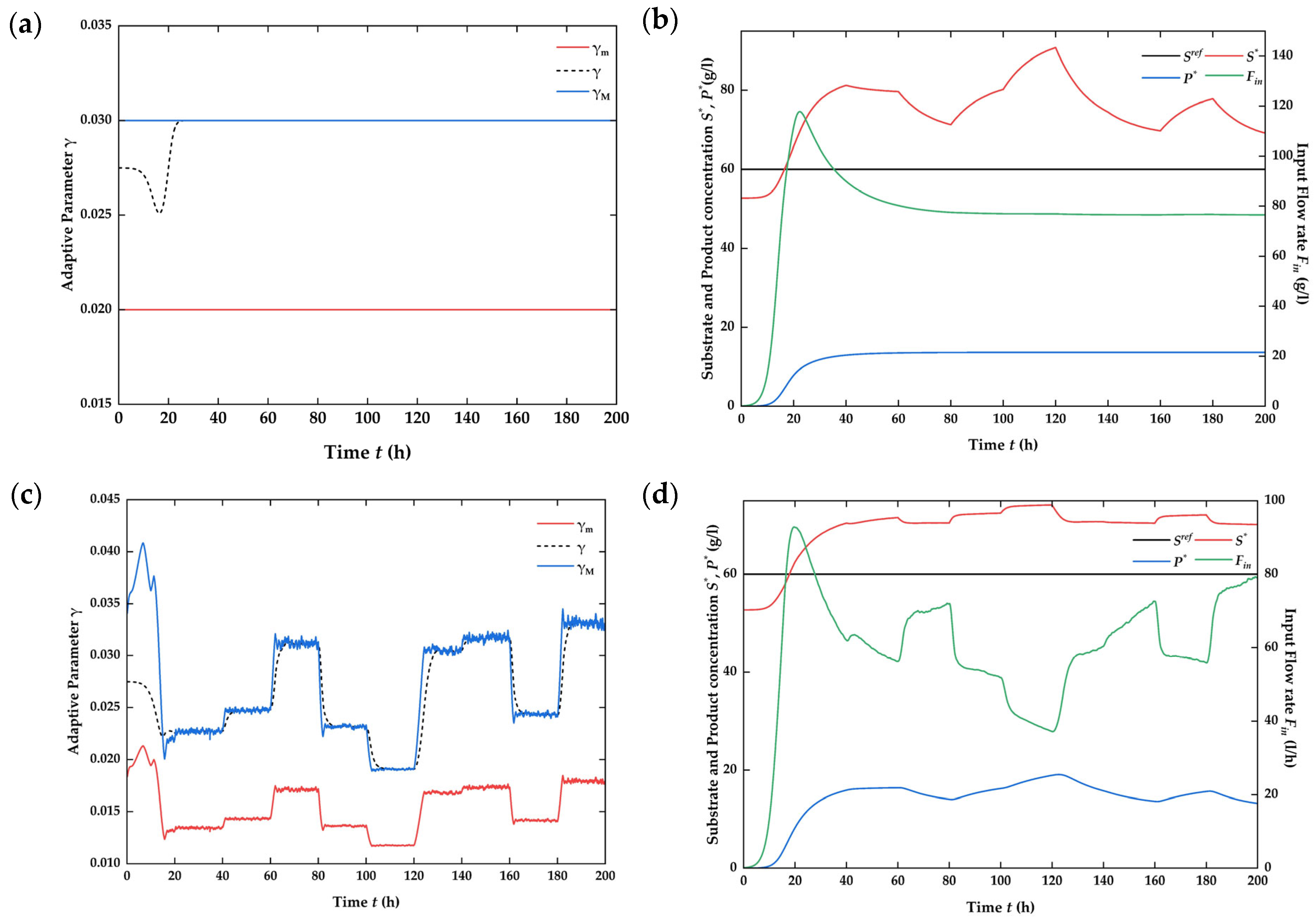
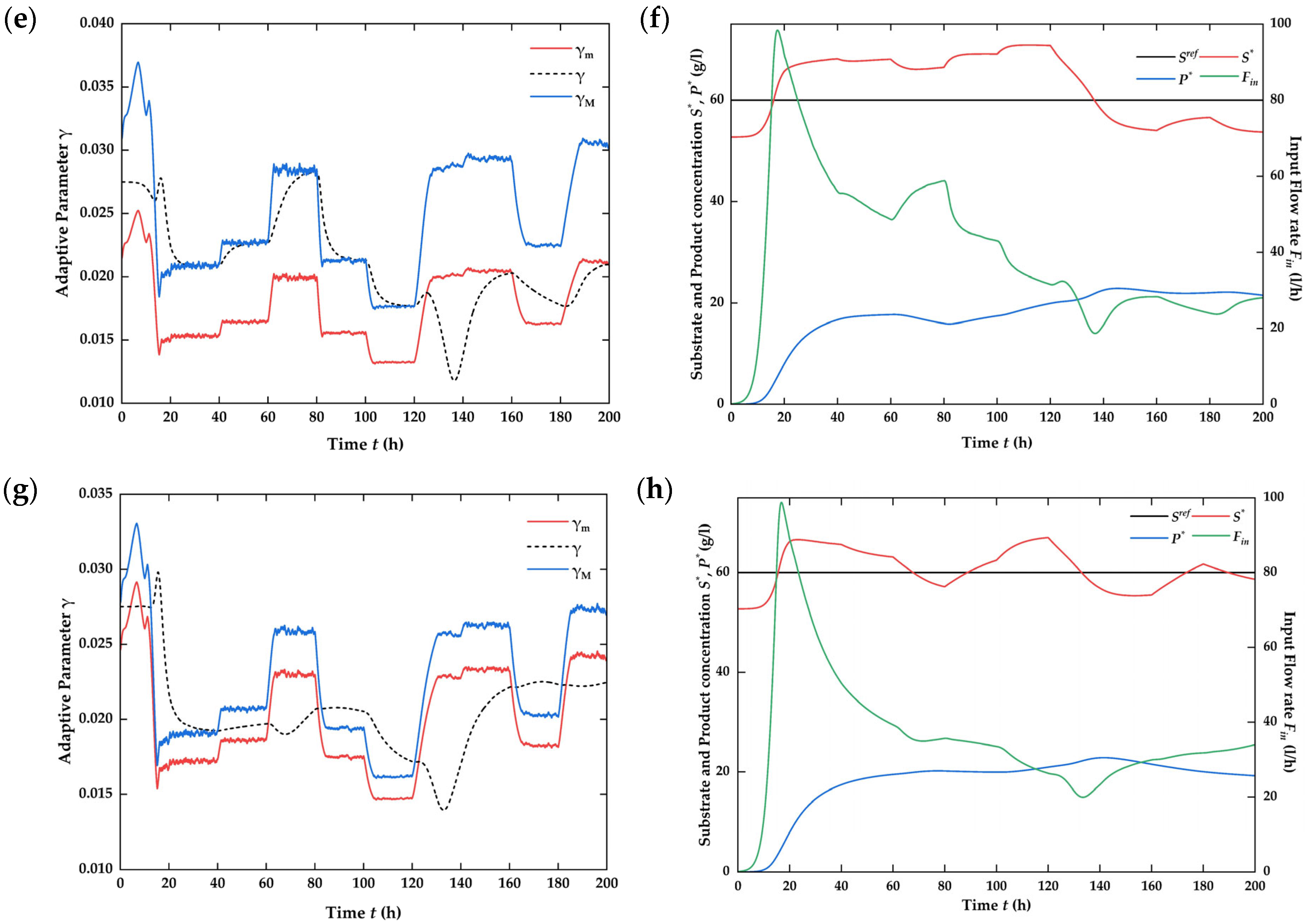
4.3. Numerical Simulation on the Closed-Loop System
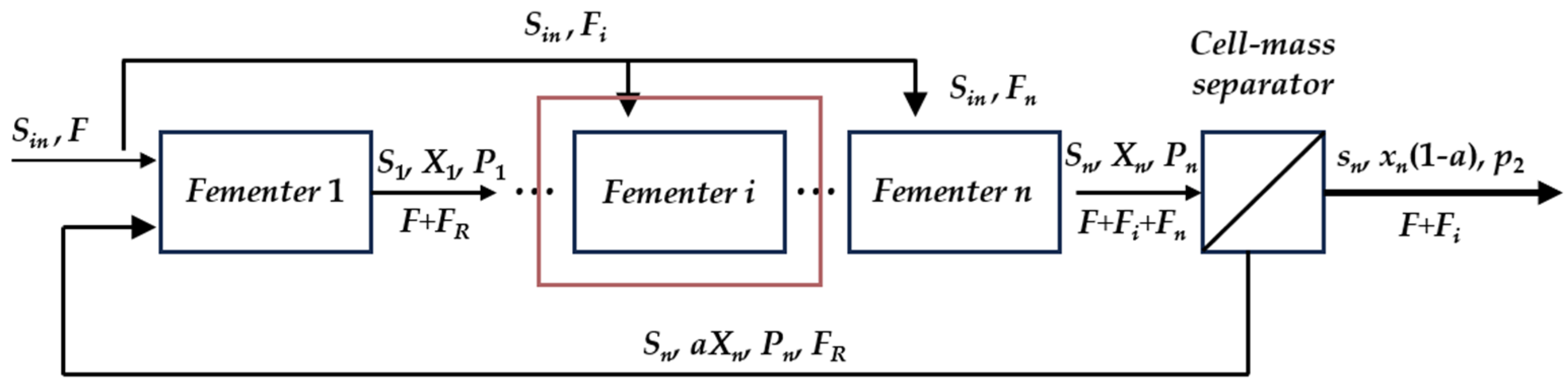
4.4. Assessment of Process Improvement [41]
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gonçalves, F.; Perna, R.; Lopes, E.; Maciel, R.; Tovar, L.; Lopes, M. Strategies to improve the environmental efficiency and the profitability of sugarcane mills. Biomass Bioenerg. 2021, 148, 106052. [Google Scholar] [CrossRef]
- Bilal, M.; Wang, Z.; Cui, J.D.; Ferreira, L.F.R.; Bharagava, R.N.; Iqbal, H.M.N. Environmental impact of lignocellulosic wastes and their effective exploitation as smart carriers–A drive towards greener and eco-friendlier biocatalytic systems. Sci. Total Environ. 2020, 722, 137903. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.P.; Feng, Y.C.; Fu, J.; Guo, H.W.; Guo, Y.; Han, B.X.; Jiang, Z.C.; Liu, H.C.; Nguyen, P.T.T.; Ren, P.N.; et al. Catalytic conversion of lignocellulosic biomass into chemicals and fuels. Green Energy Environ. 2023, 8, 10–114. [Google Scholar] [CrossRef]
- Daugulis, A.J.; McLellan, P.J.; Li, J. Experimental investigation and modeling of oscillatory behavior in the continuous culture of Zymomonas mobilis. Biotechnol. Bioeng. 1997, 56, 99–105. [Google Scholar] [CrossRef]
- Herrera, W.E.; Rivera, E.C.; Alvarez, L.A.; Tovar, L.P.; Rojas, S.T.; Yamakawa, C.K.; Bonomi, A.; Maciel, R. Modeling and control of a continuous ethanol fermentation using a mixture of enzymatic hydrolysate and molasses from sugarcane. In Proceedings of the 2nd International Conference on Biomass, Taormina, Italy, 19–22 June 2016. [Google Scholar]
- Quintero, O.L.; Amicarelli, A.A.; Scaglia, G.; di Sciascio, F. Control based on numerical methods and recursive Bayesian estimation in a continuous alcoholic fermentation process. BioResources 2009, 4, 1372–1395. [Google Scholar] [CrossRef]
- Blanco-Sanchez, P.; Taylor, D.; Cooper, S. IEA Bioenergy Task 33 UK Country Report; International Energy Agency Bioenergy: Paris, France, 2021. [Google Scholar]
- Skupin, P.; Laszczyk, P.; Goud, E.C.; Vooradi, R.; Ambati, S.R. Robust nonlinear model predictive control of cascade of fermenters with recycle for efficient bioethanol production. Comput. Chem. Eng. 2022, 160, 107735. [Google Scholar] [CrossRef]
- Das, S. Mathematical Modelling of Bioenergy Systems for Stability Analysis and Parametric Sensitivity. Ph.D. Thesis, UiT The Arctic University of Norway, Tromsø, Norway, 2021. [Google Scholar]
- Zhai, C.; Yang, C.X.; Na, J. Bifurcation Control on the Un-Linearizable Dynamic System via Washout Filters. Sensors 2022, 22, 9334. [Google Scholar] [CrossRef] [PubMed]
- Straathof, A.J.J. Modelling of end-product inhibition in fermentation. Biochem. Eng. J. 2023, 191, 108796. [Google Scholar] [CrossRef]
- Kurth, J.M.; Nobu, M.K.; Tamaki, H.; de Jonge, N.; Berger, S.; Jetten, M.S.M.; Yamamoto, K.; Mayumi, D.; Sakata, S.; Bai, L.P.; et al. Methanogenic archaea use a bacteria-like methyltransferase system to demethoxylate aromatic compounds. ISME J. 2021, 15, 3549–3565. [Google Scholar] [CrossRef] [PubMed]
- Tu, B.P.; Kudlicki, A.; Rowicka, M.; McKnight, S.L. Logic of the yeast metabolic cycle: Temporal compartmentalization of cellular processes. Science 2005, 310, 1152–1158. [Google Scholar] [CrossRef] [PubMed]
- Sriputorn, B.; Laopaiboon, P.; Phukoetphim, N.; Polsokchuak, N.; Butkun, K.; Laopaiboon, L. Enhancement of ethanol production efficiency in repeated-batch fermentation from sweet sorghum stem juice: Effect of initial sugar, nitrogen and aeration. Electron. J. Biotechnol. 2020, 46, 55–64. [Google Scholar] [CrossRef]
- Peng, P.; Lan, Y.; Liang, L.; Jia, L. Membranes for bioethanol production by pervaporation. Biotechnol. Biofuels 2021, 14, 10. [Google Scholar] [CrossRef] [PubMed]
- Chai, W.Y.; Teo, K.T.K.; Tan, M.K.; Tham, H.J. Fermentation Process Control and Optimization. Chem. Eng. Technol. 2022, 45, 1731–1747. [Google Scholar] [CrossRef]
- Chai, W.Y.; Teo, K.T.K.; Tan, M.K.; Tham, H.J. Model predictive control in fermentation process—A review. In Proceedings of the 2nd Energy Security and Chemical Engineering Congress, Gambang, Malaysia, 29 August 2022. [Google Scholar]
- Shen, Y.; Zhao, X.Q.; Ge, X.M.; Bai, F.W. Metabolic flux and cell cycle analysis indicating new mechanism underlying process oscillation in continuous ethanol fermentation with Saccharomyces cerevisiae under VHG conditions. Biotechnol. Adv. 2009, 27, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Prasad, D.; Kumar, M.; Srivastav, A.; Singh, R.S. Modelling of Multiple Steady-state Behavior and Control of a Continuous Bioreactor. Indian J. Sci. Technol. 2019, 12, 140476. [Google Scholar] [CrossRef]
- Bai, F.W.; Zhao, X.Q. High gravity ethanol fermentations and yeast tolerance. In Microbial Stress Tolerance for Biofuels; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Navarro-Tapia, E.; Nana, R.K.; Querol, A.; Pérez-Torrado, R. Ethanol cellular defense induce unfolded protein response in yeast. Front. Microbiol. 2016, 7, 189. [Google Scholar] [CrossRef] [PubMed]
- Lopez, P.C.; Feldman, H.; Mauricio-Iglesias, M.; Junicke, H.; Huusom, J.K.; Gernaey, K.V. Benchmarking real-time monitoring strategies for ethanol production from lignocellulosic biomass. Biomass Bioenerg. 2019, 127, 105296. [Google Scholar]
- Periyasamy, S.; Isabel, J.B.; Kavitha, S.; Karthik, V.; Mohamed, B.A.; Gizaw, D.G.; Sivashanmugam, P.; Aminabhavi, T.M. Recent advances in consolidated bioprocessing for conversion of lignocellulosic biomass into bioethanol—A review. Chem. Eng. J. 2022, 453, 139783. [Google Scholar] [CrossRef]
- Petre, E.; Selişteanu, D.; Roman, M. Advanced nonlinear control strategies for a fermentation bioreactor used for ethanol production. Bioresour. Technol. 2021, 328, 124836. [Google Scholar] [CrossRef] [PubMed]
- Ciesielski, A.; Grzywacz, R. Nonlinear analysis of cybernetic model for aerobic growth of Saccharomyces cerevisiae in a continuous stirred tank bioreactor. Static bifurcations. Biochem. Eng. J. 2019, 146, 88–96. [Google Scholar] [CrossRef]
- Perrier, M.; Dochain, D. Evaluation of control strategies for anaerobic digestion processes. Int. J. Adapt. Control. Signal Process. 1993, 7, 309–321. [Google Scholar] [CrossRef]
- Czyżniewski, M.; Łangowski, R. A robust sliding mode observer for non-linear uncertain biochemical systems. ISA Trans. 2022, 123, 25–45. [Google Scholar] [CrossRef]
- Petre, E.; Selişteanu, D.; Roman, M. Control schemes for a complex biorefinery plant for bioenergy and biobased products. Bioresour. Technol. 2020, 295, 122245. [Google Scholar] [CrossRef]
- Pachauri, N.; Rani, A.; Singh, V. Bioreactor temperature control using modified fractional order IMC-PID for ethanol production. Chem. Eng. Res. Des. 2017, 122, 97–112. [Google Scholar] [CrossRef]
- Pachauri, N.; Singh, V.; Rani, A. Two degrees-of-freedom fractional-order proportional–integral–derivative-based temperature control of fermentation process. J. Dyn. Syst. Meas. Control. 2018, 140, 071006. [Google Scholar] [CrossRef]
- Sun, S.Y.; Gresham, D. Cellular quiescence in budding yeast. Yeast 2021, 38, 12–29. [Google Scholar] [CrossRef] [PubMed]
- Oh, T.H.; Park, H.M.; Kim, J.W.; Lee, J.M. Integration of reinforcement learning and model predictive control to optimize semi-batch bioreactor. AICHE J. 2022, 68, e17658. [Google Scholar] [CrossRef]
- Pinto, A.S.S.; Pereira, S.C.; Ribeiro, M.P.A.; Farinas, C.S. Monitoring of the cellulosic ethanol fermentation process by near-infrared spectroscopy. Bioresour. Technol. 2016, 203, 334–340. [Google Scholar] [CrossRef] [PubMed]
- Tiernan, H.; Byrne, B.; Kazarian, S.G. ATR-FTIR spectroscopy and spectroscopic imaging for the analysis of biopharmaceuticals. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 241, 118636. [Google Scholar] [CrossRef] [PubMed]
- Bernard, P.; Andrieu, V.; Astolfi, D. Observer design for continuous-time dynamical systems. Annu. Rev. Control 2022, 53, 224–248. [Google Scholar] [CrossRef]
- Bayen, T.; Rapaport, A.; Tani, F.Z. Improvement of performances of the chemostat used for continuous biological water treatment with periodic controls. Automatica 2020, 121, 109199. [Google Scholar] [CrossRef]
- Wang, J.; Chae, M.; Beyene, D.; Sauvageau, D.; Bressler, D.C. Co-production of ethanol and cellulose nanocrystals through self-cycling fermentation of wood pulp hydrolysate. Bioresour. Technol. 2021, 330, 124969. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Prasad, D.; Giri, B.S.; Singh, R.S. Temperature control of fermentation bioreactor for ethanol production using IMC-PID controller. Biotechnol. Rep. 2019, 22, e00319. [Google Scholar] [CrossRef] [PubMed]
- Kurth, A.C.; Sawodny, O. Control of age-structured population dynamics with intra specific competition in context of bioreactors. Automatica 2023, 152, 110944. [Google Scholar] [CrossRef]
- De Battista, H.; Jamilis, M.; Garelli, F.; Picó, J. Global stabilisation of continuous bioreactors: Tools for analysis and design of feeding laws. Automatica 2018, 89, 340–348. [Google Scholar] [CrossRef]
- Grisolia, G.; Fino, D.; Lucia, U. Thermodynamic optimisation of the biofuel production based on mutualism. Energy Rep. 2020, 6, 1561–1571. [Google Scholar] [CrossRef]







| Label | Description | Value | Label | Description | Value |
|---|---|---|---|---|---|
| A1 | Exponential factors in Arrhenius law | 1.57 × 109 | MCa | Mol mass of Ca | 40 g/mol |
| A2 | Exponential factors in Arrhenius law | 4.20 × 1033 | MMg | Mol mass of Mg | 24 g/mol |
| AT | Heat transfer area | 1 m2 | MCl | Mol mass of Cl | 35.5 g/mol |
| Cheat,r | Heat capacity of culture medium | 4.18 J/g/°C | Mol mass of CO3 | 60 g/mol | |
| Cheat,j | Heat capacity of the cooling agent | 4.18 J/g/°C | MNaCl | Mol mass of NaCl | 58.5 g/mol |
| Ea1 | Activation energy | 55,000 J/mol | Mol mass of NaCO3 | 100 g/mol | |
| Ea2 | Activation energy | 220,000 J/mol | Mol mass of NaMgCl2 | 95.2 g/mol | |
| HOH | Specific ionic constant of OH | 0.941 | R | Universal gas constant | 8.31 J/mol/°C |
| HH | Specific ionic constant of H | −0.774 | YSP | Ethanol produced yield | 0.3989 g/g |
| HCO3 | Specific ionic constant of HCO3 | 0.485 | YSX | Biomass produced yield | 0.607 g/g |
| HCl | Specific ionic constant of Cl | 0.844 | V | Bioreactor volume | 1000 L |
| HMg | Specific ionic constant of Mg | −0.314 | Vj | Cooling jacket volume | 50 L |
| HCa | Specific ionic constant of Ca | −0.303 | O2 consumed rate | 0.970 mg/mg | |
| HNa | Specific ionic constant of Na | −0.55 | ΔHr | Aspiration heat | 518 kJ/mol |
| Ii | Ionic strengths | – | μO2 | O2 consumption rate | 0.5 h−1 |
| KLa0 | O2 mass-transfer coefficient | 38 h−1 | μP | Ethanol production rate | 1.79 h−1 |
| O2 consumption constant | 8.886 mg/L | ρj | Density of jacket liquid | 1000 g/L | |
| KE | Inhibition constant by ethanol | 0.139 g/L | ρr | Density of the medium | 1080 g/L |
| KE1 | Inhibition constant by ethanol | 0.07 g/L | mNaCl | Quantity of NaCl | 500 g |
| KS | Substrate constant for growth | 1.03 g/L | Quantity of CaCO3 | 100 g | |
| KS1 | Substrate constant for production | 1.68 g/L | Quantity of MgCl2 | 100 g | |
| KT | Heat transfer coefficient | 3.6 × 105 J/h/m2/°C | MNa | Molecular mass of Na | 23 g/mol |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Zhai, C. Global Stabilizing Control of a Continuous Ethanol Fermentation Process Starting from Batch Mode Production. Processes 2024, 12, 819. https://doi.org/10.3390/pr12040819
Qin Y, Zhai C. Global Stabilizing Control of a Continuous Ethanol Fermentation Process Starting from Batch Mode Production. Processes. 2024; 12(4):819. https://doi.org/10.3390/pr12040819
Chicago/Turabian StyleQin, Yuxin, and Chi Zhai. 2024. "Global Stabilizing Control of a Continuous Ethanol Fermentation Process Starting from Batch Mode Production" Processes 12, no. 4: 819. https://doi.org/10.3390/pr12040819






