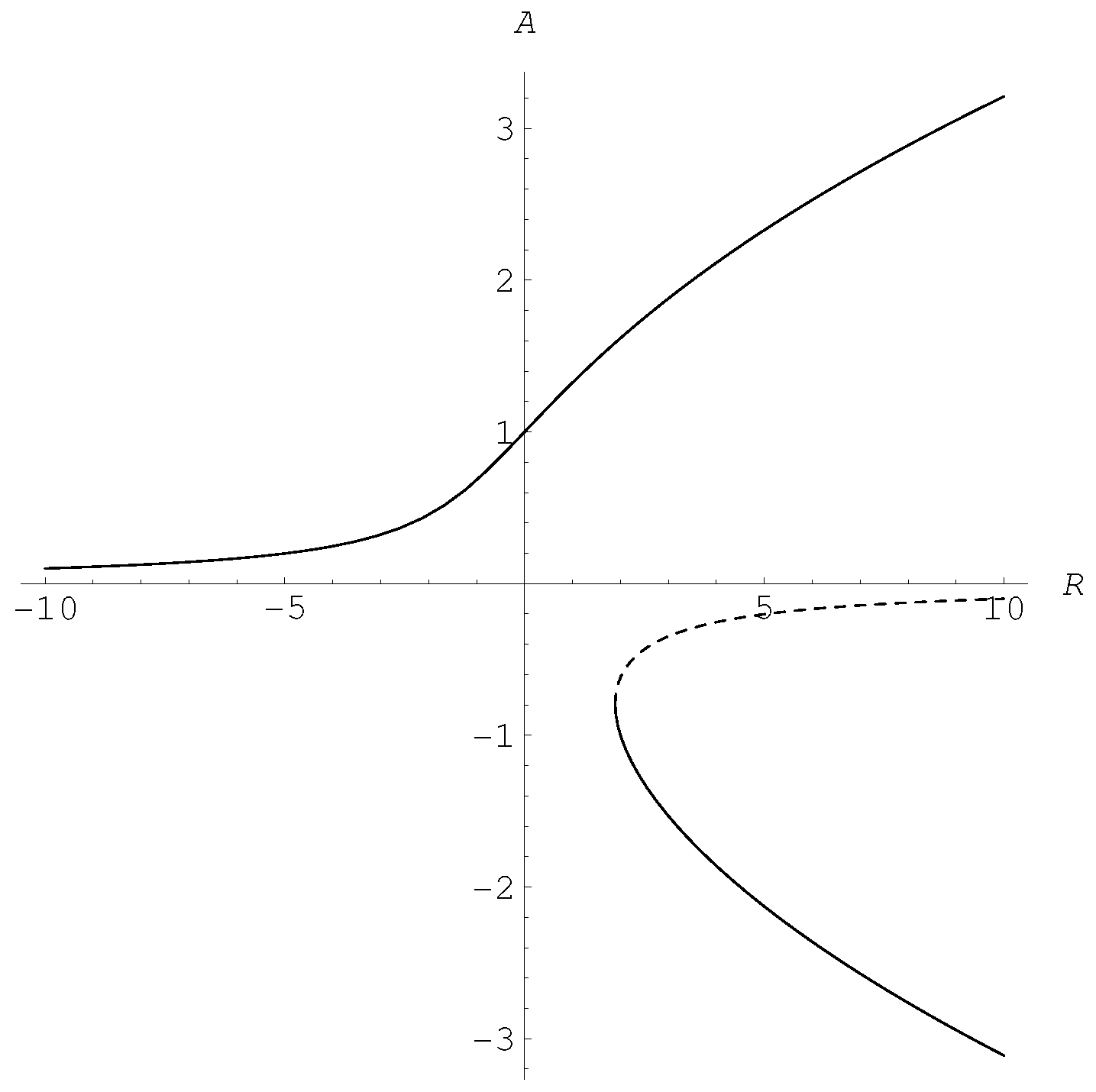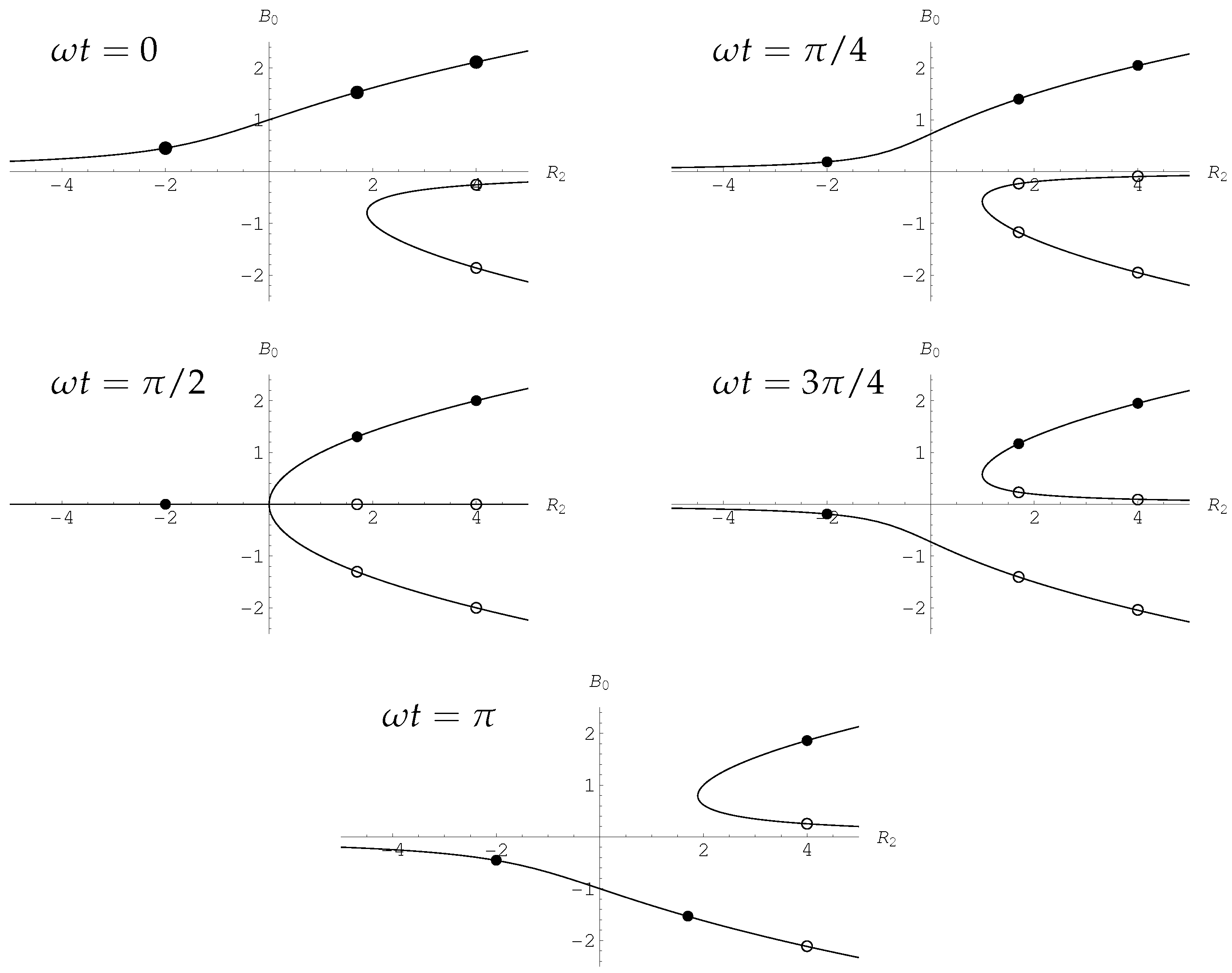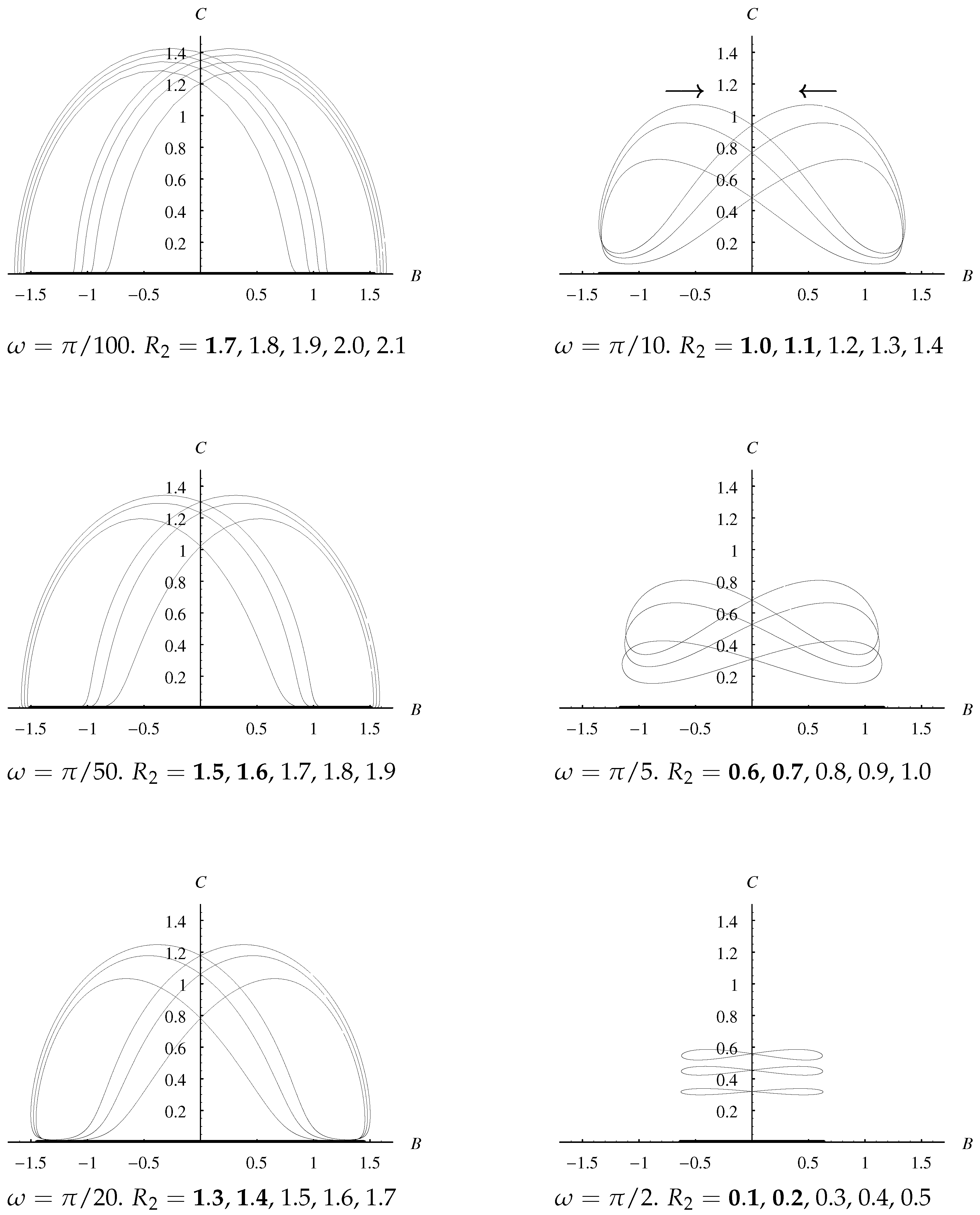1. Introduction
The classical Bénard problem as applied to a porous medium was first studied by Horton and Rogers (1945) [
1] and independently by Lapwood (1948) [
2]; these authors considered the onset of convection in a horizontal saturated porous layer heated uniformly from below. Using a linear stability theory, the neutral curve which relates the Darcy-Rayleigh number,
, to the wavenumber,
k, may be shown to take the form,
(see Rees 2000, for example) [
3] where the value of
n corresponds to the number of rolls which are stacked above one another in the layer. This variation of
with
k is shown in
Figure 1 and it may be shown easily that the minimum/critical value is
, which occurs when
and
. These values correspond to rolls with a square cross-section.
Palm et al. (1972) [
4] subsequently analysed the moderately supercritical flow using a series representation in terms of powers of
. A very detailed numerical stability analysis was undertaken by Straus (1974) [
5] who delineated the region in
-space within which steady rolls form the stable planform of convection.
The general topic of Darcy-Bénard convection continues to grow rapidly as further effects, realism and/or practical application are added to the original Horton-Rogers-Lapwood configuration [
2,
6]. Reviews have been presented by Rees (2000) [
3] and Tyvand (2002) [
7], but the topic has continued to be the subject of substantial interest in the time since then, and therefore we would refer the reader to the latest edition of Nield and Bejan (2017) [
8] for an up-to-date account of the topic.
In the present paper, we shall confine our interest to the role played by boundary imperfections, itself a well-researched subtopic. It is widely recognised that completely uniform and idealised boundary conditions are not easily achieveable in practice, and therefore authors such as Riahi (1983) [
9], Saleh et al. (2011) [
10], Motjabi and Rees (2011) [
1] and Rees and Mojtabi (2011) [
11] have concerned themselves with more realistic boundary conditions where the perfectly conducting bounding surfaces are replaced by conducting solids. The resulting stability properties are influenced profoundly by the nature of the solids used and their thickness. Thus it is possible for perfectly conducting boundary conditions on the outer surfaces to give rise to stability properties which are more closely associated with constant heat flux surfaces, and vice versa. It is also possible for roll solutions to be unstable in some circumstances, in which case convection with a square planform forms the preferred pattern (see Riahi 1993, Rees and Mojtabi 2011) [
11].
In a series of papers, Rees and Riley (1986, 1989a, 1989b) [
12,
13,
14] and Rees (1990) [
15] considered the effect of small-amplitude boundary variations on both the onset of convection and convection within the weakly nonlinear regime. Depending on the wavenumber of the variation, the preferred pattern of convection may take the form of rolls, wavy rolls, rectangular cells or exhibit other unusual properties. Other papers of this type include those by Vozovoi and Nepomnyaschii (1974) [
16], Tavantzis et al. (1978) [
17], O’Sullivan and McKibbin (1986) [
18] and Riahi (1993, 1995) [
9,
19,
20].
A little later, Mamou et al. (1996) [
21] and Banu and Rees (2001) [
22] applied thermal boundary variations of the form
, which correspond to travelling thermal waves at the critical spatial wavenumber,
. The former paper considered strongly supercritical convection using fully numerical methods, while the latter applied a weakly nonlinear theory in order to understand the subtle details which arise closer to the onset of convection. The effect of having a forcing wave speed,
U, is to cause a competition between the tendency of the rolls to remain stationary, which is what happens naturally in a layer without such imperfections, and the tendency to follow the forcing wave. It was found that there is a catastrophic transition between the wave-following regime and the quasi-stationary regime in that the amplitude and horizontal velocity of the convection pattern change suddenly as the Darcy-Rayleigh number increases. This system was also found to display hysteresis, for the reverse transition which occurs as the Rayleigh number decreases, does so at a different value of the Rayleigh number.
The present paper is concerned with a physical configuration for which convection cells also have a tendency to move. For the Darcy-Bénard problem one of the easiest ways in which this may arise is when the fluid is also subject to a horizontal pressure gradient. Prats (1967) [
23] showed that the convection cells then move with precisely the same velocity as the pressure-gradient-induced flow which exists in the absence of heating. Thus the dynamics of the ensuing convection are precisely the same as that for a layer without the background flow when it is considered in a frame of reference which is moving with the background flow. An interesting variation on this Darcy-Bénard-Prats problem was studied by Dufour and Néel (1996) [
24] where a uniform horizontal flow is injected into a horizontally semi-infinite porous layer heated from below. In general the flow remains roughly uniform near to injection and there exists a spatial transition towards the time-periodic flow described by Prats (1967) [
23]. The length of the transition region depends on the magnitudes of the injection velocity,
Q (a Péclet number) and the Darcy-Rayleigh number, increasing as Péclet number increases but decreasing as the Darcy-Rayleigh number increases; these phenomena are related to the phase diffusion speed of the convection cells. A much more recent paper by Rees and Mojtabi (2013) [
1] shows that the presence of solid conducting boundaries serves to reduce the phase speed of the convecting cells. This reduction may be attributed to what might be called a thermal drag which arises due to the fact that the time-varying convection mode has to move through a stationary boundary of finite height.
Another mechanism which relies neither on an external pressure gradient nor on moving boundary conditions to induce phase drift is when convection takes place in a cylindrical container with a circular planform. Although no studies have yet been published on such flows in porous media, it is well-known that such a variant of the classical Bénard problem may sometimes exhibit a rotating spiral convection pattern even though all the boundary conditions are steady and uniform; see Plapp et al. (1998) [
25].
In this paper we consider thermal forcing of the form
, and this may be regarded as the standing wave counterpart to the work of Banu and Rees (2001) [
22]. Although this thermal forcing is now stationary in space, we shall show later that it remains possible for rolls to exhibit a time-periodic horizontal motion. As shall be seen, the reason for this periodic motion is that the preferred phase of the convection cells depends (in a quasi-static sense) on the sign of the forcing amplitude,
, and therefore the phase of the cells is drawn towards two different fixed points during the two different parts of the forcing cycle. Our subsequent analyses involve a derivation of the weakly non-linear amplitude equations, together with both numerical simulations and asymptotic analyses of those amplitude equations. Attention is also focused on the transition between two different types of stationary motion, and on a twitching motion at high Rayleigh numbers where cells execute small-amplitude periodic movements in phase.
2. Governing Equations
Darcy’s law gives the most basic equation governing fluid flows in a porous medium. It is the macroscopic law which relates the fluid flux to the applied pressure gradient. For buoyancy-affected flows of a Boussinesq fluid, where the porous medium is assumed to be homogeneous, nondeformable and isotropic, the dimensional equations which govern the fluid motion are,
In these equations all the terms take their common meanings. The coordinates and are in the horizontal directions, while is vertically upwards. T is the temperature of the saturated medium, is the mean upper (cold) boundary temperature, is the pressure, K the permeability, the viscosity, g gravity, a reference density of the fluid, and the coefficient of cubical expansion of the fluid. The quantities , and , correspond to the fluid seepage velocities in the , and directions, respectively.
The full equations are completed by the equation of continuity,
and the heat transport equation,
where
is the thermal diffusivity of the saturated porous medium and,
is the heat capacity ratio of the saturated medium to that of the fluid. The value,
c, is the specific heat and
the density of the medium, with the subscripts
f and
s referring to the fluid and solid phases, respectively.
The nondimensionalisation of Equations (
2)–(
4) is achieved using the following substitutions,
where
d is the height of the layer. Here,
and
are the cold (upper) and hot (lower) mean temperatures of the horizontal bounding surfaces. Hence, the non-dimensional equations are,
In the above, the parameter,
is the Darcy-Rayleigh number; the usual clear-fluid Rayleigh number may be obtained by replacing the permeability,
K, by
. The Darcy-Rayleigh number expresses the balance between buoyancy and viscous forces.
Assuming that the flow is two dimensional, then
and all the derivatives with respect to
y may be neglected. Hence, by introducing the stream function,
, using
and
, not only is Equation (
8) satisfied but Equations (
9) and (
10) become,
Both of the equations above are to be solved analytically using a weakly nonlinear analysis.
The boundary surfaces are considered to be impermeable. The thermal boundary conditions comprise a combination of heating from below and a small-amplitude variation which is periodic in both time and space. Therefore the boundary conditions are
where
is the amplitude of the thermal forcing and
is its nondimensional temporal frequency.
3. Weakly Nonlinear Analysis
In this section we shall carry out a weakly nonlinear analysis in order to obtain a complex Landau equation for the amplitude of convection in the presence of the thermal boundary imperfections given in Equation (
14). This will be undertaken using the scalings which were used in Rees and Riley (1989a) [
13] and Banu and Rees (2002) [
22], and which are suitable for those cases where the wavenumber of the imperfection takes the critical value. We follow the methodology introduced by Newell and Whitehead (1969) [
26] for the Bénard problem.
Therefore we shall set the amplitude of convection to be of
and the Darcy-Rayleigh number shall be within a distance of
of its critical value,
. Given that the imperfection has the critical wavenumber, we need to set
; see Rees and Riley (1986,1989a) [
12,
13]. The appropriate time scale is of
. Equations (
12) and (
13) may now be expanded using the following asymptotic series,
and, given the above observations, we set
where
. The leading term in Equation (
16) is the linear conduction profile while the additional cosine term at
renders the thermal boundary conditions for
to be homogeneous (see Equation (
14)).
At
, the leading order disturbance equations are,
These homogeneous equations form the linearised stability problem for the uniformly heated layer, and are to be solved subject to the following homogeneous Dirichlet boundary conditions,
identical conditions will also apply for
and
,
. We choose to use the following roll eigensolutions,
where
is a complex amplitude which is a function of the slow timescale,
. The complex forms used in Equation (
21) allow for a straightforward modelling of phase variations in the solutions.
At
the equations for
and
are,
When the solutions given in Equations (
21) are substituted into Equation (
23) the latter becomes,
and therefore
and
are found to be,
At
the equations for
and
are,
After the substitution of Equations (
21) and (
25), the above equations become,
The inhomogeneous terms in Equations (
28) and (
29) contain components which are proportional to the eigensolution of the homogeneous form of the equations, namely, the solutions given in Equation (
21). The value for
is presently arbitrary but in general this system of equations cannot be solved unless
takes a specific value. The derivation of a solvability condition will yield the desired amplitude equation for
A in terms of
, the satisfaction of which guarantees the solution of Equations (
28) and (
29) up to an arbitrary multiple of the eigensolution.
If Equations (
28) and (
29) are written in the form,
and if we define the quantities,
and
, which are the coefficients of
in Equation (
21), then the following identity may be formed:
The left hand side of Equation (
31) may be shown to be precisely equal to zero by using integration by parts, and thus the solvability condition is that,
Upon application of this solvability condition to Equations (
28) and (
29) we obtain the following amplitude (i.e., Landau) equation,
The coefficients of the last two terms of Equation (
33) may be simplified by rescaling
A,
and
in order to obtain the following canonical form of the amplitude equation,
The scalings which are required to do this are,
If we omit the asterisks for simplicity of presentation, then the complex amplitude equation governing weakly nonlinear convection is,
where
has been replaced by
t for simplicity of presentation from this point onwards, and this
t should not be confused with that used in §§1 and 2. The rest of the paper is devoted to the properties of the real and complex solutions of this equation. For any given
the forcing period is
.
7. Conclusions
We have studied the behaviour of two-dimensional convective rolls in a horizontal fluid-saturated porous layer heated from below, taking into account the effect of time-periodic resonant thermal boundary imperfections of small amplitude. A weakly non-linear theory has been used to derive the governing amplitude equation and to analyse the stability of the motion.
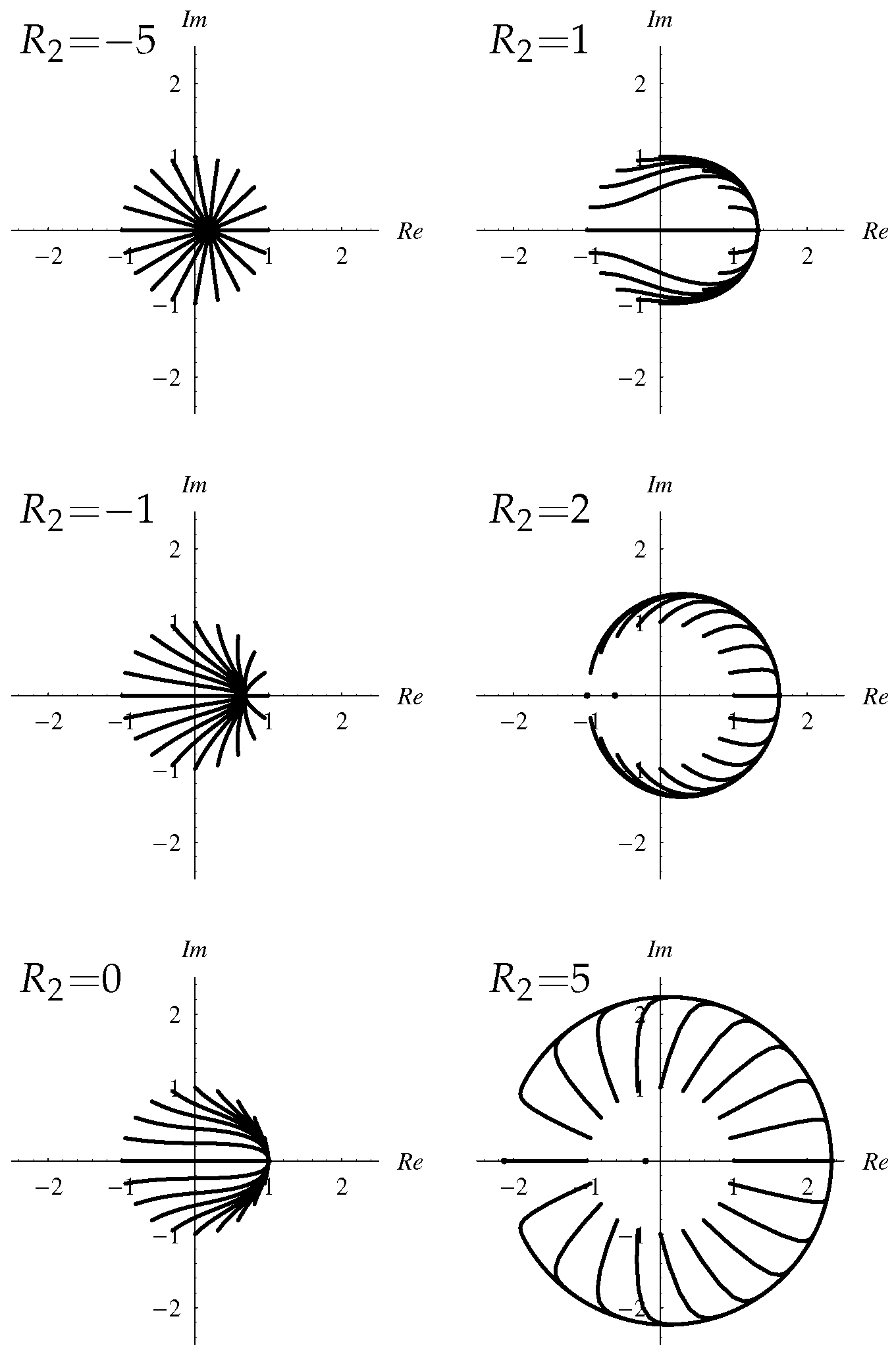
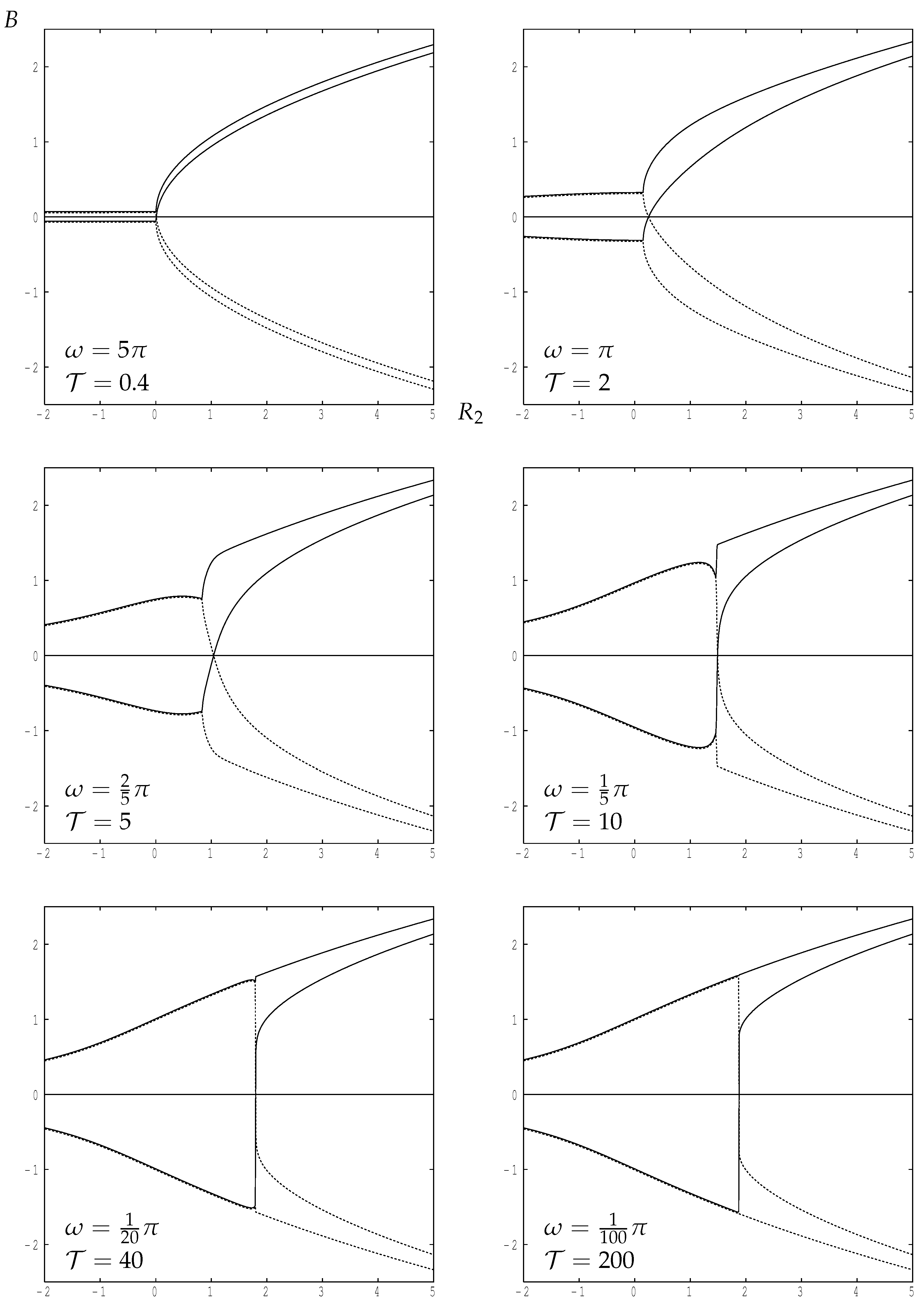
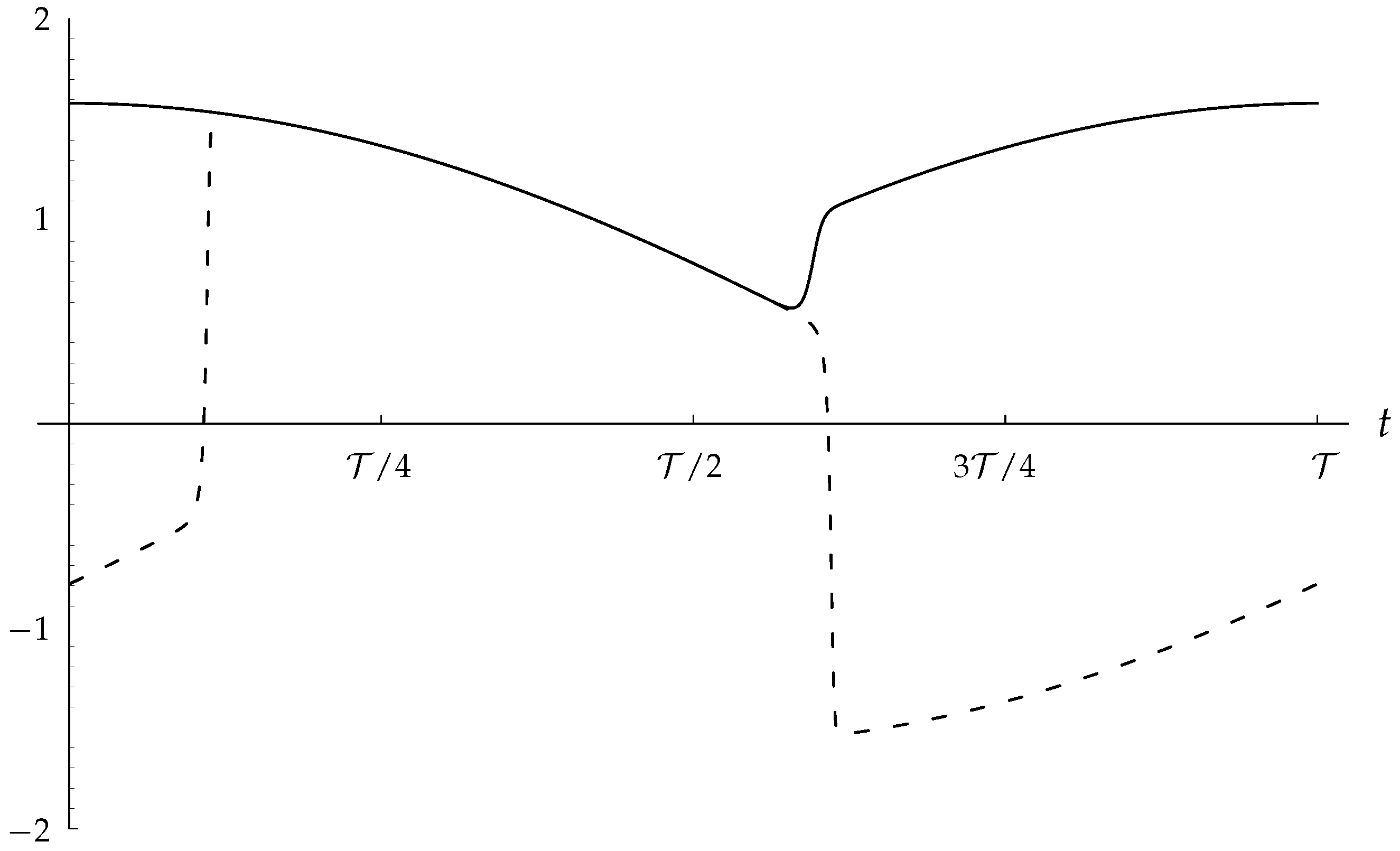
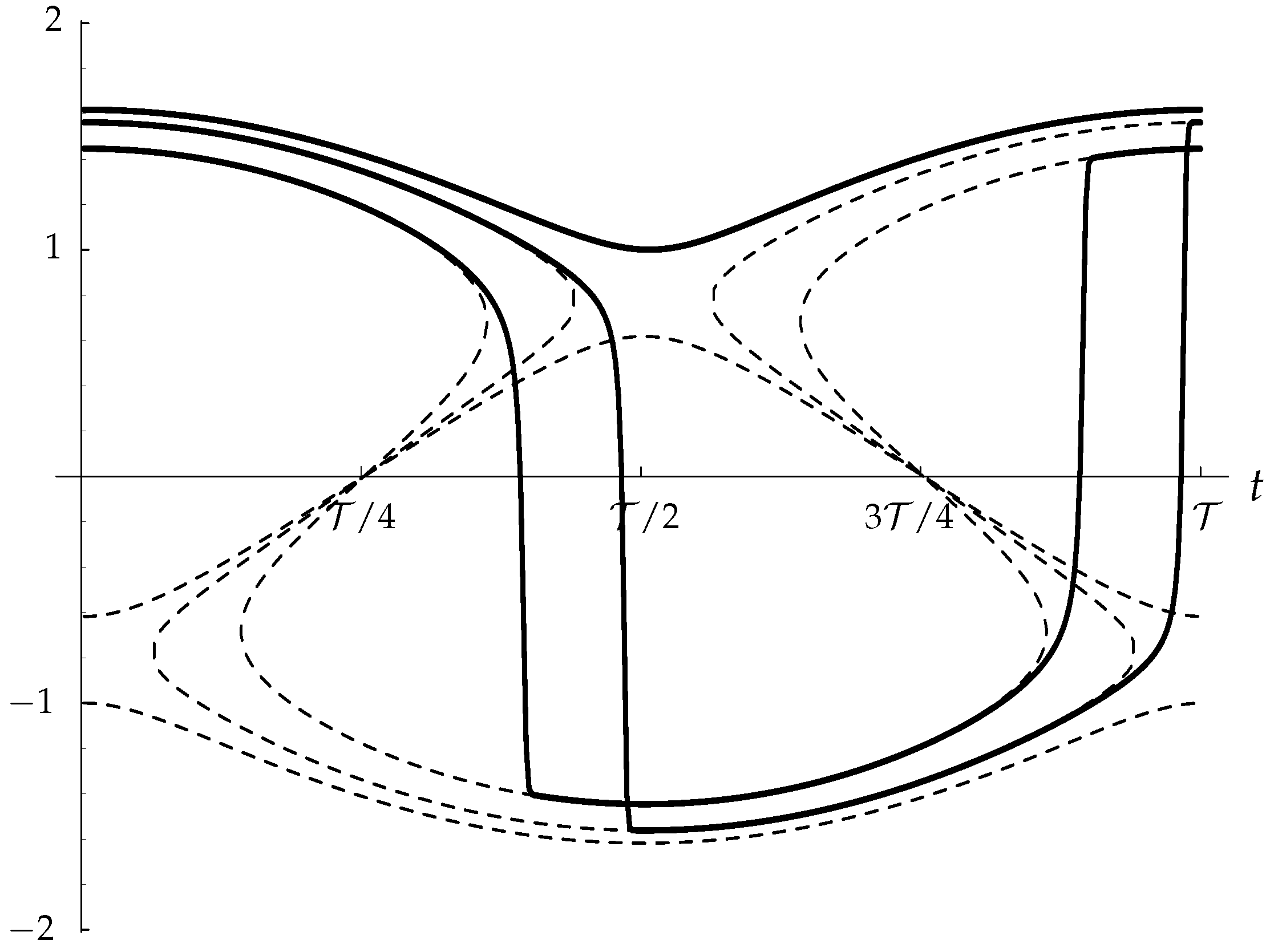
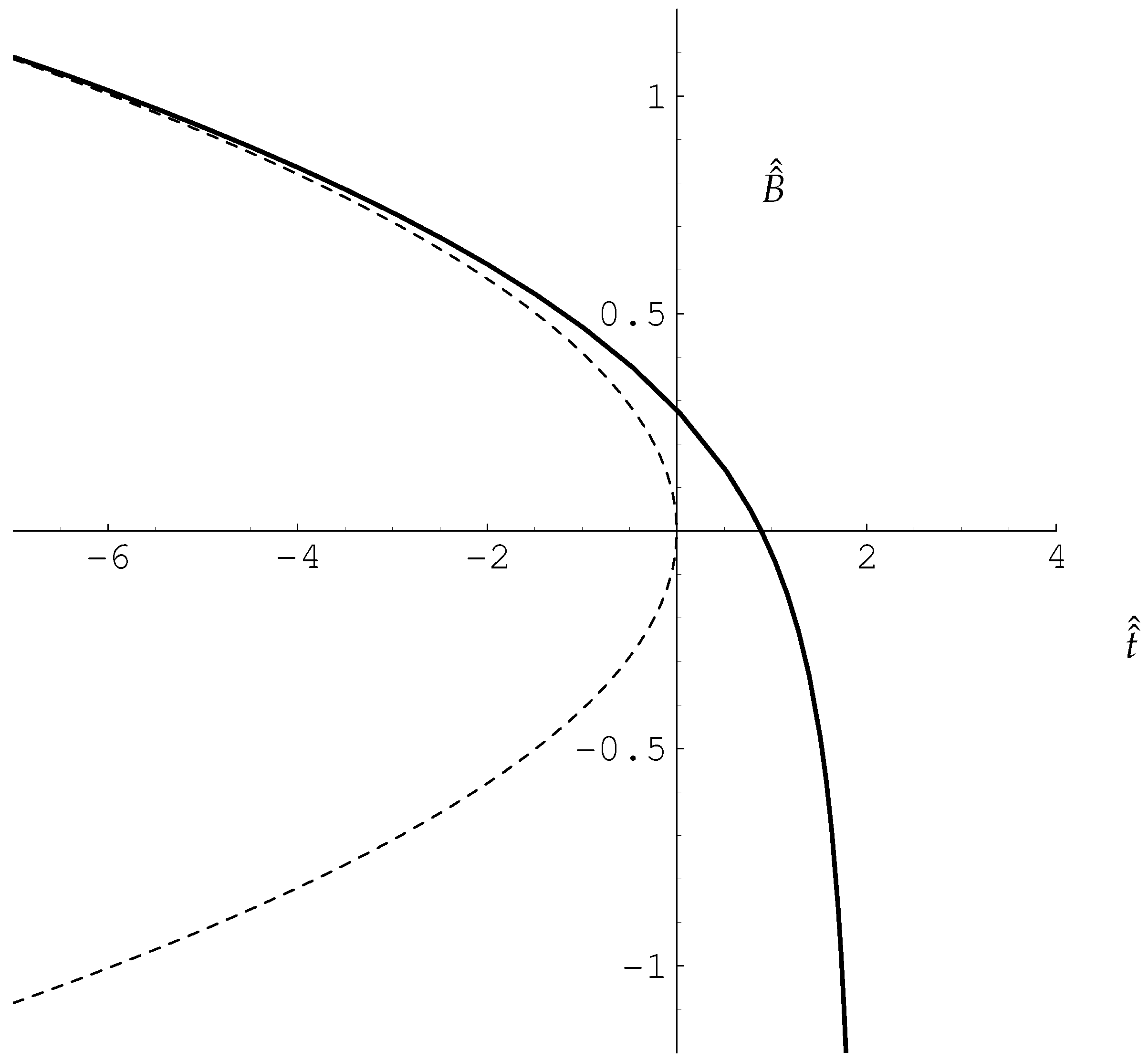
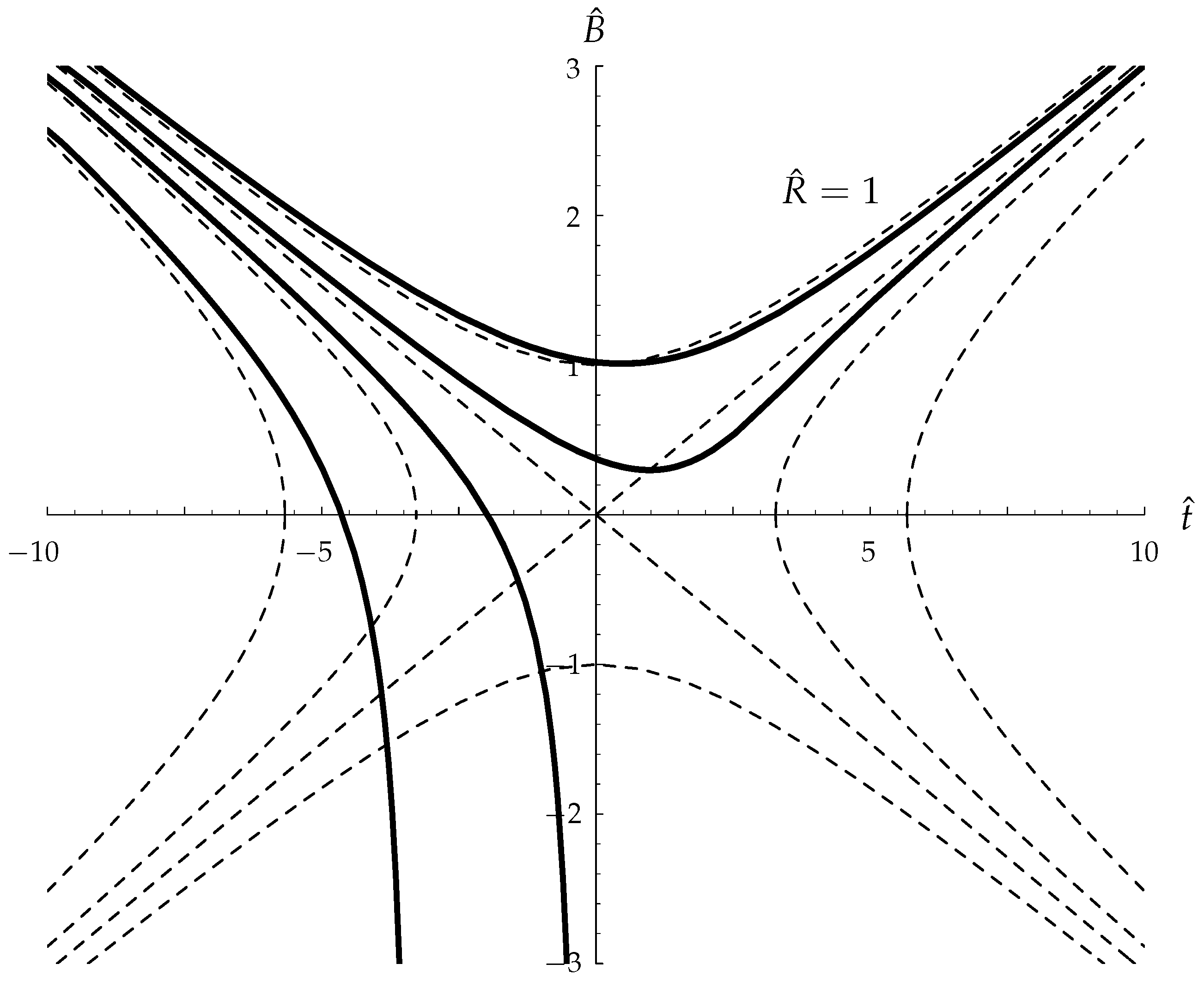
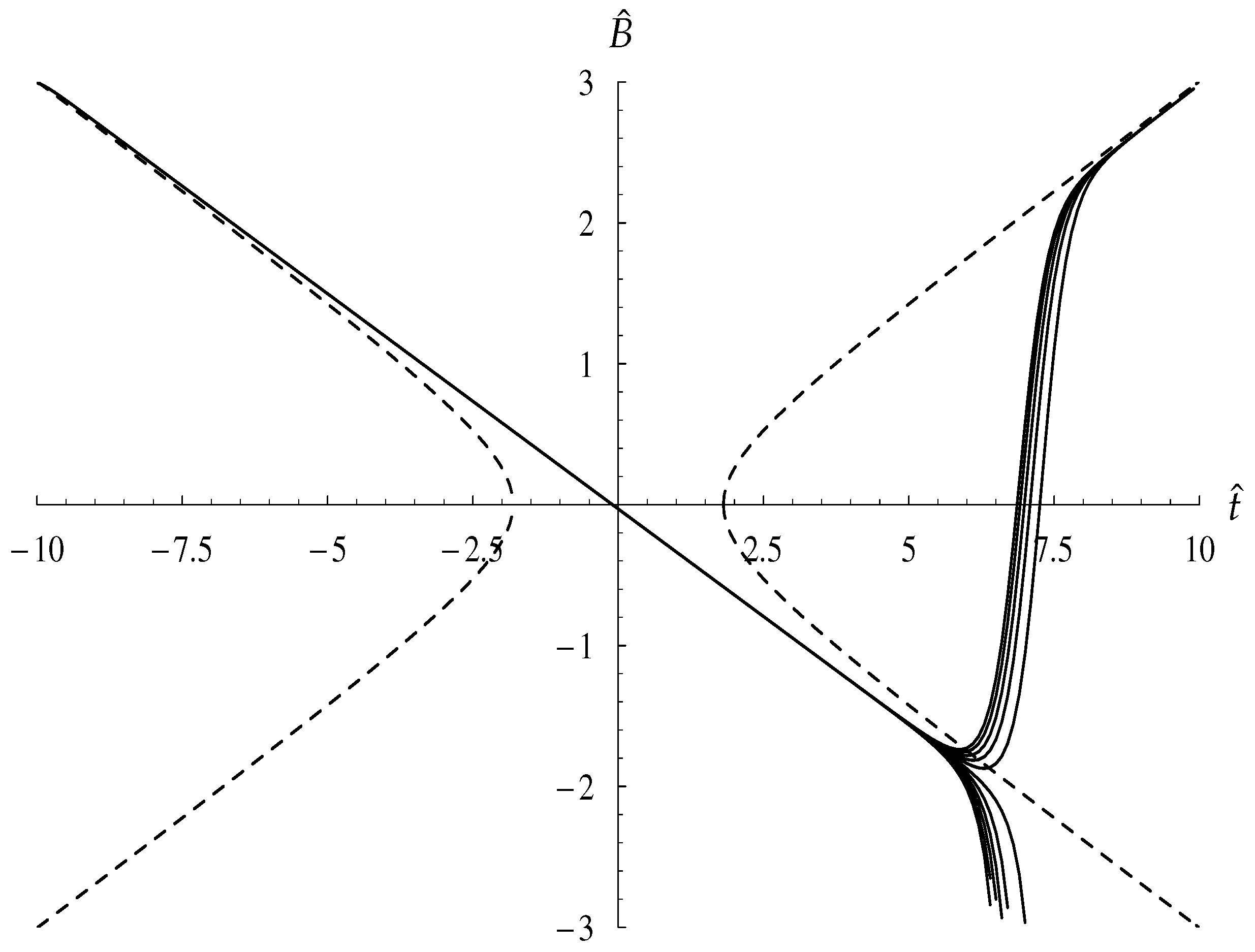
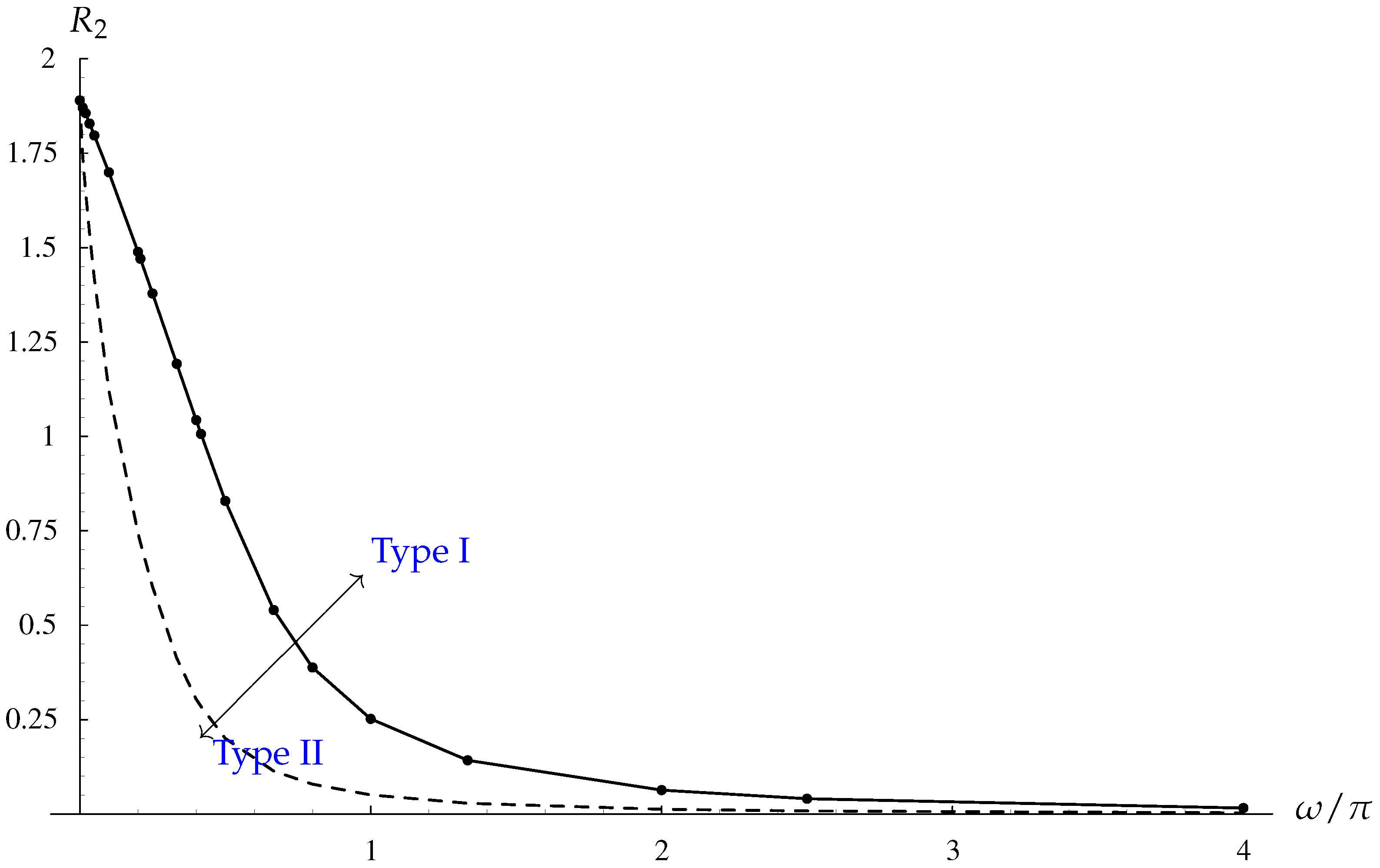
There exist different solutions of this amplitude equation in different regions of Rayleigh number/wavenumber space. If the flow is constrained to be stationary, which will happen if the layer is bounded by suitably-placed sidewalls with impermeable and insulating boundary conditions, then what is termed a Type II flow exists and is stable when is below a frequency-dependent critical value. As increases there is a supercritical bifurcation to what is termed a Type I flow. Flows of Type II are double-signed, whereas Type I flows are usually single-signed—exceptions are situated close to the bifurcation point. Detailed asymptotic solutions are presented for small frequencies where the numerical solutions display localised and quite rapid changes in sign.
When the layer is unbounded horizontally, then the real-A stationary solutions are susceptible to disturbances in phase, and we find that all Type I solutions are unstable to this type of disturbance. Type II real solutions may also be destabilised if is sufficiently large to become one with complex amplitude, which corresponds to a convection pattern which oscillates horizontally.
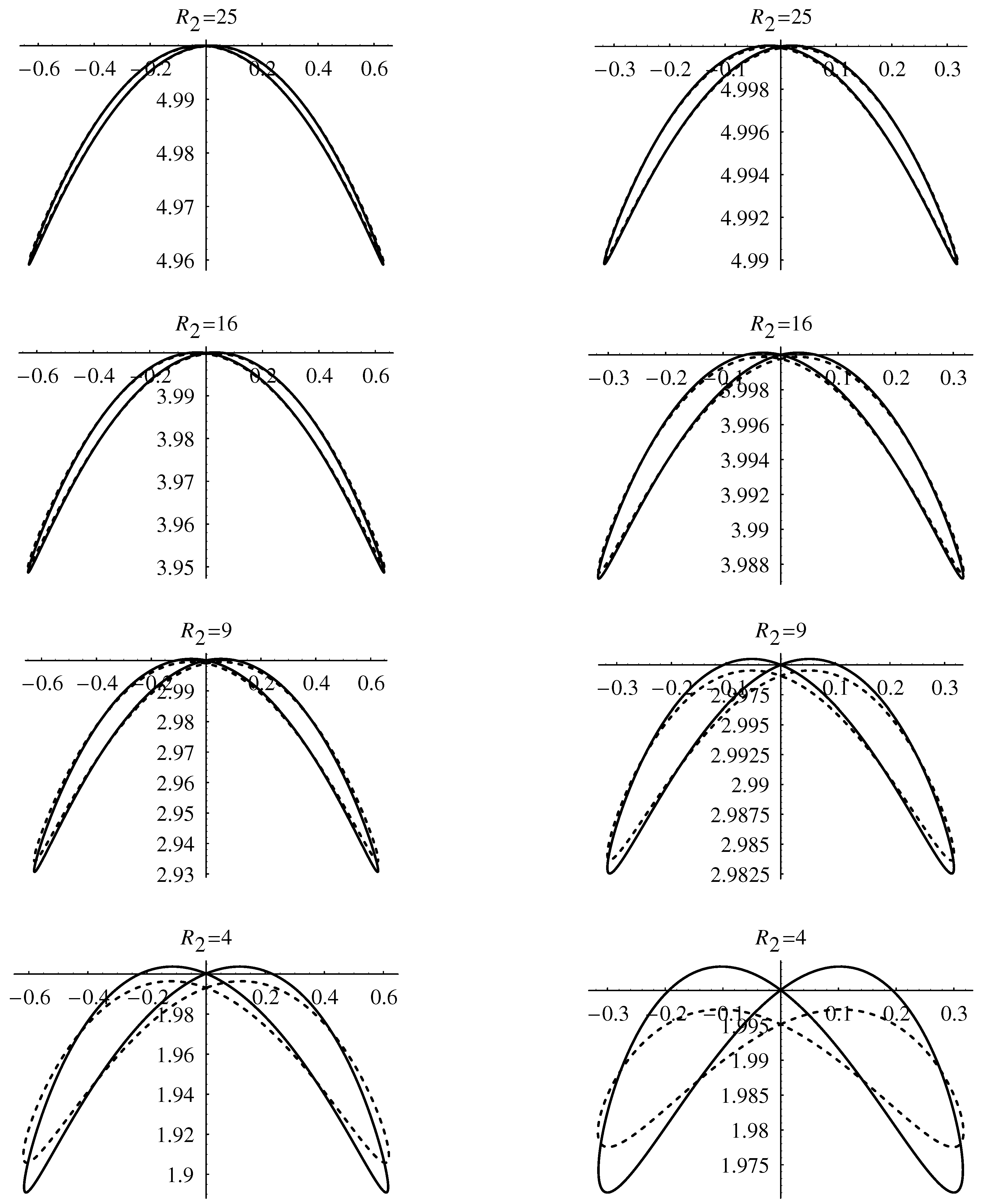
Numerical solutions have in many cases been supplemented by asymptotic solutions and these have shown excellent agreement.
Three dimensional disturbances have not been considered in this paper. Given that the boundary disturbances have a spatial pattern which has the critical wavenumber, it is our a priori expectation that three-dimensional effects are subdominant. However, we think that three-dimensional effects will be important when the spatial wavenumber of the disturbance is different from
. Certainly it is the case that such patterns are dominant when these boundary forcing terms are steady in time; see Rees and Riley 1989(a,b) [
12].
Finally we note that some of the work described here on moving cells may need to be modified if a layer of long but finite length were to be considered. It has already been stated that disturbances in phase cannot arise in a short layer due to the presence of sidewalls. However, if the layer is of finite but sufficiently large extent (which will be of ), then it may well be possible for cells to be compressed slightly near those sidewalls, and this would allow for phase movements in the bulk which then reduce in magnitude as the sidewalls are approached. In these the resulting time-dependent flow may be visualized by having stationary cells fixed or pinned to the two sidewalls, rather than being generated or annihilated, and then the magnitude of the time-variation of the phase of all other cells will increase to a maximum midwall between the sidewalls. If the layer is sufficiently long, then there will be a substantial region in the middle of the layer where the present theory is valid.
It is also intended to extend the present work well into the nonlinear regime.