Simulations of Blast Wave and Fireball Occurring Due to Rupture of High-Pressure Hydrogen Tank

Abstract

In the present study, pilot simulations of the phenomena of blast wave and fireball generated by the rupture of a high-pressure (35 MPa) hydrogen tank (volume 72 L) due to fire were carried out. The computational fluid dynamics (CFD) model includes the realizable k-ε model for turbulence and the eddy dissipation model coupled with the one-step chemical reaction mechanism for combustion. The simulation results were compared with experimental data on a stand-alone hydrogen tank rupture in a bonfire test. The simulations provided insights into the interaction between the blast wave propagation and combustion process. The simulated blast wave decay is approximately identical to the experimental data concerning pressure at various distances. Fireball is first ignited at the ground level, which is considered to be due to stagnation flow conditions. Subsequently, the flame propagates toward the interface between hydrogen and air.

1. Introduction

The mainstream solution for on-board hydrogen storage in automotive applications is compressed gaseous hydrogen (CGH2) tanks composed of carbon fiber reinforced plastic (CFRP) with either a plastic liner (Type 4) or aluminum liner (Type 3). Tank rupture in a fire, owing to localized transient heating or a failure of thermally activated pressure relief device (TPRD), remains a hazard associated with car fires. An understanding of the consequences of a tank rupture under realistic conditions and the ability to predict associated hazards are challenging safety engineering requirements critical for the effective design of hydrogen storage and infrastructure. Although the consequences of liquefied petroleum gas (LPG) tank rupture have been investigated [1,2,3,4,5], few research has been conducted with regard to the hydrogen tank [6,7,8,9,10].

Fire exposure tests of Type 3 and Type 4 hydrogen fuel tanks without TPRD were conducted by Weyandt et al. [6,7,8]. The stand-alone Type 4 tank in their study had a length of 0.84 m, a diameter of 0.41 m and a volume of 72.4 L. The initial storage pressure in the tank was 35 MPa, and it was installed 0.20 m above the ground. The tank ruptured catastrophically after 6 min 27 s of exposure to a propane bonfire. Experimental measurements revealed blast pressures of 300 kPa, 83 kPa and 41 kPa at distances 1.9 m, 4.2 m and 6.5 m, respectively. The maximum observed diameter of the fireball was approximately 7.7 m. Tank fragment projectiles were observed at distances from 34 m to 82 m. In the test with a Type 3 tank, which was installed under a vehicle, the blast wave overpressure registered during the experiment ranged from 140 kPa at 1.2 m to 12 kPa at 15 m, and the maximum fireball diameter was 24 m. In this test, the projectiles were observed at distances up to 107 m. Similar experimental results indicate that tank rupture is likely to result in devastating consequences, causing damage to life and property at substantial distances from the tank location. Recently, a methodology for the prediction of the decay of blast wave caused by high-pressure hydrogen tank rupture due to fire has been developed [10]. This new model was applied as a safety engineering tool to analyze the consequences of catastrophic failure of onboard vehicle storage tanks and stand-alone tanks.

The objective of this numerical study was to obtain insights into the blast wave and fireball phenomena as a consequence of high-pressure hydrogen storage tank rupture due to fire, and to compare simulation results with experimental results [6,7,8].

2. Numerical Model

The governing equations include three-dimensional Favre-averaged compressible conservation equations for mass, momentum, energy, and species that are listed as follows:

$$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x_j}\left(\rho u_i\right)=0$$

(1)

$$\frac{\partial \overline{\rho }{u}_i}{\partial t}+\frac{\partial }{\partial x_j}\left(\overline{\rho }{u}_i{u}_j\right)=-\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial }{\partial x_j}\left(\mu +{\mu }_t\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k}{\delta }_{ij}\right)+\rho g_i$$

(2)

$$\begin{array}{l}\frac{\partial }{\partial t}\left(\overline{\rho }E\right)+\frac{\partial }{\partial x_j}\left(u_j(\overline{\rho }E+p)\right)\\ =\frac{\partial }{\partial x_j}\left[\left(k+\frac{{\mu }_t{c}_p}{{\mathrm{Pr}}_t}\right)\frac{\partial T}{\partial x_j}-{\displaystyle \sum _m{h}_m}\left(-\left(\rho D_{H_2}+\frac{{\mu }_t}{S{c}_t}\right)\frac{\partial Y_{H_2}}{\partial x_j}\right)+u_i\left(\mu +{\mu }_t\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k}{\delta }_{ij}\right)\right]+S_E\end{array}$$

(3)

$$\frac{\partial \overline{\rho }{Y}_{H_2}}{\partial t}+\frac{\partial }{\partial x_j}\left(\overline{\rho }{u}_j{Y}_{H_2}\right)=\frac{\partial }{\partial x_j}\left[\left(\rho D_{H_2}+\frac{{\mu }_t}{S{c}_t}\right)\frac{\partial Y_{H_2}}{\partial x_j}\right]+S_{H_2}$$

(4)

where ρ is the density; t is the time; x_i, x_j and x_k are the Cartesian coordinates; u_i, u_j and u_k are the velocity components; p is the pressure; g_i is the gravity acceleration in direction i; μ_t is the turbulent dynamic viscosity; δ_ij is the Kronecker symbol; E is the total energy; T is the temperature; Y_H2 is the hydrogen mass fraction; c_p is the specific heat at constant pressure; Sc_t is the turbulent Schmidt number; Pr_t is the turbulent Prandtl number; D_H2 is the hydrogen molecular diffusivity; and S_E and S_H2 are the source terms in the equations of energy conservation and hydrogen conservation during combustion [11].

The turbulence is accounted for using the realizable k-ε model [12]. The transport equation of turbulence kinetic energy, k, and its rate of dissipation, ε, are as follows:

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_j}\left(\rho k{u}_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho \epsilon -Y_M$$

(5)

$$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_j}\left(\rho \epsilon u_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}S\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}+C_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_b$$

(6)

where $C_1=\max \left[0.43,\frac{\eta }{\eta +5}\right],\eta =S\frac{k}{\epsilon },S=\sqrt{2S_{ij}{S}_{ij}}$.

In these equations, G_k is the generation of turbulent kinetic energy by the mean velocity gradients; G_b is the generation of turbulent kinetic energy by buoyancy; Y_M is the contribution of the fluctuating dilatation in compressible turbulence flow to the dissipation rate; C₂, C_1ε and C_3ε are constants; and σ_k and σ_ε are the turbulent Prandtl numbers for k and ε, respectively. In this simulation, the initial values of both k and ε are assumed to be 1.

The Eddy Dissipation model based on the concept of Magnussen and Hjertager [13] is employed to the model the combustion and turbulence-chemistry interaction. The net rate of production of species i in reaction r, R_i,r is expressed by:

$$R_{i,r}={\nu }_{i,r}^{\prime }{M}_{w,i}A\rho \frac{\epsilon }{k}\min R\left(\frac{Y_R}{{\nu }_{R,r}^{\prime }{M}_{w,R}}\right)$$

(7)

$$R_{i,r}={\nu }_{i,r}^{\prime }{M}_{w,i}AB\rho \frac{\epsilon }{k}\frac{{\displaystyle {\sum }_P{Y}_P}}{{\displaystyle {\sum }_j^N{\nu }_{j,r}^{″}}{M}_{w,j}}$$

(8)

where ${\nu }_{i,r}^{\prime }$, ${\nu }_{j,r}^{″}$ are the stoichiometric coefficients for reactants i and j due to the reaction; M_w,i, M_w,j are the molecular weights of species i and j; Y_p and Y_R are the mass fractions of the product and reactant, respectively; and A = 4.0 and B = 0.5 are empirical constants. The chemical reaction is regulated by the large-eddy mixing time scale. Combustion occurs whenever turbulence is present, i.e., k/ε > 0, and an ignition source is not required to initiate combustion [14]. In this simulation, the one-step chemical reaction mechanism of hydrogen combustion in the air is applied, i.e., 2H₂ + (O₂ + 3.76N₂) → 2H₂O + 3.76N₂, and the model is therefore incapable of predicting kinetics of intermediate species.

3. Numerical Details

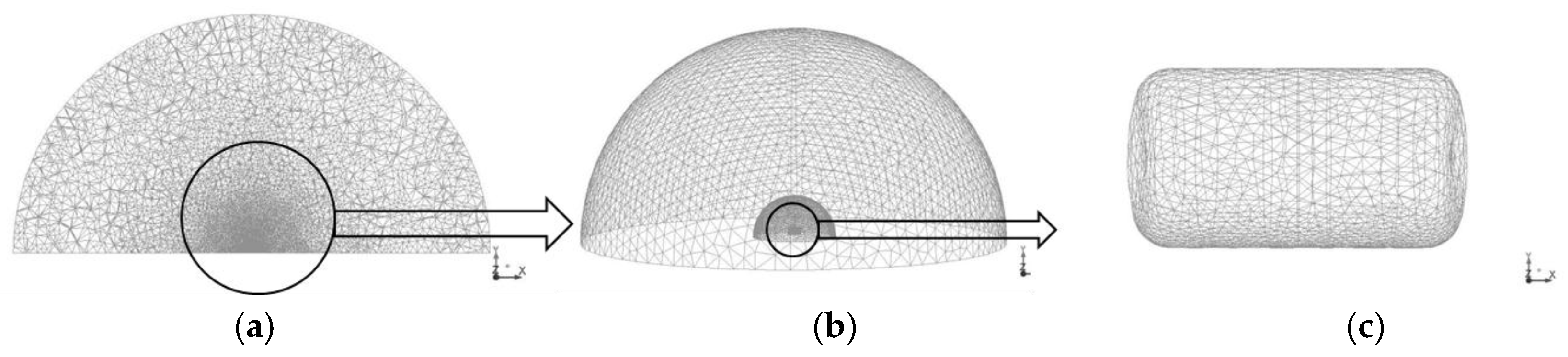
The computational domain is illustrated in Figure 1. The domain was a 100-m diameter hemisphere designed to account for both the blast wave and fireball propagation. In particular, a large domain was adopted in order to evaluate the hazard distance of blast wave. In this study, the domain was separated into the tank area (2-m diameter), fireball (10-m diameter), and blast wave (50-m diameter), because of variations between the generation rates of blast wave and fireball.

The hydrogen tank was meshed using a tetrahedral mesh with a control volume (CV) size varying from 0.010 m to 0.017 m. The domain for the tank area (area surrounding the tank) was a 2-m diameter hemisphere, and it was discretized by CVs of sizes ranging from 0.01 m to 0.10 m. The calculation domain for fireball propagation was a 10-m diameter hemisphere meshed using tetrahedral CVs of sizes ranging from 0.015 to 0.1 m. The rest of the domain was meshed using CVs of sizes ranging from 0.1–1.5 m. Blast wave generation is less sensitive than a fireball accompanied by combustion because hydrodynamic effects dominate during the generation. The total number of CVs was 944,868. In the simulations, the initial hydrogen mass fraction in the tank was set to Y_H2 = 1.0 and the initial pressure was set to p = 35 MPa. The ground was modeled as a non-slip impermeable adiabatic boundary. A far-field non-reflective boundary was set as the interface with the ambient atmosphere. ANSYS Fluent software was used as the computational fluid dynamics (CFD) platform. A coupled compressible solver with an explicit time stepping was used in the simulations with the Courant-Friedrichs-Lewy (CFL) number equal to 0.8. Convective terms were discretized using a second-order upwind scheme and diffusive terms were discretized using a second-order central difference scheme. Tank rupture was modeled as the instantaneous disappearance of the tank wall.

4. Results and Discussion

4.1. Blast Wave

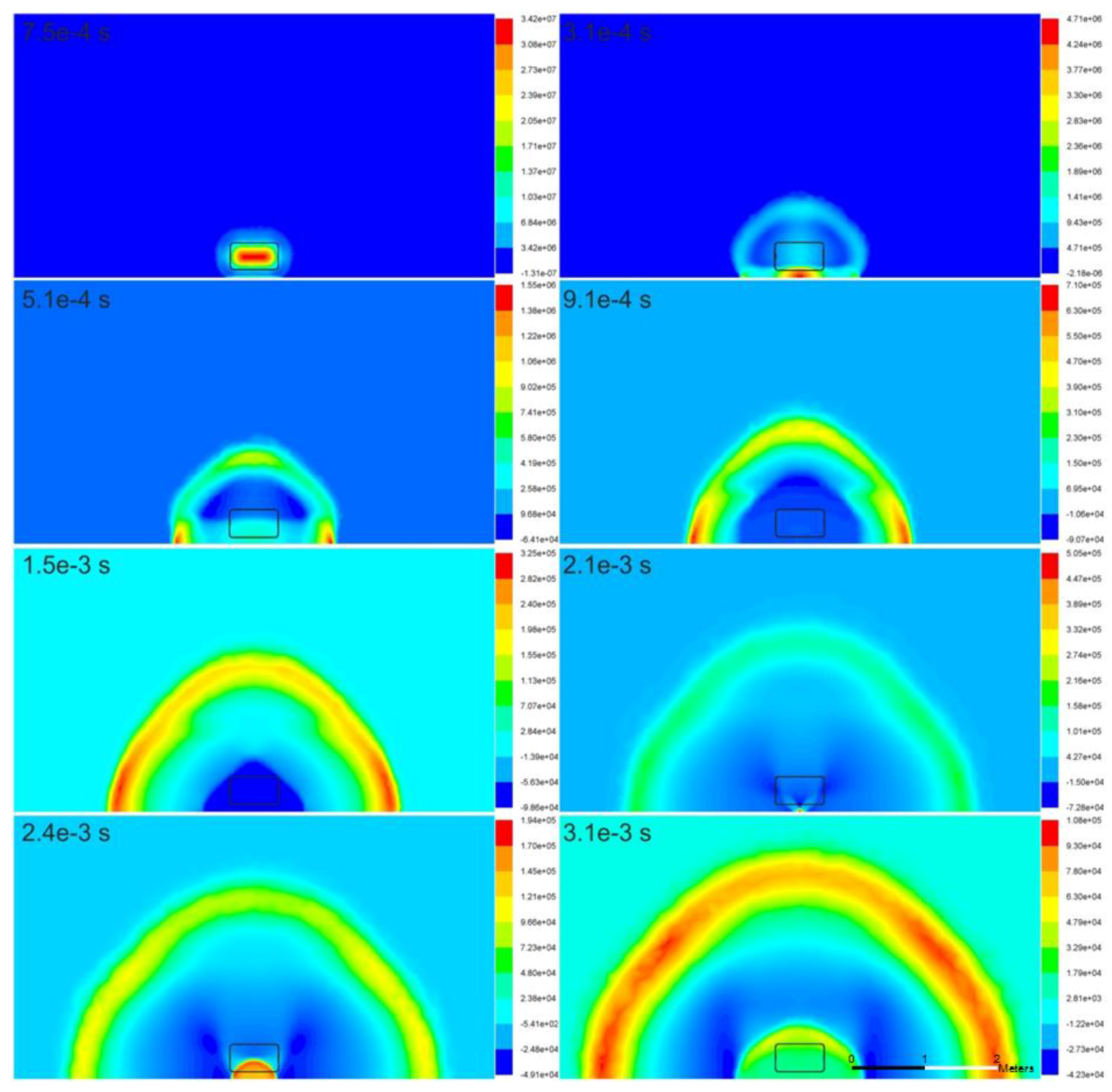
Figure 2 illustrates the pressure wave propagation at various moments in the tank area (area surrounding the tank) as a result of the rupture of the high-pressure hydrogen tank. After the tank rupture, the high pressure is instantaneously released. The initial shock propagates and is reflected from the ground. The reflected wave catches up with the head blast wave. The pressure decays rapidly due to spherical, and subsequently hemispherical expansion. The reproduced blast wave propagation exhibits the predicted physical behavior—the wave shape is generally hemispherical, with marginally larger overpressure formed in the vicinity of the ground (instances t = 5.1 × 10⁻⁴, 9.1 × 10⁻⁴, and 1.5 × 10⁻³ s). This is possibly owing to the stagnation conditions. Figure 2 (instance t = 3.1 × 10⁻⁴ s) also illustrates the formation of a secondary pressure wave, which, being reflected from the ground, provides the largest overpressure of approximately 47 bar at this instant. This wave continues to travel back and forth between the ground and hydrogen-air interface, providing high pressure at the focal point on the ground, e.g., approximately 5 bar overpressure at t = 2.1 × 10⁻³ s, which generates the next oscillation in the pressure wave propagating through hydrogen to approach the initial blast wave propagating through the air with a slower velocity.

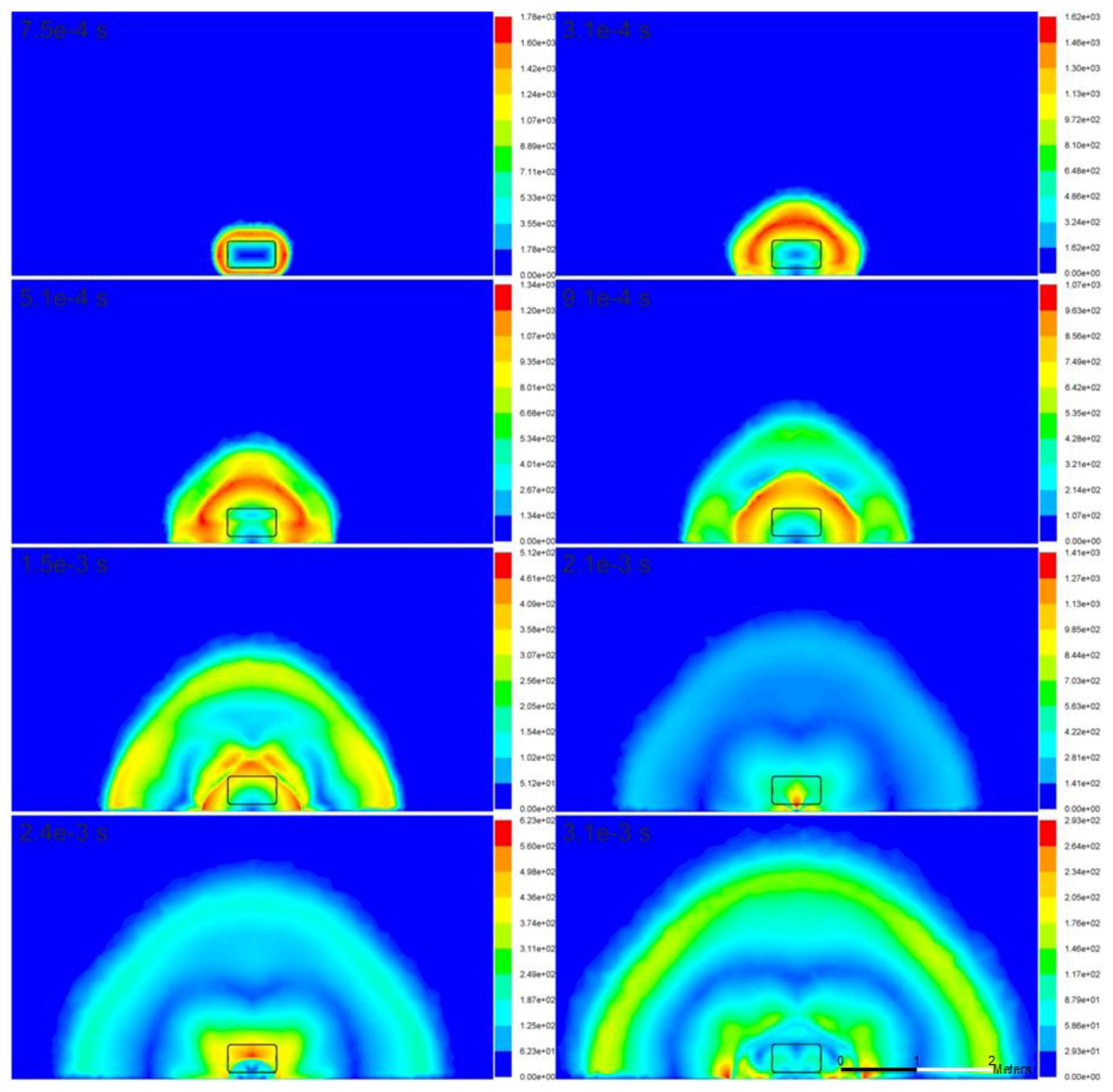
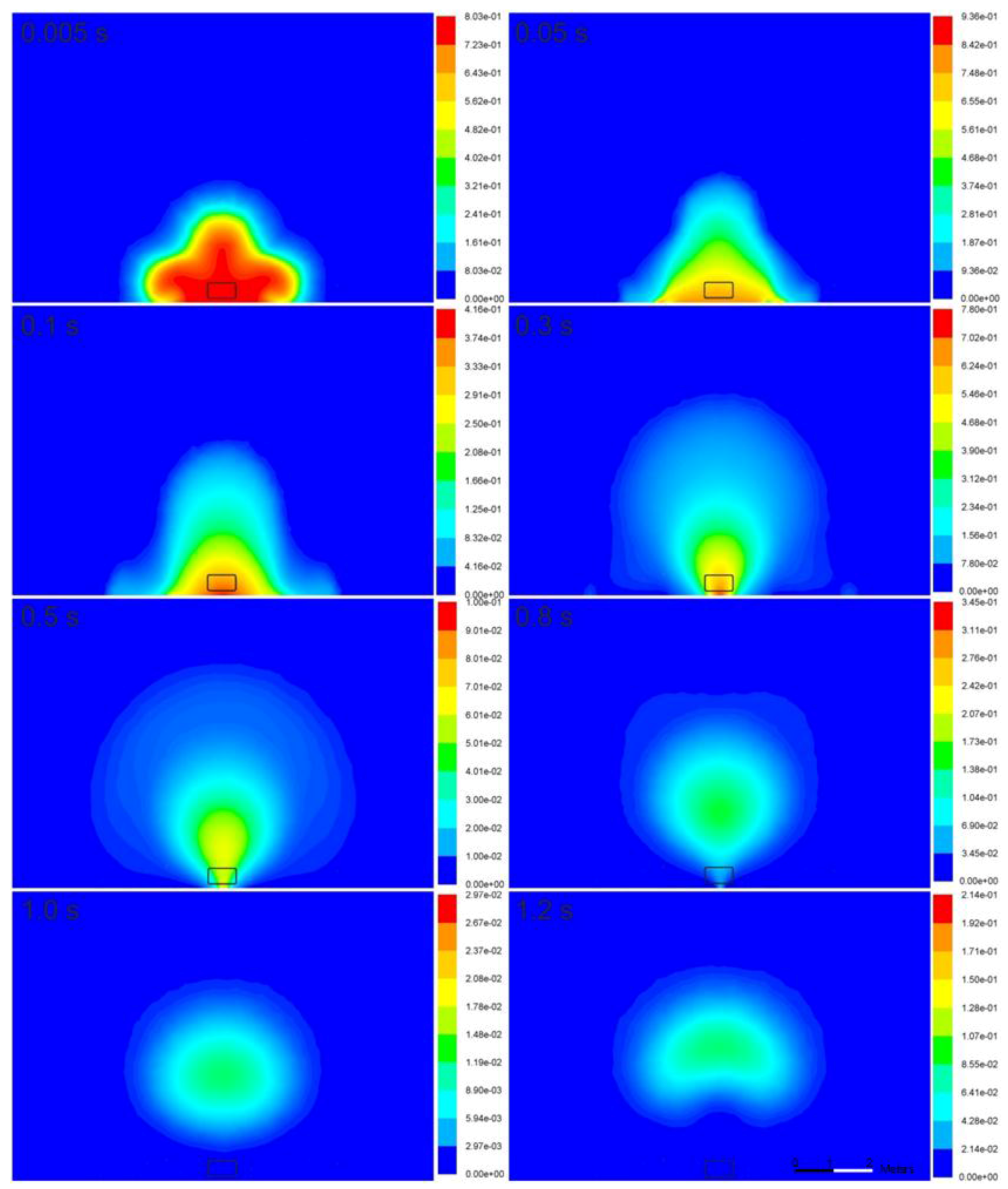
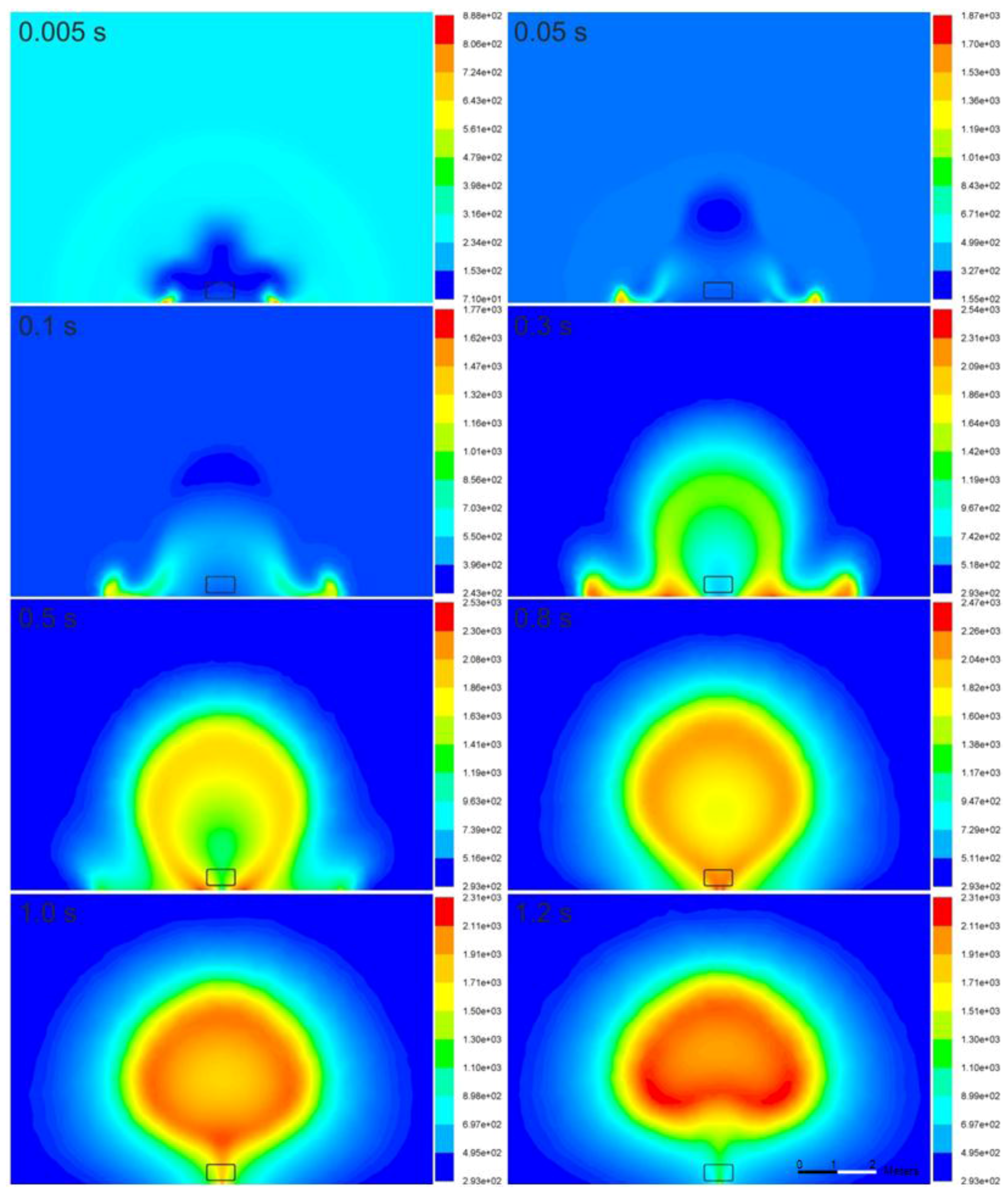
The variations in the temperature and velocity in the surrounding atmosphere due to the rupture of the high-pressure hydrogen tank are illustrated in Figure 3 and Figure 4, respectively. The temperature profiles are generally physical. Air temperature increases in the area of adiabatic compression due to the blast wave. Hydrogen, on the other hand, adiabatically expands, and its temperature reduces to below the ambient temperature. The contribution of combustion to temperature increase in these simulations is not large during the blast wave propagation through the domain, although the combustion model is formally engaged from the start of the simulations. As a result, the largest temperatures are observed in the area of flow stagnation and pressure wave reflection in the vicinity of the ground. Thus, the maximum temperature on the ground increases to 1750 K at t = 3.1 × 10⁻⁴ s. It can be observed that although the high-temperature profile coincides with the blast wave propagation and is generally hemispherical, the low temperature area of the expanding hydrogen envelope is not hemispherical. The low temperature area exhibits preferential propagation direction along the longitudinal and transverse tank axes, and the authors consider that this is, to a certain extent, the result of the cylindrical shape of the high-pressure hydrogen charge and the effect of buoyancy.

The velocity profile reflects the development of the blast wave during the high-pressure hydrogen expansion. Initially, the expansion provides a single high-velocity profile, which is visible in Figure 4 at t = 7.5 × 10⁻⁵ s and t = 3.1 × 10⁻⁴ s. At t = 5.1 × 10⁻⁴ s, the velocity profile is affected by the reflection wave travelling through hydrogen between the interface with the heavier air and the ground. The maximum velocity of 1780 m/s is observed as anticipated at the beginning of the process (t = 7.5 × 10⁻⁴ s in Figure 4), when the pressure in the blast wave is maximum (starting shock).

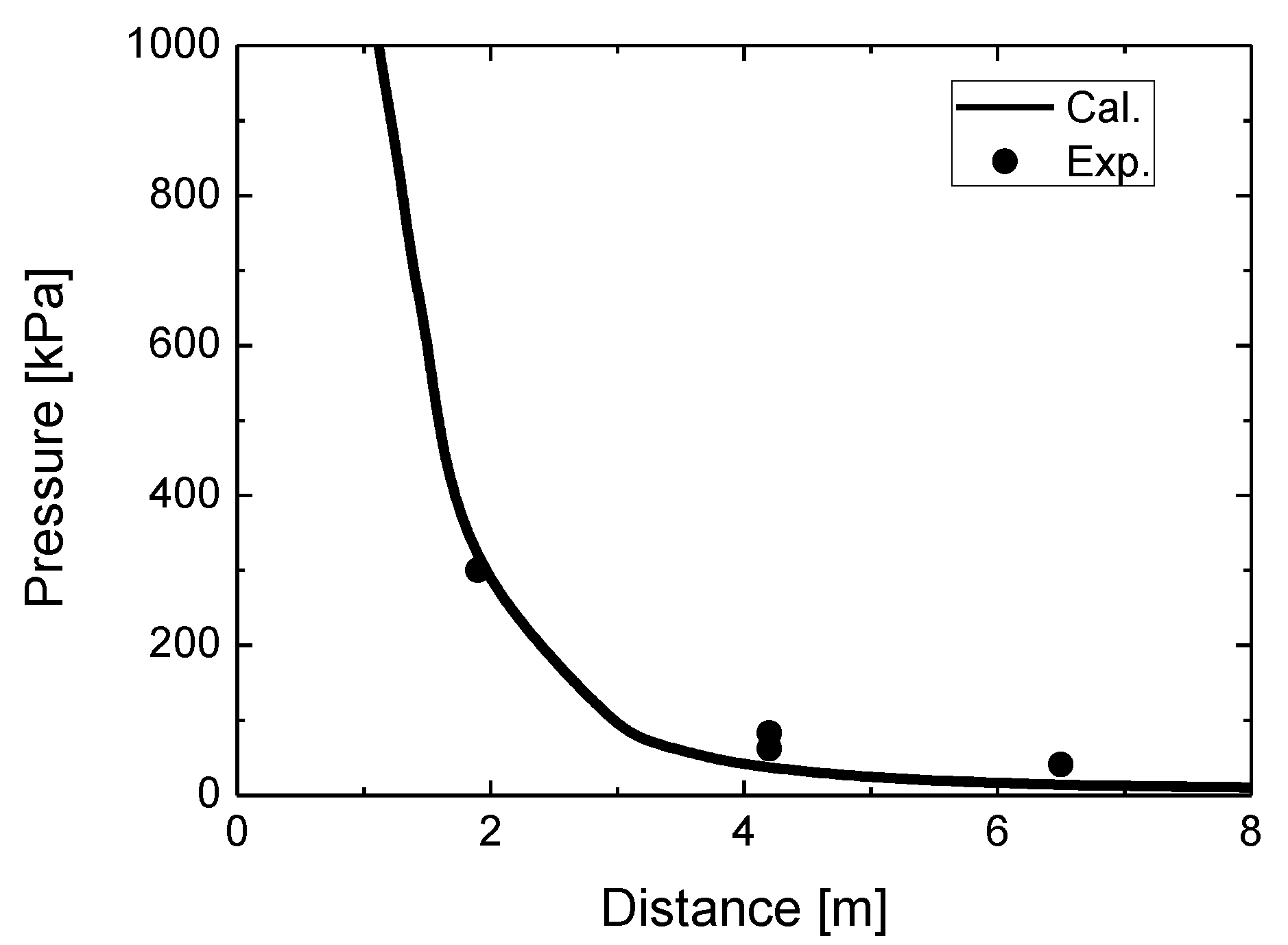
Figure 5 compares the simulated overpressure in the blast wave with the experimental overpressure at various distances for the stand-alone tank test. The simulated overpressure at 1.9 m is practically equal to the experimental value. However, the simulated values at 4.2 m and 6.5 m underestimate the measured overpressures. A probable cause of this underestimation is the insufficient contribution of combustion to the blast wave strength.

4.2. Fireball

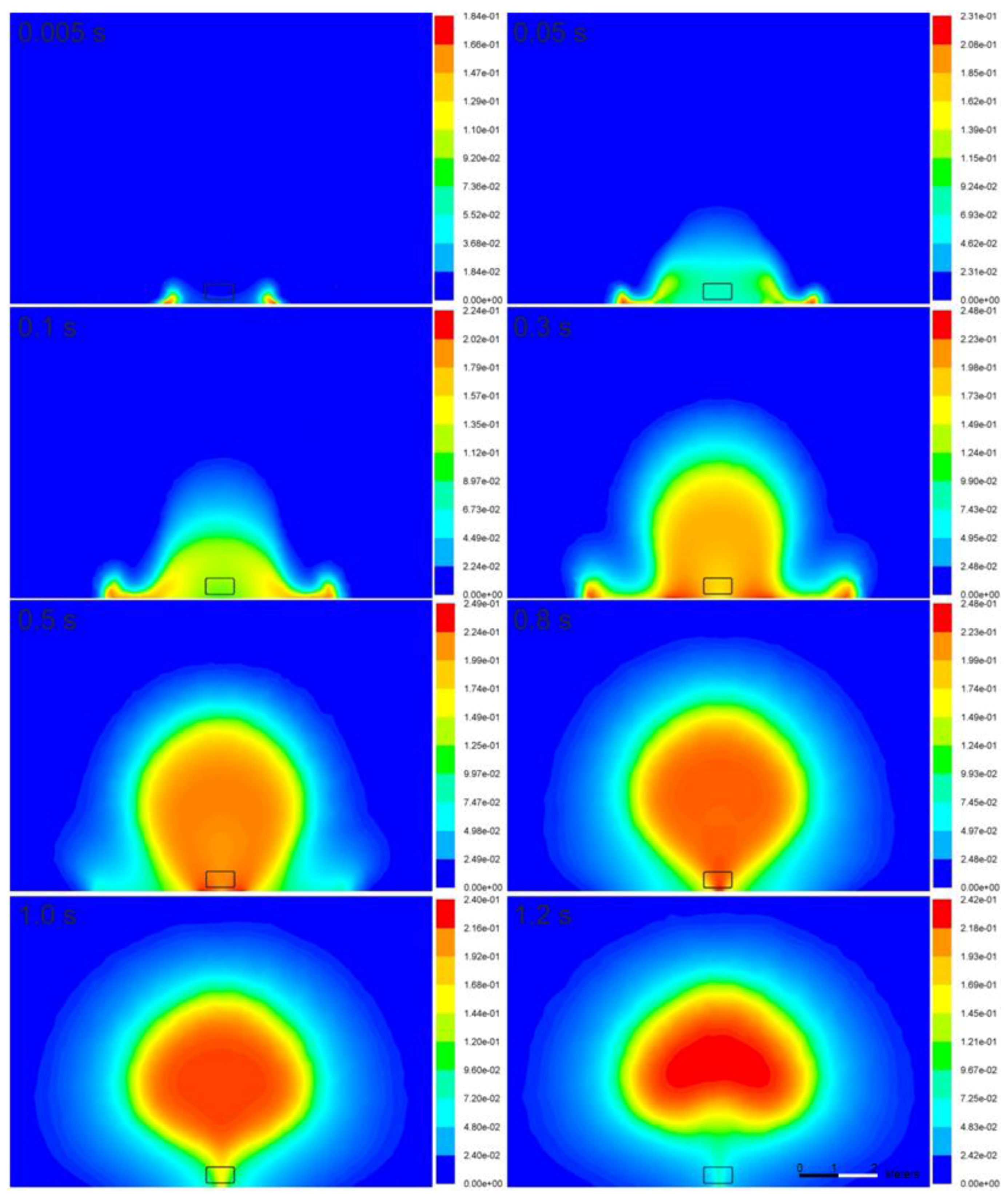
During the blast wave propagation, the fireball is formed behind the shock as a result of the mixing of hydrogen and air behind the contact surface. Because of the heat released by combustion and the buoyancy force acting on hydrogen, the fireball lifts up from the ground at later stages of the process, when the blast leaves the calculation domain (Figure 6). The surrounding air mixes with the hydrogen cloud owing to intensive convection and turbulent diffusion processes, and the remaining hydrogen burns continuously in the surrounding air. Figure 6 illustrates the hydrogen mass fraction in the fireball. At the initial stage of the rapid hydrogen expansion, i.e., t = 0–5.1 × 10⁻³ s, combustion practically has negligible effect, and its role becomes apparent later at approximately t = 5.0 × 10⁻³ s. Hydrogen concentration starts to decrease owing to combustion, beginning with the area of intensive hydrogen-air mixing at the hydrogen-air interface, while it remains unchanged at the ground (see t = 0.1–0.3 s in Figure 6). Once the reacting hydrogen cloud (fireball) is affected by the buoyancy force, mixing with air and combustion start to occur in the vicinity of the ground as well (t = 0.3–0.5 s). The fireball development progresses, and it assumes the shape characteristic of a thermic attached to the ground by a narrow “leg” (t = 0.5–0.8 s). Then, the “leg” burns completely, and the mushroom-shaped fireball continues to burn in the air and rise upward (t = 1.0–1.2 s).

Figure 7 and Figure 8 illustrate the time-dependence of the temperature and mass fraction of water vapor in the fireball cross-section. In the simulations, the flame is initiated in the vicinity of the ground, where the stagnation conditions and highest generation of turbulence (vorticity) exist, resulting in the combustion rate presented in Equations (7) and (8). On the other hand, in the experiment, the source of ignition is the bonfire test burner. The flame propagates to the area of unburned hydrogen at the initial location of the tank. Then, the flame assumes a more spherical shape at 0.8 s and is lifted off the ground 1.2 s after the tank rupture. The temperature of the fireball on the ground increases to 2540 K at 0.3 s, and the fireball becomes hemispherical. Its cross-section resembles the characteristic mushroom-shape.

The calculated maximum diameter of the fireball is 5.3 m at 1.0 s, which is moderately below the experimentally determined size—7.7 m [8]. A probable cause of this is the insufficient combustion intensity at the beginning of the process, as mentioned previously. Experimental images [9] suggest that the inhomogeneous luminosity of fireball is possibly caused by the combustion of tank debris and the presence of the surrounding dust within the hydrogen envelope. These “additional” fuels could significantly affect the luminosity of the observed flame, which may be another cause of the larger visible fireball size reported in experiments.

5. Concluding Remarks

The blast wave and fireball formed after the high-pressure (35 MPa) hydrogen tank (72 L) rupture due to fire have been simulated. The CFD model is based on the realizable k-ε model for turbulence, and the eddy dissipation model for combustion. These pilot simulations reproduced general experimental observations in a stand-alone cylindrical hydrogen tank, including the blast wave decay with distance. Reflected pressure waves travelling through the expanding hydrogen back and forth between the ground and the hydrogen-air interface were reproduced in the simulations. Combustion had negligible effect during the initial stage of hydrogen expansion, and the maximum temperature reached 1750 K at time t = 3.1 × 10⁻⁴ s. Hydrogen expansion was considered to be affected by the cylindrical shape of the hydrogen tank, with preferential expansion directions along the main and transversal tank axes.

The simulation results of the fireball indicate that the blast wave and combustion develop in these simulations in dissimilar time scales, as most of the combustion occurred after the blast wave propagated to a large distance from the tank location. In the simulations, the flame was initiated in the vicinity of the ground, and it then propagated along the hydrogen-air mixing interface. The flame assumed a spherical shape at 0.8 s, and lifted off the ground at 1.2 s; this phenomenon is similar to the experimental observations.

While the simulated overpressure at 1.9 m agrees adequately with the measured overpressure, the simulated values at 4.2 m and 6.5 m are more or less underestimated. This is considered to be caused by insufficient combustion intensity at the beginning of the process. This is in agreement with the observation that the maximum diameter of the simulated fireball is approximately 5 m at 1 s, although the maximum measured fireball size is approximately 7.7 m at 0.045 s. A probable cause of this variation is the contribution of various fuels and particles—such as polyethylene and resin decomposition products and fragments of carbon fibers—and ground and atmospheric dust, whose combustion and luminosity are not accounted for in simulations.

It is recommended that future work be focused on the study of various combustion models and the effect of the real gas equation and radiation on the parameters of the blast wave and fireball.