A Green’s Function Molecular Dynamics Approach to the Mechanical Contact between Thin Elastic Sheets and Randomly Rough Surfaces
Abstract
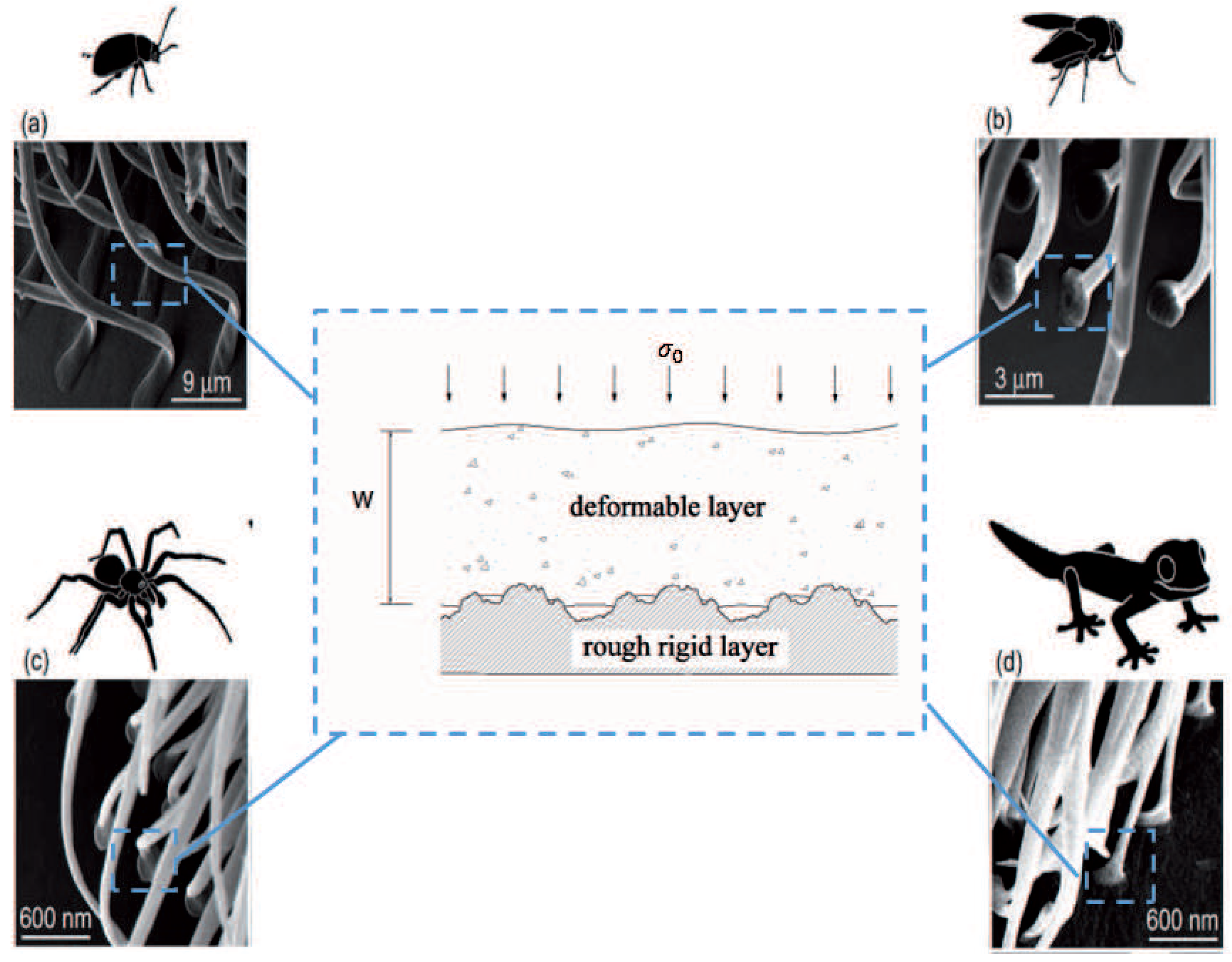
:1. Introduction
2. Materials and Methods
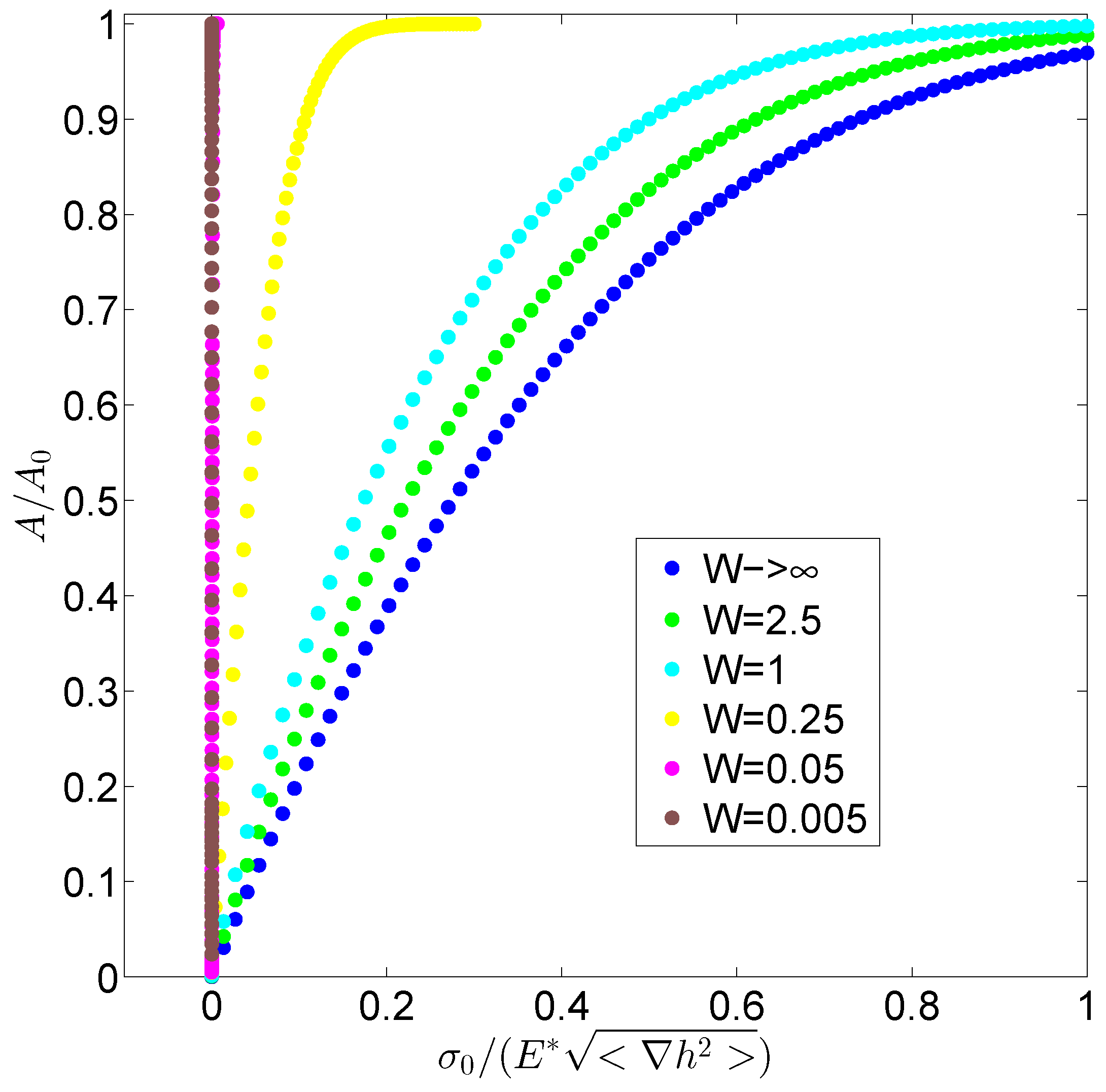
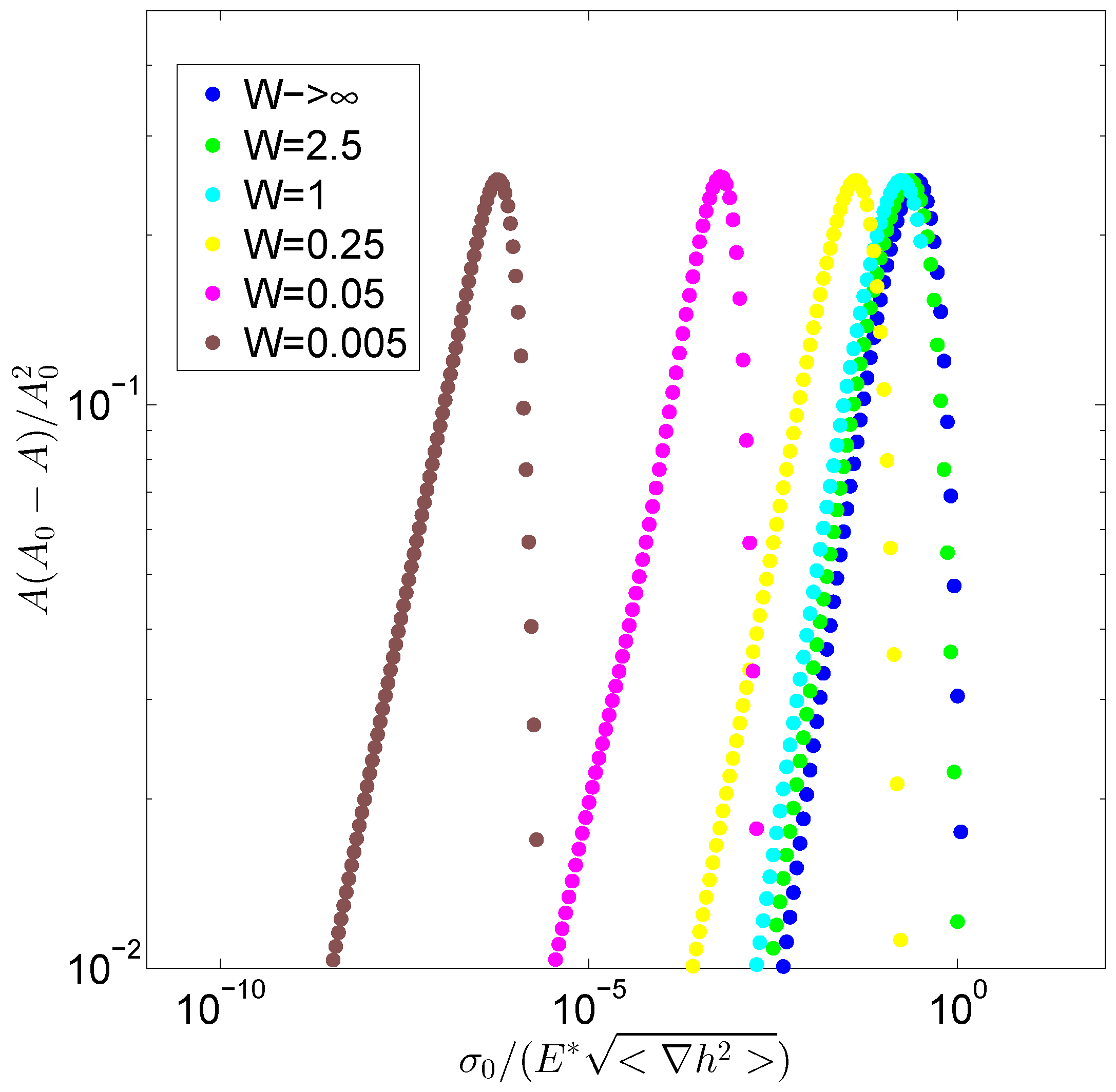
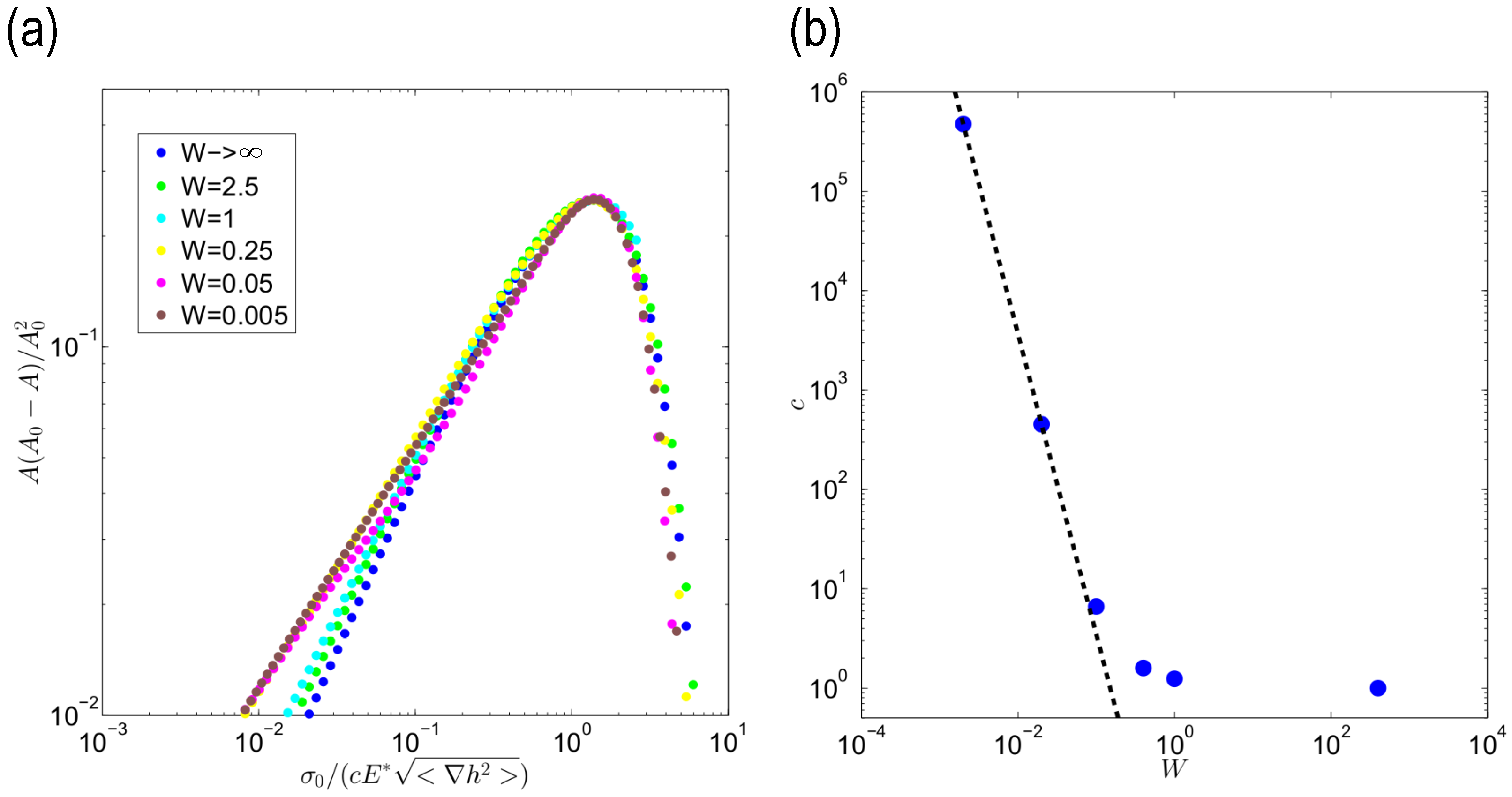
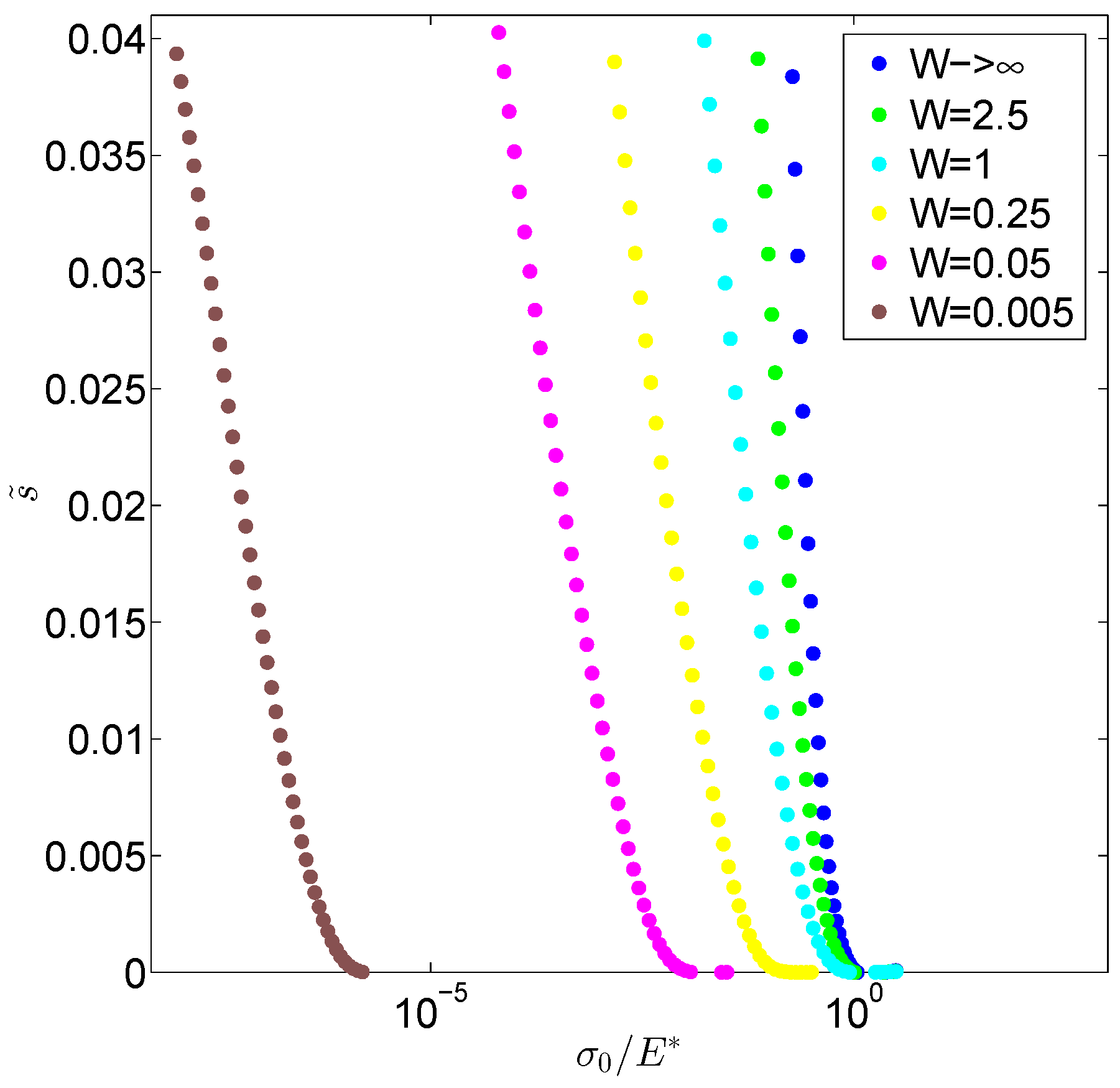
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Geim, A.K.; Dubonos, S.V.; Gricorieva, I.V.; Novoselov, K.S.; Zhukov, A.A.; Shapoval, S. Microfabricated adhesive mimicking gecko foot-hair. Nat. Mater. 2003, 2, 461–463. [Google Scholar] [CrossRef] [PubMed]
- Carbone, G.; Mangialardi, L. Adhesion and friction of an elastic half-space in contact with a slightly wavy rigid surface. J. Mech. Phys. Solids 2004, 52, 1267–1287. [Google Scholar] [CrossRef]
- Carbone, G.; Pierro, E.; Gorb, S. Origin of the superior adhesive performance of mushroom shaped microstructured surfaces. Soft Matter 2011, 7, 5545–5552. [Google Scholar] [CrossRef]
- Carbone, G.; Pierro, E. Sticky bio-inspired micropillars: Finding the best shape. SMALL 2012, 8, 1449–1454. [Google Scholar] [CrossRef] [PubMed]
- Carbone, G.; Pierro, E. Effect of interfacial air entrapment on the adhesion of bio-inspired mushroom-shaped micro-pillars. Soft Matter 2012, 8, 7904–7908. [Google Scholar] [CrossRef]
- Afferrante, L.; Carbone, G.; Pugno, D.N. Adhesion of Elastic Thin Films: Double Peeling of Tapes Versus Axisymmetric Peeling of Membranes. Tribol. Lett. 2013. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Mangialardi, L.; Carbone, G. Equilibrium states and stability of pre-tensioned adhesive tapes Beilstein. J. Nanotechnol. 2014, 5, 1725–1731. [Google Scholar]
- Varenberg, M.; Pugno, N.M.; Gorb, S.N. Spatulate structures in biological fibrillar adhesion. Soft Matter 2010, 6, 3269–3272. [Google Scholar] [CrossRef]
- Kendall, K. The adhesion and surface energy of elastic solids. J. Phys. D Appl. Phys. 1971, 4, 1186–1195. [Google Scholar] [CrossRef]
- Paggi, M.; Reinoso, J. An anisotropic large displacement cohesive zone model for fibrillar and crazing interfaces. Int. J. Solids Struct. 2015, 69, 106–120. [Google Scholar] [CrossRef]
- Borri, C.; Paggi, M.; Reinoso, J.; Borodich, F.M. Adhesive behaviour of bonded paper layers: Mechanical testing and statistical modelling. Proc. Inst. Mech. Eng. Part C 2016, 230, 1440–1448. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Greenwood, J.A. A simplified elliptic model of rough surface contact. Wear 2006, 261, 191–200. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Putignano, C.; Ciavarella, M. A Greenwood & Williamson theory for line contact. Wear 2011, 270, 332–334. [Google Scholar]
- Bush, A.W.; Gibson, R.D.; Thomas, T.R. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Ciavarella, M.; Delfine, V.; Demelio, G. A “re-vitalized” Greenwood and Williamson model of elastic contat between fractal surfaces. J. Mech. Phys. Solids 2006, 54, 2569–2591. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Persson, B.N.J. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. The influence of the statistical properties of self-affine surfaces in elastic contact: A numerical investigation. J. Mech. Phys. Solids 2012, 60, 973–982. [Google Scholar] [CrossRef]
- Dapp, W.B.; Prodanov, N.; Müser, M.H. Systematic analysis of Persson’s contact mechanics theory of randomly rough elastic surfaces. J. Phys. Condens. Matter 2014, 26, 355002. [Google Scholar] [CrossRef] [PubMed]
- Hyun, S.; Pei, L.; Molinari, J.-F.; Robbins, M.O. Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E 2004, 70, 026117. [Google Scholar] [CrossRef] [PubMed]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. A new efficient numerical method for contact mechanics of rough surfaces. Int. J. Solids Struct. 2012, 49, 338–343. [Google Scholar] [CrossRef]
- Geike, T.; Popov, V.L. Mapping of three-dimensional contact problems into one dimension. Phys. Rev. E 2007, 76, 036710. [Google Scholar] [CrossRef] [PubMed]
- Paggi, M.; Ciavarella, M. The coefficient of proportionality between real contact area and load, with new asperity models. Wear 2010, 268, 1020–1029. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. A novel methodology to predict sliding/rolling friction in viscoelastic materials: Theory and experiments. J. Mech. Phys. Solids 2013, 61, 1822–1834. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. Rough viscoelastic sliding contact: Theory and experiments. Phys. Rev. E 2014, 89, 032408. [Google Scholar] [CrossRef] [PubMed]
- Putignano, C.; Carbone, G.; Dini, D. Theory of reciprocating contact for viscoelastic solids. Phys. Rev. E 2016, 93, 043003. [Google Scholar] [CrossRef] [PubMed]
- Borri, C.; Paggi, M. Topological characterization of antireflective and hydrophobic rough surfaces: Are random process theory and fractal modeling applicable? J. Phys. D Appl. Phys. 2015, 48, 045301. [Google Scholar] [CrossRef]
- Yang, C.; Persson, B.N.J. Molecular Dynamics Study of Contact Mechanics: Contact Area and Interfacial Separation from Small to Full Contac. Phys. Rev. Lett. 2008, 100, 024303. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Tartaglino, U.; Persson, B.N.J. A multiscale molecular dynamics approach to contact mechanics. Eur. Phys. J. E 2006, 19, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Campana, C.; Muser, M.H. Contact mechanics of real vs. randomly rough surfaces: A Green’s function moleculardynamics study. Europhys. Lett. 2007, 77, 38005. [Google Scholar] [CrossRef]
- Hyun, S.; Robbins, M.O. Elastic contact between rough surfaces: Effect of roughness at large and small wavelengths. Tribol. Int. 2007, 40, 413–1422. [Google Scholar] [CrossRef]
- Luan, B.Q.; Hyun, S.; Molinari, J.F.; Bernstein, N.; Robbins, M.O. Multiscale modeling of two-dimensional contacts. Phys. Rev. E 2006, 74, 046710. [Google Scholar] [CrossRef] [PubMed]
- Campañá, C.; Müser, M.H. Practical Green’s function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B 2006, 74, 075420. [Google Scholar] [CrossRef]
- Pastewka, L.; Sharp, T.A.; Robbins, M.O. Seamless elastic boundaries for atomistic calculations. Phys. Rev. B 2012, 86, 075459. [Google Scholar] [CrossRef]
- Prodanov, N.; Dapp, W.B.; Muser, M.H. On the contact area and mean gap of rough, elastic contacts: Dimensional analysis, numerical corrections and reference data. Tribol. Lett. 2014, 53, 433–448. [Google Scholar] [CrossRef]
- Carbone, G.; Lorenz, B.; Persson, N.J.; Wohlers, A. Contact mechanics and rubber friction for randomly rough surfaces with anisotropic statistical properties. Eur. Phys. J. E 2009, 29, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Carbone, G.; Mangialardi, L.; Persson, B.N.J. Adhesion between a thin elastic plate and a hard randomly rough substrate. Phys. Rev. B 2014, 70, 125407. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon: London, UK, 1959. [Google Scholar]
- Müser, M.N. A dimensionless measure for adhesion and effects of the range of adhesion in contacts of nominally flat surfaces. Tribol. Int. 2015. [Google Scholar] [CrossRef]
- Scaraggi, M.; Putignano, C.; Carbone, G. Elastic contact of rough surfaces: A simple criterion to make 2D isotropic roughness equivalent to 1D one. Wear 2013, 297, 1811–817. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G.; Dini, D. Mechanics of rough contacts in elastic and viscoelastic thin layers. Int. J. Solids Struct. 2015, 69, 507–517. [Google Scholar] [CrossRef]
- Campana, C.; Persson, B.N.J.; Mueser, M.H. Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys. 2011, 23, 085001. [Google Scholar]

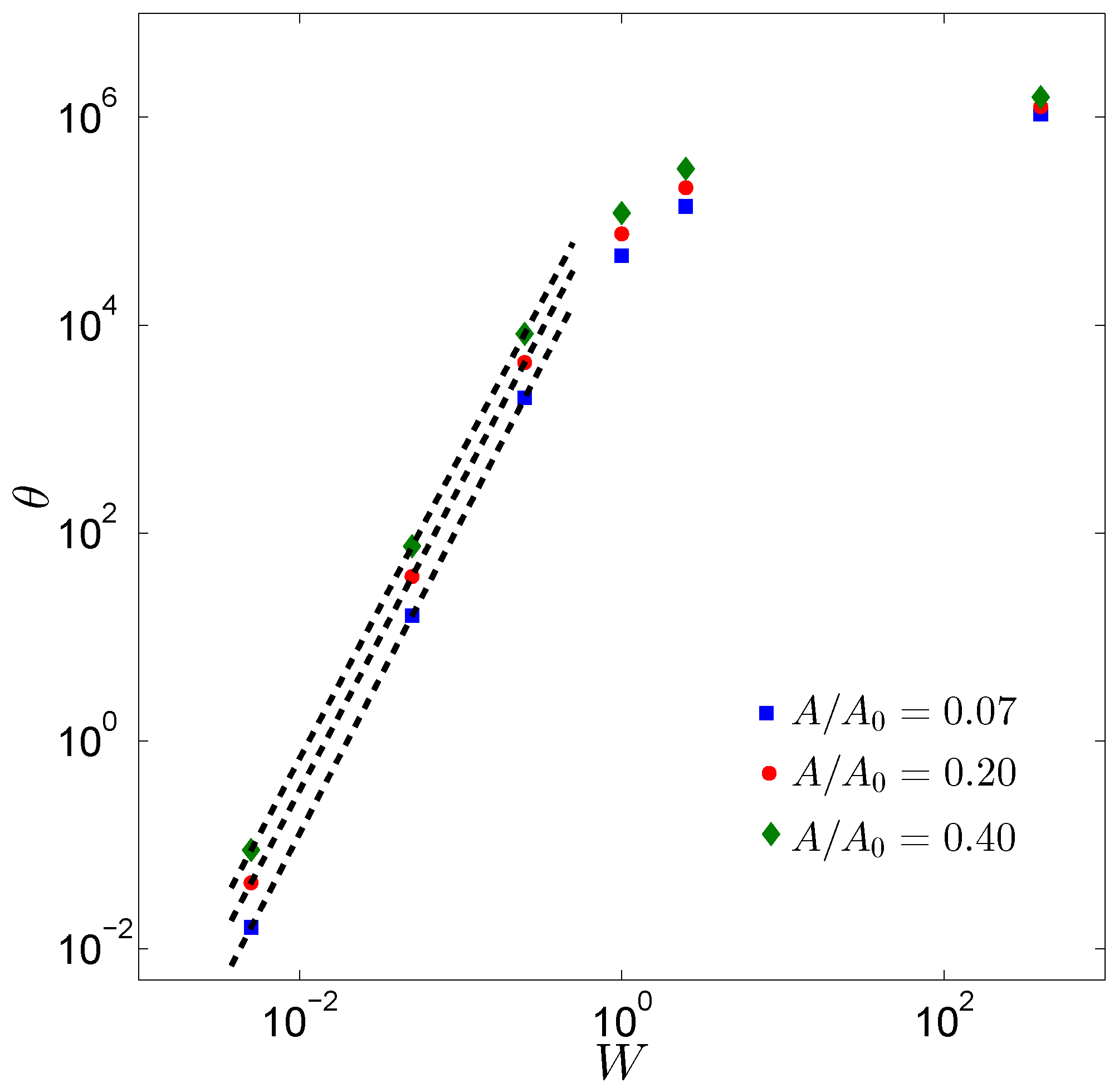
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putignano, C.; Dapp, W.B.; Müser, M.H. A Green’s Function Molecular Dynamics Approach to the Mechanical Contact between Thin Elastic Sheets and Randomly Rough Surfaces. Biomimetics 2016, 1, 7. https://doi.org/10.3390/biomimetics1010007
Putignano C, Dapp WB, Müser MH. A Green’s Function Molecular Dynamics Approach to the Mechanical Contact between Thin Elastic Sheets and Randomly Rough Surfaces. Biomimetics. 2016; 1(1):7. https://doi.org/10.3390/biomimetics1010007
Chicago/Turabian StylePutignano, Carmine, Wolf B. Dapp, and Martin H. Müser. 2016. "A Green’s Function Molecular Dynamics Approach to the Mechanical Contact between Thin Elastic Sheets and Randomly Rough Surfaces" Biomimetics 1, no. 1: 7. https://doi.org/10.3390/biomimetics1010007
APA StylePutignano, C., Dapp, W. B., & Müser, M. H. (2016). A Green’s Function Molecular Dynamics Approach to the Mechanical Contact between Thin Elastic Sheets and Randomly Rough Surfaces. Biomimetics, 1(1), 7. https://doi.org/10.3390/biomimetics1010007






