Hyperonic Interactions in Neutron Stars
Abstract
:1. Introduction
2. Methods
2.1. Skyrme Potential
2.2. Neutron Star Matter and Tidal Deformability
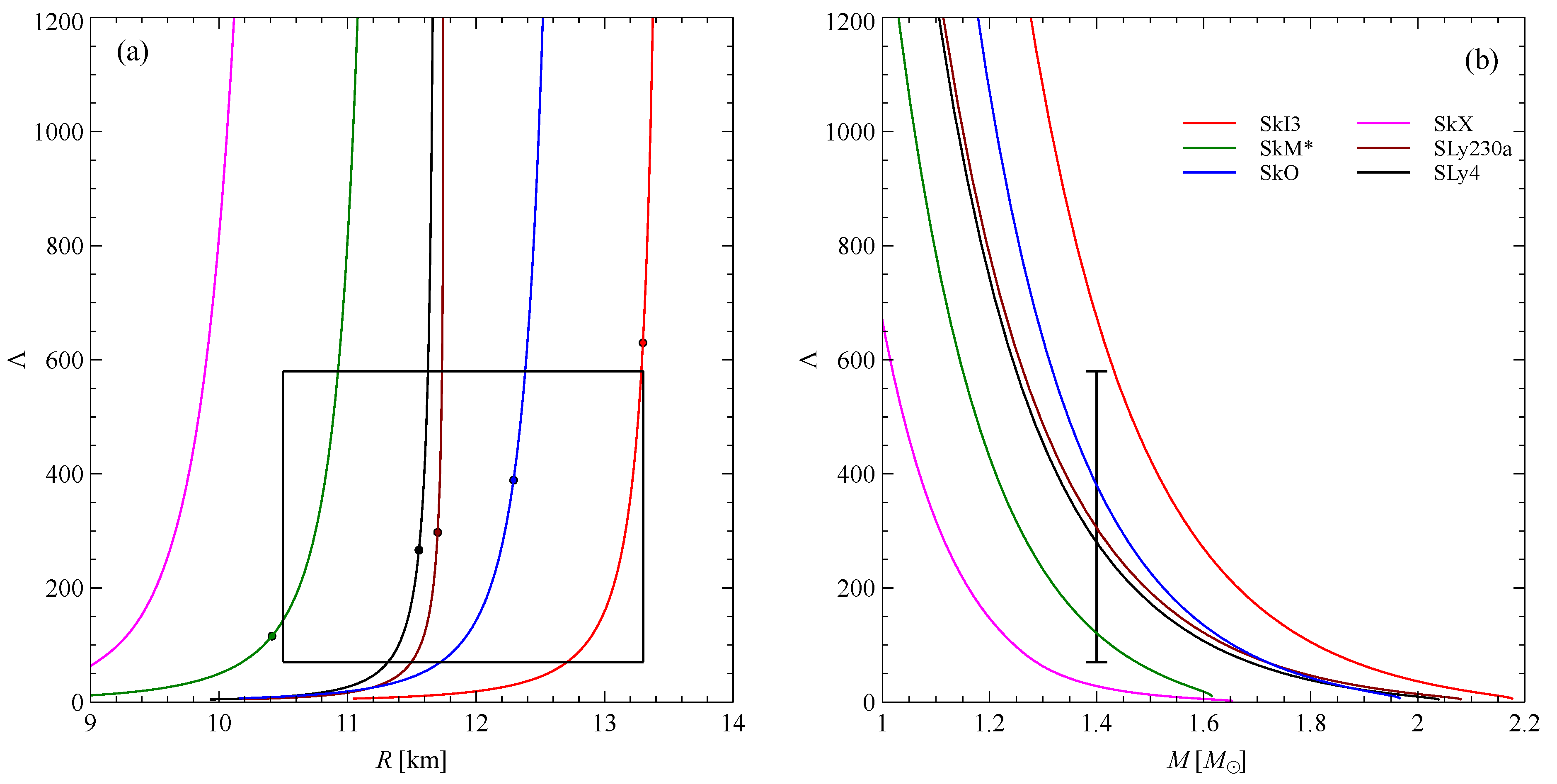
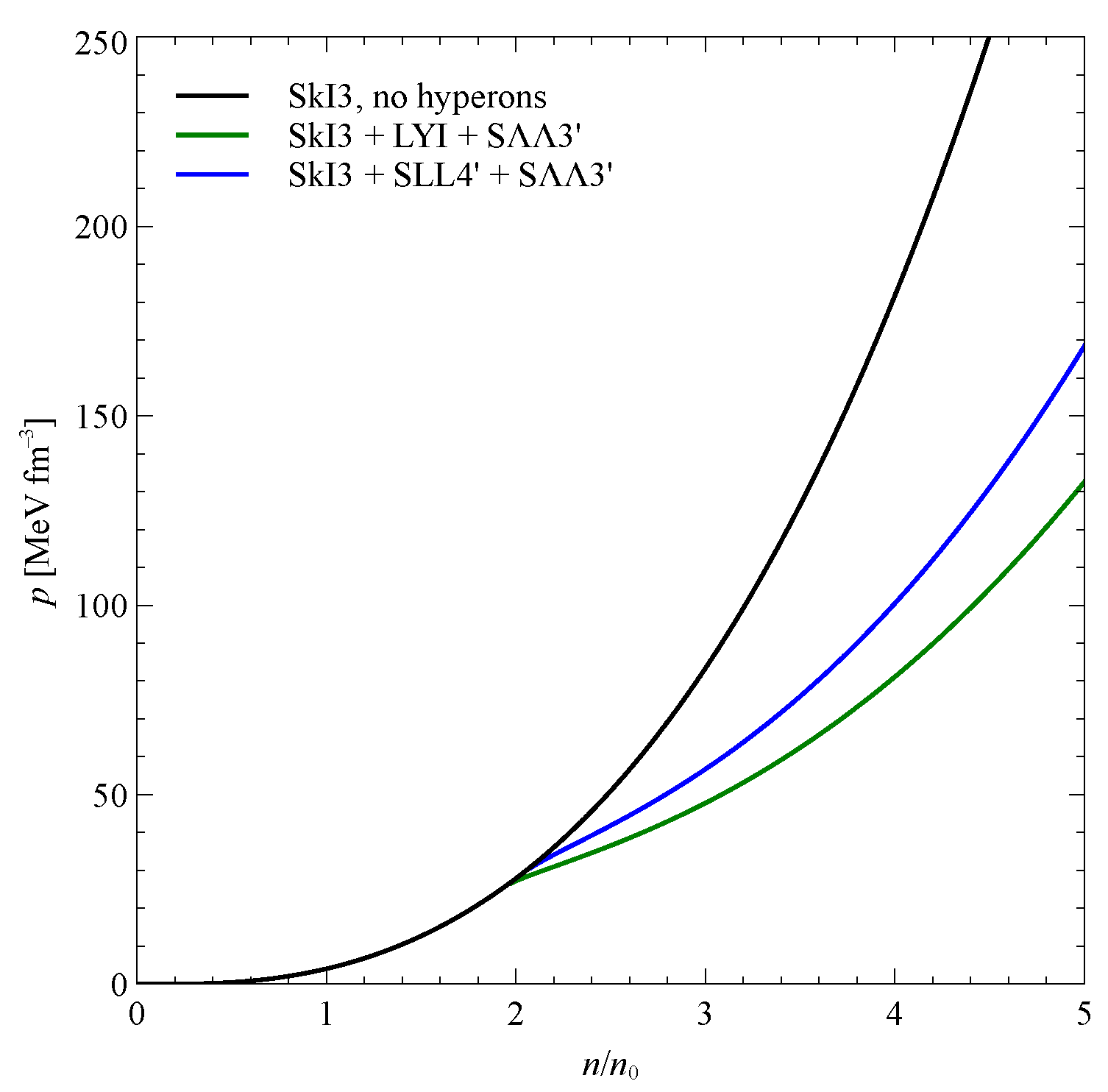
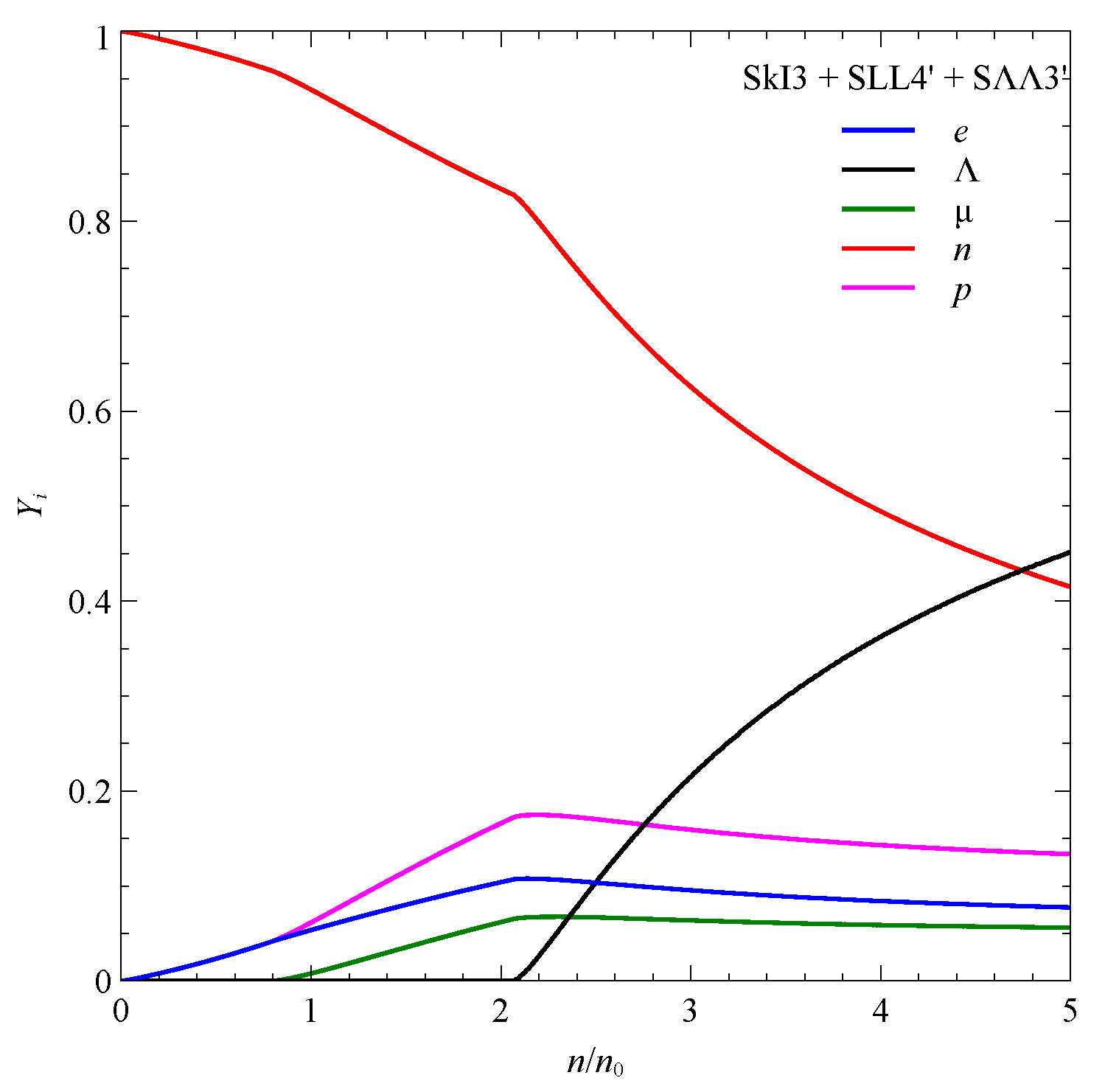
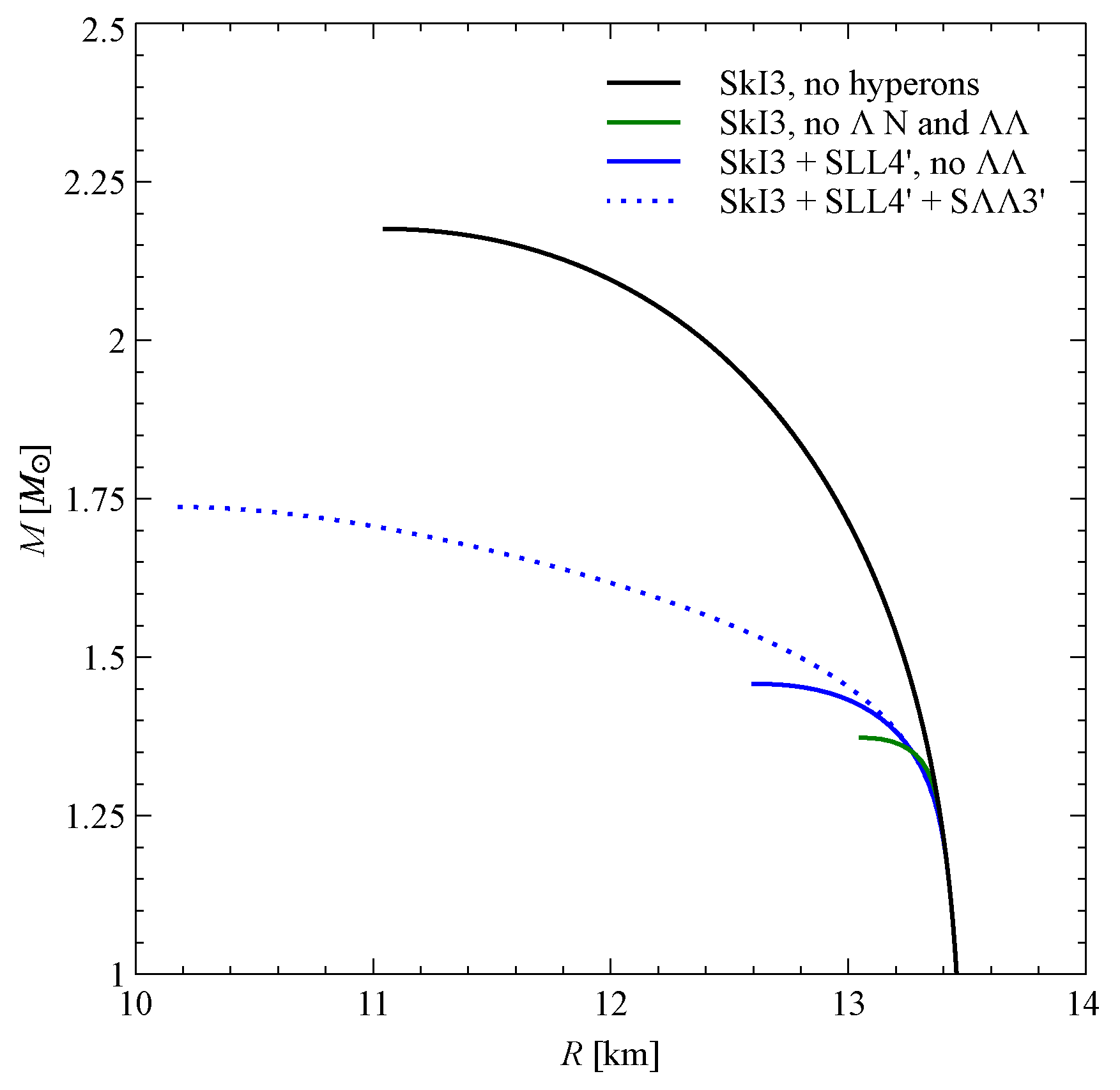
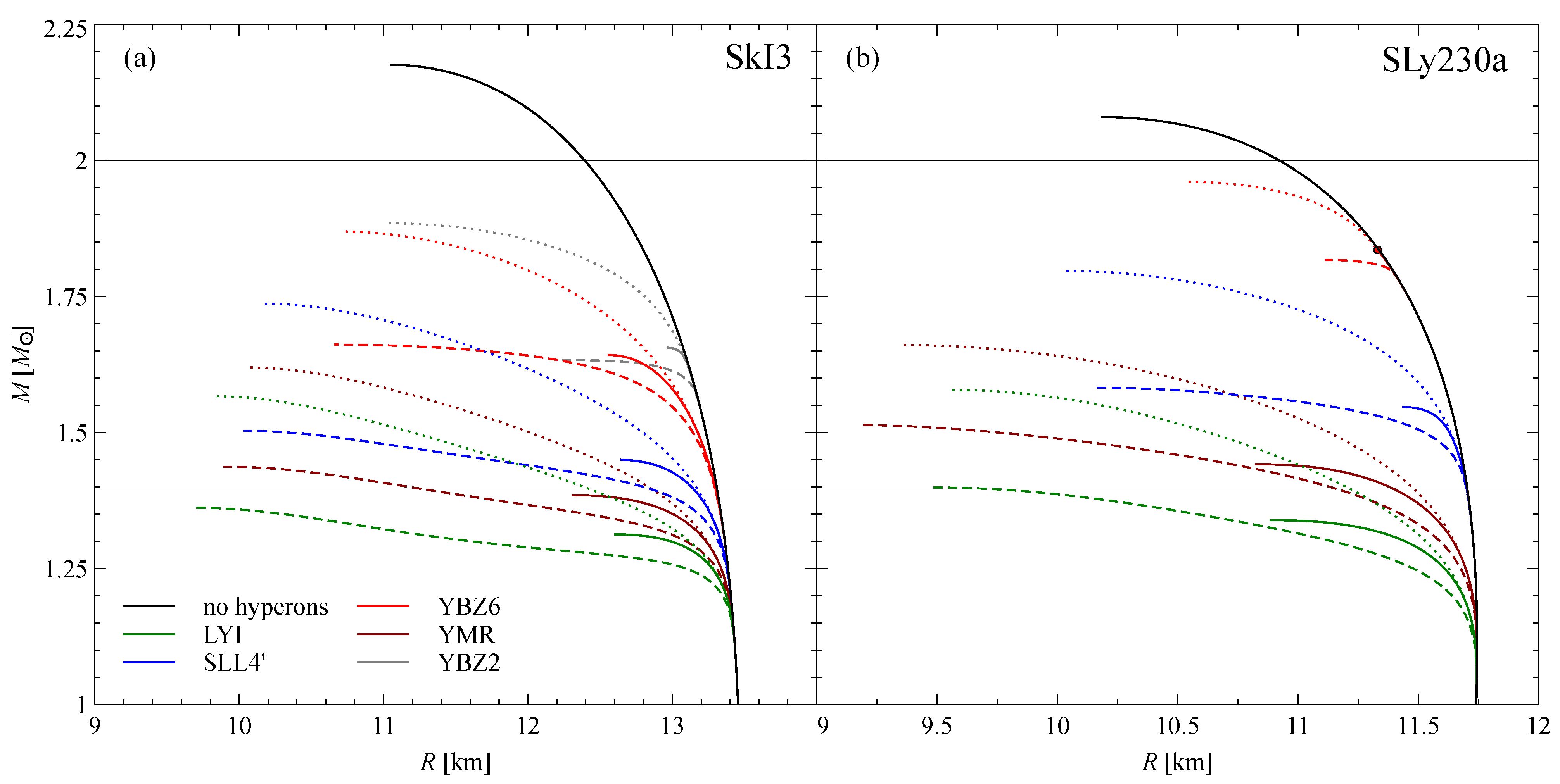
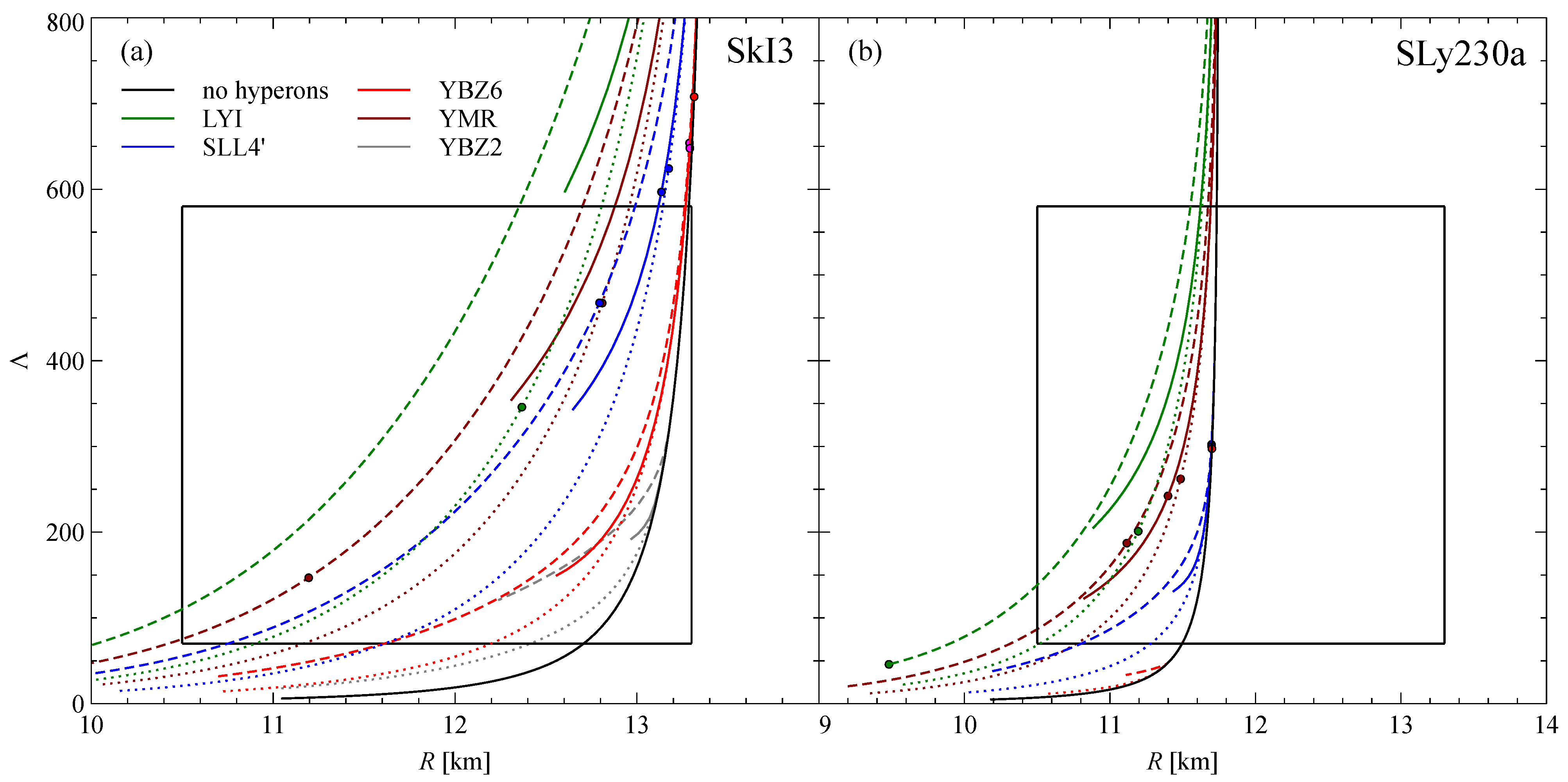
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952–0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Salmi, T.; Vinciguerra, S.; Choudhury, D.; Riley, T.E.; Watts, A.L.; Remillard, R.A.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Arzoumanian, Z.; et al. The Radius of PSR J0740+6620 from NICER with NICER Background Estimates. Astrophys. J. 2022, 941, 150. [Google Scholar] [CrossRef]
- Bombaci, I. The Hyperon Puzzle in Neutron Stars. J. Phys. Soc. Jpn. Conf. Proc. 2017, 17, 101002. [Google Scholar] [CrossRef]
- Friedman, E.; Gal, A. Constraints from Λ hypernuclei on the ΛNN content of the Λ-nucleus potential. Phys. Lett. B 2023, 837, 137669. [Google Scholar] [CrossRef]
- Vidaña, I. Neutron stars and the hyperon puzzle. EPJ Web Conf. 2022, 271, 09001. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Yamamoto, Y. Necessity of extra repulsion in hypernuclear systems: Suggestion from neutron stars. Eur. Phys. J. A 2002, 13, 213–215. [Google Scholar] [CrossRef]
- Lonardoni, D.; Lovato, A.; Gandolfi, S.; Pederiva, F. Hyperon Puzzle: Hints from Quantum Monte Carlo Calculations. Phys. Rev. Lett. 2015, 114, 092301. [Google Scholar] [CrossRef]
- Gerstung, D.; Kaiser, N.; Weise, W. Hyperon–nucleon three-body forces and strangeness in neutron stars. Eur. Phys. J. A 2020, 56, 175. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Martins, S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Del Popolo, A.; Deliyergiyev, M.; Le Delliou, M. Solution to the hyperon puzzle using dark matter. Phys. Dark Universe 2020, 30, 100622. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Sedrakian, A.; Li, J.J.; Weber, F. Heavy baryons in compact stars. Prog. Part. Nucl. Phys. 2023, 131, 104041. [Google Scholar] [CrossRef]
- Bednarek, I.; Manka, R. The role of nonlinear vector meson interactions in hyperon stars. J. Phys. G Nucl. Part. Phys. 2009, 36, 095201. [Google Scholar] [CrossRef]
- Bednarek, I. Hyperon puzzle in compact stars. Phys. Part. Nucl. 2015, 46, 816–820. [Google Scholar] [CrossRef]
- Oertel, M.; Providência, C.; Gulminelli, F.; Raduta, A. Hyperons in neutron star matter within relativistic mean-field models. J. Phys. G Nucl. Part. Phys. 2014, 42, 075202. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Making a soft relativistic mean-field equation of state stiffer at high density. Phys. Rev. C 2015, 92, 052801. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802. [Google Scholar] [CrossRef]
- van Dalen, E.N.E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with Λ-hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef]
- Fortin, M.; Avancini, S.S.; Providência, C.; Vidaña, I. Hypernuclei and massive neutron stars. Phys. Rev. C 2017, 95, 065803. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Sedrakian, A. Hypernuclear stars from relativistic Hartree-Fock density functional theory. Eur. Phys. J. A 2018, 54, 133. [Google Scholar] [CrossRef]
- Lim, Y.; Lee, C.-H.; Oh, Y. Effective interactions of hyperons and mass-radius relation of neutron stars. Phys. Rev. D 2018, 97, 023010. [Google Scholar] [CrossRef]
- Li, Z.; Ren, Z.; Hong, B.; Lu, H.; Bai, D. Neutron stars within a relativistic mean field theory compatible with nucleon-nucleon short-range correlations. Nucl. Phys. A 2019, 990, 118–136. [Google Scholar] [CrossRef]
- Fu, H.R.; Li, J.J.; Sedrakian, A.; Weber, F. Massive relativistic compact stars from SU(3) symmetric quark models. Phys. Lett. B 2022, 834, 137470. [Google Scholar] [CrossRef]
- Rikovska Stone, J.; Miller, J.C.; Koncewicz, R.; Stevenson, P.D.; Strayer, M.R. Nuclear matter and neutron-star properties calculated with the Skyrme interaction. Phys. Rev. C 2003, 68, 034324. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Lim, Y.; Hyun, C.H.; Kwak, K.; Lee, C.-H. Hyperon puzzle of neutron stars with Skyrme force models. Int. J. Mod. Phys. E 2015, 24, 1550100. [Google Scholar] [CrossRef]
- Mornas, L. Neutron stars in a Skyrme model with hyperons. Eur. Phys. J. A 2005, 24, 293–312. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Watson, D.; Hansen, C.J.; Selsing, J.; Koch, A.; Malesani, D.B.; Andersen, A.C.; Fynbo, J.P.U.; Arcones, A.; Bauswein, A.; Covino, S.; et al. Identification of strontium in the merger of two neutron stars. Nature 2019, 574, 497–500. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Thorne, K.S. Tidal stabilization of rigidly rotating, fully relativistic neutron stars. Phys. Rev. D 1998, 58, 124031. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Rayet, M. Skyrme parametrization of an effective Λ-nucleon interaction. Nucl. Phys. A 1981, 367, 381–397. [Google Scholar] [CrossRef]
- Hiyama, E.; Nakazawa, K. Structure of S =−2 Hypernuclei and hyperon-hyperon interactions. Annu. Rev. Nucl. Part. Sci. 2018, 68, 131–159. [Google Scholar] [CrossRef]
- Lanskoy, D.E. Double-Λ hypernuclei in the Skyrme-Hartree-Fock approach and nuclear core polarization. Phys. Rev. C 1998, 58, 3351–3358. [Google Scholar] [CrossRef]
- Millener, D.J.; Dover, C.B.; Gal, A. Λ-nucleus single-particle potentials. Phys. Rev. C 1988, 38, 2700–2708. [Google Scholar] [CrossRef]
- Lanskoi, D.E.; Tret’yakova, T.Y. Skyrme interactions in calculations of hypernuclei by the Hartree–Fock method. Sov. J. Nucl. Phys. (Engl. Transl.) 1989, 49, 987–991. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Krastev, P.G.; Li, B.-A. Imprints of the nuclear symmetry energy on the tidal deformability of neutron stars. J. Phys. Nucl. Part. Phys. 2019, 46, 074001. [Google Scholar] [CrossRef]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Cutler, C.; Flanagan, É.É. Gravitational waves from merging compact binaries: How accurately can one extract the binary’s parameters from the inspiral waveform? Phys. Rev. D 1994, 49, 2658–2697. [Google Scholar] [CrossRef]
- Favata, M. Systematic Parameter Errors in Inspiraling Neutron Star Binaries. Phys. Rev. Lett. 2014, 112, 101101. [Google Scholar] [CrossRef] [PubMed]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Part II. Nuclei far from stablities. Nucl. Phys. A 1998, 635, 231–256, Erratum: Nucl. Phys. A 1998, 643, 441–441. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Flocard, H. Nuclear effective forces and isotope shifts. Nucl. Phys. A 1995, 584, 467–488. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Dean, D.J.; Nazarewicz, W.; Dobaczewski, J.; Maruhn, J.A.; Strayer, M.R. Shape coexistence and the effective nucleon-nucleon interaction. Phys. Rev. C 1999, 60, 014316. [Google Scholar] [CrossRef]
- Bartel, J.; Quentin, P.; Brack, M.; Guet, C.; Håkansson, H.-B. Towards a better parametrisation of Skyrme-like effective forces: A critical study of the SkM force. Nucl. Phys. A 1982, 386, 79–100. [Google Scholar] [CrossRef]
- Brown, B.A. New Skyrme interaction for normal and exotic nuclei. Phys. Rev. C 1998, 58, 220–231. [Google Scholar] [CrossRef]
- Mikheev, S.A.; Lanskoy, D.E.; Tretyakova, T.Y. Correlations between Properties of Nuclear Matter and Characteristics of Neutron Stars. Phys. Part. Nucl. 2022, 53, 409–414. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Motoba, T.; Rijken, T.A. G-Matrix Approach to Hyperon-Nucleus Systems. Prog. Theor. Phys. Suppl. 2010, 185, 72–105. [Google Scholar] [CrossRef]
- Lanskoy, D.E.; Yamamoto, Y. Skyrme-Hartree-Fock treatment of Λ and ΛΛ hypernuclei with G-matrix motivated interactions. Phys. Rev. C 1997, 55, 2330–2339. [Google Scholar] [CrossRef]
- Schulze, H.-J.; Hiyama, E. Skyrme force for light and heavy hypernuclei. Phys. Rev. C 2014, 90, 047301. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Bandō, H.; Žofka, J. On the Λ-Hypernuclear Single Particle Energies. Prog. Theor. Phys. 1988, 80, 757–761. [Google Scholar] [CrossRef]
- Takahashi, H.; Ahn, J.K.; Akikawa, H.; Aoki, S.; Arai, K.; Bahk, S.Y.; Baik, K.M.; Bassalleck, B.; Chung, J.H.; Chung, M.S.; et al. Observation of a Double Hypernucleus. Phys. Rev. Lett. 2001, 87, 212502. [Google Scholar] [CrossRef]
- Minato, F.; Chiba, S. Fission barrier of actinide nuclei with double-Λ particles within the Skyrme–Hartree–Fock method. Nucl. Phys. A 2011, 856, 55–67. [Google Scholar] [CrossRef]
- Imasheva, L.T.; Lanskoy, D.E.; Tretyakova, T.Y. Neutron Star Matter and Baryonic Interactions. Phys. At. Nucl. 2019, 82, 402–407. [Google Scholar] [CrossRef]
- Balberg, S.; Barnea, N. S-wave pairing of Λ hyperons in dense matter. Phys. Rev. C 1998, 57, 409–416. [Google Scholar] [CrossRef]
- Sun, T.T.; Hiyama, E.; Sagawa, H.; Schulze, H.-J.; Meng, J. Mean-field approaches for Ξ− hypernuclei and current experimental data. Phys. Rev. C 2016, 94, 064319. [Google Scholar] [CrossRef]
- Jin, Y.; Zhou, X.-R.; Cheng, Y.-Y.; Schulze, H.-J. Study of Ξ− hypernuclei in the Skyrme-Hartree-Fock approach. Eur. Phys. J. A 2020, 56, 135. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, X.-R.; Schulze, H.-J. Skyrme force for all known Ξ− hypernuclei. Phys. Rev. C 2021, 104, L061307. [Google Scholar] [CrossRef]



| Model | L | |||||||
|---|---|---|---|---|---|---|---|---|
| SkI3 | 258.19 | 34.83 | 100.53 | 73.04 | 0.58 | 2.19 | 10.93 | |
| SLy230a | 229.89 | 31.99 | 44.32 | 0.70 | 2.08 | 10.18 |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| YBZ2 | −0.085 | 56.95 | 48.05 | 3000 | 0 | 1 | |
| YBZ6 | −372.2 | −0.107 | 100.4 | 79.6 | 2000 | 0 | 1 |
| SLL4 * | −326 | 0 | 62 | 20 | 1880 | 0 | 1 |
| YMR | −1056.2 | 0 | 96.248 | 8.743 | 2811.2 | 0 | 1/8 |
| LYI | −476 | −0.0452 | 42 | 23 | 1514.1 | −0.280 | 1/3 |
| Model | ||
|---|---|---|
| S1 | −37.9 | 14.1 |
| S2 | −437.7 | 240.7 |
| S3 | −156.4 | 347.2 |
| SkI3 | SLy230a | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| LYI | S1 | - | - | 1.31 | 12.6 | - | - | 1.34 | 10.9 |
| S2 | - | - | 1.36 | 9.7 | 9.5 | 46 | 1.40 | 9.5 | |
| S3 | 12.4 | 346 | 1.58 | 9.8 | 11.2 | 201 | 1.58 | 9.6 | |
| SLL4 | S1 | 13.1 | 597 | 1.45 | 12.6 | 11.7 | 300 | 1.55 | 11.4 |
| S2 | 12.8 | 468 | 1.50 | 10.0 | 11.7 | 302 | 1.58 | 10.2 | |
| S3 | 13.1 | 624 | 1.74 | 10.2 | 11.7 | 301 | 1.80 | 10.0 | |
| YBZ6 | S1 | 13.3 | 648 | 1.64 | 12.6 | 11.7 | 297 | 1.84 | 11.3 |
| S2 | 13.3 | 654 | 1.66 | 10.7 | 11.7 | 297 | 1.82 | 11.1 | |
| S3 | 13.3 | 649 | 1.87 | 10.7 | 11.7 | 297 | 1.96 | 10.5 | |
| YBZ2 * | S1 | 13.3 | 708 | 1.66 | 13.0 | 11.7 | 297 | 2.08 | 10.2 |
| S2 | 13.3 | 708 | 1.57 | 10.5 | 11.7 | 297 | 2.08 | 10.2 | |
| S3 | 13.3 | 708 | 1.83 | 10.7 | 11.7 | 297 | 2.08 | 10.2 | |
| YMR | S1 | - | - | 1.39 | 12.3 | 11.4 | 242 | 1.44 | 10.8 |
| S2 | 11.2 | 147 | 1.44 | 9.9 | 11.1 | 187 | 1.51 | 9.2 | |
| S3 | 12.9 | 503 | 1.62 | 10.0 | 11.5 | 262 | 1.66 | 9.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikheev, S.; Lanskoy, D.; Nasakin, A.; Tretyakova, T. Hyperonic Interactions in Neutron Stars. Particles 2023, 6, 847-863. https://doi.org/10.3390/particles6030054
Mikheev S, Lanskoy D, Nasakin A, Tretyakova T. Hyperonic Interactions in Neutron Stars. Particles. 2023; 6(3):847-863. https://doi.org/10.3390/particles6030054
Chicago/Turabian StyleMikheev, Semyon, Dmitry Lanskoy, Artur Nasakin, and Tatiana Tretyakova. 2023. "Hyperonic Interactions in Neutron Stars" Particles 6, no. 3: 847-863. https://doi.org/10.3390/particles6030054








