The Agent-Based Model and Simulation of Sexual Selection and Pair Formation Mechanisms
Abstract
:1. Introduction
- An agent is a physical or virtual entity, capable of operating in the environment and able to communicate with other agents.
- In its activities, it strives to achieve its own goals.
- It may possess some resources.
- It may observe the environment, but only locally.
- It possesses only partial knowledge about the environment.
- It has some skills and can offer some services.
- It can also be able to reproduce.
- an environment,
- objects—passive elements of the system,
- agents—active elements of the system,
- relations between the environment, objects and agents,
- operations that allow agents to observe and interact with other system components,
- operators that represent the reactions of other system components to agents’ activities.
- Allopatric models—the speciation takes place as a result of the geographic separation of subpopulations, which reduces the flow of genes between subpopulations and ultimately leads to reproductive isolation and emergence of new species.
- Parapatric models—subpopulations of primary species live in habitats that only partially overlap, which limits the flow of genes. Such limitation potentially leads to the reproductive isolation and emergence of new species.
- Sympatric models—the speciation takes place within the population of primary species only as a result of co-evolutionary interactions with another species or as a result of sexual selection. The selective pressure caused by interactions between co-evolving species or sexes (within a single species) potentially leads to reproductive isolation and emergence of a new species. The space of environment, in which a population is located, does not play any role in the sympatric speciation.
- a cost of reproduction for one of the sexes (usually these are females) is much higher than for the other,
- proportions of both sexes in the population are almost equal.
2. A Review of Entropy-Based Measures of Population Diversity
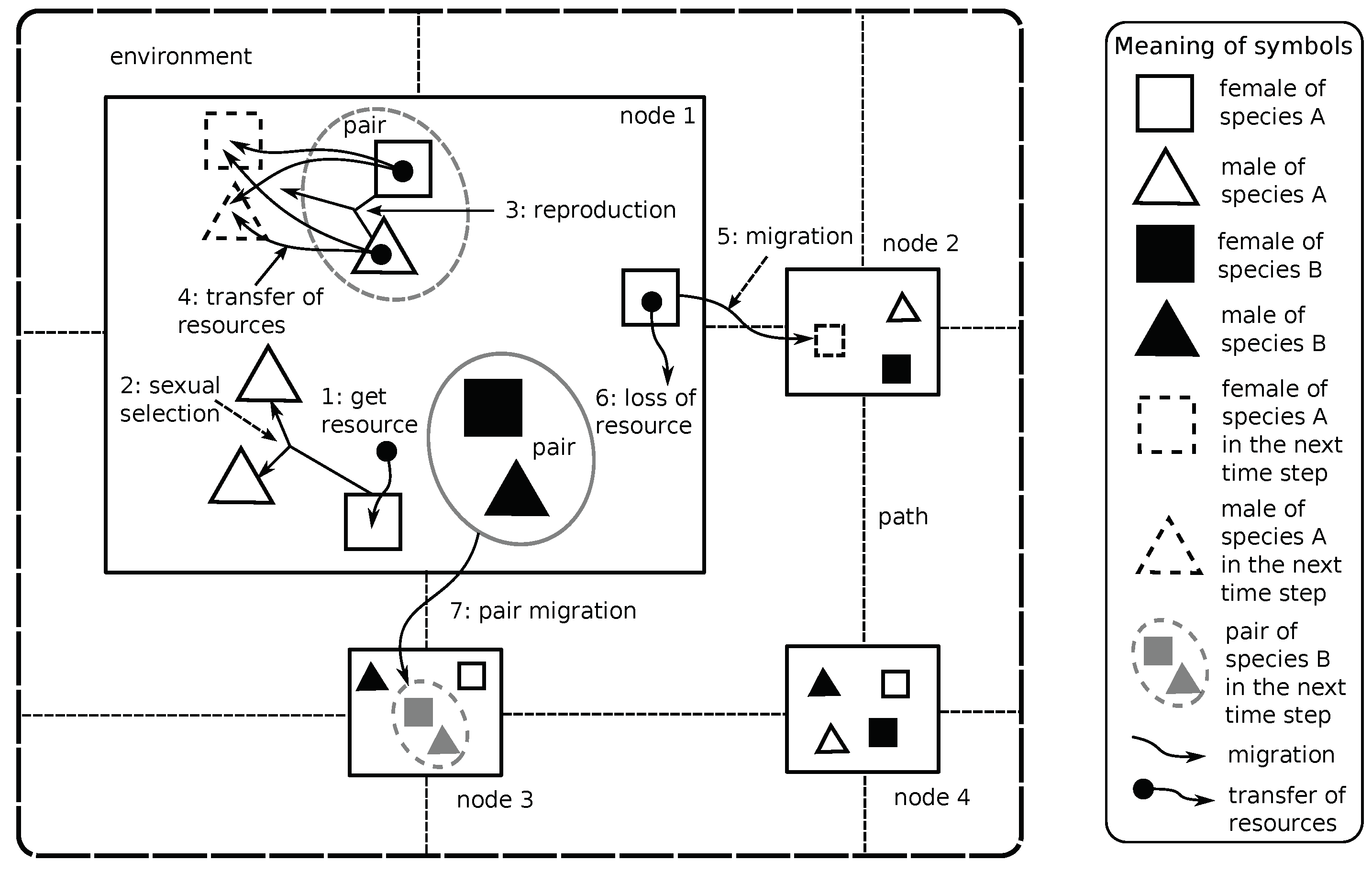
3. The Agent-Based Simulation Model of Sexual Selection and Pair Formation Mechanisms
3.1. Environment
3.2. Selection
3.3. Fitness Functions
3.4. Agents
3.5. Reproduction, Sexual Selection and Pair Formation
3.6. Recombination and Mutation
4. The Results of Simulation Experiments
- maximum age of pair : different values are used during the experiment (0, 1000, 2000, 3000, 4000 and 5000)—the information is provided with the results,
- probability of mutation: ,
- probability of recombination: ,
- coefficient determining the minimal level of resource that is required for reproduction: ,
- coefficient determining how much of the resource is given to offspring by a agent during reproduction: ,
- coefficient determining how much of the resource is given to offspring by a agent during reproduction: ,
- coefficient determining how much of the resource is given back to the environment during migration to another node: .
4.1. Speciation Processes
4.2. Maintaining Population Diversity
- Sympatric speciation can be triggered by sexual selection.
- The pair formation mechanism is necessary for a stable existence of species. It reduces the energetic effort necessary for finding a partner for reproduction greatly.
- In the cases when reproduction partners can be found in the nearest neighborhood and the energetic effort needed to find them is not very high, dissolution of existing pairs of agents can intensify speciation processes and increase the population diversity. Such phenomenon occurs because female agents are forced to choose male partners that do not fit their preferences perfectly—simply because there are no other partners in the nearest neighborhood. In such a case, children have much more diverse preferences and features because their parents differ significantly in genetic terms. Such situation can lead to forming new sub-populations, and possibly also new species.
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. The Agent-Based Model of Evolving Population with Sexual Selection and Pair Formation Mechanisms
Appendix A.1. Agent-Based Simulation System
- is the set of environment types in time t;
- is the set of environments in time t;
- is the set of types of elements that can exist within the system in time t;
- is the set of types of vertices that can exist within the system in time t;
- is the set of object (passive elements) types that can exist within the system in time t;
- is the set of agent types that can exist within the system in time t;
- is the set of resource types that can exist within the system in time t, the amount of resource of type will be denoted as ;
- is the set of information types that exist in the system, the information of type will be denoted as ;
- is the set of relations between sets of agents, objects, and vertices;
- is the set of attributes of agents, objects, and vertices—the are two possible attributes: and of an agent;
- is the set of actions that can be executed by agents, objects, and vertices.
Appendix A.2. Environment
- is the set of environment types that may be connected with environment of type .
- is the set of types of vertices that may exist within the environment of type .
- is the set of resource types that may exist within the environment of type .
- is the set of information types that may exist within the environment of type .
- is the set of vertices.
- is the set of arches.
- Function computes an amount of resource, that an agent migrating between two nodes would lose.
- is the set of attributes of vertex at the beginning of its existence;
- is the set of actions, which vertex can execute at the beginning of its existence, when asked for it;
- is the set of resource types, which can exist within vertex at the beginning of its existence;
- is the set of information, which can exist within vertex at the beginning of its existence;
- is the set of types of vertices that can be connected with vertex at the beginning of its existence;
- is the set of types of objects that can be located within vertex at the beginning of its existence;
- is the set of types of agents that can be located within vertex at the beginning of its existence;
- is the action of giving a certain amount of resource to an agent.
- is the set of attributes of vertex —this set can change during a vertex’s lifetime;
- is the set of actions, which vertex can execute, when asked for it—this set can change during a vertex’s lifetime;
- is the set of resources of types from set;
- is the set of information of types from set;
- is the set of types of vertices from set that are connected with vertex ;
- is the set of objects of types from set that are located in vertex ;
- is the set of agents of types from set that are located in vertex .
Appendix A.3. Agents
Appendix A.3.1. Female Agent
- is the set of goals of agent at the beginning of its existence;
- is the set of attributes of a agent at the beginning of its existence, is the current age, contains the encoded preferences (two independent variables) and the parameters of mutation (standard deviations)—compare Section 3.4 and Section 3.6;
- is the set of actions, which a agent can execute at the beginning of its existence;
- is the set of types of resources, which can be used by a agent at the beginning of its existence;
- is the set of information types, which can be used by a agent at the beginning of its existence;
- is the set of types of objects that can be located within a agent at the beginning of its existence;
- is the set of types of agents that can be located within a agent at the beginning of its existence.
- is the goal of getting a certain amount of resource from the environment;
- is the goal of reproducing;
- is the goal of migrating to another vertex.
- is the action of death—an agent dies when it runs out of resources.
- is the action of getting a certain amount of resource from the environment.
- is the action of choosing a partner for reproduction from a set of agents that are located within the same vertex and are ready for reproduction (that is, which executed action).
- is the action of reproducing with the use of recombination and mutation operators. A agent executes this action when it is ready for reproduction, and a partner was chosen (with the use of action), or a agent is already paired with a agent. During the reproduction, a agent gives a certain amount of resources to its offspring.
- is the action of forming a pair with a selected agent.
- is the action of dissolving a pair if it is older than .
- is the action of migrating to another vertex in search of resources or partners for reproduction.
| Algorithm 1: The pseudocode of activities of the agent. |
 |
- is the set of goals, which the agent tries to realize—this set can change during the agent’s lifetime;
- is the set of attributes of the agent—this set can change during the agent’s lifetime;
- is the set of actions, which the agent can execute in order to realize its goals—this set can change during the agent’s lifetime;
- is the set of resources (of types from set) which are used by the agent;
- is the set of information (of types from the set), which the agent can possess and use;
- is the set of objects (of types from the set), that are located within the agent;
- is the set of agents (of types from the set), that are located within the agent.
Appendix A.3.2. Male Agent
- —getting resource from the environment,
- —reproducing,
- —migrating to another vertex.
- is the action of death—an agent dies when it runs out of resources.
- is the action of getting a certain amount of resource from the environment.
- is the action executed when a given agent is ready for reproduction. Then, a agent that is also ready for reproduction chooses the agent (by executing action) or a agent that is paired with the agent, and is also ready for reproduction, executes action.
- is the action of reproducing (with the use of recombination and mutation operators)— a agent executes this action when it is ready for reproduction and has a partner.
- is the action of forming a pair with a agent.
- is the action of dissolving a pair if it is older than .
- is the action of migrating to another vertex.
| Algorithm 2: The pseudocode of activities of the agent. |
 |
Appendix A.4. Relations
References
- Wooldridge, M. An Introduction to MultiAgent Systems; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ferber, J. Multi-Agent Systems: An Introduction to Distributed Artificial Intelligence; Addison-Wesley: Boston, MA, USA, 1999. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson: London, UK, 2010. [Google Scholar]
- Sterling, L.S. The Art of Agent-Oriented Modeling; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Grimm, V.; Railsback, S.F. Agent-Based and Individual-Based Modeling: A Practical Introduction; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Uhrmacher, A.M.; Weyns, D. (Eds.) Multi-Agent Systems. Simulation and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sarker, R.A.; Ray, T. (Eds.) Agent-Based Evolutionary Search; Springer: Berlin, Germany, 2010. [Google Scholar]
- Floreano, D.; Mattiussi, C. Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Engelbrecht, A.P. Fundamentals of Computational Swarm Intelligence; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Lee, R.S.T. (Ed.) Computational Intelligence for Agent-Based Systems; Springer: Berlin, Germany, 2007. [Google Scholar]
- Dreżewski, R.; Cetnarowicz, K.; Dziuban, G.; Martynuska, S.; Byrski, A. Agent-Based Neuro-Evolution Algorithm. Agent and Multi-Agent Systems: Technologies and Applications. In Proceedings of the 2015 9th KES International Conference on KES-AMSTA, Sorrento, Italy, 17–19 June 2015; Jezic, G., Howlett, R.J., Jain, L.C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 38, pp. 95–108. [Google Scholar]
- Grimm, V.; Railsback, S.F. Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Gilbert, N. Agent-Based Models; SAGE Publications: Thousand Oaks, CA, USA, 2008. [Google Scholar]
- North, M.J.; Macal, C.M. Managing Business Complexity: Discovering Strategic Solutions with Agent-Based Modeling and Simulation; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Epstein, J.M. Generative Social Science. Studies in Agent-Based Computational Modeling; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Epstein, J.M.; Axtell, R. Growing Artificial Societes. Social Science from Bottom Up; Brookings Institution Press: Washington, DC, USA; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Gilbert, N.; Troitzsch, K.G. Simulation for the Social Scientist; Open University Press: Berkshire, UK, 2005. [Google Scholar]
- Hamill, L.; Gilbert, N. Agent-Based Modelling in Economics; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Laver, M.; Sergenti, E. Party Competition: An Agent-Based Model; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Billari, F.C.; Prskawetz, A. (Eds.) Agent-Based Computational Demography: Using Simulation to Improve Our Understanding of Demographic Behaviour; Physica-Verlag: Heidelberg, Germany, 2003. [Google Scholar]
- Billari, F.C.; Fent, T.; Prskawetz, A.; Scheffran, J. (Eds.) Agent-Based Computational Modelling: Applications in Demography, Social, Economic and Environmental Sciences; Physica-Verlag: Heidelberg, Germany, 2006. [Google Scholar]
- Macal, C.M.; North, M.J. Agent-based modeling and simulation. In Proceedings of the 2009 Winter Simulation Conference, Austin, TX, USA, 13–16 December 2009. [Google Scholar]
- Luke, S.; Cioffi-Revilla, C.; Panait, L.; Sullivan, K. MASON: A New Multi-Agent Simulation Toolkit. Proc. 2004 Swarmfest Workshop 2004, 2, 316–327. [Google Scholar]
- Luke, S.; Cioffi-Revilla, C.; Panait, L.; Sullivan, K.; Balan, G. MASON: A Multi-Agent Simulation Environment. Simul. Trans. Soc. Model. Simul. Int. 2005, 82, 517–527. [Google Scholar]
- Klügl, F.; Herrler, R.; Oechslein, C. From Simulated to Real Environments: How to Use SeSAm for Software Development; Number 2831 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 13–24. [Google Scholar]
- Kravari, K.; Bassiliades, N. A Survey of Agent Platforms. J. Artif. Soc. Soc. Simul. 2015, 18. [Google Scholar] [CrossRef]
- Cetnarowicz, K.; Kisiel-Dorohinicki, M.; Nawarecki, E. The application of Evolution Process in Multi-Agent World to the Prediction System. In Proceedings of the 2nd International Conference on Multi-Agent Systems (ICMAS 1996), Kyoto, Japan, 9–13 December 1996; Tokoro, M., Ed.; AAAI Press: Menlo Park, CA, USA, 1996. [Google Scholar]
- Cetnarowicz, K.; Dreżewski, R. Maintaining Functional Integrity in Multi-Agent Systems for Resource Allocation. Comput. Inform. 2010, 29, 947–973. [Google Scholar]
- Dreżewski, R. A Model of Co-evolution in Multi-agent System. In Proceedings of the 3rd International Central and Eastern European Conference on Multi-Agent Systems, CEEMAS 2003, Prague, Czech Republic, 16–18 June 2003; Marik, V., Muller, J., Pechoucek, M., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2003; Volume 2691, pp. 314–323. [Google Scholar]
- Dreżewski, R. A Co-Evolutionary Multi-Agent System for Multi-Modal Function Optimization. In Proceedings of the 4th International Conference on Computational Science, Kraków, Poland, 6–9 June 2004; Bubak, M., van Albada, G.D., Sloot, P.M.A., Dongarra, J.J., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2004; Volume 3038, pp. 654–661. [Google Scholar]
- Dreżewski, R. Co-Evolutionary Multi-Agent System with Speciation and Resource Sharing Mechanisms. Comput. Inform. 2006, 25, 305–331. [Google Scholar]
- Dreżewski, R.; Siwik, L. Multi-objective Optimization Using Co-evolutionary Multi-agent System with Host-Parasite Mechanism. In Proceedings of the 6th International Conference on Computational Science, Reading, UK, 28–31 May 2006; Alexandrov, V.N., van Albada, G.D., Sloot, P.M.A., Dongarra, J., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2006; Volume 3993, pp. 871–878. [Google Scholar]
- Dreżewski, R.; Siwik, L. Co-evolutionary Multi-agent System with Predator-Prey Mechanism for Multi-objective Optimization. In Proceedings of the 8th International Conference on Adaptive and Natural Computing Algorithms ICANNGA 2007, Warsaw, Poland, 11–14 April 2007; Beliczynski, B., Dzielinski, A., Iwanowski, M., Ribeiro, B., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 4431, pp. 67–76. [Google Scholar]
- Dreżewski, R.; Obrocki, K.; Siwik, L. Comparison of Multi-Agent Co-Operative Co-Evolutionary and Evolutionary Algorithms for Multi-Objective Portfolio Optimization. In Proceedings of the Applications of Evolutionary Computing, EvoWorkshops 2009: EvoCOMNET, EvoENVIRONMENT, EvoFIN, EvoGAMES, EvoHOT, EvoIASP, EvoINTERACTION, EvoMUSART, EvoNUM, EvoSTOC, EvoTRANSLOG, Tübingen, Germany, 15–17 April 2009; Volume 5484, pp. 223–232. [Google Scholar]
- Dreżewski, R.; Obrocki, K.; Siwik, L. Agent-Based Co-Operative Co-Evolutionary Algorithms for Multi-Objective Portfolio Optimization. In Natural Computing in Computational Finance; Brabazon, A., O’Neill, M., Maringer, D.G., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2010; Volume 3, pp. 63–84. [Google Scholar]
- Dreżewski, R.; Doroz, K. An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization. Symmetry 2017, 9, 168. [Google Scholar] [CrossRef]
- Dreżewski, R.; Sepielak, J. Evolutionary System for Generating Investment Strategies. In Proceedings of the Applications of Evolutionary Computing, EvoWorkshops 2008: EvoCOMNET, EvoFIN, EvoHOT, EvoIASP, EvoMUSART, EvoNUM, EvoSTOC, and EvoTransLog, Naples, Italy, 26–28 March 2008; Volume 4974, pp. 83–92. [Google Scholar]
- Dreżewski, R.; Sepielak, J.; Siwik, L. Classical and Agent-Based Evolutionary Algorithms for Investment Strategies Generation. In Natural Computing in Computational Finance; Brabazon, A., O’Neill, M., Eds.; Springer-Verlag: Berlin/Heidelberg, Germnay, 2009; Volume 2, pp. 181–205. [Google Scholar]
- Dreżewski, R.; Cetnarowicz, K. Sexual Selection Mechanism for Agent-Based Evolutionary Computation. In Proceedings of the 7th International Conference on Computational Science—ICCS 2007, Beijing, China, 27–30 May 2007; Shi, Y., van Albada, G.D., Dongarra, J., Sloot, P.M.A., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 4488, pp. 920–927. [Google Scholar]
- Dreżewski, R.; Siwik, L. Techniques for Maintaining Population Diversity in Classical and Agent-Based Multi-objective Evolutionary Algorithms. In Proceedings of the 7th International Conference on Computational Science—ICCS 2007, Beijing, China, 27–30 May 2007; Shi, Y., van Albada, G.D., Dongarra, J., Sloot, P.M.A., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 4488, pp. 904–911. [Google Scholar]
- Dreżewski, R. Agent-Based Modeling and Simulation of Species Formation Processes. In Multi-Agent Systems—Modeling, Interactions, Simulations and Case Studies; Alkhateeb, F., Al Maghayreh, E., Abu Doush, I., Eds.; InTech: Rijeka, Croatia, 2011; pp. 3–28. [Google Scholar]
- Gavrilets, S.; Waxman, D. Sympatric speciation by sexual conflict. Proc. Natl. Acad. Sci. USA 2002, 99, 10533–10538. [Google Scholar] [CrossRef] [PubMed]
- Gavrilets, S. Models of speciation: What have we learned in 40 years? Evolution 2003, 57, 2197–2215. [Google Scholar] [CrossRef] [PubMed]
- Krebs, J.; Davies, N. An Introduction to Behavioural Ecology; Blackwell Science Ltd.: Hoboken, NJ, USA, 1993. [Google Scholar]
- M’Gonigle, L.K.; Mazzucco, R.; Otto, S.P.; Dieckmann, U. Sexual selection enables longterm coexistence despite ecological equivalence. Nature 2012, 484, 506–509. [Google Scholar] [CrossRef] [PubMed]
- Dreżewski, R. Agent-Based Simulation Model of Sexual Selection Mechanism. In Proceedings of the 9th KES International Conference on Agent and Multi-Agent Systems: Technologies and Applications KES-AMSTA 2015, Sorrento, Italy, 17–19 June 2015; Jezic, G., Howlett, R.J., Jain, L.C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 38, pp. 155–166. [Google Scholar]
- Hurlbert, S. The Nonconcept of Diversity: a Critique and Alternative Parameters. Ecology 1971, 52, 577–586. [Google Scholar] [CrossRef] [PubMed]
- Jost, L. Entropy and Diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Tothmeresz, B. Comparison of Different Methods for Diversity Ordering. J. Veg. Sci. 1995, 6, 283–290. [Google Scholar] [CrossRef]
- Ricotta, C. Parametric Scaling from Species Relative Abundances to Absolute Abundances in the Computation of Biological Diversity: A First Proposal Using Shannon’s Entropy. Acta Biotheor. 2003, 51, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Keylock, C. Simpson Diversity and Shannon–Wiener Index as Special Cases of a Generalized Entropy. Oikos 2005, 109, 2003–2007. [Google Scholar] [CrossRef]
- Renyi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Neymann, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Pielou, E. Ecological Diversity; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Hill, M. Diversity and Evenness: A Unifying Notation and its Consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer-Verlag: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Potter, M.A. The Design and Analysis of a Computational Model of Cooperative Coevolution. Ph.D. Thesis, George Mason University, Fairfax, VA, USA, 1997. [Google Scholar]
- Ursem, R.K. Multinational Evolutionary Algorithms. In Proceedings of the 1999 Congress on Evolutionary Computation (CEC-1999), Washington, DC, USA, 6–9 July 1999; Angeline, P.J., Michalewicz, Z., Schoenauer, M., Yao, X., Zalzala, A., Eds.; IEEE Press: Piscataway, NJ, USA, 1999; pp. 1633–1640. [Google Scholar]
- Bäck, T.; Schwefel, H.P. Evolutionary Computation: An Overview. In Proceedings of the Third IEEE Conference on Evolutionary Computation, Orlando, FL, USA, 26–29 June 1994; Fukuda, T., Furuhashi, T., Eds.; IEEE Press: Piscataway, NJ, USA, 1996. [Google Scholar]
- Booker, L.B.; Fogel, D.B.; Whitley, D.; Angeline, P.J. Recombination. In Handbook of Evolutionary Computation; Bäck, T., Fogel, D., Michalewicz, Z., Eds.; IOP Publishing: Bristol, UK; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Bäck, T.; Fogel, D.B.; Whitley, D.; Angeline, P.J. Mutation. In Handbook of Evolutionary Computation; Bäck, T., Fogel, D., Michalewicz, Z., Eds.; IOP Publishing: Bristol, UK; Oxford University Press: Oxford, UK, 1997. [Google Scholar]















© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dreżewski, R. The Agent-Based Model and Simulation of Sexual Selection and Pair Formation Mechanisms. Entropy 2018, 20, 342. https://doi.org/10.3390/e20050342
Dreżewski R. The Agent-Based Model and Simulation of Sexual Selection and Pair Formation Mechanisms. Entropy. 2018; 20(5):342. https://doi.org/10.3390/e20050342
Chicago/Turabian StyleDreżewski, Rafał. 2018. "The Agent-Based Model and Simulation of Sexual Selection and Pair Formation Mechanisms" Entropy 20, no. 5: 342. https://doi.org/10.3390/e20050342
APA StyleDreżewski, R. (2018). The Agent-Based Model and Simulation of Sexual Selection and Pair Formation Mechanisms. Entropy, 20(5), 342. https://doi.org/10.3390/e20050342




