Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling
Abstract
:1. Introduction
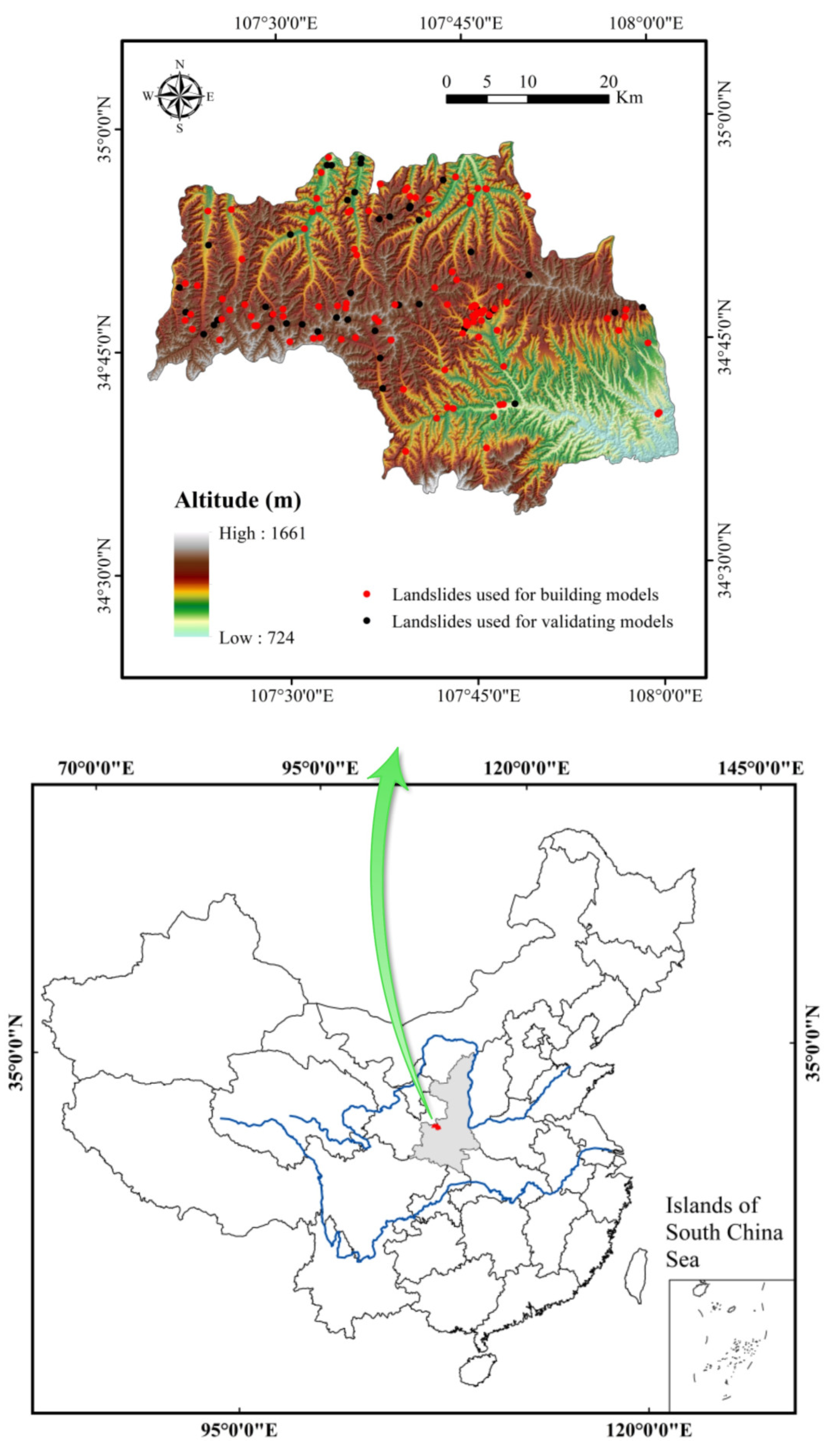
2. Study Area
3. Materials and Methods
3.1. Data Preparation
3.2. Index of Entropy (IoE)
3.3. Credal Decision Tree
3.4. Rotation Forest
3.5. Bagging
3.6. MultiBoostAB
4. Results and Analysis
4.1. Selection of Landslide Conditioning Factors
4.2. Generation of Landslide Susceptibility Maps
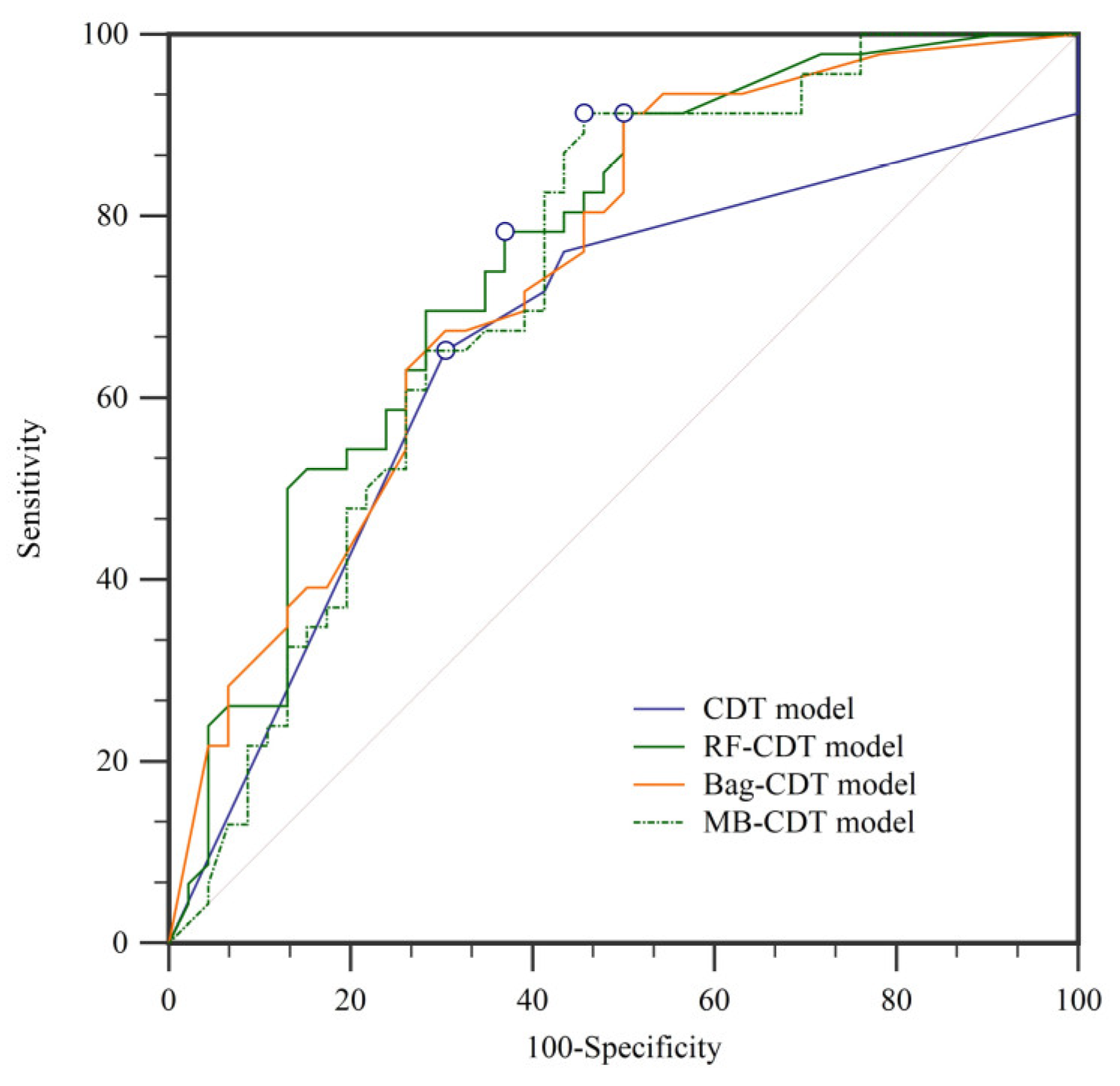
4.3. Model Validation and Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ambrosi, C.; Strozzi, T.; Scapozza, C.; Wegmüller, U. Landslide hazard assessment in the himalayas (nepal and bhutan) based on earth-observation data. Eng. Geol. 2018, 237, 217–228. [Google Scholar] [CrossRef]
- Palmisano, F.; Vitone, C.; Cotecchia, F. Methodology for landslide damage assessment. PProcedia Eng. 2016, 161, 511–515. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? CATENA 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Samodra, G.; Chen, G.; Sartohadi, J.; Kasama, K. Generating landslide inventory by participatory mapping: An example in purwosari area, yogyakarta, java. Geomorphology 2018, 306, 306–313. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in loess plateau: A case study in shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. CATENA 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Chen, F.; Yu, B.; Xu, C.; Li, B. Landslide detection using probability regression, a case study of wenchuan, northwest of chengdu. Appl. Geogr. 2017, 89, 32–40. [Google Scholar] [CrossRef]
- Ko, F.W.Y.; Lo, F.L.C. Rainfall-based landslide susceptibility analysis for natural terrain in hong kong—A direct stock-taking approach. Eng. Geol. 2016, 215, 95–107. [Google Scholar] [CrossRef]
- Raška, P.; Zábranský, V.; Brázdil, R.; Lamková, J. The late little ice age landslide calamity in north bohemia: Triggers, impacts and post-landslide development reconstructed from documentary data (case study of the kozí vrch hill landslide). Geomorphology 2016, 255, 95–107. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. CATENA 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Martino, S.; Lenti, L.; Bourdeau, C. Composite mechanism of the büyükçekmece (turkey) landslide as conditioning factor for earthquake-induced mobility. Geomorphology 2018, 308, 64–77. [Google Scholar] [CrossRef]
- Schmaltz, E.M.; Steger, S.; Glade, T. The influence of forest cover on landslide occurrence explored with spatio-temporal information. Geomorphology 2017, 290, 250–264. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, jiangxi province, china. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Nicu, I.C. Frequency ratio and gis-based evaluation of landslide susceptibility applied to cultural heritage assessment. J. Cult. Herit. 2017, 28, 172–176. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M.; et al. A novel ensemble approach of bivariate statistical-based logistic model tree classifier for landslide susceptibility assessment. Geocarto Int. 2018, 33, 1398–1420. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.; Panahi, M.; Hong, H.; et al. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in cameron highlands, malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. A comparative study of landslide susceptibility maps produced using support vector machine with different kernel functions and entropy data mining models in china. Bull. Eng. Geol. Environ. 2018, 77, 647–664. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I.; Hong, H.; Chen, W.; Xu, C. Applying information theory and gis-based quantitative methods to produce landslide susceptibility maps in nancheng county, china. Landslides 2017, 14, 1091–1111. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at al-hasher area, jizan (saudi arabia) using gis-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in nepal himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Regmi, A.D.; Poudel, K. Assessment of landslide susceptibility using gis-based evidential belief function in patu khola watershed, dang, nepal. Environ. Earth Sci. 2016, 75, 1–20. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Revhaug, I.; Nguyen, D.B.; Pham, H.V.; Bui, Q.N. A novel hybrid evidential belief function-based fuzzy logic model in spatial prediction of rainfall-induced shallow landslides in the lang son city area (vietnam). Geomat. Nat. Hazards Risk 2015, 6, 243–271. [Google Scholar]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of gis-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of ambon, indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, W.; Hong, H. Application of frequency ratio, weights of evidence and evidential belief function models in landslide susceptibility mapping. Geocarto Int. 2017, 32, 619–639. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, F.; Chen, H.; Wu, Y.; Li, T.; Li, W.; Wang, Q.; Liu, P. Gis-based landslide susceptibility analysis using frequency ratio and evidential belief function models. Environ. Earth Sci. 2016, 75, 1–12. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Prefac, Z.; Dumitru, S.; Chendeș, V.; Sîrodoev, I.; Cracu, G. Assessment of landslide susceptibility using the certainty factor model: Răşcuţa catchment (curvature subcarpathians) case study. Carpath. J. Earth Environ. Sci. 2016, 11, 617–626. [Google Scholar]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using gis. Earth Sci. Inf. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Mohammadi, M.; Moradi, H.R. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at haraz watershed, iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility mapping of shallow landslides using kernel-based gaussian process, support vector machines and logistic regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of logistic regression and random forests techniques for shallow landslide susceptibility assessment in giampilieri (ne sicily, italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and naïve bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. CATENA 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Chang, S.K.; Lee, D.H.; Wu, J.H.; Juang, C.H. Rainfall-based criteria for assessing slump rate of mountainous highway slopes: A case study of slopes along highway 18 in alishan, taiwan. Eng. Geol. 2011, 118, 63–74. [Google Scholar] [CrossRef]
- Lin, H.-M.; Chang, S.-K.; Wu, J.-H.; Juang, C.H. Neural network-based model for assessing failure potential of highway slopes in the alishan, taiwan area: Pre- and post-earthquake investigation. Eng. Geol. 2009, 104, 280–289. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.-J.; Lee, H.-J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using aster images and gis. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the turbolo river catchment (northern calabria, italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Lin, G.-F.; Chang, M.-J.; Huang, Y.-C.; Ho, J.-Y. Assessment of susceptibility to rainfall-induced landslides using improved self-organizing linear output map, support vector machine, and logistic regression. Eng. Geol. 2017, 224, 62–74. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the multiboost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2018, 1–22. [Google Scholar] [CrossRef]
- Ada, M.; San, B.T. Comparison of machine-learning techniques for landslide susceptibility mapping using two-level random sampling (2lrs) in alakir catchment area, antalya, turkey. Nat. Hazards 2018, 90, 237–263. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I. A novel hybrid model of bagging-based naïve bayes trees for landslide susceptibility assessment. Bull. Eng. Geol. Environ. 2017, 1–15. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. Gis-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, naïve-bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I. Landslide susceptibility assessment using bagging ensemble based alternating decision trees, logistic regression and j48 decision trees methods: A comparative study. Geotech. Geol. Eng. 2017, 35, 2597–2611. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Dholakia, M.; Prakash, I.; Pham, H.V. A comparative study of least square support vector machines and multiclass alternating decision trees for spatial prediction of rainfall-induced landslides in a tropical cyclones area. Geotech. Geol. Eng. 2016, 34, 1807–1824. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the yihuang area (china) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. CATENA 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in shangnan county, china using gis-based data mining algorithms. Bull. Eng. Geol. Environ. 2018, 77, 611–629. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2018, 1–23. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Nasiri Aghdam, I.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (wi) and adaptive neuro-fuzzy inference system (anfis) model at alborz mountains (iran). Environ. Earth Sci. 2016, 75, 1–20. [Google Scholar]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at hoa binh province (vietnam) using an adaptive neuro-fuzzy inference system and gis. Comput. Geosci. 2012, 45, 199–211. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin, asir region, saudi arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Chen, W.; Sun, Z.; Han, J. Landslide susceptibility modeling using integrated ensemble weights of evidence with logistic regression and random forest models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef]
- Ozcift, A.; Gulten, A. Classifier ensemble construction with rotation forest to improve medical diagnosis performance of machine learning algorithms. Comput. Meth. Prog. Biomed. 2011, 104, 443–451. [Google Scholar] [CrossRef] [PubMed]
- Abellán, J.; Moral, S. Building classification trees using the total uncertainty criterion. Int. J. Intell. Syst. 2003, 18, 1215–1225. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Amthauer, H.A.; Tsatsoulis, C. Classifying genes to the correct gene ontology slim term in saccharomyces cerevisiae using neighbouring genes with classification learning. BMC Genom. 2010, 11, 340. [Google Scholar] [CrossRef] [PubMed]
- Available online: Http://www.Linyou.Gov.Cn/ (accessed on 18 December 2018).
- Demir, G. Landslide susceptibility mapping by using statistical analysis in the north anatolian fault zone (nafz) on the northern part of suşehri town, turkey. Nat. Hazards 2018, 92, 133–154. [Google Scholar] [CrossRef]
- ESRI. Arcgis Desktop: Release 10.2 Redlands, CA: Environmental Systems Research Institute. Available online: Https://www.esri.com/zh-cn/home (accessed on 15 December 2018).
- Hungr, O.; Leroueil, S.; Picarelli, L. The varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Hong, H.; Ilia, I.; Tsangaratos, P.; Chen, W.; Xu, C. A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the wuyuan area, china. Geomorphology 2017, 290, 1–16. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using support vector machine for mandakini river basin, garhwal himalaya, india. Geomorphology 2017, 295, 115–125. [Google Scholar]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Characterization and quantification of path dependency in landslide susceptibility. Geomorphology 2017, 292, 16–24. [Google Scholar] [CrossRef]
- Wu, C.-H. Landslide susceptibility mapping by using landslide ratio-based logistic regression: A case study in the southern taiwan. J. Mt. Sci. 2015, 12, 721–736. [Google Scholar] [CrossRef]
- Sterlacchini, S.; Ballabio, C.; Blahut, J.; Masetti, M.; Sorichetta, A. Spatial agreement of predicted patterns in landslide susceptibility maps. Geomorphology 2011, 125, 51–61. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.K.; Wallinga, J.; Stuiver, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Implementing landslide path dependency in landslide susceptibility modelling. Landslides 2018, 15, 2129–2144. [Google Scholar] [CrossRef]
- Available online: Https://www.Nasa.Gov/ (accessed on 18 December 2018).
- Pradhan, B.; Sameen, M.I. Effects of the spatial resolution of digital elevation models and their products on landslide susceptibility mapping. In Laser Scanning Applications in Landslide Assessment; Pradhan, B., Ed.; Springer International Publishing: Berlin, Germany, 2017; pp. 133–150. [Google Scholar]
- Chen, W.; Li, W.; Chai, H.; Hou, E.; Li, X.; Ding, X. Gis-based landslide susceptibility mapping using analytical hierarchy process (ahp) and certainty factor (cf) models for the baozhong region of baoji city, china. Environ. Earth Sci. 2015, 75, 63. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Muhammad, S. Analysis of satellite-derived landslide at central nepal from 2011 to 2016. Environ. Earth Sci. 2018, 77, 331. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Lo, H.-M.; Chou, W.-C.; Lin, W.-T. Vegetation recovery assessment at the jou-jou mountain landslide area caused by the 921 earthquake in central taiwan. Ecol. Model. 2004, 176, 75–81. [Google Scholar] [CrossRef]
- Aksoy, B.; Ercanoglu, M. Landslide identification and classification by object-based image analysis and fuzzy logic: An example from the azdavay region (kastamonu, turkey). Comput. Geosci. 2012, 38, 87–98. [Google Scholar] [CrossRef]
- Jiang, J.-W.; Xiang, W.; Rohn, J.; Zeng, W.; Schleier, M. Research on water–rock (soil) interaction by dynamic tracing method for huangtupo landslide, three gorges reservoir, pr china. Environ. Earth Sci. 2015, 74, 557–571. [Google Scholar] [CrossRef]
- Alvioli, M.; Guzzetti, F.; Rossi, M. Scaling properties of rainfall induced landslides predicted by a physically based model. Geomorphology 2014, 213, 38–47. [Google Scholar] [CrossRef]
- Mugagga, F.; Kakembo, V.; Buyinza, M. Land use changes on the slopes of mount elgon and the implications for the occurrence of landslides. CATENA 2012, 90, 39–46. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Chen, H.; Lin, G.-W.; Lu, M.-H.; Shih, T.-Y.; Horng, M.-J.; Wu, S.-J.; Chuang, B. Effects of topography, lithology, rainfall and earthquake on landslide and sediment discharge in mountain catchments of southeastern taiwan. Geomorphology 2011, 133, 132–142. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity–duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Bayer, B.; Simoni, A.; Mulas, M.; Corsini, A.; Schmidt, D. Deformation responses of slow moving landslides to seasonal rainfall in the northern apennines, measured by insar. Geomorphology 2018, 308, 293–306. [Google Scholar] [CrossRef]
- Available online: Http://www.Sxmb.Gov.Cn/ (accessed on 18 December 2018).
- Abellán, J.; Masegosa, A.R. Combining Decision Trees Based on Imprecise Probabilities and Uncertainty Measures; Springer: Berlin/Heidelberg, Germany, 2007; pp. 512–523. [Google Scholar]
- Shafer, G.A. Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Yager, R.R., Liu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. [Google Scholar]
- Abellan, J.; Moral, S. A non-specificity measure for convex sets of probability distributions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2000, 8, 357–367. [Google Scholar] [CrossRef]
- Abellan, J.; Moral, S. Completing a total uncertainty measure in the dempster-shafer theory. Int. J. Gen. Syst. 1999, 28, 299–314. [Google Scholar] [CrossRef]
- Walley, P. Inferences from multinomial data: Learning about a bag of marbles. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 3–57. [Google Scholar] [CrossRef]
- Mantas, C.J.; Abellán, J. Hybrid Artificial Intelligence Systems. In Credal Decision Trees to Classify Noisy Data Sets; Polycarpou, M., de Carvalho, A.C.P.L.F., Pan, J.-S., Woźniak, M., Quintian, H., Corchado, E., Eds.; Springer International Publishing: Berlin, Germany, 2014; pp. 689–696. [Google Scholar]
- Pham, B.T.; Nguyen, V.-T.; Ngo, V.-L.; Trinh, P.T.; Ngo, H.T.T.; Tien Bui, D. A novel hybrid model of rotation forest based functional trees for landslide susceptibility mapping: A case study at kon tum province, Vietnam. In Advances and Applications in Geospatial Technology and Earth Resources; Tien Bui, D., Ngoc Do, A., Bui, H.-B., Hoang, N.-D., Eds.; Springer International Publishing: Berlin, Germany, 2018; pp. 186–201. [Google Scholar]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using j48 decision tree with adaboost, bagging and rotation forest ensembles in the guangchang area (china). CATENA 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: A case study in the himalayan area, india. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
- Rodríguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef]
- Kotsianti, S.B.; Kanellopoulos, D. Combining bagging, boosting and dagging for classification problems. In Knowledge-Based Intelligent Information and Engineering Systems; Apolloni, B., Howlett, R.J., Jain, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 493–500. [Google Scholar]
- Skurichina, M.; Duin, R.P.W. The role of combining rules in bagging and boosting. In Advances in Pattern Recognition; Ferri, F.J., Iñesta, J.M., Amin, A., Pudil, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 631–640. [Google Scholar]
- Webb, G.I. Multiboosting: A technique for combining boosting and wagging. Mach. Learn. 2000, 40, 159–196. [Google Scholar] [CrossRef]
- Kotsiantis, S. Combining bagging, boosting, rotation forest and random subspace methods. Artif. Intell. Rev. 2011, 35, 223–240. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.; Rezaeian, J.; Sattarian, A. Gis-based frequency ratio and index of entropy models for landslide susceptibility assessment in the caspian forest, northern iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Mark, A.H. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Ching, J.; Phoon, K.-K. Quantile value method versus design value method for calibration of reliability-based geotechnical codes. Struct. Saf. 2013, 44, 47–58. [Google Scholar] [CrossRef]
- Zhao, W.; Lian, H. Quantile index coefficient model with variable selection. J. Multivar. Anal. 2017, 154, 40–58. [Google Scholar] [CrossRef]
- Lee, C.-F.; Huang, W.-K.; Chang, Y.-L.; Chi, S.-Y.; Liao, W.-C. Regional landslide susceptibility assessment using multi-stage remote sensing data along the coastal range highway in northeastern taiwan. Geomorphology 2018, 300, 113–127. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C.; et al. Gis-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive bayes and rbfnetwork models for the long county area (china). Bull. Eng. Geol. Environ. 2018, 1–20. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Pourghasemi, H.R.; Indra, P.; Dholakia, M. Landslide susceptibility assesssment in the uttarakhand area (india) using gis: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Plant-soil reinforcement response under different soil hydrological regimes. Geoderma 2017, 285, 141–150. [Google Scholar] [CrossRef]
- Ordak, M.; Wesolowski, M.; Radecka, I.; Muszynska, E.; Bujalska-Zazdrozny, M. Seasonal variations of mercury levels in selected medicinal plants originating from poland. Biol. Trace Elem. Res. 2016, 173, 514–524. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-B.; Chen, L.-H.; Jiang, J. Why fine tree roots are stronger than thicker roots: The role of cellulose and lignin in relation to slope stability. Geomorphology 2014, 206, 196–202. [Google Scholar] [CrossRef]
- Persichillo, M.G.; Bordoni, M.; Meisina, C. The role of land use changes in the distribution of shallow landslides. Sci. Total Environ. 2017, 574, 924–937. [Google Scholar] [CrossRef] [PubMed]
- Bozo, L.; Cela, K. Problems with landslide stabilization of dukat in the road vlora—Saranda. Procedia Eng. 2016, 143, 1435–1442. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. Gis-based support vector machine modeling of earthquake-triggered landslide susceptibility in the jianjiang river watershed, china. Geomorphology 2012, 145–146, 70–80. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in lianhua county (china): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ann, maxent, and svm machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Truong, X.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Truong, X.; Do, T.; Tien Bui, D.; Lee, S. Enhancing prediction performance of landslide susceptibility model using hybrid machine learning approach of bagging ensemble and logistic model tree. Appl. Sci. 2018, 8, 146. [Google Scholar] [CrossRef]
- Barrios, E.; Gajardo, P.; Vasilieva, O. Sustainable thresholds for cooperative epidemiological models. Math. Biosci. 2018, 302, 9–18. [Google Scholar] [CrossRef]
- Kim, M.-H.; Baik, H.; Lee, S. Response threshold model based uav search planning and task allocation. J. Intell. Robot. Syst. 2014, 75, 625–640. [Google Scholar] [CrossRef]









| Name | Lithology | Geological Age |
|---|---|---|
| Group A | Loess | Quaternary |
| Group B | Gravel, fine sandstone, argillaceous silt | Quaternary |
| Group C | Brown-red calcareous clay rock interbedded with sandy clay rock, sandstone, and glutenite | Neogene |
| Group D | Sandstone interbedded with mudstone; mudstone and siltstone interbedded with sandstone | Cretaceous |
| Group E | Powder-fine sandstone, mudstone interbedded with tuff and marlstone | Cretaceous |
| Group F | Sandstone interbedded with conglomerate | Cretaceous |
| Group G | Conglomerate interbedded with glutenite and sandstone | Cretaceous |
| Group H | Feldspathic sandstone, mudstone, siltstone, coarse sandstone, fine conglomerate | Jurassic |
| Group I | Interbedded sandstone and mudstone, coarse sandstone, sandstone, coal seam | Jurassic |
| Group J | Interbedded sandstone and mudstone, marlstone, conglomerate, sandstone, siltstone, shale, oil shale | Triassic |
| Group K | Sandstone interbedded with mudstone, siltstone, and coal seam | Permian |
| Group L | Conglomerate, siliceous dolomite, shale, shale interbedded with sandstone | Ordovician |
| Group M | Upper: argillaceous dolomite Middle: fine-grained dolomite Bottom: spatulate dolomite, oolitic dolomite | Cambrian |
| Conditioning Factor | Classes | Percentage of Domain | Percentage of Landslides | (Pij) | Ij | Wj |
|---|---|---|---|---|---|---|
| Altitude (m) | 724–800 | 0.103 | 0.000 | 0.000 | 0.203 | 0.168 |
| 800–900 | 0.779 | 1.887 | 0.292 | |||
| 900–1000 | 2.705 | 0.000 | 0.000 | |||
| 1000–1100 | 7.581 | 6.604 | 0.105 | |||
| 1100–1200 | 14.306 | 21.698 | 0.183 | |||
| 1200–1300 | 24.928 | 27.358 | 0.132 | |||
| 1300–1400 | 30.262 | 21.698 | 0.086 | |||
| 1400–1500 | 17.504 | 19.811 | 0.136 | |||
| 1500–1600 | 1.733 | 0.943 | 0.066 | |||
| 1600–1661 | 0.099 | 0.000 | 0.000 | |||
| Slope angle (°) | 0–10 | 22.910 | 23.585 | 0.244 | 0.229 | 0.162 |
| 10–20 | 42.375 | 41.509 | 0.232 | |||
| 20–30 | 27.160 | 26.415 | 0.230 | |||
| 30–40 | 6.829 | 8.491 | 0.294 | |||
| 40–50 | 0.700 | 0.000 | 0.000 | |||
| 50–64.67 | 0.027 | 0.000 | 0.000 | |||
| Slope aspect | Flat | 0.028 | 0.000 | 0.000 | 0.095 | 0.085 |
| North | 11.352 | 6.604 | 0.072 | |||
| Northeast | 13.563 | 10.377 | 0.094 | |||
| East | 14.844 | 16.038 | 0.133 | |||
| Southeast | 11.877 | 22.642 | 0.235 | |||
| South | 10.414 | 14.151 | 0.168 | |||
| Southwest | 12.378 | 15.094 | 0.151 | |||
| West | 13.614 | 7.547 | 0.068 | |||
| Northwest | 11.928 | 7.547 | 0.078 | |||
| Plan curvature | Concave | 45.118 | 34.906 | 0.240 | 0.020 | 0.021 |
| Plan | 8.877 | 11.321 | 0.396 | |||
| Convex | 46.005 | 53.774 | 0.363 | |||
| Profile curvature | Concave | 45.281 | 48.113 | 0.361 | 0.002 | 0.002 |
| Plan | 7.095 | 6.604 | 0.316 | |||
| Convex | 47.624 | 45.283 | 0.323 | |||
| STI | <10 | 76.576 | 82.075 | 0.324 | 0.345 | 0.228 |
| 10–20 | 17.018 | 12.264 | 0.218 | |||
| 20–30 | 3.726 | 5.660 | 0.459 | |||
| 30–40 | 1.317 | 0.000 | 0.000 | |||
| >40 | 1.363 | 0.000 | 0.000 | |||
| SPI | <10 | 56.676 | 59.434 | 0.223 | 0.054 | 0.051 |
| 10–20 | 19.037 | 23.585 | 0.263 | |||
| 20–30 | 7.932 | 2.830 | 0.076 | |||
| 30–40 | 4.124 | 5.660 | 0.291 | |||
| >40 | 12.230 | 8.491 | 0.147 | |||
| TWI | <2 | 56.140 | 62.264 | 0.332 | 0.160 | 0.107 |
| 2–3 | 35.052 | 31.132 | 0.266 | |||
| 3–4 | 6.804 | 5.660 | 0.249 | |||
| 4–5 | 1.845 | 0.943 | 0.153 | |||
| >5 | 0.159 | 0.000 | 0.000 | |||
| Distance to rivers (m) | <200 | 26.385 | 28.302 | 0.219 | 0.018 | 0.017 |
| 200–400 | 22.387 | 28.302 | 0.258 | |||
| 400–600 | 17.492 | 19.811 | 0.231 | |||
| 600–800 | 12.379 | 9.434 | 0.156 | |||
| >800 | 21.357 | 14.151 | 0.135 | |||
| Distance to roads (m) | <500 | 16.524 | 27.358 | 0.299 | 0.036 | 0.040 |
| 500–1000 | 14.614 | 20.755 | 0.257 | |||
| 1000–1500 | 12.738 | 9.434 | 0.134 | |||
| 1500–2000 | 10.994 | 11.321 | 0.186 | |||
| >2000 | 45.130 | 31.132 | 0.125 | |||
| NDVI | −0.02–0.23 | 7.755 | 16.981 | 0.288 | 0.216 | 0.328 |
| 0.23–0.32 | 10.093 | 28.302 | 0.369 | |||
| 0.32–0.38 | 18.757 | 41.509 | 0.291 | |||
| 0.38–0.44 | 34.724 | 11.321 | 0.043 | |||
| 0.44–0.58 | 28.672 | 1.887 | 0.009 | |||
| Soil | Fimic Anthrosol | 0.328 | 0.000 | 0.000 | 0.436 | 0.325 |
| Calcaric Cambisol | 82.702 | 79.245 | 0.214 | |||
| Eutric Cambisol | 12.653 | 14.151 | 0.250 | |||
| Gleyic Cambisol | 2.750 | 6.604 | 0.536 | |||
| Calcaric Regosol | 0.377 | 0.000 | 0.000 | |||
| Eutric Regosol | 1.190 | 0.000 | 0.000 | |||
| Land use | Farmland | 34.928 | 65.094 | 0.282 | 0.477 | 0.525 |
| Forestland | 16.617 | 0.943 | 0.009 | |||
| Grassland | 48.185 | 33.019 | 0.104 | |||
| Water | 0.008 | 0.000 | 0.000 | |||
| Residential areas | 0.236 | 0.943 | 0.605 | |||
| Bareland | 0.025 | 0.000 | 0.000 | |||
| Lithology | A | 65.720 | 52.830 | 0.043 | 0.239 | 0.343 |
| B | 0.021 | 0.000 | 0.000 | |||
| C | 5.811 | 5.660 | 0.052 | |||
| D | 0.251 | 0.943 | 0.201 | |||
| E | 3.165 | 9.434 | 0.160 | |||
| F | 7.254 | 7.547 | 0.056 | |||
| G | 2.576 | 12.264 | 0.255 | |||
| H | 0.965 | 2.830 | 0.157 | |||
| I | 0.245 | 0.000 | 0.000 | |||
| J | 8.257 | 6.604 | 0.043 | |||
| K | 3.074 | 1.887 | 0.033 | |||
| L | 2.336 | 0.000 | 0.000 | |||
| M | 0.326 | 0.000 | 0.000 | |||
| Rainfall (mm/yr) | <400 | 2.041 | 0.000 | 0.000 | 0.210 | 0.161 |
| 400–500 | 7.117 | 6.604 | 0.303 | |||
| 500–600 | 74.158 | 74.528 | 0.328 | |||
| >600 | 16.684 | 18.868 | 0.369 |
| Landslide Conditioning Factor | Average Merit (AM) | Standard Deviation (SD) |
|---|---|---|
| NDVI | 0.273 | ±0.019 |
| Distance to roads | 0.242 | ±0.014 |
| Land use | 0.191 | ±0.020 |
| Distance to rivers | 0.127 | ±0.019 |
| Rainfall | 0.092 | ±0.017 |
| STI | 0.091 | ±0.026 |
| SPI | 0.090 | ±0.032 |
| Profile curvature | 0.072 | ±0.017 |
| Plan curvature | 0.060 | ±0.023 |
| Lithology | 0.055 | ±0.015 |
| TWI | 0.048 | ±0.021 |
| Soil | 0.044 | ±0.016 |
| Slope aspect | 0.025 | ±0.017 |
| Slope angle | 0.015 | ±0.015 |
| Altitude | 0.014 | ±0.010 |
| Model | AUC | SE | 95% CI |
|---|---|---|---|
| CDT | 0.779 | 0.0328 | 0.717 to 0.833 |
| RF-CDT | 0.813 | 0.0300 | 0.754 to 0.863 |
| Bag-CDT | 0.809 | 0.0302 | 0.750 to 0.860 |
| MB-CDT | 0.788 | 0.0320 | 0.727 to 0.841 |
| Model | AUC | SE | 95% CI |
|---|---|---|---|
| CDT | 0.663 | 0.0547 | 0.557 to 0.758 |
| RF-CDT | 0.759 | 0.0504 | 0.658 to 0.842 |
| Bag-CDT | 0.740 | 0.0515 | 0.638 to 0.826 |
| MB-CDT | 0.729 | 0.0537 | 0.626 to 0.816 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy 2019, 21, 106. https://doi.org/10.3390/e21020106
He Q, Xu Z, Li S, Li R, Zhang S, Wang N, Pham BT, Chen W. Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy. 2019; 21(2):106. https://doi.org/10.3390/e21020106
Chicago/Turabian StyleHe, Qingfeng, Zhihao Xu, Shaojun Li, Renwei Li, Shuai Zhang, Nianqin Wang, Binh Thai Pham, and Wei Chen. 2019. "Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling" Entropy 21, no. 2: 106. https://doi.org/10.3390/e21020106
APA StyleHe, Q., Xu, Z., Li, S., Li, R., Zhang, S., Wang, N., Pham, B. T., & Chen, W. (2019). Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy, 21(2), 106. https://doi.org/10.3390/e21020106






