A Continuous-Time Random Walk Extension of the Gillis Model
Abstract
:1. Introduction
2. Review of Previous Work
2.1. Gillis Random Walk
2.2. CTRW
3. Results
3.1. Probability of Being at the Origin
3.1.1. Gillis Way
- is the probability of being (arriving) at j at (within) time t;
- is the probability of arriving at j at time t.
3.1.2. Recurrence Relation: First-Return Time to the Origin
3.1.3. Finite-Mean Waiting-Time Distributions
3.1.4. Infinite-Mean Waiting-Time Distributions
3.2. Survival Probability on the Positive Semi-Axis
3.3. Occupation Times
3.3.1. Occupation Time of the Origin
3.3.2. Occupation Time of the Positive Semi-Axis
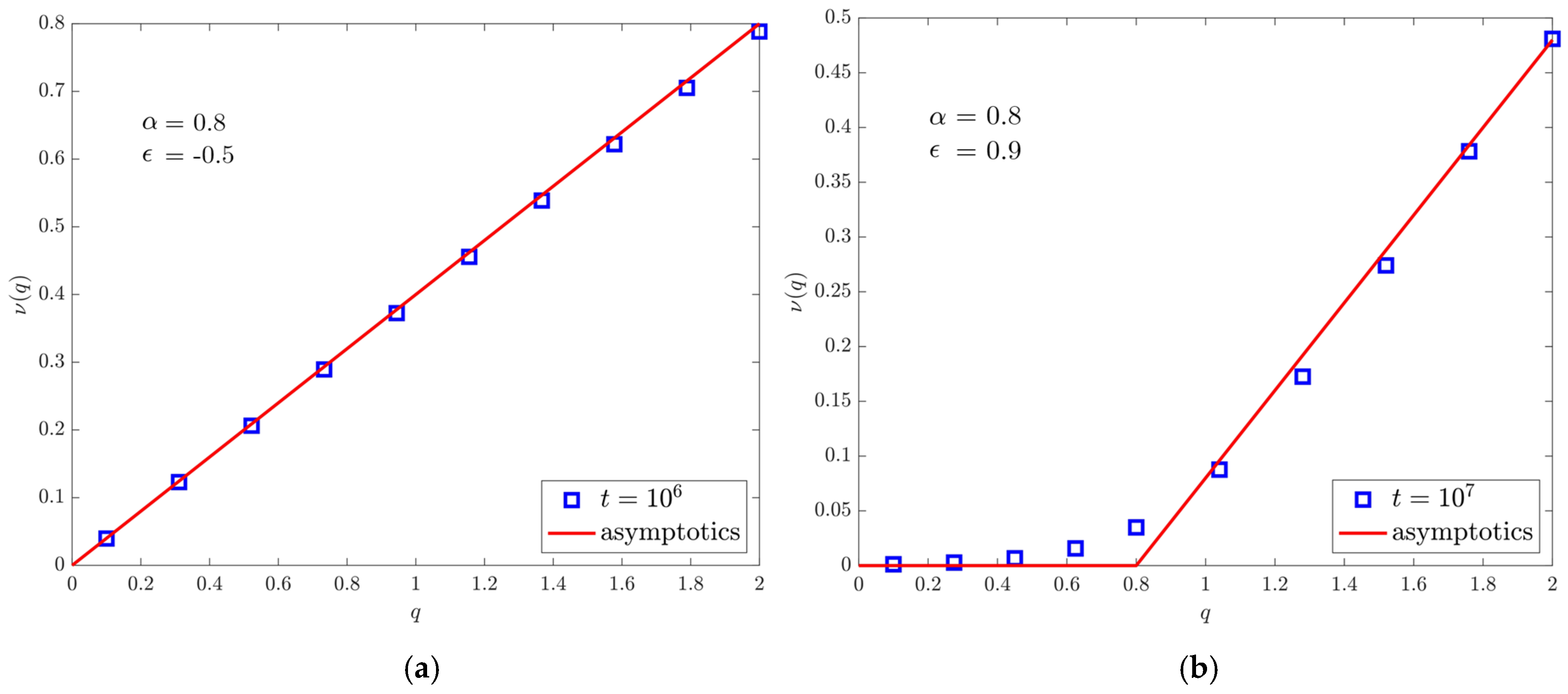
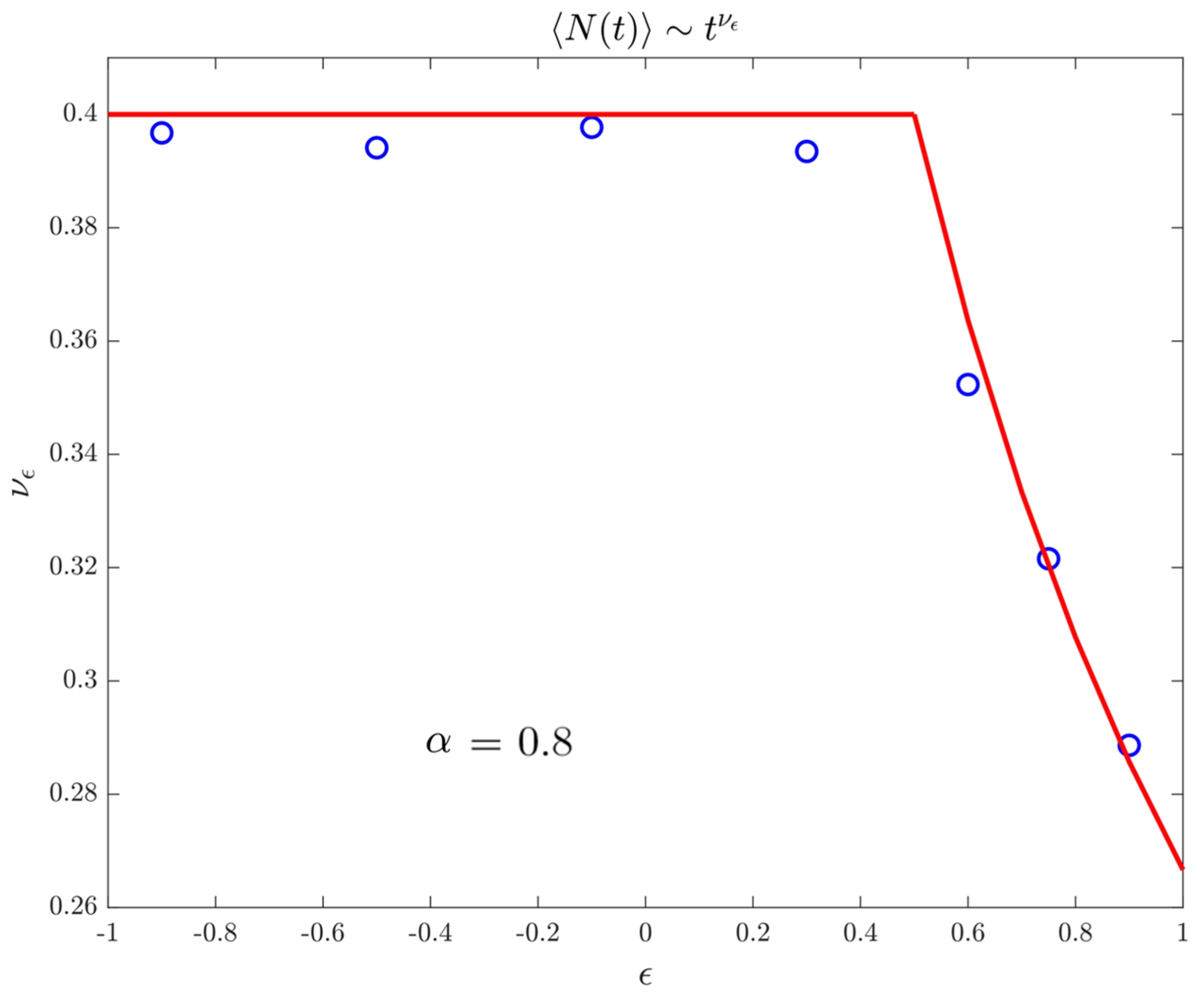
3.4. Moments Spectrum
3.5. Statistics of Records
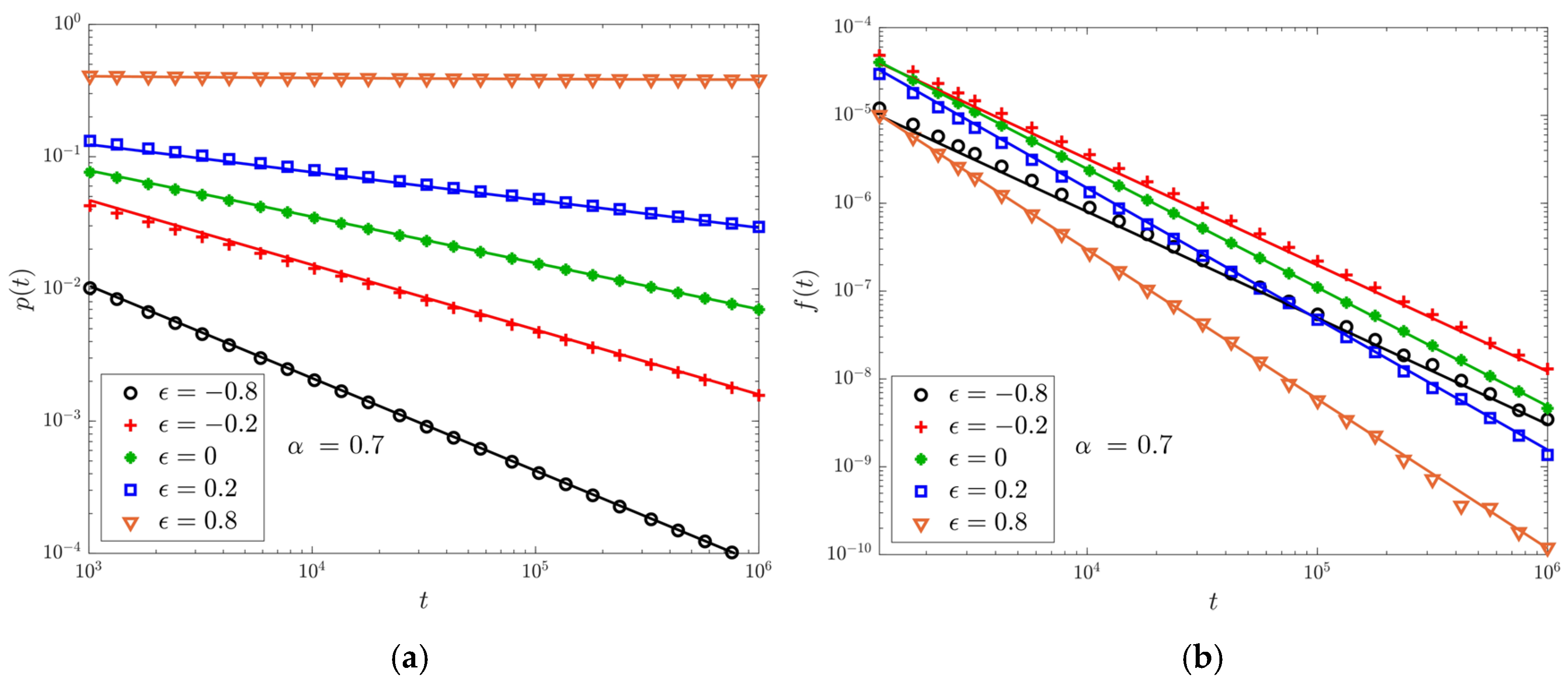
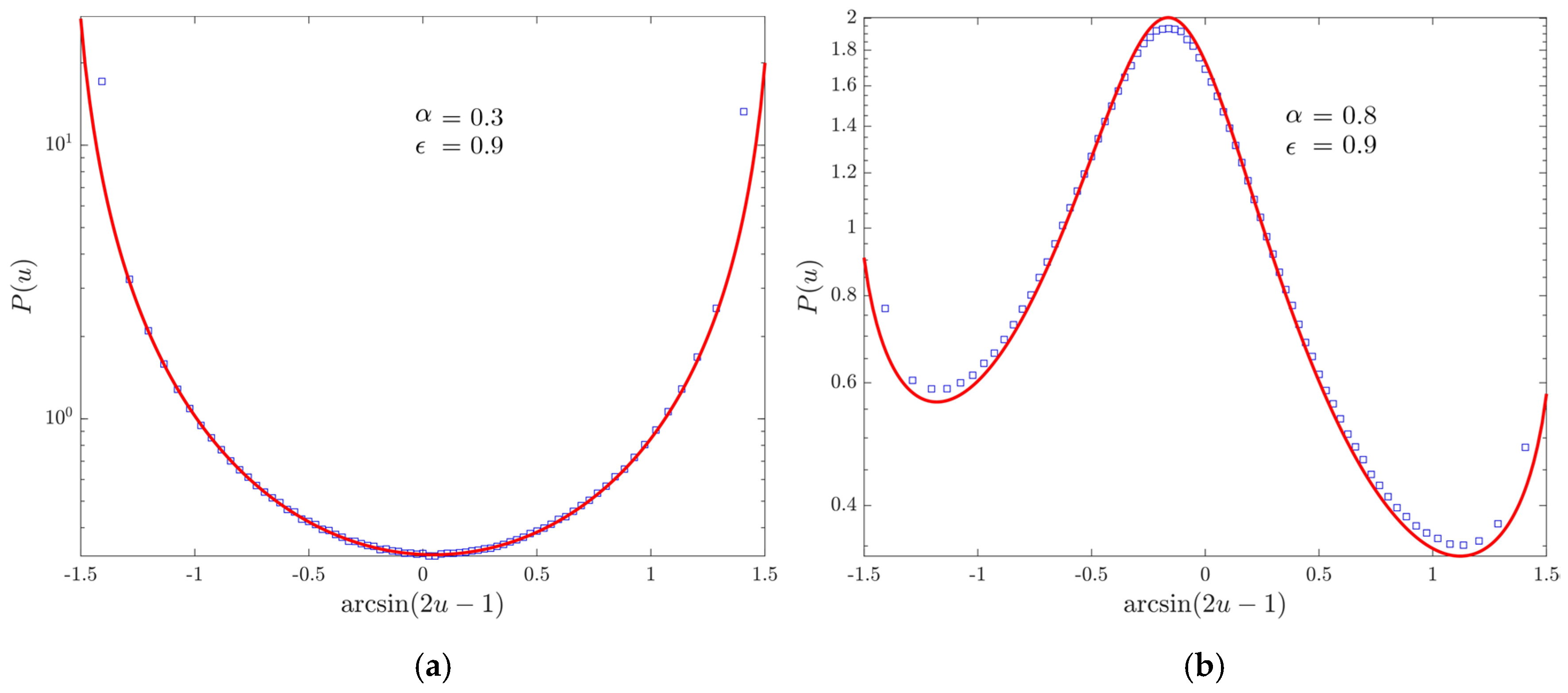
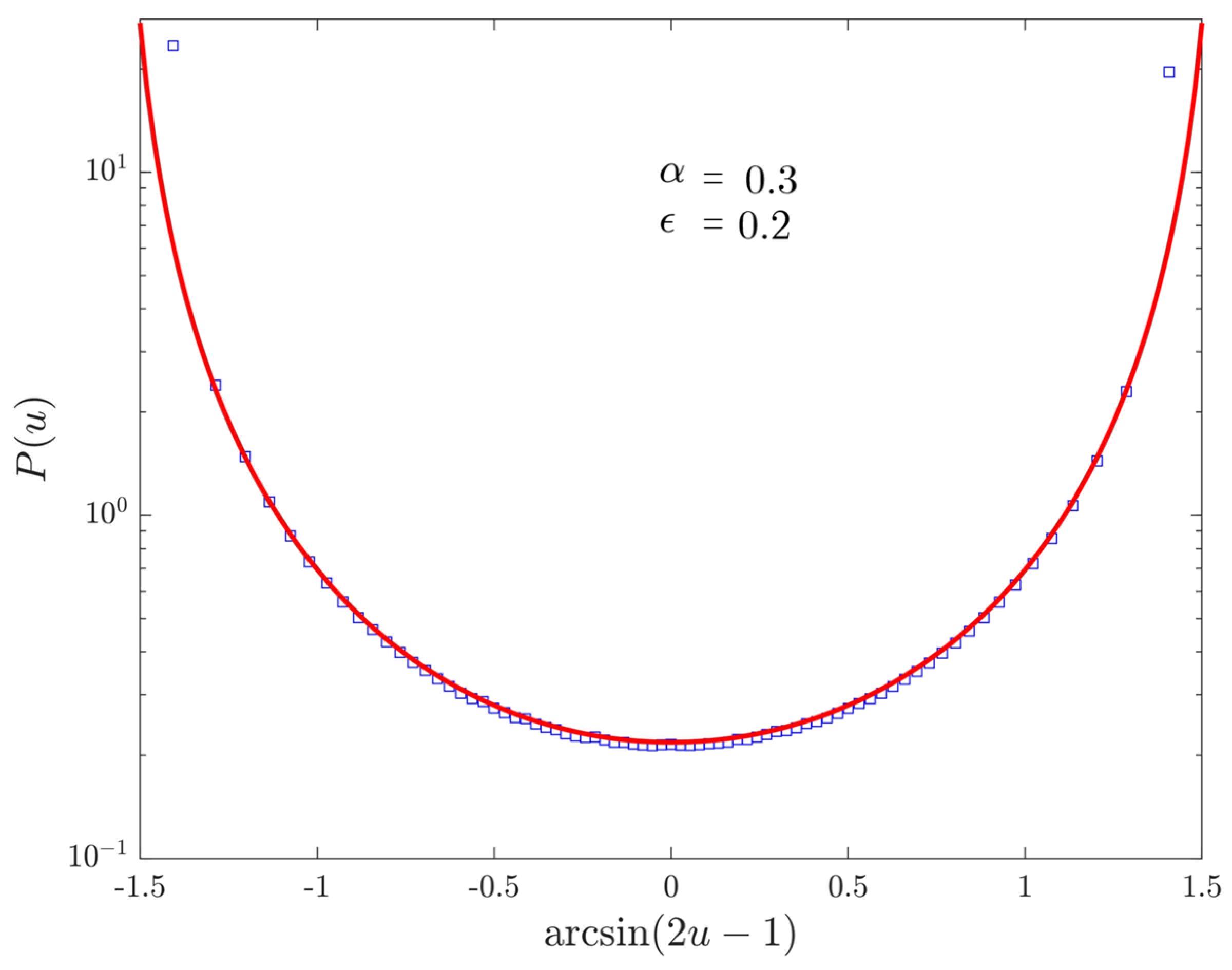
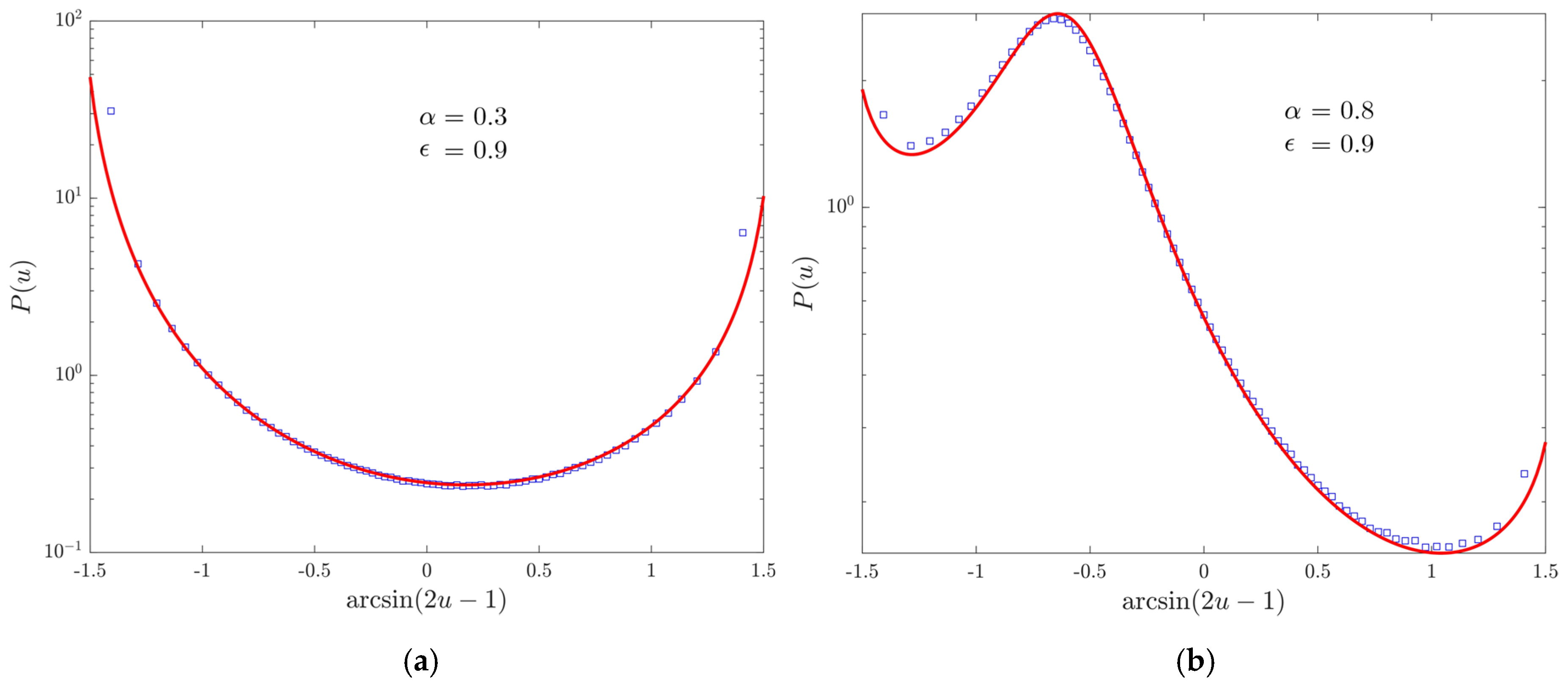
4. Numerical Results
4.1. Return and First-Return Events
4.2. Occupation Times
4.3. Moments Spectrum
4.4. Records
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CTRW | Continuous Time Random Walk |
| Probability Density Function | |
| i.i.d. | Independent Identically Distributed |
Appendix A. Gillis-Type Proof
Appendix B. Hitting Time PDF of the Origin: Exact Results
Appendix C. First-Hitting Time PDF: Exact Results
Appendix C.1. First-Return
Appendix C.2. First-Hitting
Appendix D. CTRW on
References
- Hughes, B.D. Random Walks and Random Environments. Volume I: Random Walks; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Menshikov, M.; Popov, S.; Wade, A. Non-Homogeneous Random Walks. Lyapunov Function Methods for Near-Critical Stochastic Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; Wiley–VHC: Berlin, Germany, 2008. [Google Scholar]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.S. A Lévy flight for light. Nature 2008, 453, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Dentz, M.; Cortis, A.; Scher, H.; Berkowitz, B. Time behavior of solute transport in heterogeneous media: Transition from anomalous to normal transport. Adv. Water Resour. 2004, 27, 155–173. [Google Scholar] [CrossRef]
- Cortis, A.; Berkowitz, B. Anomalous transport in “classical” soil and sand columns. Soil Sci. Soc. Am. J. 2004, 68, 1539–1548. [Google Scholar] [CrossRef]
- Kühn, T.; Ihalainen, T.O.; Hyväluoma, J.; Dross, N.; Willman, S.F.; Langowski, J.; Vihinen-Ranta, M.; Timonen, J. Protein Diffusion in Mammalian Cell Cytoplasm. PLoS ONE 2011, 6, e22962. [Google Scholar] [CrossRef] [Green Version]
- Nissan, A.; Berkowitz, B. Inertial Effects on Flow and Transport in Heterogeneous Porous Media. Phys. Rev. Lett. 2018, 120, 054504. [Google Scholar] [CrossRef]
- Barkai, E.; Garini, Y.; Metzler, R. Strange kinetics of single molecules in living cells. Phys. Today 2012, 65, 29–35. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Burov, S.; Metzler, R.; Barkai, E. Random Time-Scale Invariant Diffusion and Transport Coefficients. Phys. Rev. Lett. 2008, 101, 058101. [Google Scholar] [CrossRef]
- Burov, S.; Jeon, J.H.; Metzler, R.; Barkai, E. Single particle tracking in systems showing anomalous diffusion: The role of weak ergodicity breaking. Phys. Chem. Chem. Phys. 2010, 13, 1800–1812. [Google Scholar] [CrossRef] [Green Version]
- Gillis, J. Centrally biased discrete random walk. Q. J. Math. 1956, 7, 144–152. [Google Scholar]
- Percus, O.E. Phase transition in one-dimensional random walk with partially reflecting boundaries. Adv. Appl. Probab. 1985, 17, 594–606. [Google Scholar] [CrossRef]
- Montroll, E.W. Random Walks on Lattices. III. Calculation of First-Passage Times with Application to Exciton Trapping on Photosynthetic Units. J. Math. Phys. 1969, 10, 153–165. [Google Scholar] [CrossRef]
- Hill, J.M.; Gulati, C.M. The random walk associated by the game of roulette. J. Appl. Probab. 1981, 18, 931–936. [Google Scholar] [CrossRef]
- Hughes, B.D.; Sahimi, M. Random walks on the Bethe lattice. J. Stat. Phys. 1982, 23, 1688–1692. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483. [Google Scholar] [CrossRef] [Green Version]
- Shlesinger, M.F.; Klafter, J. Lévy Walks Versus Lévy Flights. In On Growth and Form. Fractal and Non–Fractal Patterns in Physics; Stanley, H.E., Ostrowsky, N., Eds.; NATO ASI Series E: Applied Sciences-No. 100; Martinus Nijhoff Publihers: Dordrecht, The Netherlands; Boston, MA, USA; Lancaster, UK, 1986; pp. 279–283. [Google Scholar]
- Montroll, E.W.; Weiss, G.H. Random walks on lattices, II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks. From Tools to Applications; Oxford University Press Inc.: New York, NY, USA, 2011; pp. 1–51. [Google Scholar]
- Scalas, E. The application of continuous-time random walks in finance and economics. Physica A 2006, 362, 225–239. [Google Scholar] [CrossRef]
- Wolfgang, P.; Baschnagel, J. Stochastic Processes. From Physics to Finance; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Scher, H.; Shlesinger, M.F.; Bendler, J.T. Time-scale invariance in transport and relaxation. Phys. Today 1991, 44, 26–34. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef] [Green Version]
- Boano, F.; Packman, A.I.; Cortis, A.; Ridolfi, R.R.L. A continuous time random walk approach to the stream transport of solutes. Water Resour. Res. 2007, 43, W10425. [Google Scholar] [CrossRef]
- Geiger, S.; Cortis, A.; Birkholzer, J.T. Upscaling solute transport in naturally fractured porous media with the continuous time random walk method. Water Resour. Res. 2010, 46, W12530. [Google Scholar] [CrossRef] [Green Version]
- Onofri, M.; Pozzoli, G.; Radice, M.; Artuso, R. Exploring the Gillis model: a discrete approach to diffusion in logarithmic potentials. J. Stat. Mech. 2020, 2020, 113201. [Google Scholar] [CrossRef]
- Redner, S. A Guide to First-Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications Inc.: New York, NY, USA, 1970. [Google Scholar]
- Hughes, B.D. On returns to the starting site in lattice random walks. Physica A 1986, 134, 443–457. [Google Scholar] [CrossRef]
- Castiglione, P.; Mazzino, A.; Muratore-Ginanneschi, P.; Vulpiani, A. On strong anomalous diffusion. Physica D 1999, 134, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Hryniv, O.; Menshikov, M.V.; Wade, A.R. Excursions and path functionals for stochastic processes with asymptotically zero drifts. Stoch. Process. Their Appl. 2013, 123, 1891–1921. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Straka, P. Inverse Stable Subordinators. Math. Model. Nat. Phenom. 2013, 8, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Janson, S. Stable Distributions. (Lecture Notes). arXiv 2011, arXiv:1112.0220v2. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley and Sons, Inc.: New York, NY, USA, 1971; Volume II. [Google Scholar]
- Sparre Andersen, E. On the fluctuations of sums of random variables II. Math. Scand. 1954, 2, 195–223. [Google Scholar]
- Mounaix, P.; Majumdar, S.N.; Schehr, G. Statistics of the number of records for random walks and Lévy Flights on a 1D Lattice. J. Phys. A Math. Theor. 2020, 53, 415003. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley and Sons, Inc.: New York, NY, USA, 1968; Volume I. [Google Scholar]
- Artuso, R.; Cristadoro, G.; Degli Esposti, M.; Knight, G.S. Sparre-Andersen theorem with spatiotemporal correlations. Phys. Rev. E 2014, 89, 052111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radice, M.; Onofri, M.; Artuso, R.; Pozzoli, G. Statistics of occupation times and connection to local properties of nonhomogeneous random walks. Phys. Rev. E 2020, 101, 042103. [Google Scholar]
- Darling, D.A.; Kac, M. On occupation times for Markoff processes. Trans. Am. Math. Soc. 1957, 84, 444–458. [Google Scholar] [CrossRef]
- Lamperti, J. An occupation time theorem for a class of stochastic processes. Trans. Am. Math. Soc. 1958, 88, 380–387. [Google Scholar] [CrossRef]
- Godrèche, C.; Luck, J.M. Statistics of the occupation time for renewal processes. J. Stat. Phys. 2001, 104, 489–524. [Google Scholar] [CrossRef]
- Barkai, E. Residence time statistics for normal and fractional diffusion in a force field. J. Stat. Phys. 2006, 123, 883–907. [Google Scholar] [CrossRef] [Green Version]
- Bel, G.; Barkai, E. Occupation time and ergodicity breaking in biased continuous time random walks. J. Phys. Condens. Matter 2005, 17, S4287–S4304. [Google Scholar] [CrossRef] [Green Version]
- Bel, G.; Barkai, E. Random walk to a nonergodic equilibrium concept. Phys. Rev. E 2006, 73, 16125. [Google Scholar] [CrossRef] [Green Version]
- Bel, G.; Barkai, E. Weak ergodicity breaking in continuous-time random walk. Phys. Rev. Lett. 2005, 94, 240602. [Google Scholar] [CrossRef] [Green Version]
- Widder, D.V. The Laplace Transform; Princeton University Press: London, UK, 1946. [Google Scholar]
- Dechant, A.; Lutz, E.; Barkai, E.; Kessler, D.A. Solution of the Fokker-Planck Equationation with a Logarithmic Potential. J. Stat. Phys. 2011, 145, 1524–1545. [Google Scholar] [CrossRef]
- Lamperti, J. Criteria for the Recurrence or Transience of Stochastic Process I. J. Math. Anal. Appl. 1960, 1, 314–330. [Google Scholar] [CrossRef] [Green Version]
- Lamperti, J. Criteria for Stochastic Processes II: Passage-Time Moments. J. Math. Anal. Appl. 1963, 7, 127–145. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozzoli, G.; Radice, M.; Onofri, M.; Artuso, R. A Continuous-Time Random Walk Extension of the Gillis Model. Entropy 2020, 22, 1431. https://doi.org/10.3390/e22121431
Pozzoli G, Radice M, Onofri M, Artuso R. A Continuous-Time Random Walk Extension of the Gillis Model. Entropy. 2020; 22(12):1431. https://doi.org/10.3390/e22121431
Chicago/Turabian StylePozzoli, Gaia, Mattia Radice, Manuele Onofri, and Roberto Artuso. 2020. "A Continuous-Time Random Walk Extension of the Gillis Model" Entropy 22, no. 12: 1431. https://doi.org/10.3390/e22121431
APA StylePozzoli, G., Radice, M., Onofri, M., & Artuso, R. (2020). A Continuous-Time Random Walk Extension of the Gillis Model. Entropy, 22(12), 1431. https://doi.org/10.3390/e22121431




