Hybrid Adaptive Lossless Image Compression Based on Discrete Wavelet Transform
Abstract
:1. Introduction
2. Materials and Methods
2.1. Predictive and Transform Coding
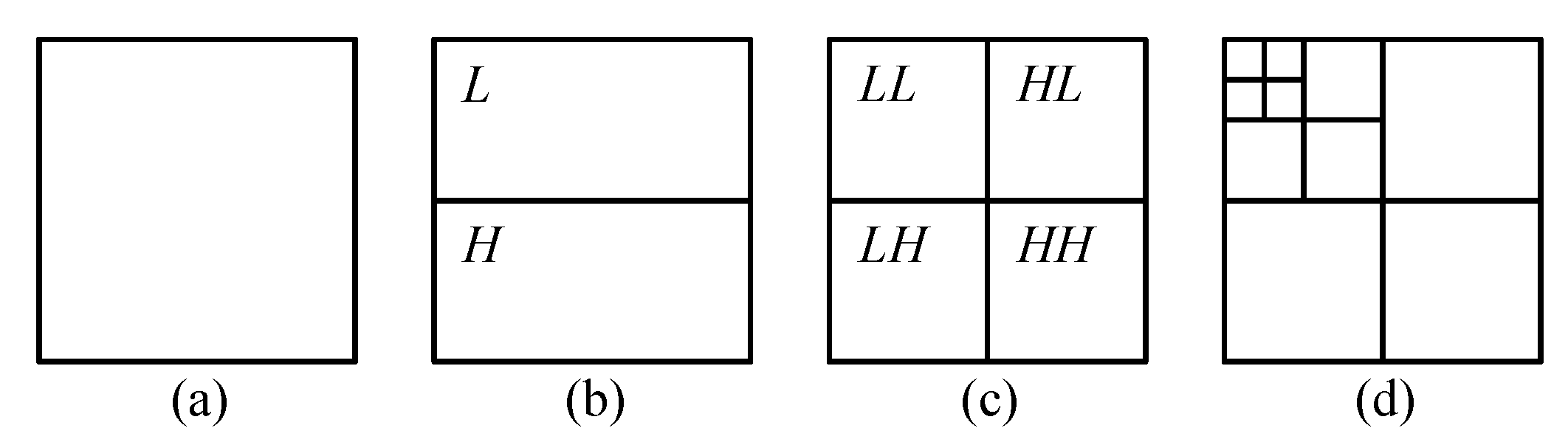
2.2. Reversible Discrete Wavelet Transform
2.3. Application of Reversible Denoising and Lifting Steps with Step Skipping to DWT
2.4. Hybrid Transform that Combines DWT with Prediction
| Predictor | Prediction |
|---|---|
| NOP | 0 |
| MED | median(W, N, W + N − NW) |
| AVG | (W + N)/2 |
| LEFT | W |
| UPPER | N |
2.5. Filter Selection Heuristics for the Hybrid Transform
- For each of the denoising filters, check the bitrate obtained for an image, using this filter in RDLS-SS-DWT+Pred steps for all subbands at all transform levels. Then for all subbands at all levels, select the filter that resulted in the best overall bitrate.
- For each transform level a (starting from level 1) and for each subband b (at a specific level analyzed in the H, L, HL, HH, LL, and LH order), try to find a better filter by checking for each filter (except for the one already selected) the bitrate obtained using this filter for subband b at level a, while the filters selected so far are used for other subbands. If the Null filter gets selected for a prediction step, then select it also for the complementary update step.
- B1.
- If the Null filter was selected in step A, then for each transform level a (starting from level 1) and for subbands b at a specific level analyzed in the H, HL, and HH order, try to find a better filter by checking for each filter (except for the one already selected) the bitrate obtained using this filter for subband b at level a, while the filters selected so far are used for other subbands.
- B2.
- If a filter other than Null was selected in step A, then for each transform level (starting from level 1) and for subbands b at a specific level analyzed in the L, HH, LL, and LH order, try to find a better filter by checking for each filter (except for the one already selected) the bitrate obtained using this filter for subband b at level a, while the filters selected so far are used for other subbands. If the Null filter gets selected for HH, then select it for the complementary LH.
2.6. Test Data, Experimental Procedure, and Implementations
3. Experimental Results and Discussion
3.1. Effects of Integrating DWT with Prediction

- Skipping the entire DWT and applying prediction to an untransformed image, which has not been decomposed into subbands, this variant, compared to three-level DWT with all the steps skipped and actual prediction applied to all subbands, is simpler and should obtain similar bitrates so it may be effective for many images.
- Application of the unmodified typical-level DWT with prediction applied to the LL subband only will almost always be better than DWT without prediction, although the difference will be small because of the small size of the LL subband.
3.2. Employing Entropy Estimation to Speed Up the Heuristic
3.3. Schemes Extending the Heuristic with Prediction Applied to Untransformed Image
4. Conclusions and Further Work
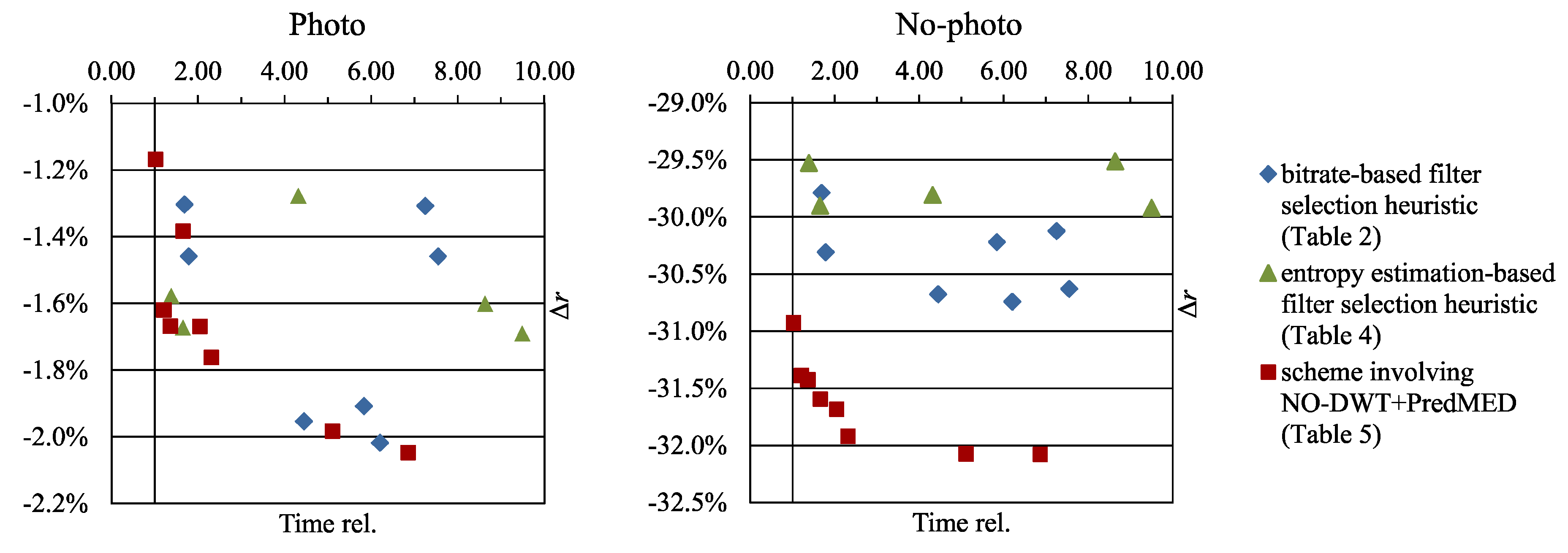
- The scheme using NO-DWT+PredMED and RDLS-SS-DWT+Pred, compared to the unmodified JPEG 2000, improves the compression ratios of Photo and No-photo images by about 1.6% and 31.4%, respectively, at the expense of a small increase in the compression time (by 21%). Larger bitrate improvements, exceeding 2% and 32%, respectively, are possible at the expense of increasing the compression time several times.
- The scheme employing DWT+PredMED_LL instead of RDLS-SS-DWT+Pred is also interesting despite improving compression ratios to a smaller extent. It can be applied by introducing only minimal and simple modifications to JPEG 2000 and allows for improving the bitrates by 1.2% and 30.9%, respectively, at a negligible cost of 2% compression time increase.
Supplementary Materials
Acknowledgments
Conflicts of Interest
Nomenclature
| the greatest integer less than or equal to v | |
| ∆rvariant | average bitrate change due to applying specific transform variant |
| cden | cost of denoising of a sample |
| cenc | cost of entropy coding of a single prediction error |
| cest | cost of estimating bitrate per single sample |
| cLS | cost of a single LS |
| cpred | cost of predicting a sample |
| f | number of filters |
| l | transform level |
| M | number of samples in the subband |
| MaxPE | the greatest prediction error obtained |
| MinPE | the smallest prediction error obtained |
| N | upper neighbor of the pixel being predicted |
| n | number of iterations of the step B of the heuristic |
| NW | upper-left neighbor of the pixel being predicted |
| P | size of the image (number of pixels) |
| p | number of predictors |
| pi | probability of occurrence of the prediction error value i in the subband |
| q | signal length |
| rDWT | average bitrate of unmodified JPEG 2000 |
| S | discrete signal |
| i-th signal sample | |
| denoised sample | |
| cost of applying RDLSs while computing all subbands by NH | |
| cost of applying RDLSs while computing all subbands by RH | |
| cost of applying prediction and entropy coding of final subbands by entropy estimation-based variant of RH | |
| cost of applying prediction and entropy coding of final subbands by NH | |
| cost of applying prediction and entropy coding of final subbands by RH | |
| TJ | time of unmodified JPEG 2000 compression |
| W | left-hand neighbor of the pixel being predicted |
References
- Clunie, D. What is different about medical image compression? IEEE Commun. Soc. MMTC E Lett. 2011, 6, 31–37. [Google Scholar]
- Liu, F.; Hernandez-Cabronero, M.; Sanchez, V.; Marcellin, M.; Bilgin, A. The current role of image compression standards in medical imaging. Information 2017, 8, 131. [Google Scholar] [CrossRef] [Green Version]
- Taubman, D.; Marcellin, M. JPEG2000 Image Compression Fundamentals, Standards and Practice; Springer: New York, NY, USA, 2004. [Google Scholar]
- ISO/IEC; ITU-T. Information Technology—JPEG 2000 Image Coding System: Core Coding System; ISO/IEC International Standard 15444-1 and ITU-T Recommendation T.800; ISO/IEC; ITU-T: Geneva, Switzerland, 2016. [Google Scholar]
- ISO/IEC; ITU-T. Information Technology—JPEG 2000 Image Coding System: Extensions for Three-Dimensional Data; ISO/IEC International Standard 15444-10 and ITU-T Recommendation T.809; ISO/IEC; ITU-T: Geneva, Switzerland, 2011. [Google Scholar]
- National Electrical Manufacturers Association. Digital Imaging and Communications in Medicine (DICOM) Part 5: Data Structures and Encoding; NEMA Standard PS3.5 2019e; NEMA: Arlington, VA, USA, 2019. [Google Scholar]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS. IEEE Trans. Image Process. 2000, 9, 1309–1324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ISO/IEC; ITU-T. Information Technology—Lossless and Near-Lossless Compression of Continuous-Tone Still Images—Baseline; ISO/IEC International Standard 14495-1 and ITU-T Recommendation T.87; ISO/IEC; ITU-T: Geneva, Switzerland, 2006. [Google Scholar]
- Dufaux, F.; Sullivan, G.J.; Ebrahimi, T. The JPEG XR image coding standard [Standards in a Nutshell]. IEEE Signal Process. Mag. 2009, 26, 195–204. [Google Scholar] [CrossRef] [Green Version]
- ISO/IEC; ITU-T. Information Technology—JPEG XR Image Coding System—Image Coding Specification; ISO/IEC International Standard 29199-2 and ITU-T Recommendation T.832; ISO/IEC; ITU-T: Geneva, Switzerland, 2019. [Google Scholar]
- Addison, P. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I.; Sweldens, W. Factoring wavelet transforms into lifting steps. J. Fourier Anal. Appl. 1998, 4, 247–269. [Google Scholar] [CrossRef]
- Sweldens, W. The lifting scheme: A custom-design construction of biorthogonal wavelets. Appl. Comput. Harmon. Anal. 1996, 3, 186–200. [Google Scholar] [CrossRef] [Green Version]
- Bruylants, T.; Munteanu, A.; Schelkens, P. Wavelet based volumetric medical image compression. Signal Process. Image Commun. 2015, 31, 112–133. [Google Scholar] [CrossRef] [Green Version]
- Starosolski, R. Application of reversible denoising and lifting steps to DWT in lossless JPEG 2000 for improved bitrates. Signal Process. Image Commun. 2015, 39, 249–263. [Google Scholar] [CrossRef]
- Starosolski, R. Skipping selected steps of DWT computation in lossless JPEG 2000 for improved bitrates. PLoS ONE 2016, 11, e0168704. [Google Scholar] [CrossRef] [Green Version]
- Starosolski, R. Application of Reversible Denoising and Lifting Steps with Step Skipping to Color Space Transforms for Improved Lossless Compression. J. Electron. Imaging 2016, 25, 043025. [Google Scholar] [CrossRef] [Green Version]
- Matsuda, I.; Ozaki, N.; Umezu, Y.; Itoh, S. Lossless coding using variable block-size adaptive prediction optimized for each image. In Proceedings of the 13th European Signal Processing Conference (EUSIPCO 2005), Antalya, Turkey, 4–8 September 2005. [Google Scholar]
- Hudson, G.; Léger, A.; Niss, B.; Sebestyén, I.; Vaaben, J. JPEG-1 standard 25 years: Past, present, and future reasons for a success. J. Electron. Imaging 2018, 27, 040901. [Google Scholar] [CrossRef]
- ISO/IEC. Information Technology—Coding of Moving Pictures and Associated Audio for Digital Storage Media at up to about 1,5 Mbit/s—Part 2: Video; ISO/IEC International Standard 11172-2; ISO/IEC: Geneva, Switzerland, 1993. [Google Scholar]
- Wiegand, T.; Sullivan, G.; Bjontegaard, G.; Luthra, A. Overview of the H.264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 560–576. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Ye, Y.; Kim, S. JVET-N1002: Algorithm description for Versatile Video Coding and Test Model 5 (VTM 5). In Proceedings of the Joint Video Experts Team (JVET), 14th Meeting, Geneva, Switzerland, 19–27 March 2019. [Google Scholar]
- Malvar, H.S.; Sullivan, G.J.; Srinivasan, S. Lifting-based reversible color transformations for image compression. Proc. SPIE 2008, 7073, 707307. [Google Scholar] [CrossRef]
- Strutz, T. Multiplierless reversible colour transforms and their automatic election for image data compression. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 1249–1259. [Google Scholar] [CrossRef]
- Starosolski, R. New simple and efficient color space transformations for lossless image compression. J. Vis. Commun. Image Represent. 2014, 25, 1056–1063. [Google Scholar] [CrossRef]
- ISO/IEC; ITU-T. Information Technology—JPEG 2000 Image Coding System: Extensions; ISO/IEC International Standard 15444-2 and ITU-T Recommendation T.801; ISO/IEC; ITU-T: Geneva, Switzerland, 2004. [Google Scholar]
- Kim, S.; Cho, N.I. Hierarchical Prediction and Context Adaptive Coding for Lossless Color Image Compression. IEEE Trans. Image Process. 2014, 23, 445–449. [Google Scholar] [CrossRef]
- Claypoole, R.; Davis, G.; Sweldens, W.; Baraniuk, R. Nonlinear wavelet transforms for image coding via lifting. IEEE Trans. Image Process. 2003, 12, 1449–1459. [Google Scholar] [CrossRef]
- Boulgouris, N.; Tzovaras, D.; Strintzis, M. Lossless image compression based on optimal prediction, adaptive lifting and conditional arithmetic coding. IEEE Trans. Image Process. 2001, 10, 1–14. [Google Scholar] [CrossRef]
- Bernas, T.; Starosolski, R.; Wójcicki, R. Application of detector precision characteristics for the denoising of biological micrographs in the wavelet domain. Biomed. Signal Process. Control 2015, 19, 1–13. [Google Scholar] [CrossRef]
- Liu, C.; Szeliski, R.; Kang, S.B.; Zitnick, C.L.; Freeman, W.T. Automatic Estimation and Removal of Noise from a Single Image. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Tanaka, M.; Okutomi, M. Single-Image Noise Level Estimation for Blind Denoising. IEEE Trans. Image Process. 2013, 22, 5226–5237. [Google Scholar] [CrossRef] [PubMed]
- Set CT2 of Color Images. Available online: http://www1.hft-leipzig.de/strutz/Papers/Testimages/CT2/ (accessed on 24 May 2020).
- Strutz, T.; Leipnitz, A. Reversible Colour Spaces without Increased Bit Depth and Their Adaptive Selection. IEEE Signal Proc. Lett. 2015, 22, 1269–1273. [Google Scholar] [CrossRef]
- Peng, W.; Walls, F.; Cohen, R.; Xu, J.; Ostermann, J.; MacInnis, A.; Lin, T. Overview of screen content video coding: Technologies, standards, and beyond. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 393–408. [Google Scholar] [CrossRef]
- RDLS-SS-DWT+Pred Implementation, Version 1.0. Available online: http://sun.aei.polsl.pl/~rstaros/rdls-ss-dwt/ (accessed on 24 May 2020).
- Starosolski, R. Reversible denoising and lifting based color component transformation for lossless image compression. Multimed. Tools Appl. 2019, 79, 11269–11294. [Google Scholar] [CrossRef] [Green Version]


| Transform Variant | Time | Images | ||
|---|---|---|---|---|
| Rel. | Photo | No-Photo | ||
| 1 | rDWT | 1.00 | 3.9975 | 2.9162 |
| 2 | ∆rDWT+Pred(5) | 1.07 | −0.18% | −1.33% |
| 3 | ∆rRDLS-SS-DWT, NH(6,2,1) | 55.85 | −1.08% | −17.59% |
| 4 | ∆rRDLS-SS-DWT+Pred, NH(6,2,5) | 59.32 | −2.08% | −31.19% |
| 5 | ∆rRDLS-SS-DWT+Pred, NH(6,1,5) | 33.43 | −2.05% | −31.16% |
| 6 | ∆rRDLS-SS-DWT+Pred, NH(6,0,5) | 7.55 | −1.46% | −30.63% |
| 7 | ∆rRDLS-SS-DWT+Pred, NH(6,1,2) | 32.08 | −1.94% | −30.66% |
| 8 | ∆rSS-DWT+Pred, NH(2,1,5) | 6.20 | −2.02% | −30.74% |
| 9 | ∆rSS-DWT+Pred, NH(2,1,2) | 5.84 | −1.91% | −30.22% |
| 10 | ∆rSS-DWT+Pred, RH(2,1,5) | 4.45 | −1.95% | −30.68% |
| 11 | ∆rRDLS-SS-DWT+Pred, NH(6,0,2) | 7.25 | −1.31% | −30.12% |
| 12 | ∆rSS-DWT+Pred, NH(2,0,5) | 1.79 | −1.46% | −30.31% |
| 13 | ∆rSS-DWT+Pred, NH(2,0,2) | 1.69 | −1.30% | −29.79% |
| Description | Time (ms per 106 Pixels) | Percentage of TJ |
|---|---|---|
| Unmodified JPEG 2000 compression (TJ) | 258.6 | 100.0% |
| 3-level DWT transform | 19.7 | 7.6% |
| Entropy coding | 167.0 | 64.6% |
| Remaining JPEG 2000 operations | 72.0 | 27.8% |
| Entropy estimation | 1.3 | 0.5% |
| Prediction (MED predictor) | 3.0 | 1.1% |
| Denosing | 62.7 | 24.3% |
| Transform Variant | Time | Images | ||
|---|---|---|---|---|
| Rel. | Photo | No-Photo | ||
| 1 | ∆rRDLS-SS-DWT+Pred, H0_RH(6,2,5) | 14.67 | −1.71% | −29.92% |
| 2 | ∆rRDLS-SS-DWT+Pred, H0_RH(6,1,5) | 9.50 | −1.69% | −29.92% |
| 3 | ∆rRDLS-SS-DWT+Pred, H0_RH(6,0,5) | 4.32 | −1.28% | −29.81% |
| 4 | ∆rRDLS-SS-DWT+Pred, H0_RH(6,1,2) | 8.64 | −1.60% | −29.51% |
| 5 | ∆rSS-DWT+Pred, H0_RH(2,1,5) | 1.65 | −1.67% | −29.90% |
| 6 | ∆rSS-DWT+Pred, H0_RH(2,1,2) | 1.39 | −1.58% | −29.53% |
| Transform Variant/Scheme | Time | Images | ||
|---|---|---|---|---|
| Rel. | Photo | No-Photo | ||
| 1 | ∆rNO-DWT+PredMED | 0.94 | −0.19% | −31.49% |
| 2 | ∆rDWT+PredMED_LL | 1.00 | −0.24% | −0.82% |
| 3 | ∆rH0_sel(NO-DWT+PredMED; DWT+PredMED_LL) | 1.02 | −1.17% | −30.93% |
| 4 | ∆rH0_sel(NO-DWT+PredMED; SS-DWT+Pred, H0_RH(2,1,2)) | 1.21 | −1.62% | −31.39% |
| 5 | ∆rH0_sel(NO-DWT+PredMED; SS-DWT+Pred, H0_RH(2,1,5)) | 1.36 | −1.67% | −31.43% |
| 6 | ∆rmin_bpp(NO-DWT+PredMED; DWT+PredMED_LL) | 1.66 | −1.38% | −31.59% |
| 7 | ∆rmin_bpp(NO-DWT+PredMED; SS-DWT+Pred, H0_RH(2,1,2)) | 2.04 | −1.67% | −31.68% |
| 8 | ∆rmin_bpp(NO-DWT+PredMED; SS-DWT+Pred, H0_RH(2,1,5)) | 2.31 | −1.76% | −31.92% |
| 9 | ∆rmin_bpp(NO-DWT+PredMED; SS-DWT+Pred, RH(2,1,5)) | 5.11 | −1.98% | −32.07% |
| 10 | ∆rmin_bpp(NO-DWT+PredMED; SS-DWT+Pred, NH(2,1,5)) | 6.86 | −2.05% | −32.08% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starosolski, R. Hybrid Adaptive Lossless Image Compression Based on Discrete Wavelet Transform. Entropy 2020, 22, 751. https://doi.org/10.3390/e22070751
Starosolski R. Hybrid Adaptive Lossless Image Compression Based on Discrete Wavelet Transform. Entropy. 2020; 22(7):751. https://doi.org/10.3390/e22070751
Chicago/Turabian StyleStarosolski, Roman. 2020. "Hybrid Adaptive Lossless Image Compression Based on Discrete Wavelet Transform" Entropy 22, no. 7: 751. https://doi.org/10.3390/e22070751
APA StyleStarosolski, R. (2020). Hybrid Adaptive Lossless Image Compression Based on Discrete Wavelet Transform. Entropy, 22(7), 751. https://doi.org/10.3390/e22070751





