In this section, the traditional intuitionistic fuzzy distance and the intuitionistic fuzzy cross-entropy distance are used to analyze and compare the ranking of earthquake shelters.
4.1. Intuitionistic Fuzzy Cross-Entropy Distance and Grey Correlation Analysis
The stability and reliability of the method of intuitionistic fuzzy cross-entropy and the grey correlation coefficient are analyzed through comparative experiments. Assume that the government carries out shelter assessment and optimization for the five areas with a large disaster impact, and use
,
,
,
, and
to represent them. The government analyzes and evaluates the geographical location
, disaster risk
, rescue facilities
, and feasibility
of the five disaster areas. The decision-maker adopts an IFN to express the objective evaluation value of alternatives under different attributes, and the intuitionistic fuzzy decision matrix
is shown in
Table 4.
The decision maker’s subjective preference values for alternatives A, B, C, D, and E are also expressed by IFNs: , , , , and . In order to choose the best alternative to build a shelter in the earthquake disaster area, the government adopts the intuitionistic fuzzy cross-entropy and grey correlation analysis method to make a decision.
Step 1. Determine the values of alternative , , , , and ; the objective evaluation attribute values ,,,; the decision makers’ objective evaluation matrix ; and subjective preference values ,,,,.
Step 2. According to model (17), the intuitionistic fuzzy cross-entropy distance between the objective evaluation value and the subjective preference value of each alternative is calculated to form the distance matrix:
Step 3. Assuming that the grey resolution coefficient is
, the grey correlation coefficient between the decision-maker’s subjective preference value and the objective evaluation value is calculated according to model (16). The coefficient matrix is as follows:
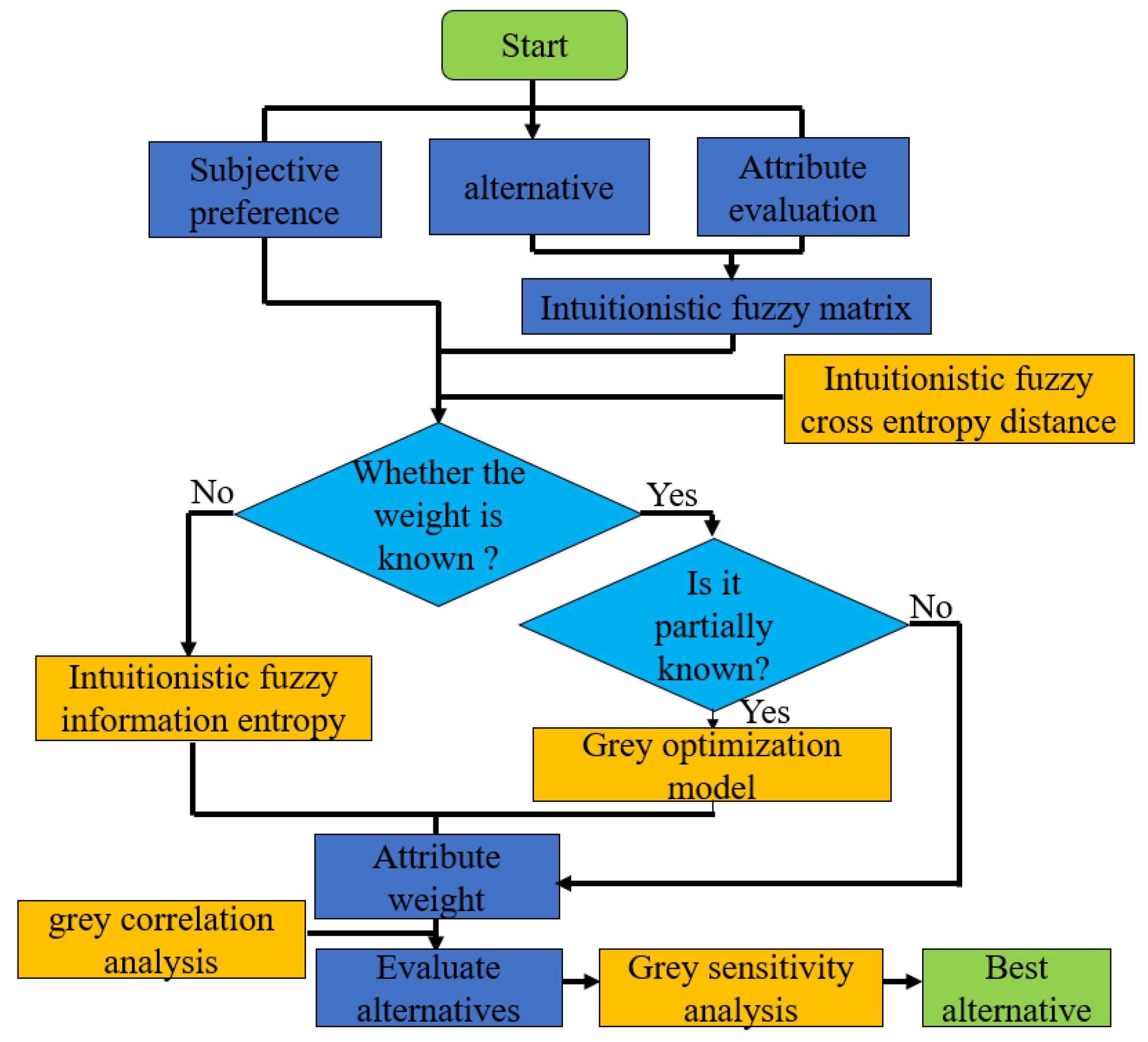
Step 4. Calculate the attribute weight according to the known information provided by the above case. When the attribute weight is known, the model is relatively easy to solve. The following focuses on the analysis of two situations: The attribute weight is completely unknown and the attribute weight range is known.
Case 1. The weight of attributes is completely unknown. According to the idea of intuitionistic fuzzy entropy, the average intuitionistic fuzzy entropy of the attribute is obtained by combining model (18): , , , . Then, according to model (19), we obtain the attribute weight , , and . The attribute weight obtained is substituted into model (22), and the comprehensive grey correlation coefficient of the alternatives under the attribute condition is calculated: , , , , and . From the comprehensive grey correlation coefficient of the alternatives, the result is and . Therefore, the alternative D is the best and the government should give priority to building earthquake shelters in the region.
For proving the superiority and stability of the intuitionistic fuzzy cross-entropy and the comprehensive grey correlation analysis algorithm proposed in this paper, different resolution coefficients
are set for sensitivity analysis to compare and analyze whether the above alternatives will produce fluctuations. Set
0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.00. The results of the comprehensive correlation coefficient are shown in
Table 5. The ranking results of alternatives did not fluctuate with the change in resolution coefficient.
In order to verify the reliability and stability of the method proposed in this paper more intuitively, we use Python graphics to carry out simulation experiments on the sequencing and gray resolution coefficient of each alternative, and the specific results are shown in
Figure 2 (G is the grey resolution coefficient).
It can be seen from
Figure 2 that in the seven experiments of sensitivity analysis of grey resolution coefficient, the ranking results of alternatives have not changed, and
is always maintained. The simulation experiment shows that
is the best alternative to build a shelter in the earthquake disaster area, and the decision result does not fluctuate, which shows the strong stability.
Case 2. The value range of attribute weight is known:
,
,
, and
. Through the linear programming model (21), the objective function
to maximize the grey correlation coefficient of alternatives is constructed and solved:
The attribute weight is
,
,
, and
by MATLAB. Combined with model (22), the comprehensive grey correlation coefficient of each alternative is obtained:
,
,
,
,
. According to the comprehensive grey correlation coefficient
of the alternatives, we can obtain
. Therefore, the order of alternatives is
, and, thus, alternative
is the best. The government should give priority to building earthquake shelters in area
, which is the same as the decision-making result when the attribute weight is unknown.
In order to further verify the stability and superiority of the algorithm of intuitionistic fuzzy cross-entropy and comprehensive grey correlation analysis when the attribute weight range is known, different resolution coefficients are also set for sensitivity analysis, and the optimal alternative and decision results are compared. Taking
0.40, 0.50, 0.60, 0.70, 0.80, 0.90, and 1.00, and attribute weight and comprehensive grey correlation analysis when the attribute weight range is known, different resolution coefficients are also set for sensitivity analysis, and the optimal alternative and decision results are compared. The attribute weight and comprehensive grey correlation coefficient of each alternative are shown in
Table 6 and
Table 7. From the table data, the change in the grey resolution coefficient does not affect the attribute weight and the decision-making result of the alternative, which is still
. It is always the best alternative to build the seismic shelter in the
area. In addition, when the weight is completely unknown, the comprehensive grey correlation coefficient of the alternatives is higher than that of the alternatives with known range of attribute weight.
More importantly, when the grey resolution coefficient fluctuates from 0.4 to 1.0, whether the weight is known or unknown, the change range of the comprehensive grey correlation coefficient of alternative
is the smallest, which is 0.0300 and 0.0302, respectively (see
Table 8). Alternative
is always the worst, and its fluctuation is also the largest, which is 0.1438 and 0.1239, respectively. Based on this, the stability of the proposed method is proved.
From
Table 7, Python simulation results are shown in
Figure 3. Compared to
Figure 2, the comprehensive grey correlation coefficient decreases but does not change the overall trend of each alternative, and the decision results remain unchanged. Whether the attribute weights are known or not, the optimal alternative and ranking results are the same, which shows the superiority and stability of the method.
Through the above comparative analysis, the intuitionistic fuzzy entropy and grey correlation analysis method has achieved good results in solving the MAEDM problems. In this way, the ranking results have strong stability and environmental adaptability.
4.2. Traditional Intuitionistic Fuzzy Distance and Grey Correlation Analysis
Based on the data given by the above problem of ranking earthquake shelters, the traditional intuitionistic fuzzy distance and grey correlation degree are used to analyze and give the ranking results.
The traditional intuitionistic fuzzy distance model (4) has been given; thus, the corresponding grey correlation coefficient
is
where
denotes the objective evaluation value,
denotes the subjective preference information, and grey resolution coefficient
.
Step 1. Calculating the grey correlation coefficient of each alternative between the objective evaluation value and subjective preference information.
Step 2. Determining the attribute weight. Due to the fact that the range of attribute weight values is known, utilize model (21) to establish the following single-objective programming model:
Solving this model, attribute weight can be obtained:
,
,
, and
.
Step 3. On the basis of model (20), the comprehensive grey correlation coefficient is calculated: , , , , .
Step 4. Determining the alternatives ranking. Rank the alternatives according to the size of the comprehensive grey correlation coefficient . Thus, is the ranking result.
4.3. Comparative Analysis
Based on the ranking problem of earthquake shelters, this paper makes a comparative analysis from two aspects:
(1). The attribute weight is completely unknown and the attribute weight range is known
For a more intuitive comparison, it is further explored based on
Figure 2 and
Figure 3. Regardless of whether the attribute weight is known or unknown, the ranking results of alternatives maintain high stability. The best alternative is always
, and the worst is always
. The comprehensive grey correlation coefficient of the alternative is positively correlated with the grey resolution coefficient, which indicates that the larger the resolution coefficient, the greater the correlation coefficient of the corresponding alternative.
Moreover, in the case of unknown weight, the comprehensive grey correlation coefficient of each alternative is always better than that of the known weight range, which also indirectly proves the fact that attribute weights are uncertain in most fields of decision problems (see
Figure 4 and
Figure 5). In addition, the results obtained by using a reasonable method to determine the attribute weights are more practical.
Meanwhile, based on the data in
Table 8, we can further analyze the volatility of the comprehensive grey correlation coefficient in two cases. From
Figure 6 (deviation 1 represents unknown weights and deviation 2 represents known weights range), the deviation curves of the comprehensive grey correlation coefficient in the two kinds of weights situation almost coincide. However, when the weight is unknown, the fluctuation amplitude of the comprehensive grey correlation coefficient is still less than that of the known attribute weight range.
Through the comparative analysis, we can see that the ranking result with unknown weight is more reasonable and more consistent with the uncertainty of the decision environment in MAEDM problems.
(2). The traditional intuitionistic fuzzy distance with the intuitionistic fuzzy cross-entropy distance
Through the above solution, the ranking results of the intuitionistic fuzzy cross-entropy method is
. Under the sufficient sensitivity analysis, the results maintain a high stability. However, by using the traditional intuitionistic fuzzy distance method, the result of ranking becomes
. Although the ranking result has little change, the best alternative is still
and the worst one is
(see
Table 9). This also fully proves that the method based on intuitionistic fuzzy cross-entropy and grey correlation analysis proposed in this paper has strong stability.
According to the above two groups of comparative analysis, it can be concluded from many aspects that is the best alternative. For the decision maker to make rescue measures, it is the most reasonable decision to give priority to the establishment of earthquake shelters in the area.