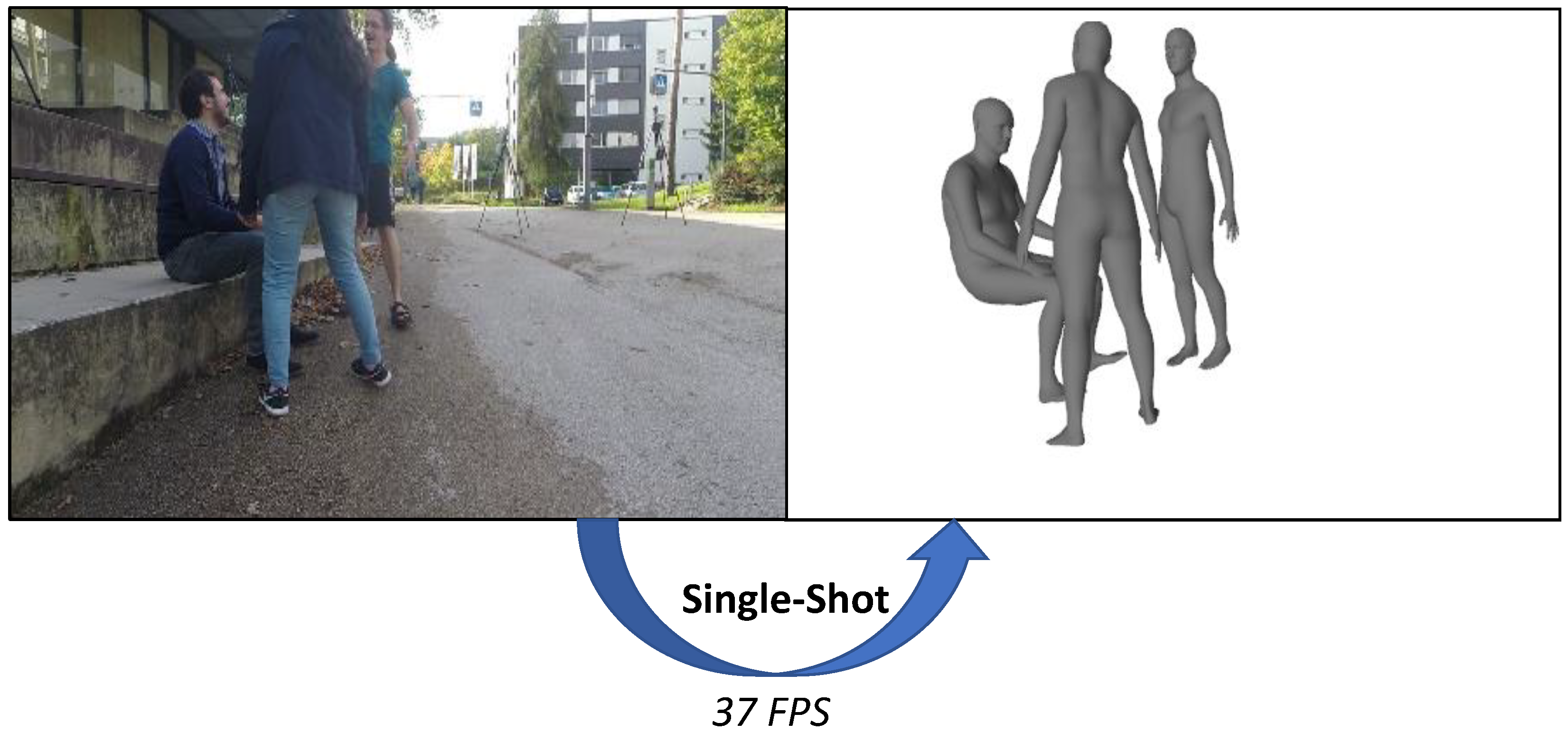
Single-Shot 3D Multi-Person Shape Reconstruction from a Single RGB Image
Abstract
:1. Introduction
2. Related Works
2.1. 2D Multi-Person Pose Estimation
2.2. 3D Multi-Person Pose Estimation
2.3. 3D Human Shape Reconstruction
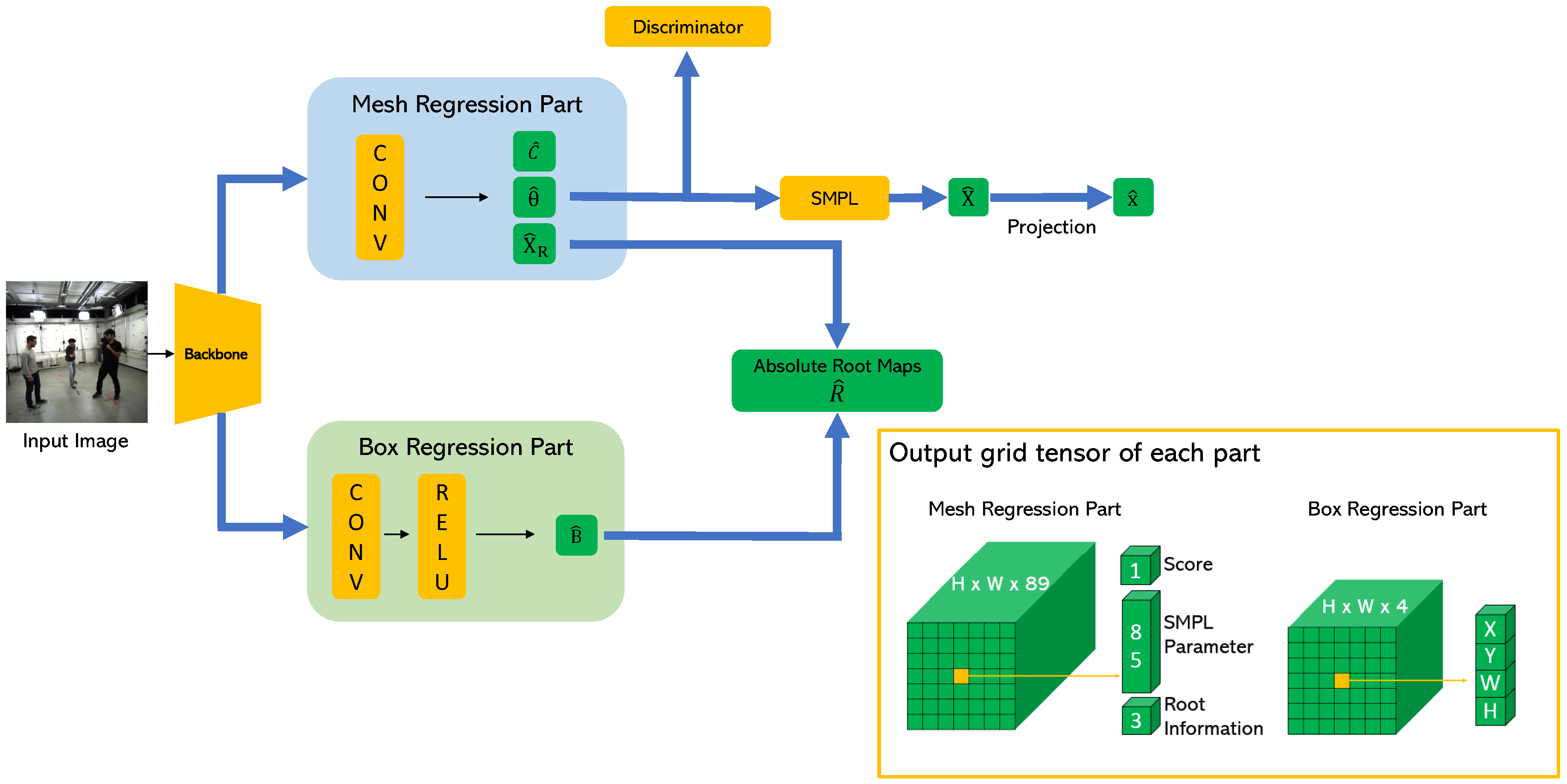
3. Proposed Methods
3.1. 3D Body Representation
3.2. Box Regression Part
3.3. Mesh Regression Part
3.4. Implementation Details
| Algorithm 1 Procedure of obtaining the shapes of multiple persons from an input RGB image. |
| Input: Single RGB Image I Output: List of human body vertices V
|
4. Experimental Results
4.1. Datasets and Evaluation Metrics
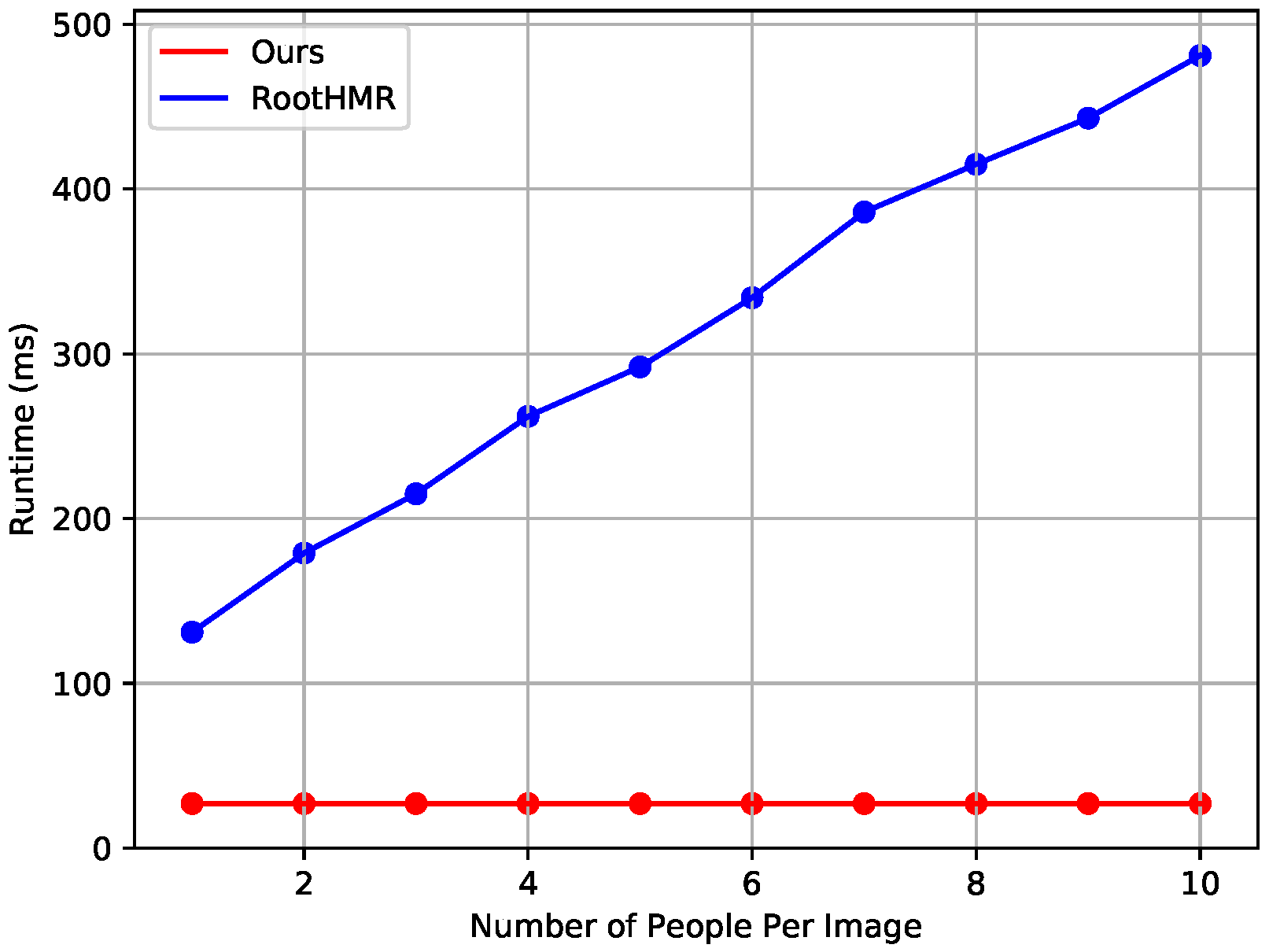
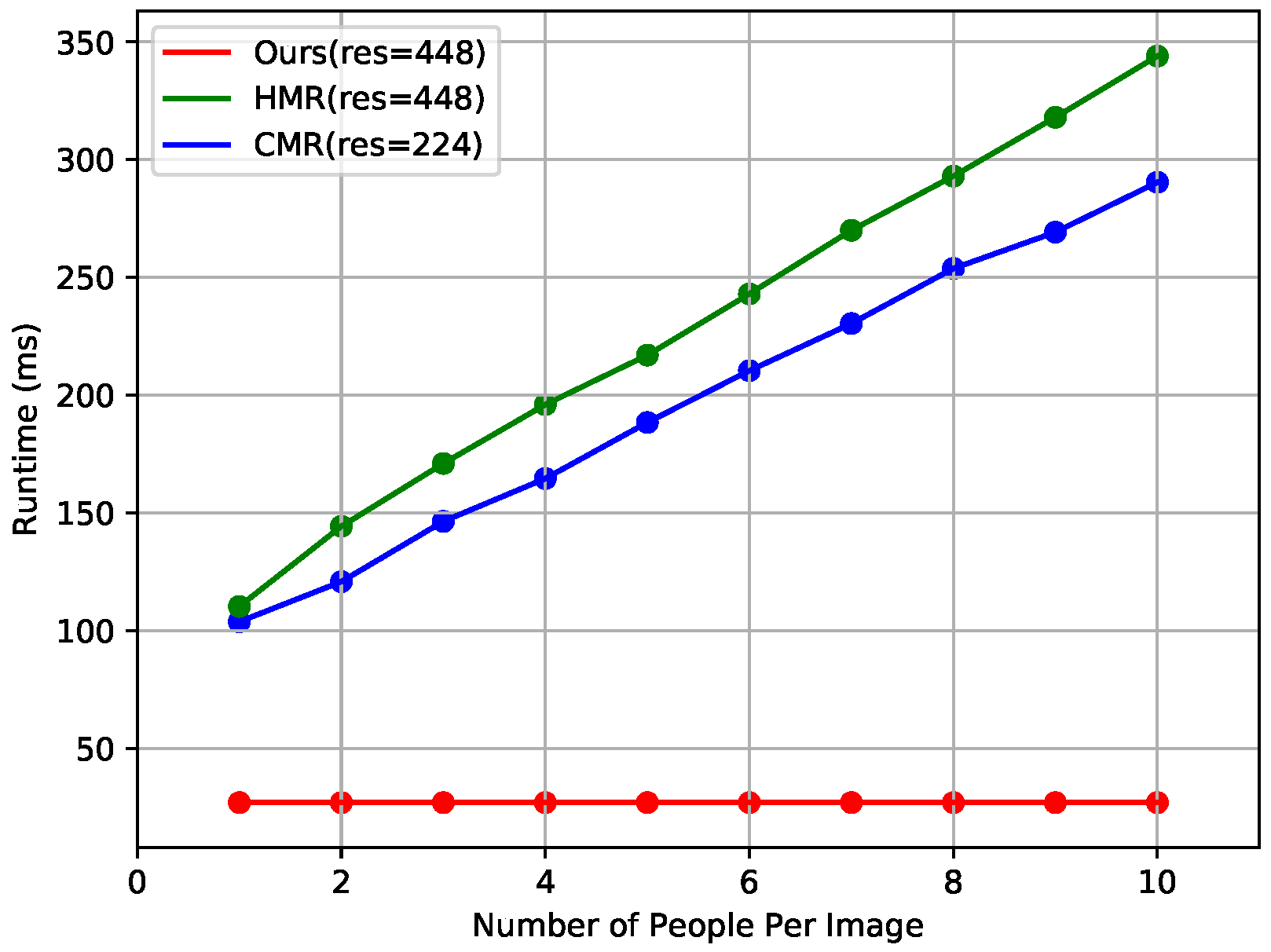
4.2. Comparison with the Baseline Method
4.3. Comparison with State-of-the-Art Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kanazawa, A.; Black, M.J.; Jacobs, D.W.; Malik, J. End-to-end recovery of human shape and pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7122–7131. [Google Scholar]
- Omran, M.; Lassner, C.; Pons-Moll, G.; Gehler, P.; Schiele, B. Neural body fitting: Unifying deep learning and model based human pose and shape estimation. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 484–494. [Google Scholar]
- Pavlakos, G.; Zhu, L.; Zhou, X.; Daniilidis, K. Learning to estimate 3d human pose and shape from a single color image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 459–468. [Google Scholar]
- Tan, J.K.V.; Budvytis, I.; Cipolla, R. Indirect deep structured learning for 3d human shape and pose prediction. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017; Volume 3, p. 6. [Google Scholar]
- Tung, H.Y.; Tung, H.W.; Yumer, E.; Fragkiadaki, K. Self-supervised learning of motion capture. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5236–5246. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. Graph. (TOG) 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Leo, M.; Mosca, N.; Spagnolo, P.; Mazzeo, P.L.; D’Orazio, T.; Distante, A. Real-time multiview analysis of soccer matches for understanding interactions between ball and players. In Proceedings of the International Conference on Content-based Image and Video Retrieval, Niagara Falls, ON, Canada, 7–9 July 2008; pp. 525–534. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. PoseFix: Model-agnostic general human pose refinement network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zanfir, A.; Marinoiu, E.; Zanfir, M.; Popa, A.I.; Sminchisescu, C. Deep network for the integrated 3d sensing of multiple people in natural images. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 3–8 December 2018; pp. 8410–8419. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. Camera distance-aware top-down approach for 3d multi-person pose estimation from a single rgb image. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 10133–10142. [Google Scholar]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Yu, G.; Sun, J. Cascaded pyramid network for multi-person pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7103–7112. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. Multi-scale aggregation r-cnn for 2d multi-person pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Long Beach, CA, USA, 15–20 June 2019; pp. 1–9. [Google Scholar]
- Papandreou, G.; Zhu, T.; Kanazawa, N.; Toshev, A.; Tompson, J.; Bregler, C.; Murphy, K. Towards accurate multi-person pose estimation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4903–4911. [Google Scholar]
- Xiao, B.; Wu, H.; Wei, Y. Simple baselines for human pose estimation and tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 466–481. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime multi-person 2d pose estimation using part affinity fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 7291–7299. [Google Scholar]
- Kocabas, M.; Karagoz, S.; Akbas, E. Multiposenet: Fast multi-person pose estimation using pose residual network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 417–433. [Google Scholar]
- Kreiss, S.; Bertoni, L.; Alahi, A. Pifpaf: Composite fields for human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11977–11986. [Google Scholar]
- Newell, A.; Huang, Z.; Deng, J. Associative embedding: End-to-end learning for joint detection and grouping. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 2277–2287. [Google Scholar]
- Rogez, G.; Weinzaepfel, P.; Schmid, C. Lcr-net: Localization-classification-regression for human pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3433–3441. [Google Scholar]
- Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Sridhar, S.; Pons-Moll, G.; Theobalt, C. Single-shot multi-person 3d pose estimation from monocular rgb. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 120–130. [Google Scholar]
- Chen, Y.; Kim, T.K.; Cipolla, R. Inferring 3d shapes and deformations from single views. In Proceedings of the European Conference on Computer Vision (ECCV), Heraklion, Crete, Greece, 5–11 September 2010; pp. 300–313. [Google Scholar]
- Guan, P.; Weiss, A.; Balan, A.O.; Black, M.J. Estimating human shape and pose from a single image. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 Septemper–2 October 2009; pp. 1381–1388. [Google Scholar]
- Hasler, N.; Ackermann, H.; Rosenhahn, B.; Thormählen, T.; Seidel, H.P. Multilinear pose and body shape estimation of dressed subjects from image sets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 1823–1830. [Google Scholar]
- Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.; Romero, J.; Black, M.J. Keep it smpl: Automatic estimation of 3d human pose and shape from a single image. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 561–578. [Google Scholar]
- Pishchulin, L.; Insafutdinov, E.; Tang, S.; Andres, B.; Andriluka, M.; Gehler, P.V.; Schiele, B. Deepcut: Joint subset partition and labeling for multi person pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4929–4937. [Google Scholar]
- Varol, G.; Ceylan, D.; Russell, B.; Yang, J.; Yumer, E.; Laptev, I.; Schmid, C. Bodynet: Volumetric inference of 3d human body shapes. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 20–36. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Black, M.J.; Daniilidis, K. Learning to reconstruct 3d human pose and shape via model-fitting in the loop. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 2252–2261. [Google Scholar]
- Wu, S.; Rupprecht, C.; Vedaldi, A. Unsupervised learning of probably symmetric deformable 3d objects from images in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, DC, USA, 16–18 June 2020; pp. 1–10. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. Eur. Conf. Comput. Vis. 2016, 9905, 21–37. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Loper, M.; Mahmood, N.; Black, M.J. MoSh: Motion and shape capture from sparse markers. ACM Trans. Graph. (TOG) 2014, 33, 1–13. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference for Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the Advances in Neural Information Processing Systems (NIPS) Workshops, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3. 6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2d human pose estimation: New benchmark and state of the art analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3686–3693. [Google Scholar]
- Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3d human pose estimation in the wild using improved cnn supervision. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 506–516. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. arXiv 2014, arXiv:1405.0312. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Daniilidis, K. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4501–4510. [Google Scholar]
- Lassner, C.; Romero, J.; Kiefel, M.; Bogo, F.; Black, M.J.; Gehler, P.V. Unite the people: Closing the loop between 3d and 2d human representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6050–6059. [Google Scholar]


| Methods | MPJPE ↓ |
|---|---|
| RootHMR | 80.8 |
| Ours | 92.8 |
| Methods | MRPE ↓ | MRPE ↓ | MRPE ↓ | MRPE ↓ |
|---|---|---|---|---|
| RootHMR | 27.5 | 35.9 | 93.7 | 115.3 |
| Ours | 22.8 | 21.0 | 115.5 | 126.1 |
| Methods | 3DPCK ↑ | AUC ↑ | 3DPCK ↑ |
|---|---|---|---|
| RootHMR | 68.2 | 31.5 | 17.4 |
| Ours | 51.1 | 22.8 | 19.1 |
| Methods | Rec. Error ↓ |
|---|---|
| Lassner et al. [41] | 93.9 |
| SMPLify [24] | 82.3 |
| Pavlakos et al. [3] | 75.9 |
| NBF [2] | 59.9 |
| HMR [1] | 56.8 |
| CMR [40] | 50.1 |
| Ours | 65.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.H.; Chang, J.Y. Single-Shot 3D Multi-Person Shape Reconstruction from a Single RGB Image. Entropy 2020, 22, 806. https://doi.org/10.3390/e22080806
Kim SH, Chang JY. Single-Shot 3D Multi-Person Shape Reconstruction from a Single RGB Image. Entropy. 2020; 22(8):806. https://doi.org/10.3390/e22080806
Chicago/Turabian StyleKim, Seong Hyun, and Ju Yong Chang. 2020. "Single-Shot 3D Multi-Person Shape Reconstruction from a Single RGB Image" Entropy 22, no. 8: 806. https://doi.org/10.3390/e22080806
APA StyleKim, S. H., & Chang, J. Y. (2020). Single-Shot 3D Multi-Person Shape Reconstruction from a Single RGB Image. Entropy, 22(8), 806. https://doi.org/10.3390/e22080806






