Figure 1.
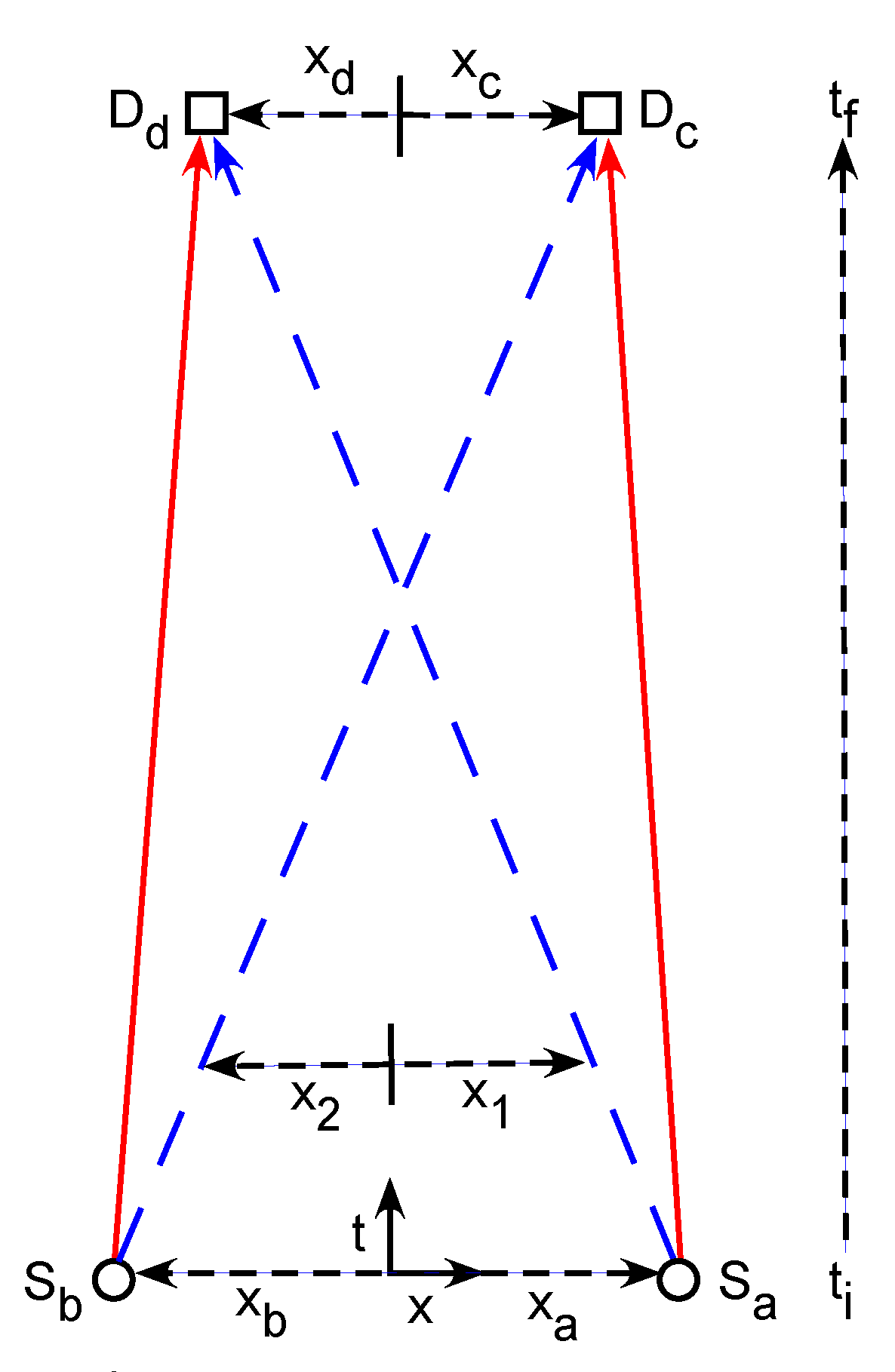
A (1 + 1)-dimensional spacetime diagram of the Gedankenexperimental setup. The sources
and
are at fixed locations
and
, while the detectors
and
are at variable locations
and
. The sources and detectors are colinear in space. The sources each emit one quantum on command at the initial time
. The locations of these quanta are
and
. We analyze only those runs where the detectors each absorb one quantum at the final time
. The red (solid) and blue (dashed) lines between the sources and detectors show two possible ways this can happen. This is a lower dimensional version of the Hanbury Brown–Twiss effect experiment [
19,
20,
21]. If the two detectors are both moved to the outside of the two sources, the experimental topology becomes equivalent to that of the Einstein–Podolsky–Rosen experiment [
23].
Figure 1.
A (1 + 1)-dimensional spacetime diagram of the Gedankenexperimental setup. The sources
and
are at fixed locations
and
, while the detectors
and
are at variable locations
and
. The sources and detectors are colinear in space. The sources each emit one quantum on command at the initial time
. The locations of these quanta are
and
. We analyze only those runs where the detectors each absorb one quantum at the final time
. The red (solid) and blue (dashed) lines between the sources and detectors show two possible ways this can happen. This is a lower dimensional version of the Hanbury Brown–Twiss effect experiment [
19,
20,
21]. If the two detectors are both moved to the outside of the two sources, the experimental topology becomes equivalent to that of the Einstein–Podolsky–Rosen experiment [
23].
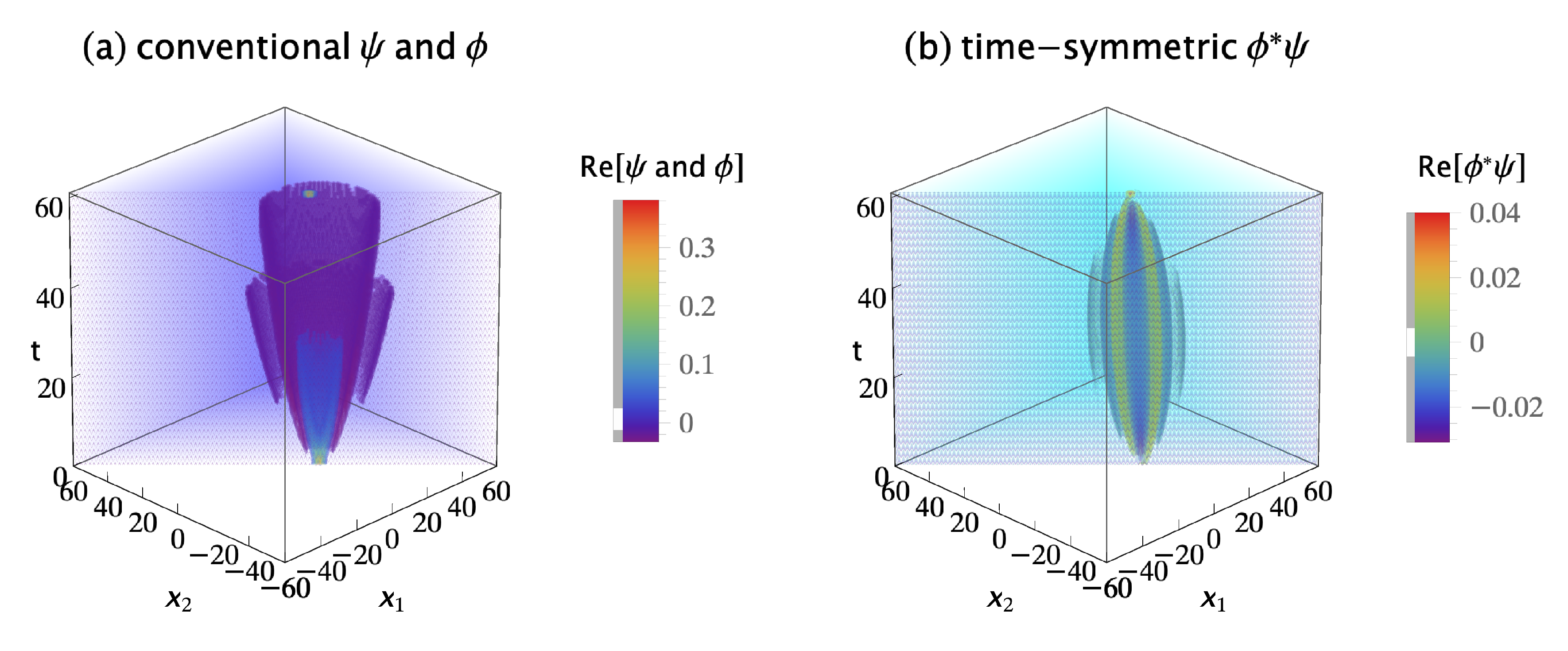
Figure 2.
(a) The conventional explanation of a Gedankenexperiment with one quantum: the one-quantum wavefunction is emitted by source at , evolves in time, then abruptly collapses onto the wavefunction and is absorbed by detector at . The conventional formulation assumes the wavefunction is a 1-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the quantum that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the one-quantum complex transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by source and absorbed by detector . There is no abrupt collapse. The time-symmetric formulation assumes the complex transition amplitude density is a (1 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the quantum that is in principle possible. Configuration spacetime is the usual quantum configuration space with a time axis added. The transition amplitude density is normalized to give a transition probability of one, and only the real parts of , , and are shown.
Figure 2.
(a) The conventional explanation of a Gedankenexperiment with one quantum: the one-quantum wavefunction is emitted by source at , evolves in time, then abruptly collapses onto the wavefunction and is absorbed by detector at . The conventional formulation assumes the wavefunction is a 1-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the quantum that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the one-quantum complex transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by source and absorbed by detector . There is no abrupt collapse. The time-symmetric formulation assumes the complex transition amplitude density is a (1 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the quantum that is in principle possible. Configuration spacetime is the usual quantum configuration space with a time axis added. The transition amplitude density is normalized to give a transition probability of one, and only the real parts of , , and are shown.
![Entropy 23 00179 g002]()
Figure 3.
(a) The conventional explanation of a Gedankenexperiment with two distinguishable quanta: only the first of the four possible distinguishable path permutations is shown. The two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the two-quanta wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: only the first of the four possible distinguishable path permutations is shown. The two-quanta transition amplitude density (where is the complex conjugate of in the conventional explanation) is emitted by sources and and absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
Figure 3.
(a) The conventional explanation of a Gedankenexperiment with two distinguishable quanta: only the first of the four possible distinguishable path permutations is shown. The two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the two-quanta wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: only the first of the four possible distinguishable path permutations is shown. The two-quanta transition amplitude density (where is the complex conjugate of in the conventional explanation) is emitted by sources and and absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
![Entropy 23 00179 g003]()
Figure 4.
(a) The conventional prediction for the Gedankenexperiment with two distinguishable quanta for all four possible distinguishable results: the probability that the two quanta emitted from the sources are absorbed in the two detectors as the locations of the two detectors are varied, averaged over many runs. Since the two quanta are distinguishable, there is no interference. (b) The time-symmetric prediction for the same Gedankenexperiment. The predictions are identical.
Figure 4.
(a) The conventional prediction for the Gedankenexperiment with two distinguishable quanta for all four possible distinguishable results: the probability that the two quanta emitted from the sources are absorbed in the two detectors as the locations of the two detectors are varied, averaged over many runs. Since the two quanta are distinguishable, there is no interference. (b) The time-symmetric prediction for the same Gedankenexperiment. The predictions are identical.
Figure 5.
(a) The conventional explanation of a Gedankenexperiment with two indistinguishable bosons: the symmetrized two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the symmetrized two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the two-quanta wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the symmetrized two-quanta transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by sources and , and the quanta are absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the symmetrized complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
Figure 5.
(a) The conventional explanation of a Gedankenexperiment with two indistinguishable bosons: the symmetrized two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the symmetrized two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the two-quanta wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the symmetrized two-quanta transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by sources and , and the quanta are absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the symmetrized complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
![Entropy 23 00179 g005]()
Figure 6.
(a) The conventional formulation prediction for the interference pattern for two indistinguishable bosons: the probability that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. (b) The time-symmetric formulation prediction for the same Gedankenexperiment: the probability that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. The interference patterns are identical, and have a maximum when the two detectors are located at , as expected for indistinguishable bosons. The interference patterns are normalized to give a transition probability of one.
Figure 6.
(a) The conventional formulation prediction for the interference pattern for two indistinguishable bosons: the probability that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. (b) The time-symmetric formulation prediction for the same Gedankenexperiment: the probability that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. The interference patterns are identical, and have a maximum when the two detectors are located at , as expected for indistinguishable bosons. The interference patterns are normalized to give a transition probability of one.
Figure 7.
(a) The conventional explanation of a Gedankenexperiment with two indistinguishable fermions: the antisymmetrized two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the antisymmetrized two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the antisymmetrized wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the antisymmetrized two-quanta transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by sources and , and the quanta are absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the antisymmetrized complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
Figure 7.
(a) The conventional explanation of a Gedankenexperiment with two indistinguishable fermions: the antisymmetrized two-quanta wavefunction is emitted by sources at and at , evolves in time, then abruptly collapses onto the antisymmetrized two-quanta wavefunction and is absorbed by detectors at and at . The conventional formulation assumes the antisymmetrized wavefunction is a 2-dimensional object which lives in configuration space, evolves in time, and gives the most complete description of the two quanta that is in principle possible. (b) The time-symmetric explanation of the same Gedankenexperiment: the antisymmetrized two-quanta transition amplitude density (where is the complex conjugate of the in the conventional explanation) is emitted by sources and , and the quanta are absorbed by detectors and . There is no abrupt collapse. The time-symmetric formulation assumes the antisymmetrized complex transition amplitude density is a (2 + 1)-dimensional object which lives in configuration spacetime and gives the most complete description of the two quanta that is in principle possible. The transition amplitude density is normalized to give a transition probability of one, only the real parts of , , and are shown, and half of the plots are cut away to show the interiors.
![Entropy 23 00179 g007]()
Figure 8.
(a) The conventional formulation prediction for the interference pattern for two indistinguishable fermions: the probability Pc that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. (b) The time-symmetric formulation prediction for the same Gedankenexperiment: the probability Pt that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. The interference patterns are identical, and have a minimum when the two detectors are located at (xc, xd) = (0, 0), as expected for indistinguishable fermions. The interference patterns are normalized to give a transition probability of one.
Figure 8.
(a) The conventional formulation prediction for the interference pattern for two indistinguishable fermions: the probability Pc that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. (b) The time-symmetric formulation prediction for the same Gedankenexperiment: the probability Pt that the two quanta emitted from the sources are absorbed in the two detectors, as the locations of the two detectors are varied, averaged over many runs. The interference patterns are identical, and have a minimum when the two detectors are located at (xc, xd) = (0, 0), as expected for indistinguishable fermions. The interference patterns are normalized to give a transition probability of one.
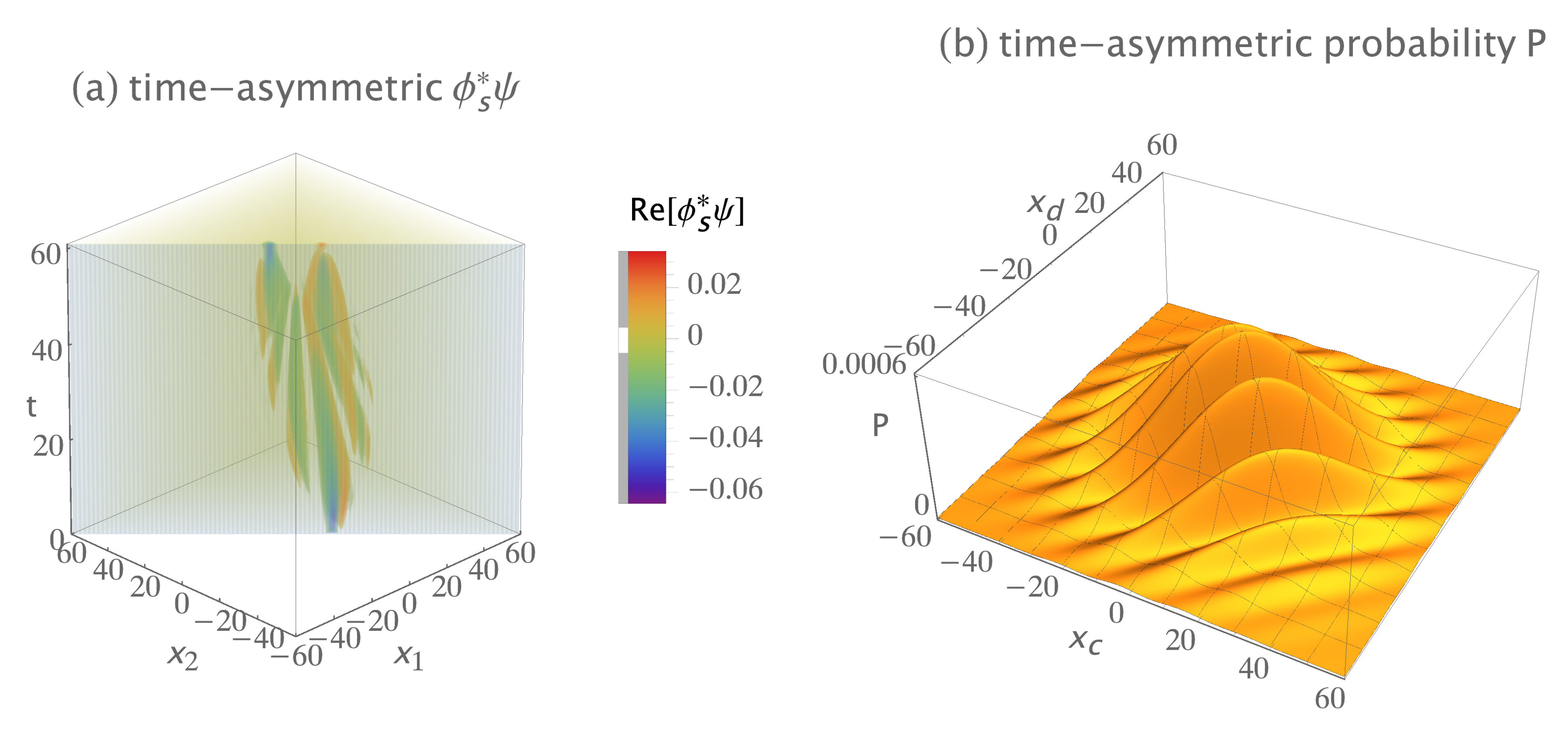
Figure 9.
The (1 + 1)-dimensional predictions of Fano, Feynman, and Mandel’s analyses of the Hanbury Brown–Twiss experiment, for the same locations of sources and detectors used earlier. They assumed only two possible indistinguishable path permutations: quantum 1 goes from
to
, while concurrently quantum 2 goes from
to
; and quantum 1 goes from
to
, while concurrently quantum 2 goes from
to
. (
a) The two-quanta transition amplitude density
is time asymmetric: compare to
Figure 5b. This is because two other possible indistinguishable path permutations are missing. The complex transition amplitude density
is normalized to give a transition probability of one, only the real part of
is shown, and half of the
plot is cut away to show the interior. (
b) The predicted probability of the transition as a function of the detector locations. It is identical to the time-symmetric experimental prediction because it is normalized to give a transition probability of one.
Figure 9.
The (1 + 1)-dimensional predictions of Fano, Feynman, and Mandel’s analyses of the Hanbury Brown–Twiss experiment, for the same locations of sources and detectors used earlier. They assumed only two possible indistinguishable path permutations: quantum 1 goes from
to
, while concurrently quantum 2 goes from
to
; and quantum 1 goes from
to
, while concurrently quantum 2 goes from
to
. (
a) The two-quanta transition amplitude density
is time asymmetric: compare to
Figure 5b. This is because two other possible indistinguishable path permutations are missing. The complex transition amplitude density
is normalized to give a transition probability of one, only the real part of
is shown, and half of the
plot is cut away to show the interior. (
b) The predicted probability of the transition as a function of the detector locations. It is identical to the time-symmetric experimental prediction because it is normalized to give a transition probability of one.
![Entropy 23 00179 g009]()