Enhancing Predictability Assessment: An Overview and Analysis of Predictability Measures for Time Series and Network Links
Abstract
:1. Introduction
- We formalize the predictability measure concept, specifying measures of realized and intrinsic predictability;
- We provide a comprehensive survey of predictability measures for time series and network links, encompassing both realized and intrinsic predictability measures;
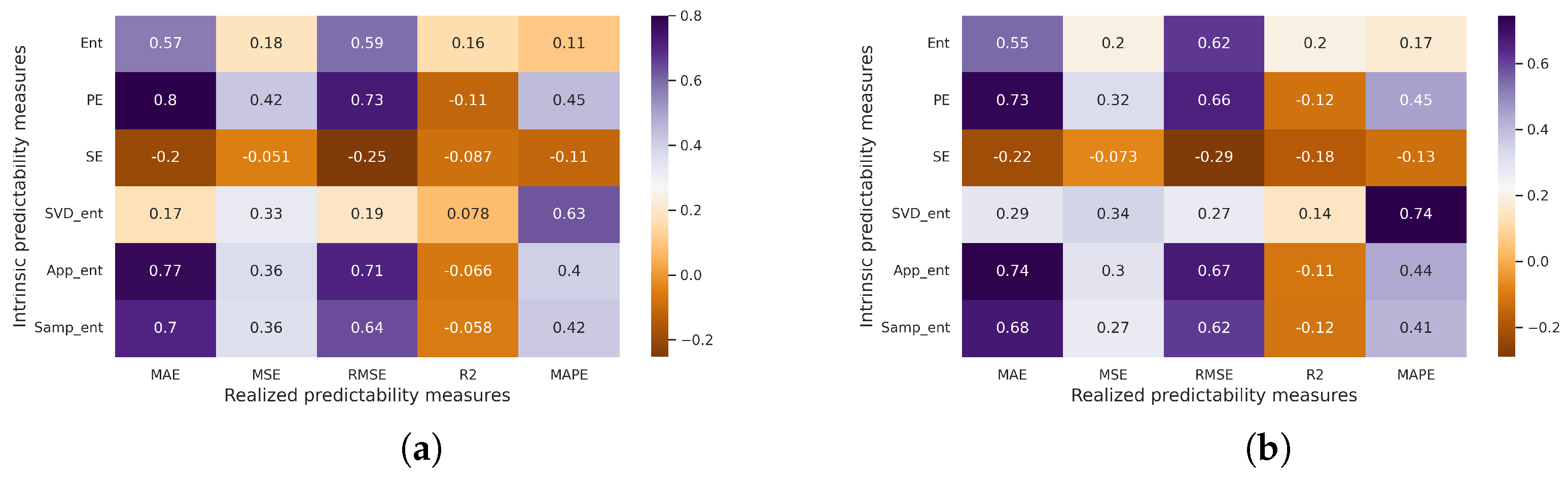
- We provide the correlation analysis results between intrinsic and realized time series predictability measures, offering valuable insights for assessing achievable forecast accuracy levels prior to the forecasting moment.
2. Overview of Predictability Measures
2.1. General Predictability Concepts
2.2. Time Series Predictability
2.2.1. Univariate Time Series
- Form a sequence of vectors in , a real m-dimensional space, defined by ;
- Use the sequence to construct, for each i, , ;
- Define ;
- Calculate the Approximate entropy value:
2.2.2. Multivariate Time Series
2.2.3. Categorical Time Series
2.3. Network Link Predictability
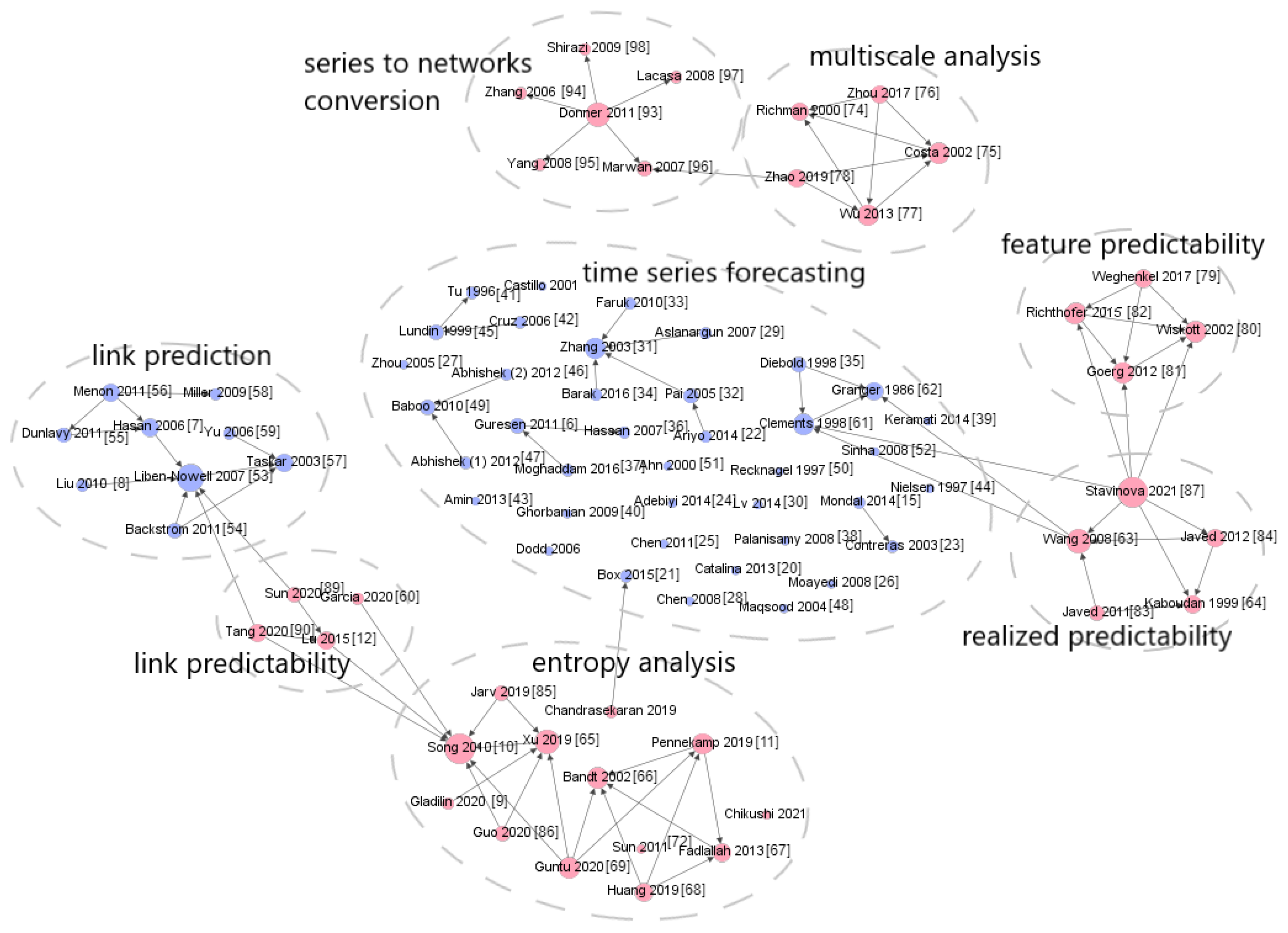
2.4. Overview Summary
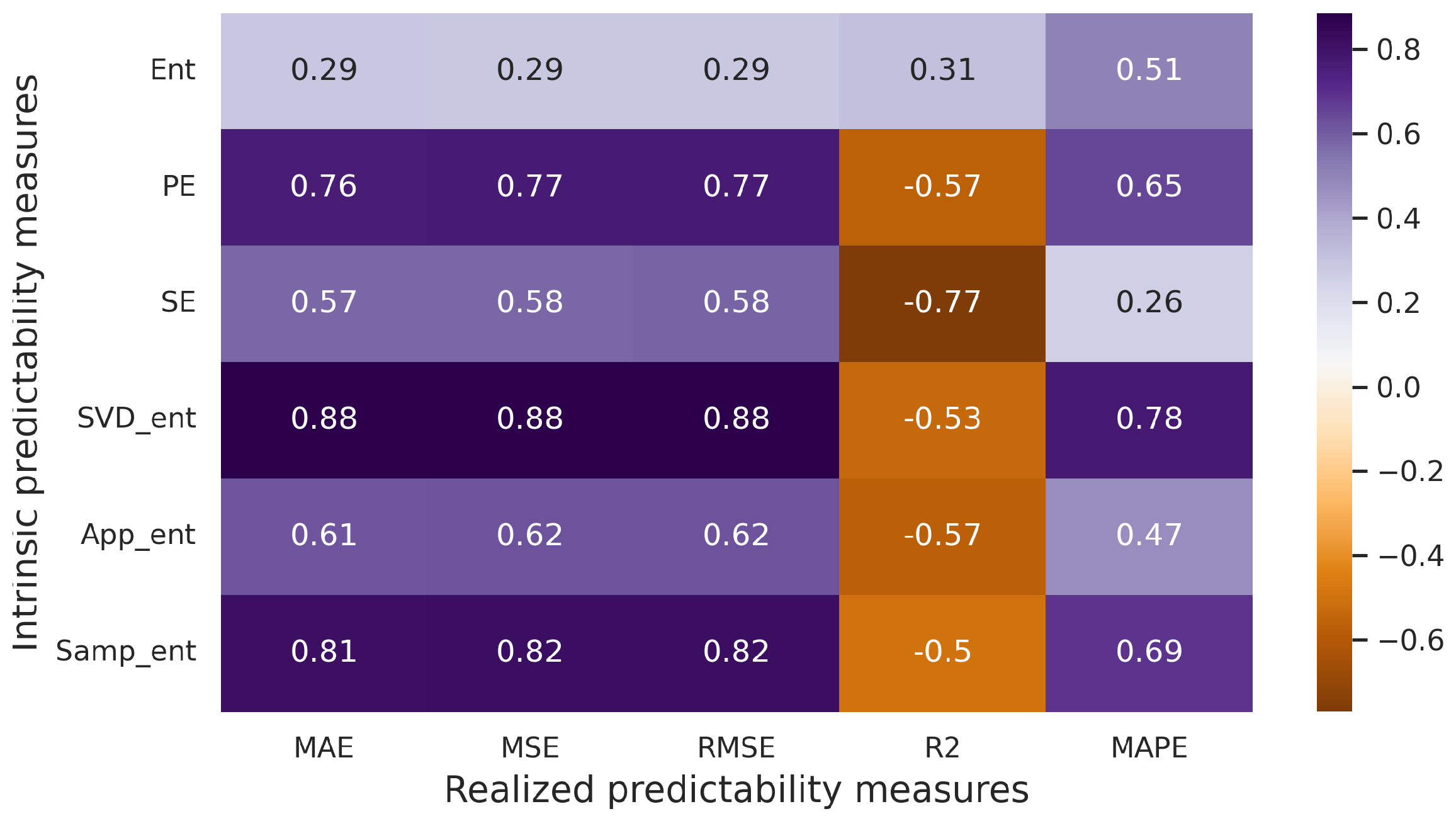
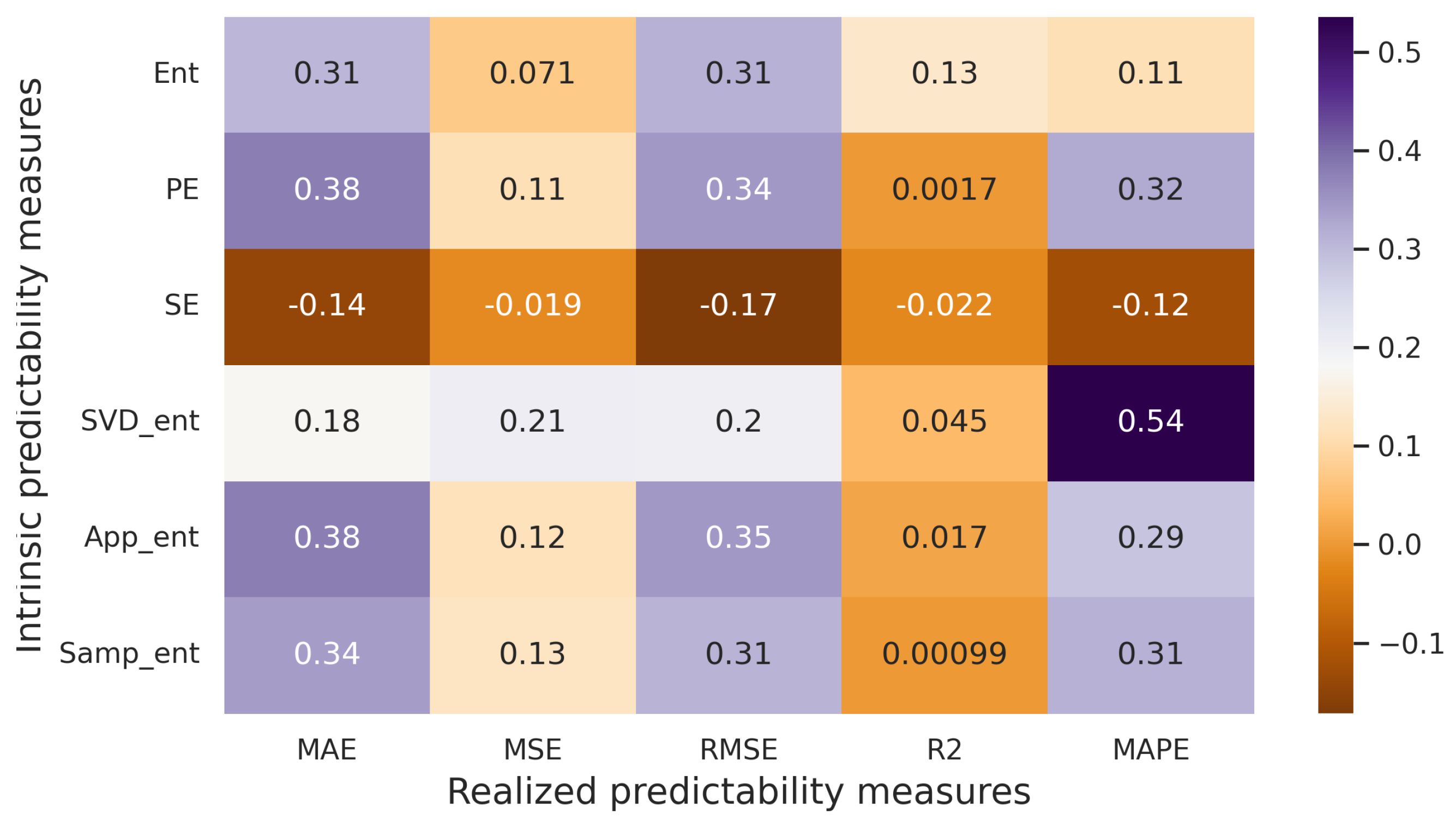
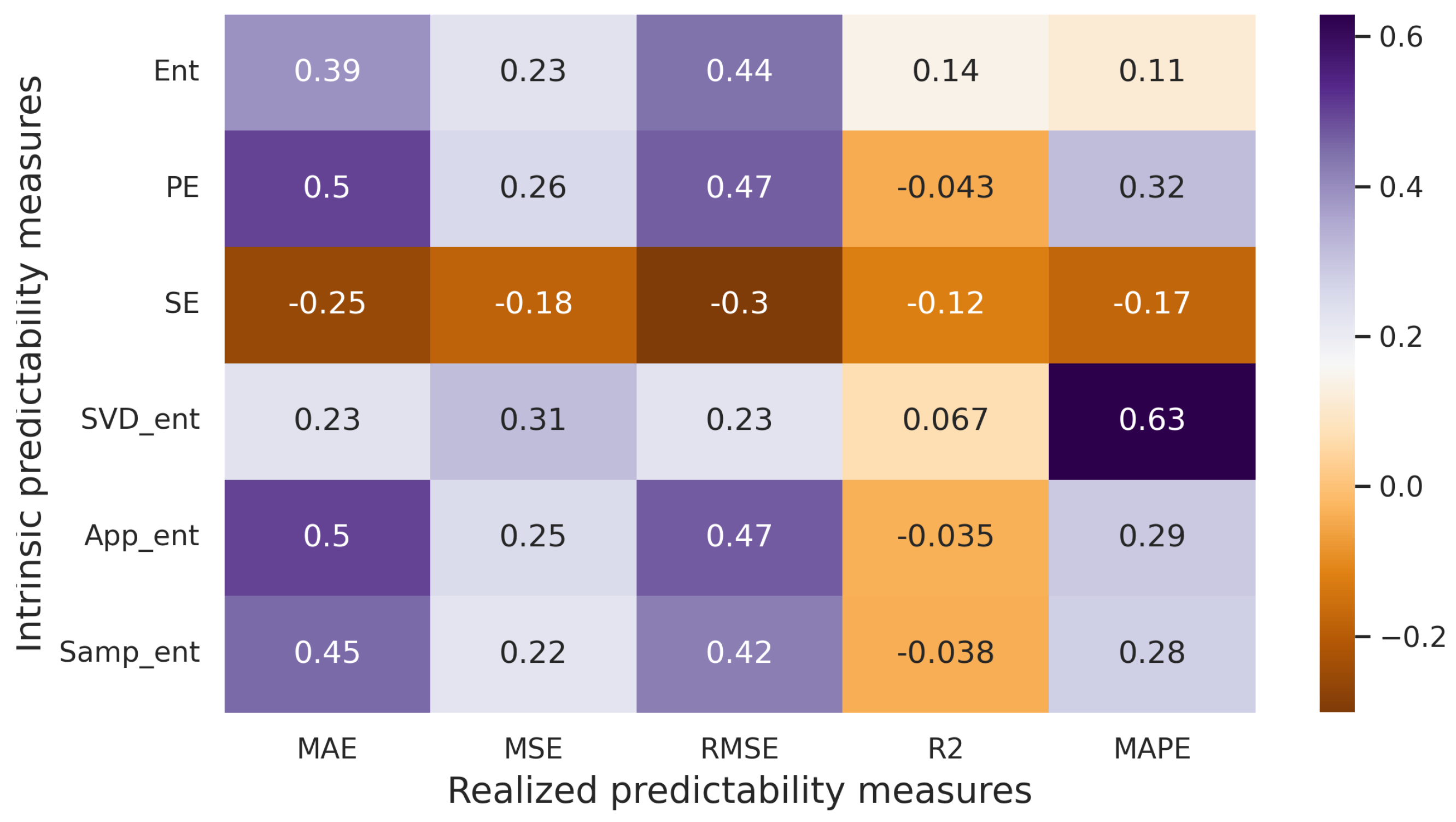
3. Correlation Rate between Intrinsic and Realized Predictability
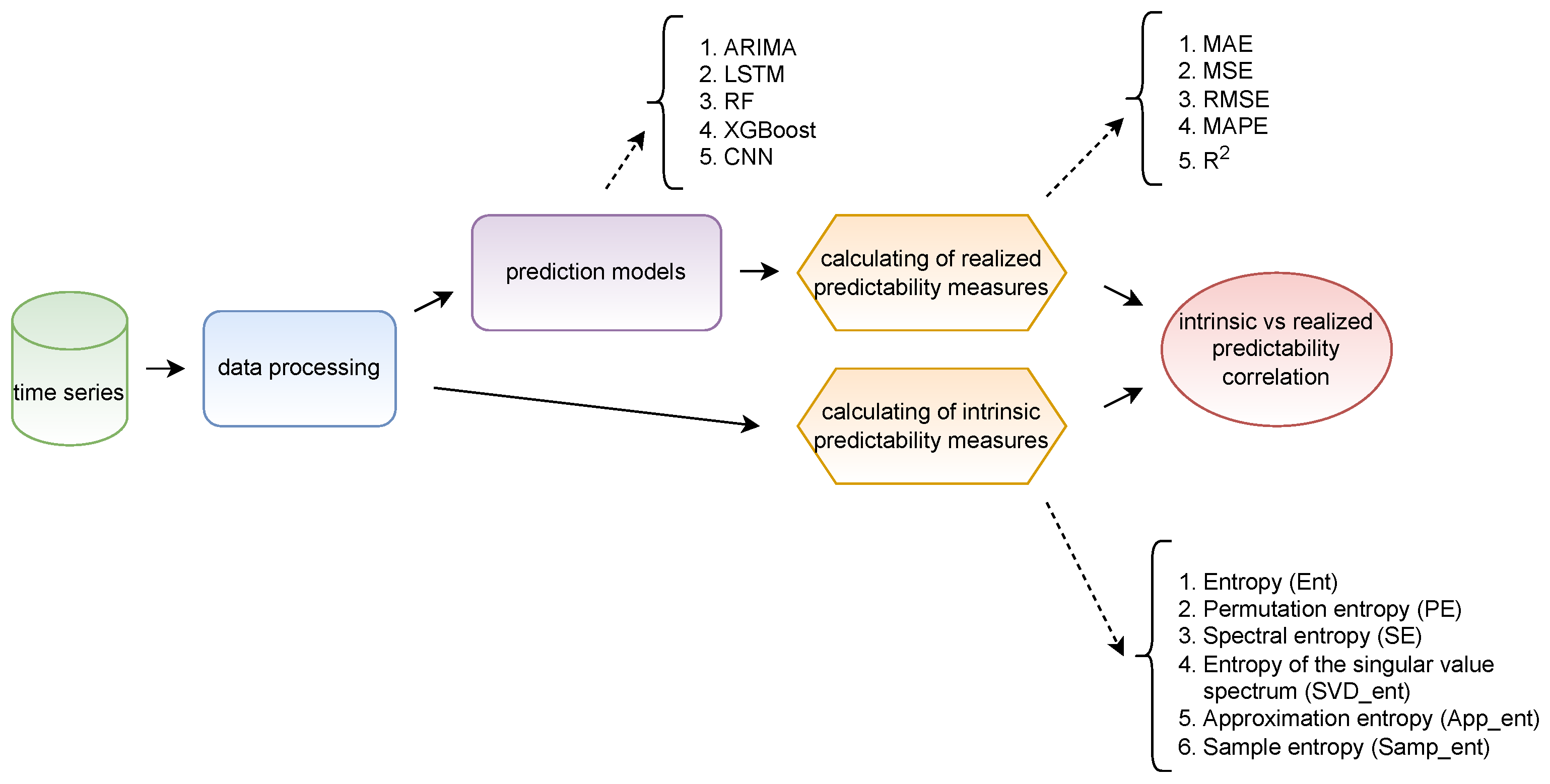
3.1. Method Description
3.1.1. Problem Statement
3.1.2. Pipeline
3.1.3. Forecasting Models and Predictability Measures
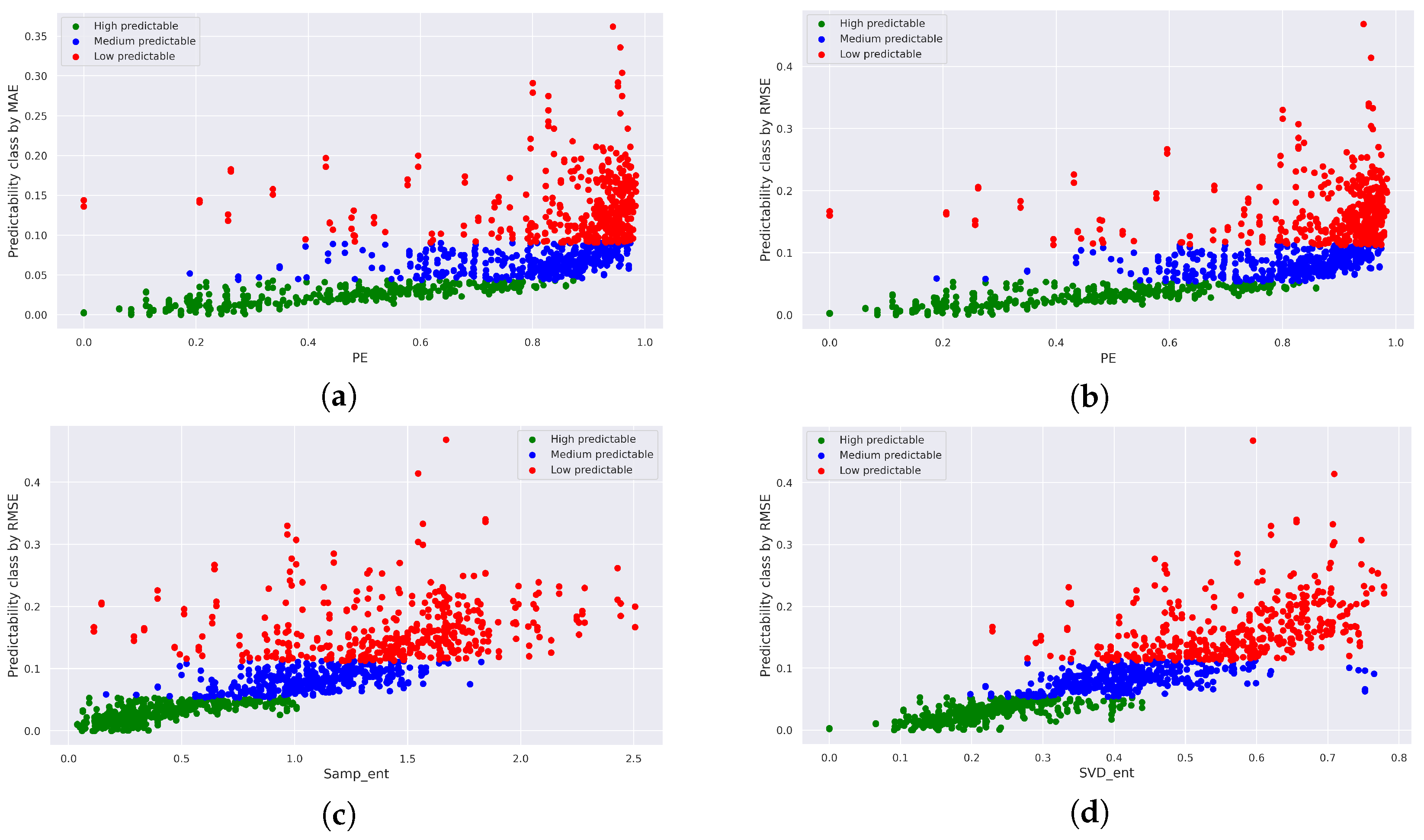
3.2. Experiments and Results
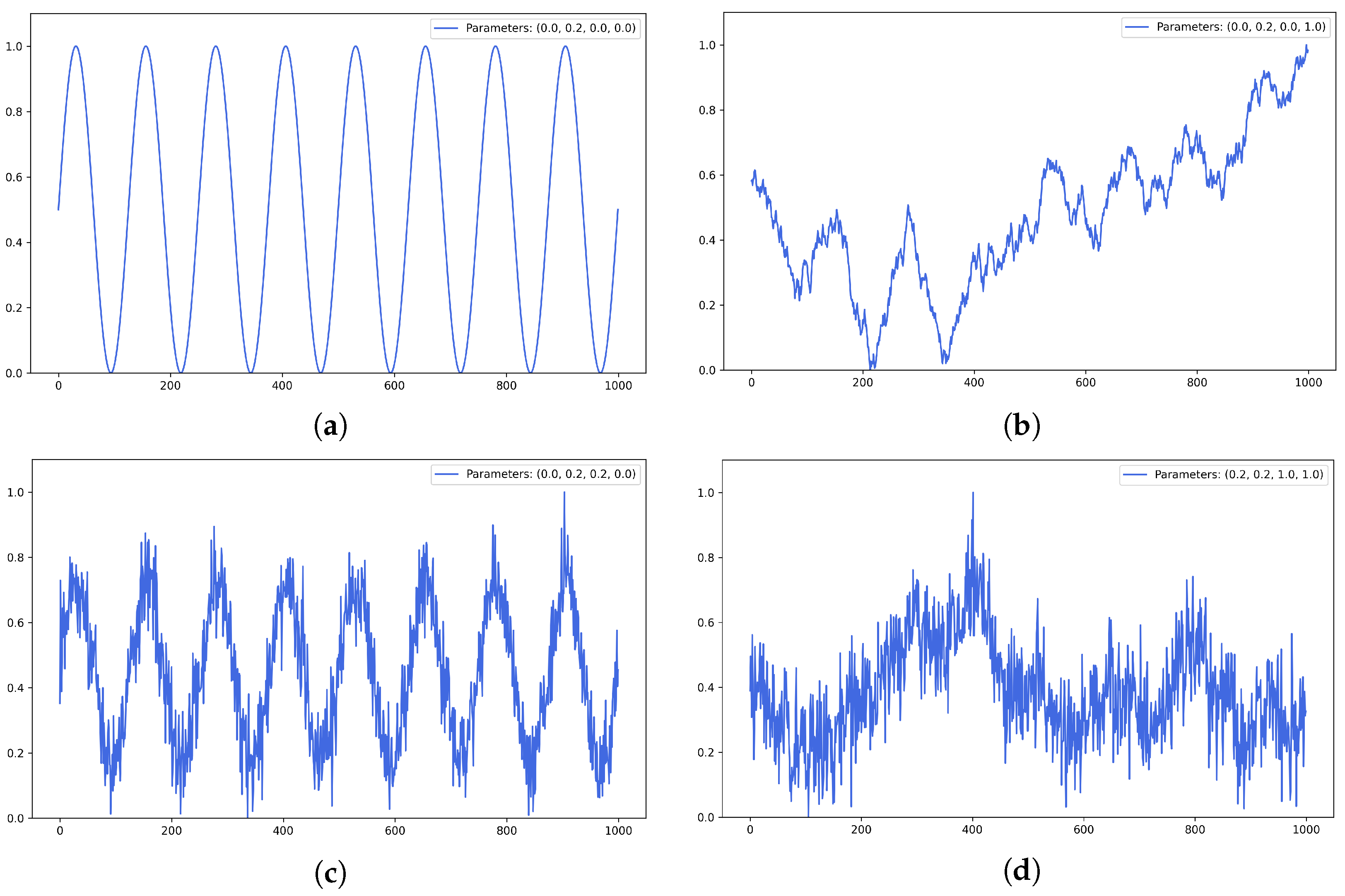
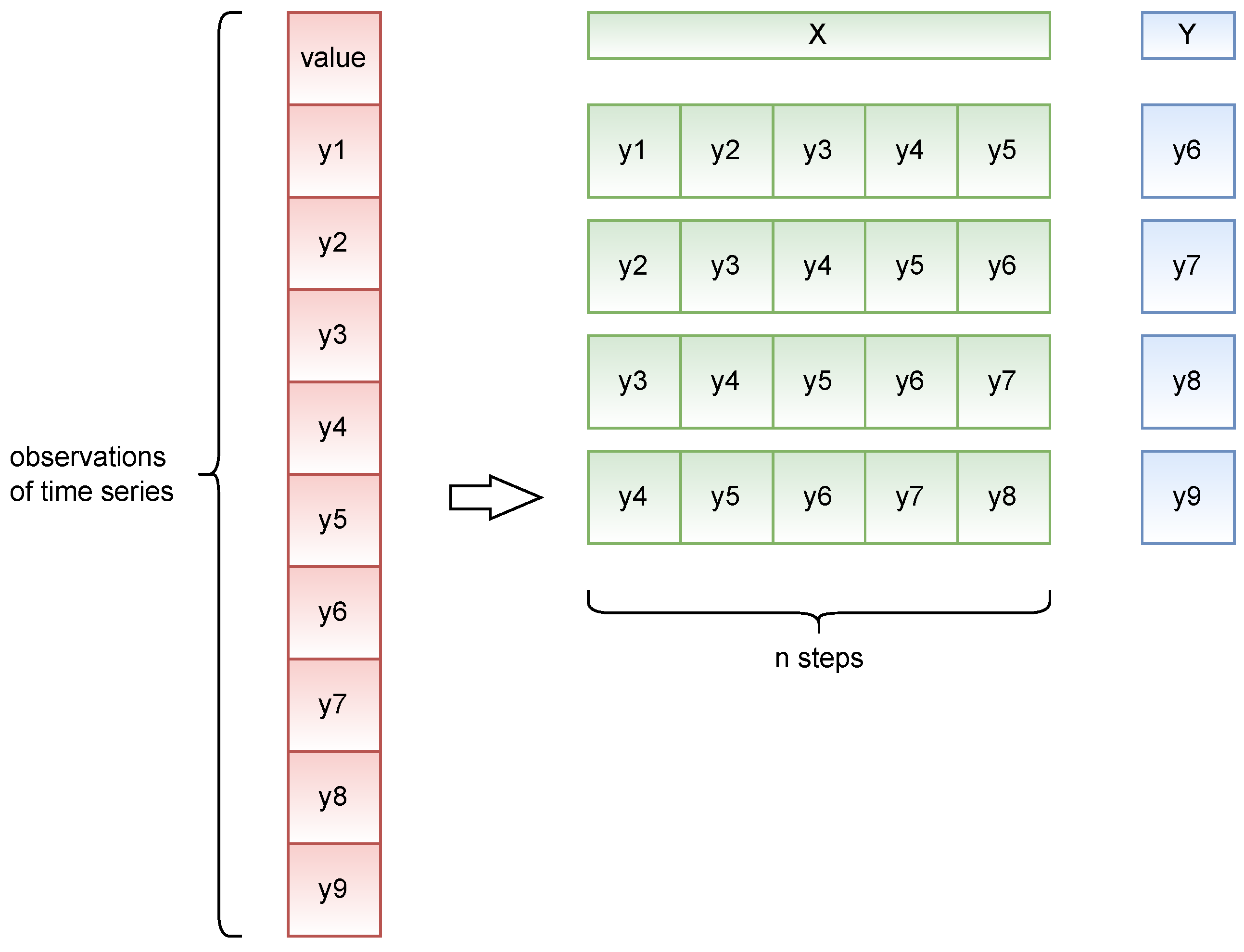
3.2.1. Data Description, Generation, and Processing
3.2.2. Experiments with Artificial Time Series
3.2.3. Experiments with Real-World Time Series
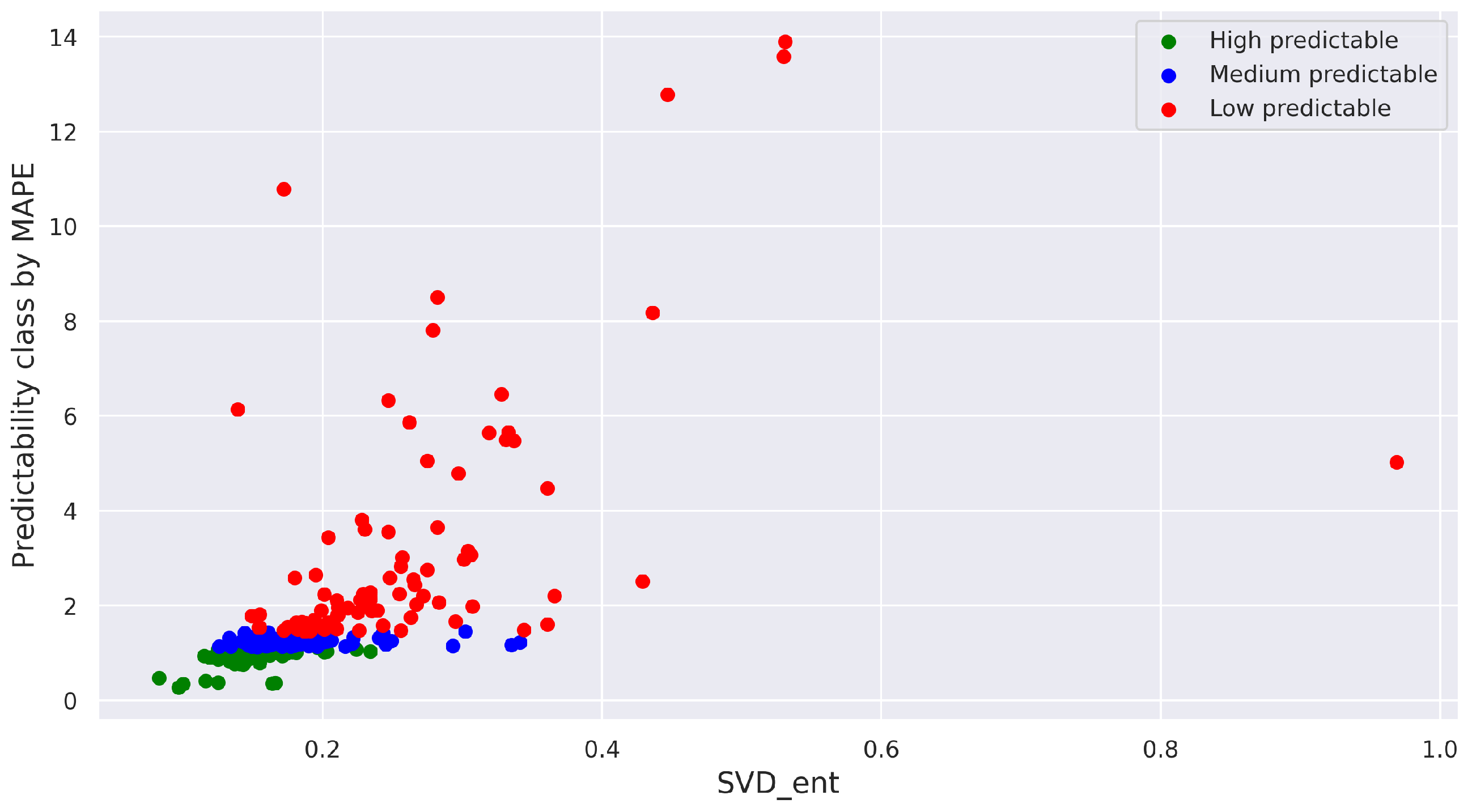
3.3. Experiments Summary
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Mahalakshmi, G.; Sridevi, S.; Rajaram, S. A survey on forecasting of time series data. In Proceedings of the 2016 International Conference on Computing Technologies and Intelligent Data Engineering (ICCTIDE’16), Kovilpatti, India, 7–9 January 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Martínez, V.; Berzal, F.; Cubero, J.C. A survey of link prediction in complex networks. ACM Comput. Surv. 2016, 49, 1–33. [Google Scholar] [CrossRef]
- Shaikh, S.; Gala, J.; Jain, A.; Advani, S.; Jaidhara, S.; Edinburgh, M.R. Analysis and prediction of COVID-19 using regression models and time series forecasting. In Proceedings of the 2021 11th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 28–29 January 2021; pp. 989–995. [Google Scholar] [CrossRef]
- Guresen, E.; Kayakutlu, G.; Daim, T.U. Using artificial neural network models in stock market index prediction. Expert Syst. Appl. 2011, 38, 10389–10397. [Google Scholar] [CrossRef]
- Al Hasan, M.; Chaoji, V.; Salem, S.; Zaki, M. Link prediction using supervised learning. In Proceedings of the SDM06: Workshop on Link Analysis, Counter-Terrorism and Security, Bethesda, MD, USA, 20 April 2006; Volume 30, pp. 798–805. [Google Scholar]
- Liu, W.; Lü, L. Link prediction based on local random walk. Europhys. Lett. 2010, 89, 58007. [Google Scholar] [CrossRef]
- Kovantsev, A.; Gladilin, P. Analysis of multivariate time series predictability based on their features. In Proceedings of the 2020 International Conference on Data Mining Workshops (ICDMW), Sorrento, Italy, 17–20 November 2020; pp. 348–355. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef]
- Pennekamp, F.; Iles, A.C.; Garland, J.; Brennan, G.; Brose, U.; Gaedke, U.; Jacob, U.; Kratina, P.; Matthews, B.; Munch, S.; et al. The intrinsic predictability of ecological time series and its potential to guide forecasting. Ecol. Monogr. 2019, 89, e01359. [Google Scholar] [CrossRef]
- Lü, L.; Pan, L.; Zhou, T.; Zhang, Y.C.; Stanley, H.E. Toward link predictability of complex networks. Proc. Natl. Acad. Sci. USA 2015, 112, 2325–2330. [Google Scholar] [CrossRef]
- Krollner, B.; Vanstone, B.; Finnie, G. Financial time series forecasting with machine learning techniques: A survey. In Proceedings of the European Symposium on Artificial Neural Networks: Computational Intelligence and Machine Learning, Bruges, Belgium, 28–30 April 2010; pp. 25–30. [Google Scholar]
- Caillault, É.P.; Bigand, A. Comparative study on univariate forecasting methods for meteorological time series. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2380–2384. [Google Scholar] [CrossRef]
- Mondal, P.; Shit, L.; Goswami, S. Study of effectiveness of time series modeling (ARIMA) in forecasting stock prices. Int. J. Comput. Sci. Eng. Appl. 2014, 4, 13. [Google Scholar] [CrossRef]
- Daud, N.N.; Ab Hamid, S.H.; Saadoon, M.; Sahran, F.; Anuar, N.B. Applications of link prediction in social networks: A review. J. Netw. Comput. Appl. 2020, 166, 102716. [Google Scholar] [CrossRef]
- Gu, S.; Li, K.; Liang, Y.; Yan, D. A transportation network evolution model based on link prediction. Int. J. Mod. Phys. B 2021, 35, 2150316. [Google Scholar] [CrossRef]
- Coşkun, M.; Koyutürk, M. Node similarity-based graph convolution for link prediction in biological networks. Bioinformatics 2021, 37, 4501–4508. [Google Scholar] [CrossRef] [PubMed]
- Imai, C.; Hashizume, M. A systematic review of methodology: Time series regression analysis for environmental factors and infectious diseases. Trop. Med. Health 2015, 43, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock price prediction using the ARIMA model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and artificial neural networks models for stock price prediction. J. Appl. Math. 2014, 2014. [Google Scholar] [CrossRef]
- Chen, C.; Hu, J.; Meng, Q.; Zhang, Y. Short-time traffic flow prediction with ARIMA-GARCH model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 607–612. [Google Scholar] [CrossRef]
- Moayedi, H.Z.; Masnadi-Shirazi, M. Arima model for network traffic prediction and anomaly detection. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; Volume 4, pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, B.; He, D.; Sun, Z.; Ng, W.H. Network traffic modeling and prediction with ARIMA/GARCH. In Proceedings of the HET-NETs Conference, Ilkley, UK, 18–20 July 2005; pp. 1–10. [Google Scholar]
- Chen, P.; Yuan, H.; Shu, X. Forecasting crime using the arima model. In Proceedings of the 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinan, China, 18–20 October 2008; Volume 5, pp. 627–630. [Google Scholar] [CrossRef]
- Aslanargun, A.; Mammadov, M.; Yazici, B.; Yolacan, S. Comparison of ARIMA, neural networks and hybrid models in time series: Tourist arrival forecasting. J. Stat. Comput. Simul. 2007, 77, 29–53. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Pai, P.F.; Lin, C.S. A hybrid ARIMA and support vector machines model in stock price forecasting. Omega 2005, 33, 497–505. [Google Scholar] [CrossRef]
- Faruk, D.Ö. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 92–104. [Google Scholar] [CrossRef]
- Diebold, F.X. Elements of Forecasting; Citeseer: State College, PA, USA, 1998. [Google Scholar]
- Hassan, M.R.; Nath, B.; Kirley, M. A fusion model of HMM, ANN and GA for stock market forecasting. Expert Syst. Appl. 2007, 33, 171–180. [Google Scholar] [CrossRef]
- Moghaddam, A.H.; Moghaddam, M.H.; Esfandyari, M. Stock market index prediction using artificial neural network. J. Econ. Financ. Adm. Sci. 2016, 21, 89–93. [Google Scholar] [CrossRef]
- Palanisamy, P.; Rajendran, I.; Shanmugasundaram, S. Prediction of tool wear using regression and ANN models in end-milling operation. Int. J. Adv. Manuf. Technol. 2008, 37, 29–41. [Google Scholar] [CrossRef]
- Keramati, A.; Jafari-Marandi, R.; Aliannejadi, M.; Ahmadian, I.; Mozaffari, M.; Abbasi, U. Improved churn prediction in telecommunication industry using data mining techniques. Appl. Soft Comput. 2014, 24, 994–1012. [Google Scholar] [CrossRef]
- Ghorbanian, K.; Gholamrezaei, M. An artificial neural network approach to compressor performance prediction. Appl. Energy 2009, 86, 1210–1221. [Google Scholar] [CrossRef]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Cruz, J.A.; Wishart, D.S. Applications of machine learning in cancer prediction and prognosis. Cancer Inform. 2006, 2, 117693510600200030. [Google Scholar] [CrossRef]
- Amin, S.U.; Agarwal, K.; Beg, R. Genetic neural network based data mining in prediction of heart disease using risk factors. In Proceedings of the 2013 IEEE Conference on Information & Communication Technologies, Thuckalay, India, 11–12 April 2013; pp. 1227–1231. [Google Scholar] [CrossRef]
- Nielsen, H.; Engelbrecht, J.; Brunak, S.; von Heijne, G. Identification of prokaryotic and eukaryotic signal peptides and prediction of their cleavage sites. Protein Eng. 1997, 10, 1–6. [Google Scholar] [CrossRef]
- Lundin, M.; Lundin, J.; Burke, H.; Toikkanen, S.; Pylkkänen, L.; Joensuu, H. Artificial neural networks applied to survival prediction in breast cancer. Oncology 1999, 57, 281–286. [Google Scholar] [CrossRef] [PubMed]
- Abhishek, K.; Kumar, A.; Ranjan, R.; Kumar, S. A rainfall prediction model using artificial neural network. In Proceedings of the 2012 IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 16–17 July 2012; pp. 82–87. [Google Scholar] [CrossRef]
- Abhishek, K.; Singh, M.; Ghosh, S.; Anand, A. Weather forecasting model using artificial neural network. Procedia Technol. 2012, 4, 311–318. [Google Scholar] [CrossRef]
- Maqsood, I.; Khan, M.R.; Abraham, A. An ensemble of neural networks for weather forecasting. Neural Comput. Appl. 2004, 13, 112–122. [Google Scholar] [CrossRef]
- Baboo, S.S.; Shereef, I.K. An efficient weather forecasting system using artificial neural network. Int. J. Environ. Sci. Dev. 2010, 1, 321. [Google Scholar] [CrossRef]
- Recknagel, F.; French, M.; Harkonen, P.; Yabunaka, K.I. Artificial neural network approach for modelling and prediction of algal blooms. Ecol. Model. 1997, 96, 11–28. [Google Scholar] [CrossRef]
- Ahn, B.S.; Cho, S.; Kim, C. The integrated methodology of rough set theory and artificial neural network for business failure prediction. Expert Syst. Appl. 2000, 18, 65–74. [Google Scholar] [CrossRef]
- Sinha, S.K.; Wang, M.C. Artificial neural network prediction models for soil compaction and permeability. Geotech. Geol. Eng. 2008, 26, 47–64. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Backstrom, L.; Leskovec, J. Supervised random walks: Predicting and recommending links in social networks. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, Hong Kong, China, 9–12 February 2011; pp. 635–644. [Google Scholar] [CrossRef]
- Dunlavy, D.M.; Kolda, T.G.; Acar, E. Temporal link prediction using matrix and tensor factorizations. ACM Trans. Knowl. Discov. Data 2011, 5, 1–27. [Google Scholar] [CrossRef]
- Menon, A.K.; Elkan, C. Link prediction via matrix factorization. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Athens, Greece, 5–9 September 2011; pp. 437–452. [Google Scholar] [CrossRef]
- Taskar, B.; Wong, M.F.; Abbeel, P.; Koller, D. Link prediction in relational data. Adv. Neural Inf. Process. Syst. 2003, 16, 659–666. [Google Scholar]
- Miller, K.; Jordan, M.; Griffiths, T. Nonparametric latent feature models for link prediction. Adv. Neural Inf. Process. Syst. 2009, 22, 1276–1284. [Google Scholar]
- Yu, K.; Chu, W.; Yu, S.; Tresp, V.; Xu, Z. Stochastic relational models for discriminative link prediction. In Proceedings of the NIPS, Vancouver, BC, Canada, 4–7 December 2006; Voume 6, pp. 1553–1560. [Google Scholar] [CrossRef]
- García-Pérez, G.; Aliakbarisani, R.; Ghasemi, A.; Serrano, M.Á. Precision as a measure of predictability of missing links in real networks. Phys. Rev. E 2020, 101, 052318. [Google Scholar] [CrossRef] [PubMed]
- Clements, M.; Hendry, D. Forecasting Economic Time Series; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Granger, C.; Newbold, P. Forecasting Economic Time Series; Technical Report; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.; Vrijling, J. Measuring predictability of daily streamflow processes based on univariate time series model. In Proceedings of the iEMSs 2008 Conference, Barcelona, Spain, 7–10 July 2008. [Google Scholar]
- Kaboudan, M. A measure of time series’ predictability using genetic programming applied to stock returns. J. Forecast. 1999, 18, 345–357. [Google Scholar] [CrossRef]
- Xu, P.; Yin, L.; Yue, Z.; Zhou, T. On predictability of time series. Phys. A Stat. Mech. Appl. 2019, 523, 345–351. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Principe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef]
- Huang, Y.; Fu, Z. Enhanced time series predictability with well-defined structures. Theor. Appl. Climatol. 2019, 138. [Google Scholar] [CrossRef]
- Guntu, R.K.; Yeditha, P.K.; Rathinasamy, M.; Perc, M.; Marwan, N.; Kurths, J.; Agarwal, A. Wavelet entropy-based evaluation of intrinsic predictability of time series. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 033117. [Google Scholar] [CrossRef]
- Inouye, T.; Shinosaki, K.; Sakamoto, H.; Toi, S.; Ukai, S.; Iyama, A.; Katsuda, Y.; Hirano, M. Quantification of EEG irregularity by use of the entropy of the power spectrum. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 204–210. [Google Scholar] [CrossRef]
- Roberts, S.J.; Penny, W.; Rezek, I. Temporal and spatial complexity measures for electroencephalogram based brain–computer interfacing. Med Biol. Eng. Comput. 1999, 37, 93–98. [Google Scholar] [CrossRef]
- Sun, L.; Xiong, Z.; Li, Z. Time-Dependent Entropy for Studying Time-Varying Visual ERP Series. In Future Intelligent Information Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 517–524. [Google Scholar] [CrossRef]
- Pincus, S.M.; Gladstone, I.M.; Ehrenkranz, R.A. A regularity statistic for medical data analysis. J. Clin. Monit. 1991, 7, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J.-Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Yang, C.; Wan, J.; Zhang, W.; Guan, B.; Xiong, N. Measuring complexity and predictability of time series with flexible multiscale entropy for sensor networks. Sensors 2017, 17, 787. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Zhao, X.; Liang, C.; Zhang, N.; Shang, P. Quantifying the Multiscale Predictability of Financial Time Series by an Information-Theoretic Approach. Entropy 2019, 21, 684. [Google Scholar] [CrossRef] [PubMed]
- Weghenkel, B.; Fischer, A.; Wiskott, L. Graph-based predictable feature analysis. Mach. Learn. 2017, 106, 1359–1380. [Google Scholar] [CrossRef]
- Wiskott, L.; Sejnowski, T.J. Slow feature analysis: Unsupervised learning of invariances. Neural Comput. 2002, 14, 715–770. [Google Scholar] [CrossRef]
- Goerg, G.M. Forecastable component analysis (ForeCA). arXiv 2012, arXiv:1205.4591. [Google Scholar]
- Richthofer, S.; Wiskott, L. Predictable feature analysis. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 190–196. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zemouri, R.; Zerhouni, N. Improving data-driven prognostics by assessing predictability of features. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM’11, Montreal, QC, Canada, 25–29 September 2011; pp. 555–560. [Google Scholar]
- Javed, K.; Gouriveau, R.; Zemouri, R.; Zerhouni, N. Features selection procedure for prognostics: An approach based on predictability. IFAC Proc. Vol. 2012, 45, 25–30. [Google Scholar] [CrossRef]
- Järv, P. Predictability limits in session-based next item recommendation. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 146–150. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, S.; Zhu, J.; Ni, R. Measuring the Gap Between the Maximum Predictability and Prediction Accuracy of Human Mobility. IEEE Access 2020, 8, 131859–131869. [Google Scholar] [CrossRef]
- Stavinova, E.; Bochenina, K.; Chunaev, P. Predictability classes for forecasting clients behavior by transactional data. In Proceedings of the International Conference on Computational Science, Krakov, Poland, 16–18 June 2021; pp. 187–199. [Google Scholar] [CrossRef]
- Bezbochina, A.; Stavinova, E.; Kovantsev, A.; Chunaev, P. Dynamic Classification of Bank Clients by the Predictability of Their Transactional Behavior. In Proceedings of the International Conference on Computational Science, London, UK, 21–23 June 2022; pp. 502–515. [Google Scholar] [CrossRef]
- Sun, J.; Feng, L.; Xie, J.; Ma, X.; Wang, D.; Hu, Y. Revealing the predictability of intrinsic structure in complex networks. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Du, W.; Shekhtman, L.; Wang, Y.; Havlin, S.; Cao, X.; Yan, G. Predictability of real temporal networks. Natl. Sci. Rev. 2020, 7, 929–937. [Google Scholar] [CrossRef] [PubMed]
- Stavinova, E.; Evmenova, E.; Antonov, A.; Chunaev, P. Link predictability classes in complex networks. In Proceedings of the Complex Networks & Their Applications X: Volume 1, Madrid, Spain, 30 November–2 December 2022; pp. 376–387. [Google Scholar] [CrossRef]
- Antonov, A.; Stavinova, E.; Evmenova, E.; Chunaev, P. Link predictability classes in large node-attributed networks. Soc. Netw. Anal. Min. 2022, 12, 81. [Google Scholar] [CrossRef]
- Donner, R.V.; Small, M.; Donges, J.F.; Marwan, N.; Zou, Y.; Xiang, R.; Kurths, J. Recurrence-based time series analysis by means of complex network methods. Int. J. Bifurc. Chaos 2011, 21, 1019–1046. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, X.; Small, M. Detecting chaos in pseudoperiodic time series without embedding. Phys. Rev. E 2006, 73, 016216. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, H. Complex network-based time series analysis. Phys. A Stat. Mech. Appl. 2008, 387, 1381–1386. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- Shirazi, A.; Jafari, G.R.; Davoudi, J.; Peinke, J.; Tabar, M.R.R.; Sahimi, M. Mapping stochastic processes onto complex networks. J. Stat. Mech. Theory Exp. 2009, 2009, P07046. [Google Scholar] [CrossRef]
- Kovantsev, A.; Chunaev, P.; Bochenina, K. Evaluating time series predictability via transition graph analysis. In Proceedings of the 2021 International Conference on Data Mining Workshops (ICDMW), Auckland, New Zealand, 7–10 December 2021; pp. 1039–1046. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]


| Measure | Formula |
|---|---|
| Mean Absolute Error (MAE) | |
| Mean Squared Error (MSE) | |
| Root Mean Square Error (RMSE) | |
| Mean Absolute Percentage Error (MAPE) | |
| Coefficient of determination () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezbochina, A.; Stavinova, E.; Kovantsev, A.; Chunaev, P. Enhancing Predictability Assessment: An Overview and Analysis of Predictability Measures for Time Series and Network Links. Entropy 2023, 25, 1542. https://doi.org/10.3390/e25111542
Bezbochina A, Stavinova E, Kovantsev A, Chunaev P. Enhancing Predictability Assessment: An Overview and Analysis of Predictability Measures for Time Series and Network Links. Entropy. 2023; 25(11):1542. https://doi.org/10.3390/e25111542
Chicago/Turabian StyleBezbochina, Alexandra, Elizaveta Stavinova, Anton Kovantsev, and Petr Chunaev. 2023. "Enhancing Predictability Assessment: An Overview and Analysis of Predictability Measures for Time Series and Network Links" Entropy 25, no. 11: 1542. https://doi.org/10.3390/e25111542
APA StyleBezbochina, A., Stavinova, E., Kovantsev, A., & Chunaev, P. (2023). Enhancing Predictability Assessment: An Overview and Analysis of Predictability Measures for Time Series and Network Links. Entropy, 25(11), 1542. https://doi.org/10.3390/e25111542






