Community-CL: An Enhanced Community Detection Algorithm Based on Contrastive Learning
Abstract
1. Introduction
- We present a novel end-to-end algorithm for community detection, which leverages a joint contrastive framework to simultaneously learn the community-level and node-level representations.
- We propose a learnable augmentation view generation scheme that captures the significance of edges in embedding space and generates more informative and diverse augmented data for community detection.
- We conduct extensive experiments on multiple real-world graph datasets to evaluate the proposed method. The results demonstrate that our approach achieves competitive performance on community detection tasks and the learnable augmentation scheme is effective and robust.
2. Related Work
2.1. Community Detection
2.2. Graph Contrastive Learning
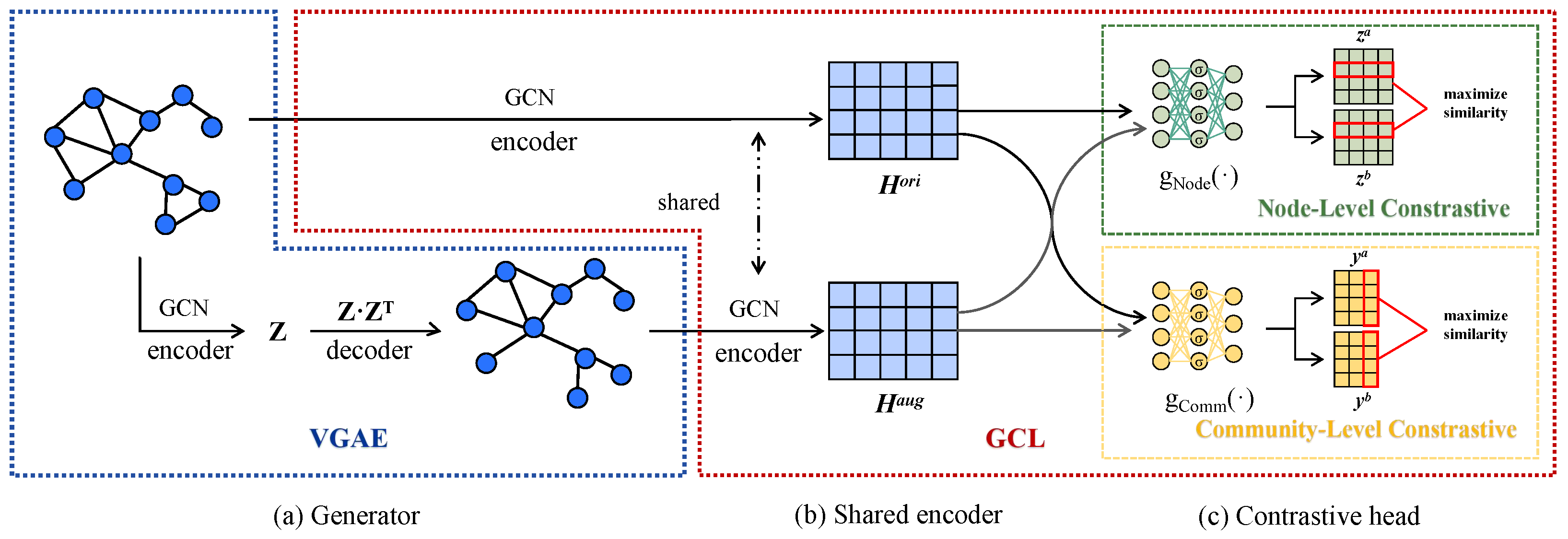
3. Methods
3.1. Generator
| Algorithm 1 The framework of generator |
| Require: Original Graph G, Augmented level , Training Epoch and Structure of |
| Ensure: Augmentation View |
3.2. Shared Graph Convolution Encoder
3.3. Node-Level Constrastive Head
3.4. Community-Level Contrastive Head
3.5. Object Function
| Algorithm 2 The framework of contrastive learning |
| Require: Original Graph, G, Augmentation View, , Training Epoch, , Temperature parameter, , Community number, M, Structure of f, , and . |
| Ensure: Community assignments. |
|
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets
4.1.2. Implementation Details
4.1.3. Evaluation Metrics
4.1.4. Leading Example
- Step 1: We downloaded the Cora dataset using PyG. The Cora dataset consists of 2708 nodes, 5429 edges, and a total of 7 categories. The dataset includes 1433 features, each of which is represented by only 0/1. Thus, we obtained the adjacency matrix and feature matrix .
- Step 3: Next, we use A, and X as input data for the shared convolution encoder, with a learned dimension of 128. As a result, we obtain the learned represention and .
- Step 4: We take the learned representations and as inputs to two MLP encoders, namely, and . In , we set the output dimension to 32 and obtain the node-level representations and . In , the output dimension is set to the number of classes (which is 7 in this case), resulting in the community-level representations and .
- Step 6: Finally, We use the Equation (14) to compute the overall loss, where the hyper-parameters and are set to 0.5. We update all the parameters according to Algorithm 2.
- Step 7: Once the training is complete, we take the original graph’s adjacency matrix A and feature matrix X as inputs to our model, resulting in the final community-level representation . We then use the argmax function to assign nodes to communities based on their highest probability of membership.
4.1.5. Baselines
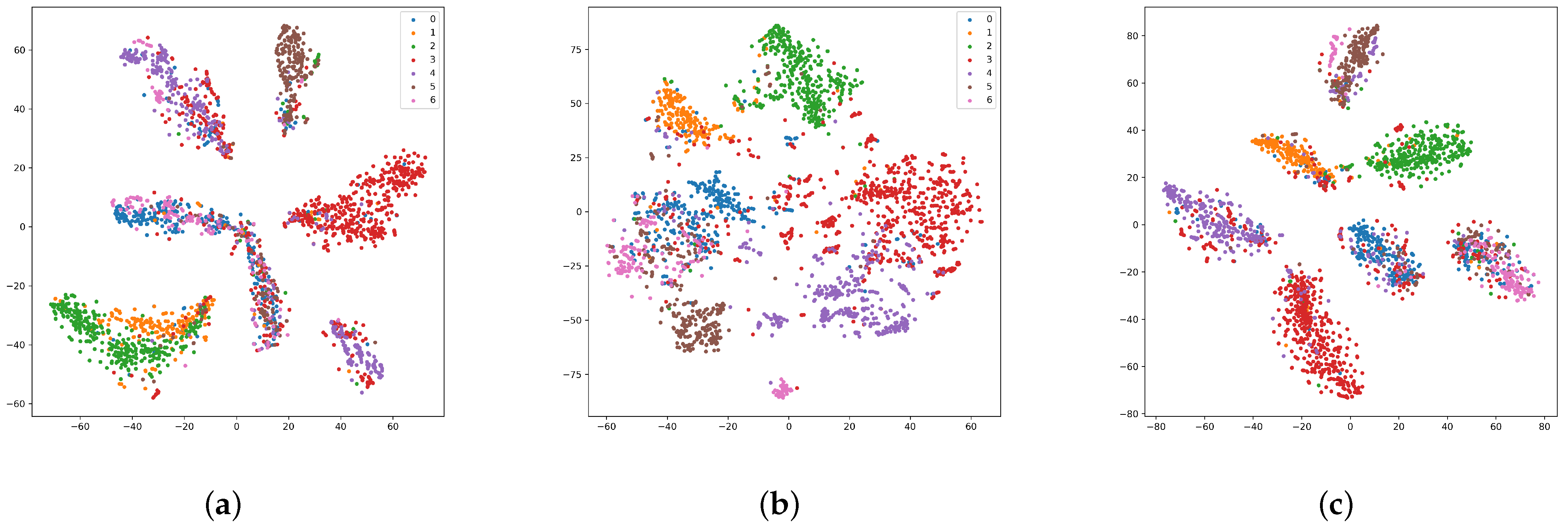
4.2. Overall Performance
4.3. Ablation Study
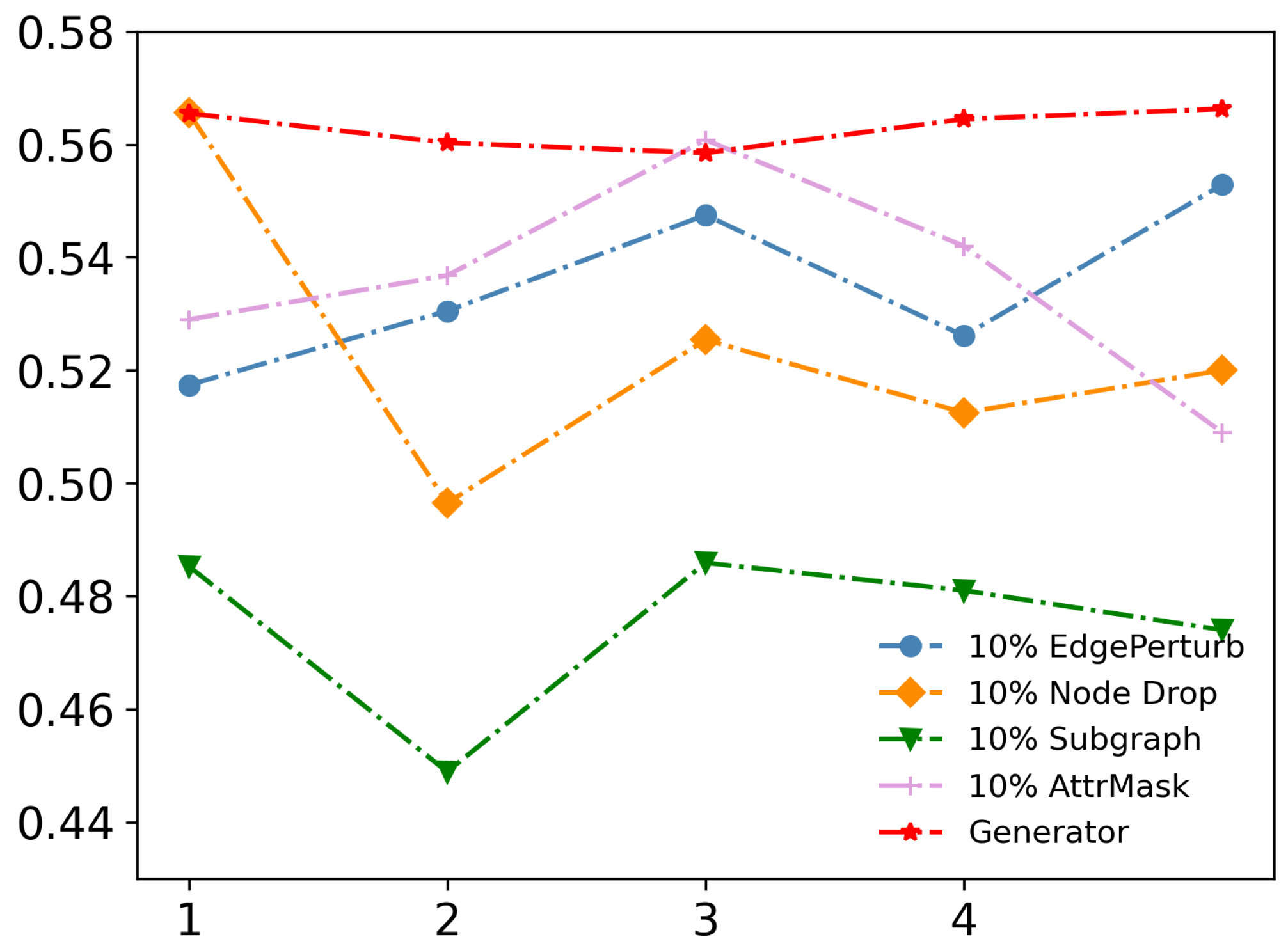
4.3.1. Importance of Generator
4.3.2. Effect of Augmented-Level
4.3.3. Importance of Double-Contrastive Head
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bedi, P.; Sharma, C. Community detection in social networks. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2016, 6, 115–135. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Kompatsiaris, Y.; Vakali, A.; Spyridonos, P. Community detection in social media: Performance and application considerations. Data Min. Knowl. Discov. 2012, 24, 515–554. [Google Scholar] [CrossRef]
- Gasparetti, F.; Sansonetti, G.; Micarelli, A. Community detection in social recommender systems: A survey. Appl. Intell. 2021, 51, 3975–3995. [Google Scholar] [CrossRef]
- Mokaddem, M.; Khodja, I.I.; Setti, H.A.; Atmani, B.; Mokaddem, C.E. Communities Detection in Epidemiology: Evolutionary Algorithms Based Approaches Visualization. In Proceedings of the Modelling and Implementation of Complex Systems: 7th International Symposium, MISC 2022, Mostaganem, Algeria, 30–31 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 319–332. [Google Scholar]
- Bonifazi, G.; Cecchini, S.; Corradini, E.; Giuliani, L.; Ursino, D.; Virgili, L. Investigating community evolutions in TikTok dangerous and non-dangerous challenges. J. Inf. Sci. 2022, 01655515221116519. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, L.; Liu, L.; Yao, J.; Ali, M.E. User interest community detection on social media using collaborative filtering. Wirel. Netw. 2022, 28, 1169–1175. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Su, X.; Xue, S.; Liu, F.; Wu, J.; Yang, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Jin, D.; et al. A comprehensive survey on community detection with deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- He, D.; Song, Y.; Jin, D.; Feng, Z.; Zhang, B.; Yu, Z.; Zhang, W. Community-centric graph convolutional network for unsupervised community detection. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 3515–3521. [Google Scholar]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 18661–18673. [Google Scholar]
- Zhu, Y.; Xu, Y.; Yu, F.; Liu, Q.; Wu, S.; Wang, L. Deep graph contrastive representation learning. arXiv 2020, arXiv:2006.04131. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, Q.; Huang, S.; Xiong, H.; Zhang, X. Autogcl: Automated graph contrastive learning via learnable view generators. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 8892–8900. [Google Scholar]
- Chunaev, P. Community detection in node-attributed social networks: A survey. Comput. Sci. Rev. 2020, 37, 100286. [Google Scholar] [CrossRef]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar]
- Li, Y.; Hu, P.; Liu, Z.; Peng, D.; Zhou, J.T.; Peng, X. Contrastive clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 8547–8555. [Google Scholar]
- Amini, A.A.; Chen, A.; Bickel, P.J.; Levina, E. Pseudo-likelihood methods for community detection in large sparse networks. Ann. Statist. 2013, 41, 2097–2122. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Society. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef]
- Tandon, A.; Albeshri, A.; Thayananthan, V.; Alhalabi, W.; Radicchi, F.; Fortunato, S. Community detection in networks using graph embeddings. Phys. Rev. E 2021, 103, 022316. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Wang, C.; Pan, S.; Long, G.; Zhu, X.; Jiang, J. Mgae: Marginalized graph autoencoder for graph clustering. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 889–898. [Google Scholar]
- Chen, Z.; Li, X.; Bruna, J. Supervised community detection with line graph neural networks. arXiv 2017, arXiv:1705.08415. [Google Scholar]
- Akbas, E.; Zhao, P. Attributed graph clustering: An attribute-aware graph embedding approach. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, Sydney, Australia, 31 July–3 August 2017; pp. 305–308. [Google Scholar]
- Jia, Y.; Zhang, Q.; Zhang, W.; Wang, X. Communitygan: Community detection with generative adversarial nets. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 784–794. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Velickovic, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep graph infomax. ICLR (Poster) 2019, 2, 4. [Google Scholar]
- Zhu, Y.; Xu, Y.; Yu, F.; Liu, Q.; Wu, S.; Wang, L. Graph contrastive learning with adaptive augmentation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2069–2080. [Google Scholar]
- Hassani, K.; Khasahmadi, A.H. Contrastive multi-view representation learning on graphs. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 4116–4126. [Google Scholar]
- Qiu, J.; Chen, Q.; Dong, Y.; Zhang, J.; Yang, H.; Ding, M.; Wang, K.; Tang, J. Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1150–1160. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Hight, C.; Perry, C. Collective intelligence in design. Archit. Des. 2006, 76, 5–9. [Google Scholar] [CrossRef]
- Shchur, O.; Mumme, M.; Bojchevski, A.; Günnemann, S. Pitfalls of graph neural network evaluation. arXiv 2018, arXiv:1811.05868. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Jing, B.; Park, C.; Tong, H. Hdmi: High-order deep multiplex infomax. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2414–2424. [Google Scholar]
- Li, B.; Jing, B.; Tong, H. Graph communal contrastive learning. In Proceedings of the ACM Web Conference 2022, Austin, TX, USA, 1–5 May 2022; pp. 1203–1213. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
| Dataset | Type | Nodes | Edges | Attributes | Classes |
|---|---|---|---|---|---|
| Cora | reference | 2708 | 10,556 | 1433 | 7 |
| Citeseer | reference | 3327 | 9104 | 3703 | 6 |
| Amazon-Photo | co-purchase | 7487 | 119,043 | 745 | 8 |
| Amazon-Computers | co-purchase | 13,381 | 245,778 | 767 | 10 |
| Coauthor-CS | co-author | 18,333 | 81,894 | 6805 | 15 |
| WikiCS | reference | 11,701 | 216,123 | 300 | 10 |
| Dataset | Cora | Citeseer | Amazon-Photo | Amazon-Computers | Coauthor-CS | WikiCS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | NMI | ARI | NMI | ARI | NMI | ARI | NMI | ARI | NMI | ARI | NMI | ARI |
| k-means | 0.167 | 0.229 | 0.17 | 0.27 | 0.235 | 0.112 | 0.192 | 0.086 | 0.498 | 0.315 | 0.244 | 0.022 |
| DeepWalk | 0.243 | 0.224 | 0.276 | 0.105 | 0.494 | 0.338 | 0.227 | 0.118 | 0.727 | 0.612 | 0.323 | 0.095 |
| MVGRL | 0.502 | 0.479 | 0.392 | 0.394 | 0.343 | 0.242 | 0. 244 | 0.141 | 0.733 | 0.637 | 0.254 | 0.101 |
| DGI | 0.498 | 0.447 | 0.378 | 0.381 | 0.365 | 0.253 | 0.318 | 0.165 | 0.754 | 0.639 | 0.309 | 0.130 |
| HDI | 0.449 | 0.352 | 0.350 | 0.341 | 0.430 | 0.310 | 0.347 | 0.216 | 0.725 | 0.616 | 0.240 | 0.104 |
| GAE | 0.389 | 0.293 | 0.174 | 0.141 | 0.614 | 0.493 | 0.441 | 0.258 | 0.727 | 0.613 | 0.241 | 0.094 |
| VGAE | 0.414 | 0.347 | 0.163 | 0.101 | 0.531 | 0.354 | 0.423 | 0.238 | 0.733 | 0.605 | 0.259 | 0.072 |
| GCA | 0.503 | 0.342 | 0.443 | 0.384 | 0.592 | 0.504 | 0.426 | 0.246 | 0.735 | 0.618 | 0.298 | 0.101 |
| gCooLe | 0.494 | 0.422 | 0.388 | 0.347 | 0.618 | 0.508 | 0.474 | 0.277 | 0.747 | 0.634 | 0.321 | 0.155 |
| Our Method | 0.563 | 0.487 | 0.476 | 0.450 | 0.714 | 0.629 | 0.550 | 0.434 | 0.757 | 0.657 | 0.455 | 0.305 |
| Augmented Level | NMI | ARI | Predicted Q | Original Q |
|---|---|---|---|---|
| 1 | 0.533 ± 0.0327 | 0.465 ± 0.0753 | 0.734 ± 0.0082 | 0.6401 |
| 2 | 0.545 ± 0.0022 | 0.481 ± 0.0253 | 0.743 ± 0.0095 | |
| 3 | 0.573 ± 0.0082 | 0.501 ± 0.0277 | 0.735 ± 0.0127 | |
| 4 | 0.557 ± 0.0245 | 0.482 ± 0.0400 | 0.726 ± 0.0083 | |
| 5 | 0.558 ± 0.0107 | 0.486 ± 0.0294 | 0.717 ± 0.0150 |
| Dataset | Contrastive Head | NMI | ARI |
|---|---|---|---|
| Cora | Node+Community | 0.5368 + 0.018 | 0.4837 + 0.024 |
| Node | 0.4848 + 0.024 | 0.3847 + 0.045 | |
| Community | 0.4532 + 0.011 | 0.4051 + 0.015 | |
| Amazon-Photo | Node + Community | 0.7140 + 0.010 | 0.6293 + 0.008 |
| Node | 0.3824 + 0.030 | 0.2741 + 0.030 | |
| Community | 0.5752 + 0.000 | 0.5741 + 0.001 | |
| Amazon-Computers | Node + Community | 0.5506 + 0.0035 | 0.4338 + 0.0033 |
| Node | 0.4678 + 0.020 | 0.3053 + 0.032 | |
| Community | 0.4804 + 0.0014 | 0.3202 + 0.0020 | |
| Coauthor-CS | Node + Community | 0.7519 + 0.0132 | 0.6579 + 0.0108 |
| Node | 0.6432 + 0.0105 | 0.4357 + 0.0110 | |
| Community | 0.7243 + 0.0055 | 0.6378 + 0.0083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Xu, W.; Zhuo, X. Community-CL: An Enhanced Community Detection Algorithm Based on Contrastive Learning. Entropy 2023, 25, 864. https://doi.org/10.3390/e25060864
Huang Z, Xu W, Zhuo X. Community-CL: An Enhanced Community Detection Algorithm Based on Contrastive Learning. Entropy. 2023; 25(6):864. https://doi.org/10.3390/e25060864
Chicago/Turabian StyleHuang, Zhaoci, Wenzhe Xu, and Xinjian Zhuo. 2023. "Community-CL: An Enhanced Community Detection Algorithm Based on Contrastive Learning" Entropy 25, no. 6: 864. https://doi.org/10.3390/e25060864
APA StyleHuang, Z., Xu, W., & Zhuo, X. (2023). Community-CL: An Enhanced Community Detection Algorithm Based on Contrastive Learning. Entropy, 25(6), 864. https://doi.org/10.3390/e25060864





