Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay
Abstract
1. Introduction
- (1)
- The approach, model-free robust control of nonlinear dynamic systems with input delay, is general and concise for analytical expansions, simulation demonstrations, and applications.
- (2)
- The stability analysis for stabilizing the systems has established a platform for positively considering input delay into control system design. It can be even used for intentionally introducing delay into control system design (Jin, Niculescu, Boussaada, and Gu 2017).
- (3)
- The approach requests less knowledge of plants and merely assumes that the open loop is stable, output controllable, and closed loop stabilizable. There is no need for model structures/parameters and input delay time in the control system design, which, by trial-and-error, tunes the delay regulator output feedback gain within a narrow numerical range of , within which the values have role in reducing the time delay effect in control system stabilization. The approach can increase the system gain stability margin times and phase stability margin to a degree. Obviously, it is robust against uncertainties (the whole plant plus delay is treated as an uncertain black box with measurable output and enabled input at the two ends).
- (4)
- It provides a simulation portfolio for demonstrating the design procedure and explaining the transparent application procedure.
- (5)
- The study has application potential/significance in terms of providing simplicity (solutions) while dealing with unknown input-delayed dynamic complexity (problems).
2. Preliminaries
2.1. Problem Formulation—Control of the Dynamic Plants with Delayed Input
2.2. Assumptions
2.3. Linear Control Systems with Input Delay
2.4. Routh–Hurwitz Stability Criterion (Patil 2021)
2.5. Poles of Control System with Input Time Delay
2.6. Non-Predictive Low Gain Control
3. Stabilization of Dynamic Systems with Input Delay
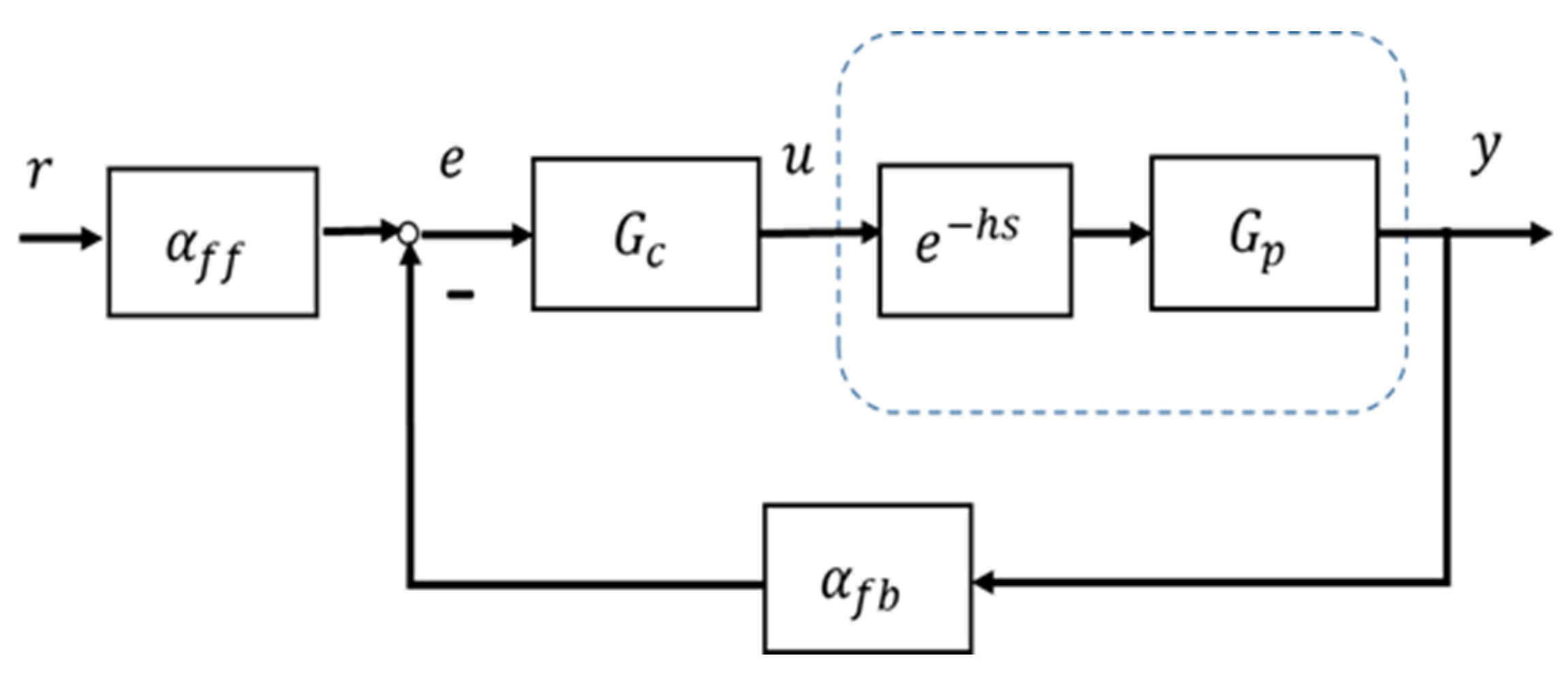
3.1. Configuration of Linear Equivalent Control Systems
3.2. Controller Design
- (1)
- Use the feedback gain to stabilize the system. It is not analytically calculated as there is no plant model available and the design follows a trial-and-error approach to select a proper in the range of . The smaller of the , the more of a stability margin, which is possibly a monotonic response. Increasing could generate a decayed oscillatory response, further increasing will drive the system to instability.
- (2)
- Use the feedforward gain to remove steady errors in response to a step reference input. This is achieved by the final value theorem referring to Figure 2. First assign it has,
- (3)
- Use the cascade controller in conjunction with to improve the system dynamic/static performance. This is left for future studies and this study sets .
3.3. Stability Analysis
3.3.1. Open-Loop-Based Stability Analysis (Frequency Response/Gain and Phase Margins)
3.3.2. Closed-Loop-Based Stability Analysis (Laplace Transfer Function/Routh Criterion)
4. Examples
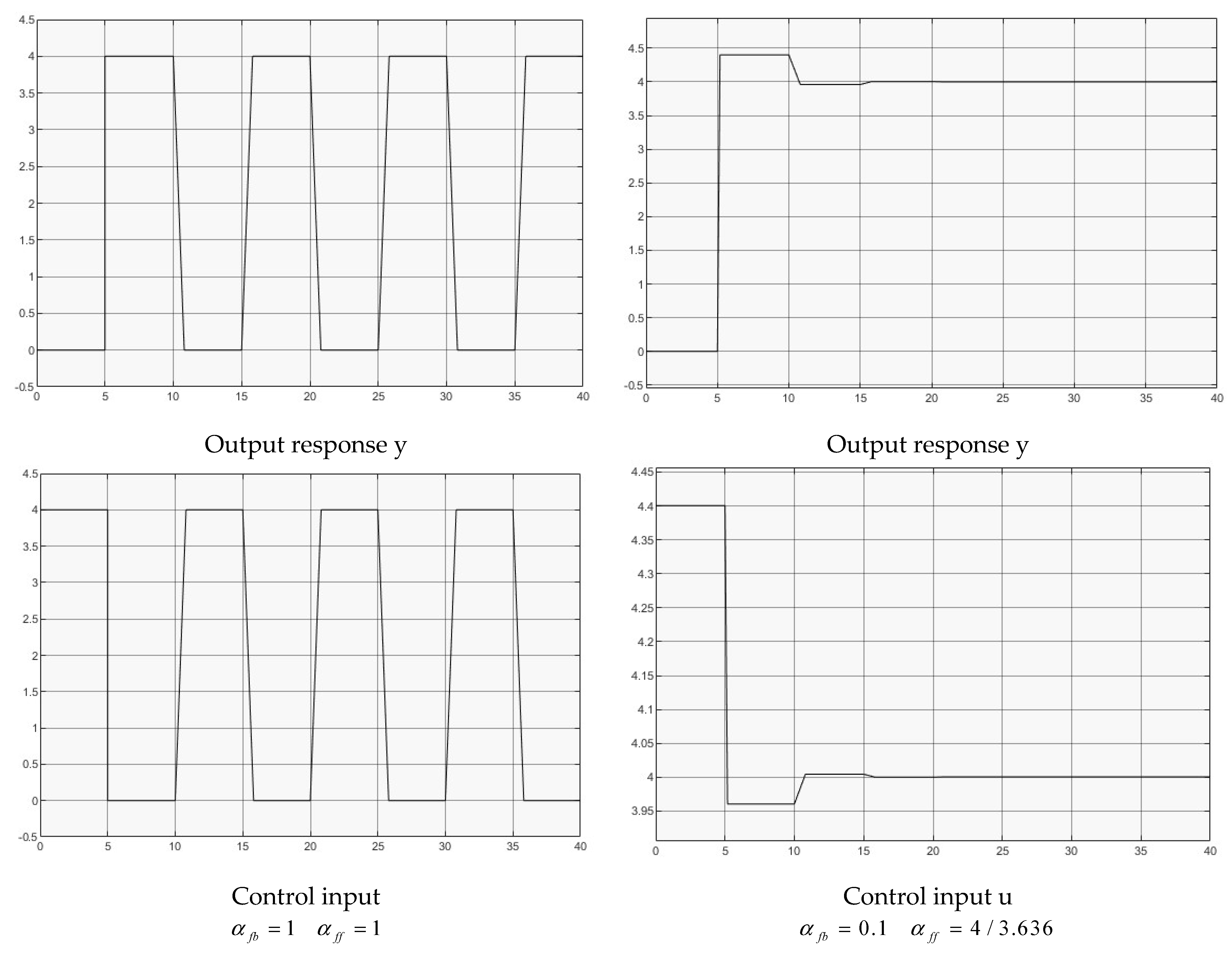
- (1)
- The operating point is assigned as a step reference with amplitude four for all of the examples.
- (2)
- Time delay for all the examples, and is only used for simulation, not for controller design, which means that the time delay is unknown.
- (3)
- The controller for all of the examples.
- (4)
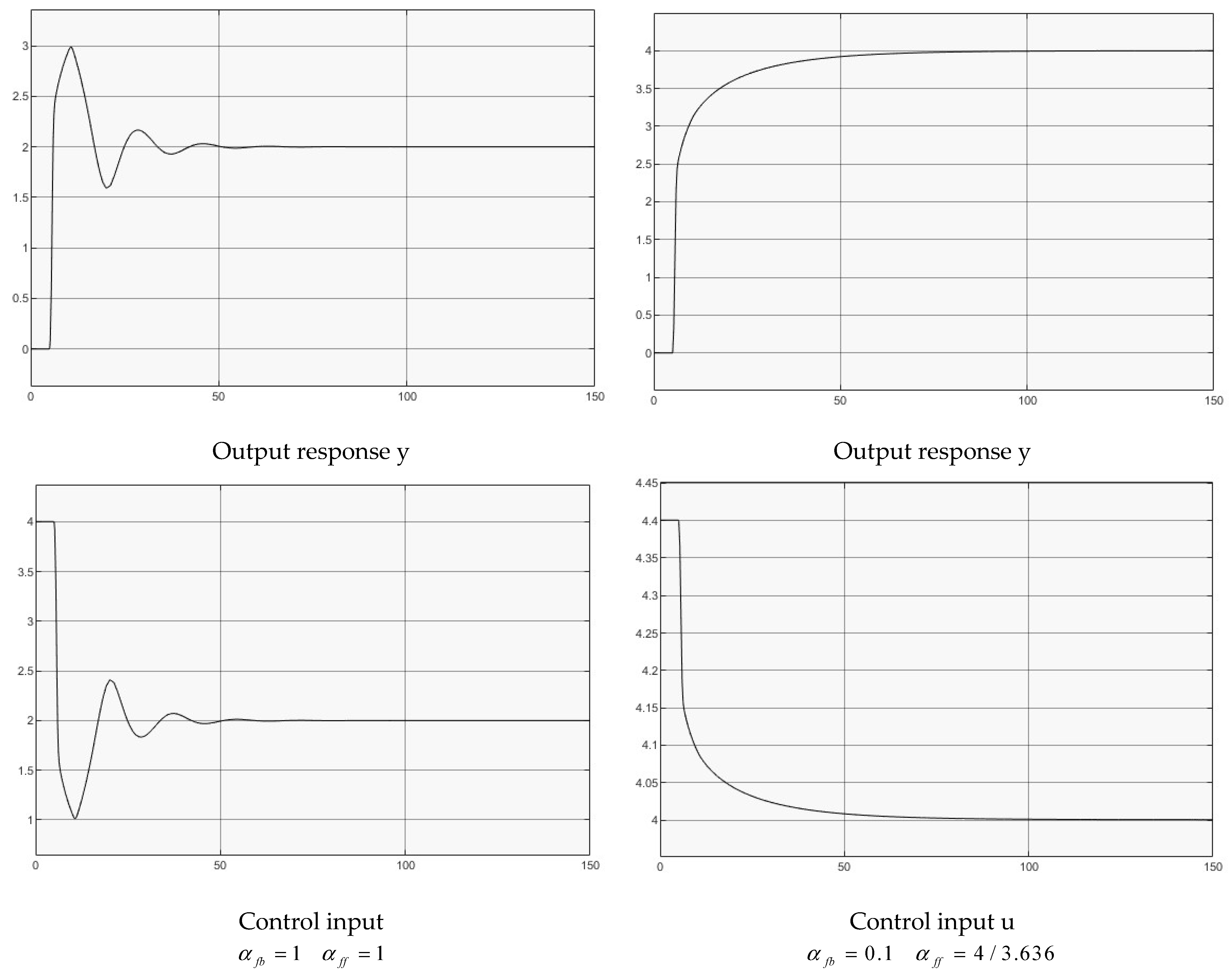
- Using a trial-and-error iterative approach to determine the feedback gain case by case, which starts from the value 0.5 in the middle of the feedback controller boundaries and then tries the two directions (increase/decrease) until a desired value is determined. Once is selected, calculate the feedforward gain . It should be noted that this simulation study uses a unique choice for all the simulated control systems for comparison.
4.1. Pure Time Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
4.2. First Order Linear Plant with Input Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
4.3. Second Order Plant with Input Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
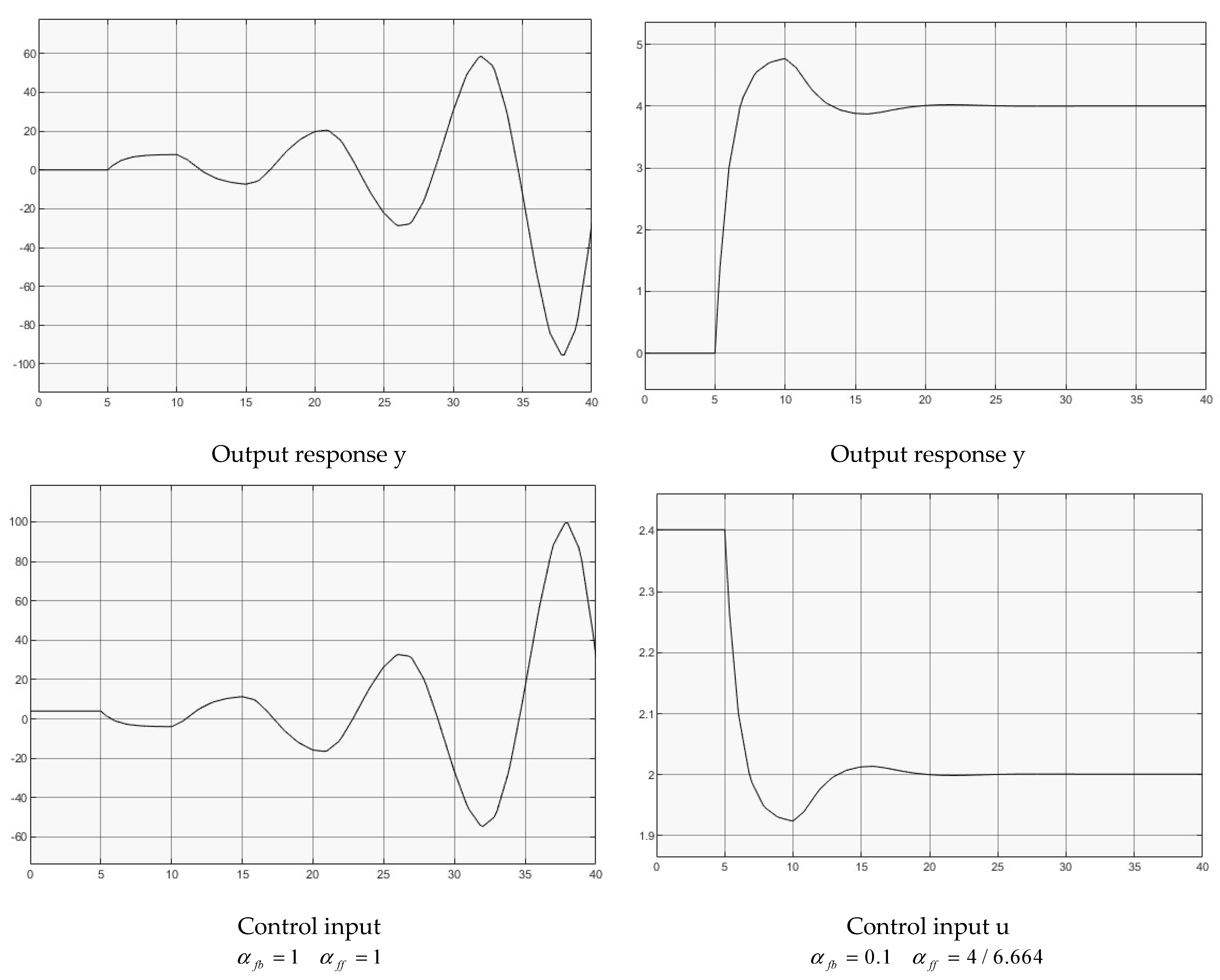
4.4. Van de Pol (VDP) Oscillator Dynamics with Input Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
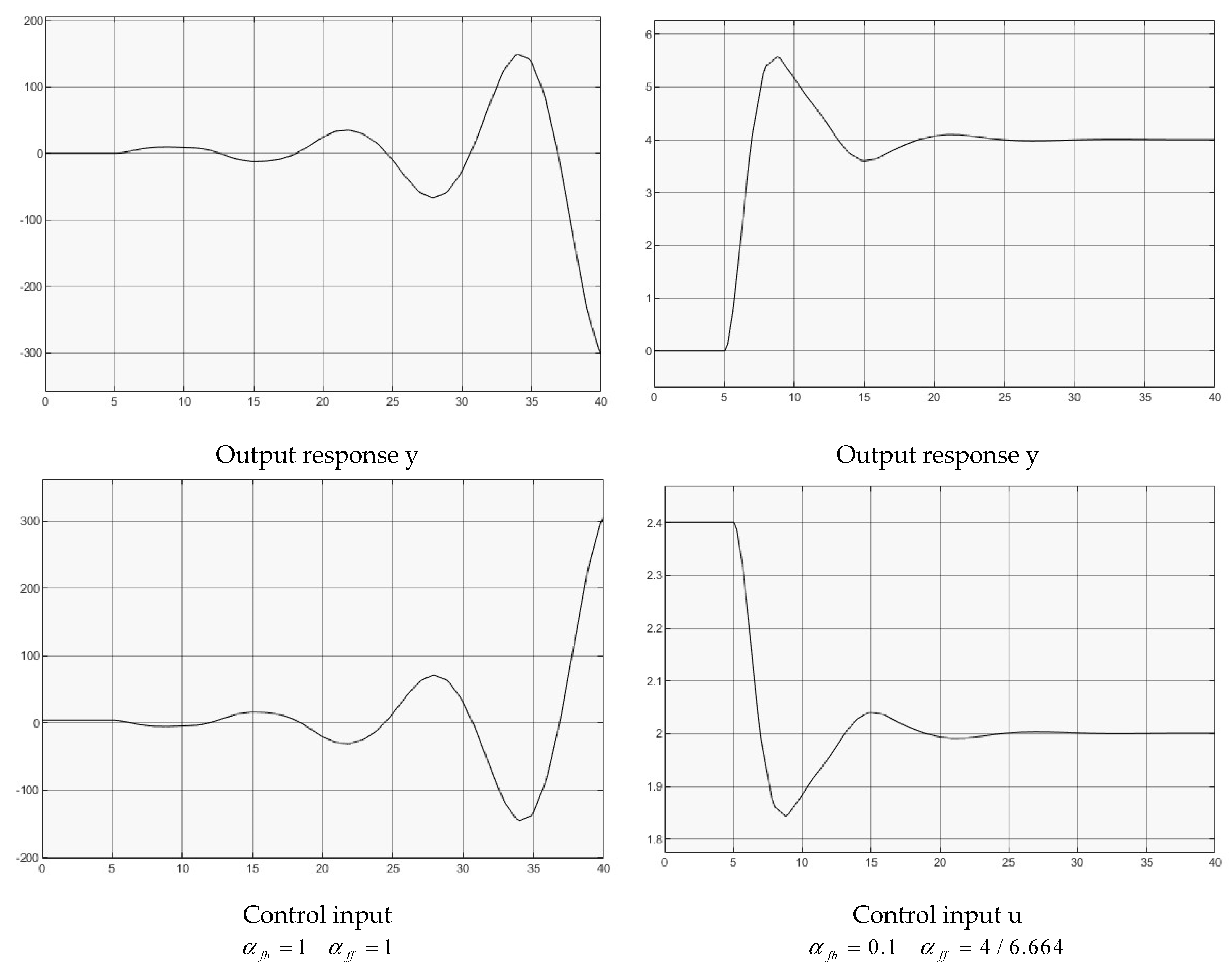
4.5. Nonlinear Nonaffine Plant with Input Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
4.6. Nonlinear Rational Plant with Input Delay
- (1)
- , for full delay feedback;
- (2)
- , for reduced delay feedback.
- (1)
- The simulation tests demonstrate the analytical results derived from stability analysis and control system design.
- (2)
- The input delay increases the dynamic order of the characteristic equation, which easily drives open loop stable systems into instability with full delay feedback in the corresponding closed loop systems. It is observed that through reducing output feedback gain (regulating delay feedback), the systems can be comfortably stabilized for the closed loop stabilizable systems.
- (3)
- All tests show that unstable responses are oscillatory (instead of monotonic unstable). The oscillatory instability comes from the fact of at least one pair of complex conjugate poles have a positive real part, which is due to the exponential components in the system transfer function.
- (4)
- The approach is a model-free control for linear/nonlinear systems with unknown constant input delay. There is no need for prediction, non-physical design parameters of an ultra-local model, when compared with aforementioned popular model-free control approaches.
- (5)
- Regarding the decay regulation, tuning within a narrow trial-and-error range provides an easy iterative testing/tuning procedure (similar to engineering tuning on site–connect to tune). The selection of increases stability gain/phase margins, robustness, etc. Both limits of represent the open loop operation and full decay feedback operation, respectively.
- (6)
- The simulations–computational experiments are mainly designed for validating feedback stabilization using the decay regulator . For dealing with the steady error referring to a step reference, the feedforward gain has been determined by case by case. For a unilateral approach to remove such steady errors, a simulation was assigned to the cascade controller with a Proportional and Integral (PI) transfer function, which has been tested (not shown in the figures) with the nonlinear nonaffine dynamic system of (37). The results confirm the feedforward gain , which is consistent with that derived in Section 3. Using integral control to remove the steady error against step/level reference has been the general procedure in analytical work and applications. As explained in Section 3, will be systematically studied in the future work.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krstic, M.; Bekiaris-Liberis, N. Control of nonlinear delay systems: A tutorial. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Richard, J.P. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Deng, Y.L.; Léchappé, V.; Moulay, E.; Chen, Z.; Liang, B.; Plestan, F.; Han, Q.L. Predictor-based control of time-delay systems: A survey. Int. J. Syst. Sci. 2022, 53, 2496–2534. [Google Scholar] [CrossRef]
- Lin, Z.L.; Fang, H.J. On asymptotic stabilizability of linear systems with delayed input. IEEE Trans. Autom. Control 2007, 52, 998–1013. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E. Delay-dependent methods and the first delay interval. Syst. Control Lett. 2014, 64, 57–63. [Google Scholar] [CrossRef]
- Smith, O.J.M. Close control of loops with dead time. Chem Eng Prog 1957, 53, 217–219. [Google Scholar]
- Zhong, Q.C. Control of integral processes with dead time—Part 3: Deadbeat disturbance response. IEEE Trans. Autom. Control. 2003, 48, 153–159. [Google Scholar] [CrossRef]
- Gu, K.Q.; Kharitonov, V.; Chen, J. Stability of Time-Delay Systems; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Wang, Q.G.; Lee, T.H.; Tan, K.K. Finite-Spectrum Assignment for Time-Delay Systems; The Lecture Notes in Control and Information Sciences; Springer: London, UK, 1999. [Google Scholar]
- Jin, C.; Niculescu, S.I.; Boussaada, I.; Gu, K. Stability analysis of control systems subject to delay-difference feedback. In Proceedings of the IFAC 2017—20th World Congress of the International Federation of Automatic Control, Toulouse, France, 14 July 2017; pp. 13330–13335. [Google Scholar] [CrossRef]
- Michiels, W.; Engelborghs, K.; Vansevenant, P.; Roose, D. Continuous pole placement for delay equations. Automatica 2002, 38, 747–761. [Google Scholar] [CrossRef]
- Efimov, D.; Polyakov, A.; Fridman, L.; Perruquetti, W.; Richard, J.P. Delayed sliding mode control. Automatica 2016, 64, 37–43. [Google Scholar] [CrossRef]
- Han, X.; Fridman, E.; Speugeon, S.K. Sliding mode control in the presence of input delay: A singular perturbation approach. Automatica 2012, 48, 1904–1912. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, Z.Q. Modified active disturbance rejection control for time-delay systems. ISA 2014, 53, 882–888. [Google Scholar] [CrossRef]
- Chen, S.; Xue, W.; Zhong, S.; Huang, Y. On comparison of modified ADRCs for nonlinear uncertain systems with time delay. Sci. China Inf. Sci. 2018, 61, 70223. [Google Scholar] [CrossRef]
- Fliess, M and Join, C Model-free control. Int. J. Control 2013, 86, 2228–2252. [CrossRef]
- Doublet, M.; Join, C.; Hamelin, F. Model-free control for unknown delayed systems. In Proceedings of the 3rd Conference on Control and Fault-Tolerant Systems, SysTol 2016, Barcelone, Spain, 7–9 September 2016. [Google Scholar]
- Yaseen, A.A.; Bayart, M. A model-free approach to networked control system with time-varying communication delay. IFAC-Pap. 2018, 51, 558–563. [Google Scholar] [CrossRef]
- Ran, M.P.; Wang, Q.; Dong, C.Y.; Xie, L.H. Active disturbance rejection control for uncertain time-delay nonlinear systems. Automatica 2020, 112, 108692. [Google Scholar] [CrossRef]
- Baldi, S.; Sun, D.; Xia, X.; Zhou, G.; Liu, D. ArduPilot-based adaptive autopilot: Architecture and software-in-the-loop experiments. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4473–4485. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, B.; Tan, C.; Ge, S.S. Adaptive control of uncertain nonlinear time-delay systems with external disturbance. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1288–1295. [Google Scholar] [CrossRef]
- Zhu, Q.M. Complete model-free sliding mode control (CMFSMC). Sci. Rep. 2021, 11, 22565. [Google Scholar] [CrossRef]
- Zhu, Q.M.; Mobayen, S.; Nemati, H.; Zhang, J.H.; Wei, W. A new configuration of composite nonlinear feedback control for nonlinear systems with input saturation. J. Vib. Control 2023, 29, 1417–1430. [Google Scholar] [CrossRef]
- Patil, A. Routh-Hurwitz Criterion for Stability: An Overview and Its Implementation on Characteristic Equation Vectors Using MATLAB. In Emerging Technologies in Data Mining and Information Security; Advances in Intelligent Systems and Computing; Hassanien, A.E., Bhattacharyya, S., Chakrabati, S., Bhattacharya, A., Dutta, S., Eds.; Springer: Singapore, 2021; Volume 1286. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, W.D.; Gu, D.Y. Analytical design of two-degree-of-freedom control scheme for open-loop unstable processes with time delay. J. Process Control 2005, 15, 559–572. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 1990. [Google Scholar]
- Zítek, P.; Vyhlídal, T. Quasi-polynomial based design of time delay control systems. IFAC Proc. 2003, 36, 233–238. [Google Scholar] [CrossRef]
- Wei, Y.; Hu, Y.; Dai, Y.; Wang, Y. A generalized Padé approximation of time delay operator. Int. J. Control Autom. Syst. 2016, 14, 181–187. [Google Scholar] [CrossRef]
- Popov, V.M. Stability criteria for systems containing non-univocal elements. In Probleme de Automatizare III; Editura Academiei: Bucharest, Romania, 1960; pp. 143–151. (In Romanian) [Google Scholar]
- Rasvan, V.; Popescu, D. Control of systems with input delay—An elementary approach. In Advances in Time Delay Systems; Lecture Notes in Computational Sciences and Engineering No.38; Niculescu, S.I., Gu, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 103–110. [Google Scholar] [CrossRef]
- Johansson, M. Piecewise Linear Control Systems; Department of Automatic Control, Lund Institute of Technology (LTH): Lund, Sweden, 1999. [Google Scholar]
- Zhu, Q.M.; Guo, L.Z. Stable adaptive neurocontrol for nonlinear discrete-time systems. IEEE Trans. Neural Netw. 2004, 15, 653–662. [Google Scholar] [CrossRef]
- Casaleiro, J.C.F.d.A.; Oliveira, L.A.B.G.; Filanovsky, I.M. Van der Pol Oscillator. In Quadrature RC−Oscillators; Analog Circuits and Signal Processing; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Zhu, Q.M.; Wang, Y.J.; Zhao, D.Y.; Li, S.Y.; Billings, S.A. Review of rational (total) nonlinear dynamic system modelling, identification and control. Int. J. Syst. Sci. 2015, 46, 122–133. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasapathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.M.; Liu, L.; Zhang, W.C.; Li, S.Y. Control of complex nonlinear dynamic rational systems. Complexity 2018, 2018, 8953035. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Zhang, J.; Zhang, W. Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay. Entropy 2023, 25, 1076. https://doi.org/10.3390/e25071076
Zhu Q, Zhang J, Zhang W. Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay. Entropy. 2023; 25(7):1076. https://doi.org/10.3390/e25071076
Chicago/Turabian StyleZhu, Quanmin, Jianhua Zhang, and Weicun Zhang. 2023. "Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay" Entropy 25, no. 7: 1076. https://doi.org/10.3390/e25071076
APA StyleZhu, Q., Zhang, J., & Zhang, W. (2023). Non-Predictive Model-Free Control of Nonlinear Systems with Unknown Input Time Delay. Entropy, 25(7), 1076. https://doi.org/10.3390/e25071076







