Corrected Thermodynamics of Black Holes in f(R) Gravity with Electrodynamic Field and Cosmological Constant
Abstract
:1. Introduction
2. Thermodynamics of Spherically Symmetric BHs in Gravity Theory with Electrodynamic Field and Cosmological Constant
2.1.
2.2.
3. Corrected Thermodynamics of Spherically Symmetric BHs in the Framework of -Modified Theory
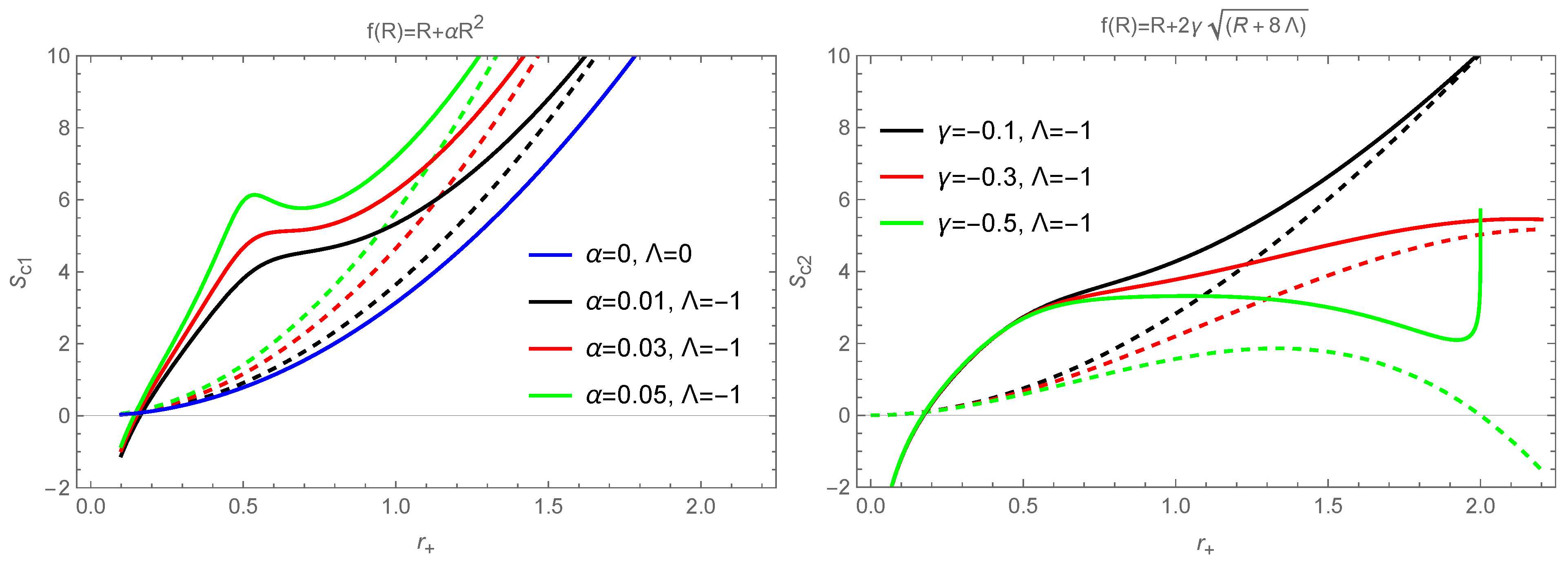
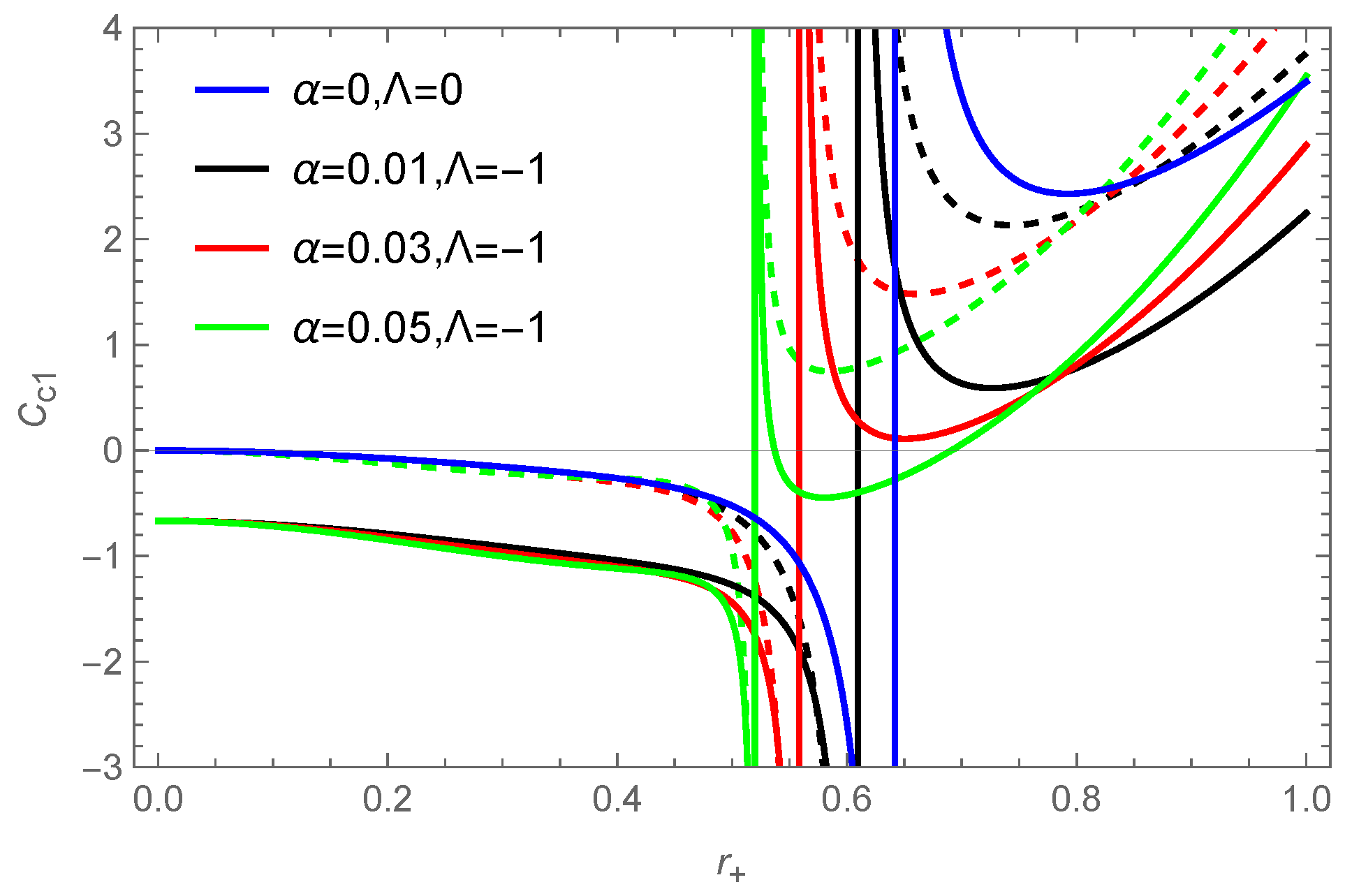
3.1. Corrected Entropy of Black Holes
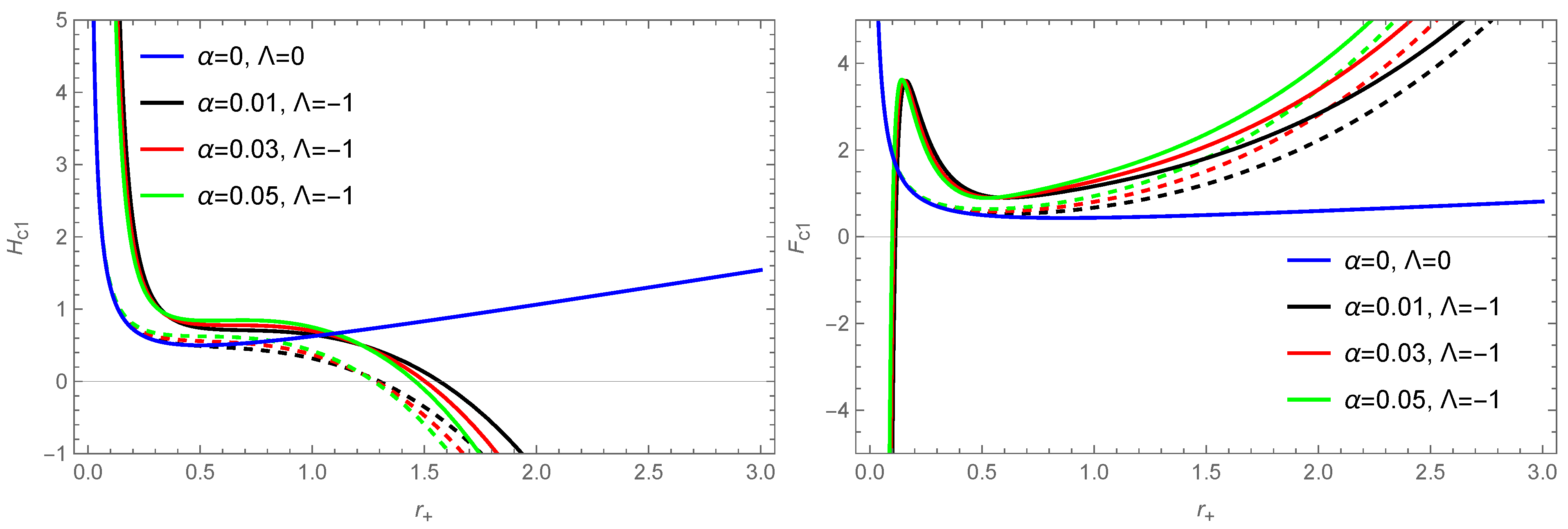
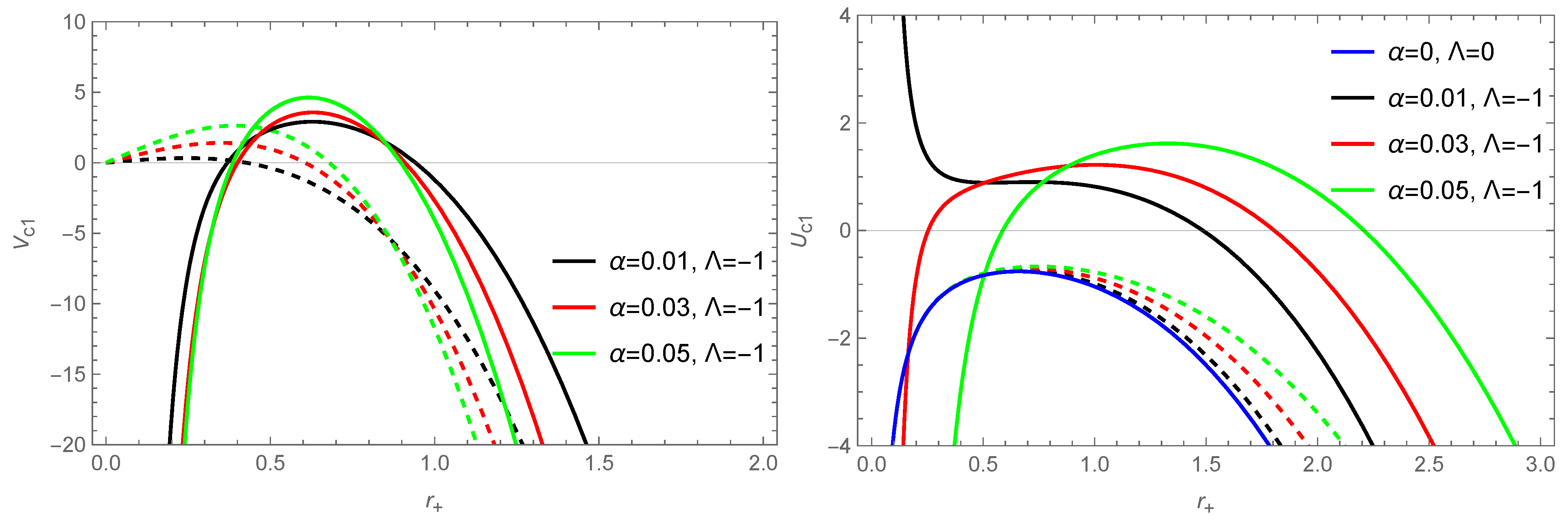
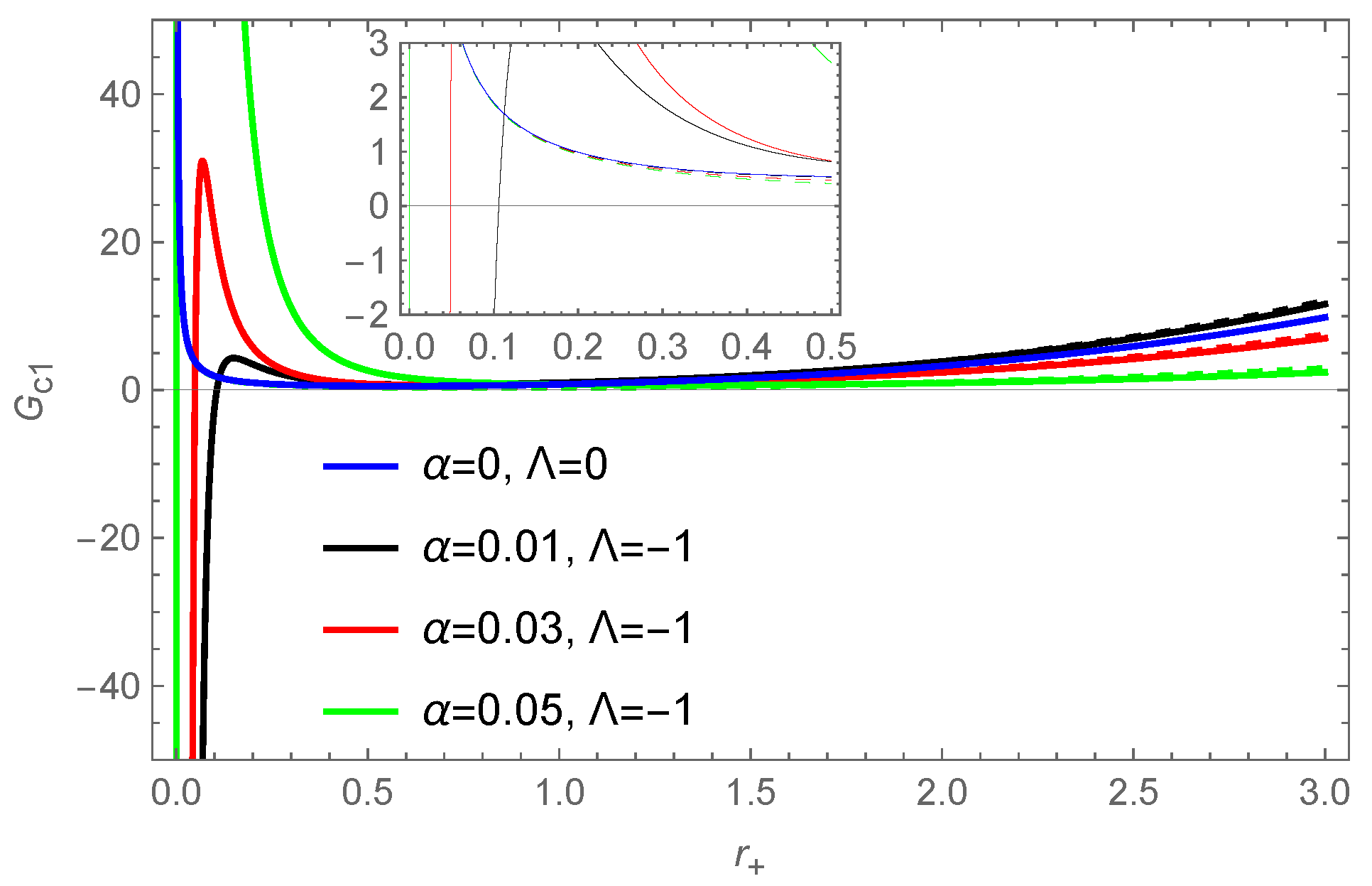
3.2. Corrected Thermodynamics of Black Holes
3.2.1.
3.2.2.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Clemence, G.M. The Relativity Effect in Planetary Motions. Rev. Mod. Phys. 1947, 19, 361–364. [Google Scholar]
- Will, C.M. New General Relativistic Contribution to Mercury’s Perihelion Advance. Phys. Rev. Lett. 2018, 120, 191101. [Google Scholar] [CrossRef]
- Fomalont, E.B.; Kopeikin, S.M.; Lanyi, G.; Benson, J. Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA. Astrophys. J. 2009, 699, 1395–1402. [Google Scholar]
- Nordtvedt, J. Equivalence Principle for Massive Bodies. II. Theory. Phys. Rev. 1968, 169, 1017–1025. [Google Scholar]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Progress in Lunar Laser Ranging Tests of Relativistic Gravity. Phys. Rev. Lett. 2004, 93, 1017–1025. [Google Scholar]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett. 2019, 875, L2. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; Princeton University Press: Princeton, NJ, USA, 1990. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ωand Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Lu, J.; Li, J.; Guo, H.; Zhuang, Z.; Zhao, X. Linearized Physics and Gravitational-Waves Polarizations in the Palatini Formalism of GBD Theory. Phys. Lett. B 2020, 811, 135985. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Harko, T. Modified gravity with arbitrary coupling between matter and geometry. Phys. Lett. B 2008, 669, 376–379. [Google Scholar] [CrossRef]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry-matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef]
- Zubair, M.; Abbas, G.; Noureen, I. Possible formation of compact stars in f(R,T) gravity. Astrophys. Space Sci. 2016, 361, 8. [Google Scholar] [CrossRef]
- Houndjo, M.J.S.; Rodrigues, M.E.; Momeni, D.; Myrzakulov, R. Exploring cylindrical solutions in modified f(G) gravity. Can. J. Phys. 2014, 92, 1528–1540. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss-Bonnet and F(R,G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295–310. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. f(R) constant-roll inflation. Eur. Phys. J. C 2017, 77, 538. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Corda, C. Primordial production of massive relic gravitational waves from a weak modification of General Relativity. Astropart. Phys. 2008, 30, 209–215. [Google Scholar] [CrossRef]
- Corda, C. Massive relic gravitational waves from f(R) theories of gravity: Production and potential detection. Eur. Phys. J. C 2010, 65, 257–267. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Shankaranarayanan, S. Quasinormal modes as a distinguisher between general relativity and f(R) gravity. Phys. Rev. D 2017, 96, 064044. [Google Scholar] [CrossRef]
- Aragon, A.; Gonzalez, P.A.; Papantonopoulos, E.; Vasquez, Y. Quasinormal modes and their anomalous behavior for black holes in f(R) gravity. Eur. Phys. J. C 2021, 81, 407. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity unifying Rm inflation with LCDM epoch. Phys. Rev. D 2008, 77, 026007. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with LCDM epoch in modified f(R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238–245. [Google Scholar] [CrossRef]
- Saffari, R.; Rahvar, S. f(R) gravity: From the Pioneer anomaly to cosmic acceleration. Phys. Rev. D 2008, 77, 104028. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Kunz, J.; Lammerzahl, C. Analytical solutions of the geodesic equation in the spacetime of a black hole in f(R) gravity. Phys. Rev. D 2015, 92, 044010. [Google Scholar] [CrossRef]
- Maso-Ferrando, A.; Sanchis-Gual, N.; Font, J.A.; Olmo, G.J. Numerical evolutions of boson stars in Palatini f(R) gravity. Phys. Rev. D 2024, 109, 044042. [Google Scholar] [CrossRef]
- Gomes, D.A.; Briffa, R.; Kozak, A.; Said, J.L.; Saal, M.; Wojnar, A. Cosmological constraints of Palatini f(R) gravity. arXiv 2023, arXiv:2310.17339. [Google Scholar] [CrossRef]
- Fabris, J.C.; Junior, E.L.B.; Rodrigues, M.E. Generalized models for black-bounce solutions in f(R) Gravity. Eur. Phys. J. C 2023, 83, 884. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H. f(R) gravity theory and CMBR constraints. Phys. Lett. B 2001, 506, 13. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Hanafy, W.E.; Odintsov, S.D.; Oikonomou, V.K. Thermodynamical correspondence of f(R) gravity in Jordan and Einstein frames. Int. J. Mod. Phys. D 2020, 29, 1750154. [Google Scholar] [CrossRef]
- Priyadarshinee, S.; Mahapatra, S. Analytic three-dimensional primary hair charged black holes and thermodynamics. Phys. Rev. D 2023, 108, 044017. [Google Scholar] [CrossRef]
- Jusufi, K.; Jamil, M.; Sheykhi, A. Three dimensional charged black holes in Gauss-Bonnet gravity. Eur. Phys. J. C 2023, 83, 1039. [Google Scholar] [CrossRef]
- Wu, D.; Wu, P.; Yu, H.; Wu, S.Q. Notes on the thermodynamics of superentropic AdS black holes. Phys. Rev. D 2020, 101, 024057. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Notes on the thermodynamics of superentropic AdS black holes. Class. Quantum Gravity 1994, 11, L33. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. D 2019, 99, 104018. [Google Scholar] [CrossRef]
- Xiao, Y.; Tian, Y.; Liu, Y.X. Extended black hole thermodynamics from extended Iyer-Wald formalism. Phys. Rev. Lett. 2024, 132, 021401. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.W.; Liu, Y.X. Topology of black hole thermodynamics. Phys. Rev. D 2022, 105, 104003. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Testing the microstructure of d-dimensional charged Gauss-Bonnet anti-de Sitter black holes. Phys. Rev. D 2021, 104, 024062. [Google Scholar] [CrossRef]
- Chen, S.B.; Liu, X.F.; Liu, C.Q. P-V criticality of AdS black hole in f(R) gravity. Chin. Phys. Lett. 2013, 30, 060401. [Google Scholar] [CrossRef]
- Chen, S.B.; Wang, B.; Su, R. Hawking radiation in a d-dimensional static spherically-symmetric black hole surrounded by quintessence. Phys. Rev. D 2008, 77, 124011. [Google Scholar] [CrossRef]
- Guo, Y.; Miao, Y.G. On heat properties of charged AdS black holes in Gauss-Bonnet gravity coupled with nonlinear electrodynamics. Phys. Lett. B 2023, 840, 137884. [Google Scholar] [CrossRef]
- Miao, Y.G.; Xu, Z.M. Thermodynamics of Horndeski black holes with non-minimal derivative coupling. Eur. Phys. J. C 2016, 76, 638. [Google Scholar] [CrossRef]
- Xu, M.; Lu, J.; Yang, S.; Jiang, H. Properties of Spherically Symmetric Black Holes in the Generalized Brans–Dicke Modified Gravitational Theory. Entropy 2023, 25, 814. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Page, D.N. Hawking Radiation and Black Hole Thermodynamics. New J. Phys. 2005, 7, 203. [Google Scholar] [CrossRef]
- Ashtekar, A. Black Hole evaporation: A Perspective from Loop Quantum Gravity. Universe 2020, 6, 21. [Google Scholar] [CrossRef]
- Pourhassan, B. Exponential corrected thermodynamics of black holes. J. Stat. Mech. 2021, 073102. [Google Scholar] [CrossRef]
- Auffinger, J. Primordial black hole constraints with Hawking radiation-a review. arXiv 2022, arXiv:2206.02672. [Google Scholar] [CrossRef]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Lynch, M.H. Analysis of the CERN-NA63 radiation reaction data set, assuming the Rindler bath is composed of microscopic black holes. Phys. Rev. D 2024, 109, 105009. [Google Scholar] [CrossRef]
- Traschen, J. An Introduction to Black Hole Evaporation. arXiv 2000, arXiv:gr-qc/0010055. [Google Scholar]
- Upadhyay, S.; Hendi, S.H.; Panahiyan, S.; Eslam Panah, B. Thermal fluctuations of charged black holes in gravity’s rainbow. Prog. Theor. Exp. Phys. 2018, 2018, 093E01. [Google Scholar] [CrossRef]
- Dehghani, M. Thermal fluctuations of AdS black holes in three-dimensional rainbow gravity. Phys. Lett. B 2019, 793, 234. [Google Scholar] [CrossRef]
- Pourhassan, B.; Upadhyay, S. Thermal fluctuations of charged black hole solution in Rastall theory. arXiv 2019, arXiv:1910.11698. [Google Scholar]
- Strominger, A.; Vafa, C. Microscopic Origin of the Bekenstein-Hawking Entropy. Phys. Lett. B 1996, 379, 99. [Google Scholar] [CrossRef]
- Shahzad, M.U.; Jawad, A. Thermodynamics of Black holes With Higher Order Corrected Entropy. arXiv 2018, arXiv:1811.10873. [Google Scholar] [CrossRef]
- Dijkgraaf, R.; Verlinde, E.P.; Verlinde, H.L. Counting dyons in N = 4 string theory. Nucl. Phys. B 1997, 484, 543. [Google Scholar] [CrossRef]
- Meissner, K.A. Black hole entropy in Loop Quantum Gravity. Class. Quantum Gravity 2004, 21, 5245. [Google Scholar] [CrossRef]
- Dabholkar, A.; Gomes, J.; Murthy, S. Nonperturbative black hole entropy and Kloosterman sums. J. High Energy Phys. 2015, 1503, 74. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Rostami, M. P-V criticality of logarithm-corrected dyonic charged AdS black holes. Phys. Rev. D 2016, 94, 064006. [Google Scholar] [CrossRef]
- Castro, A.; Godet, V.; Larsen, F.; Zeng, Y. Logarithmic Corrections to Black Hole Entropy: The Non-BPS Branch. J. High Energy Phys. 2018, 2018, 79. [Google Scholar] [CrossRef]
- Pourhassan, B.; Faizal, M.; Ketabi, S.A. Logarithmic correction of the BTZ black hole and adaptive model of Graphene. Int. J. Mod. Phys. D 2018, 27, 1850118. [Google Scholar] [CrossRef]
- Pourhassan, B.; Faizal, M. Thermodynamics of a Sufficient Small Singly Spinning Kerr-AdS Black Hole. Nucl. Phys. B 2016, 913, 834. [Google Scholar] [CrossRef]
- Upadhyay, S. Quantum corrections to thermodynamics of quasitopological black holes. Phys. Lett. B 2017, 775, 130. [Google Scholar] [CrossRef]
- Bak, D.; Rey, S.J. Holographic principle and string cosmology. Class. Quantum Gravity 2000, 17, L1. [Google Scholar] [CrossRef]
- Rama, S.K. Holographic principle in the closed universe: A resolution with negative pressure matter. Phys. Lett. B 1999, 457, 268. [Google Scholar] [CrossRef]
- Banerjee, S.; Gupta, R.K.; Mandal, I.; Sen, A. Logarithmic Corrections to N = 4 and N = 8 Black Hole Entropy: A One Loop Test of Quantum Gravity. J. High Energy Phys. 2011, 1111, 143. [Google Scholar] [CrossRef]
- Mahapatra, S. Logarithmic black hole entropy corrections and holographic Rényi entropy. Eur. Phys. J. C 2018, 78, 23. [Google Scholar] [CrossRef]
- Pourhassan, B.; Faizal, M.; Capozziello, S. Testing Quantum Gravity through Dumb Holes. Annals Phys. 2017, 377, 108. [Google Scholar] [CrossRef]
- Foit, V.F.; Kleban, M. Testing Quantum Black Holes with Gravitational Waves. Class. Quantum Gravity 2019, 36, 035006. [Google Scholar] [CrossRef]
- Pourhassan, B.; Chougule, S.; Dey, S.; Faizal, M. Quantum Corrections to a Finite Temperature BIon. Class. Quantum Gravity 2020, 37, 135004. [Google Scholar] [CrossRef]
- Upadhyay, S.; Islam, N.; Ganai, P. A modified thermodynamics of rotating and charged BTZ black hole. J. Hologr. Appl. Phys. 2022, 2, 25. [Google Scholar]
- Upadhyay, S.; Pourhassan, B.; Farahani, H. P-V criticality of first-order entropy corrected AdS black holes in massive gravity. Phys. Rev. D 2017, 95, 106014. [Google Scholar] [CrossRef]
- Islam, N.; Ganai, P.A. Quantum corrections to AdS black hole in massive gravity. Int. J. Mod. Phys. A 2019, 34, 1950225. [Google Scholar] [CrossRef]
- Pourdarvish, A.; Sadeghi, J.; Farahani, H.; Pourhassan, B. Thermodynamics and Statistics of Goedel Black Hole with Logarithmic Correction. Int. J. Theor. Phys. 2013, 52, 3560. [Google Scholar] [CrossRef]
- Jing, J.; Yan, M.L. Statistical Entropy of a Stationary Dilaton Black Hole from Cardy Formula. Phys. Rev. D 2001, 63, 024003. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Hendi, S.H.; Momeni, D. Black hole solutions in F(R) gravity with conformal anomaly. Eur. Phys. J. C 2011, 71, 1823. [Google Scholar] [CrossRef]
- Hassaine, M.; Martinez, C. Higher-dimensional black holes with a conformally invariant Maxwell source. Phys. Rev. D 2007, 75, 027502. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter universe. J. Cosmol. Astropart. Phys. 2005, 2005, 010. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Rotating charged black hole spacetimes in quadratic f(R) gravitational theories. Int. J. Mod. Phys. D 2018, 27, 1850074. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged black holes in f(R) gravitational theories. Eur. Phys. J. Plus 2018, 133, 18. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Mandal, S.; Das, S.; Gogoi, D.J. Leading-order corrections to the thermodynamics of Rindler modified Schwarzschild black hole. Phys. Dark Universe 2023, 42, 101349. [Google Scholar] [CrossRef]
- Kubiznak, D.; Mann, R.B. P-V criticality of charged AdS black holes. J. High Energy Phys. 2012, 1207, 033. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quantum Gravity 2009, 26, 195011. [Google Scholar] [CrossRef]
- Sajadi, S.N.; Riazi, N.; Hendi, S.H. Dynamical and Thermal Stabilities of Nonlinearly Charged AdS Black Holes. Eur. Phys. J. C 2019, 79, 775. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Tang, Z.Y.; Wang, B.; Papantonopoulos, E. Exact charged black hole solutions in D-dimensions in f(R) gravity. Eur. Phys. J. C 2021, 81, 346. [Google Scholar] [CrossRef]
- Hurtado, R.A.; Arenas, R. Spherically symmetric and static solutions in f(R) gravity coupled with electromagnetic fields. Phys. Rev. D 2020, 102, 104019. [Google Scholar] [CrossRef]
- Karakasis, T.; Papantonopoulos, E.; Tang, Z.Y.; Wang, B. Exact Black Hole Solutions with a Conformally Coupled Scalar Field and Dynamic Ricci Curvature in f(R) Gravity Theories. Eur. Phys. J. C 2021, 81, 897. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Rahimi, F. Logarithmic corrections of charged hairy black hole in (2+1) dimension. Can. J. Phys. 2014, 92, 1638. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Akhtar, Z.; Ovgün, A. Thermodynamics and logarithmic corrections of symmergent black holes. Results Phys. 2023, 46, 106300. [Google Scholar] [CrossRef]
- Das, S.; Majumdar, P.; Bhaduri, R.K. General logarithmic corrections to black-hole entropy. Class. Quantum Gravity 2002, 19, 2355. [Google Scholar] [CrossRef]
- Govindarajan, T.R.; Kaul, R.K.; Suneeta, V. Logarithmic correction to the Bekenstein-Hawking entropy of the BTZ black hole. Class. Quantum Gravity 2001, 18, 2877–2886. [Google Scholar] [CrossRef]
- Hendi, S.H.; Vahidinia, M.H. Extended phase space thermodynamics and P-V criticality of black holes with a nonlinear source. Phys. Rev. D 2013, 88, 084045. [Google Scholar] [CrossRef]
- Ma, M.S.; Zhao, R. Stability of black holes based on horizon thermodynamics. Phys. Lett. B 2015, 751, 278. [Google Scholar] [CrossRef]
- Hendi, S.H.; Eslam Panah, B.; Momennia, M.; Panahiyan, S. Three dimensional nonlinear magnetic AdS solutions through topological defects. Eur. Phys. J. C 2015, 75, 457. [Google Scholar] [CrossRef]
- Cai, R.G.; Wang, A. Thermodynamics and Stability of Hyperbolic Charged Black Holes. Phys. Rev. D 2004, 70, 064013. [Google Scholar] [CrossRef]
- Akhtar, Z.; Babar, R.; Ali, R. Thermal Fluctuations Evolution of the New Schwarzschild Black Hole. arXiv 2022, arXiv:2212.06205. [Google Scholar] [CrossRef]
- Bukhari, S.; Pourhassan, B.; Aounallah, H.; Wang, L. On the microstructure of higher-dimensional Reissner-Nordström black holes in quantum regime. Class. Quantum Gravity 2023, 40, 225007. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Kamvar, N. Thermodynamic geometry of black holes in f(R) gravity. Eur. Phys. J. C 2016, 76, 476. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Zhang, Y.; Yang, L.; Yang, S.; Lu, J. Corrected Thermodynamics of Black Holes in f(R) Gravity with Electrodynamic Field and Cosmological Constant. Entropy 2024, 26, 868. https://doi.org/10.3390/e26100868
Xu M, Zhang Y, Yang L, Yang S, Lu J. Corrected Thermodynamics of Black Holes in f(R) Gravity with Electrodynamic Field and Cosmological Constant. Entropy. 2024; 26(10):868. https://doi.org/10.3390/e26100868
Chicago/Turabian StyleXu, Mou, Yuying Zhang, Liu Yang, Shining Yang, and Jianbo Lu. 2024. "Corrected Thermodynamics of Black Holes in f(R) Gravity with Electrodynamic Field and Cosmological Constant" Entropy 26, no. 10: 868. https://doi.org/10.3390/e26100868
APA StyleXu, M., Zhang, Y., Yang, L., Yang, S., & Lu, J. (2024). Corrected Thermodynamics of Black Holes in f(R) Gravity with Electrodynamic Field and Cosmological Constant. Entropy, 26(10), 868. https://doi.org/10.3390/e26100868






