Minimum Information Variability in Linear Langevin Systems via Model Predictive Control
Abstract
:1. Introduction
2. Preliminaries
2.1. Information Length (IL)
2.2. Information–Thermodynamic Relation
2.3. Minimum Information Variability Problem
2.4. BIBO Stability of the Linear Stochastic Process
3. Main Results
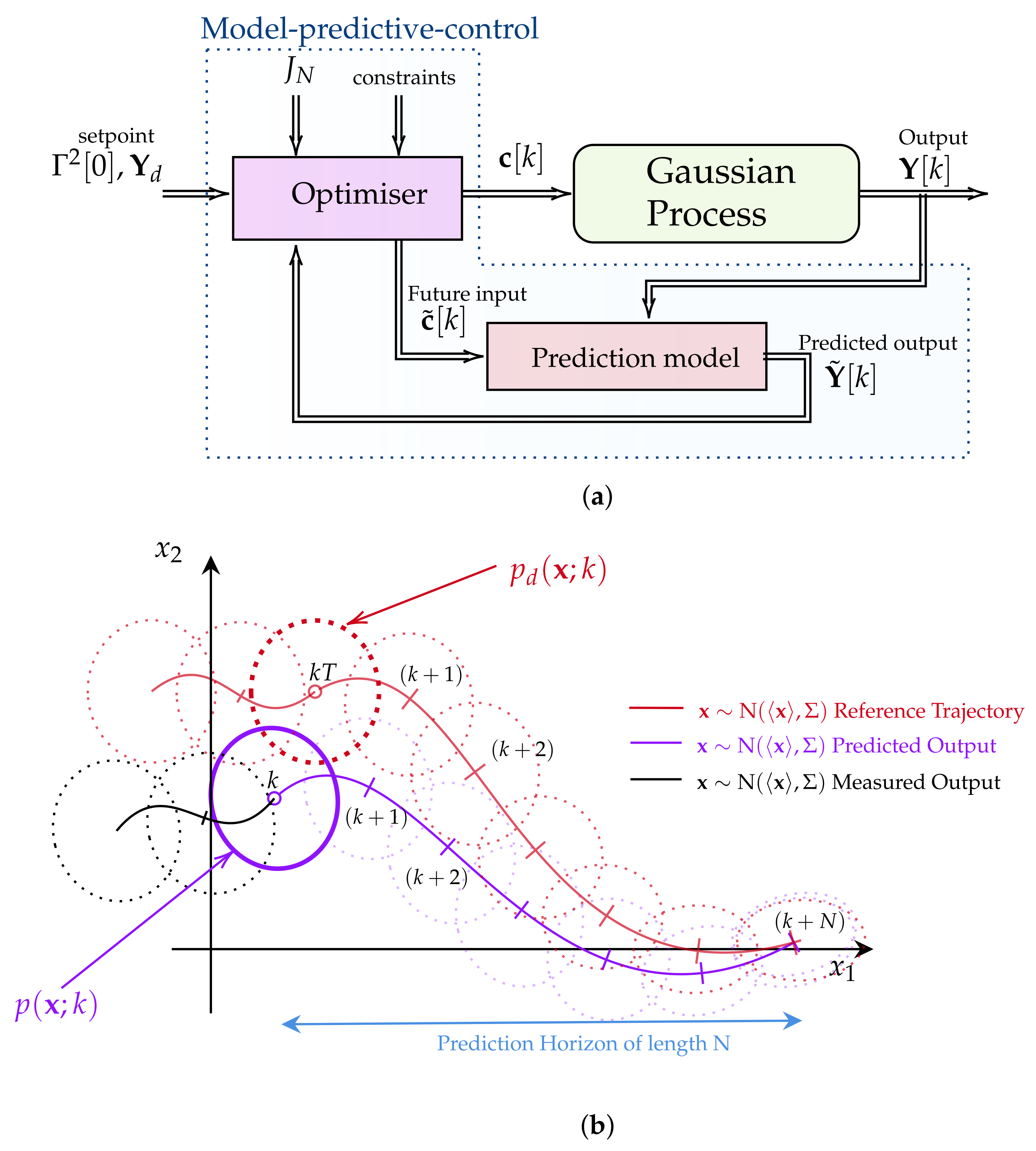
Model Predictive Control
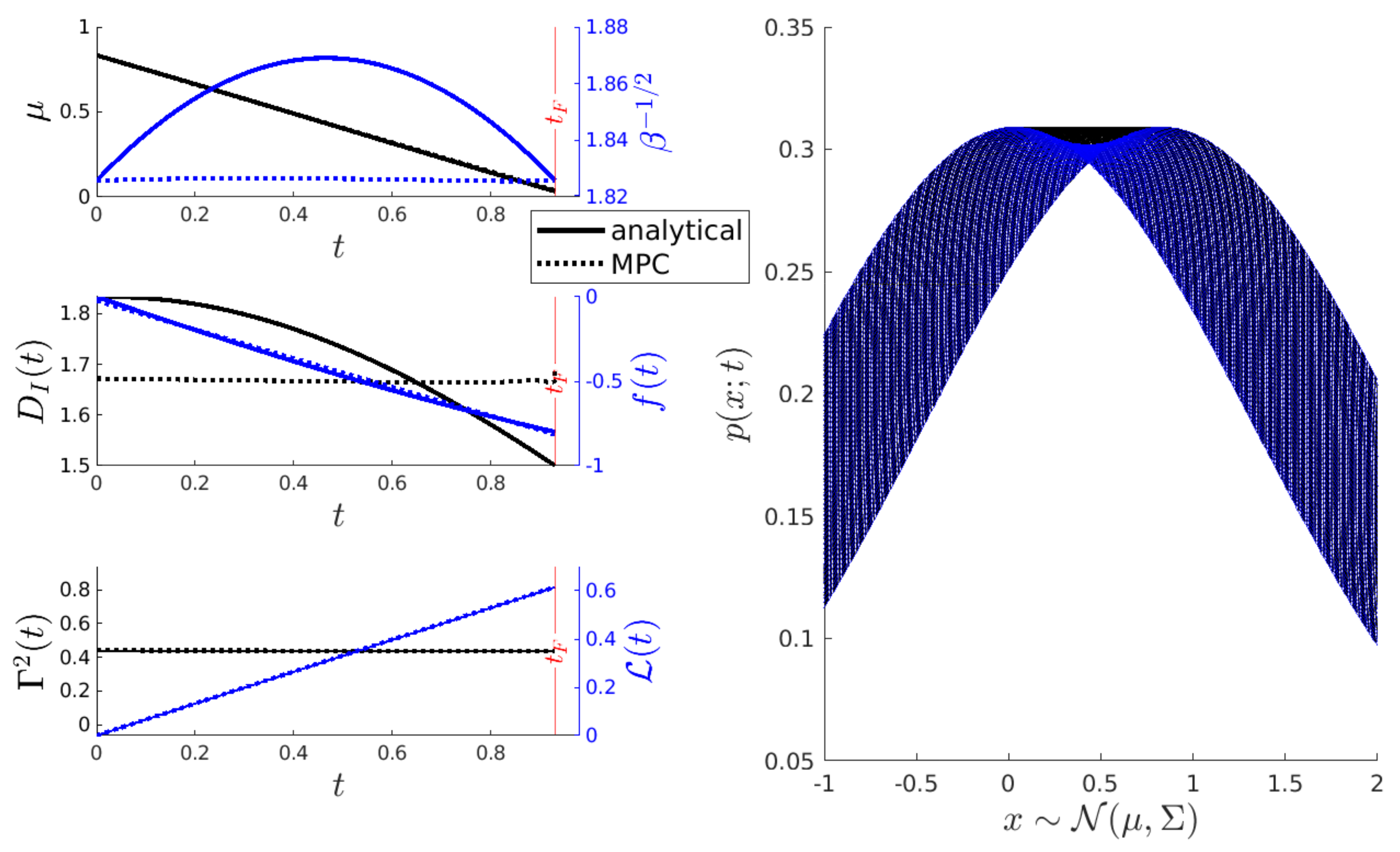
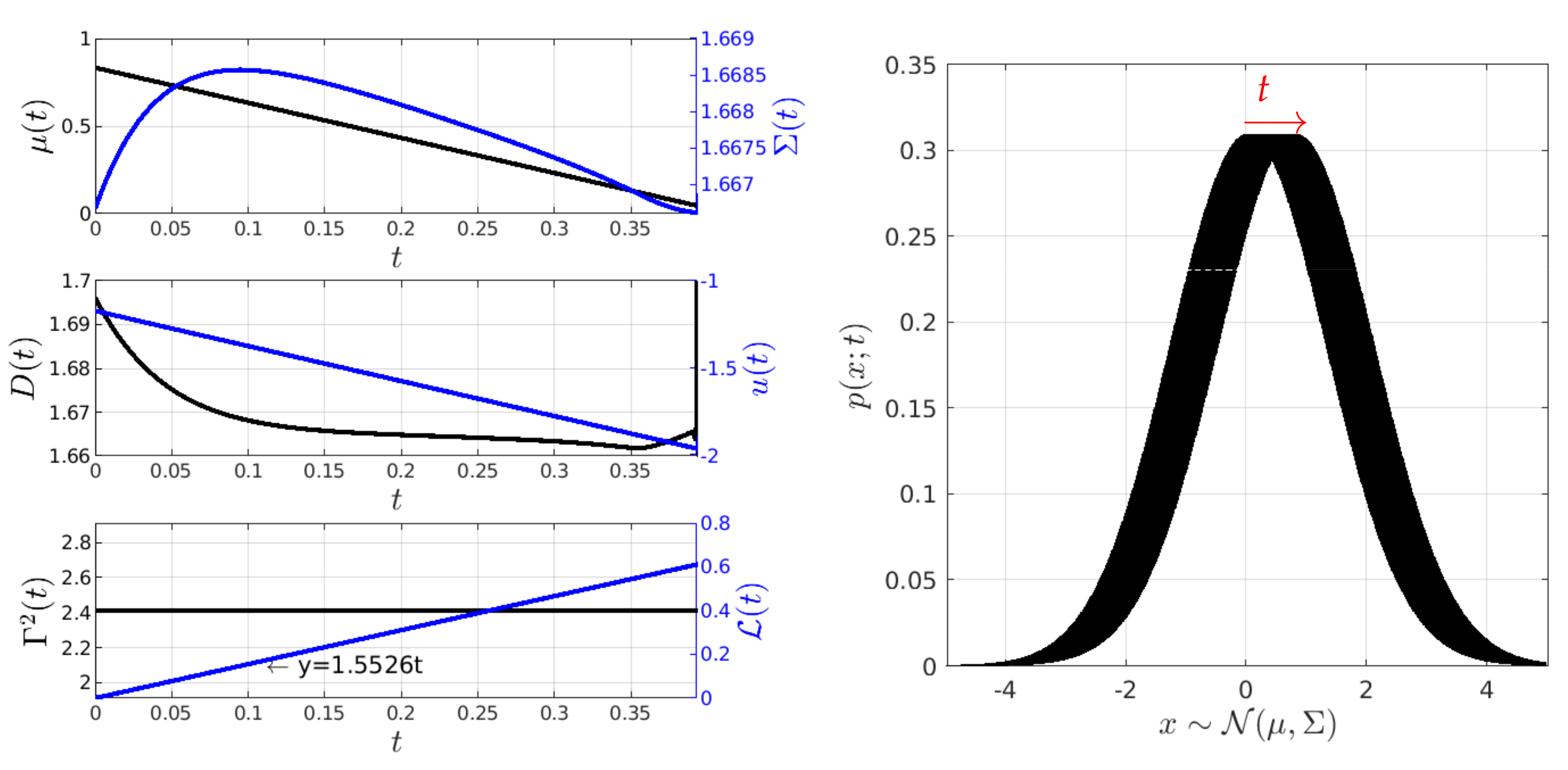
4. Simulation Results
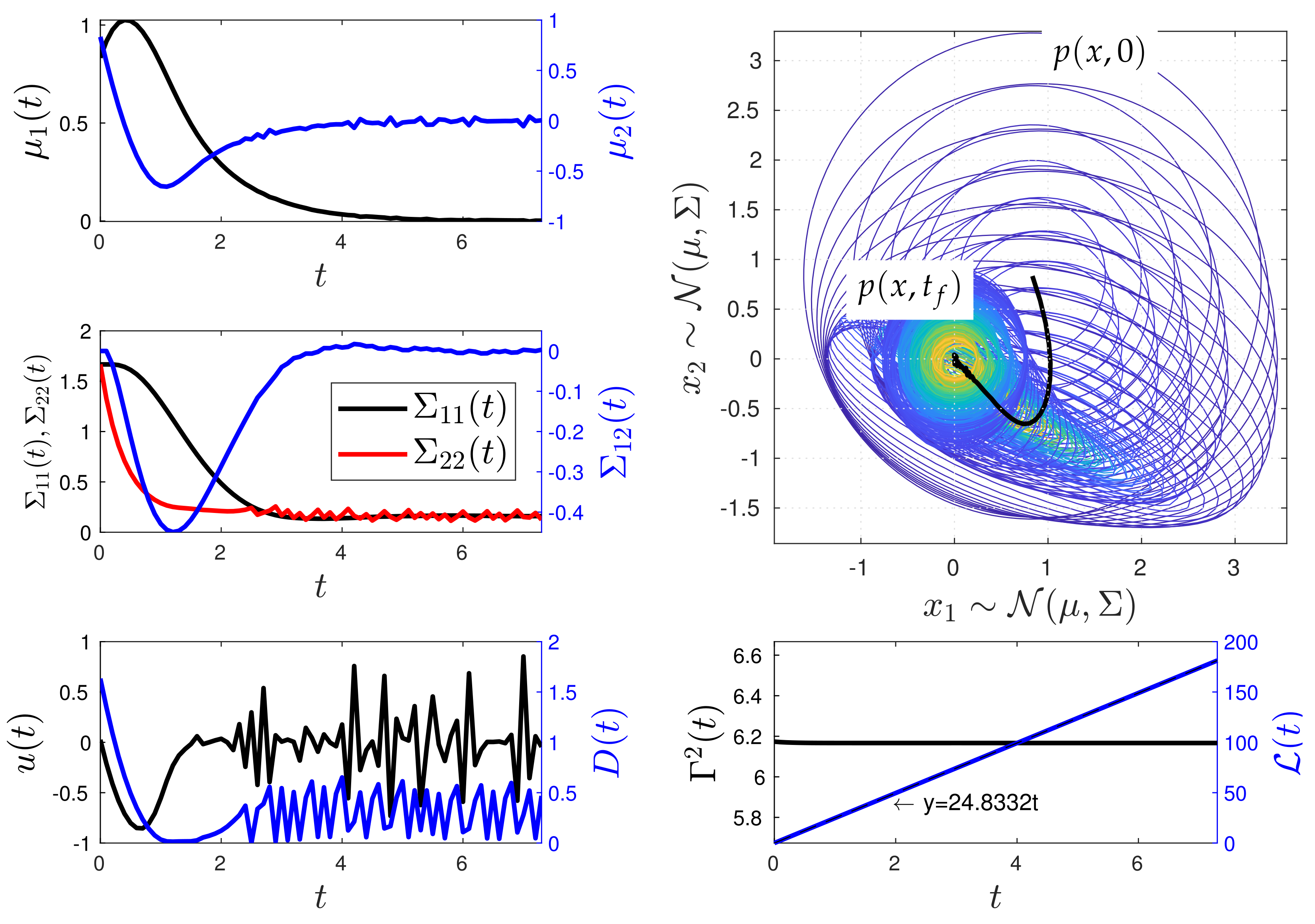
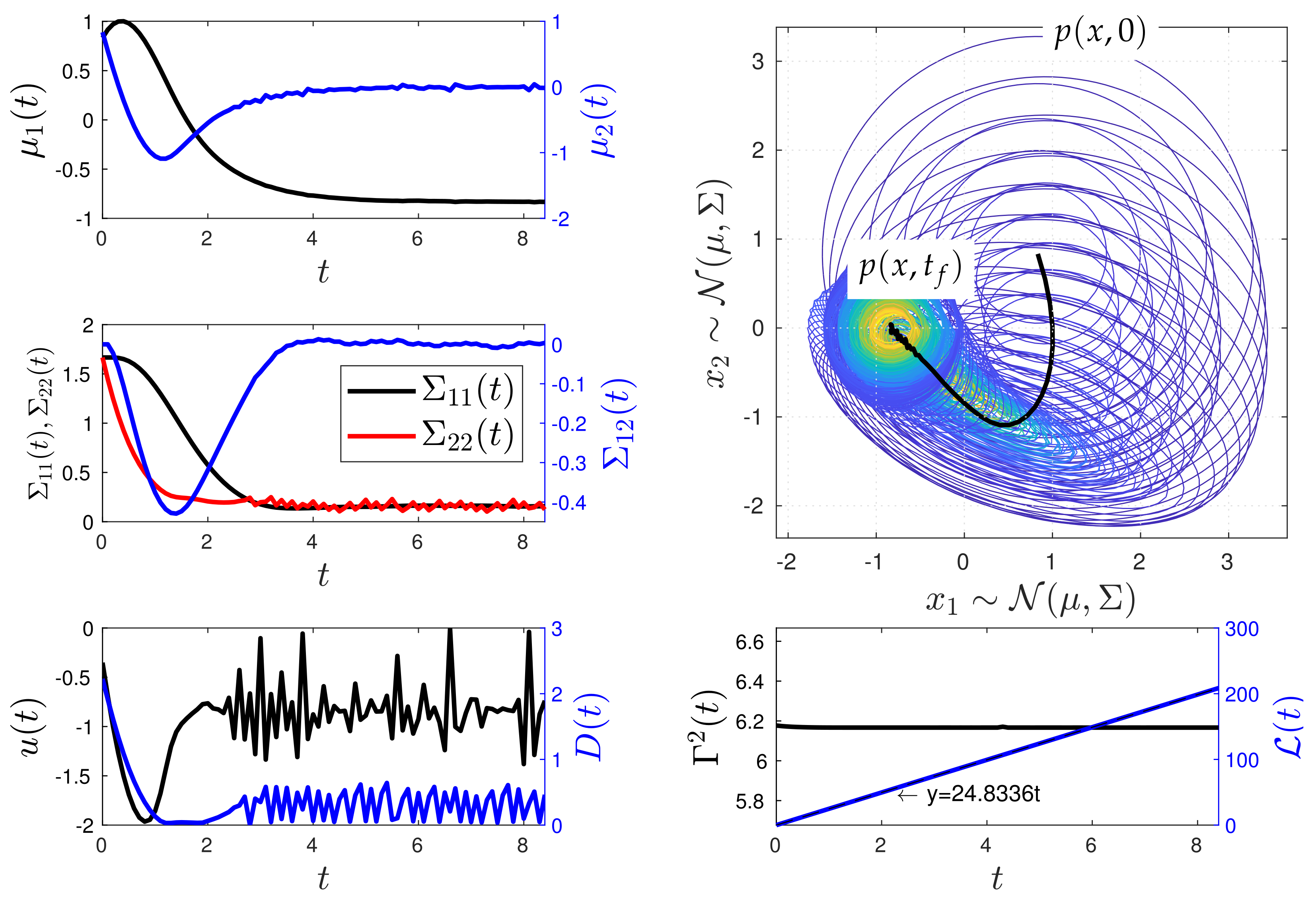
4.1. The O-U Process
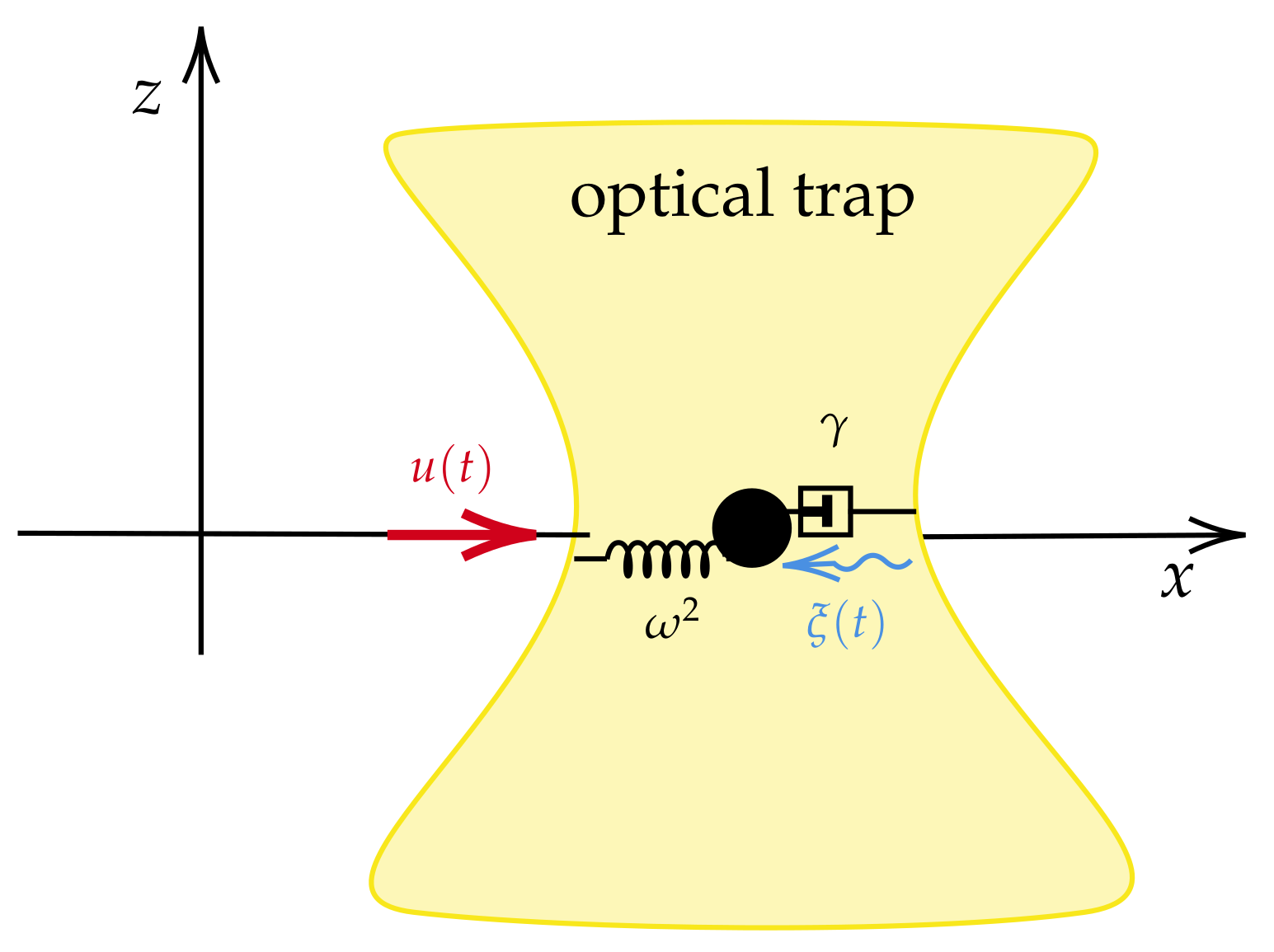
4.2. Kramers Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PDFs | Probability density functions |
| FP | Fokker–Planck |
| IL | Information length |
| MPC | Model predictive control |
| QR | Quadratic regulator |
| BIBO | Bounded-input, bounded-output |
Appendix A. A Solution by the Euler–Lagrange Equation

Appendix B. Geodesic Dynamics Derivation
Appendix C. Entropy Rate in the O-U Process
References
- Smith, R.; Friston, K.J.; Whyte, C.J. A step-by-step tutorial on active inference and its application to empirical data. J. Math. Psychol. 2022, 107, 102632. [Google Scholar] [CrossRef]
- Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Bechhoefer, J. Control Theory for Physicists; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Kim, E.j.; Lee, U.; Heseltine, J.; Hollerbach, R. Geometric structure and geodesic in a solvable model of nonequilibrium process. Phys. Rev. E 2016, 93, 062127. [Google Scholar] [CrossRef]
- Pesce, G.; Jones, P.H.; Maragò, O.M.; Volpe, G. Optical tweezers: Theory and practice. Eur. Phys. J. Plus 2020, 135, 949. [Google Scholar] [CrossRef]
- Deffner, S.; Bonança, M.V. Thermodynamic control—An old paradigm with new applications. EPL (Europhys. Lett.) 2020, 131, 20001. [Google Scholar] [CrossRef]
- Salapaka, M.V. Control of Optical Tweezers. Encyclopedia of Systems and Control; Springer: London, UK, 2021; pp. 361–368. [Google Scholar]
- Guéry-Odelin, D.; Jarzynski, C.; Plata, C.A.; Prados, A.; Trizac, E. Driving rapidly while remaining in control: Classical shortcuts from Hamiltonian to stochastic dynamics. Rep. Prog. Phys. 2023, 86, 035902. [Google Scholar] [CrossRef]
- Iram, S.; Dolson, E.; Chiel, J.; Pelesko, J.; Krishnan, N.; Güngör, Ö.; Kuznets-Speck, B.; Deffner, S.; Ilker, E.; Scott, J.G.; et al. Controlling the speed and trajectory of evolution with counterdiabatic driving. Nat. Phys. 2021, 17, 135–142. [Google Scholar] [CrossRef]
- Annunziato, M.; Borzi, A. Optimal control of probability density functions of stochastic processes. Math. Model. Anal. 2010, 15, 393–407. [Google Scholar] [CrossRef]
- Annunziato, M.; Borzì, A. A Fokker–Planck control framework for multidimensional stochastic processes. J. Comput. Appl. Math. 2013, 237, 487–507. [Google Scholar] [CrossRef]
- Risken, H. Fokker-planck equation. In The Fokker-Planck Equation; Springer: Berlin/Heidelberg, Germany, 1996; pp. 63–95. [Google Scholar]
- Fleig, A.; Guglielmi, R. Optimal control of the Fokker–Planck equation with space-dependent controls. J. Optim. Theory Appl. 2017, 174, 408–427. [Google Scholar] [CrossRef]
- Aronna, M.S.; Tröltzsch, F. First and second order optimality conditions for the control of Fokker-Planck equations. ESAIM Control. Optim. Calc. Var. 2021, 27, 15. [Google Scholar] [CrossRef]
- Martínez, I.A.; Petrosyan, A.; Guéry-Odelin, D.; Trizac, E.; Ciliberto, S. Engineered swift equilibration of a Brownian particle. Nat. Phys. 2016, 12, 843–846. [Google Scholar] [CrossRef] [PubMed]
- Baldassarri, A.; Puglisi, A.; Sesta, L. Engineered swift equilibration of a Brownian gyrator. Phys. Rev. E 2020, 102, 030105. [Google Scholar] [CrossRef] [PubMed]
- Martinez, I.; Petrosyan, A.; Guéry-Odelin, D.; Trizac, E.; Ciliberto, S. Faster than nature: Engineered swift equilibration of a brownian particle. arXiv 2015, arXiv:1512.07821. [Google Scholar]
- Saridis, G.N. Entropy in Control Engineering; World Scientific: Singapore, 2001; Volume 12. [Google Scholar]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Limon, A.; Bedeaux, D.; Kjelstrup, S. A simple example of control to minimize entropy production. J. Non-Equilib. Thermodyn. 2002, 27, 45–55. [Google Scholar] [CrossRef]
- Nicholson, S.B.; del Campo, A.; Green, J.R. Nonequilibrium uncertainty principle from information geometry. Phys. Rev. E 2018, 98, 032106. [Google Scholar] [CrossRef]
- Kim, E.J. Information Geometry, Fluctuations, Non-Equilibrium Thermodynamics, and Geodesics in Complex Systems. Entropy 2021, 23, 1393. [Google Scholar] [CrossRef]
- Nielsen, F. An elementary introduction to information geometry. Entropy 2020, 22, 1100. [Google Scholar] [CrossRef] [PubMed]
- Miura, K. An introduction to maximum likelihood estimation and information geometry. Interdiscip. Inf. Sci. 2011, 17, 155–174. [Google Scholar] [CrossRef]
- Leung, L.Y.; North, G.R. Information theory and climate prediction. J. Clim. 1990, 3, 5–14. [Google Scholar] [CrossRef]
- Guel-Cortez, A.J.; Kim, E.J. Information Geometric Theory in the Prediction of Abrupt Changes in System Dynamics. Entropy 2021, 23, 694. [Google Scholar] [CrossRef]
- Kim, E.J.; Guel-Cortez, A.J. Causal Information Rate. Entropy 2021, 23, 1087. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- San Liang, X. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, J.M.; Sandberg, H. Second-law-like inequalities with information and their interpretations. New J. Phys. 2014, 16, 125007. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Janzing, D.; Mahler, G. Thermodynamic efficiency of information and heat flow. J. Stat. Mech. Theory Exp. 2009, 2009, P09011. [Google Scholar] [CrossRef]
- Crooks, G.E. Measuring thermodynamic length. Phys. Rev. Lett. 2007, 99, 100602. [Google Scholar] [CrossRef] [PubMed]
- Flynn, S.W.; Zhao, H.C.; Green, J.R. Measuring disorder in irreversible decay processes. J. Chem. Phys. 2014, 141, 104107. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Garcia-Pintos, L.P.; del Campo, A.; Green, J.R. Time—Information uncertainty relations in thermodynamics. Nat. Phys. 2020, 16, 1211–1215. [Google Scholar] [CrossRef]
- Guel-Cortez, A.J.; Kim, E.J. Information length analysis of linear autonomous stochastic processes. Entropy 2020, 22, 1265. [Google Scholar] [CrossRef]
- Ito, S.; Dechant, A. Stochastic time evolution, information geometry, and the Cramér-Rao bound. Phys. Rev. X 2020, 10, 021056. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. PID control. IEEE Control Syst. Mag. 2006, 1066, 30–31. [Google Scholar]
- Guel-Cortez, A.J.; Méndez-Barrios, C.F.; González-Galván, E.J.; Mejía-Rodríguez, G.; Félix, L. Geometrical design of fractional PDμ controllers for linear time-invariant fractional-order systems with time delay. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2019, 233, 815–829. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control Autom. Syst. 2011, 9, 415–424. [Google Scholar] [CrossRef]
- Mehrez, M.W.; Worthmann, K.; Cenerini, J.P.; Osman, M.; Melek, W.W.; Jeon, S. Model predictive control without terminal constraints or costs for holonomic mobile robots. Robot. Auton. Syst. 2020, 127, 103468. [Google Scholar] [CrossRef]
- Kristiansen, B.A.; Gravdahl, J.T.; Johansen, T.A. Energy optimal attitude control for a solar-powered spacecraft. Eur. J. Control 2021, 62, 192–197. [Google Scholar] [CrossRef]
- Salesch, T.; Gesenhues, J.; Habigt, M.; Mechelinck, M.; Hein, M.; Abel, D. Model based optimization of a novel ventricular assist device. At-Automatisierungstechnik 2021, 69, 619–631. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Bemporad, A. Hybrid Toolbox—User’s Guide. 2004. Available online: http://cse.lab.imtlucca.it/~bemporad/hybrid/toolbox (accessed on 1 December 2023).
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: Chelmsford, MA, USA, 2007. [Google Scholar]
- Görges, D. Relations between model predictive control and reinforcement learning. IFAC-PapersOnLine 2017, 50, 4920–4928. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E.J. Comparing Information Metrics for a Coupled Ornstein–Uhlenbeck Process. Entropy 2019, 21, 775. [Google Scholar] [CrossRef]
- Gieseler, J.; Gomez-Solano, J.R.; Magazzù, A.; Castillo, I.P.; García, L.P.; Gironella-Torrent, M.; Viader-Godoy, X.; Ritort, F.; Pesce, G.; Arzola, A.V.; et al. Optical tweezers—From calibration to applications: A tutorial. Adv. Opt. Photonics 2021, 13, 74–241. [Google Scholar] [CrossRef]
- Kim, E.J. Information geometry and non-equilibrium thermodynamic relations in the over-damped stochastic processes. J. Stat. Mech. Theory Exp. 2021, 2021, 093406. [Google Scholar] [CrossRef]
- Maybeck, P.S. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Kamen, E.W.; Levine, W. Fundamentals of linear time-varying systems. In The Control Handbook; CRC Press: Boca Raton, FL, USA, 1996; Volume 1. [Google Scholar]
- Jenks, S.; Mechanics, S., II. Introduction to Kramers Equation; Drexel University: Philadelphia, PA, USA, 2006. [Google Scholar]
- Pavliotis, G.A. Stochastic Processes and Applications: Diffusion Processes, the Fokker-Planck and Langevin Equations; Springer: Berlin/Heidelberg, Germany, 2014; Volume 60. [Google Scholar]
- Chamorro, H.; Guel-Cortez, A.; Kim, E.J.; Gonzalez-Longat, F.; Ortega, A.; Martinez, W. Information Length Quantification and Forecasting of Power Systems Kinetic Energy. IEEE Trans. Power Syst. 2022, 37, 4473–4484. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Entropy production in nonequilibrium systems at stationary states. Phys. Rev. Lett. 2012, 108, 020601. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, S.N.; Müller, F.; Marques, J.C.; Bastianoni, S.; Jørgensen, S.E. Thermodynamics in ecology—An introductory review. Entropy 2020, 22, 820. [Google Scholar] [CrossRef] [PubMed]
- Haddad, W.M. A Dynamical Systems Theory of Thermodynamics; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Van der Schaft, A. Classical thermodynamics revisited: A systems and control perspective. IEEE Control Syst. Mag. 2021, 41, 32–60. [Google Scholar] [CrossRef]
- Chen, C.T. Linear System Theory and Design; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Behr, M.; Benner, P.; Heiland, J. Solution formulas for differential Sylvester and Lyapunov equations. Calcolo 2019, 56, 51. [Google Scholar] [CrossRef]
- Lindgren, F.; Bolin, D.; Rue, H. The SPDE approach for Gaussian and non-Gaussian fields: 10 years and still running. arXiv 2021, arXiv:2111.01084. [Google Scholar] [CrossRef]
- Erban, R.; Chapman, J.; Maini, P. A practical guide to stochastic simulations of reaction-diffusion processes. arXiv 2007, arXiv:0704.1908. [Google Scholar]
- Reutlinger, A.; Hangleiter, D.; Hartmann, S. Understanding (with) toy models. Br. J. Philos. Sci. 2018, 69, 1069–1099. [Google Scholar] [CrossRef]
- Ackermann, J. Robust Control: Systems with Uncertain Physical Parameters; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lee, S.H.; Kapral, R. Friction and diffusion of a Brownian particle in a mesoscopic solvent. J. Chem. Phys. 2004, 121, 11163–11169. [Google Scholar] [CrossRef] [PubMed]
- Hadeler, K.P.; Hillen, T.; Lutscher, F. The Langevin or Kramers approach to biological modeling. Math. Models Methods Appl. Sci. 2004, 14, 1561–1583. [Google Scholar] [CrossRef]
- Balakrishnan, V. Diffusion in an External Potential. In Elements of Nonequilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 168–190. [Google Scholar]
- Guel-Cortez, A.J.; Kim, E.J. Information geometry control under the Laplace assumption. Phys. Sci. Forum 2022, 5, 25. [Google Scholar] [CrossRef]
- Van Der Merwe, R.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No. 01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 6, pp. 3461–3464. [Google Scholar]
- Elfring, J.; Torta, E.; Van De Molengraft, R. Particle filters: A hands-on tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef]
- Petersen, K.B.; Pedersen, M.S. The matrix cookbook. Tech. Univ. Den. 2008, 7, 510. [Google Scholar]






| Symbol | Description |
|---|---|
| Random vector variable | |
| Spatial variable of the PDF | |
| Gaussian stochastic variable | |
| Bounded smooth external input (any time-dependent function) | |
| Time-dependent noise amplitude matrix | |
| Mean value vector of the random vector | |
| Covariance matrix of the random vector | |
| Probability density function (PDF) | |
| Information length | |
| Information rate | |
| Entropy rate | |
| Entropy production | |
| Entropy flow | |
| Vector state composed by the elements of and at time t. The vector describes the current PDF at time t. | |
| Desired vector state. The vector describes the desired Gaussian PDF. | |
| Vector of controls including u and the elements of the amplitude noise matrix | |
| Weight matrix regulating the error between and | |
| Weight matrix regulating the control action | |
| Weight factor of the error between the current information rate at time t and the initial information rate to keep it constant at all t | |
| Predicted information rate. The symbol implies prediction. | |
| Discrete time mean value vector. The brackets , where , refers to the discrete time sampled at time period . | |
| Damping constant | |
| Undamped natural frequency constant | |
| Sampling period | |
| N | Prediction horizon length |
| System | Experiment | Figure | Y(0) | Yd(t) | (0) | ||||
|---|---|---|---|---|---|---|---|---|---|
| O-U | 1 | 5, 6 | 2.4 | ||||||
| 2 | 7, 8 | 0.41 | |||||||
| Kramers | 1 | 10 | 6.16667 | ||||||
| 2 | 11 | 6.16667 | |||||||
| System | Experiment | Figure | γ | ω | Ts | N | IL | R | Q |
| O-U | 1 | 5, 6 | 1 | - | 50 | and | |||
| 2 | 7, 8 | 1 | - | 50 | and | ||||
| Kramers | 1 | 10 | 2 | 1 | 50 | ||||
| 2 | 11 | 2 | 1 | 50 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guel-Cortez, A.-J.; Kim, E.-j.; Mehrez, M.W. Minimum Information Variability in Linear Langevin Systems via Model Predictive Control. Entropy 2024, 26, 323. https://doi.org/10.3390/e26040323
Guel-Cortez A-J, Kim E-j, Mehrez MW. Minimum Information Variability in Linear Langevin Systems via Model Predictive Control. Entropy. 2024; 26(4):323. https://doi.org/10.3390/e26040323
Chicago/Turabian StyleGuel-Cortez, Adrian-Josue, Eun-jin Kim, and Mohamed W. Mehrez. 2024. "Minimum Information Variability in Linear Langevin Systems via Model Predictive Control" Entropy 26, no. 4: 323. https://doi.org/10.3390/e26040323
APA StyleGuel-Cortez, A.-J., Kim, E.-j., & Mehrez, M. W. (2024). Minimum Information Variability in Linear Langevin Systems via Model Predictive Control. Entropy, 26(4), 323. https://doi.org/10.3390/e26040323







