Dynamical Tunneling in More than Two Degrees of Freedom
Abstract
1. Introduction
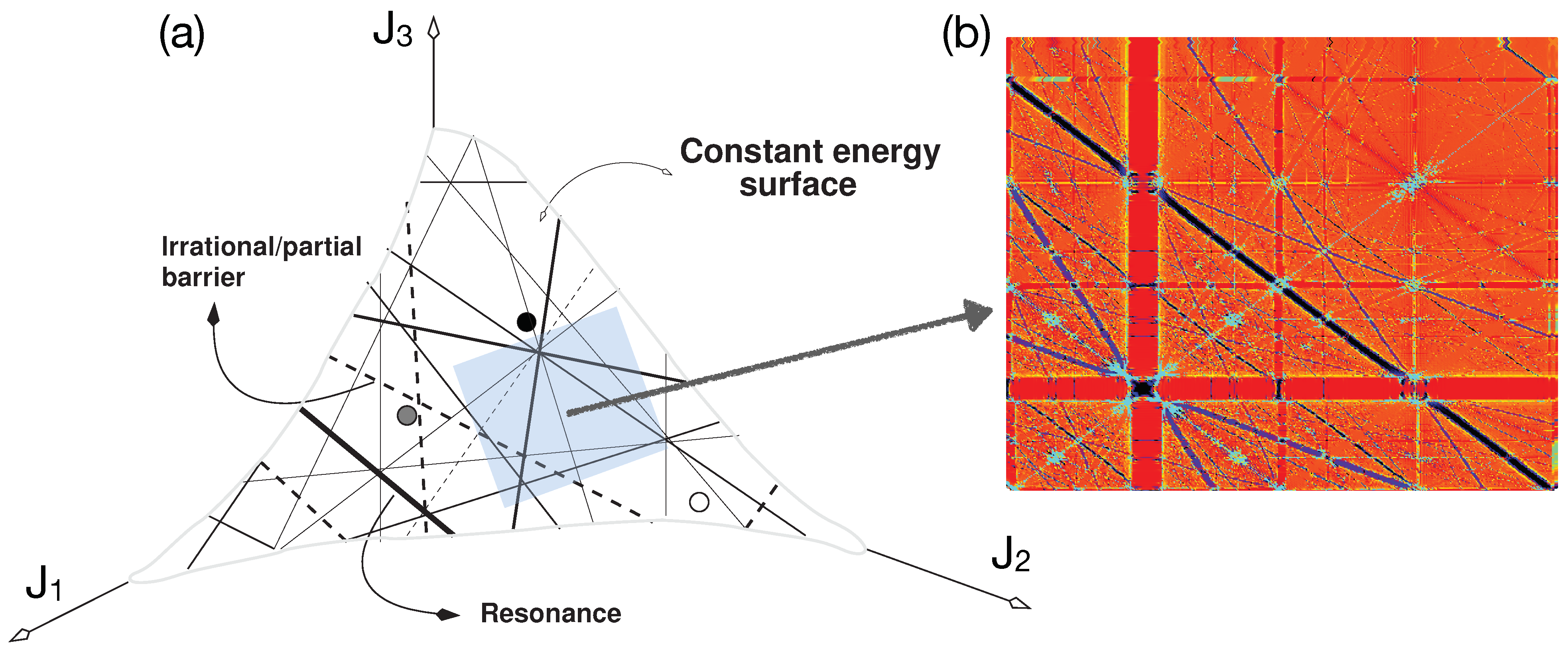
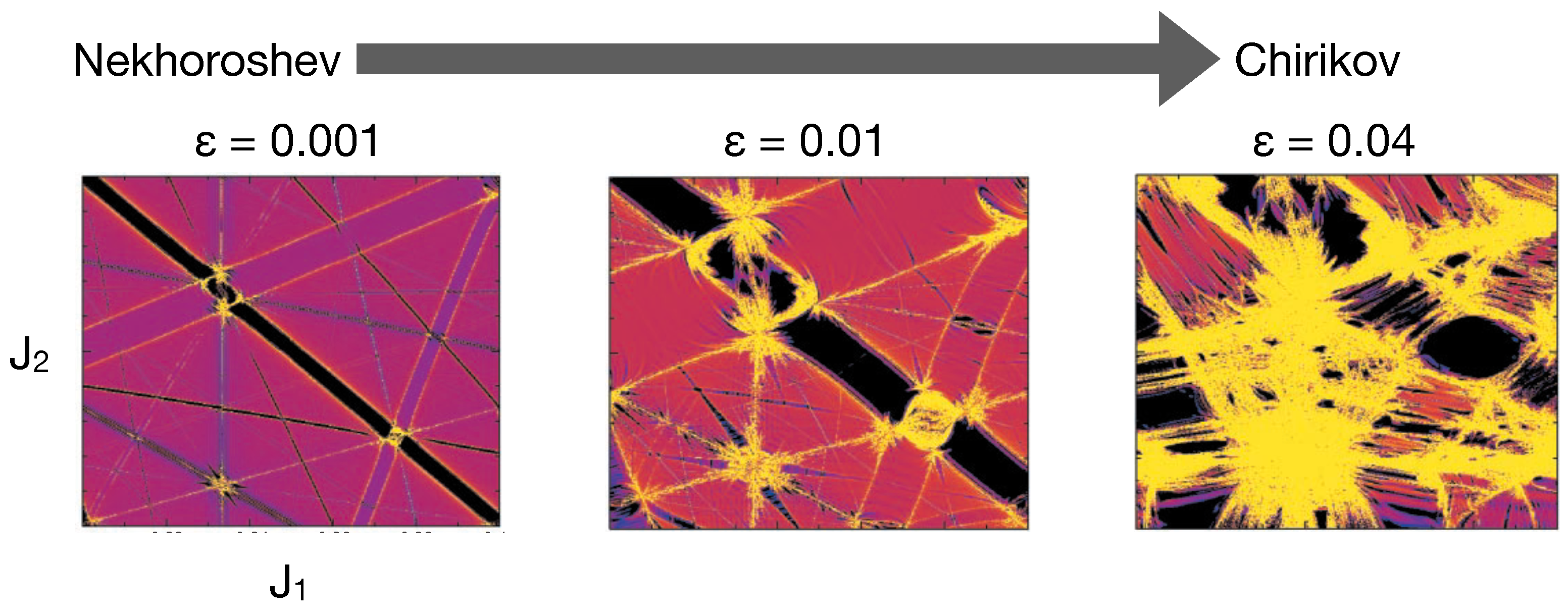
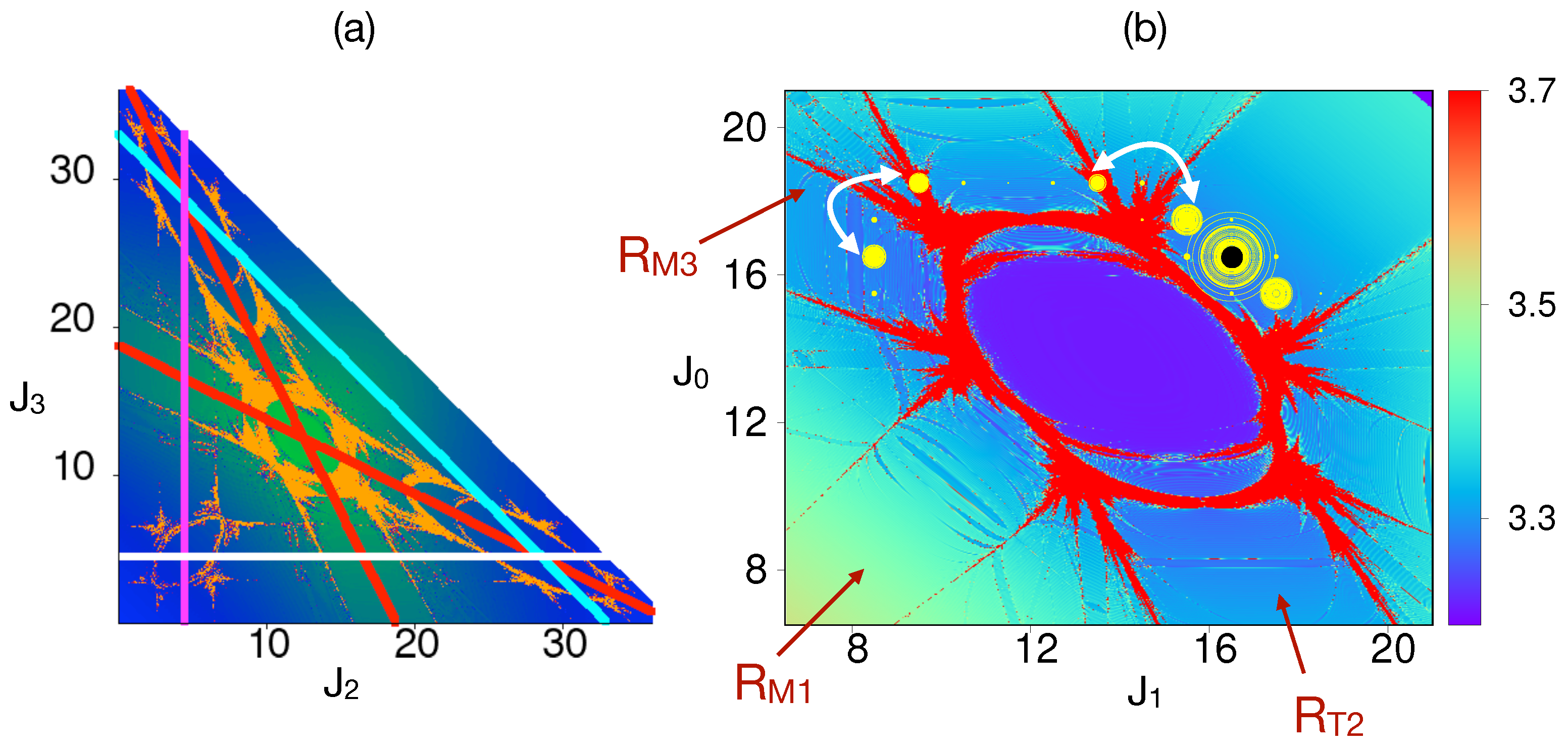
2. Arnold Web: Definition, Construction, and Examples
Construction of the Arnold Web
3. Dynamical Tunneling and the Arnold Web: Some Examples
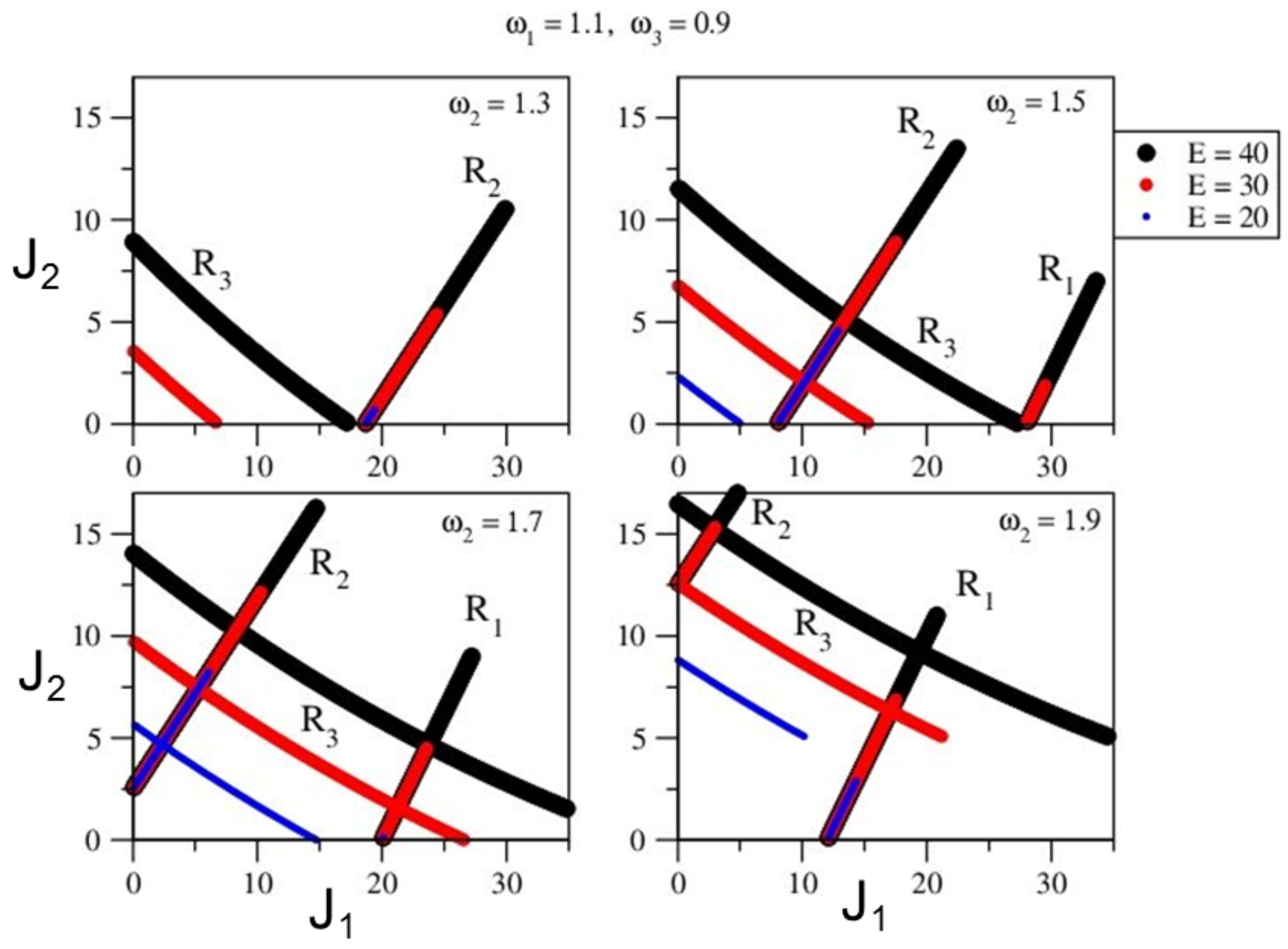
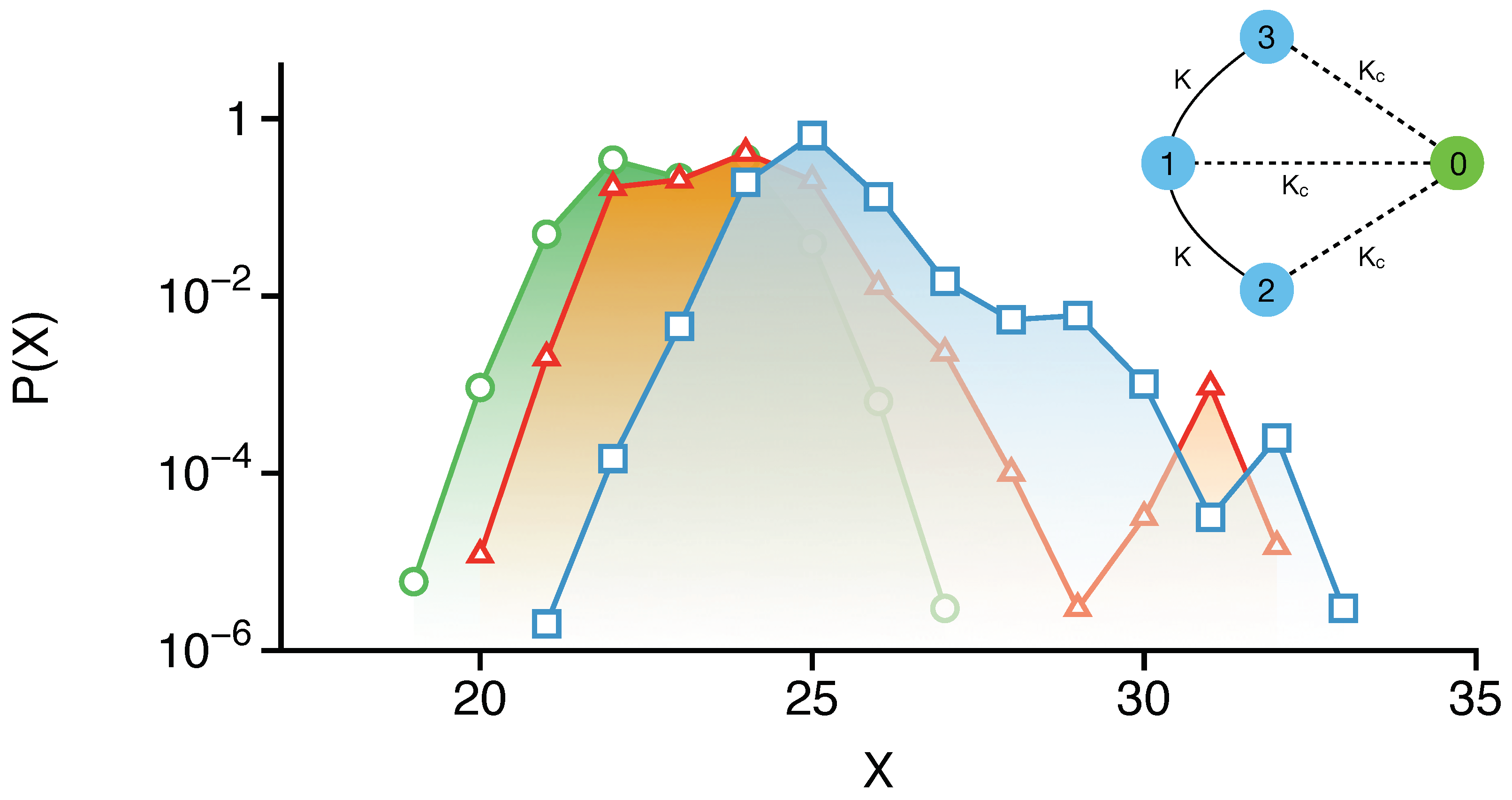
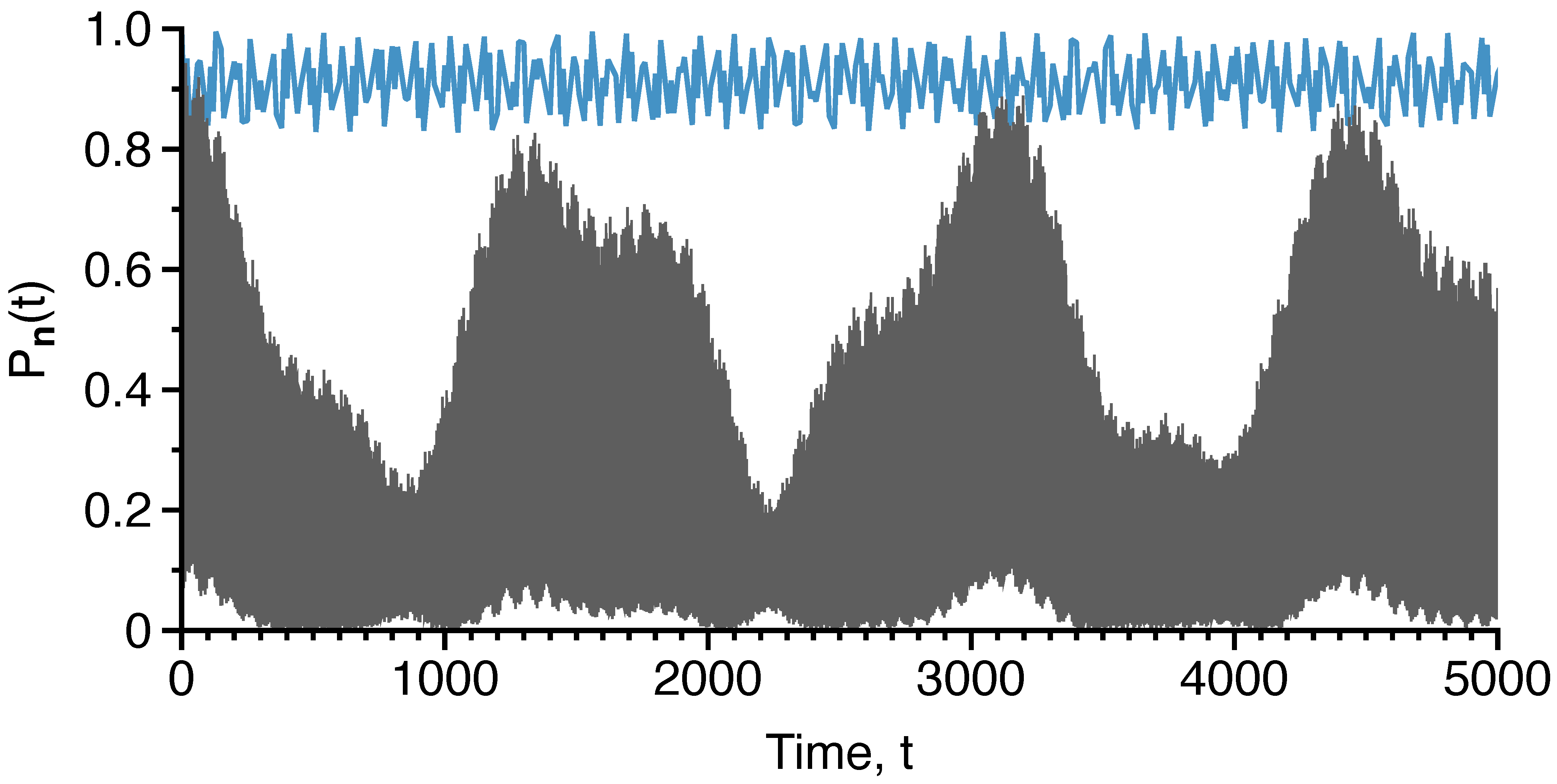
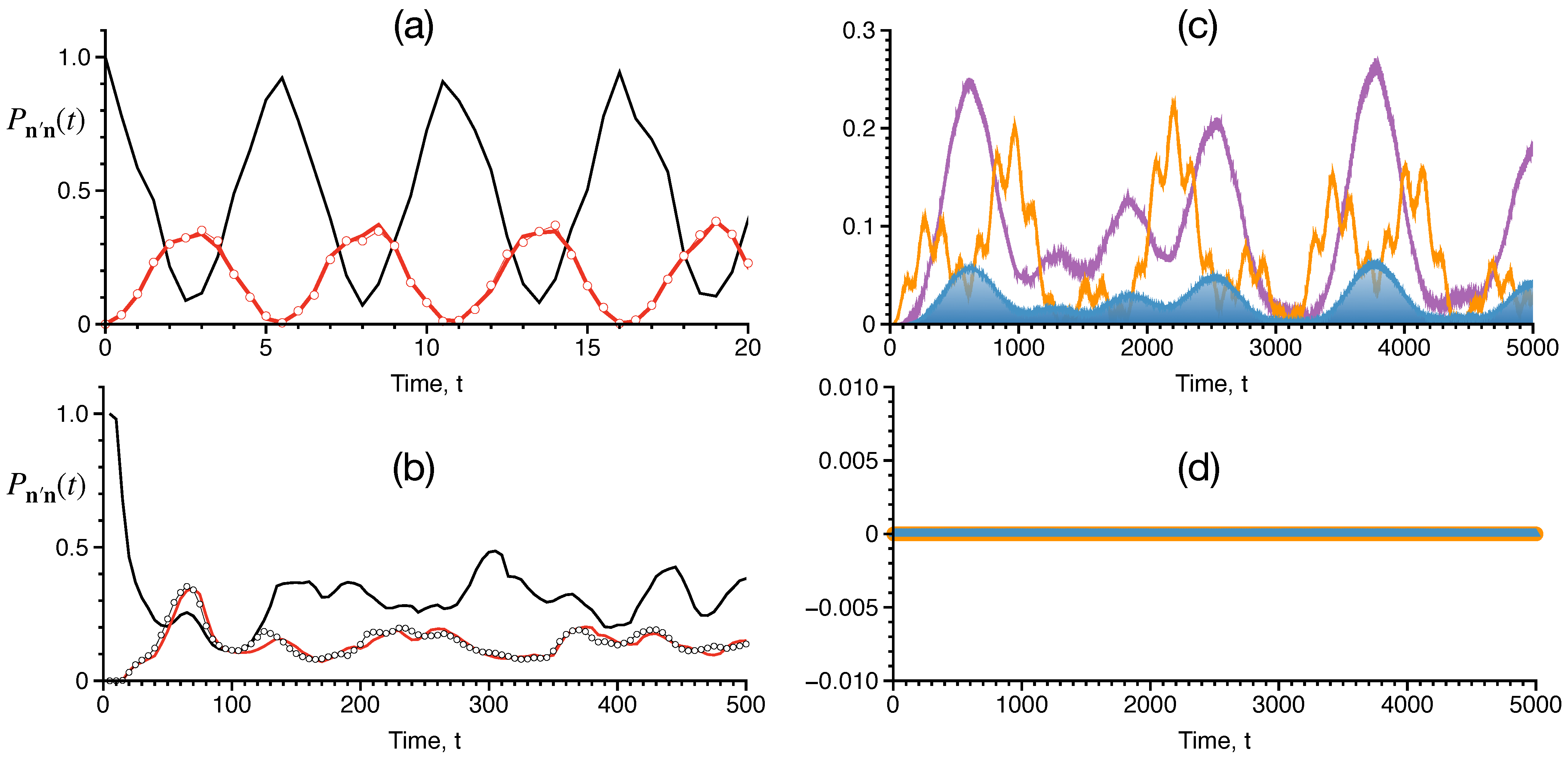
3.1. Martens’ Three-Resonance Model
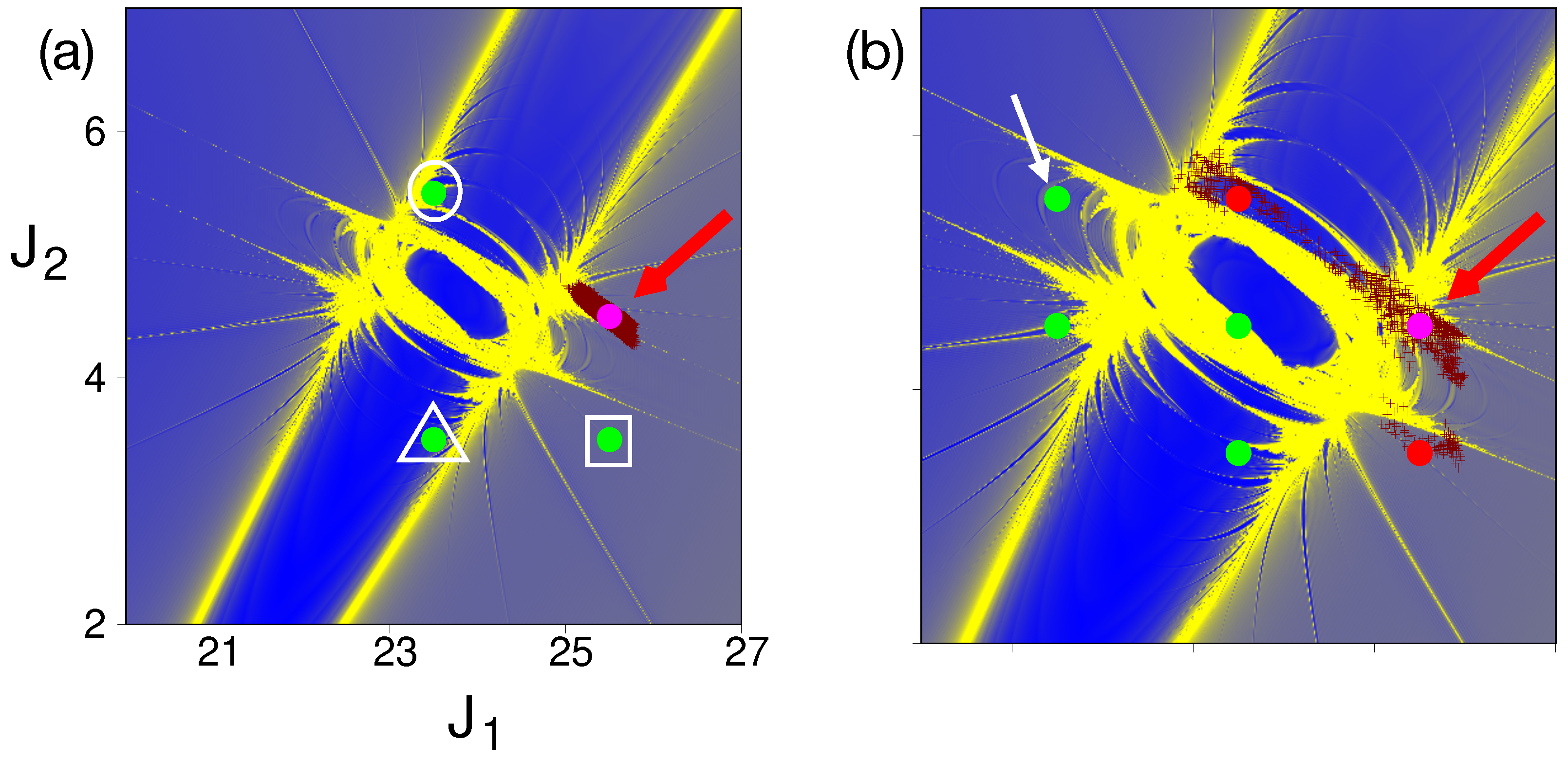
3.2. Trapped Ultracold Atoms
4. Final Thoughts
- Almost all the examples shown here suffer from one key issue. There is simply no accurate estimate of classical stability times and their comparison to the DT timescales. Moreover, a careful study of the DT process by scaling the effective ℏ needs to be done. In this regard, it may be worthwhile to study Martens’ model from the stochastic pumping (or three-resonance) model perspective.
- For mixed regular–chaotic phase spaces in , a combination of RAT and CAT is operative. Models combining the nonlinear resonances and random matrix theory have been relatively successful in understanding tunneling splittings. For , the local chaos near the junctions may not be amenable to a random matrix approach. How does one account for the role of CAT, if relevant, near junctions?
- The focus, understandably so, has been on systems. What about systems? Higher rank junctions are now possible. Moreover, the argument [80] that quantum Arnold diffusion may delocalized in analogy with the transport along disordered wires is no longer valid. Similarly, whether the destruction of quantum localization on the Arnold web due to classical drift [87] holds in the presence of higher rank junctions is not clear at the present moment. Already for , the results in Figure 7 and Figure 10b seem to suggest a stronger Nekhoroshev stability for the quantum dynamics. Of course, one needs to ask: is there a “quantum” Nekhoroshev theorem? Some subtle issues in this regard have been outlined in the paper by Fontanari et al. [119].
- Much of the arguments invoking the Nekhoroshev exponential stability need modification when the quasi-convexity or steepness assumptions are violated. In such instances, one can have fast transport on the Arnold web. Does this then invalidate the notion of DT in such systems? Even for such systems, are there phase space regions that are classically disconnected over physically relevant timescales? In an impressive study, Pittman, Tannenbaum, and Heller have [50] made a start in terms of non-convex model Hamiltonians. In fact, and relevant to the previous point, they studied DT in systems with , and 5 and argued that DT can be faster than the fast classical transport and hint at mechanisms different from RAT. However, certain coupling schemes can result in comparable timescales for classical and quantum transport. More extensive studies on this and other such models would yield important insights.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DT | Dynamical Tunneling |
| IVR | Intramolecular Vibrational energy Redistribution |
| KAM | Kolmogorov-Arnold-Moser |
| RAT | Resonance-assisted Tunneling |
| CAT | Chaos-assisted Tunneling |
| FLI | Fast Lyapunov Indicator |
| MEGNO | Mean Exponential Growth of Nearby Orbits |
| SALI | Smaller Alignment Index |
| GALI | Generalized Alignment Index |
| MQST | Macroscopic Quantum Self-Trapping |
| BHH | Bose–Hubbard Hamiltonian |
References
- Davis, M.J.; Heller, E.J. Quantum dynamical tunneling in bound states. J. Chem. Phys. 1981, 75, 246–254. [Google Scholar] [CrossRef]
- Keshavamurthy, S. Dynamical tunnelling in molecules: Quantum routes to energy flow. Int. Rev. Phys. Chem. 2007, 26, 521–584. [Google Scholar] [CrossRef][Green Version]
- Heller, E.J. Dynamic Tunneling and Molecular Spectra. J. Phys. Chem. 1995, 99, 2625–2634. [Google Scholar] [CrossRef]
- Stuchebrukhov, A.A.; Mehta, A.; Marcus, R.A. Vibrational superexchange mechanism of intramolecular vibrational relaxation in 3,3-dimethylbut-1-yne molecules. J. Phys. Chem. 1993, 97, 12491–12499. [Google Scholar] [CrossRef]
- Callegari, A.; Pearman, R.; Choi, S.; Engels, P.H.; Srivastava, H.; Gruebele, M.; Lehmann, K.K.; Scoles, G. Intramolecular vibrational relaxation in aromatic molecules. 2: An experimental and computational study of pyrrole and triazine near the IVR threshold. Mol. Phys. 2003, 101, 551–568. [Google Scholar] [CrossRef]
- Keshavamurthy, S. Scaling Perspective on Intramolecular Vibrational Energy Flow: Analogies, Insights, and Challenges. Adv. Chem. Phys. 2013, 153, 43–110. [Google Scholar]
- Karmakar, S.; Keshavamurthy, S. Intramolecular vibrational energy redistribution and the quantum ergodicity transition: A phase space perspective. Phys. Chem. Chem. Phys. 2020, 22, 11139–11173. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.M. Quantum ergodicity and energy flow in molecules. Adv. Phys. 2015, 64, 445–517. [Google Scholar] [CrossRef]
- Vanhaele, G.; Schlagheck, P. NOON states with ultracold bosonic atoms via resonance- and chaos-assisted tunneling. Phys. Rev. A 2021, 103, 013315. [Google Scholar] [CrossRef]
- Vanhaele, G.; Bäcker, A.; Ketzmerick, R.; Schlagheck, P. Creating triple-NOON states with ultracold atoms via chaos-assisted tunneling. Phys. Rev. A 2022, 106, L011301. [Google Scholar] [CrossRef]
- Sethi, A.; Keshavamurthy, S. Bichromatically driven double well: Parametric perspective of the strong field control landscape reveals the influence of chaotic states. J. Chem. Phys. 2008, 128, 164117. [Google Scholar] [CrossRef] [PubMed]
- Sethi, A.; Keshavamurthy, S. Local phase space control and interplay of classical and quantum effects in dissociation of a driven Morse oscillator. Phys. Rev. A 2009, 79, 033416. [Google Scholar] [CrossRef]
- Shukla, A.; Keshavamurthy, S. One Versus Two Photon Control of Dynamical Tunneling: Influence of the Irregular Floquet States. J. Phys. Chem. B 2015, 119, 11326–11335. [Google Scholar] [CrossRef] [PubMed]
- Shukla, A.; Keshavamurthy, S. Controlling the quantum rotational dynamics of a driven planar rotor by rebuilding barriers in the classical phase space. J. Chem. Sci. 2017, 129, 1005–1016. [Google Scholar] [CrossRef]
- Krithika, V.R.; Santhanam, M.S.; Mahesh, T.S. NMR investigations of dynamical tunneling in spin systems. Phys. Rev. A 2023, 108, 032207. [Google Scholar] [CrossRef]
- Chaudhury, S.; Smith, A.; Anderson, B.E.; Ghose, S.; Jessen, P.S. Quantum signatures of chaos in a kicked top. Nature 2009, 461, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Pinto, R.A.; Flach, S. Quantum breathers in capacitively coupled Josephson junctions: Correlations, number conservation, and entanglement. Phys. Rev. B 2008, 77, 024308. [Google Scholar] [CrossRef]
- Igumenshchev, K.; Ovchinnikov, M.; Maniadis, P.; Prezhdo, O. Signatures of discrete breathers in coherent state quantum dynamics. J. Chem. Phys. 2013, 138, 054104. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, S.; Keshavamurthy, S. Arnold web and dynamical tunneling in a four-site Bose–Hubbard model. Phys. D 2021, 427, 133006. [Google Scholar] [CrossRef]
- Satpathi, U.; Ray, S.; Vardi, A. Chaos-assisted many-body tunnelling. Phys. Rev. E 2022, 106, L042204. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Liu, Y.; Xiao, S.; Wang, Z.; Fan, Y.; Han, J.; Ge, L.; Song, Q. Direct observation of chaotic resonances in optical microcavities. Light. Sci. Appl. 2021, 10, 135. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.H.; Kullig, J.; Wiersig, J. Pair of Exceptional Points in a Microdisk Cavity under an Extremely Weak Deformation. Phys. Rev. Lett. 2018, 120, 093902. [Google Scholar] [CrossRef] [PubMed]
- Arnal, M.; Chatelain, G.; Martinez, M.; Dupont, N.; Giraud, O.; Ullmo, D.; Georgeot, B.; Lemarié, G.; Billy, J.; Guéry-Odelin, D. Chaos-assisted tunneling resonances in a synthetic Floquet superlattice. Sci. Adv. 2020, 6, eabc4886. [Google Scholar] [CrossRef] [PubMed]
- Bäcker, A.; Ketzmerick, R.; Löck, S.; Robnik, M.; Vidmar, G.; Höhmann, R.; Kuhl, U.; Stöckmann, H.J. Dynamical Tunneling in Mushroom Billiards. Phys. Rev. Lett. 2008, 100, 174103. [Google Scholar] [CrossRef] [PubMed]
- Saini, R.K.; Sehgal, R.; Jain, S.R. Protection of qubits by nonlinear resonances. Eur. Phys. J. Plus 2022, 137, 356. [Google Scholar] [CrossRef]
- Cohen, J.; Petrescu, A.; Shillito, R.; Blais, A. Reminiscence of Classical Chaos in Driven Transmons. PRX Quantum 2023, 4, 020312. [Google Scholar] [CrossRef]
- Lenz, M.; Wüster, S.; Vale, C.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H.; Holmes, C.A.; Milburn, G.J.; Davis, M.J. Dynamical tunneling with ultracold atoms in magnetic microtraps. Phys. Rev. A 2013, 88, 013635. [Google Scholar] [CrossRef]
- Jangid, P.; Chauhan, A.K.; Wüster, S. Dynamical tunneling of a nanomechanical oscillator. Phys. Rev. A 2020, 102, 043513. [Google Scholar] [CrossRef]
- Fritzsch, F.; Ketzmerick, R.; Bäcker, A. Resonance-assisted tunneling in deformed optical microdisks with a mixed phase space. Phys. Rev. E 2019, 100, 042219. [Google Scholar] [CrossRef]
- Kwak, H.; Shin, Y.; Moon, S.; Lee, S.B.; Yang, J.; An, K. Nonlinear resonance-assisted tunneling induced by microcavity deformation. Sci. Rep. 2015, 5, 9010. [Google Scholar] [CrossRef]
- Gehler, S.; Löck, S.; Shinohara, S.; Bäcker, A.; Ketzmerick, R.; Kuhl, U.; Stöckmann, H.J. Experimental Observation of Resonance-Assisted Tunneling. Phys. Rev. Lett. 2015, 115, 104101. [Google Scholar] [CrossRef]
- Martinez, M.; Giraud, O.; Ullmo, D.; Billy, J.; Guéry-Odelin, D.; Georgeot, B.; Lemarié, G. Chaos-Assisted Long-Range Tunneling for Quantum Simulation. Phys. Rev. Lett. 2021, 126, 174102. [Google Scholar] [CrossRef] [PubMed]
- de Moura, A.P.S.; Lai, Y.C.; Akis, R.; Bird, J.P.; Ferry, D.K. Tunneling and Nonhyperbolicity in Quantum Dots. Phys. Rev. Lett. 2002, 88, 236804. [Google Scholar] [CrossRef]
- Liu, S.; Wiersig, J.; Sun, W.; Fan, Y.; Ge, L.; Yang, J.; Xiao, S.; Song, Q.; Cao, H. Transporting the Optical Chirality through the Dynamical Barriers in Optical Microcavities. Laser Photonics Rev. 2018, 12, 1800027. [Google Scholar] [CrossRef]
- Brodier, O.; Schlagheck, P.; Ullmo, D. Resonance-Assisted Tunneling in Near-Integrable Systems. Phys. Rev. Lett. 2001, 87, 064101. [Google Scholar] [CrossRef] [PubMed]
- Eltschka, C.; Schlagheck, P. Resonance- and Chaos-Assisted Tunneling in Mixed Regular-Chaotic Systems. Phys. Rev. Lett. 2005, 94, 014101. [Google Scholar] [CrossRef]
- Keshavamurthy, S. On dynamical tunneling and classical resonances. J. Chem. Phys. 2005, 122, 114109. [Google Scholar] [CrossRef] [PubMed]
- Keshavamurthy, S. Dynamical tunneling in molecules: Role of the classical resonances and chaos. J. Chem. Phys. 2003, 119, 161–164. [Google Scholar] [CrossRef]
- Löck, S.; Bäcker, A.; Ketzmerick, R.; Schlagheck, P. Regular-to-chaotic tunneling rates: From the quantum to the semiclassical regime. Phys. Rev. Lett. 2010, 104, 114101. [Google Scholar] [CrossRef]
- Wimberger, S.; Schlagheck, P.; Eltschka, C.; Buchleitner, A. Resonance-Assisted Decay of Nondispersive Wave Packets. Phys. Rev. Lett. 2006, 97, 043001. [Google Scholar] [CrossRef]
- Bohigas, O.; Tomsovic, S.; Ullmo, D. Manifestations of classical phase space structures in quantum mechanics. Phys. Rep. 1993, 223, 43–133. [Google Scholar] [CrossRef]
- Tomsovic, S.; Ullmo, D. Chaos-assisted tunneling. Phys. Rev. E 1994, 50, 145–162. [Google Scholar] [CrossRef] [PubMed]
- Reichl, L.E. Chaos-Assisted Tunneling. Entropy 2024, 26, 144. [Google Scholar] [CrossRef] [PubMed]
- Tomsovic, S. Tunneling in Complex Systems; World Scientific: Singapore, 1998. [Google Scholar]
- Keshavamurthy, S.; Schlagheck, P. Dynamical Tunnelling: Theory and Experiment; Taylor and Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Iijima, R.; Koda, R.; Hanada, Y.; Shudo, A. Quantum tunneling in ultra-near-integrable systems. Phys. Rev. E 2022, 106, 064205. [Google Scholar] [CrossRef] [PubMed]
- Koda, R.; Hanada, Y.; Shudo, A. Ergodicity of complex dynamics and quantum tunneling in nonintegrable systems. Phys. Rev. E 2023, 108, 054219. [Google Scholar] [CrossRef] [PubMed]
- Hanada, Y.; Ikeda, K.S.; Shudo, A. Dynamical tunneling across the separatrix. Phys. Rev. E 2023, 108, 064210. [Google Scholar] [CrossRef] [PubMed]
- Keshavamurthy, S. Resonance-assisted tunneling in three degrees of freedom without discrete symmetry. Phys. Rev. E 2005, 72, 045203. [Google Scholar] [CrossRef] [PubMed]
- Pittman, S.M.; Tannenbaum, E.; Heller, E.J. Dynamical tunneling versus fast diffusion for a non-convex Hamiltonian. J. Chem. Phys. 2016, 145, 054303. [Google Scholar] [CrossRef]
- Karmakar, S.; Keshavamurthy, S. Relevance of the Resonance Junctions on the Arnold Web to Dynamical Tunneling and Eigenstate Delocalization. J. Phys. Chem. A 2018, 122, 8636–8649. [Google Scholar] [CrossRef]
- Firmbach, M.; Fritzsch, F.; Ketzmerick, R.; Bäcker, A. Resonance-assisted tunneling in four-dimensional normal-form Hamiltonians. Phys. Rev. E 2019, 99, 042213. [Google Scholar] [CrossRef]
- Cincotta, P.M.; Giordano, C.M. Estimation of diffusion time with the Shannon entropy approach. Phys. Rev. E 2023, 107, 064101. [Google Scholar] [CrossRef] [PubMed]
- Konishi, T. Slow Dynamics in Multidimensional Phase Space: Arnold Model Revisited. In Geometric Structures of Phase Space in Multidimensional Chaos; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; Chapter 21; pp. 423–436. [Google Scholar]
- Chirikov, B.V.; Vecheslavov, V.V. Theory of fast arnold diffusion in many-frequency systems. J. Stat. Phys. 1993, 71, 243–258. [Google Scholar] [CrossRef][Green Version]
- Laskar, J. Frequency analysis for multi-dimensional systems. Global dynamics and diffusion. Phys. D 1993, 67, 257–281. [Google Scholar] [CrossRef]
- Haller, G. Diffusion at intersecting resonances in Hamiltonian systems. Phys. Lett. A 1995, 200, 34–42. [Google Scholar] [CrossRef]
- Honjo, S.; Kaneko, K. Structure of Resonances and Transport in Multidimensional Hamiltonian Dynamical Systems. In Geometric Structures of Phase Space in Multidimensional Chaos; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; Chapter 22; pp. 437–463. [Google Scholar]
- Guillery, N.; Meiss, J.D. Diffusion and drift in volume-preserving maps. Reg. Chaot. Dyn. 2017, 22, 700–720. [Google Scholar] [CrossRef]
- Guzzo, M.; Lega, E.; Froeschlé, C. Diffusion and stability in perturbed non-convex integrable systems. Nonlinearity 2006, 19, 1049. [Google Scholar] [CrossRef]
- Wood, B.P.; Lichtenberg, A.J.; Lieberman, M.A. Arnold diffusion in weakly coupled standard maps. Phys. Rev. A 1990, 42, 5885–5893. [Google Scholar] [CrossRef] [PubMed]
- Martens, C.C.; Davis, M.J.; Ezra, G.S. Local frequency analysis of chaotic motion in multidimensional systems: Energy transport and bottlenecks in planar OCS. Chem. Phys. Lett. 1987, 142, 519–528. [Google Scholar] [CrossRef]
- Manikandan, P.; Keshavamurthy, S. Dynamical traps lead to the slowing down of intramolecular vibrational energy flow. Proc. Natl. Acad. Sci. USA 2014, 111, 14354–14359. [Google Scholar] [CrossRef]
- Atkins, K.M.; Logan, D.E. Intersecting resonances as a route to chaos: Classical and quantum studies of a three-oscillator model. Phys. Lett. A 1992, 162, 255–262. [Google Scholar] [CrossRef]
- Toda, M. Dynamics of Chemical Reactions and Chaos; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; Chapter 3; pp. 153–198. [Google Scholar]
- Shojiguchi, A.; Li, C.B.; Komatsuzaki, T.; Toda, M. Fractional behavior in multidimensional Hamiltonian systems describing reactions. Phys. Rev. E 2007, 76, 056205. [Google Scholar] [CrossRef]
- Yadav, P.K.; Keshavamurthy, S. Breaking of a bond: When is it statistical? Faraday Disc. 2015, 177, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, S.; Yadav, P.K.; Keshavamurthy, S. Stable chaos and delayed onset of statisticality in unimolecular dissociation reactions. Commun. Chem. 2020, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Sethi, A.; Keshavamurthy, S. Driven coupled Morse oscillators: Visualizing the phase space and characterizing the transport. Mol. Phys. 2012, 110, 717–727. [Google Scholar] [CrossRef][Green Version]
- Lopez-Pina, A.; Losada, J.C.; Benito, R.M.; Borondo, F. Frequency analysis of the laser driven nonlinear dynamics of HCN. J. Chem. Phys. 2016, 145, 244309. [Google Scholar] [CrossRef] [PubMed]
- Lange, S.; Bäcker, A.; Ketzmerick, R. What is the mechanism of power-law distributed Poincaré recurrences in higher-dimensional systems? Europhys. Lett. 2016, 116, 30002. [Google Scholar] [CrossRef]
- Firmbach, M.; Lange, S.; Ketzmerick, R.; Bäcker, A. Three-dimensional billiards: Visualization of regular structures and trapping of chaotic trajectories. Phys. Rev. E 2018, 98, 022214. [Google Scholar] [CrossRef] [PubMed]
- Firmbach, M.; Bäcker, A.; Ketzmerick, R. Partial barriers to chaotic transport in 4D symplectic maps. Chaos 2023, 33, 013125. [Google Scholar] [CrossRef] [PubMed]
- Richter, M.; Lange, S.; Bäcker, A.; Ketzmerick, R. Visualization and comparison of classical structures and quantum states of four-dimensional maps. Phys. Rev. E 2014, 89, 022902. [Google Scholar] [CrossRef]
- Agaoglou, M.; García-Garrido, V.J.; Katsanikas, M.; Wiggins, S. Visualizing the phase space of the HeI2 van der Waals complex using Lagrangian descriptors. Commun. Nonlin. Sci. Num. Simul. 2021, 103, 105993. [Google Scholar] [CrossRef]
- Efthymiopoulos, C.; Harsoula, M. The speed of Arnold diffusion. Phys. D 2013, 251, 19–38. [Google Scholar] [CrossRef][Green Version]
- Cincotta, P.M.; Efthymiopoulos, C.; Giordano, C.M.; Mestre, M.F. Chirikov and Nekhoroshev diffusion estimates: Bridging the two sides of the river. Phys. D 2014, 266, 49–64. [Google Scholar] [CrossRef]
- Guzzo, M.; Lega, E. The numerical detection of the Arnold web and its use for long-term diffusion studies in conservative and weakly dissipative systems. Chaos 2013, 23, 023124. [Google Scholar] [CrossRef] [PubMed]
- Martens, C.C. Quantum qualitative dynamics. J. Stat. Phys. 1992, 68, 207–237. [Google Scholar] [CrossRef]
- Leitner, D.M.; Wolynes, P.G. Quantization of the Stochastic Pump Model of Arnold Diffusion. Phys. Rev. Lett. 1997, 79, 55–58. [Google Scholar] [CrossRef]
- Demikhovskii, V.; Izrailev, F.; Malyshev, A. Quantum Arnol’d diffusion in a rippled waveguide. Phys. Lett. A 2006, 352, 491–495. [Google Scholar] [CrossRef]
- Malyshev, A.I.; Chizhova, L.A. Arnol’d diffusion in a system with 2.5 degrees of freedom: Classical and quantum mechanical approaches. J. Exp. Theor. Phys. 2010, 110, 837–844. [Google Scholar] [CrossRef]
- Demikhovskii, V.Y.; Izrailev, F.M.; Malyshev, A.I. Manifestation of Arnol’d Diffusion in Quantum Systems. Phys. Rev. Lett. 2002, 88, 154101. [Google Scholar] [CrossRef]
- Manikandan, P.; Keshavamurthy, S. Intramolecular vibrational energy redistribution from a high frequency mode in the presence of an internal rotor: Classical thick-layer diffusion and quantum localization. J. Chem. Phys. 2007, 127, 064303. [Google Scholar] [CrossRef]
- Boretz, Y.; Reichl, L.E. Arnold diffusion in a driven optical lattice. Phys. Rev. E 2016, 93, 032214. [Google Scholar] [CrossRef]
- Stöber, J.; Bäcker, A.; Ketzmerick, R. Quantum Transport through Partial Barriers in Higher-Dimensional Systems. Phys. Rev. Lett. 2024, 132, 047201. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.R.; Bäcker, A.; Ketzmerick, R. Classical Drift in the Arnold Web Induces Quantum Delocalization Transition. Phys. Rev. Lett. 2023, 131, 187201. [Google Scholar] [CrossRef] [PubMed]
- Gligorić, G.; Bodyfelt, J.D.; Flach, S. Interactions destroy dynamical localization with strong and weak chaos. Europhys. Lett. 2011, 96, 30004. [Google Scholar] [CrossRef]
- Basko, D. Weak chaos in the disordered nonlinear Schrödinger chain: Destruction of Anderson localization by Arnold diffusion. Ann. Phys. 2011, 326, 1577–1655. [Google Scholar] [CrossRef]
- Madsen, D.; Pearman, R.; Gruebele, M. Approximate factorization of molecular potential surfaces. I. Basic approach. J. Chem. Phys. 1997, 106, 5874–5893. [Google Scholar] [CrossRef]
- Nekhoroshev, N.N. An exponential estimate of the time of stability of nearly-integrable hamiltonian systems. Russ. Math. Surv. 1977, 32, 1. [Google Scholar] [CrossRef]
- Karmakar, S. Nonstatistical Reaction Dynamics: Junctions, Traps, and Tunnelling on the Arnold Web. Ph.D. Thesis, Indian Institute of Technology Kanpur, Uttar Pradesh, India, 2021. [Google Scholar]
- Morbidelli, A.; Guzzo, M. The Nekhoroshev theorem and the asteroid belt dynamical system. Celest. Mech. Dyn. Astron. 1996, 65, 107–136. [Google Scholar] [CrossRef]
- Froeschlé, C.; Guzzo, M.; Lega, E. Graphical Evolution of the Arnold Web: From Order to Chaos. Science 2000, 289, 2108–2110. [Google Scholar] [CrossRef] [PubMed]
- Morbidelli, A.; Froeschlé, C. On the relationship between Lyapunov times and macroscopic instability times. Celest. Mech. Dyn. Astron. 1995, 63, 227–239. [Google Scholar] [CrossRef]
- Barrio, R. Sensitivity tools vs. Poincaré sections. Chaos Solitons Fractals 2005, 25, 711–726. [Google Scholar] [CrossRef]
- Cincotta, P.; Giordano, C.; Simó, C. Phase space structure of multi-dimensional systems by means of the mean exponential growth factor of nearby orbits. Phys. D 2003, 182, 151–178. [Google Scholar] [CrossRef]
- Skokos, C.; Bountis, T.; Antonopoulos, C. Geometrical properties of local dynamics in Hamiltonian systems: The Generalized Alignment Index (GALI) method. Phys. D 2007, 231, 30–54. [Google Scholar] [CrossRef]
- Sándor, Z.; Érdi, B.; Széll, A.; Funk, B. The Relative Lyapunov Indicator: An Efficient Method of Chaos Detection. Celest. Mech. Dyn. Astron. 2004, 90, 127–138. [Google Scholar] [CrossRef]
- Darriba, L.A.; Maffione, N.P.; Cincotta, P.M.; Giordano, C.M. Comparative study of variational chaos indicators and ODES’ numerical integrators. Int. J. Bifur. Chaos 2012, 22, 1230033. [Google Scholar] [CrossRef]
- Skokos, C.H.; Gottwald, G.A.; Laskar, J. (Eds.) Chaos Detection and Predictability; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Giordano, C.; Cincotta, P. The Shannon entropy as a measure of diffusion in multidimensional dynamical systems. Celest. Mech. Dyn. Astron. 2018, 130, 35. [Google Scholar] [CrossRef]
- Daquin, J.; Charalambous, C. Detection of separatrices and chaotic seas based on orbit amplitudes. Celest. Mech. Dyn. Astron. 2023, 135, 31. [Google Scholar] [CrossRef]
- von Milczewski, J.; Diercksen, G.H.F.; Uzer, T. Computation of the Arnol’d Web for the Hydrogen Atom in Crossed Electric and Magnetic Fields. Phys. Rev. Lett. 1996, 76, 2890–2893. [Google Scholar] [CrossRef] [PubMed]
- Vela-Arevalo, L.V.; Wiggins, S. Time-frequency analysis of classical trajectories of polyatomic molecules. Int. J. Bifur. Chaos 2001, 11, 1359–1380. [Google Scholar] [CrossRef]
- Chandre, C.; Wiggins, S.; Uzer, T. Time-frequency analysis of chaotic systems. Phys. D 2003, 181, 171–196. [Google Scholar] [CrossRef]
- Cordani, B. Frequency modulation indicator, Arnold’s web and diffusion in the Stark–Quadratic-Zeeman problem. Phys. D 2008, 237, 2797–2815. [Google Scholar] [CrossRef]
- Fuji, K.; Toda, M. Time series analysis for multi-dimensional dynamical systems combining wavelet transformation and local principal component analysis. Prog. Theor. Exp. Phys. 2019, 2019, 123A03. [Google Scholar] [CrossRef]
- Seibert, A.; Denisov, S.; Ponomarev, A.V.; Hänggi, P. Mapping the Arnold web with a graphic processing unit. Chaos 2011, 21, 043123. [Google Scholar] [CrossRef] [PubMed]
- Tailleur, J.; Kurchan, J. Probing rare physical trajectories with Lyapunov weighted dynamics. Nat. Phys. 2007, 3, 203–207. [Google Scholar] [CrossRef]
- Hensinger, W.K.; Häffner, H.; Browaeys, A.; Heckenberg, N.R.; Helmerson, K.; McKenzie, C.; Milburn, G.J.; Phillips, W.D.; Rolston, S.L.; Rubinsztein-Dunlop, H.; et al. Dynamical tunnelling of ultracold atoms. Nature 2001, 412, 52–55. [Google Scholar] [CrossRef] [PubMed]
- Folling, S.; Trotzky, S.; Cheinet, P.; Feld, M.; Saers, R.; Widera, A.; Müller, T.; Bloch, I. Direct observation of second-order atom tunnelling. Nature 2007, 448, 1029–1032. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef] [PubMed]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Wüster, S.; Dąbrowska Wüster, B.J.; Davis, M.J. Macroscopic Quantum Self-Trapping in Dynamical Tunneling. Phys. Rev. Lett. 2012, 109, 080401. [Google Scholar] [CrossRef] [PubMed]
- Khripkov, C.; Cohen, D.; Vardi, A. Thermalization of Bipartite Bose–Hubbard Models. J. Phys. Chem. A 2016, 120, 3136–3141. [Google Scholar] [CrossRef]
- Khripkov, C.; Vardi, A.; Cohen, D. Quantum thermalization: Anomalous slow relaxation due to percolation-like dynamics. New J. Phys. 2015, 17, 023071. [Google Scholar] [CrossRef][Green Version]
- Leitner, D.M. Molecules and the Eigenstate Thermalization Hypothesis. Entropy 2018, 20, 673. [Google Scholar] [CrossRef] [PubMed]
- Fontanari, D.; Fassò, F.; Sadovskií, D.A. Quantum manifestations of Nekhoroshev stability. Phys. Lett. A 2016, 380, 3167–3172. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshavamurthy, S. Dynamical Tunneling in More than Two Degrees of Freedom. Entropy 2024, 26, 333. https://doi.org/10.3390/e26040333
Keshavamurthy S. Dynamical Tunneling in More than Two Degrees of Freedom. Entropy. 2024; 26(4):333. https://doi.org/10.3390/e26040333
Chicago/Turabian StyleKeshavamurthy, Srihari. 2024. "Dynamical Tunneling in More than Two Degrees of Freedom" Entropy 26, no. 4: 333. https://doi.org/10.3390/e26040333
APA StyleKeshavamurthy, S. (2024). Dynamical Tunneling in More than Two Degrees of Freedom. Entropy, 26(4), 333. https://doi.org/10.3390/e26040333





