Bayesian Spatio-Temporal Modeling of the Dynamics of COVID-19 Deaths in Peru
Abstract
1. Introduction
2. Materials and Methods
2.1. The Data
- (i)
- Records of COVID-19 deaths across Peru sourced from the Ministerio de Salud (MINSA) and accessible through the Plataforma Nacional De Datos Abiertos (www.datosabiertos.gob.pe/);
- (ii)
- Records of COVID-19 cases across Peru sourced from the MINSA;
- (iii)
- Vaccination records against COVID-19, also obtained from the MINSA.
2.2. Bayesian Spatio-Temporal Model
- is the average time;
- is a latent component for the province k and day t embracing one or more sets of spatio-temporally autocorrelated random effects, which are known as correlated linear time trends [26];
- is a binary neighborhood matrix , with if (diagonal elements equal to zero), if the provinces k and j share a common border, and if the provinces k and j do not share a common border;
- The random effects and are modeled as spatially autocorrelated by the CAR (conditional autoregressive) prior, satisfying to avoid a lack of identifiability, with and denoting the vectors and without their corresponding kth entries, respectively;
- The quantities , , , and are given, respectively, byand
3. Results and Discussion
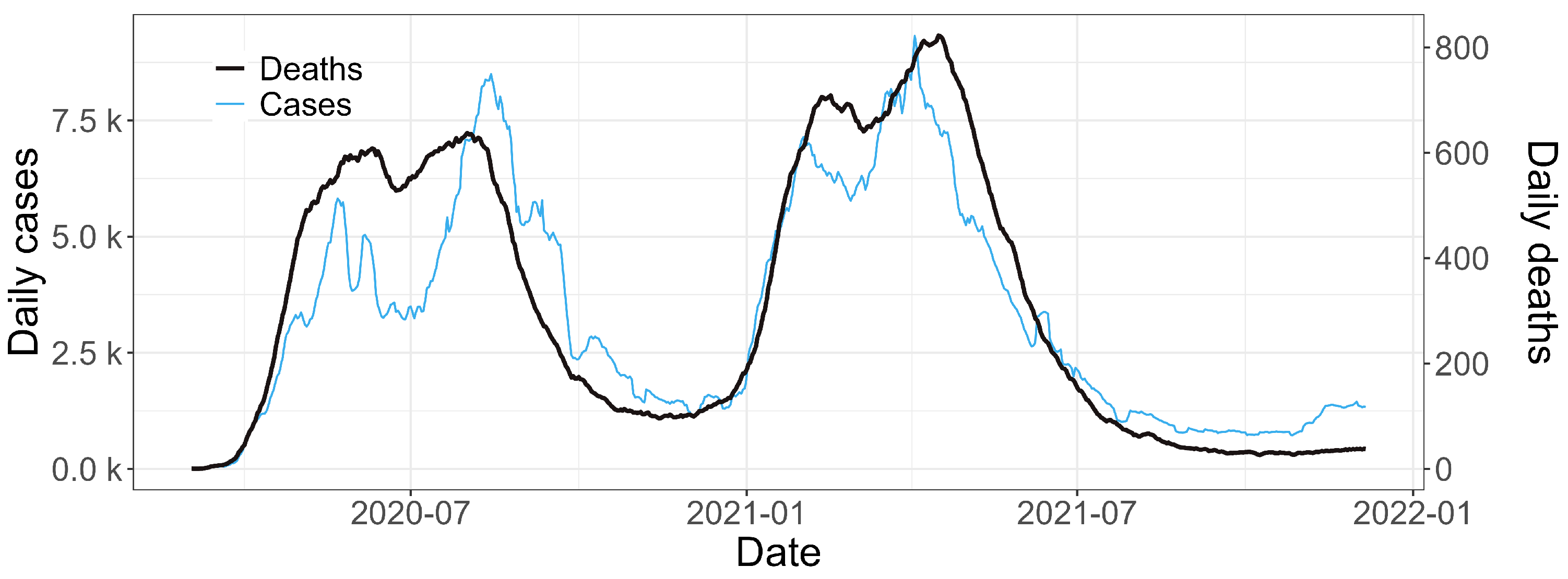
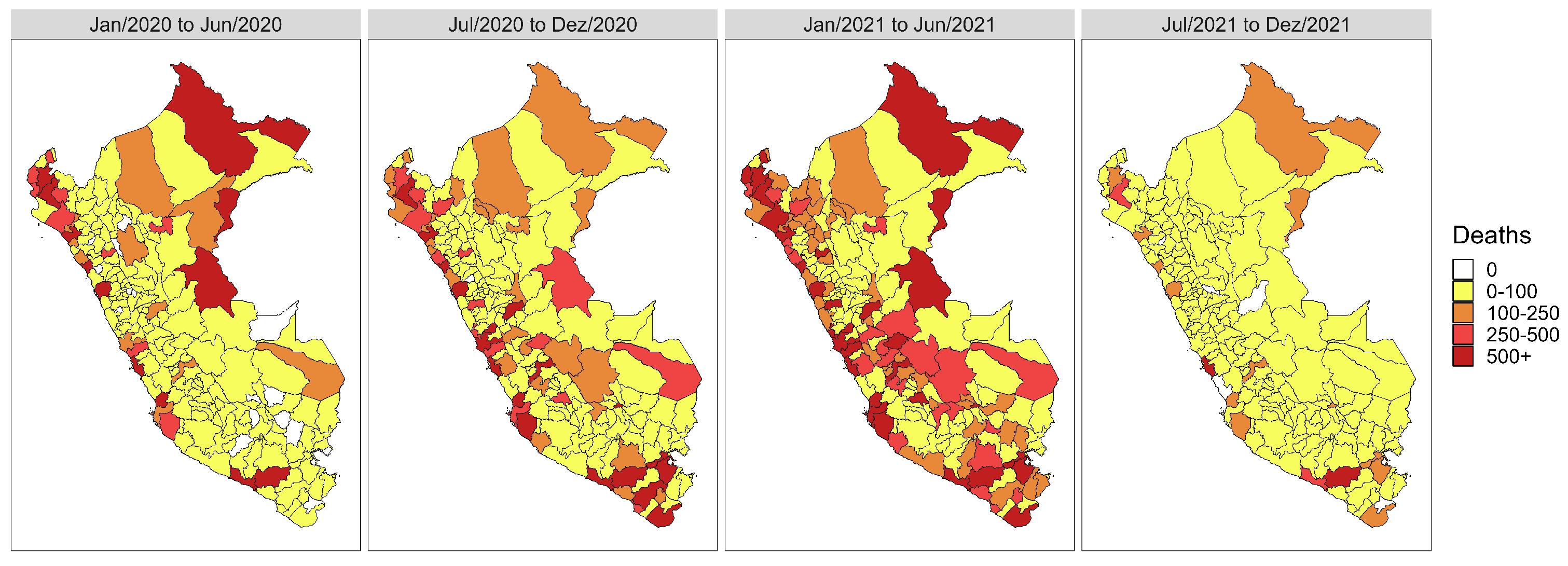
3.1. Descriptive and Exploratory Analysis
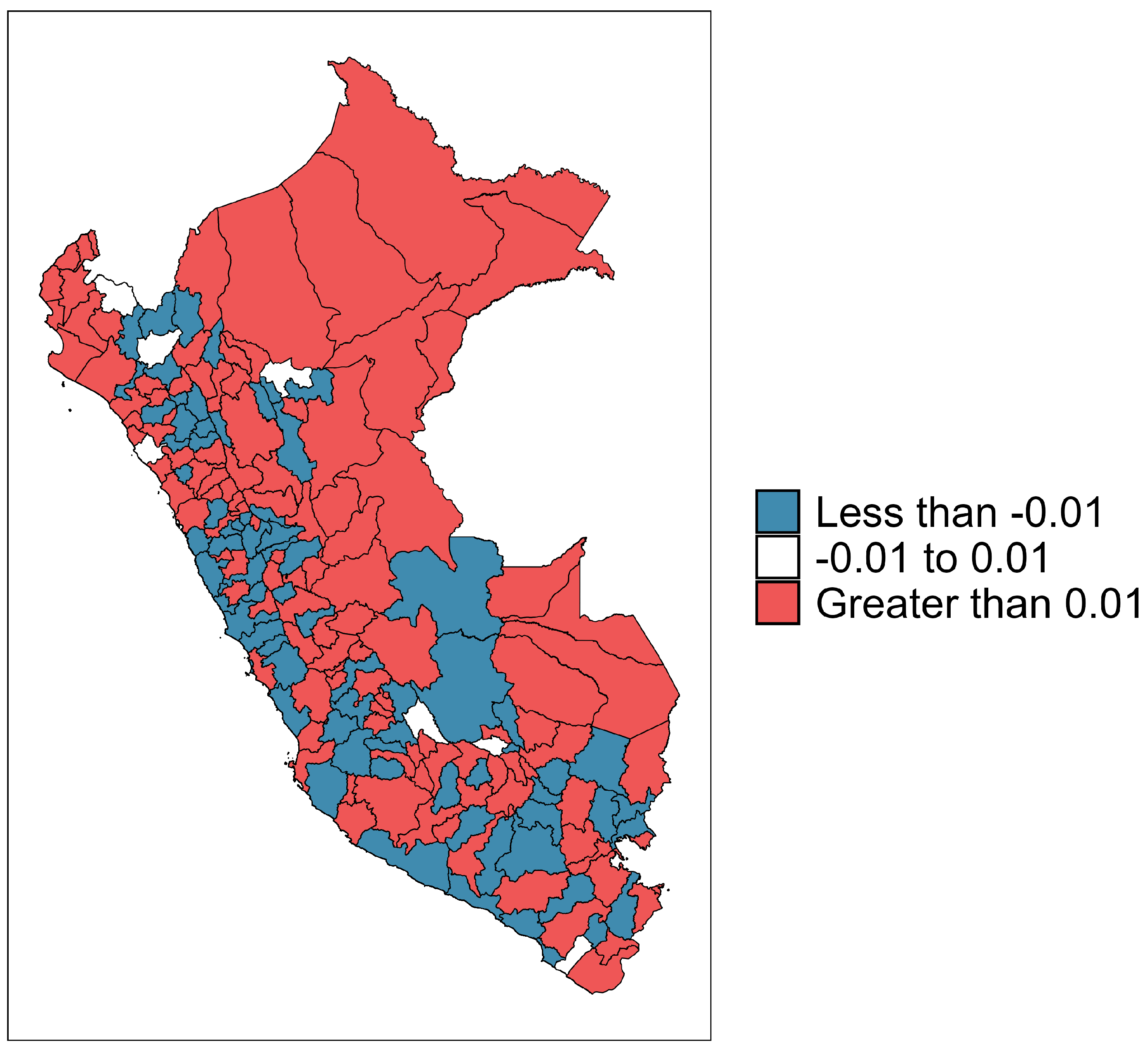
3.2. Bayesian Spatio-Temporal Modeling
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Supplementary Figures

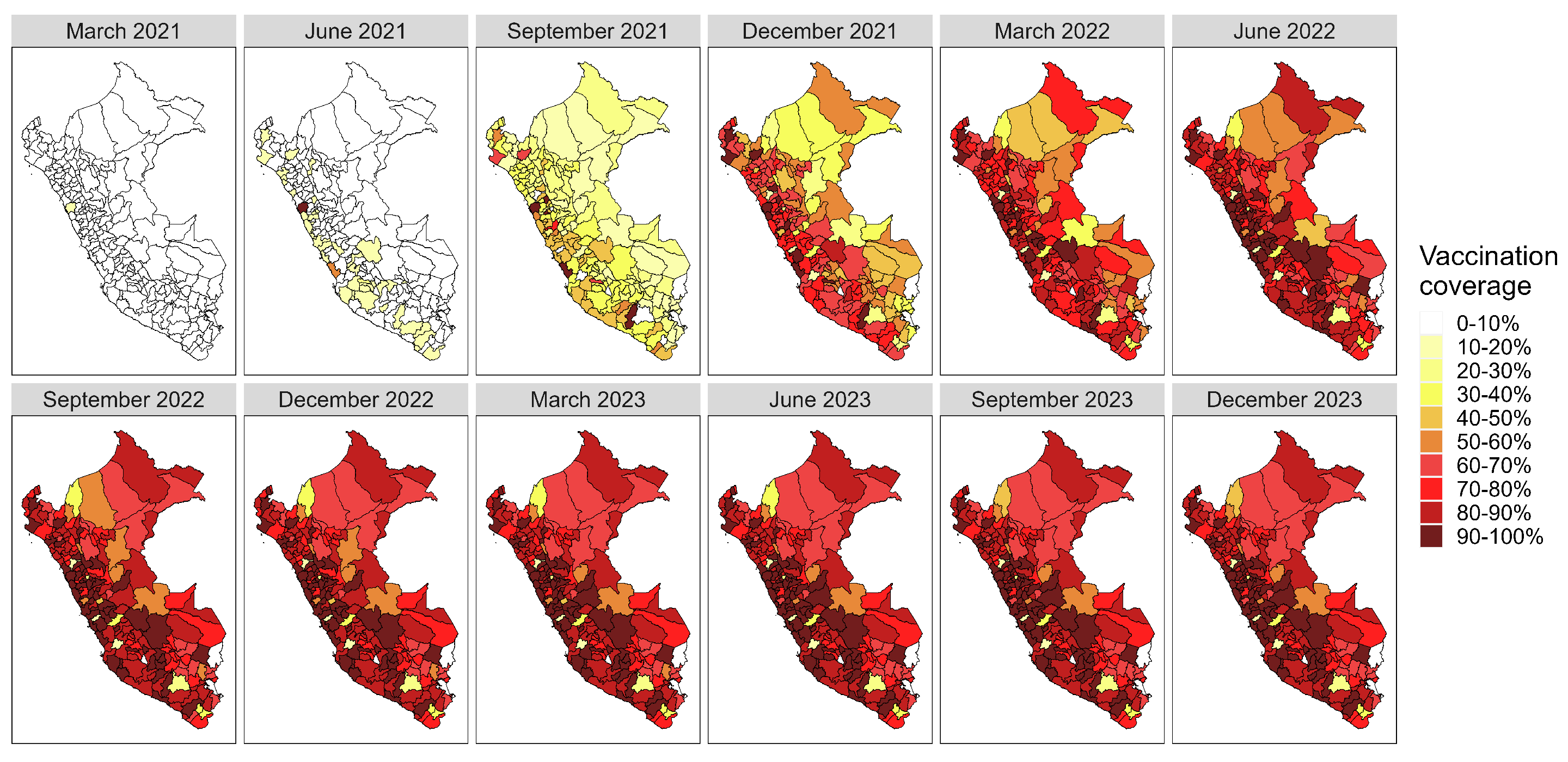
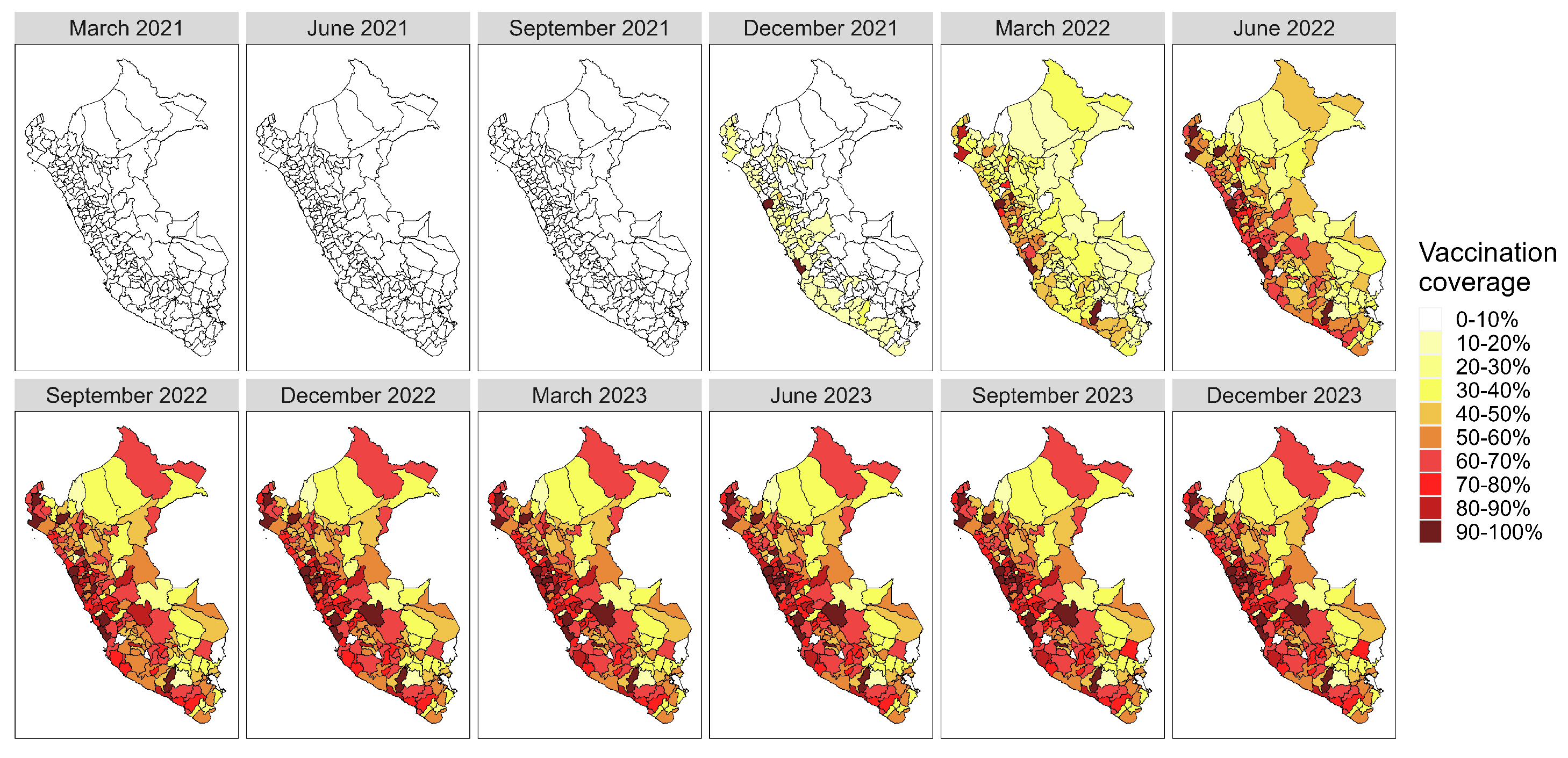

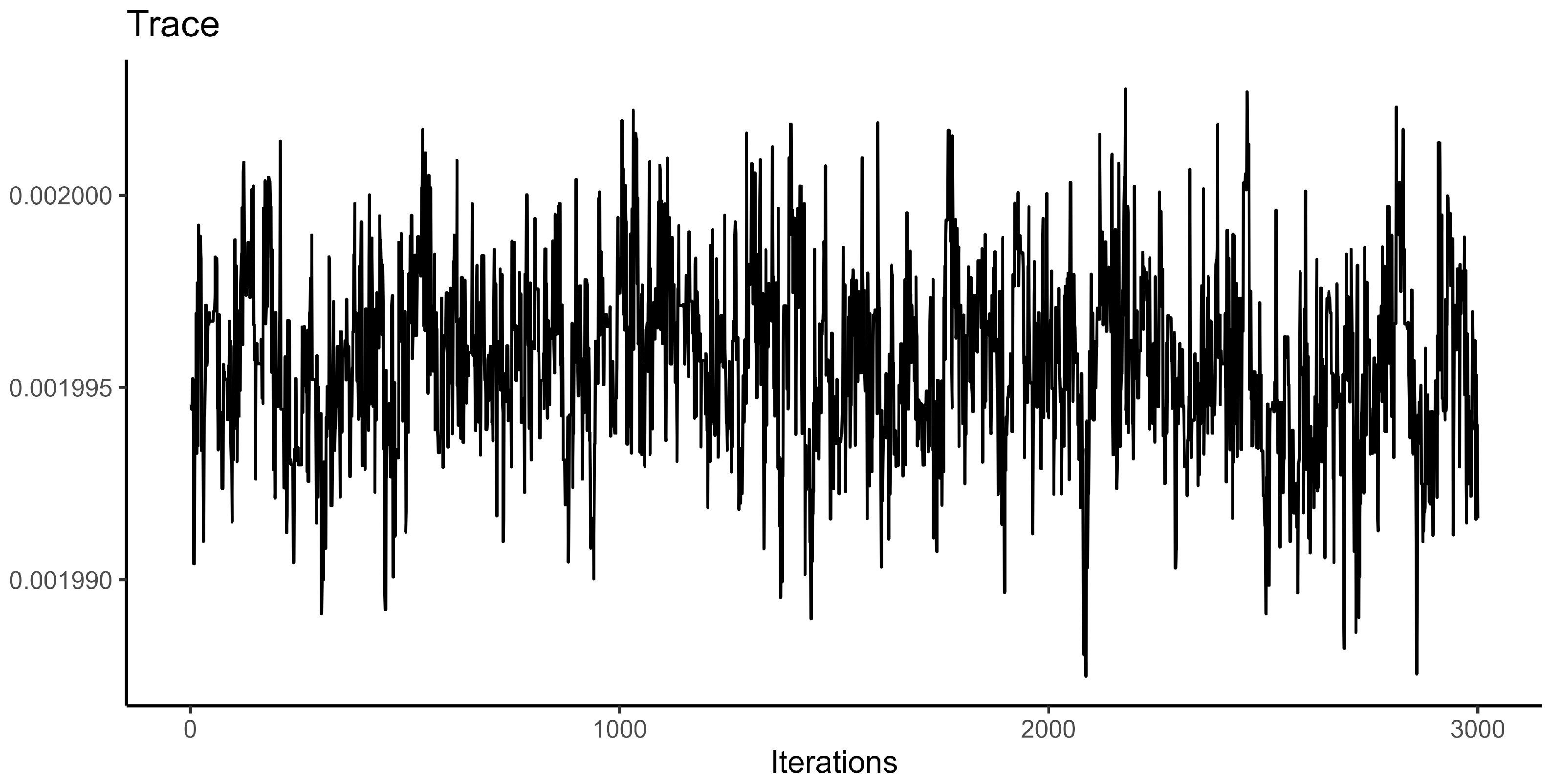
References
- Baloch, S.; Baloch, M.A.; Zheng, T.; Pei, X. The coronavirus disease 2019 (COVID-19) pandemic. Tohoku J. Exp. Med. 2020, 250, 271–278. [Google Scholar] [CrossRef] [PubMed]
- Ciotti, M.; Ciccozzi, M.; Terrinoni, A.; Jiang, W.C.; Wang, C.B.; Bernardini, S. The COVID-19 pandemic. Crit. Rev. Clin. Lab. Sci. 2020, 57, 365–388. [Google Scholar] [CrossRef] [PubMed]
- Abenavoli, L.; Gentile, I. COVID-19: Where We Are and Where We Are Going. Diseases 2023, 11, 40. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Risco, A.; Mejia, C.R.; Delgado-Zegarra, J.; Del-Aguila-Arcentales, S.; Arce-Esquivel, A.A.; Valladares-Garrido, M.J.; Del Portal, M.R.; Villegas, L.F.; Curioso, W.H.; Sekar, M.C.; et al. The Peru approach against the COVID-19 infodemic: Insights and strategies. Am. J. Trop. Med. Hyg. 2020, 103, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Schwalb, A.; Seas, C. The COVID-19 pandemic in Peru: What went wrong? Am. J. Trop. Med. Hyg. 2021, 104, 1176. [Google Scholar] [CrossRef] [PubMed]
- Karlinsky, A.; Kobak, D. Tracking excess mortality across countries during the COVID-19 pandemic with the World Mortality Dataset. eLife 2021, 10, e69336. [Google Scholar] [CrossRef] [PubMed]
- Ndwandwe, D.; Wiysonge, C.S. COVID-19 vaccines. Curr. Opin. Immunol. 2021, 71, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Lopez Bernal, J.; Andrews, N.; Gower, C.; Gallagher, E.; Simmons, R.; Thelwall, S.; Stowe, J.; Tessier, E.; Groves, N.; Dabrera, G.; et al. Effectiveness of COVID-19 vaccines against the B. 1.617. 2 (Delta) variant. N. Engl. J. Med. 2021, 385, 585–594. [Google Scholar] [CrossRef]
- Calina, D.; Docea, A.O.; Petrakis, D.; Egorov, A.M.; Ishmukhametov, A.A.; Gabibov, A.G.; Shtilman, M.I.; Kostoff, R.; Carvalho, F.; Vinceti, M.; et al. Towards effective COVID-19 vaccines: Updates, perspectives and challenges. Int. J. Mol. Med. 2020, 46, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Pardo-Figueroa, B.; Mindreau-Ganoza, E.; Reyes-Calderon, A.; Yufra, S.P.; Solorzano-Ortiz, I.M.; Donayre-Torres, A.J.; Antonini, C.; Renom, J.M.; Quispe, A.M.; Mota, C.R.; et al. Spatiotemporal surveillance of SARS-CoV-2 in the sewage of three major urban areas in Peru: Generating valuable data where clinical testing is extremely limited. Acs Es T Water 2022, 2, 2144–2157. [Google Scholar] [CrossRef]
- Wang, P.; Zheng, X.; Liu, H. Simulation and forecasting models of COVID-19 taking into account spatio-temporal dynamic characteristics: A review. Front. Public Health 2022, 10, 1033432. [Google Scholar] [CrossRef] [PubMed]
- Mingione, M.; Di Loro, P.A.; Farcomeni, A.; Divino, F.; Lovison, G.; Maruotti, A.; Lasinio, G.J. Spatio-temporal modelling of COVID-19 incident cases using Richards’ curve: An application to the Italian regions. Spat. Stat. 2022, 49, 100544. [Google Scholar] [CrossRef] [PubMed]
- Bartolucci, F.; Farcomeni, A. A spatio-temporal model based on discrete latent variables for the analysis of COVID-19 incidence. Spat. Stat. 2022, 49, 100504. [Google Scholar] [CrossRef] [PubMed]
- Briz-Redón, Á. The impact of modelling choices on modelling outcomes: A spatio-temporal study of the association between COVID-19 spread and environmental conditions in Catalonia (Spain). Stoch. Environ. Res. Risk Assess. 2021, 35, 1701–1713. [Google Scholar] [CrossRef] [PubMed]
- Sartorius, B.; Lawson, A.; Pullan, R. Modelling and predicting the spatio-temporal spread of COVID-19, associated deaths and impact of key risk factors in England. Sci. Rep. 2021, 11, 5378. [Google Scholar] [CrossRef] [PubMed]
- Gomes, D.S.; Andrade, L.A.; Ribeiro, C.J.N.; Peixoto, M.; Lima, S.; Duque, A.; Cirilo, T.M.; Góes, M.; Lima, A.; Santos, M.; et al. Risk clusters of COVID-19 transmission in northeastern Brazil: Prospective space–time modelling. Epidemiol. Infect. 2020, 148, e188. [Google Scholar] [CrossRef] [PubMed]
- Pereira, C.A.d.B.; Nakamura, L.R.; Rodrigues, P.C. Naive statistical analyses for COVID-19: Application to data from Brazil and Italy. Rev. Bras. Biom. 2021, 39, 158–176. [Google Scholar] [CrossRef]
- Griffith, D.; Li, B. Spatial-temporal modeling of initial COVID-19 diffusion: The cases of the Chinese Mainland and Conterminous United States. Geo-Spat. Inf. Sci. 2021, 24, 340–362. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Ejima, K.; Kim, K.S.; Ludema, C.; Bento, A.I.; Iwanami, S.; Fujita, Y.; Ohashi, H.; Koizumi, Y.; Watashi, K.; Aihara, K.; et al. Estimation of the incubation period of COVID-19 using viral load data. Epidemics 2021, 35, 100454. [Google Scholar] [CrossRef]
- Men, K.; Li, Y.; Wang, X.; Zhang, G.; Hu, J.; Gao, Y.; Han, A.; Liu, W.; Han, H. Estimate the incubation period of coronavirus 2019 (COVID-19). Comput. Biol. Med. 2023, 158, 106794. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Lee, D.; Rushworth, A.; Napier, G. Spatio-temporal areal unit modeling in R with conditional autoregressive priors using the CARBayesST package. J. Stat. Softw. 2018, 84, 1–39. [Google Scholar] [CrossRef]
- Bernardinelli, L.; Clayton, D.; Pascutto, C.; Montomoli, C.; Ghislandi, M.; Songini, M. Bayesian analysis of space—Time variation in disease risk. Stat. Med. 1995, 14, 2433–2443. [Google Scholar] [CrossRef] [PubMed]
- Leroux, B.; Lei, X.; Breslow, N. Estimation of Disease Rates in Small Areas: A new Mixed Model for Spatial Dependence. In Statistical Models in Epidemiology, the Environment, and Clinical Trials; Bernado, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 179–191. [Google Scholar]
- Lee, D. A tutorial on spatio-temporal disease risk modelling in R using Markov chain Monte Carlo simulation and the CARBayesST package. Spat. Spatio-Temporal Epidemiol. 2020, 34, 100353. [Google Scholar] [CrossRef] [PubMed]
- Geweke, J. Evaluating the Accuracy of Sampling-Based Approaches to the Calculation of Posterior Moments. In Bayesian Statistics; Bernado, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Oxford University Press: Oxford, UK, 1992; Volume 4. [Google Scholar]
- Ganesan, S.; Subramani, D. Spatio-temporal predictive modeling framework for infectious disease spread. Sci. Rep. 2021, 11, 6741. [Google Scholar] [CrossRef] [PubMed]
- López-Gonzales, J.L.; Gómez Lamus, A.M.; Torres, R.; Canas Rodrigues, P.; Salas, R. Self-Organizing Topological Multilayer Perceptron: A Hybrid Method to Improve the Forecasting of Extreme Pollution Values. Stats 2023, 6, 1241–1259. [Google Scholar] [CrossRef]
- Solci, C.C.; Reisen, V.A.; Rodrigues, P.C. Robust local bootstrap for weakly stationary time series in the presence of additive outliers. Stoch. Environ. Res. Risk Assess. 2023, 37, 2977–2992. [Google Scholar] [CrossRef]
- da Silva, K.L.S.; López-Gonzales, J.L.; Turpo-Chaparro, J.E.; Tocto-Cano, E.; Rodrigues, P.C. Spatio-temporal visualization and forecasting of PM 10 in the Brazilian state of Minas Gerais. Sci. Rep. 2023, 13, 3269. [Google Scholar] [CrossRef] [PubMed]
- Aubrecht, C.; Fuchs, S.; Neuhold, C. Spatio-temporal aspects and dimensions in integrated disaster risk management. Nat. Hazards 2013, 68, 1205–1216. [Google Scholar] [CrossRef]
- Awe, O.O.; Mahmoudvand, R.; Rodrigues, P.C. Non-negative time series reconstruction via singular spectrum analysis: A case study of precipitation dynamics in Nigeria. Fluct. Noise Lett. 2020, 19, 2050045. [Google Scholar] [CrossRef]
- Oliveira Filho, F.M.; Guedes, E.F.; Rodrigues, P.C. Networks analysis of Brazilian climate data based on the DCCA cross-correlation coefficient. PLoS ONE 2023, 18, e0290838. [Google Scholar] [CrossRef] [PubMed]
- Laurini, M.P. A spatio-temporal approach to estimate patterns of climate change. Environmetrics 2019, 30, e2542. [Google Scholar] [CrossRef]

| Parameter | Posterior | 2.5th Perc. | 97.5th Perc. | % Accept. | Effective | Geweke |
|---|---|---|---|---|---|---|
| Mean | Samples | |||||
| Intercept | 0.0722 | 0.0657 | 0.0789 | 13 | 128 | −0.3 |
| 0.0020 | 0.0020 | 0.0020 | 13 | 285 | 0.4 | |
| −0.1354 | −0.1462 | −0.1243 | 13 | 105 | −0.1 | |
| −0.4078 | −0.4334 | −0.3808 | 13 | 105 | −0.1 | |
| −0.1337 | −0.1535 | −0.1148 | 38 | 2263 | −1.4 | |
| 0.0888 | 0.0675 | 0.1228 | 100 | 1610 | −0.2 | |
| 0.1506 | 0.1124 | 0.2063 | 100 | 1907 | 0.1 | |
| 0.0335 | 0.0010 | 0.1171 | 41.6 | 1523 | 0.1 | |
| 0.0287 | 0.0008 | 0.1003 | 43.2 | 1524 | −0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galarza, C.R.C.; Sánchez, O.N.D.; Pimentel, J.S.; Bulhões, R.; López-Gonzales, J.L.; Rodrigues, P.C. Bayesian Spatio-Temporal Modeling of the Dynamics of COVID-19 Deaths in Peru. Entropy 2024, 26, 474. https://doi.org/10.3390/e26060474
Galarza CRC, Sánchez OND, Pimentel JS, Bulhões R, López-Gonzales JL, Rodrigues PC. Bayesian Spatio-Temporal Modeling of the Dynamics of COVID-19 Deaths in Peru. Entropy. 2024; 26(6):474. https://doi.org/10.3390/e26060474
Chicago/Turabian StyleGalarza, César Raúl Castro, Omar Nolberto Díaz Sánchez, Jonatha Sousa Pimentel, Rodrigo Bulhões, Javier Linkolk López-Gonzales, and Paulo Canas Rodrigues. 2024. "Bayesian Spatio-Temporal Modeling of the Dynamics of COVID-19 Deaths in Peru" Entropy 26, no. 6: 474. https://doi.org/10.3390/e26060474
APA StyleGalarza, C. R. C., Sánchez, O. N. D., Pimentel, J. S., Bulhões, R., López-Gonzales, J. L., & Rodrigues, P. C. (2024). Bayesian Spatio-Temporal Modeling of the Dynamics of COVID-19 Deaths in Peru. Entropy, 26(6), 474. https://doi.org/10.3390/e26060474








