The Application of Pinch Technology to a Novel Closed-Loop Spray Drying System with a Condenser and Reheater
Abstract
:1. Introduction
2. Materials and Methods
2.1. Modelling of Spray Dryer
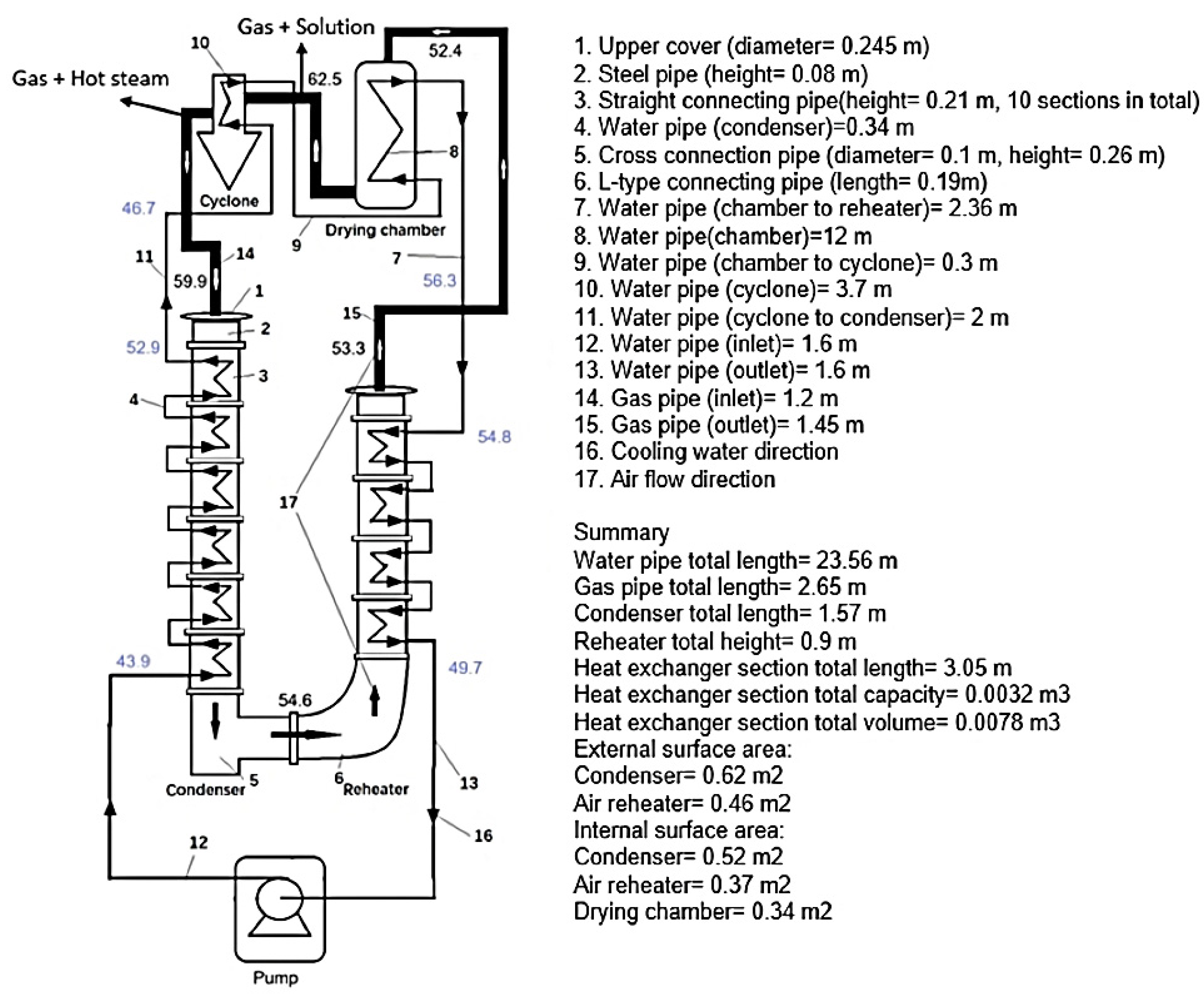
2.2. Experimental Setup
2.3. Operating Conditions and Parameters
2.4. Preliminary Pinch Analysis Information
3. Results
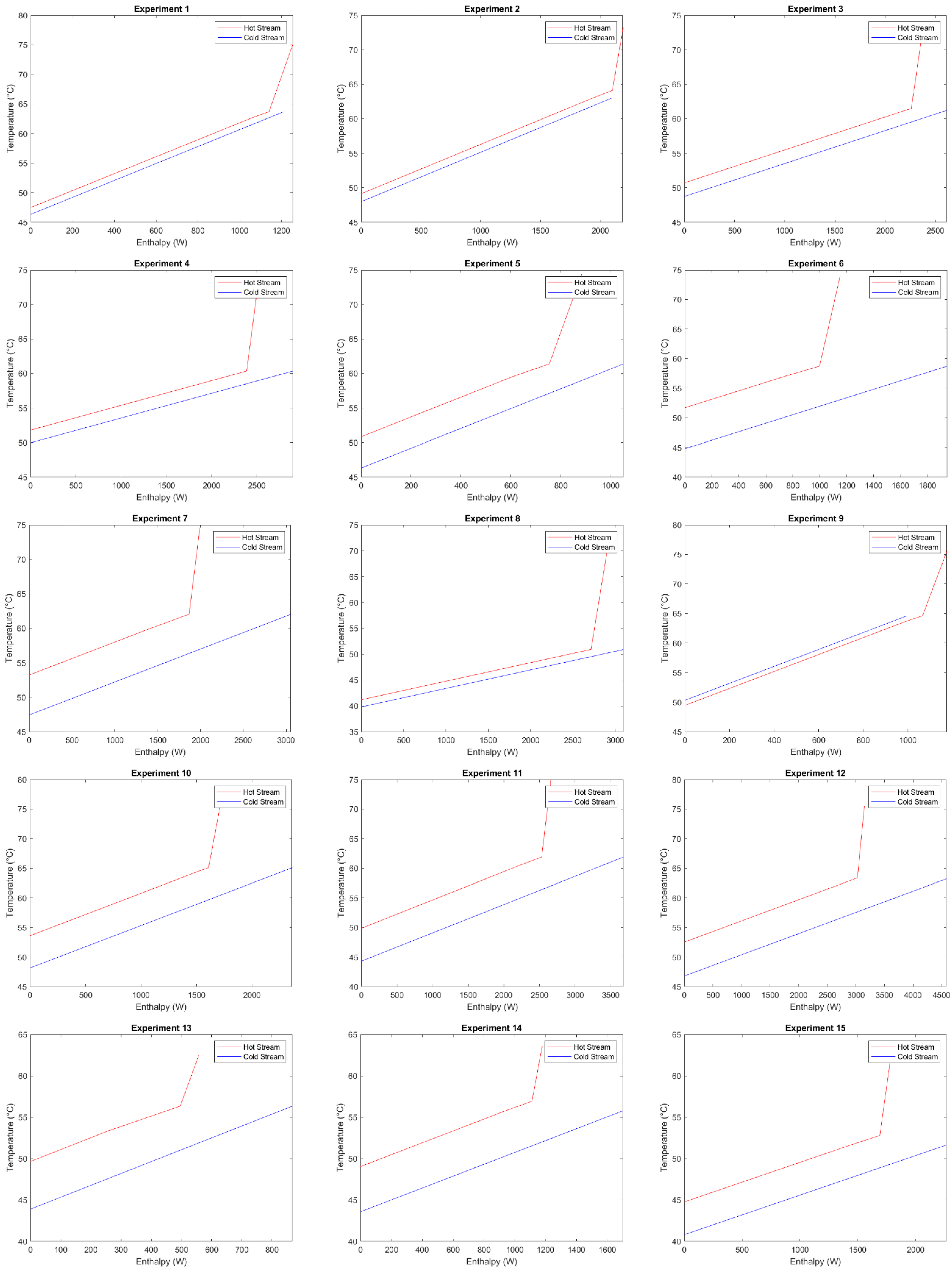
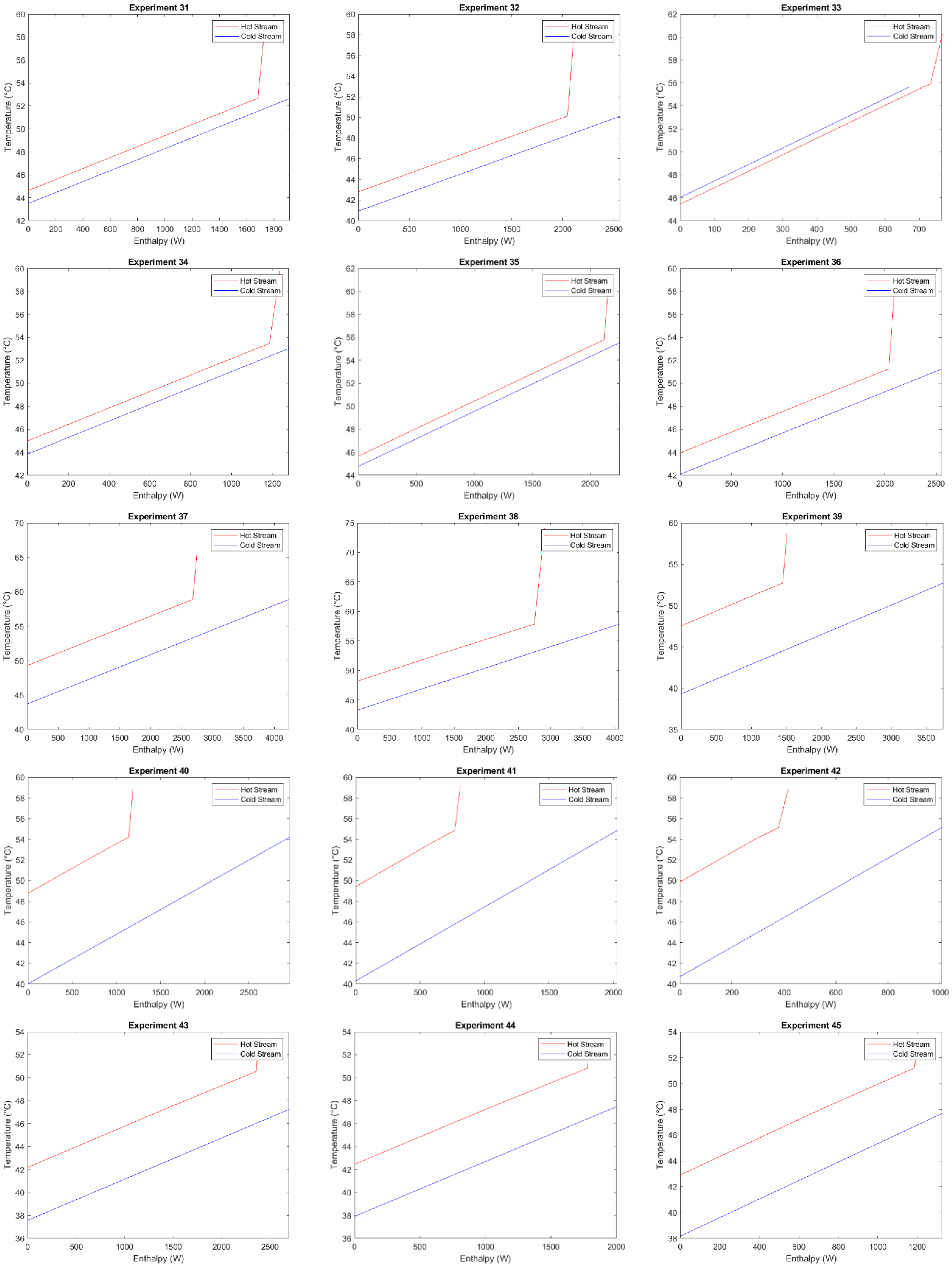
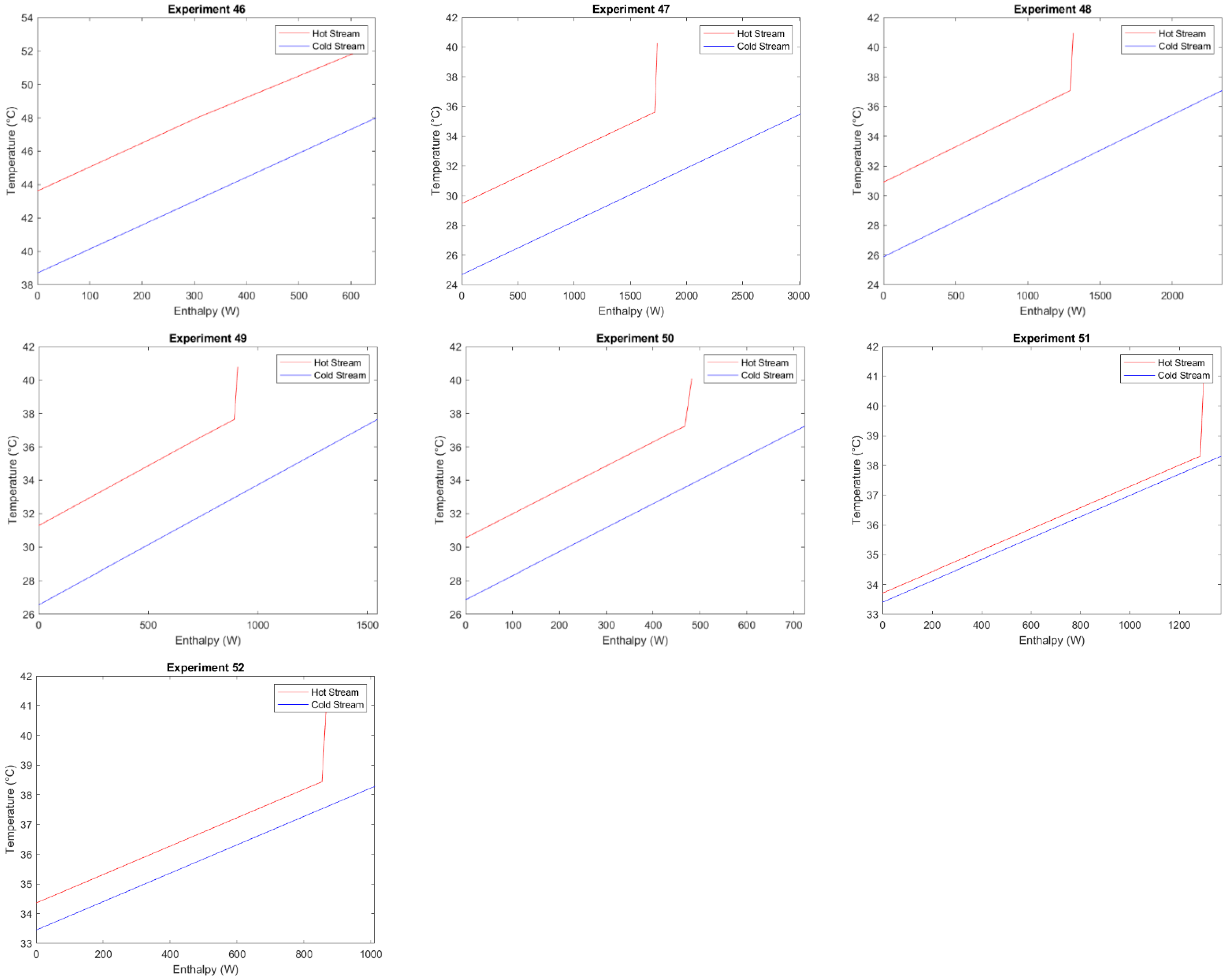
3.1. Sample Data and Typical Pinch Analysis
3.2. Pinch Analysis for All Data and Approach Temperatures
4. Discussion
4.1. Approach Temperature and Heat-Transfer Performance
4.2. Comparison with Existing Studies
4.3. Future Research Suggestions and Prospects for Practical Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Run | Aspirator m/s | Pump Flow mL/min | Water Flow L/min | Spray Dryer °C | Dryer Out °C | Condenser in (Dry) °C | Condenser In (Wet) °C | Condenser Out (Dry) °C | Condenser Out (Wet) °C | Reheater out (Dry) °C | Reheater out (Wet) °C | Dryer Return °C | Water Condenser in °C | Water Condenser Out °C | Water Cyclone in °C | Water Cyclone Out °C | Reheater in °C | Reheater Out °C | Ambient °C | Solid Conc. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.6 | 2.5 | 1 | 200 | 75.1716 | 71.5650 | 69.5969 | 63.2492 | 60.7077 | 62.7212 | 59.8997 | 59.7385 | 46.3419 | 48.7322 | 46.8536 | 63.6960 | 61.3804 | 47.4942 | 23 | 0 |
| 2 | 6.6 | 2.5 | 2 | 200 | 73.2676 | 71.0983 | 70.0348 | 65.2042 | 60.9506 | 64.1115 | 56.0566 | 62.8647 | 47.9838 | 51.5853 | 50.2930 | 63.0232 | 62.6006 | 49.1362 | 23 | 0 |
| 3 | 6.6 | 2.5 | 3 | 200 | 73.0557 | 70.0414 | 69.2088 | 62.4383 | 58.5395 | 61.4970 | 54.7905 | 55.0064 | 48.7362 | 53.3926 | 51.2943 | 61.2199 | 60.8099 | 50.7123 | 23 | 0 |
| 4 | 6.6 | 2.5 | 4 | 200 | 73.7805 | 69.5490 | 68.4137 | 61.6641 | 60.1421 | 60.1850 | 58.5497 | 57.1121 | 49.9603 | 54.1536 | 52.8001 | 60.3432 | 59.1038 | 51.7962 | 23 | 0 |
| 5 | 6.6 | 2.5 | 1 | 200 | 74.4379 | 72.7546 | 66.2832 | 61.9347 | 60.5871 | 59.5908 | 53.6764 | 53.8572 | 46.3158 | 52.0430 | 49.4764 | 61.3903 | 61.1379 | 50.8397 | 23 | 0 |
| 6 | 6.6 | 2.5 | 2 | 200 | 74.0747 | 72.5767 | 65.4560 | 59.8542 | 58.4660 | 57.0368 | 51.3401 | 45.7998 | 44.7938 | 51.1428 | 49.2957 | 58.7424 | 55.5523 | 51.7058 | 23 | 0 |
| 7 | 6.6 | 2.5 | 3 | 200 | 74.5935 | 72.9138 | 66.3253 | 62.4347 | 60.9557 | 59.9065 | 54.2300 | 48.2158 | 47.4468 | 53.9761 | 52.8337 | 62.0548 | 60.6574 | 53.2377 | 23 | 0 |
| 8 | 6.6 | 2.5 | 4 | 200 | 72.4710 | 70.8197 | 68.3685 | 53.1593 | 51.6917 | 50.4036 | 45.9238 | 41.4590 | 39.8112 | 45.5723 | 44.1722 | 50.9115 | 51.8605 | 41.2088 | 23 | 0 |
| 9 | 6.6 | 2.5 | 1 | 200 | 75.6280 | 72.8485 | 68.3470 | 64.5862 | 56.2058 | 63.7678 | 54.1171 | 62.7215 | 50.3387 | 53.9736 | 51.8090 | 64.6282 | 63.3372 | 49.4757 | 23 | 0 |
| 10 | 6.6 | 2.5 | 2 | 200 | 75.9942 | 73.2409 | 68.7054 | 65.1826 | 56.7303 | 64.3810 | 56.4642 | 63.3208 | 48.1746 | 54.3728 | 52.4255 | 65.0997 | 63.4728 | 53.6270 | 23 | 0 |
| 11 | 6.6 | 2.5 | 3 | 200 | 74.9366 | 72.4010 | 67.3160 | 62.0967 | 54.1391 | 60.4718 | 52.3614 | 60.2352 | 44.3232 | 53.9788 | 53.1835 | 61.9069 | 61.2913 | 49.8882 | 23 | 0 |
| 12 | 6.6 | 2.5 | 4 | 200 | 75.5303 | 72.5411 | 68.6941 | 64.4329 | 57.1152 | 63.3840 | 55.7056 | 62.0126 | 46.8143 | 53.0367 | 51.0812 | 63.2462 | 63.5067 | 52.5463 | 23 | 0 |
| 13 | 6.6 | 2.5 | 1 | 150 | 62.4818 | 59.8986 | 58.4787 | 54.5915 | 52.7616 | 53.3468 | 51.7184 | 52.3748 | 43.9004 | 52.8560 | 46.7391 | 56.3396 | 54.8420 | 49.6587 | 23 | 0 |
| 14 | 6.6 | 2.5 | 2 | 150 | 63.5980 | 60.9155 | 60.1536 | 57.3471 | 55.0795 | 56.9267 | 51.8611 | 56.4997 | 43.5770 | 52.3766 | 46.4599 | 55.7672 | 54.2420 | 49.0446 | 23 | 0 |
| 15 | 6.6 | 2.5 | 3 | 150 | 62.3273 | 59.9560 | 58.2200 | 53.7477 | 50.7739 | 52.7936 | 49.9203 | 52.3815 | 40.8085 | 46.3682 | 44.8120 | 51.6500 | 50.2093 | 44.7691 | 23 | 0 |
| 16 | 6.6 | 2.5 | 4 | 150 | 65.1282 | 62.5910 | 62.5837 | 61.1674 | 59.9958 | 59.3121 | 59.0479 | 57.2354 | 43.2633 | 46.4472 | 45.3751 | 51.2969 | 50.3529 | 45.7208 | 23 | 0 |
| 17 | 6.6 | 2.5 | 1 | 150 | 64.7488 | 63.0570 | 59.0870 | 56.3066 | 49.4585 | 55.0577 | 47.0135 | 54.2013 | 43.5524 | 46.6839 | 44.7374 | 54.8074 | 55.0495 | 44.2170 | 23 | 0 |
| 18 | 6.6 | 2.5 | 2 | 150 | 63.7057 | 62.3226 | 58.1949 | 53.7238 | 47.1978 | 52.5861 | 43.0198 | 50.2714 | 42.2570 | 46.3626 | 45.0676 | 52.2475 | 51.6151 | 44.8941 | 23 | 0 |
| 19 | 6.6 | 2.5 | 3 | 150 | 63.9824 | 62.7074 | 53.5206 | 58.6963 | 50.8856 | 54.8860 | 48.6885 | 54.1493 | 43.1828 | 47.0230 | 46.2847 | 53.3903 | 51.2280 | 43.4638 | 23 | 0 |
| 20 | 6.6 | 2.5 | 4 | 150 | 60.9944 | 59.8292 | 55.6201 | 43.6803 | 38.0877 | 41.9691 | 35.8439 | 41.0740 | 35.5947 | 38.5845 | 37.6436 | 42.3927 | 42.1432 | 35.8157 | 23 | 0 |
| 21 | 6.6 | 2.5 | 1 | 150 | 64.3330 | 62.1136 | 60.3219 | 60.1368 | 52.4636 | 58.6439 | 50.8940 | 58.0908 | 43.0850 | 52.0906 | 49.5797 | 58.7382 | 58.7667 | 50.4560 | 23 | 0 |
| 22 | 6.6 | 2.5 | 2 | 150 | 64.5907 | 62.0912 | 60.4948 | 59.8218 | 52.0853 | 58.8620 | 51.1193 | 58.0709 | 42.0560 | 49.5240 | 49.4595 | 59.1631 | 58.4987 | 51.3731 | 23 | 0 |
| 23 | 6.6 | 2.5 | 3 | 150 | 64.3372 | 61.9280 | 60.3121 | 59.4930 | 52.2952 | 58.5138 | 51.3354 | 57.8387 | 43.0070 | 49.3454 | 49.1745 | 58.8703 | 57.8698 | 49.9273 | 23 | 0 |
| 24 | 6.6 | 2.5 | 4 | 150 | 64.8557 | 62.3371 | 60.6978 | 59.9265 | 53.0794 | 59.1275 | 52.2994 | 58.2776 | 43.5429 | 49.8127 | 49.0696 | 59.4424 | 58.5646 | 50.1417 | 23 | 0 |
| 25 | 3.7 | 4.8 | 1 | 150 | 43.0610 | 42.0934 | 40.3255 | 40.1900 | 38.1705 | 40.2316 | 37.5786 | 39.0654 | 33.8959 | 37.1251 | 35.1198 | 40.0699 | 38.0944 | 34.7726 | 23 | 0 |
| 26 | 3.7 | 4.8 | 2 | 150 | 42.4005 | 41.4332 | 39.6324 | 39.5595 | 38.1670 | 39.2535 | 37.3231 | 39.3341 | 33.2073 | 34.7687 | 34.3833 | 39.1461 | 37.4963 | 33.5128 | 23 | 0 |
| 27 | 3.7 | 4.8 | 3 | 150 | 41.2514 | 40.1174 | 38.5030 | 38.2831 | 37.3100 | 38.3046 | 36.0507 | 37.1052 | 32.4036 | 34.2982 | 33.3714 | 38.4294 | 37.0754 | 34.3952 | 23 | 0 |
| 28 | 3.7 | 4.8 | 4 | 150 | 41.1735 | 40.0006 | 38.2505 | 37.9444 | 36.0789 | 37.8402 | 35.8396 | 37.2014 | 32.4063 | 34.9469 | 33.7657 | 37.9237 | 36.2974 | 34.1599 | 23 | 0 |
| 29 | 5.6 | 7 | 1 | 150 | 59.2081 | 57.4708 | 59.3151 | 54.4179 | 53.6905 | 54.7271 | 51.8439 | 53.1262 | 45.7232 | 48.2874 | 47.4704 | 55.2689 | 51.1556 | 45.1504 | 23 | 0 |
| 30 | 5.6 | 7 | 2 | 150 | 59.3290 | 57.1404 | 59.5271 | 55.7261 | 53.5567 | 54.6225 | 51.7653 | 52.5403 | 44.4190 | 48.1995 | 47.3811 | 55.1818 | 50.5180 | 45.3199 | 23 | 0 |
| 31 | 5.6 | 7 | 3 | 150 | 58.6593 | 57.3873 | 58.0530 | 53.2880 | 51.1264 | 52.3019 | 49.7926 | 50.3541 | 43.4999 | 46.1538 | 45.4126 | 52.6616 | 48.6706 | 44.6377 | 23 | 0 |
| 32 | 5.6 | 7 | 4 | 150 | 58.0039 | 56.7561 | 56.4113 | 51.0477 | 48.7600 | 49.9113 | 46.8551 | 48.7583 | 40.9359 | 44.2051 | 43.3998 | 50.1217 | 47.0328 | 42.8005 | 23 | 0 |
| 33 | 5.6 | 7 | 1 | 150 | 60.2479 | 60.0823 | 58.6729 | 55.5879 | 54.8087 | 55.9241 | 52.9660 | 54.3096 | 46.0346 | 48.5657 | 47.9026 | 55.6471 | 52.4247 | 45.4455 | 23 | 0 |
| 34 | 5.6 | 7 | 2 | 150 | 59.7842 | 59.1857 | 58.5144 | 54.4414 | 52.2584 | 53.4521 | 50.9325 | 51.5064 | 43.8380 | 46.5052 | 45.7740 | 53.0387 | 49.0197 | 44.9693 | 23 | 0 |
| 35 | 5.6 | 7 | 3 | 150 | 60.4843 | 60.6462 | 58.2358 | 56.8068 | 54.6468 | 55.7730 | 52.9022 | 53.6931 | 44.7731 | 48.5299 | 47.7378 | 55.5464 | 50.8544 | 45.6664 | 23 | 0 |
| 36 | 5.6 | 7 | 4 | 150 | 59.1500 | 57.8984 | 57.5606 | 52.1893 | 49.9024 | 51.0592 | 48.0026 | 49.9234 | 42.0854 | 45.3556 | 44.6207 | 51.2414 | 48.1909 | 43.9458 | 23 | 0 |
| 37 | 6.6 | 4.8 | 4 | 150 | 65.5202 | 63.5964 | 60.2444 | 59.4349 | 52.7282 | 58.5134 | 51.9039 | 57.5938 | 43.7100 | 49.3801 | 49.3509 | 58.8914 | 57.5729 | 49.2975 | 23 | 0.3 |
| 38 | 6.6 | 4.8 | 4 | 150 | 74.1482 | 70.8732 | 64.9347 | 55.3062 | 51.8788 | 52.9377 | 47.3341 | 52.6062 | 43.2956 | 48.5530 | 45.6755 | 57.8701 | 56.6894 | 48.2075 | 23 | 0.5 |
| 39 | 6.6 | 9 | 4 | 120 | 58.7008 | 55.3529 | 54.1977 | 52.1243 | 50.9580 | 52.1098 | 51.7835 | 49.2899 | 39.3090 | 44.8927 | 44.6517 | 52.7253 | 51.4744 | 47.5482 | 23 | 0 |
| 40 | 6.6 | 9 | 3 | 120 | 58.9906 | 56.5364 | 55.5239 | 54.1905 | 52.3673 | 53.2020 | 50.6812 | 52.9003 | 40.0378 | 45.9908 | 45.7216 | 54.2073 | 53.0120 | 48.8041 | 23 | 0 |
| 41 | 6.6 | 9 | 2 | 120 | 59.0826 | 57.0488 | 56.1272 | 54.8524 | 52.9781 | 53.7834 | 50.9993 | 53.0240 | 40.2975 | 46.7175 | 46.3749 | 54.8557 | 53.5224 | 49.4213 | 23 | 0 |
| 42 | 6.6 | 9 | 1 | 120 | 58.8236 | 57.3330 | 56.5013 | 55.2390 | 53.4838 | 53.9600 | 51.2352 | 52.7683 | 40.7103 | 46.7482 | 45.0560 | 55.1297 | 54.2785 | 49.8648 | 23 | 0 |
| 43 | 5.6 | 7 | 4 | 120 | 52.8293 | 52.5631 | 51.9299 | 50.8960 | 50.1603 | 50.5494 | 49.7287 | 49.2378 | 37.5746 | 44.2184 | 43.5480 | 47.2485 | 47.2162 | 42.1930 | 23 | 0 |
| 44 | 5.6 | 7 | 3 | 120 | 53.1210 | 52.6973 | 52.0626 | 51.0922 | 49.8989 | 50.8235 | 49.4071 | 50.3030 | 37.9161 | 44.4559 | 43.8870 | 47.4720 | 46.6733 | 42.4596 | 23 | 0 |
| 45 | 5.6 | 7 | 2 | 120 | 53.1719 | 52.8854 | 52.3538 | 51.3648 | 50.6249 | 51.2039 | 49.7381 | 50.2266 | 38.1805 | 44.2317 | 43.2023 | 47.6719 | 46.8098 | 42.9117 | 23 | 0 |
| 46 | 5.6 | 7 | 1 | 120 | 53.4273 | 53.5152 | 52.9259 | 52.0160 | 51.2489 | 51.9207 | 50.8454 | 50.3537 | 38.7065 | 45.2893 | 44.6410 | 47.9875 | 47.9033 | 43.6178 | 23 | 0 |
| 47 | 3.7 | 4.8 | 4 | 120 | 40.2615 | 39.0251 | 36.0683 | 37.7155 | 34.6997 | 35.6237 | 31.2515 | 35.3360 | 24.6923 | 32.6744 | 30.4618 | 35.5018 | 34.1155 | 29.4740 | 23 | 0 |
| 48 | 3.7 | 4.8 | 3 | 120 | 40.9498 | 39.6639 | 38.4730 | 37.3453 | 33.5291 | 37.0186 | 32.8360 | 36.7503 | 25.8874 | 32.1705 | 30.0846 | 37.0857 | 35.4825 | 30.9051 | 23 | 0 |
| 49 | 3.7 | 4.8 | 2 | 120 | 40.7862 | 39.4800 | 38.3624 | 37.4973 | 33.5539 | 36.3201 | 32.2930 | 36.5932 | 26.5587 | 32.2572 | 29.9923 | 37.6397 | 36.0107 | 31.2878 | 23 | 0 |
| 50 | 3.7 | 4.8 | 1 | 120 | 40.0784 | 38.7690 | 37.7959 | 37.3102 | 33.5756 | 36.8201 | 32.1513 | 36.0919 | 26.8681 | 33.4480 | 31.6668 | 37.2357 | 35.5271 | 30.5587 | 23 | 0 |
| 51 | 3.7 | 4.8 | 4 | 120 | 41.7119 | 40.4313 | 38.6167 | 38.7246 | 37.2602 | 38.1673 | 34.2688 | 37.0507 | 33.4071 | 36.2079 | 34.4072 | 38.3118 | 37.5670 | 33.7110 | 23 | 0 |
| 52 | 3.7 | 4.8 | 3 | 120 | 41.6239 | 40.2819 | 38.8122 | 38.4959 | 37.3783 | 38.4377 | 36.9453 | 37.1426 | 33.4491 | 36.4336 | 34.4005 | 38.2860 | 37.6939 | 34.3605 | 23 | 0 |
| 53 | 3.7 | 4.8 | 2 | 120 | 41.4106 | 39.9888 | 38.7140 | 38.3102 | 37.4186 | 38.4001 | 37.1410 | 36.9191 | 33.5626 | 36.4908 | 34.7835 | 38.2930 | 37.6616 | 34.3045 | 23 | 0 |
| 54 | 3.7 | 4.8 | 1 | 120 | 40.6386 | 39.2694 | 38.4597 | 38.1633 | 37.1657 | 37.7989 | 36.7037 | 36.4290 | 33.2502 | 36.3121 | 34.3388 | 38.0856 | 37.4039 | 33.8363 | 23 | 0 |

References
- Aghbashlo, M.; Kianmehr, M.H.; Samimi-Akhijahani, H. Influence of Drying Conditions on the Effective Moisture Diffusivity, Energy of Activation and Energy Consumption during the Thin-Layer Drying of Berberis Fruit (Berberidaceae). Energy Convers. Manag. 2008, 49, 2865–2871. [Google Scholar] [CrossRef]
- Nummer, B.A.; Brian, A. Historical Origins of Food Preservation. Ph.D. Thesis, National Center for Home Food Preservation, Athens, GA, USA, 2002. [Google Scholar]
- Mujumdar, A.S. Handbook of Industrial Drying, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Erbay, Z.; Koca, N.; Kaymak-Ertekin, F.; Ucuncu, M. Optimization of Spray Drying Process in Cheese Powder Production. Food Bioprod. Process. 2015, 93, 156–165. [Google Scholar] [CrossRef]
- Patel, S.K.; Bade, M.H. Energy Targeting and Process Integration of Spray Dryer with Heat Recovery Systems. Energy Convers. Manag. 2020, 221, 113148. [Google Scholar] [CrossRef]
- Pakowski, Z.; Druzdzel, A.; Drwiega, J. Validation of a Model of an Expanding Superheated Steam Flash Dryer for Cut Tobacco Based on Processing Data. Dry. Technol. 2004, 22, 45–57. [Google Scholar] [CrossRef]
- Van Heiningen, A.R.P.; Crotogino, R.H.; Douglas, W.J.M. An Experimental Study of the Falling Rate Period of Superheated Steam Impingement Drying of Paper. Dry. Technol. 1992, 10, 961–977. [Google Scholar] [CrossRef]
- Li, J.; Liang, Q.C.; Bennamoun, L. Superheated Steam Drying: Design Aspects, Energetic Performances, and Mathematical Modeling. Renew. Sustain. Energy Rev. 2016, 60, 1562–1583. [Google Scholar] [CrossRef]
- Linnhoff, B.; Alanis, F.J. Integration of a New Process Into an Existing Site: A Case Study in the Application of Pinch Technology. J. Eng. Gas. Turbine Power 1991, 113, 159–168. [Google Scholar] [CrossRef]
- Tan, R.R.; Sum Ng, D.K.; Yee Foo, D.C. Pinch Analysis Approach to Carbon-Constrained Planning for Sustainable Power Generation. J. Clean. Prod. 2009, 17, 940–944. [Google Scholar] [CrossRef]
- Dimian, A.C.; Bildea, C.S.; Kiss, A.A. Pinch Point Analysis. Comput. Aided Chem. Eng. 2014, 35, 525–564. [Google Scholar] [CrossRef]
- Di Pretoro, A.; Manenti, F. Spray Drying. In Non-Conventional Unit Operations; Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2020; pp. 65–74. [Google Scholar] [CrossRef]
- Johnson, P.W.; Langrish, T.A.G. Inversion Temperature and Pinch Analysis, Ways to Thermally Optimize Drying Processes. Dry. Technol. 2011, 29, 488–507. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Z.; Huang, S.; Li, Y. Process Integration Analysis and Improved Options for an MEA CO2 Capture System Based on the Pinch Analysis. Appl. Therm. Eng. 2015, 85, 214–224. [Google Scholar] [CrossRef]
- Langrish, T.A.G. Multi-Scale Mathematical Modelling of Spray Dryers. J. Food Eng. 2009, 93, 218–228. [Google Scholar] [CrossRef]
- Lei, Z.; Langrish, T. Energy and Exergy Analysis for a Laboratory-Scale Closed-Loop Spray Drying System: Experiments and Simulations. Dry. Technol. 2024. [Google Scholar] [CrossRef]
- B-290 Mini Spray Dryer Operation Manual 093001|Q En. Available online: https://www.scientificlabs.co.uk/handlers/libraryFiles.ashx?filename=Manuals_E_EVA4514_B.pdf (accessed on 18 September 2024).
- Ting, D. Thermofluids: From Nature to Engineering; Academic Press: Cambridge, MA, USA, 2022; pp. 1–397. [Google Scholar] [CrossRef]
- Integration, I.K.-P. Analysis and Process; Undefined. Key Concepts of Pinch Analysis. 2007. Available online: https://cir.nii.ac.jp./all?q=Key+Concepts+of+Pinch+Analysis&count=20&sortorder=0 (accessed on 18 September 2024).
- Kemp, I.C. Reducing Dryer Energy Use by Process Integration and Pinch Analysis. Dry. Technol. 2005, 23, 2089–2104. [Google Scholar] [CrossRef]
- Johnson, P.W.; Langrish, T.A.G. Interpreting Exergy Analysis as Applied to Spray Drying Systems. Int. J. Exergy 2020, 31, 120–149. [Google Scholar] [CrossRef]
- Serth, R.W.; Lestina, T.G. Process Heat Transfer: Principles, Applications and Rules of Thumb, 2nd ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Ficarella, A.; Laforgia, D. Energy Conservation in Alcohol Distillery with the Application of Pinch Technology. Energy Convers. Manag. 1999, 40, 1495–1514. [Google Scholar] [CrossRef]
- Harkin, T.; Hoadley, A.; Hooper, B. Reducing the Energy Penalty of CO2 Capture and Compression Using Pinch Analysis. J. Clean. Prod. 2010, 18, 857–866. [Google Scholar] [CrossRef]
- Kaviani, A.; Aslani, A.; Zahedi, R.; Ahmadi, H.; Malekli, M.R. A New Approach for Energy Optimization in Dairy Industry. Clean. Eng. Technol. 2022, 8, 100498. [Google Scholar] [CrossRef]
- Sarker, M.S.H.; Ibrahim, M.N.; Abdul Aziz, N.; Punan, M.S. Energy and Exergy Analysis of Industrial Fluidized Bed Drying of Paddy. Energy 2015, 84, 131–138. [Google Scholar] [CrossRef]
- Surendhar, A.; Sivasubramanian, V.; Vidhyeswari, D.; Deepanraj, B. Energy and Exergy Analysis, Drying Kinetics, Modeling and Quality Parameters of Microwave-Dried Turmeric Slices. J. Therm. Anal. Calorim. 2019, 136, 185–197. [Google Scholar] [CrossRef]
- Guo, S.; Xiao, Y.; Tian, W.; Zhang, Z. Energy and Exergy Analysis of a Novel Efficient Combined Process by Hydrothermal Degradation and Superheated Steam Drying of Degradable Organic Wastes. J. Therm. Sci. 2006, 15, 274–280. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Rafiee, S.; Madadlou, A. Energy and Exergy Analyses of the Spray Drying Process of Fish Oil Microencapsulation. Biosyst. Eng. 2012, 111, 229–241. [Google Scholar] [CrossRef]
- Amjad, W.; Hensel, O.; Munir, A.; Esper, A.; Sturm, B. Thermodynamic Analysis of Drying Process in a Diagonal-Batch Dryer Developed for Batch Uniformity Using Potato Slices. J. Food Eng. 2016, 169, 238–249. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Exergy as a Driver for Achieving Sustainability. Int. J. Green. Energy 2004, 1, 1–19. [Google Scholar] [CrossRef]
- Erbay, Z.; Hepbasli, A. Application of Conventional and Advanced Exergy Analyses to Evaluate the Performance of a Ground-Source Heat Pump (GSHP) Dryer Used in Food Drying. Energy Convers. Manag. 2014, 78, 499–507. [Google Scholar] [CrossRef]
- Johnson, P.W.; Langrish, T.A.G. Exergy Analysis of a Spray Dryer: Methods and Interpretations. Dry Technol. 2018, 36, 578–596. [Google Scholar] [CrossRef]
- Golman, B.; Julklang, W. Analysis of Heat Recovery from a Spray Dryer by Recirculation of Exhaust Air. Energy Convers. Manag. 2014, 88, 641–649. [Google Scholar] [CrossRef]
- Li, J.; Si, Z.; Han, D.; Hang, Z. Thermo-Economic Performance Enhancement in Batch Evaporation Process via Mechanical Vapor Recompression System Coupled with Steam Accumulator. Desalination 2022, 532, 115735. [Google Scholar] [CrossRef]

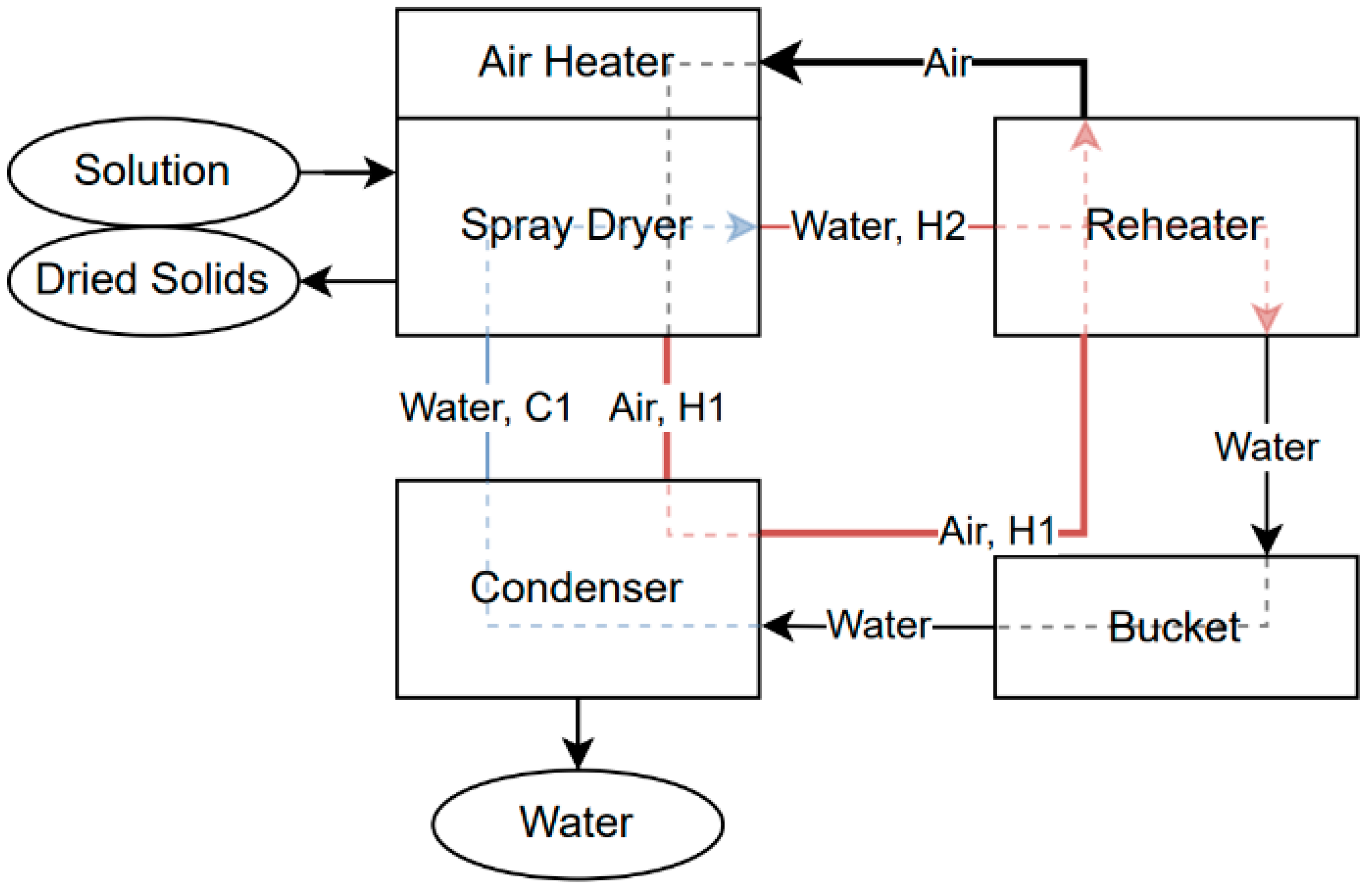
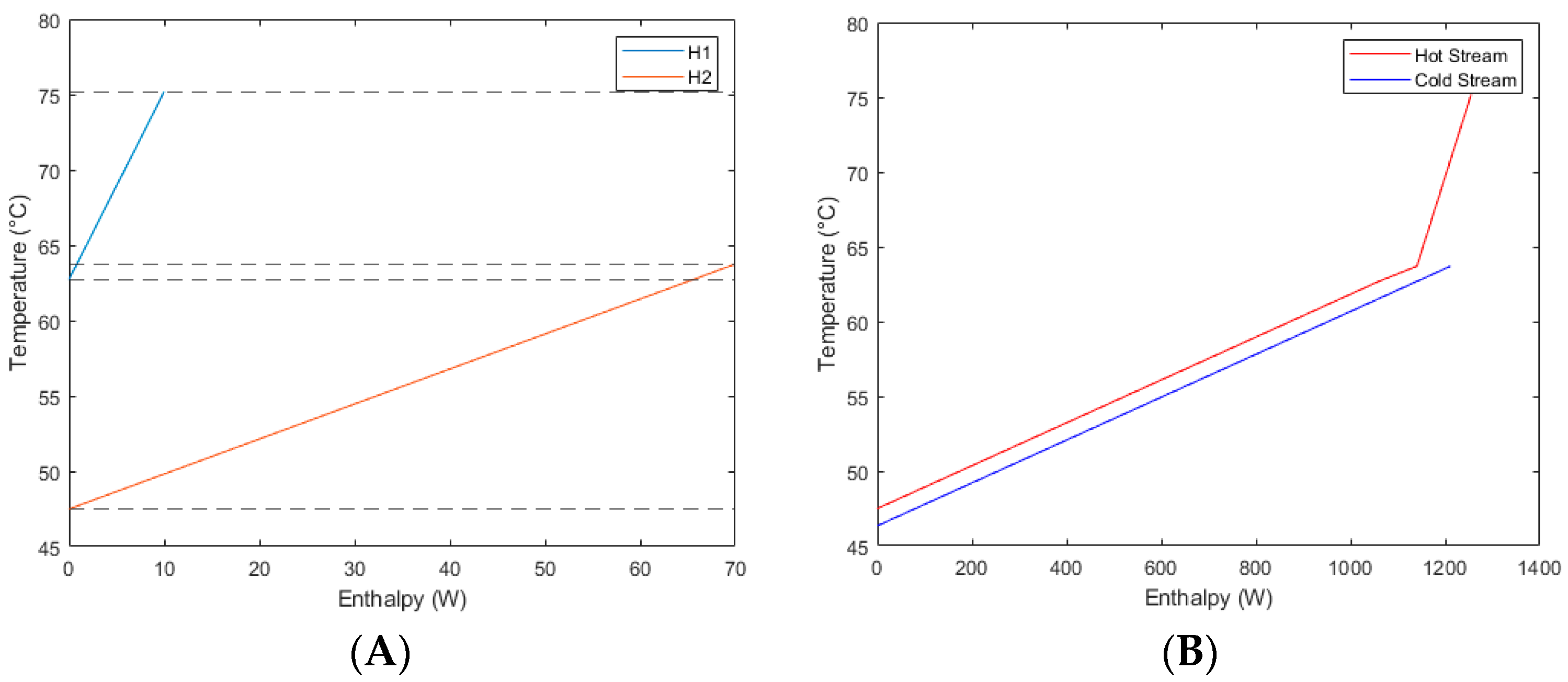
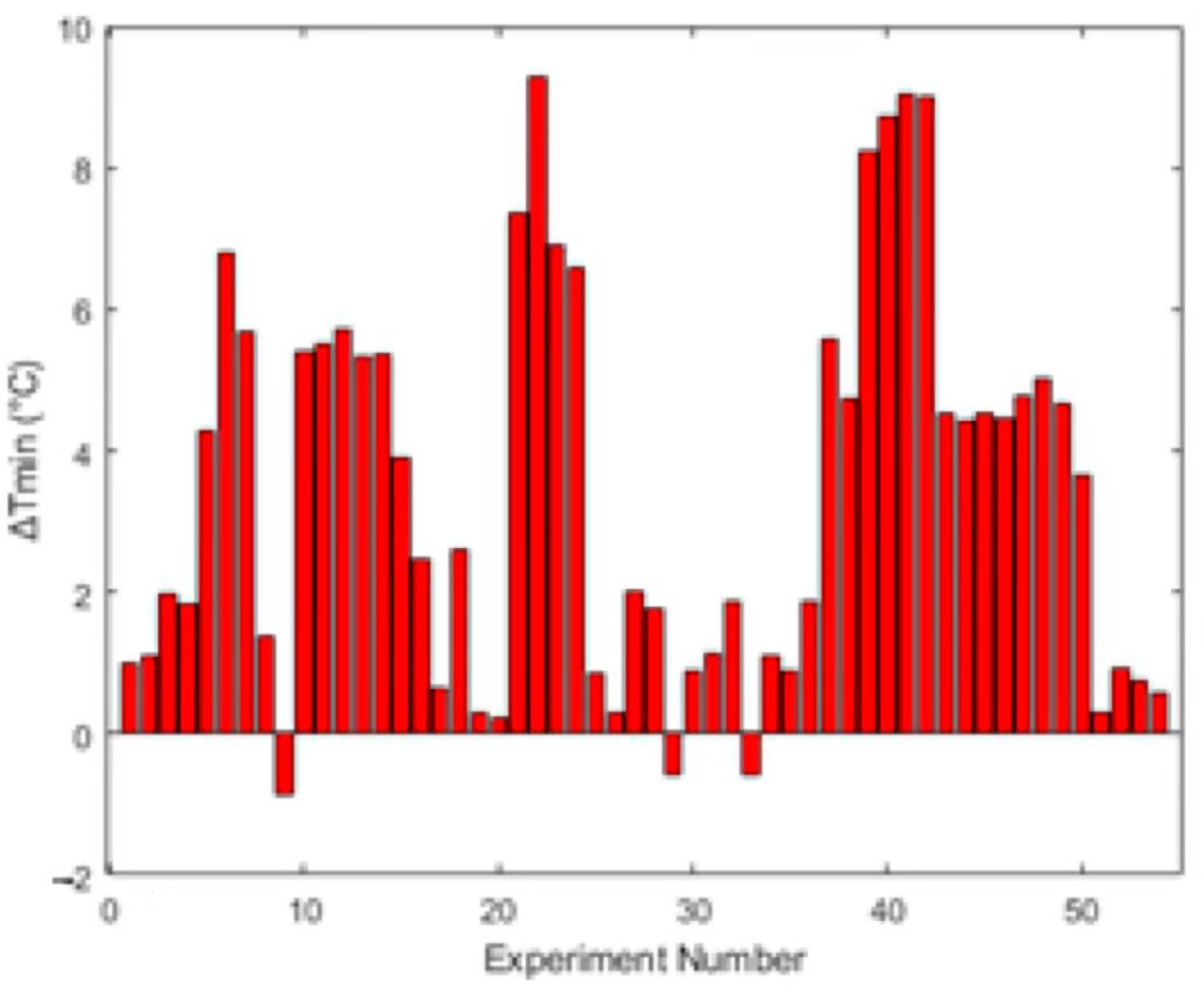
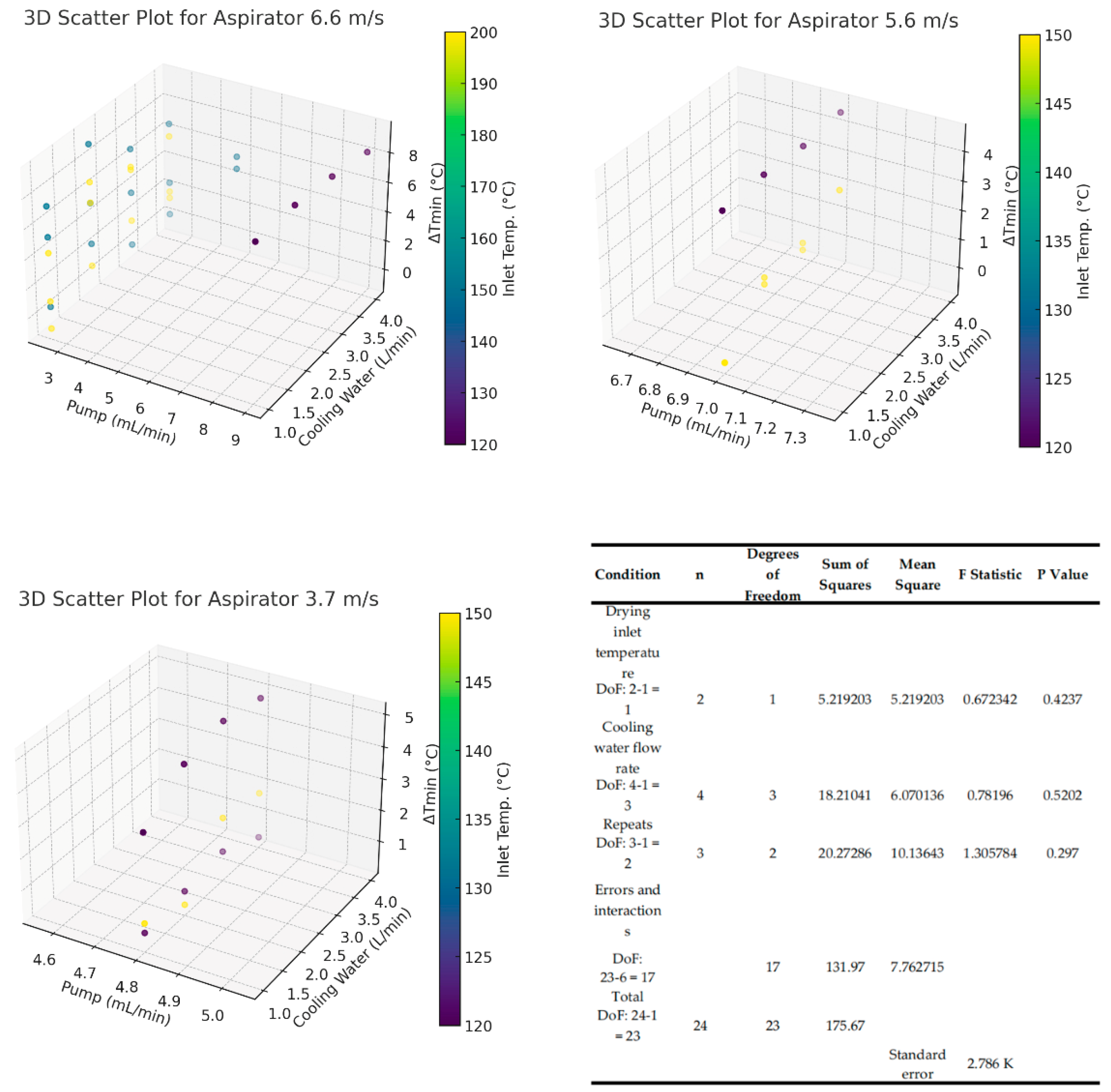
| Stream | Source Temperature (°C) | Target Temperature (°C) | Heat Capacity Rate (W/K) |
| H1 | 75.17 | 62.72 | 10 |
| H2 | 63.70 | 47.50 | 69.77 |
| C1 | 46.34 | 63.70 | 69.77 |
| Interval (°C) | Temperature Difference | Total Heat Cap Rate (W/K) | Heat Load (W) |
|---|---|---|---|
| 75.17–63.70 | 11.48 | 10 | 114.76 |
| 63.70–62.72 | 0.9748 | 79.77 | 77.75 |
| 62.72–47.50 | 15.23 | 69.77 | 1062.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; O’Neill, T.; Langrish, T. The Application of Pinch Technology to a Novel Closed-Loop Spray Drying System with a Condenser and Reheater. Entropy 2024, 26, 809. https://doi.org/10.3390/e26090809
Lei Z, O’Neill T, Langrish T. The Application of Pinch Technology to a Novel Closed-Loop Spray Drying System with a Condenser and Reheater. Entropy. 2024; 26(9):809. https://doi.org/10.3390/e26090809
Chicago/Turabian StyleLei, Zexin, Thomas O’Neill, and Timothy Langrish. 2024. "The Application of Pinch Technology to a Novel Closed-Loop Spray Drying System with a Condenser and Reheater" Entropy 26, no. 9: 809. https://doi.org/10.3390/e26090809
APA StyleLei, Z., O’Neill, T., & Langrish, T. (2024). The Application of Pinch Technology to a Novel Closed-Loop Spray Drying System with a Condenser and Reheater. Entropy, 26(9), 809. https://doi.org/10.3390/e26090809







