Thermodynamics of Morphogenesis: Beading and Branching Pattern Formation in Diffusion-Driven Salt Finger Plumes
Abstract
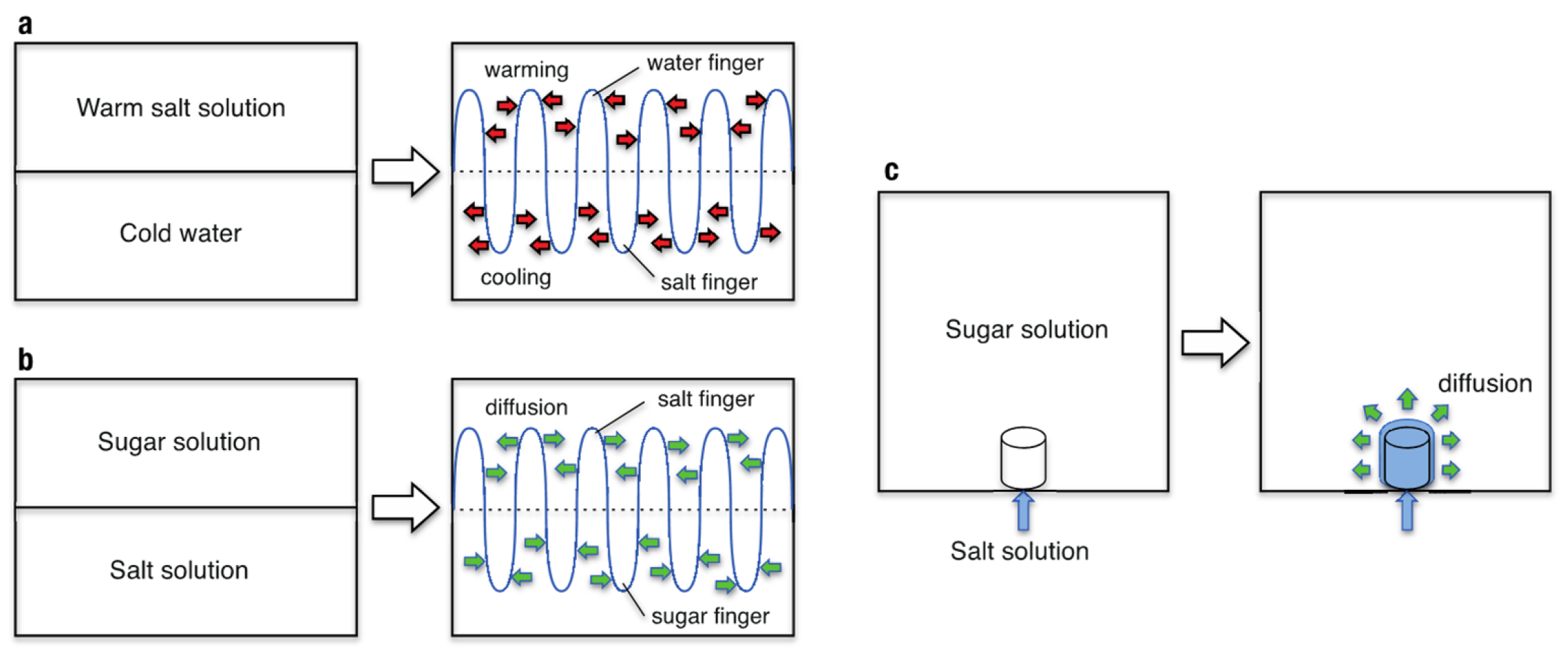
:1. Introduction
2. Results
3. Discussion
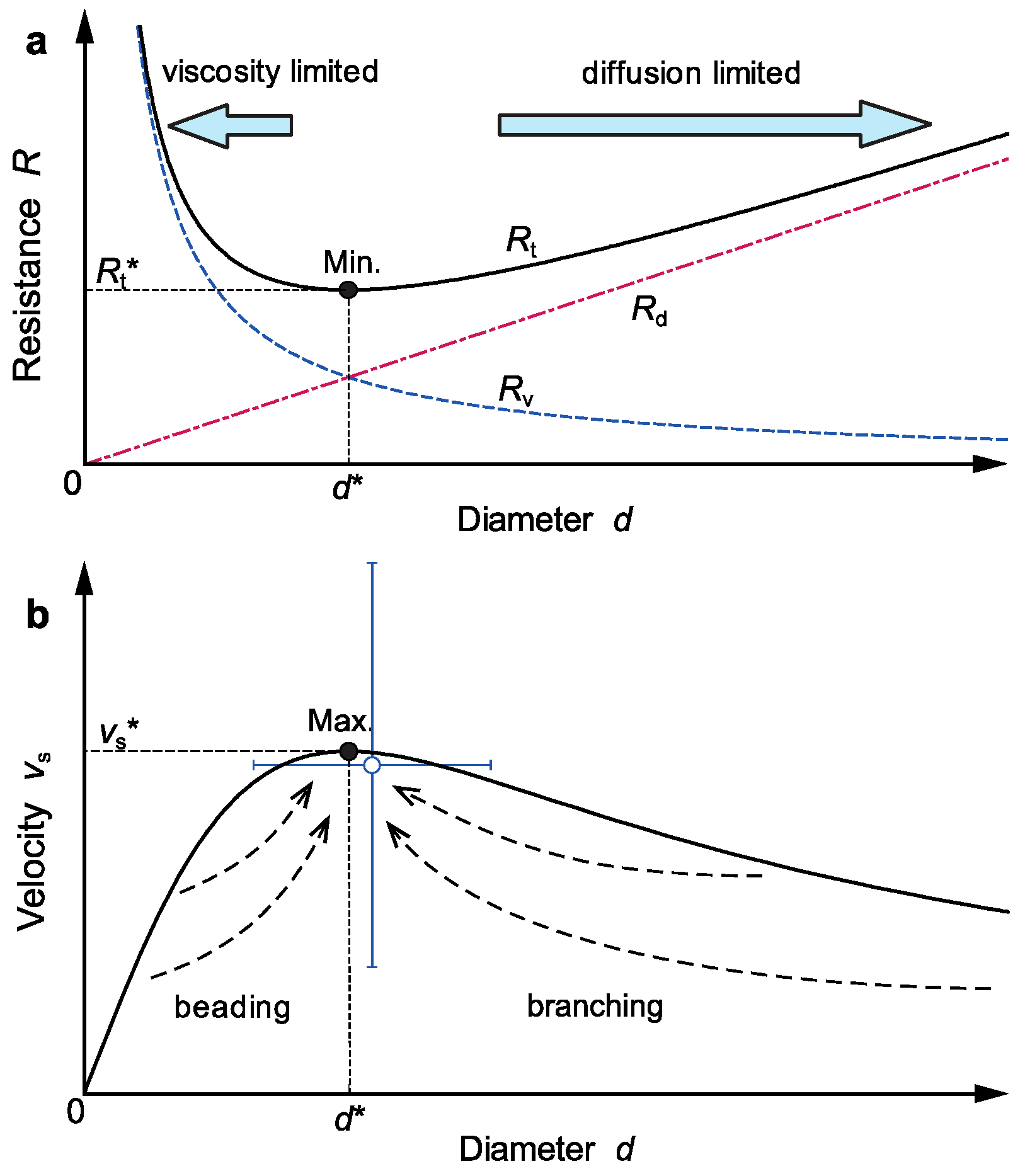
3.1. Theoretical Finger Model
3.2. Generation and Dissipation of Kinetic Energy
3.3. Implications for Other Structure Formation Phenomena
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Experimental Methods
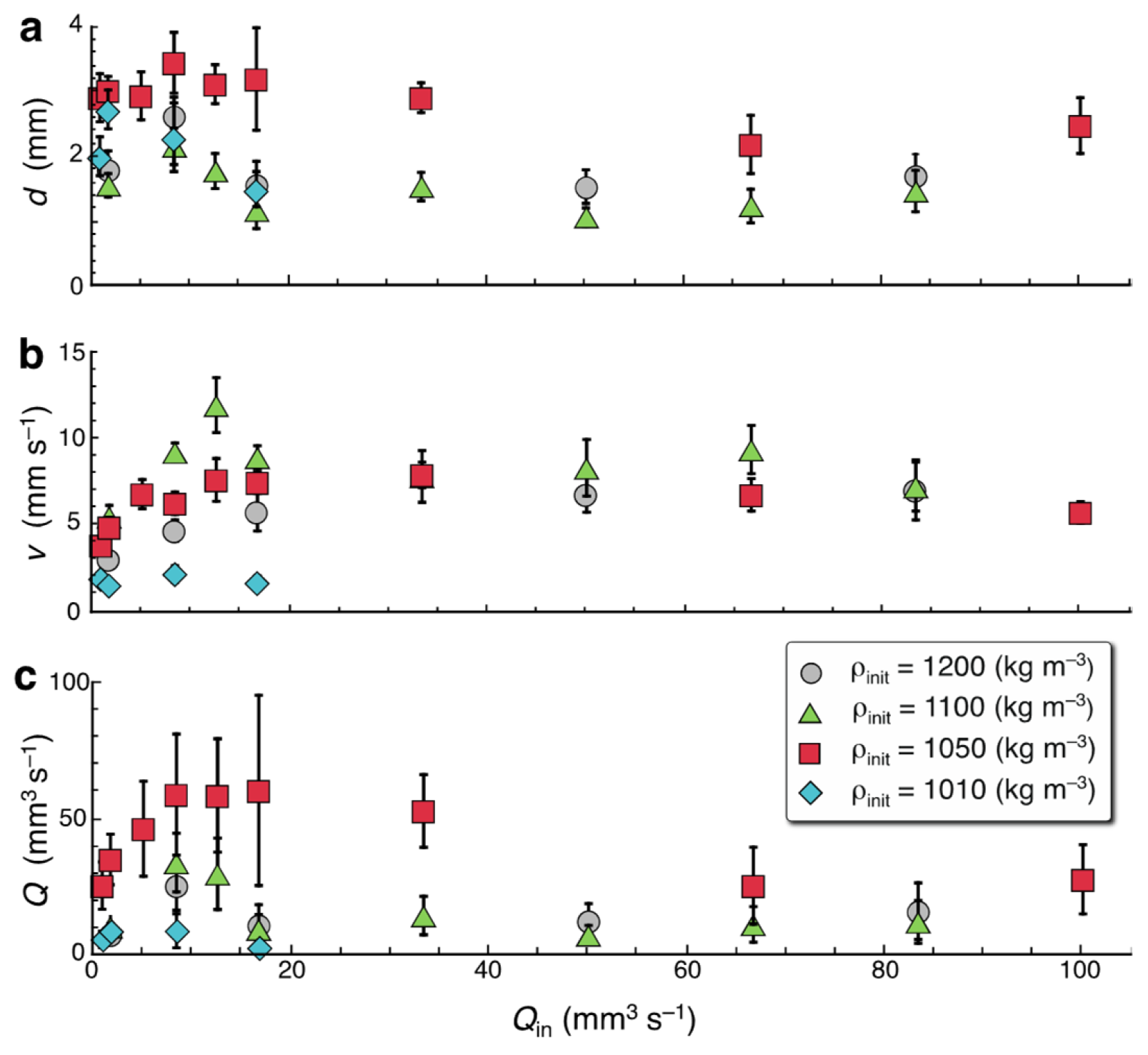
| ρinit 1 (kg m−3) | Qin (mm3 s−1) | v (mm s−1) | d (mm) | Finger Type |
|---|---|---|---|---|
| 1010 | 0.83 | 1.91 ± 0.37 | 2.02 ± 0.30 | Bd |
| 1010 | 1.67 | 1.53 ± 0.13 | 2.74 ± 0.30 | Bd, M (+) |
| 1010 | 8.33 | 2.19 ± 0.48 | 2.31 ± 0.53 | B, MB |
| 1010 | 16.7 | 1.67 ± 0.41 | 1.51 ± 0.27 | MB |
| 1050 | 0.83 | 3.85 ± 0.32 | 2.92 ± 0.37 | Bd |
| 1050 | 1.67 | 4.90 ± 0.57 | 3.03 ± 0.22 | Bd |
| 1050 | 3.33 | 7.54 ± 0.81 | 3.04 ± 0.38 | Bd (+) |
| 1050 | 5.0 | 6.82 ± 0.84 | 2.95 ± 0.37 | B |
| 1050 | 8.33 | 6.29 ± 0.65 | 3.46 ± 0.47 | MB |
| 1050 | 66.7 | 6.77 ± 0.94 | 2.20 ± 0.45 | MB |
| 1050 | 100 | 5.76 ± 0.62 | 2.49 ± 0.43 | MB |
| 1100 | 0.83 | 5.25 ± 0.76 | 1.90 ± 0.22 | Bd |
| 1100 | 1.67 | 5.51 ± 0.66 | 1.57 ± 0.18 | L (+) |
| 1100 | 5.0 | 8.40 ± 0.65 | 1.85 ± 0.35 | M |
| 1100 | 8.33 | 9.25 ± 0.52 | 2.17 ± 0.28 | M |
| 1100 | 12.5 | 11.97 ± 1.59 | 1.79 ± 0.27 | M |
| 1100 | 16.7 | 8.95 ± 0.67 | 1.18 ± 0.28 | B |
| 1100 | 33.3 | 7.84 ± 1.50 | 1.55 ± 0.22 | B |
| 1100 | 50.0 | 8.34 ± 1.64 | 1.08 ± 0.14 | MB |
| 1100 | 66.7 | 9.40 ± 1.40 | 1.25 ± 0.26 | MB |
| 1100 | 83.3 | 7.25 ± 1.42 | 1.48 ± 0.32 | MB |
| 1200 | 1.67 | 3.06 ± 0.28 | 1.81 ± 0.29 | M |
| 1200 | 8.33 | 4.71 ± 0.62 | 2.64 ± 0.29 | M (+) |
| 1200 | 16.7 | 5.80 ± 1.12 | 1.58 ± 0.36 | B, MB |
| 1200 | 50.0 | 6.81 ± 1.04 | 1.55 ± 0.26 | MB |
| 1200 | 83.3 | 7.06 ± 1.74 | 1.72 ± 0.33 | MB |
References
- Thompson, D.W. On Growth and Form, 1st ed.; Cambridge Univ. Press: Cambridge, UK, 1961. [Google Scholar]
- Nicolis, G.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Ball, P. The Self-Made Tapestry: Pattern Formation in Nature; Oxford Univ. Press: Oxford, UK, 1999. [Google Scholar]
- Bénard, H. Les tourbillons cellulaires dans une nappe liquide transportant de la chaleur par convection en régime permanent. Ann. Chim. Phys. 1901, 23, 62–144. [Google Scholar]
- Terada, T.; Hirata, M.; Yamamoto, R. Microscopic cracks produced by electric spark. Nature 1932, 129, 168–169. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Garik, P. The formation of patterns in non-equilibrium growth. Nature 1990, 343, 523–530. [Google Scholar] [CrossRef]
- Hill, A. Entropy production as the selection rule between different growth morphologies. Nature 1990, 348, 426–428. [Google Scholar] [CrossRef]
- Nohguchi, Y.; Ozawa, H. On the vortex formation at the moving front of lightweight granular particles. Phys. D 2009, 238, 20–26. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. Roy. Soc. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge Univ. Press: Cambridge, UK, 2000. [Google Scholar]
- Stommel, H.; Arons, A.B.; Blanchard, D. An oceanographical curiosity: The perpetual salt fountain. Deep-Sea Res. 1956, 3, 152–153. [Google Scholar] [CrossRef]
- Stern, M.E. The “salt-fountain” and thermohaline convection. Tellus 1960, 12, 172–175. [Google Scholar] [CrossRef]
- Stern, M.E.; Turner, J.S. Salt fingers and convecting layers. Deep-Sea Res. 1969, 16, 497–511. [Google Scholar] [CrossRef]
- Turner, J.S. Buoyancy Effects in Fluids; Cambridge Univ. Press: Cambridge, UK, 1973. [Google Scholar]
- Huppert, H.E.; Turner, J.S. Double-diffusive convection. J. Fluid Mech. 1981, 106, 299–329. [Google Scholar] [CrossRef]
- Krishnamurti, R. Double-diffusive transport in laboratory thermohaline staircases. J. Fluid Mech. 2003, 483, 287–314. [Google Scholar] [CrossRef]
- Radko, T. Double-Diffusive Convection; Cambridge Univ. Press: Cambridge, UK, 2013. [Google Scholar]
- Plateau, J. Statique Expérimentale et Théorique des Liquides Soumis aux Seules Forces Moléculaires; Gauthier-Villars: Paris, France, 1873. [Google Scholar]
- Lord Rayleigh, On the instability of jets. Proc. Lond. Math. Soc. 1878, 10, 4–13. [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes, I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Atkins, P.W. The Second Law: Energy, Chaos, and Form; Freeman: New York, NY, USA, 1984. [Google Scholar]
- Ozawa, H.; Shimokawa, S.; Sakuma, H. Thermodynamics of fluid turbulence: A unified approach to the maximum transport properties. Phys. Rev. E 2001, 64, 026303. [Google Scholar] [CrossRef] [PubMed]
- Paltridge, G.W. Global dynamics and climate–A system of minimum entropy exchange. Q. J. Roy. Meteorol. Soc. 1975, 101, 475–484. [Google Scholar] [CrossRef]
- Paltridge, G.W. Climate and thermodynamic systems of maximum dissipation. Nature 1979, 279, 630–631. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A. Thermodynamics of a global-mean state of the atmosphere–A state of maximum entropy increase. J. Clim. 1997, 10, 441–445. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Lunine, J.I.; Withers, P.G.; McKay, C.P. Titan, Mars and Earth: Entropy production by latitudinal heat transport. Geophys. Res. Lett. 2001, 28, 415–418. [Google Scholar] [CrossRef]
- Shimokawa, S.; Ozawa, H. On the thermodynamics of the oceanic general circulation: Irreversible transition to a state with higher rate of entropy production. Q. J. Roy. Meteorol. Soc. 2002, 128, 2115–2128. [Google Scholar] [CrossRef]
- Ozawa, H.; Shimokawa, S. Thermodynamics of a tropical cyclone: Generation and dissipation of mechanical energy in a self-driven convection system. Tellus A 2015, 67, 24216. [Google Scholar] [CrossRef]
- Kleidon, A.; Fraedrich, K.; Kirk, E.; Lunkeit, F. Maximum entropy production and the strength of boundary layer exchange in an atmospheric general circulation model. Geophys. Res. Lett. 2006, 33, L06706. [Google Scholar] [CrossRef]
- Yoshida, Z.; Mahajan, S.M. “Maximum” entropy production in self-organized plasma boundary layer: A thermodynamic discussion about turbulent heat transport. Phys. Plasmas 2008, 15, 032307. [Google Scholar] [CrossRef]
- Kondepudi, D.; Kay, B.; Dixon, J. End-directed evolution and the emergence of energy-seeking behaviour in a complex system. Phys. Rev. E 2015, 91, 050902. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M.; Birzina, A.I. Entropy production and stability during radial displacement of fluid in Hele-Shaw cell. J. Phys. Condens. Matter 2008, 20, 465102. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Birzina, A.I. Metastability at the displacement of a fluid in a Hele-Shaw cell. JETP Lett. 2014, 99, 446–451. [Google Scholar] [CrossRef]
- England, J. Dissipative adaptation in driven self-assembly. Nat. Nanotechnol. 2015, 10, 919–923. [Google Scholar] [CrossRef]
- Lotka, A.J. Contribution to the energetics of evolution. Proc. Nat. Acad. Sci. USA 1922, 8, 147–151. [Google Scholar] [CrossRef]
- Ulanowicz, R.E.; Hannon, B.M. Life and the production of entropy. Proc. R. Soc. Lond. B 1987, 232, 181–192. [Google Scholar]
- Sawada, Y. A thermodynamic variational principle in nonlinear non-equilibrium phenomena. Prog. Theor. Phys. 1981, 66, 68–76. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A 2003, 36, 631–641. [Google Scholar] [CrossRef]
- Kleidon, A.; Lorenz, R.D. (Eds.) Non-Equilibrium Thermodynamics and the Production of Entropy: Life, Earth, and Beyond; Springer: Berlin, Germany, 2005. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Kleidon, A. Thermodynamic Foundations of the Earth System; Cambridge Univ. Press: Cambridge, UK, 2016. [Google Scholar]
- Martyushev, L.M. Maximum entropy production principle: History and current status. Uspekhi Fiz. Nauk. 2021, 64, 558–583. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. On a general evolution criterion in macroscopic physics. Physica 1964, 30, 351–374. [Google Scholar] [CrossRef]
- Oparin, A.I. The Origin of Life; Macmillan Publication: New York, NY, USA, 1938. [Google Scholar]
- Zwicker, D.; Seyboldt, R.; Weber, C.A.; Hyman, A.A.; Jülicher, F. Growth and division of active droplets provides a model for protocells. Nat. Phys. 2017, 13, 408–413. [Google Scholar] [CrossRef]
- Mullins, W.W.; Sekerka, R.F. Morphological stability of a particle growing by diffusion or heat flow. J. Appl. Phys. 1963, 34, 323–329. [Google Scholar] [CrossRef]
- Aoki, I. Entropy principle for the evolution of living systems and the universe––From bacteria to the universe. J. Phys. Soc. Jpn 2018, 87, 104801. [Google Scholar] [CrossRef]
- Gilbert, W. The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Szostak, J.W.; Bartel, S.D.; Luisi, P.L. Synthesizing life. Nature 2001, 409, 387–390. [Google Scholar] [CrossRef]
- Weber, C.A.; Zwicker, D.; Jülicher, F.; Lee, C.F. Physics of active emulsions. Rep. Prog. Phys. 2019, 82, 064601. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 1958, 425, 312–329. [Google Scholar] [CrossRef]
- Kubota, K.; Matsumoto, T.; Kurisu, S.; Suzuki, K.; Hosaka, H. The equations regarding temperature and concentration of the density and viscosity of sugar, salt and skim milk solutions. J. Fac. Appl. Biol. Sci. Hiroshima Univ. 1980, 19, 133–145. [Google Scholar]
- Dean, J.A. Lange’s Handbook of Chemistry, 15th ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
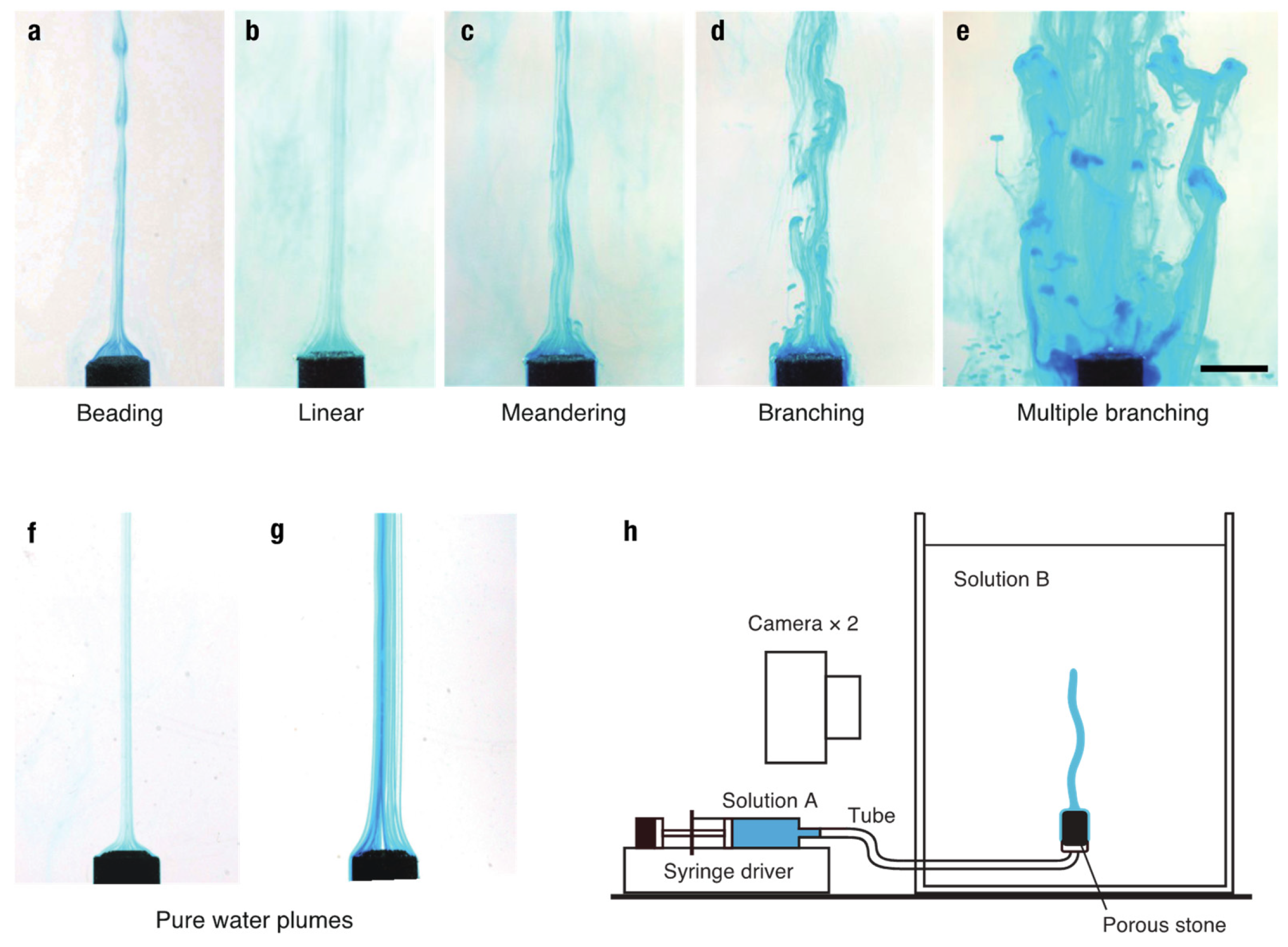
 , multiple branching. The solid (red) line indicates the flow rate for the maximum-velocity finger, Q*, as a function of the initial density, ρinit.
, multiple branching. The solid (red) line indicates the flow rate for the maximum-velocity finger, Q*, as a function of the initial density, ρinit.
 , multiple branching. The solid (red) line indicates the flow rate for the maximum-velocity finger, Q*, as a function of the initial density, ρinit.
, multiple branching. The solid (red) line indicates the flow rate for the maximum-velocity finger, Q*, as a function of the initial density, ρinit.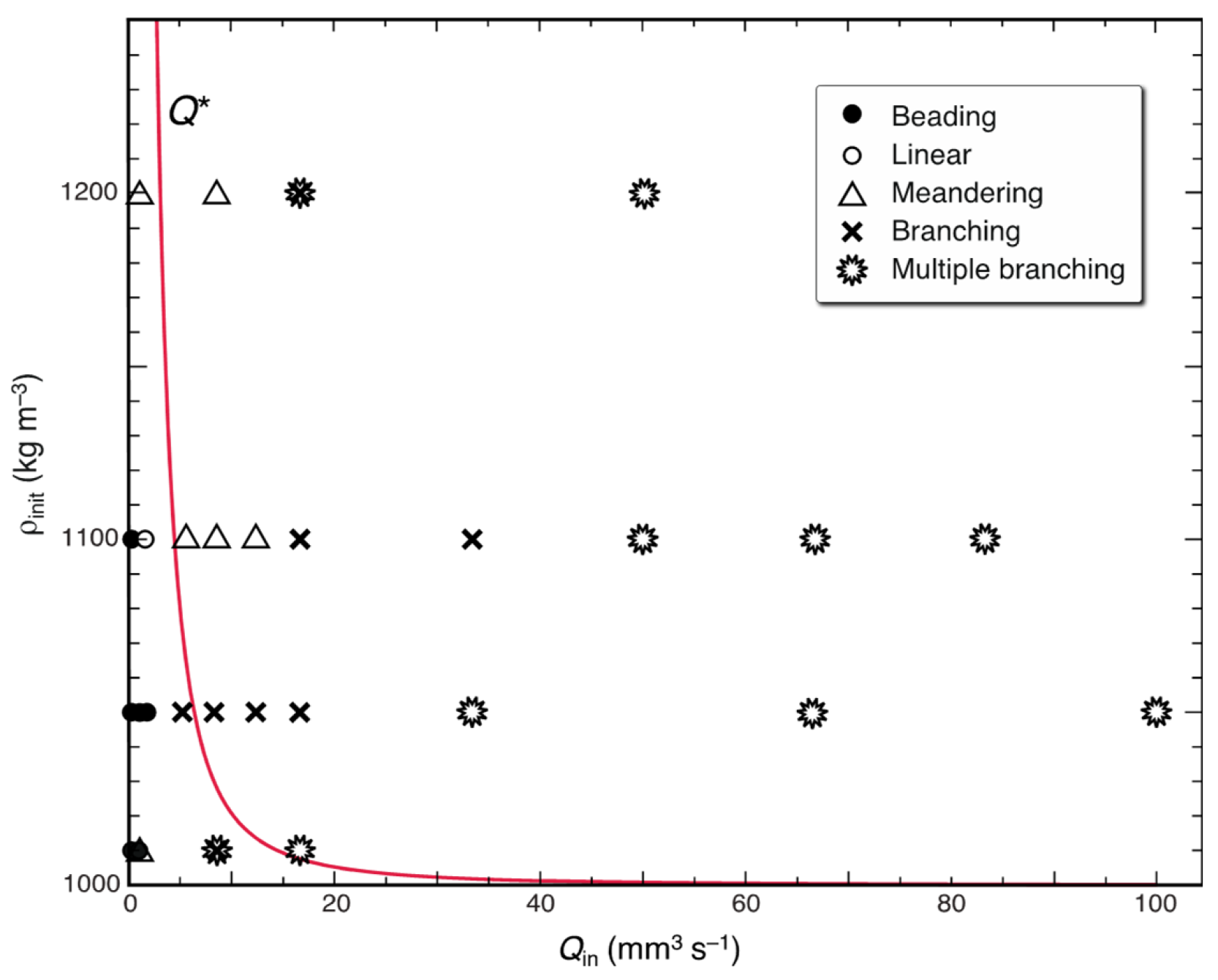

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozawa, H.; Murayama-Ogino, S.; Kleidon, A. Thermodynamics of Morphogenesis: Beading and Branching Pattern Formation in Diffusion-Driven Salt Finger Plumes. Entropy 2025, 27, 106. https://doi.org/10.3390/e27020106
Ozawa H, Murayama-Ogino S, Kleidon A. Thermodynamics of Morphogenesis: Beading and Branching Pattern Formation in Diffusion-Driven Salt Finger Plumes. Entropy. 2025; 27(2):106. https://doi.org/10.3390/e27020106
Chicago/Turabian StyleOzawa, Hisashi, Sayaka Murayama-Ogino, and Axel Kleidon. 2025. "Thermodynamics of Morphogenesis: Beading and Branching Pattern Formation in Diffusion-Driven Salt Finger Plumes" Entropy 27, no. 2: 106. https://doi.org/10.3390/e27020106
APA StyleOzawa, H., Murayama-Ogino, S., & Kleidon, A. (2025). Thermodynamics of Morphogenesis: Beading and Branching Pattern Formation in Diffusion-Driven Salt Finger Plumes. Entropy, 27(2), 106. https://doi.org/10.3390/e27020106







