The Supervised Information Bottleneck
Abstract
1. Introduction
2. Materials and Methods
2.1. Related Work
2.2. From VIB to SVIB
- Consider :
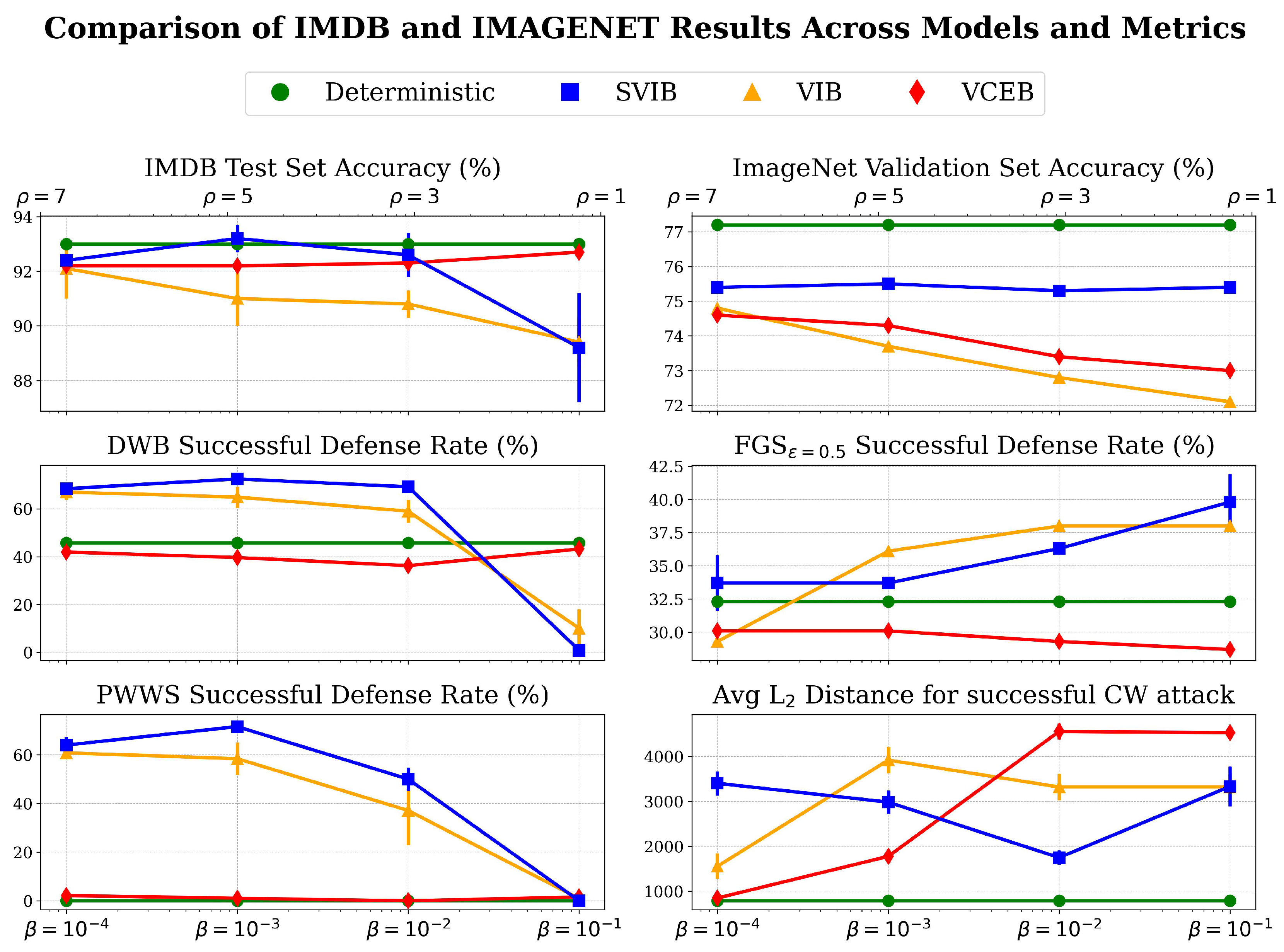
3. Results
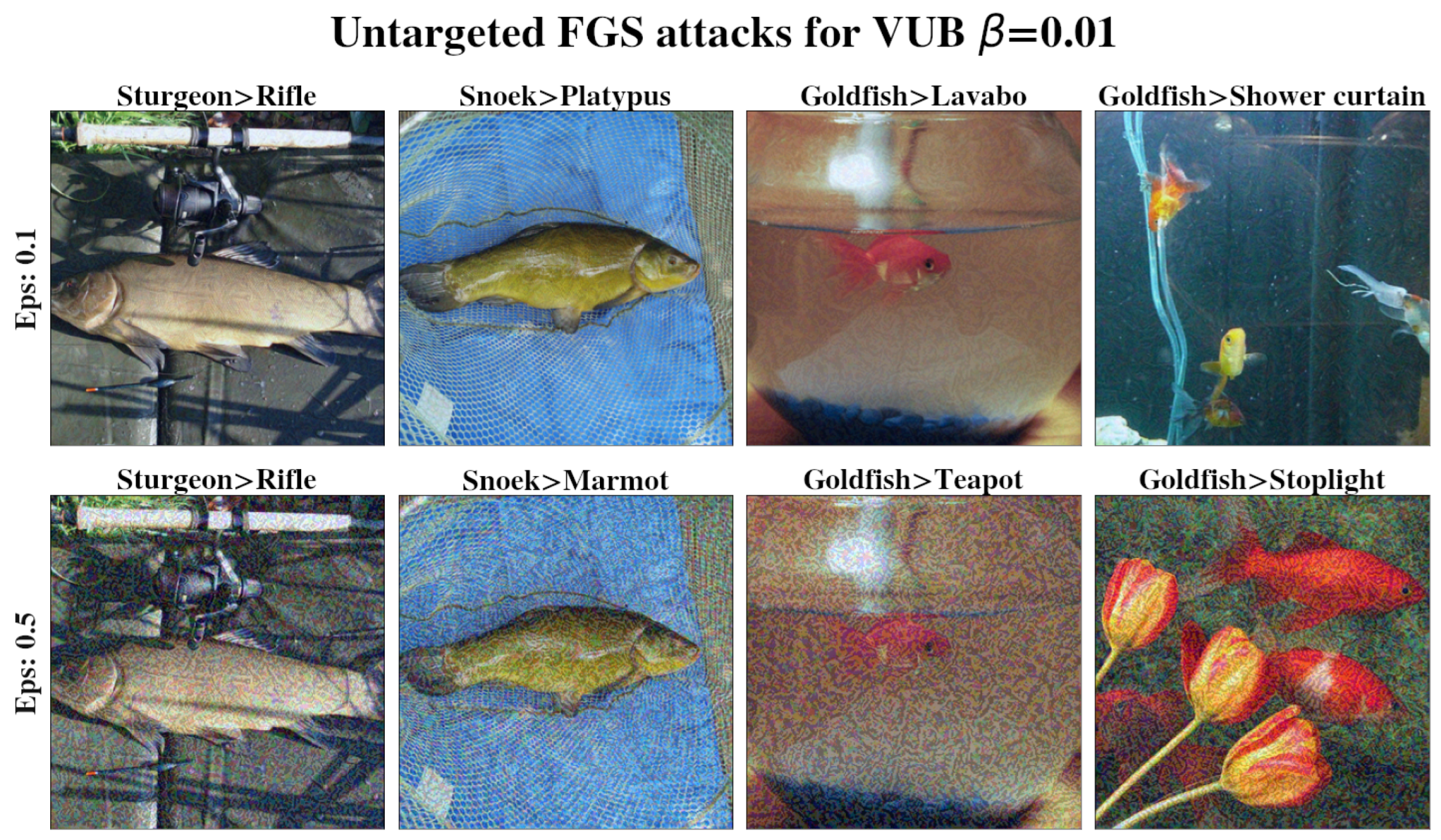
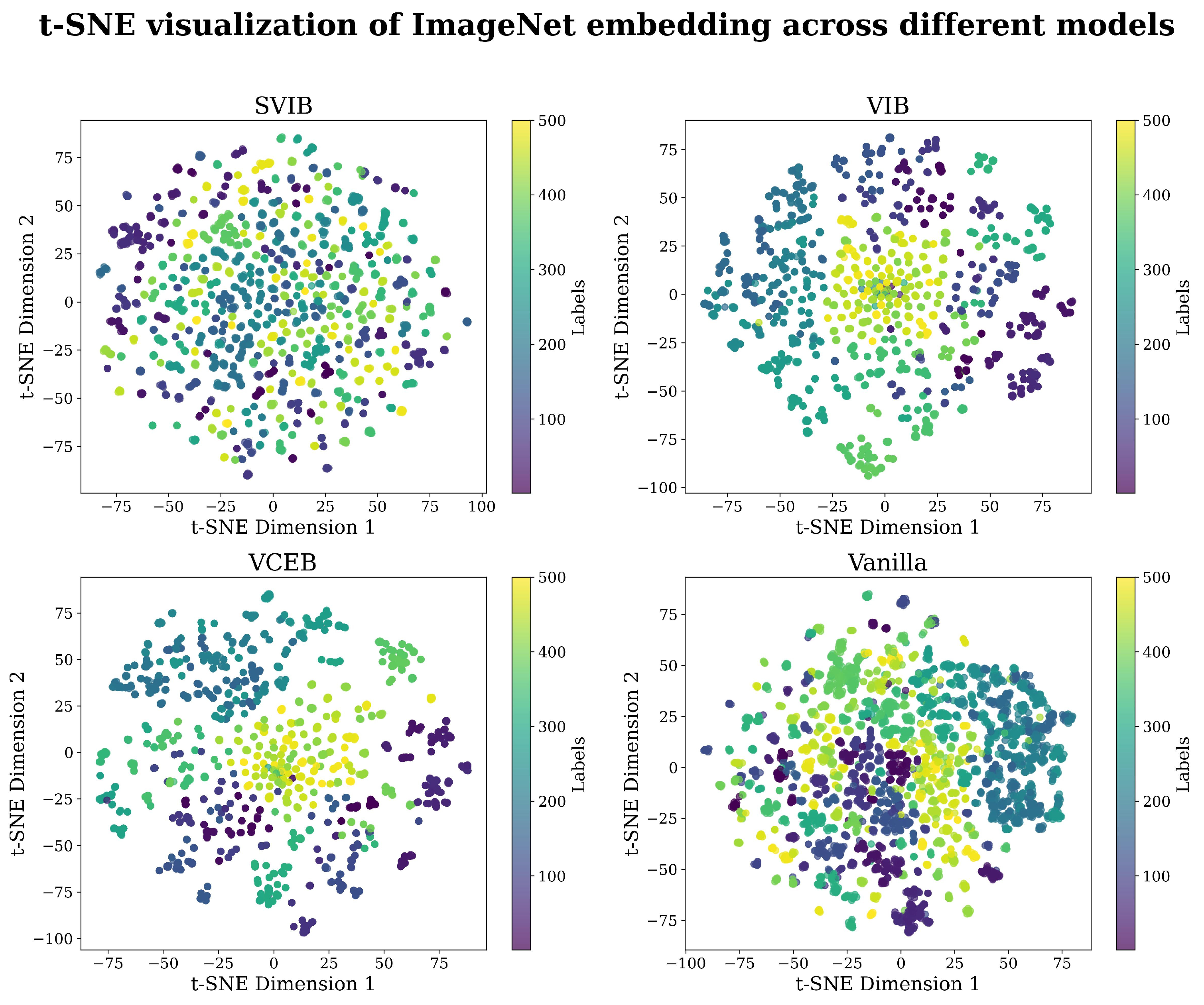
3.1. Image Classification
3.2. Text Classification
4. Discussion
Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Preliminaries
Appendix A.1. Notation
Appendix A.2. Variational Approximations
Appendix A.3. Learning Tasks
- A generator of random vectors , drawn independently from an unknown probability distribution .
- A supervisor who returns a scalar output value according to an unknown conditional probability distribution . We note that these probabilities can indeed be soft labels, where y is a continuous probability vector rather than the more commonly used hard labels.
- A learning machine capable of implementing a predefined set of functions, , where is a set of parameters.
Appendix A.4. Information Theoretic Functions
| Notation | Differential | Discrete | |
| Entropy | |||
| Conditional entropy | |||
| Cross entropy | |||
| Joint entropy | |||
| KL divergence | |||
| Mutual information (MI) |
Appendix B. Related Work Elaboration
Appendix B.1. The Information Plane

Appendix B.2. Fixing a Broken ELBO
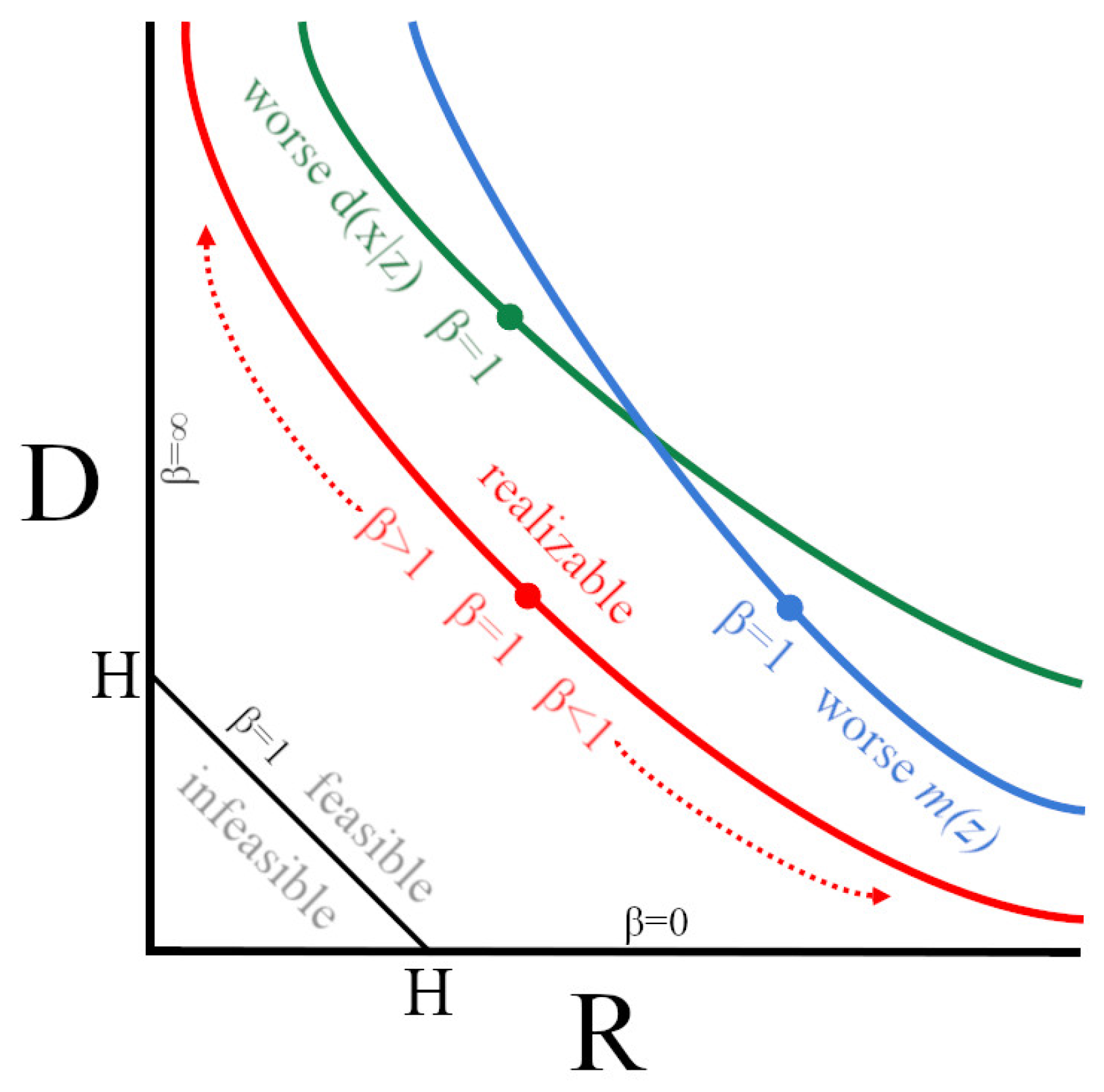
Appendix B.3. IB Theory of Deep Learning
Appendix B.4. Conditional Entropy Bottleneck
Appendix C. Experiments Elaboration
- import scipy.stats as statsvib_scores = [0.915, 0.915, 0.91, 0.92, 0.89]svib_scores = [0.93, 0.935, 0.925, 0.93, 0.94]pvalue = stats.ranksums(svib_scores, vib_scores, ‘greater’).pvalueassert pvalue < 0.05
Appendix C.1. Complete Empirical Results
| Val ↑ | CW ↑ | ||||
|---|---|---|---|---|---|
| Vanilla model | |||||
| - | - | 77.2% | 31.1% | 32.3% | 788 |
| SVIB models | |||||
| 2 | 75.4% ± | 40.1% ± | 33.7% ± | 3401 ± 267 | |
| 74.9% ± | 38.4% ± | 33.8% ± | 3293 ± 140 | ||
| 1 | 75.5% ± | 37.2% ± | 33.6% ± | 2666 ± 140 | |
| 75.4% ± | 38.1% ± | 33.7% ± | 2981 ± 260 | ||
| 75.3% ± | 38.3% ± | 33.8% ± | 3095 ± 407 | ||
| 75.3% ± | 38.5% ± | 33.9% ± | 3078 ± 443 | ||
| 74.2% ± | 42.0% ± | 35.2% ± | 2354 ± 394 | ||
| 1 | 75.0% ± | 42.4% ± | 35.7% ± | 1564 ± 218 | |
| 75.3% ± | 43.1% ± | 36.3% ± | 1748 ± 160 | ||
| 75.4% ± | 43.0% ± | 36.0% ± | 1814 ± 144 | ||
| 75.4% ± | 42.9% ± | 36.2% ± | 1749 ± 138 | ||
| SVIB models | |||||
| 73.1% ± | 39.1% ± | 32.6% ± | 3738 ± 138 | ||
| 1 | 74.8% ± | 42.1% ± | 35.2% ± | 3575 ± 456 | |
| 75.4% ± | 46.6% ± | 39.8% ± | 3332 ± 443 | ||
| 75.4% ± | 45.6% ± | 38.7% ± | 3581 ± 243 | ||
| 75.1% ± | 46.0% ± | 39.3% ± | 3536 ± 315 | ||
| Val ↑ | CW ↑ | ||||
|---|---|---|---|---|---|
| VIB models | |||||
| - | 74.8% ± | 28.3% ± | 29.3% ± | 1554 ± 280 | |
| - | 74.1% ± | 37.7% ± | 34.8% ± | 3104 ± 529 | |
| - | 73.7% ± | 40.5% ± | 36.1% ± | 3917 ± 291 | |
| - | 73.0% ± | 44.9% ± | 37.8% ± | 3358 ± 245 | |
| - | 72.8% ± | 46.5% ± | 38.0% ± | 3318 ± 293 | |
| - | 72.3% ± | 44.7% ± | 34.9% ± | 3654 ± 333 | |
| - | 72.1% ± | 41.6% ± | 38.0% ± | 3318 ± 293 | |
| - | 0.1% ± | 0% ± | 0% ± | 0 ± 0 | |
| CEB models | |||||
| - | 1 | 73.0% ± | 26.5% ± | 28.7% ± | 4527 ± 64 |
| - | 2 | 730.2% ± | 26.4% ± | 29.0% ± | 4342 ± 173 |
| - | 3 | 73.4% ± | 26.7% ± | 29.3% ± | 4556 ± 177 |
| - | 4 | 73.8% ± | 27.0% ± | 29.9% ± | 3689 ± 347 |
| - | 5 | 74.3% ± | 27.6% ± | 30.1%± | 1776 ± 146 |
| - | 6 | 74.6% ± | 27.7% ± | 30.0% ± | 1103 ± 154 |
| - | 7 | 74.6% ± | 28.0% ± | 30.1% ± | 847 ± 16 |
| Test ↑ | DWB ↑ | PWWS ↑ | ||
|---|---|---|---|---|
| Vanilla model | ||||
| - | - | 93.0% | 45.7% | 0.0% |
| SVIB models | ||||
| 1 | 92.4% ± | 68.4% ± | 63.9% ± | |
| 92.3% ± | 70.7% ± | 68.3% ± | ||
| 1 | 930.2% ± | 72.5% ± | 71.6% ± | |
| 92.3% ± | 74.7% ± | 73.1% ± | ||
| 92.4% ± | 75.9% ± | 72.4% ± | ||
| 92.3% ± | 74.5% ± | 74.4% ± | ||
| 92.4% ± | 66.1% ± | 68.3% ± | ||
| 1 | 92.6% ± | 690.2% ± | 50.0% ± | |
| SVIB models | ||||
| 92.4% ± | 64.8% ± | 40.3% ± | ||
| 92.3% ± | 58.1% ± | 28.9% ± | ||
| 92.3% ± | 54.0% ± | 22.5% ± | ||
| 920.2% ± | 1.1% ± | 0.0% ± | ||
| 1 | 890.2% ± | 0.8% ± | 0.0% ± | |
| 92.3% ± | 0.0% ± | 0.0% ± | ||
| 92.4% ± | 0.0% ± | 0.0% ± | ||
| 92.4% ± | 0.0% ± | 0.0% ± | ||
| Test ↑ | DWB ↑ | PWWS ↑ | ||
|---|---|---|---|---|
| VIB models | ||||
| - | 92.1% ± | 67.0% ± | 60.8% ± | |
| - | 920.2% ± | 680.2% ± | 64.3% ± | |
| - | 91.0% ± | 64.9% ± | 58.4% ± | |
| - | 920.2% ± | 62.9% ± | 48.3% ± | |
| - | 90.8% ± | 59.0% ± | 37.1% ± | |
| 92.4% ± | 14.4% ± | 1.0% ± | ||
| - | 89.4% ± | 10.0% ± | 0.9% ± | |
| CEB models | ||||
| - | 92.7% ± | 46.7% ± | 1.65% ± | |
| - | 1 | 92.7% ± | 430.2% ± | 1.53% ± |
| - | 2 | 92.5% ± | 40.8% ± | 0% ± |
| - | 3 | 92.3% ± | 360.2% ± | 0% ± |
| - | 4 | 92.1% ± | 38.8% ± | 0% ± |
| - | 5 | 920.2% ± | 39.6% ± | 1.0% ± |
| - | 6 | 92.1% ± | 41.9% ± | 0% ± |
| - | 7 | 920.2% ± | 41.9% ± | 2.15% ± |
| - | 8 | 920.2% ± | 45.9% ± | 0% ± |
References
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep Variational Information Bottleneck. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–27 April 2017. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 22–24 September 1999. [Google Scholar]
- Slonim, N. The Information Bottleneck: Theory and Applications. Ph.D. Thesis, Hebrew University of Jerusalem, Jerusalem, Israel, 2002. [Google Scholar]
- Shannon, C.E. Coding Theorems for a Discrete Source with a Fidelity Criterion. In Proceedings of the IRE National Convention, San Fransico, CA, USA, 18–21 August 1959. [Google Scholar]
- Chechik, G.; Globerson, A.; Tishby, N.; Weiss, Y. Information Bottleneck for Gaussian Variables. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–13 December 2003. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the Information Bottleneck Theory of Deep Learning. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Amjad, R.A.; Geiger, B.C. Learning Representations for Neural Network-Based Classification Using the Information Bottleneck Principle. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2225–2239. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Fischer, I. The Conditional Entropy Bottleneck. Entropy 2020, 22, 999. [Google Scholar] [CrossRef] [PubMed]
- Kolchinsky, A.; Tracey, B.D.; Wolpert, D.H. Nonlinear Information Bottleneck. Entropy 2019, 21, 1181. [Google Scholar] [CrossRef]
- Achille, A.; Soatto, S. Information dropout: Learning optimal representations through noisy computation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Painsky, A.; Tishby, N. Gaussian Lower Bound for the Information Bottleneck Limit. J. Mach. Learn. Res. 2017, 18, 213:1–213:29. [Google Scholar]
- Geiger, B.C.; Fischer, I.S. A Comparison of Variational Bounds for the Information Bottleneck Functional. Entropy 2020, 22, 1229. [Google Scholar] [CrossRef] [PubMed]
- Piran, Z.; Shwartz-Ziv, R.; Tishby, N. The Dual Information Bottleneck. arXiv 2020, arXiv:2006.04641. [Google Scholar] [CrossRef]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–27 April 2017. [Google Scholar]
- Cheng, P.; Hao, W.; Dai, S.; Liu, J.; Gan, Z.; Carin, L. CLUB: A Contrastive Log-ratio Upper Bound of Mutual Information. In Proceedings of the 37th International Conference on Machine Learning (ICML), Virtual, 13–18 July 2020; Volume 119, pp. 1779–1788. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. Entropy 2017, 19, 361. [Google Scholar] [CrossRef]
- Czyż, P.; Grabowski, F.; Vogt, J.; Beerenwinkel, N.; Marx, A. Beyond Normal: On the Evaluation of Mutual Information Estimators. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), New Orleans, LA, USA, 10–16 December 2023; Volume 36, pp. 16957–16990. [Google Scholar]
- Yu, X.; Yu, S.; Príncipe, J.C. Deep Deterministic Information Bottleneck with Matrix-Based Entropy Functional. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3160–3164. [Google Scholar]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999; p. 22. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Fischer, I.; Alemi, A.A. CEB Improves Model Robustness. Entropy 2020, 22, 1081. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Pereyra, G.; Tucker, G.; Chorowski, J.; Kaiser, L.; Hinton, G.E. Regularizing Neural Networks by Penalizing Confident Output Distributions. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–27 April 2017. [Google Scholar]
- Alemi, A.; Poole, B.; Fischer, I.; Dillon, J.; Saurous, R.A.; Murphy, K. Fixing a Broken ELBO. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 159–168. [Google Scholar]
- Barber, D.; Agakov, F.V. The IM algorithm: A variational approach to Information Maximization. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–13 December 2003. [Google Scholar]
- Maas, A.; Daly, R.E.; Pham, P.T.; Huang, D.; Ng, A.Y.; Potts, C. Learning word vectors for sentiment analysis. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, OR, USA, 19–24 June 2011; pp. 142–150. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Carlini, N.; Wagner, D.A. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–24 May 2017; pp. 39–57. [Google Scholar]
- Kaiwen. pytorch-cw2. GitHub Repository. 2018. Available online: https://github.com/kkew3/pytorch-cw2 (accessed on 16 April 2025).
- Gao, J.; Lanchantin, J.; Soffa, M.L.; Qi, Y. Black-box generation of adversarial text sequences to evade deep learning classifiers. In Proceedings of the IEEE Security and Privacy Workshops (SPW), San Jose, CA, USA, 24 May 2018; pp. 50–56. [Google Scholar]
- Morris, J.; Lifland, E.; Yoo, J.Y.; Grigsby, J.; Jin, D.; Qi, Y. TextAttack: A Framework for Adversarial Attacks, Data Augmentation, and Adversarial Training in NLP. In Proceedings of the Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Virtual Conference (Online), 16–20 November 2020; pp. 119–126. [Google Scholar]
- Ren, S.; Deng, Y.; He, K.; Che, W. Generating natural language adversarial examples through probability weighted word saliency. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 1085–1097. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 113–123. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–9 June 2019; pp. 4171–4186. [Google Scholar]
- Croce, F.; Hein, M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In Proceedings of the 37th International Conference on Machine Learning (ICML), Virtual (Online), 12–18 July 2020. [Google Scholar]
- Kingma, D.P.; Welling, M. An Introduction to Variational Autoencoders. Found. Trends Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; Chapter 1; pp. 17–22. [Google Scholar]
- Goldfeld, Z.; Polyanskiy, Y. The Information Bottleneck Problem and its Applications in Machine Learning. IEEE J. Sel. Areas Inf. Theory 2020, 1, 19–38. [Google Scholar] [CrossRef]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar] [CrossRef]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar] [CrossRef]


| Original Text |
|---|
| the acting, costumes, music, cinematography and sound are all astounding given the production’s austere locales. |
| Perturbed Text |
| the acting, costumes, music, cinematography and sound are all dumbfounding given the production’s austere locales. |
| Original Text |
|---|
| great historical movie, will not allow a viewer to leave once you begin to watch. View is presented differently than displayed by most school books on this subject. My only fault for this movie is it was photographed in black and white; wished it had been in color … wow ! |
| Perturbed Text |
| gnreat historical movie, will not allow a viewer to leave once you begin to watch. View is presented differently than displayed by most school books on this sSbject. My only fault for this movie is it was photographed in black and white; wished it had been in color … wow ! |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weingarten, N.Z.; Yakhini, Z.; Butman, M.; Bustin, R. The Supervised Information Bottleneck. Entropy 2025, 27, 452. https://doi.org/10.3390/e27050452
Weingarten NZ, Yakhini Z, Butman M, Bustin R. The Supervised Information Bottleneck. Entropy. 2025; 27(5):452. https://doi.org/10.3390/e27050452
Chicago/Turabian StyleWeingarten, Nir Z., Zohar Yakhini, Moshe Butman, and Ronit Bustin. 2025. "The Supervised Information Bottleneck" Entropy 27, no. 5: 452. https://doi.org/10.3390/e27050452
APA StyleWeingarten, N. Z., Yakhini, Z., Butman, M., & Bustin, R. (2025). The Supervised Information Bottleneck. Entropy, 27(5), 452. https://doi.org/10.3390/e27050452







