A Network Parameter Database False Data Injection Correction Physics-Based Model: A Machine Learning Synthetic Measurement-Based Approach
Abstract
:1. Introduction
- 1.
- Creating synthetic measurements based on weights obtained from machine learning linear regression prediction;
- 2.
- Developing an overdetermined physics-based model for parameter FDI correction;
- 3.
- Incorporating synthetic measurements in the parameter FDI correction model.
2. Background Information
2.1. State Estimation Augmented with Synthetic Measurements
2.2. Linear Regression Prediction Model
2.3. Unbalanced Parameter FDI Attack Correction Model
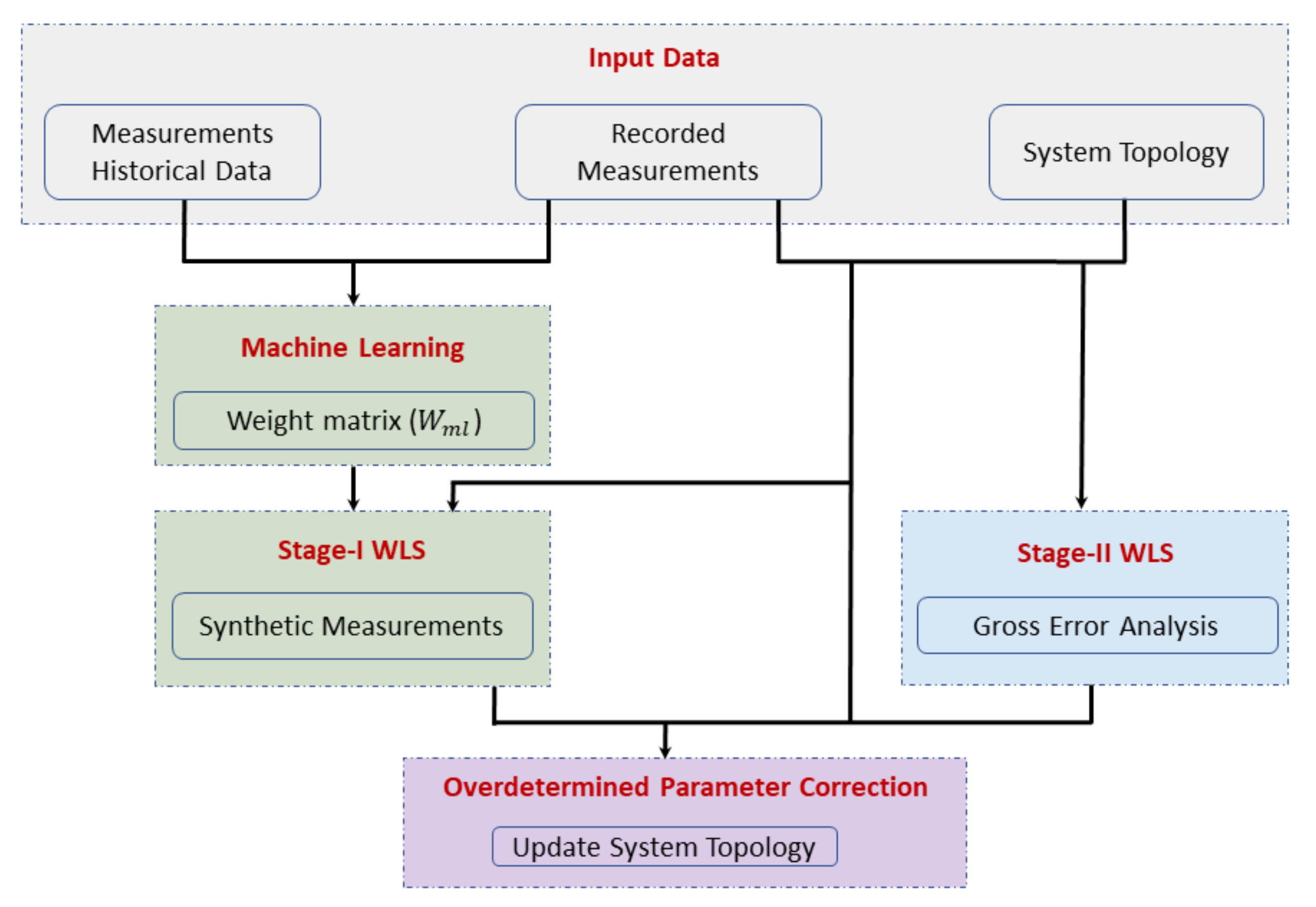
3. Synthetic Measurement Enhanced Parameter Error Correction
3.1. Framework for Parameter FDI Correction
3.2. Overdetermined Parameter FDI Correction Model
4. Case Study
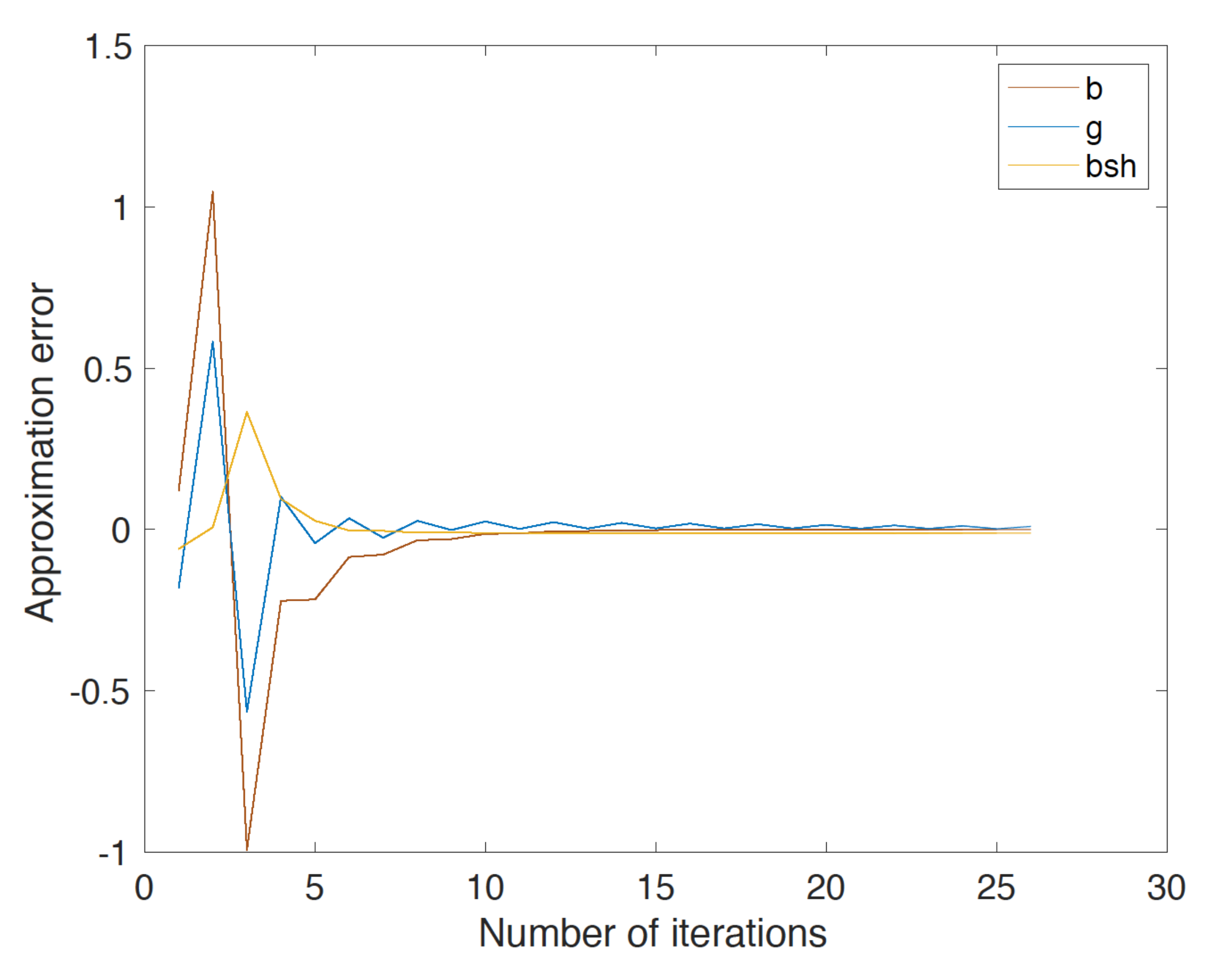
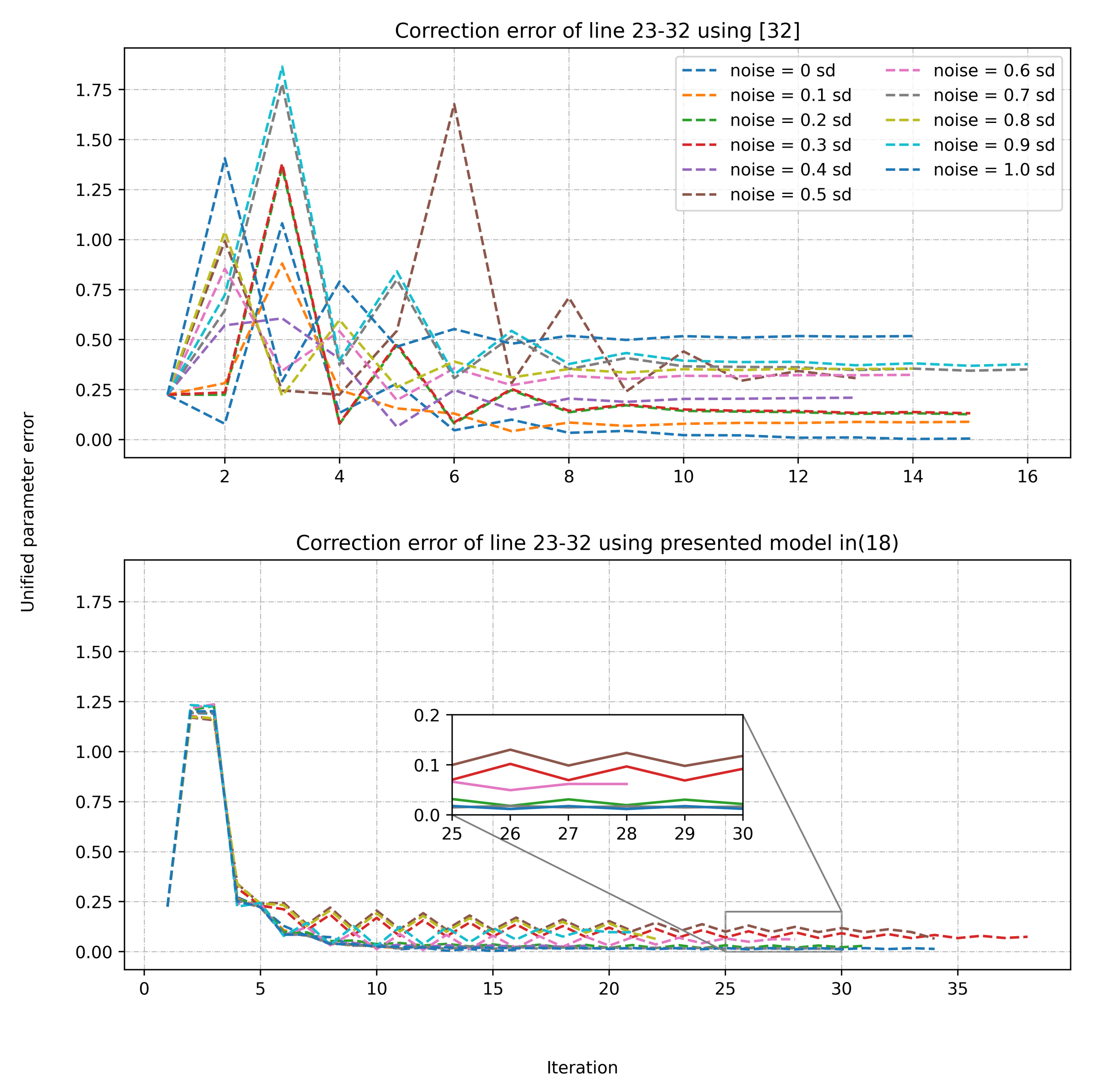
4.1. Parameter Attack Scenario I
4.2. Parameter Attack Scenario II
- A measurement cyber-attack of magnitude 5 is added to reactive power flow from bus 31 to bus 17 ().
- An unbalanced parameter FDI attack is injected to the series and shunt parameter of the line 47–69 ( on parameter g, on parameter b, on parameter ).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farag, M.; Azab, M.; Mokhtar, B. Cross-Layer Security Framework for Smart Grid: Physical Security Layer. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Istanbul, Turkey, 12–15 October 2014; pp. 1–7. [Google Scholar]
- Stefanov, A.; Liu, C. Cyber-power system security in a smart grid environment. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–3. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. TISSEC 2011, 14, 13. [Google Scholar] [CrossRef]
- Kosut, O.; Jia, L.; Thomas, R.J.; Tong, L. Malicious data attacks on the smart grid. IEEE Trans. Smart Grid 2011, 2, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Bi, S.; Zhang, Y.J.A. Graph-based Cyber Security Analysis of State Estimation in Smart Power Grid. IEEE Commun. Mag. 2017, 55, 176–183. [Google Scholar] [CrossRef]
- Li, S.; Yılmaz, Y.; Wang, X. Quickest detection of false data injection attack in wide-area smart grids. IEEE Trans. Smart Grid 2015, 6, 2725–2735. [Google Scholar] [CrossRef]
- Li, S.; Yilmaz, Y.; Wang, X. Sequential cyber-attack detection in the large-scale smart grid system. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 127–132. [Google Scholar]
- Volz, D. U.S. government concludes cyber attack caused Ukraine power outage. Reuters, 25 February 2016. [Google Scholar]
- Wang, Y.; Xia, M.; Chen, Q.; Chen, F.; Yang, X.; Han, F. Fast State Estimation of Power System based on Extreme Learning Machine Pseudo-Measurement Modeling. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1236–1241. [Google Scholar]
- Chakhchoukh, Y.; Liu, S.; Sugiyama, M.; Ishii, H. Statistical outlier detection for diagnosis of cyber attacks in power state estimation. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Ahmed, S.; Lee, Y.; Hyun, S.; Koo, I. Feature Selection–Based Detection of Covert Cyber Deception Assaults in Smart Grid Communications Networks Using Machine Learning. IEEE Access 2018, 6, 27518–27529. [Google Scholar] [CrossRef]
- Zou, T.; Aljohani, N.; Wang, P.; Bretas, A.S.; Bretas, N.G. Distributed nonlinear state estimation using adaptive penalty parameters with load characteristics in the Electricity Reliability Council of Texas. J. Ind. Inf. Integr. 2021, 24, 100223. [Google Scholar]
- Panthi, M. Anomaly Detection in Smart Grids using Machine Learning Techniques. In Proceedings of the 2020 First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 220–222. [Google Scholar]
- Cao, J.; Wang, D.; Qu, Z.; Cui, M.; Xu, P.; Xue, K.; Hu, K. A Novel False Data Injection Attack Detection Model of the Cyber-Physical Power System. IEEE Access 2020, 8, 95109–95125. [Google Scholar] [CrossRef]
- Zonouz, S.A.; Rogers, K.M.; Berthier, R.; Bobba, R.; Sanders, W.H.; Overbye, T.J. SCPSE: Security-Oriented Cyber-Physical State Estimation for Power Grid Critical Infrastructures. IEEE Trans. Smart Grid 2012, 3, 1790–1799. [Google Scholar] [CrossRef]
- Sridhar, S.; Govindarasu, M. Model-Based Attack Detection and Mitigation for Automatic Generation Control. IEEE Trans. Smart Grid 2014, 5, 580–591. [Google Scholar] [CrossRef]
- Trevizan, R.D.; Ruben, C.; Nagaraj, K.; Ibukun, L.L.; Starke, A.C.; Bretas, A.S.; McNair, J.; Zare, A. Data-driven Physics-based Solution for False Data Injection Diagnosis in Smart Grids. In Proceedings of the 2019 IEEE PES GM, Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
- Nagaraj, K.; Zou, S.; Ruben, C.; Dhulipala, S.C.; Starke, A.; Bretas, A.; Zare, A.; McNair, J. Ensemble CorrDet with Adaptive Statistics for Bad Data Detection. IET Smart Grid 2020, 3, 572–580. [Google Scholar] [CrossRef]
- Bretas, A.S.; Bretas, N.G.; Carvalho, B.E. Further contributions to smart grids cyber-physical security as a malicious data attack: Proof and properties of the parameter error spreading out to the measurements and a relaxed correction model. Int. J. Electr. Power Energy Syst. 2019, 104, 43–51. [Google Scholar] [CrossRef]
- Liu, C.; Liang, H.; Chen, T. Network Parameter Coordinated False Data Injection Attacks against Power System AC State Estimation. IEEE Trans. Smart Grid 2020. [Google Scholar] [CrossRef]
- Abur, A.; Expósito, A. Power System State Estimation: Theory and Implementation; Power Engineering (Willis); CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Abur, A.; Zhu, J. Identification of parameter errors. In Proceedings of the IEEE PES General Meeting, Detroit, MI, USA, 24–28 July 2010; pp. 1–4.
- Lin, Y.; Abur, A. Fast Correction of Network Parameter Errors. IEEE Trans. Power Syst. 2018, 33, 1095–1096. [Google Scholar] [CrossRef]
- Carvalho, B.; Bretas, N.; Bretas, A. A local state vector augmentation technique for processing network parameters errors. In Proceedings of the 2017 IEEE Power Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Wang, Q.; Tai, W.; Tang, Y.; Ni, M.; You, S. A two-layer game theoretical attack-defense model for a false data injection attack against power systems. Int. J. Electr. Power Energy Syst. 2019, 104, 169–177. [Google Scholar] [CrossRef]
- Bansal, P.; Singh, A. Smart metering in smart grid framework: A review. In Proceedings of the 2016 Fourth International Conference on Parallel, Distributed and Grid Computing (PDGC), Waknaghat, India, 22–24 December 2016; pp. 174–176. [Google Scholar]
- Bretas, A.S.; Bretas, N.G.; Carvalho, B.; Baeyens, E.; Khargonekar, P.P. Smart grids cyber-physical security as a malicious data attack: An innovation approach. Electr. Power Syst. Res. 2017, 149, 210–219. [Google Scholar] [CrossRef]
- Zou, T.; Bretas, A.S.; Aljohani, N.; Bretas, N.G. Malicious data injection attacks: A relaxed physics model based strategy for real-time monitoring. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar]
- Nagaraj, K.; Aljohani, N.; Zou, S.; Ruben, C.; Bretas, A.; Zare, A.; McNair, J. State Estimator and Machine Learning Analysis of Residual Differences to Detect and Identify FDI and Parameter Errors in Smart Grids. In Proceedings of the 2020 North American Power Symposium (NAPS), Tempe, AZ, USA, 11–13 April 2020; pp. 1–6. [Google Scholar]
- Bretas, N.G.; Bretas, A.S. The extension of the Gauss approach for the solution of an overdetermined set of algebraic non linear equations. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1269–1273. [Google Scholar] [CrossRef]
- Zou, T.; Bretas, A.S.; Ruben, C.; Dhulipala, S.C.; Bretas, N. Smart grids cyber-physical security: Parameter correction model against unbalanced false data injection attacks. Electr. Power Syst. Res. 2020, 187, 106490. [Google Scholar] [CrossRef]
- Bretas, A.S.; Rossoni, A.; Trevizan, R.D.; Bretas, N.G. Distribution networks nontechnical power loss estimation: A hybrid data-driven physics model-based framework. Electr. Power Syst. Res. 2020, 186, 106397. [Google Scholar] [CrossRef]
- Bretas, A.S.; Bretas, N.G.; London, J.B.; Carvalho, B.E. Cyber-Physical Power Systems State Estimation; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Christie, R. Power Systems Test Case Archive; Electrical Engineering Department, University of Washington: Washington, DC, USA, 2000. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Oliphant, T.E. A Guide to NumPy; 2006; Volume 1, Available online: https://ecs.wgtn.ac.nz/foswiki/pub/Support/ManualPagesAndDocumentation/numpybook.pdf (accessed on 26 August 2021).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Contributors, S. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]



| Processing Measurement Cyber-Attack Step 1 | ||
|---|---|---|
| J (x) = 1246.587 > C = 775.1861 Attack Detected! | ||
| Descending List | ||
| Measurement | ||
| 0.0395 | −8.4156 | |
| 3.9464 | 6.9948 | |
| 0.1380 | 5.9432 | |
| 0.3557 | 5.5826 | |
| 0.4774 | −4.4724 | |
| 3.9464 | 3.9948 | |
| Parameter Correction | ||||
|---|---|---|---|---|
| Parameter | Database | Erroneous | Presented Correction (Approximation Error) | State-of-the-Art Correction (Approximation Error) [31] |
| 2.2169 | 1.8179 | 2.2285 | 2.2385 | |
| −8.0635 | −9.0311 | −8.0782 | −8.0854 | |
| 0.0587 | 0.0551 | 0.0586 | 0.0589 | |
| Processing Measurement Cyber-Attack Step 1 | ||
|---|---|---|
| J (x) = 1133.8323 > C = 775.1861 Attack Detected! | ||
| Descending List | ||
| Measurement | ||
| 1.9344 | 15.6324 | |
| 0.2513 | 9.2054 | |
| 4.8151 | −7.8438 | |
| 6.0617 | −7.6539 | |
| 0.3380 | 6.2045 | |
| 2.8898 | 5.6933 | |
| 6.6911 | 4.2257 | |
| Parameter Correction | ||||
|---|---|---|---|---|
| Parameter | Database | Erroneous | Presented Correction (Approximation Error) | State-of-the-art Correction (Approximation Error) [31] |
| 1.0012 | 1.1314 | 1.0062 | 1.0088 | |
| −3.2955 | −3.0648 | −3.2876 | −3.2826 | |
| 0.0355 | 0.0383 | 0.035532 | 0.0357 | |
| Processing Measurement Cyber-Attack Step 1 | |||
|---|---|---|---|
| Attack Detected! | |||
| Descending List | |||
| Measurement | |||
| 2.8541 | 5.2318 | 5.2044 | |
| Measurement Correction | |||
|---|---|---|---|
| Measurement | Database | Erroneous | Correction Using CNE (Approximation Error) [30] |
| −0.1754 | −0.1643 | −0.1761 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, T.; Aljohani, N.; Nagaraj, K.; Zou, S.; Ruben, C.; Bretas, A.; Zare, A.; McNair, J. A Network Parameter Database False Data Injection Correction Physics-Based Model: A Machine Learning Synthetic Measurement-Based Approach. Appl. Sci. 2021, 11, 8074. https://doi.org/10.3390/app11178074
Zou T, Aljohani N, Nagaraj K, Zou S, Ruben C, Bretas A, Zare A, McNair J. A Network Parameter Database False Data Injection Correction Physics-Based Model: A Machine Learning Synthetic Measurement-Based Approach. Applied Sciences. 2021; 11(17):8074. https://doi.org/10.3390/app11178074
Chicago/Turabian StyleZou, Tierui, Nader Aljohani, Keerthiraj Nagaraj, Sheng Zou, Cody Ruben, Arturo Bretas, Alina Zare, and Janise McNair. 2021. "A Network Parameter Database False Data Injection Correction Physics-Based Model: A Machine Learning Synthetic Measurement-Based Approach" Applied Sciences 11, no. 17: 8074. https://doi.org/10.3390/app11178074
APA StyleZou, T., Aljohani, N., Nagaraj, K., Zou, S., Ruben, C., Bretas, A., Zare, A., & McNair, J. (2021). A Network Parameter Database False Data Injection Correction Physics-Based Model: A Machine Learning Synthetic Measurement-Based Approach. Applied Sciences, 11(17), 8074. https://doi.org/10.3390/app11178074







