Analytical Prediction of Balling, Lack-of-Fusion and Keyholing Thresholds in Powder Bed Fusion
Abstract
:Featured Application
Abstract
1. Introduction
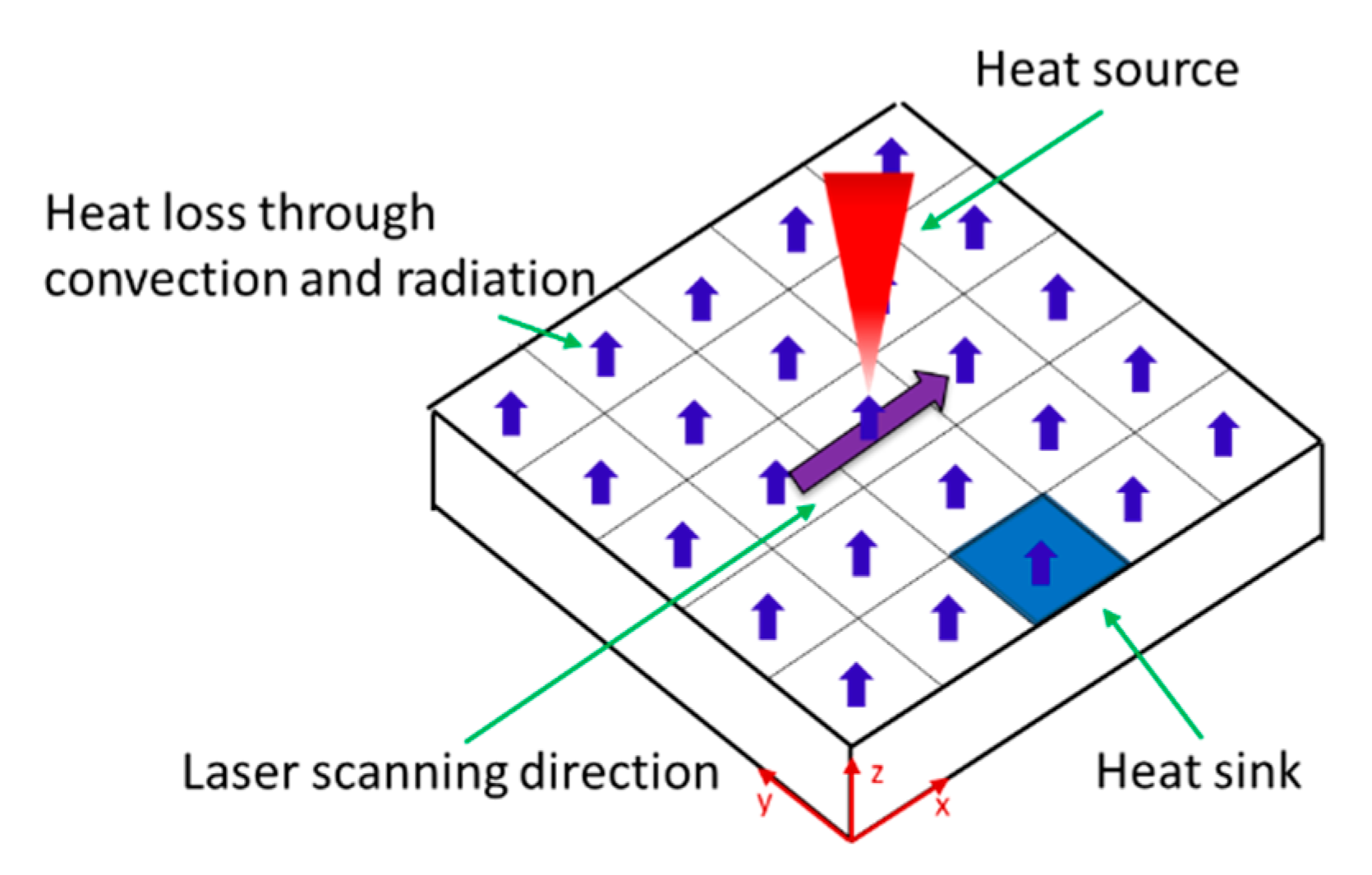
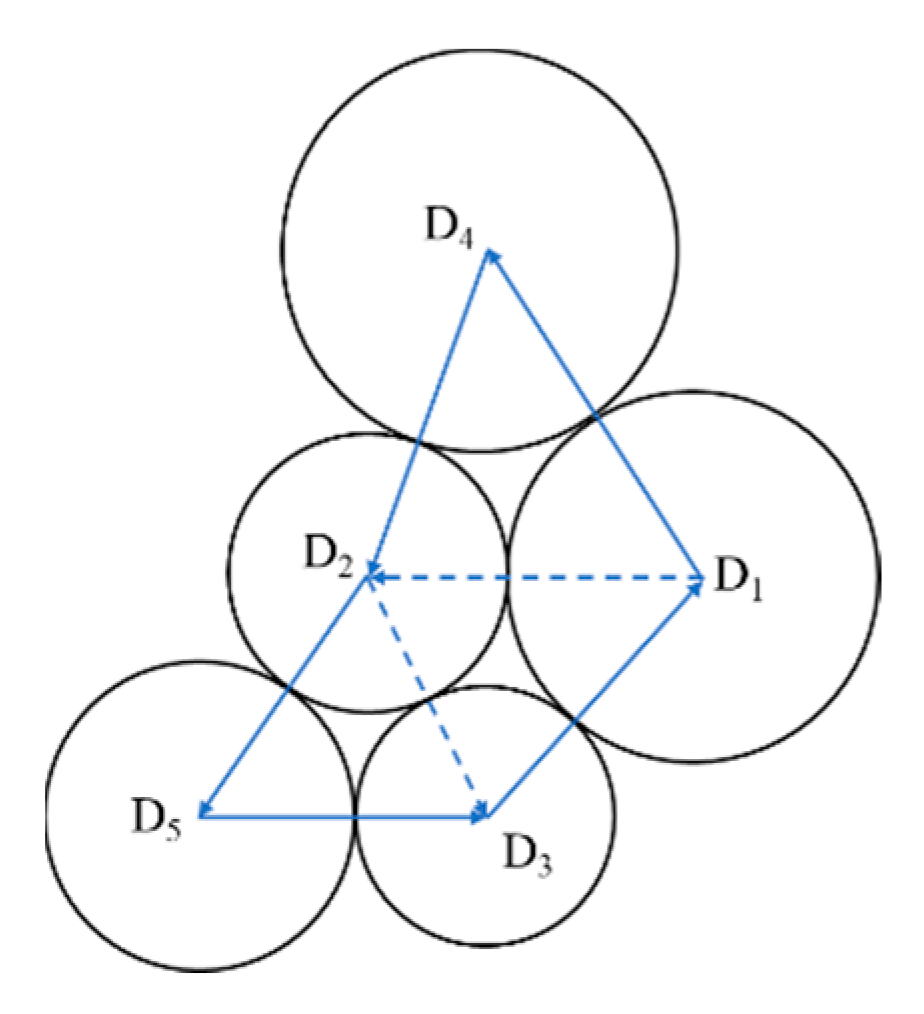
2. Analytical Modeling
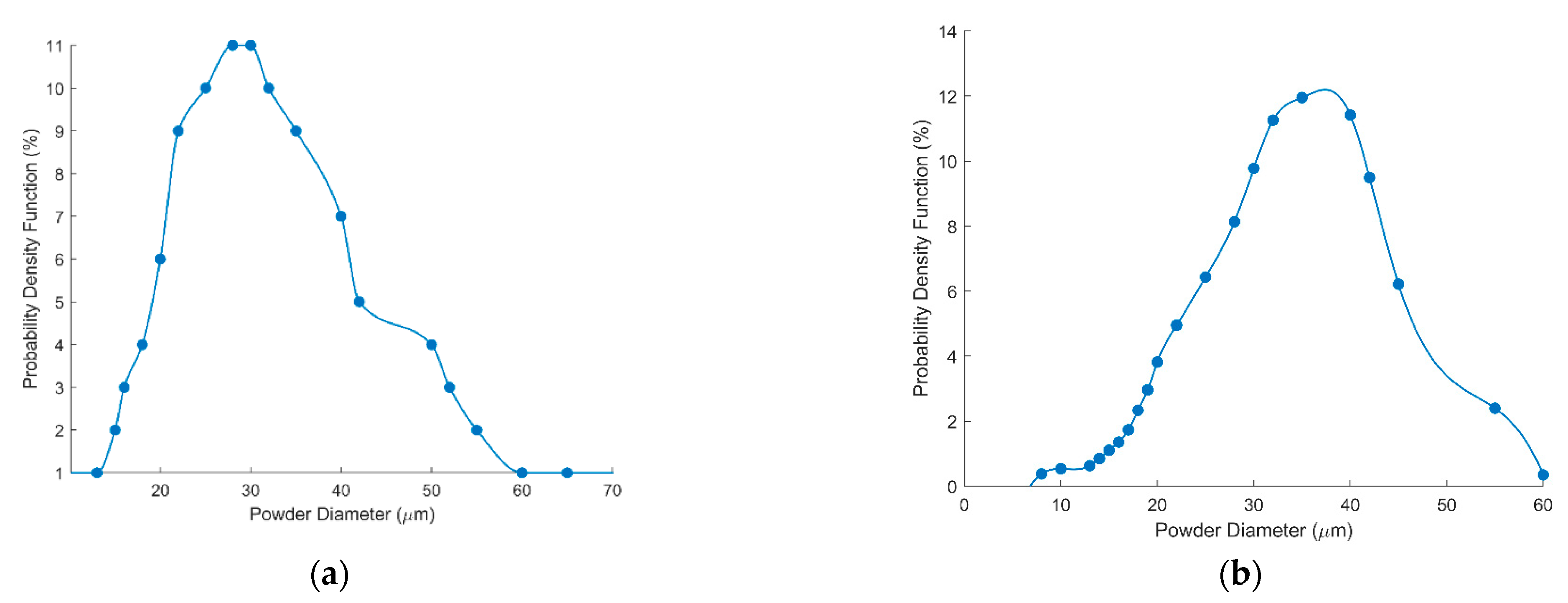
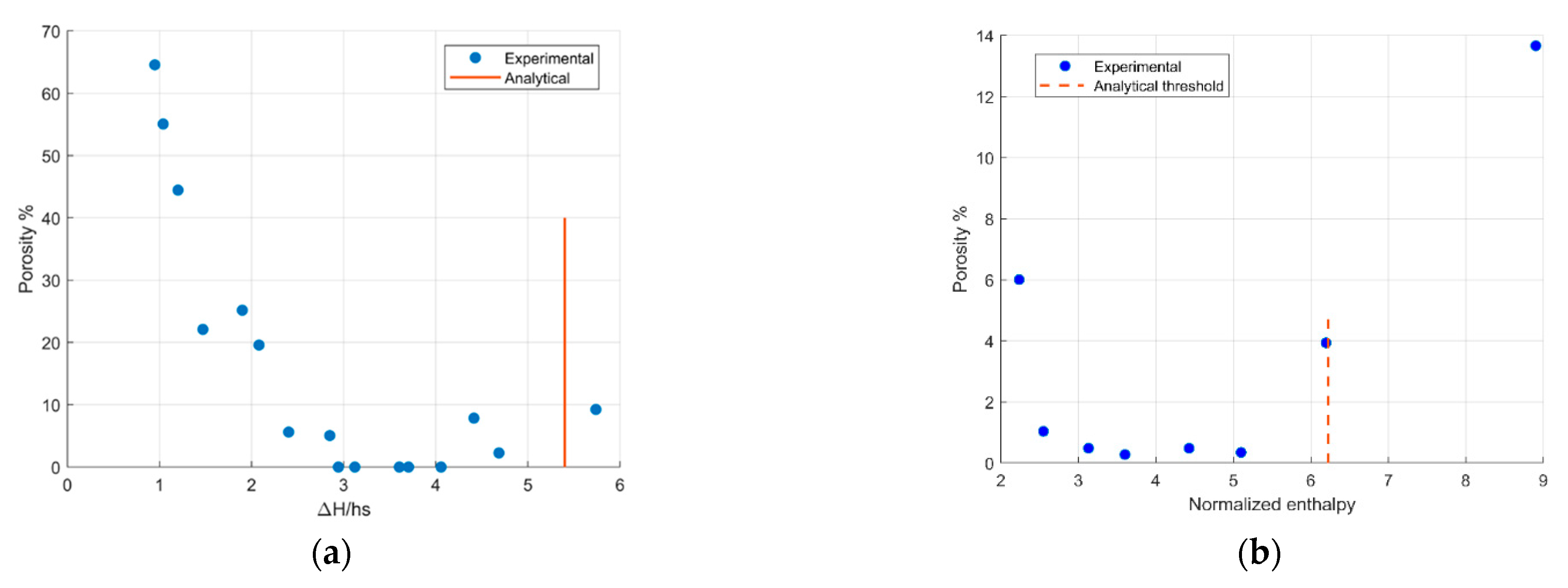
3. Experimental Validation and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cunningham, R.; Zhao, C.; Parab, N.; Kantzos, C.; Pauza, J.; Fezzaa, K.; Sun, T.; Rollett, A.D. Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed x-ray imaging. Science 2019, 363, 849–852. [Google Scholar] [CrossRef]
- Hojjatzadeh, S.M.H.; Parab, N.D.; Yan, W.; Guo, Q.; Xiong, L.; Zhao, C.; Qu, M.; Escano, L.I.; Xiao, X.; Fezzaa, K.; et al. Pore elimination mechanisms during 3D printing of metals. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sheridan, L.; Scott-Emuakpor, O.E.; George, T.; Gockel, J.E. Relating porosity to fatigue failure in additively manufactured alloy 718. Mater. Sci. Eng. A 2018, 727, 170–176. [Google Scholar] [CrossRef]
- Tang, M.; Pistorius, P.C. Oxides, porosity and fatigue performance of AlSi10Mg parts produced by selective laser melting. Int. J. Fatigue 2017, 94, 192–201. [Google Scholar] [CrossRef]
- Ning, J.; Wang, W.; Zamorano, B.; Liang, S.Y. Analytical modeling of lack-of-fusion porosity in metal additive manufacturing. Appl. Phys. A 2019, 125, 1–11. [Google Scholar] [CrossRef]
- Tang, M.; Pistorius, P.C.; Beuth, J.L. Prediction of lack-of-fusion porosity for powder bed fusion. Addit. Manuf. 2017, 14, 39–48. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Yang, Y.; Xiao, D. Theoretical and experimental study on surface roughness of 316L stainless steel metal parts obtained through selective laser melting. Rapid Prototyp. J. 2016, 22, 706–716. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.C. Analytical evaluation of defect generation for selective laser melting of metals. Int. J. Adv. Manuf. Technol. 2019, 103, 1185–1198. [Google Scholar] [CrossRef]
- Vastola, G.; Pei, Q.X.; Zhang, Y.W. Predictive model for porosity in powder-bed fusion additive manufacturing at high beam energy regime. Addit. Manuf. 2018, 22, 817–822. [Google Scholar] [CrossRef]
- Dilip, J.J.S.; Zhang, S.; Teng, C.; Zeng, K.; Robinson, C.; Pal, D.; Stucker, B. Influence of processing parameters on the evolution of melt pool, porosity, and microstructures in Ti-6Al-4V alloy parts fabricated by selective laser melting. Prog. Addit. Manuf. 2017, 2, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, S.; Starr, T.; Chou, K. A study of keyhole porosity in selective laser melting: Single-track scanning with micro-CT analysis. J. Manuf. Sci. Eng. 2019, 141, 071004. [Google Scholar] [CrossRef]
- Zhao, C.; Fezzaa, K.; Cunningham, R.W.; Wen, H.; De Carlo, F.; Chen, L.; Rollett, A.D.; Sun, T. Real-time monitoring of laser powder bed fusion process using high-speed X-ray imaging and diffraction. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Bayat, M.; Thanki, A.; Mohanty, S.; Witvrouw, A.; Yang, S.; Thorborg, J.; Tiedje, N.S.; Hattel, J.H. Keyhole-induced porosities in Laser-based Powder Bed Fusion (L-PBF) of Ti6Al4V: High-fidelity modelling and experimental validation. Addit. Manuf. 2019, 30, 100835. [Google Scholar] [CrossRef]
- Bruna-Rosso, C.; Demir, A.G.; Previtali, B. Selective laser melting finite element modeling: Validation with high-speed imaging and lack of fusion defects prediction. Mater. Des. 2018, 156, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.S.; Zhang, W. Modeling of heat transfer, fluid flow and solidification microstructure of nickel-base superalloy fabricated by laser powder bed fusion. Addit. Manuf. 2016, 12, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Van Elsen, M.; Baelmans, M.; Mercelis, P.; Kruth, J.P. Solutions for modelling moving heat sources in a semi-infinite medium and applications to laser material processing. Int. J. Heat Mass Transf. 2007, 50, 4872–4882. [Google Scholar] [CrossRef]
- Ning, J.; Mirkoohi, E.; Dong, Y.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Analytical modeling of 3D temperature distribution in selective laser melting of Ti-6Al-4V considering part boundary conditions. J. Manuf. Process. 2019, 44, 319–326. [Google Scholar] [CrossRef]
- Ji, X.; Mirkoohi, E.; Ning, J.; Liang, S.Y. Analytical modeling of post-printing grain size in metal additive manufacturing. Opt. Lasers Eng. 2020, 124, 105805. [Google Scholar] [CrossRef]
- Ning, J.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Analytical modeling of part porosity in metal additive manufacturing. Int. J. Mech. Sci. 2020, 172, 105428. [Google Scholar] [CrossRef]
- Carslaw, H.; Jaeger, J. Conduction of Heat in Solids; Oxford Science Publication: Oxford, UK, 1990. [Google Scholar]
- Feng, Y.T.; Han, K.; Owen, D.R.J. Filling domains with disks: An advancing front approach. Int. J. Numer. Methods Eng. 2003, 56, 699–713. [Google Scholar] [CrossRef]
- Xing, J.; Sun, W.; Rana, R.S.; Senior Member IEEE. 3D modeling and testing of transient temperature in selective laser sintering (SLS) process. Optik 2013, 124, 301–304. [Google Scholar] [CrossRef]
- Ning, J.; Wang, W.; Ning, X.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Analytical thermal modeling of powder bed metal additive manufacturing considering powder size variation and packing. Materials 2020, 13, 1988. [Google Scholar] [CrossRef] [PubMed]
- Yadroitsev, I.; Gusarov, A.; Yadroitsava, I.; Smurov, I. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 2010, 210, 1624–1631. [Google Scholar] [CrossRef]
- King, W.E.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mater. Process. Technol. 2014, 214, 2915–2925. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Starr, T.; Stucker, B. Analysis of defect generation in Ti–6Al–4V parts made using powder bed fusion additive manufacturing processes. Addit. Manuf. 2014, 1, 87–98. [Google Scholar] [CrossRef]
- Choi, J.P.; Shin, G.H.; Yang, S.; Yang, D.Y.; Lee, J.S.; Brochu, M.; Yu, J.H. Densification and microstructural investigation of Inconel 718 parts fabricated by selective laser melting. Powder Technol. 2017, 310, 60–66. [Google Scholar] [CrossRef]
- Yang, Y.; Knol, M.F.; Van Keulen, F.; Ayas, C. A semi-analytical thermal modelling approach for selective laser melting. Addit. Manuf. 2018, 21, 284–297. [Google Scholar] [CrossRef] [Green Version]
- Roberts, I.A.; Wang, C.J.; Esterlein, R.; Stanford, M.; Mynors, D.J. A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tools Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Philo, A.M.; Mehraban, S.; Holmes, M.; Sillars, S.; Sutcliffe, C.J.; Sienz, J.; Brown, S.G.; Lavery, N.P. A pragmatic continuum level model for the prediction of the onset of keyholing in laser powder bed fusion. Int. J. Adv. Manuf. Technol. 2019, 101, 697–714. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Liu, J.; Shi, Y.; Wang, L.; Jiang, W. Balling behavior of stainless steel and nickel powder during selective laser melting process. Int. J. Adv. Manuf. Technol. 2012, 59, 1025–1035. [Google Scholar] [CrossRef]


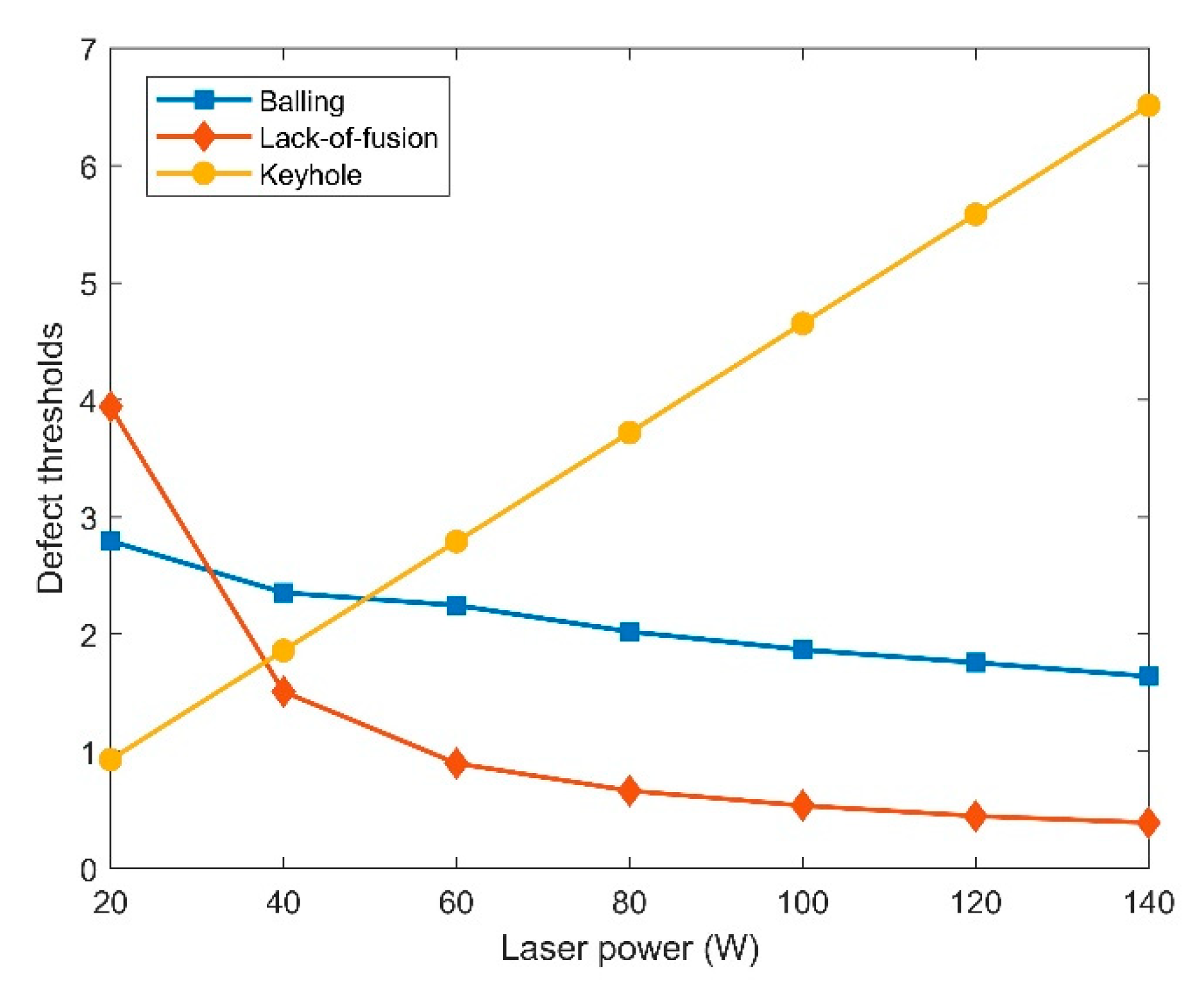
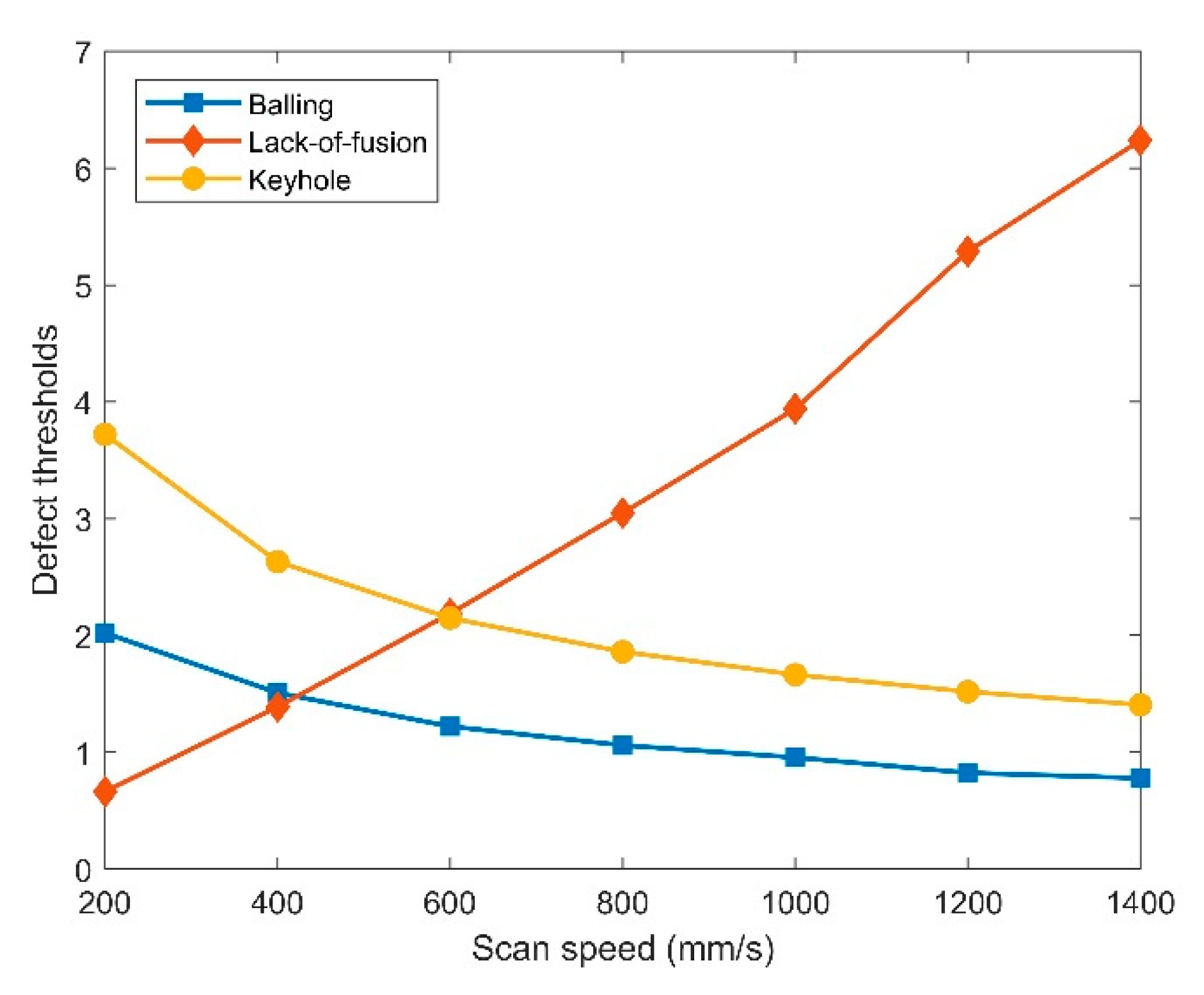
| Power (W) | Scanning Speed (mm/s) | Computed Molten Pool Depth (µm) | Computed Molten Pool Width (µm) | Energy Density (J/mm3) | Measured Porosity (%) | |
|---|---|---|---|---|---|---|
| 40 | 1200 | 20.2 | 38.1 | 11.1 | 22.6 | 9.1 |
| 40 | 1080 | 22.2 | 42.1 | 12.3 | 19.5 | 7.5 |
| 40 | 960 | 24.2 | 46.1 | 13.9 | 17.7 | 6.2 |
| 40 | 840 | 24.2 | 50.1 | 15.9 | 15.1 | 5.5 |
| 40 | 720 | 28.3 | 54.1 | 18.5 | 11.9 | 4.5 |
| 40 | 600 | 30.3 | 58.1 | 22.2 | 9.3 | 3.9 |
| 40 | 480 | 34.3 | 66.1 | 27.8 | 4.7 | 3.0 |
| 40 | 360 | 38.4 | 74.1 | 37.0 | 2.4 | 2.4 |
| 40 | 240 | 44.4 | 90.2 | 55.6 | 0.7 | 1.7 |
| 40 | 120 | 56.6 | 114.2 | 111.1 | 0.6 | 1.0 |
| Power (W) | Scanning Speed (mm/s) | Computed Molten Pool Depth (µm) | Computed Molten Pool Width (µm) | Energy Density (J/mm3) | Measured Porosity (%) | ||
|---|---|---|---|---|---|---|---|
| 90 | 1600 | 14.1 | 26.1 | 28.1 | 13.4 | 12.6 | 1.7 |
| 90 | 1200 | 18.2 | 34.1 | 37.5 | 3.8 | 7.4 | 2.0 |
| 90 | 800 | 24.2 | 46.1 | 56.3 | 0.3 | 4.1 | 2.4 |
| 90 | 600 | 28.3 | 54.1 | 75.0 | 0.4 | 3.0 | 2.8 |
| 90 | 400 | 38.4 | 74.1 | 112.5 | 0.4 | 1.6 | 3.4 |
| 90 | 300 | 46.5 | 90.2 | 150.0 | 0.5 | 1.1 | 4.0 |
| 90 | 200 | 60.6 | 118.2 | 225.0 | 0.9 | 0.6 | 4.9 |
| 90 | 100 | 88.9 | 174.3 | 450.0 | 5.9 | 0.3 | 6.9 |
| Name | Symbol | Ti6Al4V | Inconel 718 | SS316L | Unit |
|---|---|---|---|---|---|
| Density | ρ | 4428 | 8220 | 7633 | kg/m3 |
| Thermal conductivity | k | 18.4 | 11 | 25 | W/(m·°C) |
| Specific heat | c | 517 | 420 | 594 | J/(kg·°C) |
| Absorption | η | 0.48 | 0.4 | 0.35 | 1 |
| Room temperature | T0 | 20 | 20 | 20 | °C |
| Boiling temperature | Tb | / | 2917 | / | °C |
| Melting temperature | Tm | 1655 | 1336 | 1400 | °C |
| Heat convection coefficient | h | 24 | 25 | 24 | W/(m2·°C) |
| Emissivity | ε | 0.9 | 0.8 | 0.26 | 1 |
| Powder Number | Powder Bed Porosity (%) | |
|---|---|---|
| Inconel 718 | Ti6Al4V | |
| 100 | 13.66 | 12.87 |
| 200 | 14.01 | 13.21 |
| 300 | 13.96 | 12.62 |
| 400 | 13.29 | 12.76 |
| 500 | 12.41 | 12.95 |
| Average | 13.47 | 12.88 |
| Power (W) | Scanning Speed (mm/s) | Computed Molten Pool Width (µm) | Computed Molten Pool Length (µm) | |
|---|---|---|---|---|
| 190 | 20 | 427.1 | 481.0 | 2.8 |
| 190 | 50 | 306.5 | 424.8 | 2.3 |
| 190 | 150 | 185.9 | 372.7 | 1.6 |
| 190 | 200 | 155.8 | 362.7 | 1.3 |
| 190 | 250 | 135.7 | 354.7 | 1.2 |
| 190 | 300 | 125.6 | 350.7 | 1.1 |
| 190 | 350 | 105.5 | 346.7 | 1.0 |
| 190 | 400 | 105.5 | 342.7 | 1.0 |
| 190 | 450 | 95.5 | 340.7 | 0.9 |
| 190 | 500 | 85.4 | 338.7 | 0.8 |
| Power (W) | Scanning Speed (mm/s) | Energy Density (J/mm3) | Measured Porosity (%) | |
|---|---|---|---|---|
| 50 | 500 | 33 | 22.1 | 1.5 |
| 50 | 750 | 22 | 44.4 | 1.2 |
| 50 | 1000 | 16 | 55.1 | 1.0 |
| 50 | 1200 | 13 | 64.6 | 0.9 |
| 100 | 500 | 66 | 0 | 2.9 |
| 100 | 750 | 44 | 5.6 | 2.4 |
| 100 | 1000 | 33 | 19.6 | 2.1 |
| 100 | 1200 | 27 | 25.2 | 1.9 |
| 150 | 500 | 100 | 7.8 | 4.4 |
| 150 | 750 | 66 | 0 | 3.6 |
| 150 | 1000 | 50 | 0 | 3.1 |
| 150 | 1200 | 41 | 5.1 | 2.8 |
| 195 | 500 | 130 | 9.2 | 5.7 |
| 195 | 750 | 86 | 2.3 | 4.7 |
| 195 | 1000 | 65 | 0 | 4.1 |
| 195 | 1200 | 54 | 0 | 3.7 |
| Power (W) | Scanning Speed (mm/s) | ||||||
|---|---|---|---|---|---|---|---|
| 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | |
| 20 | LOF | LOF | LOF | LOF | LOF | LOF | LOF |
| 40 | LOF | LOF | LOF | LOF | LOF | LOF | LOF |
| 60 | No | LOF | LOF | LOF | LOF | LOF | Balling |
| 80 | No | LOF | LOF | LOF | Balling | Balling | Balling |
| 100 | No | LOF | LOF | Balling | Balling | Balling | Balling |
| 120 | Keyhole | No | LOF | Balling | Balling | Balling | Balling |
| 140 | Keyhole | No | Balling | Balling | Balling | Balling | Balling |
| 160 | Keyhole | No | Balling | Balling | Balling | Balling | Balling |
| 180 | Keyhole | Keyhole | Balling | Balling | Balling | Balling | Balling |
| 200 | Keyhole | Keyhole | Balling | Balling | Balling | Balling | Balling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Ning, J.; Liang, S.Y. Analytical Prediction of Balling, Lack-of-Fusion and Keyholing Thresholds in Powder Bed Fusion. Appl. Sci. 2021, 11, 12053. https://doi.org/10.3390/app112412053
Wang W, Ning J, Liang SY. Analytical Prediction of Balling, Lack-of-Fusion and Keyholing Thresholds in Powder Bed Fusion. Applied Sciences. 2021; 11(24):12053. https://doi.org/10.3390/app112412053
Chicago/Turabian StyleWang, Wenjia, Jinqiang Ning, and Steven Y. Liang. 2021. "Analytical Prediction of Balling, Lack-of-Fusion and Keyholing Thresholds in Powder Bed Fusion" Applied Sciences 11, no. 24: 12053. https://doi.org/10.3390/app112412053
APA StyleWang, W., Ning, J., & Liang, S. Y. (2021). Analytical Prediction of Balling, Lack-of-Fusion and Keyholing Thresholds in Powder Bed Fusion. Applied Sciences, 11(24), 12053. https://doi.org/10.3390/app112412053









