1. Introduction
The latent heat thermal energy storage (LHTES) units are compact storage systems, benefiting the latent heat energy of phase change materials (PCMs). The LHTES units are practical in various parts of energy systems such as solar thermal energy storage [
1], seasonal thermal energy storage [
2], thermal load management [
3], building cooling [
4], electronic thermal management [
5], and battery thermal management [
6].
The heat storage density of a latent heat thermal energy storage for a PCMs base system is high compared to sensible heat. The PCMs could absorb the excess heat of thermal systems and phase change from a solid to molten state (thermal charging). Later, they can release the heat and phase change from liquid to solid during a discharge process.
The thermal conductivity of most of these materials is poor [
7]. They cannot absorb/release energy in a reasonable time. Therefore, the main shortcoming of PCMs in LHTES units is their low heat transfer capability and long charging time and discharging process. The increase of the heat transfer rate of PMC base LHTES is a hot topic that demands further research. Some of the possible approaches for improving the heat transfer are geometrical enhancement by enhancing the shape of PCM container [
8,
9] or tube placement [
9], invoking extended surfaces and fins [
10,
11], heatpipes [
12,
13], metal foams [
14,
15], and nanoadditives [
16,
17].
Some researchers tried to use a combination of enhancement approaches to further improve the heat transfer in LHTESs and reduce the charging/discharging time. For example, Sardari et al. [
18] employed aluminum foams to design a compact wall-mounted LHTES unit for domestic applications. The LHTES unit is mounted in the gap space between a heating radiator and the wall and recovers the waste heat during its charging process. Later, it releases the heat to the room when the main heating system (radiator) is offline. The impact of various foam porosities was investigated. The results showed that an aluminum foam with a high porosity of 97% is adequate for heat transfer improvement since the heating loads were smooth. The foam could reduce the charging time by 95%. Hoseinzadeh et al. [
19] applied two different types of PCMs along in a channel passage and improved the thermal energy storage rate. Talebizadehsardari et al. [
20] applied metal foams to improve the PCM’s thermal conductivity and then tried to find the best geometrical design for heat transfer channels. They found that the geometrical design of channels in the presence of metal foams could fairly control the discharging time and uniform discharge capabilities of the LHTES unit.
Boukani et al. [
21] employed copper nanoparticles to improve the thermal conductivity of n-octadecane paraffin. The nano-enhanced phase change material (NePCM) was used in an elliptical shape enclosure. The authors investigated the influence of nanoadditives and the geometrical aspect ratio of the enclosure on the unit’s thermal charging performance. They found that nanoparticles and an elliptical enclosure with a high aspect ratio would improve the melting rate.
The natural convection effects are important in most LHTES designs when a significant portion of a unit is molten. The liquid PCM can circulate in the enclosure and contributes to the heat transfer by the natural convection mechanism. Mahdi et al. [
22] investigated the impact of fin arrangements to enhance the melting heat transfer in a shell-tube LHTES unit. The conduction heat transfer was improved using thermal conductive metal fins in the initial stages of the melting process. Moreover, there could be natural convection circulation after the melting of PCM, and the aim was to avoid the suppression of the natural convection circulations in the presence of the fins. They found that the natural convection flows tend to move upward, and thus, the top area of a unit can be melted down quickly. This is where the fins could suppress natural convection circulation. As a result, they used a few short fins at the top and more long fins at the bottom. Nie et al. [
23] utilized copper foams in a shell-tube shape LHTES unit. They modified the typical shell’s cylindrical shape to a conical shape to allow better natural convection circulation and improve the heat transfer rate. Invoking a conical shape for enclosure reduced the charging time by 9.2% for a pure PCM with no metal foam and 5.9% for a metal foam case.
As mentioned, PCMs suffer from poor thermal conductivity, and hence, the conduction heat transfer in a solid-PCM is weak. The thermal conductivity in a solid-PCM can be improved by using nanoparticles, metal foams, and fins. However, when some of the PCM melts down, the presence of nanoparticles increases the liquid viscosity and weakens the natural convection circulation. Metal foams resist the convection flows by imposing drag and friction forces on the moving liquid. The presence of fins also could block the circulation flows and suppress the natural convection. Thus, the design of an LHTES is a complex task as the internal hydrodynamic and convection heat transfer is under the influence of the molten PCM. In such systems, the conduction-dominant heat transfer mechanisms should be identified and improved in the initial charging stages, while the free convection mechanism in liquid PCM regions should be supported.
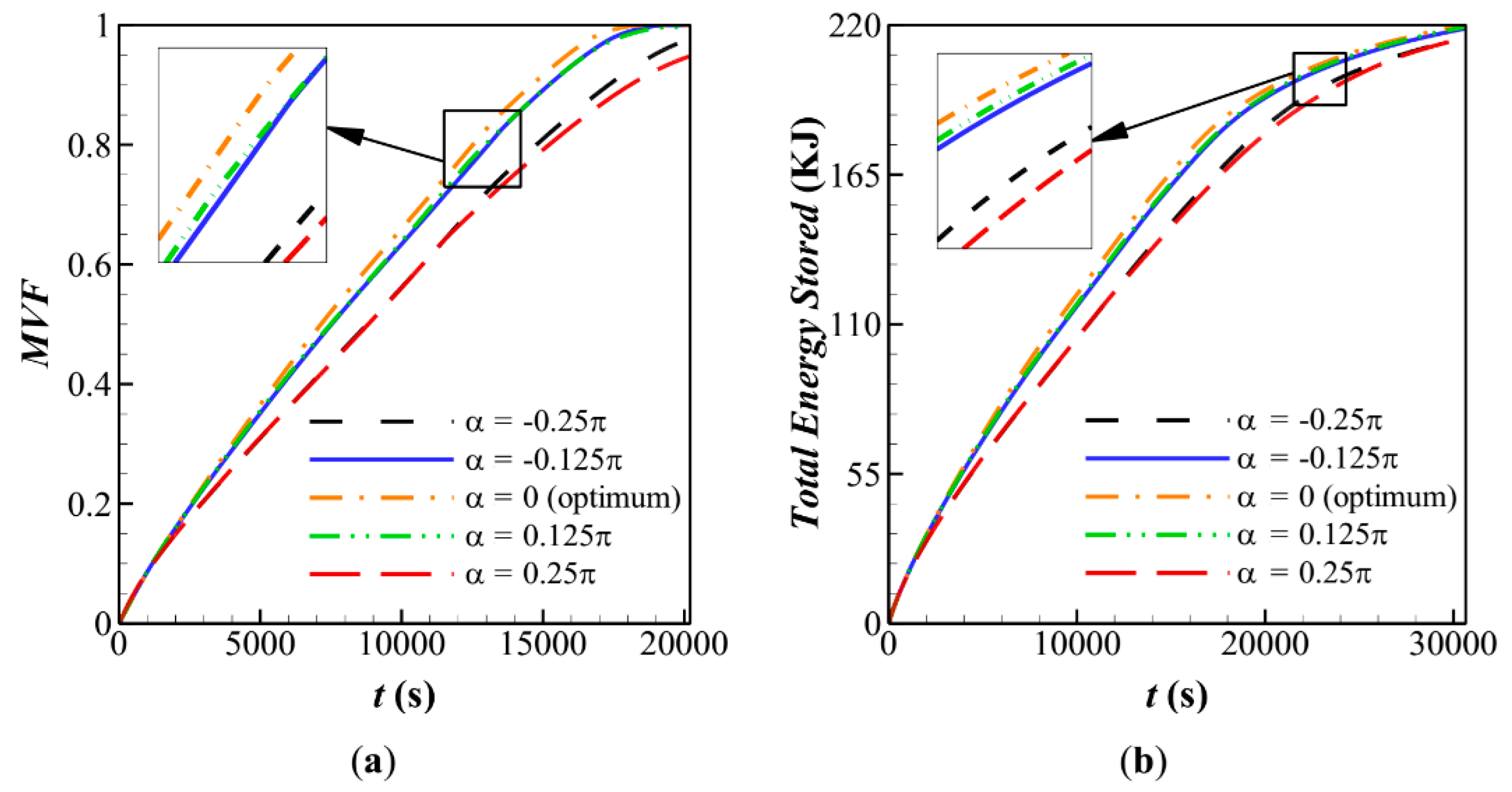
The present study aims to design a shell-tube LHTES unit with a conical shape shell and inclined fins to improve the conduction mechanism in the early stage of melting heat transfer but allow adequate space to benefit from later natural convection flows. The impact of various types of nanoparticles on the charging time is also investigated. An optimization method, the Taguchi method, is used to find an optimum design for the LHTES unit systematically.
2. Mathematical Model
In this work, a conical shell-and-tube with inclined copper fins used to store the latent heat energy is employed. As can be seen in
Figure 1a–d, the NePCM is poured into the conical units, and heat transfer fluid (HTF) passes the central copper tube. Since the tube’s thermal conductivity is high and its thickness is low, it can be ignored in the modeling process. Four different types of high thermal conductivity nano-sized particles are separately added to the pure PCM. The height of the unit is 20 cm, the inner radius of the HTF (heat transfer) tube is 0.5 cm, the outer radius of the normal unit is 5 cm. The volume of the unit is considered a constraint. The ratio of the lower radius of the conical unit to that of the normal unit is
AR. The thickness and height of the copper fins are 1 mm and 1 cm, respectively. The following assumptions are established in this study. (I) The volume changes of the NePCM during the melting is neglected; (II) the flow passing the tube and flow of the melted NePCM is laminar, incompressible, and Newtonian; (III) the linear Boussinesq approximation is reliable to model the effect of buoyancy. (IV) The nano-sized particles are considered to be spherical, and there are no sediment and accumulation. The thermal energy storage unit is axis-symmetric, and thus, a 2D axis-symmetric model of the unit is applied for the computations as depicted in
Figure 1d. Specifications of the HTF, pure PCM, and nano-sized particles are listed in
Table 1 and
Table 2.
A 2D axisymmetric model is employed to observe the melting process in the above-introduced system. The progressive melting front is captured by using the enthalpy-porosity approach with a fixed mesh. The controlling equations for the HTF, solid fins, and NePCM are as the following:
HTF domain:
htf denotes the properties of the HTF.
R and
z are the horizontal and vertical coordinates.
NePCM domain:
in which,
na refers to nano-sized particles properties,
LNP is the NePCM in the liquid phase,
LPP is the pure PCM in the liquid phase, and
fus is the fusion temperature of the pure PCM.
and
are considered to be equal to 5 × 10
5 and 10
−3.
SNP denotes the NePCM in the solid phase,
SPP, the pure PCM in the solid phase.
The imposed initial and boundary conditions are listed as follows:
At the interface of the HTF tube and NePCM domain:
At the outlet of the HTF tube:
The boundary conditions of the walls of the NePCM domain:
To obtain the total energy stored in the LHTES unit, the below-expressed relationship is employed:
The melted liquid fraction, MVF, can be defined as: