Solubility of Metal Precursors in Supercritical CO2: Measurements and Correlations
Abstract
1. Introduction
2. Results
2.1. Presentation of the Models Used
2.1.1. Density-Based Approaches
2.1.2. Equation of State Approaches
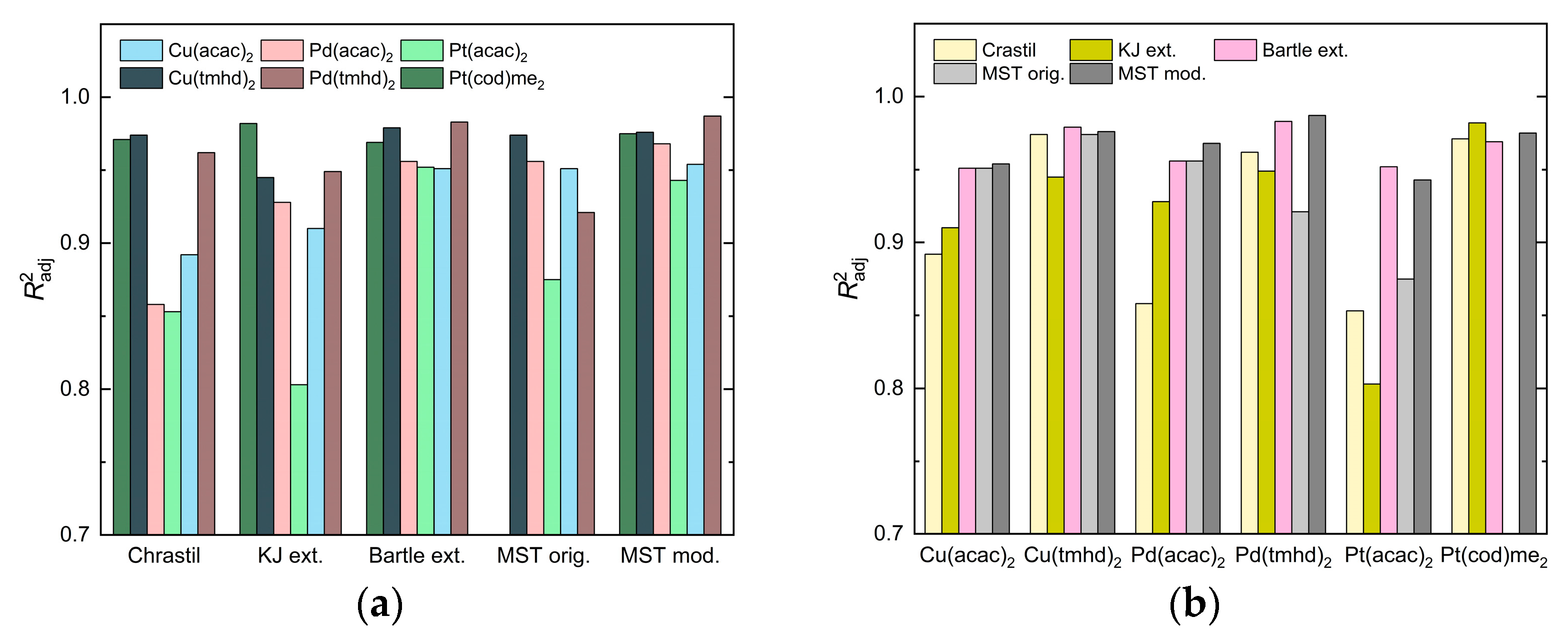
2.1.3. Evaluation of the Fitting Quality
2.2. Experimental Solubility Data
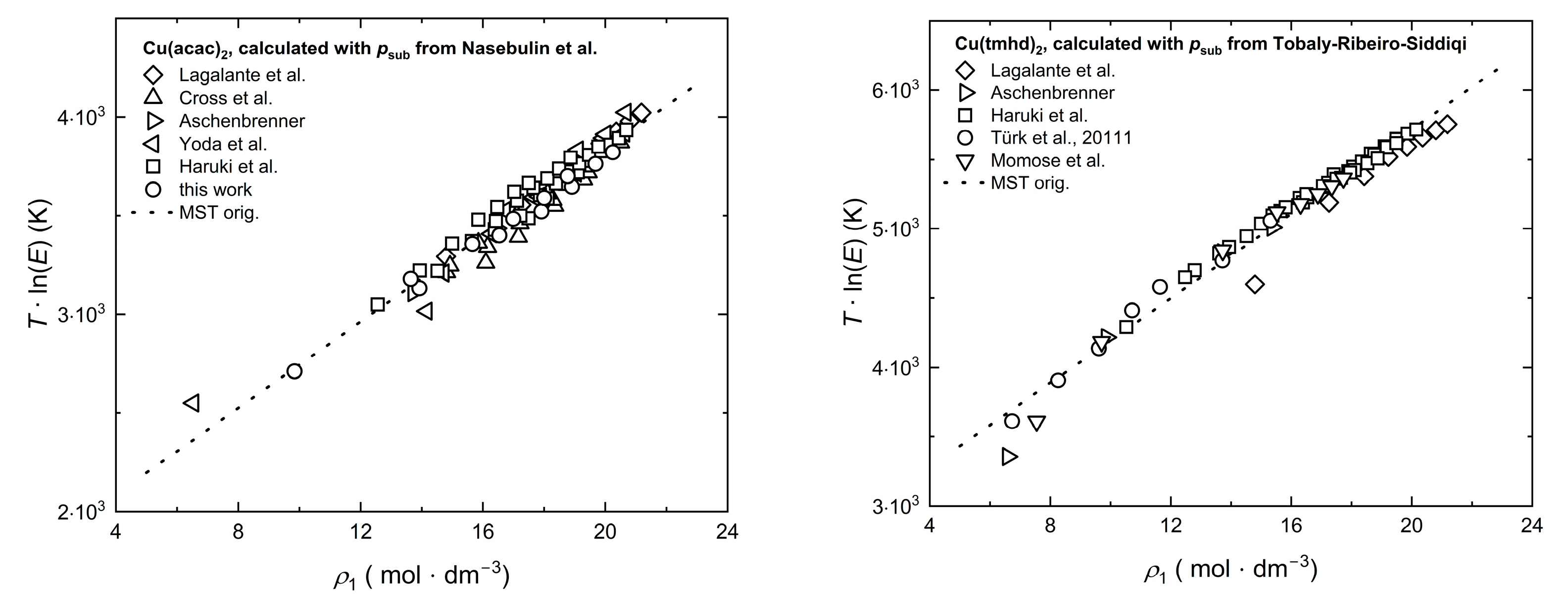
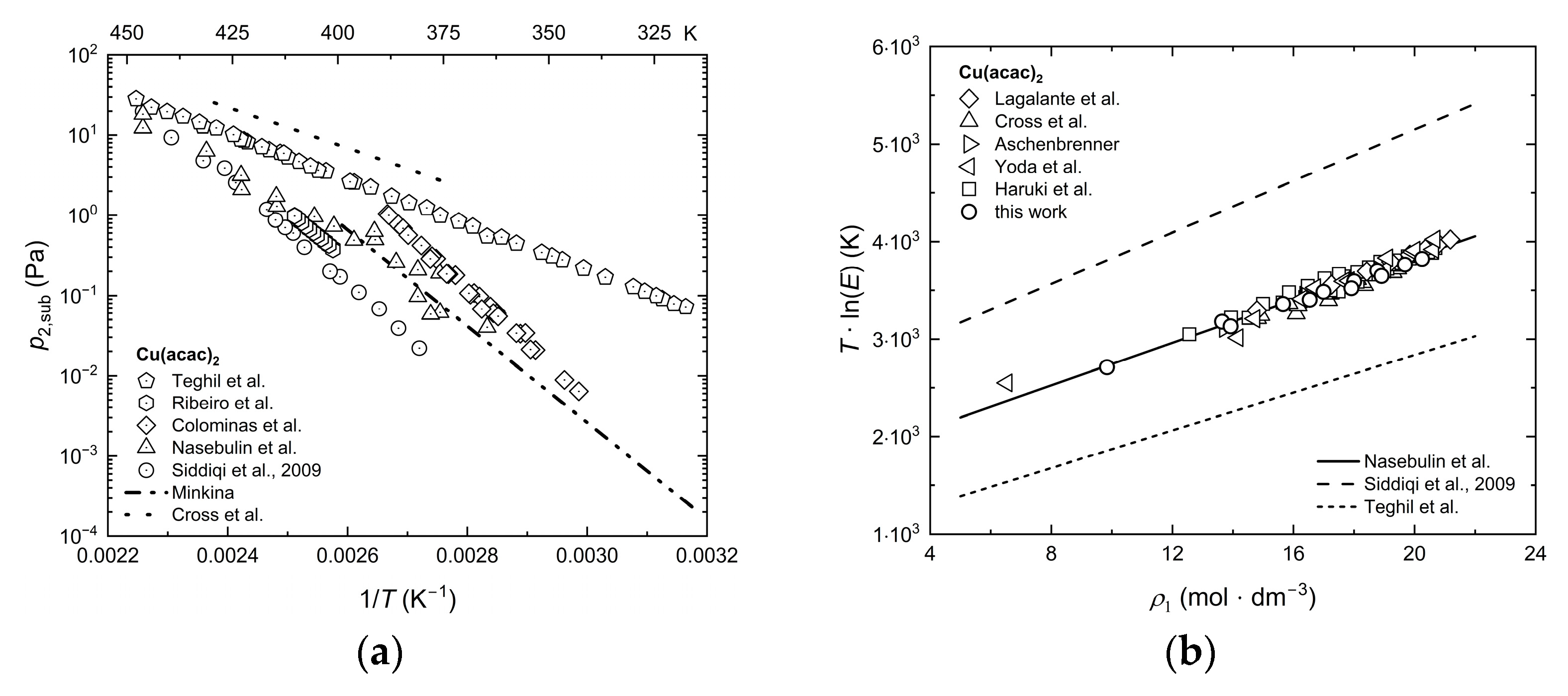
2.3. Experimental Sublimation Pressure Data from the Literature
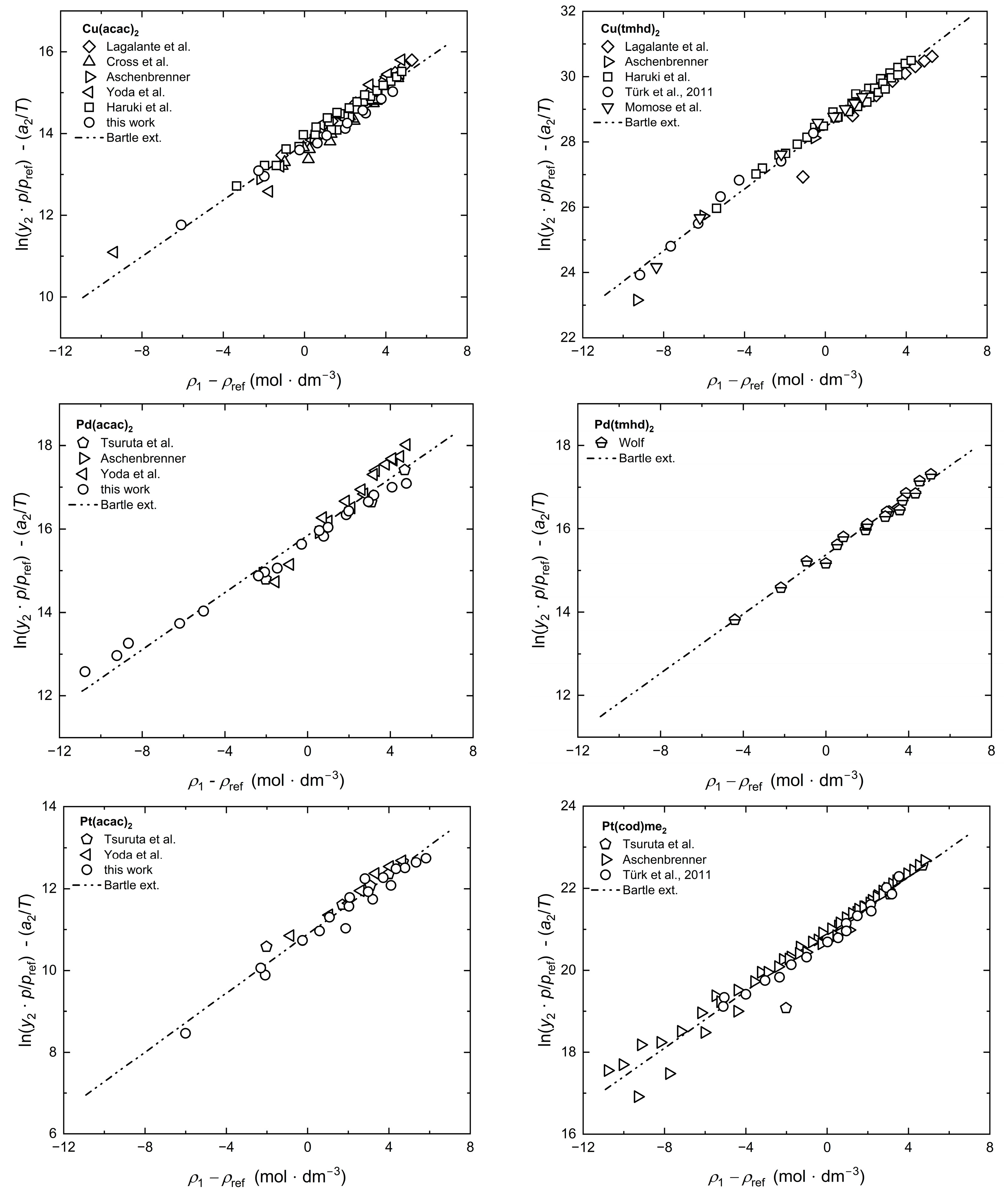
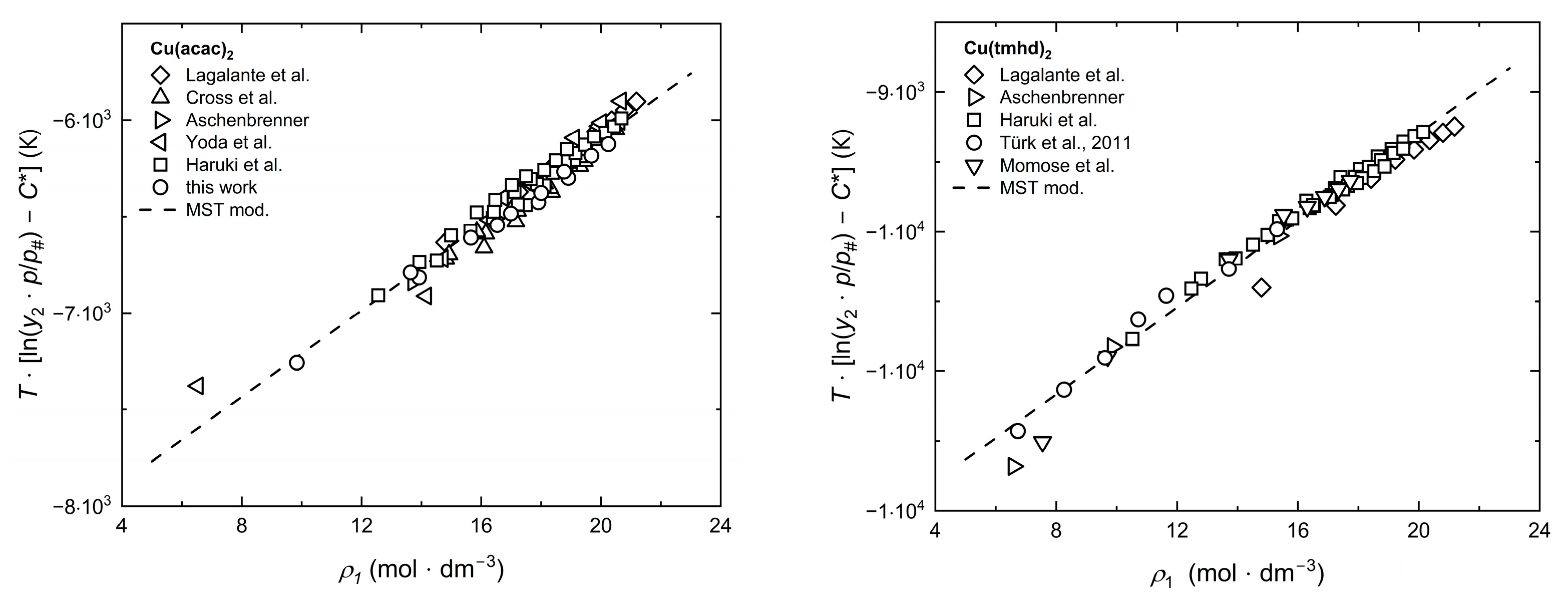
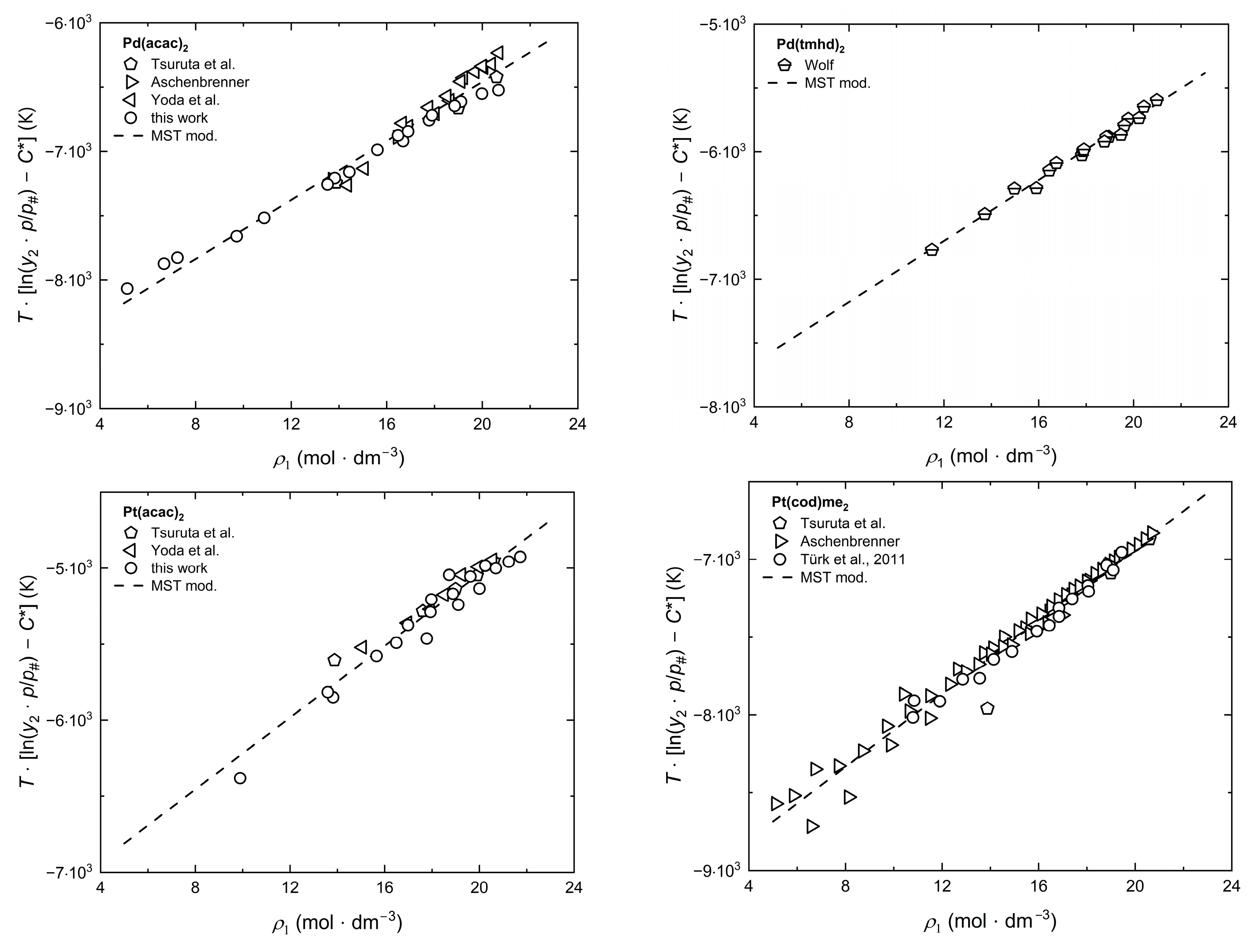
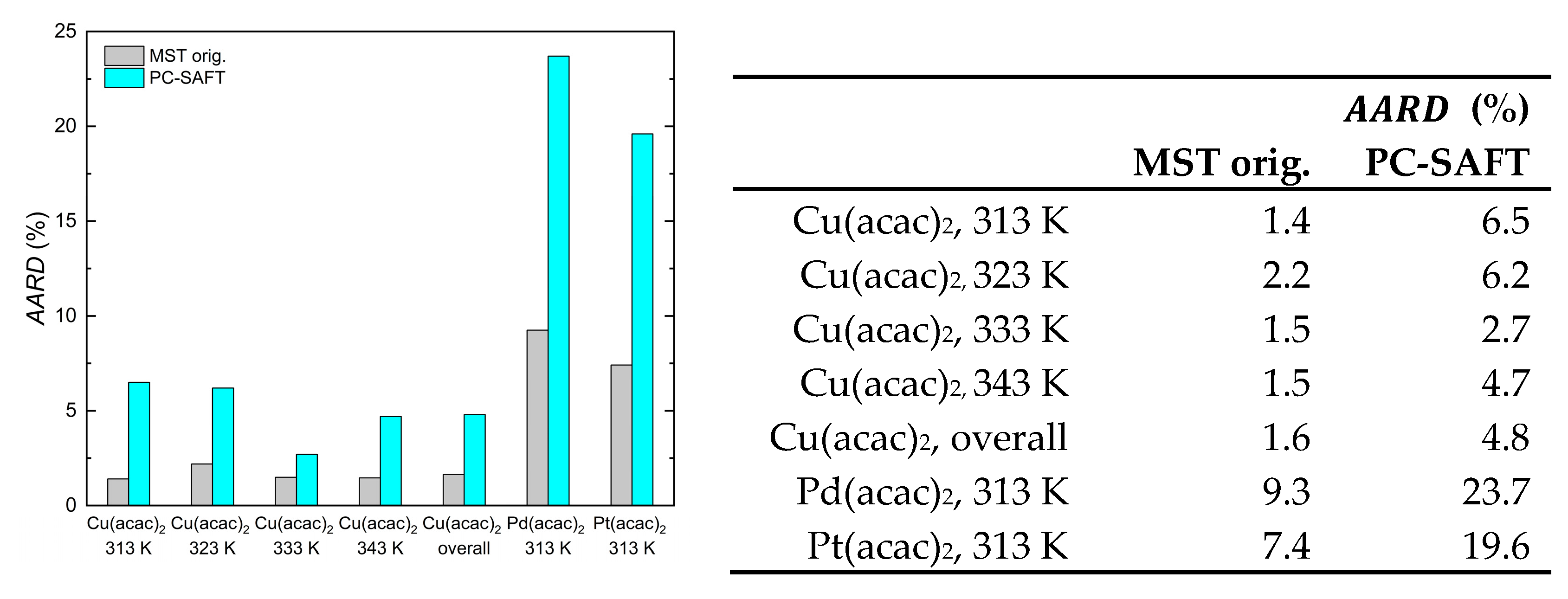
2.4. Modeling of Solubility Data
2.5. Correlation of Experimental Solubility Data
2.6. Estimation of Dissolution, Sublimation, and Solvation Enthalpies
3. Materials and Experimental Methods
3.1. Materials
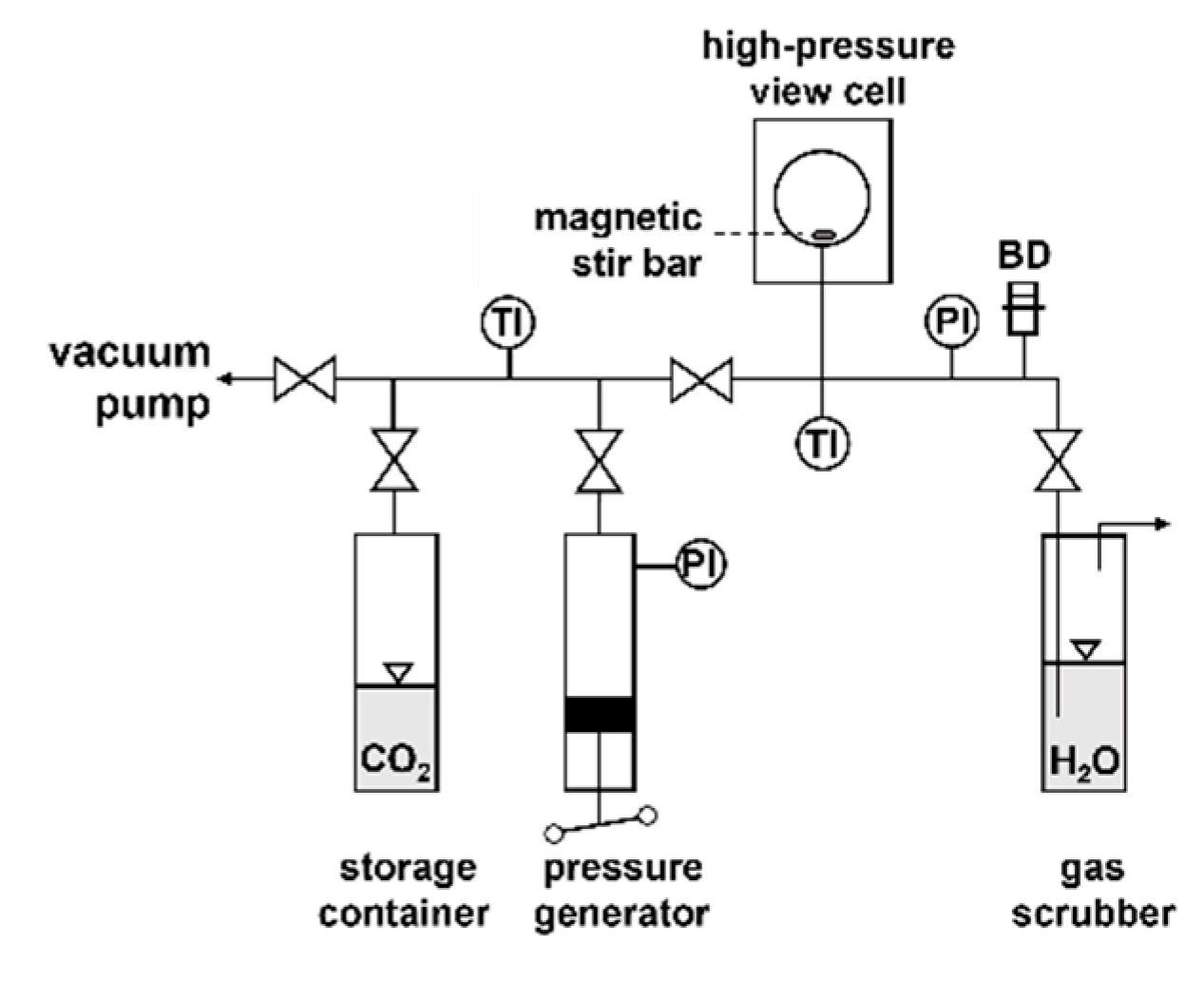
3.2. Experimental
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | unit | |
| average absolute relative deviation | ||
| acac | acetylacetonate | |
| calc | calculated | |
| CAS | Chemical Abstracts Service | |
| cod | cyclooctadiene | |
| solvation enthalpy | ||
| sublimation enthalpy | ||
| dissolution enthalpy | ||
| enhancement factor | ||
| EoS | equation of state | |
| exp | experimental | |
| ext. | extended | |
| GCM | group contribution method | |
| number of adjustable parameters in the correlation model | ||
| KJ | Kumar–Johnston | |
| molar mass | ||
| g | mass | |
| me | methyl | |
| mod. | modified | |
| MST | Méndez–Santiago–Teja | |
| number of data points | ||
| mole CO2 | ||
| mole precursor | ||
| NP | nanoparticle | |
| orig. | original | |
| pressure | ||
| , Equation (6) | ||
| , Equation (7) | ||
| , Equation (3) | ||
| sublimation pressure of the solid | ||
| PC-SAFT | perturbed-chain statistical associating fluid theory | |
| PR | Peng–Robinson | |
| ) | ||
| squared correlation coefficient | ||
| adjusted squared correlation coefficient | ||
| density of CO2 | ||
| , Equation (3) | ||
| sc | supercritical | |
| SCF | supercritical fluid | |
| SFRD | supercritical fluid reactive deposition | |
| temperature | ||
| time | ||
| tmhd | tetramethyl-3,5-heptandione | |
| precursor solubility | ||
| Parameters… | ||
| parameters of the Chrastil model, Equation (1) | ||
| parameters of the KJ ext. model, Equation (2) | ||
| parameters of the Bartle ext. model, Equation (3) | ||
| parameters of the MST orig. model, Equation (4) | ||
| parameters of the Clausius-Clapeyron equation, Equation (6) | ||
| parameters of the MST mod. model, Equation (7) |
Appendix A. Sublimation Pressures
| Range | (K) | Ref. | |||
|---|---|---|---|---|---|
| Cu(acac)2 | Nasebulin | 353–477 K | 24.5 | −9603 | [37] |
| Cu(tmhd)2 | Tobaly, Ribeiro, Siddiqi | 362–452 K | 37.7 | −14,392 | [41,53,54] |
| Pd(acac)2 | Morozova | 347–453 K | 33.6 | −13,425 | [55] |
| Pd(tmhd)2 | Igumenov | 348–398 K | 27.9 | −15,106 | [56] |
| Pt(acac)2 | Morozova | 332–453 K | 31.7 | −12,737 | [55] |
| Pt(cod)me2 | Hierso | 333–353 K | 17.2 | −5441 | [48] |
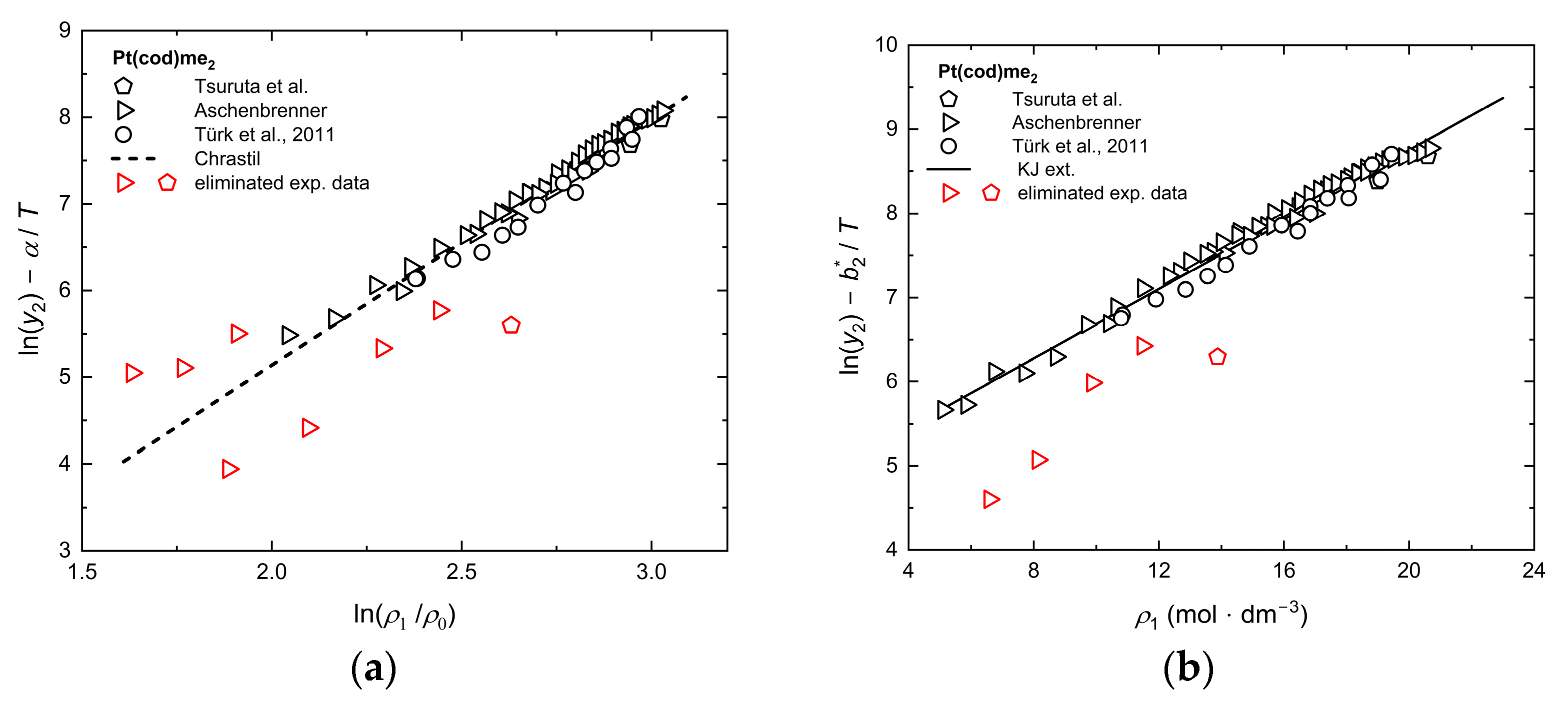
Appendix B. Tests of Consistency with Chrastil, KJ Ext., Bartle Ext., and MST Orig.

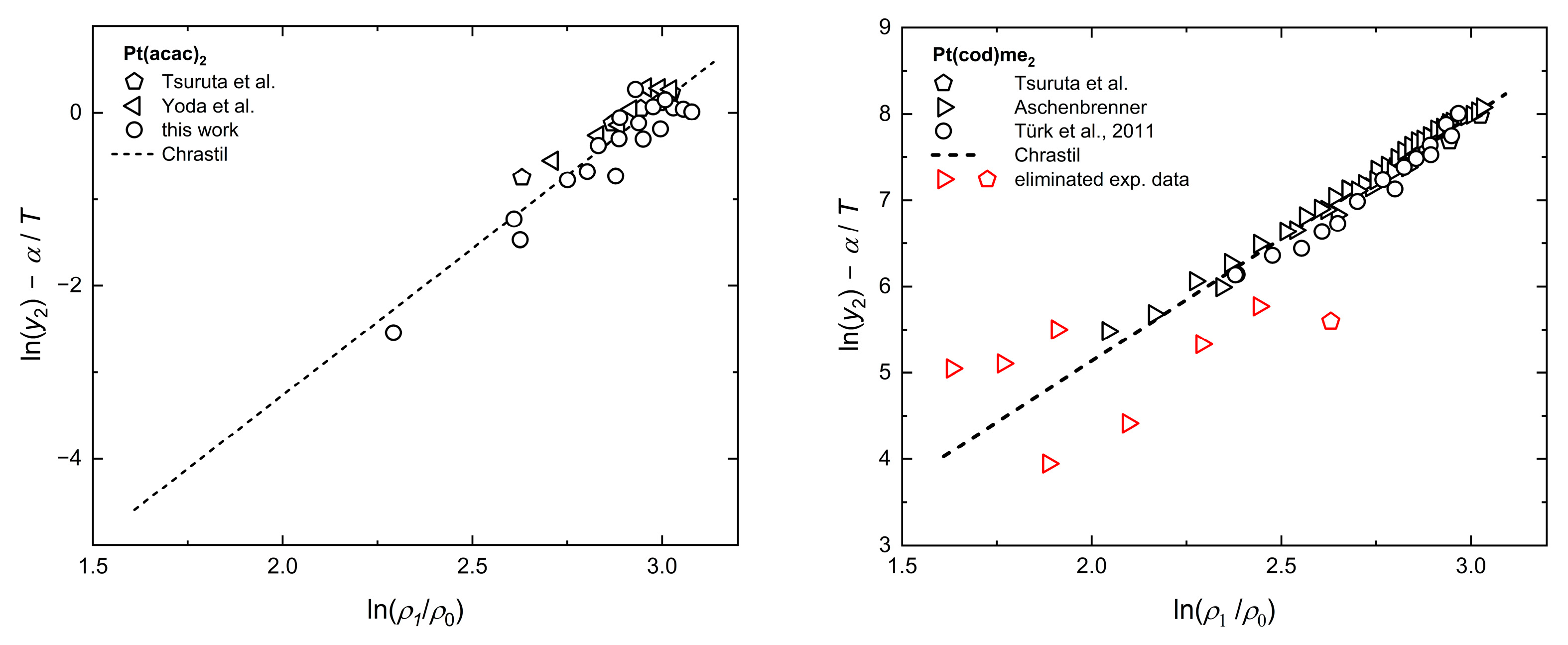

References
- Cansell, F.; Aymonier, C. Design of functional nanostructured materials using supercritical fluids. J. Supercrit. Fluids 2009, 47, 508–516. [Google Scholar] [CrossRef]
- Türk, M.; Erkey, C. Synthesis of supported nanoparticles in supercritical fluids by supercritical fluid reactive deposition: Current state, further perspectives and needs. J. Supercrit. Fluids 2018, 134, 176–183. [Google Scholar] [CrossRef]
- Incera Garrido, G.; Patcas, F.C.; Upper, G.; Türk, M.; Yilmaz, S.; Kraushaar-Czarnetzki, B. Supercritical deposition of Pt on SnO2-coated Al2O3 foams: Phase behaviour and catalytic performance. Appl. Catal. A Gen. 2008, 338, 58–65. [Google Scholar] [CrossRef][Green Version]
- Reiser, S.; Shaban, M.; Weber, A.; Türk, M. CO2 assisted deposition of R/S-ibuprofen on different porous carrier materials: Influence of carrier properties on loading and dissolution behavior. J. CO2 Util. 2018, 25, 216–225. [Google Scholar] [CrossRef]
- Crone, M.; Trinkies, L.L.; Dittmeyer, R.; Türk, M. Deposition of Pd, Pt, and PdPt nanoparticles on TiO2 powder using supercritical fluid reactive deposition: Application in the direct synthesis of H2O2. Molecules 2024, 29, 2142. [Google Scholar] [CrossRef]
- Yousefzadeh, H.; Akgün, I.S.; Barim, S.B.; Sari, T.B.; Eris, G.; Unzunlar, E.; Bozbag, S.E.; Erkey, C. Supercritical fluid reactive deposition: A process intensification technique for synthesis of nanostructured materials. Chem. Eng. Process 2022, 176, 108934. [Google Scholar] [CrossRef]
- Crone, M.; Türk, M. Adsorption of precursors on substrates in the presence of scCO2 for the synthesis of supported metallic nanoparticles: Experiments and modeling. Fluids 2023, 8, 121. [Google Scholar] [CrossRef]
- Reddy, T.A.; Garlapati, C. Dimensionless empirical model to correlate pharmaceutical compound solubility in supercritical carbon dioxide. Chem. Eng. Technol. 2019, 42, 2621–2630. [Google Scholar] [CrossRef]
- Knez, Z.; Cör, D.; Knez Hrncic, M. Solubility of solids in sub- and supercritical fluids: A review 2010–2017. J. Chem. Eng. Data 2018, 63, 860–884. [Google Scholar] [CrossRef]
- Chrastil, J. Solubility of solids and liquids in supercritical gases. J. Phys. Chem. 1982, 86, 3016–3021. [Google Scholar] [CrossRef]
- Kumar, S.K.; Johnston, K.P. Modelling the solubility of solids in supercritical fluids with density as the independent variable. J. Supercrit. Fluids 1988, 1, 15–22. [Google Scholar] [CrossRef]
- Bartle, K.D.; Clifford, A.A.; Jafar, S.A.; Shilstone, G.F. Solubilities of solids and liquids of low volatility in supercritical carbon dioxide. Phys. Chem. Ref. Data 1991, 20, 713–756. [Google Scholar] [CrossRef]
- Méndez-Santiago, J.; Teja, A.S. The Solubility of solids in supercritical fluids. Fluid Phase Equilib. 1999, 158–160, 501–510. [Google Scholar] [CrossRef]
- Ushiki, I.; Sato, Y.; Takishima, S.; Inomata, H. Thermodynamic modeling of the solubility of acetylacetonate-type metal precursors in supercritical carbon dioxide using the PC-SAFT equation of state. J. Chem. Eng. Jpn. 2019, 52, 243–252. [Google Scholar] [CrossRef]
- Ziger, D.H.; Eckert, C.A. Correlation and prediction of solid-supercritical fluid phase equilibriums. Ind. Eng. Chem. Process Des. Dev. 1983, 22, 582–588. [Google Scholar] [CrossRef]
- Harvey, A.H. Supercritical solubility of solids from near-critical dilute-mixture theory. J. Phys. Chem. 1990, 94, 8403–8406. [Google Scholar] [CrossRef]
- Türk, M.; Crone, M.; Kraska, T.H. A comparison between models based on equations of state and density-based models for describing the solubility of solutes in CO2. J. Supercrit. Fluids 2010, 55, 462–471. [Google Scholar] [CrossRef]
- Stiver, W. Chrastil revisited for supercritical carbon dioxide. J. Supercrit. Fluids 2021, 177, 105348. [Google Scholar] [CrossRef]
- Adachi, Y.; Lu, B.C.-Y. Supercritical fluid extraction with carbon dioxide and ethylene. Fluid Phase Equilibr. 1983, 14, 147–156. [Google Scholar] [CrossRef]
- Del Valle, J.M.; Aguilera, J.M. An improved equation for predicting the solubility of vegetable oils in supercritical CO2. Ind. Eng. Chem. Res. 1988, 27, 1551–1553. [Google Scholar] [CrossRef]
- Sparks, D.L.; Hernandez, R.; Estévez, L.A. Evaluation of density-based models for the solubility of solids in supercritical carbon dioxide and formulation of a new model. Chem. Eng. Sci. 2008, 63, 4292–4301. [Google Scholar] [CrossRef]
- Skerget, M.; Knez, Z.; Knez-Hrncic, M. Solubility of solids in sub- and supercritical fluids: A Review. J. Chem. Eng. Data 2011, 56, 694–719. [Google Scholar] [CrossRef]
- Miller, D.J.; Hawthorne, S.B.; Clifford, A.A.; Zhu, S. Solubility of polycyclic aromatic hydrocarbons in supercritical carbon dioxide from 313 to 523 K and pressures from 100 to 450 bar. J. Chem. Eng. Data 1996, 41, 779–786. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). Available online: http://webbook.nist.gov/ (accessed on 1 July 2024).
- Kautz, C.B.; Schneider, G.M.; Shim, J.-J.; Wagner, B.; Tuma, D. Solubilities of a 1,4-bis(alkylamino)-9,10-anthraquinone series in compressed carbon dioxide. J. Chem. Eng. Data 2008, 53, 2356–2371. [Google Scholar] [CrossRef]
- Upper, G. Reaktivabscheidung von Metallen Aus Überkritischen Fluiden zur Herstellung von Funktionsoptimierten Katalysatoren. Ph.D. Thesis, Fakultät für Chemieingenieurwesen und Verfahrenstechnik, Universität Karlsruhe (TH), Karlsruhe, Germany, 2009. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Res. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Lopez-Echeverry, J.S.; Reif-Acherman, S.; Araujo-Lopez, E. Peng-Robinson equation of state: 40 years through cubics. Fluid Phase Equilib. 2017, 447, 39–71. [Google Scholar] [CrossRef]
- Skerget, M.; Novak-Pintaric, Z.; Knez, Z.; Kravanja, Z. Estimation of solid solubilities in supercritical carbon dioxide: Peng–Robinson adjustable binary parameters in the near critical region. Fluid Phase Equilib. 2002, 203, 111–132. [Google Scholar] [CrossRef]
- Ushiki, I.; Fujimitsu, R.; Takishima, S. Predicting the solubilities of metal acetylacetonates in supercritical CO2: Thermodynamic approach using PC-SAFT. J. Supercrit. Fluids 2020, 164, 104909. [Google Scholar] [CrossRef]
- Kleiner, M.; Tumakaka, F.; Sadowski, G. Thermodynamic Modeling of Complex Systems. In Molecular Thermodynamics of Complex Systems; Lu, X., Hu, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 131, pp. 76–108. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Siebertz, K.; van Bebber, D.; Hochkirchen, T.H. Statistische Versuchsplanung, 2nd ed.; Springer-Verlag GmbH Deutschland: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-662-55742-6. [Google Scholar]
- Türk, M.; Crone, M.; Upper, G. Effect of gas pressure on the phase behaviour of organometallic compounds. J. Supercrit. Fluids 2011, 58, 1–6. [Google Scholar] [CrossRef]
- Wolf, A. Bestimmung der Löslichkeit von Metallchelaten in Überkritischem Kohlendioxid. Ph.D. Thesis, Universität-Gesamthochschule Siegen, Siegen, Germany, 1999. Available online: https://nbn-resolving.org/urn:nbn:de:hbz:467-1708.
- Teoh, W.H.; Mammucari, R.; Foster, N.R. Solubility of organometallic complexes in supercritical carbon dioxide: A review. J. Organomet. Chem. 2013, 724, 102–116. [Google Scholar] [CrossRef]
- Nasebulin, A.G.; Ahonen, P.P.; Richard, O.; Altman, I.S. Copper and copper oxide nanoparticle formation by chemical vapor nucleation from copper(II)acetylacetonate. J. Nanopart. Res. 2001, 3, 385–400. [Google Scholar] [CrossRef]
- Siddiqi, M.A.; Siddiqui, R.A.; Atakan, B. Thermal stability, sublimation pressures, and diffusion coefficients of anthracene, pyrene, and some metal b-diketonates. J. Chem. Eng. Data 2009, 54, 2795–2802. [Google Scholar] [CrossRef]
- Teghil, R.; Ferro, D.; Benecivenni, L.; Pelino, M. A thermodynamic study of the sublimation processes of aluminum and copper acetylacetonates. Thermochim. Acta 1981, 44, 213–222. [Google Scholar] [CrossRef]
- Cross, W., Jr.; Akgerman, A.; Erkey, C. Determination of metal-chelate complex solubilities in supercritical carbon dioxide. Ind. Eng. Chem. Res. 1996, 35, 1765–1770. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Monte, M.J.S.; Huinink, J. Vapour pressures and standard molar enthalpies of sublimation of seven crystalline copper (II) b-diketonates. The mean molar (Cu—O) bond-dissociation enthalpies. J. Chem. Thermodyn. 1995, 27, 175–190. [Google Scholar] [CrossRef]
- Colominas, C.; Lau, K.H.; Hildenbrand, D.L.; Crouch-Baker, S.; Sanjurjo, A. Vapor pressures of the copper and yttrium b-diketonate MOCVD precursors. J. Chem. Eng. Data 2001, 46, 446–450. [Google Scholar] [CrossRef]
- Minkina, V.G. Initial compounds for obtaining high-temperature superconducting films by the CVD-method. Russian Chem. Bull. 1993, 42, 1460–1466. [Google Scholar] [CrossRef]
- Lagalante, A.F.; Hansen, B.N.; Bruno, T.J.; Sievers, R.E. Solubilities of copper (II) and chromium (II) b-diketonates in supercritical carbon dioxide. Inorg. Chem. 1995, 34, 5781–5785. [Google Scholar] [CrossRef]
- Aschenbrenner, O. Untersuchungen zu Phasengleichgewichten und Transportvorgängen gelöster Metallverbindungen in überkritischem Kohlendioxid. Ph.D. Thesis, Fakultät für Chemieingenieurwesen und Verfahrenstechnik, Universität Karlsruhe (TH), Karlsruhe, Germany, 2007. [Google Scholar] [CrossRef]
- Yoda, S.; Mizuno, Y.; Furuya, T.; Takebayashi, Y.; Otake, K.; Tsuji, T.; Hiaki, T. Solubility measurements of noble metal acetylacetonates in supercritical carbon dioxide by high performance liquid chromatography (HPLC). J. Supercrit. Fluids 2008, 44, 139–147. [Google Scholar] [CrossRef]
- Haruki, M.; Kobayashi, F.; Kihara, S.-i.; Takishima, S. Solubility of b-diketonate complexes of copper (II) and cobalt (II) in supercritical carbon dioxide. J. Chem. Eng. Data 2011, 56, 2230–2235. [Google Scholar] [CrossRef]
- Hierso, J.-C.; Serp, P.; Feurer, R.; Kalck, P. MOCVD of rhodium, palladium and platinum complexes on fluidized divided substrates: Novel process for one-step preparation of noble-metal catalysts. Appl. Organomet. Chem. 1998, 12, 161–172. [Google Scholar] [CrossRef]
- Momose, T.; Kondo, A.; Kamiya, T.; Yamada, H.; Ohara, J.; Kitamura, Y.; Uchida, H.; Shimogaki, Y.; Sugiyama, M. Solubility of bis-(2,2,6,6-tetramethyl-3,5-heptanedionato) copper (II) in mixed supercritical CO2 and H2 systems for application in supercritical fluid deposition of Cu. J. Supercrit. Fluids 2015, 105, 193–200. [Google Scholar] [CrossRef]
- Tsuruta, N.; Yoda, S.; Hasegawa, A.; Sugeta, T.; Takebayashi, Y.; Tsuji, T.; Otake, K. Solubility measurement of noble-metal-chelates in supercritical CO2. In Proceedings of the 6th International Symposium on Supercritical Fluids, Versailles, France, 28–30 April 2003; Available online: https://supercriticalfluidsociety.net/wp-content/VERSAILLES/Versailles/Papers/PTs6.pdf.
- Galia, A.; Argentino, A.; Scialdone, O.; Filardo, G. A new simple static method for the determination of solubilities of condensed compounds in supercritical fluids. J. Supercrit. Fluids 2002, 24, 7–17. [Google Scholar] [CrossRef]
- Sherman, G.; Shenoy, S.; Weiss, R.A.; Erkey, C. A static method coupled with gravimetric analysis for the determination of solubilities of solids in supercritical carbon dioxide. Ind. Eng. Chem. Res. 2000, 39, 846–848. [Google Scholar] [CrossRef]
- Tobaly, P.; Lanchec, G. Vapour pressure and enthalpy of sublimation of a series of organometallic complexes: Cu(DPM)2, Y(DPM)3, Ba(DPM)2 and some derivatives. J. Chem. Thermodyn. 1993, 25, 503–510. [Google Scholar] [CrossRef]
- Siddiqi, M.A.; Siddiqui, R.A.; Atakan, B. Thermal stability, vapor pressures, and diffusion coefficients of some metal 2,2,6,6-tetramethyl-3,5-heptandionate [M(tmhd)n] compounds. J. Chem. Eng. Data 2010, 55, 2149–2154. [Google Scholar] [CrossRef]
- Morozova, N.B.; Zharkova, G.I.; Semyannikov, P.P.; Sysoev, S.V.; Igumenov, I.K.; Fedotova, N.E.; Gelfond, N.V. Vapor pressure of precursors for CVD on the base of platinum group metals. J Phys. IV France 2001, 11, 3–609. [Google Scholar] [CrossRef]
- Igumenov, I.K.; Zharkova, G.I.; Baidina, I.A.; Stabnikov, P.A.; Semyannikov, P.P.; Morozova, N.B.; Gelfond, N.V. Systematical investigations of new Pd (II) precursors for the MO CVD processes. In Proceedings of the Fifteenth European Conference on Chemical Vapor Deposition 2005-09 (EUROCVD-15), Bochum, Germany, 6–9 September 2005; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2005. [Google Scholar]


| (K) | (MPa) | ) | (%) | ) | ) |
|---|---|---|---|---|---|
| 333.1 | 15.23 | 13.92 | 0.87 | 1.05·10−5 | ±2.48·10−6 |
| 333.1 | 20.25 | 16.54 | 0.43 | 1.78·10−5 | ±2.26·10−6 |
| 333.1 | 25.16 | 17.91 | 0.30 | 2.05·10−5 | ±2.12·10−6 |
| 333.1 | 30.33 | 18.91 | 0.23 | 2.47·10−5 | ±2.03·10−6 |
| 333.1 | 35.52 | 19.68 | 0.19 | 2.99·10−5 | ±2.05·10−6 |
| 333.1 | 40.13 | 20.24 | 0.17 | 3.16·10−5 | ±2.02·10−6 |
| 353.2 | 15.14 | 9.84 | 1.01 | 9.66·10−6 | ±3.34·10−6 |
| 353.2 | 20.28 | 13.64 | 0.57 | 2.71·10−5 | ±2.79·10−6 |
| 353.2 | 25.21 | 15.66 | 0.37 | 3.62·10−5 | ±2.63·10−6 |
| 353.2 | 30.23 | 16.99 | 0.28 | 4.32·10−5 | ±2.54·10−6 |
| 353.2 | 35.46 | 18.00 | 0.22 | 4.98·10−5 | ±2.50·10−6 |
| 353.2 | 40.50 | 18.77 | 0.19 | 5.96·10−5 | ±2.55·10−6 |
| (K) | (MPa) | ) | (%) | ) | ) |
|---|---|---|---|---|---|
| 313.1 | 10.08 | 14.43 | 1.70 | 8.95·10−6 | ±1.71·10−6 |
| 313.1 | 12.62 | 16.68 | 0.66 | 1.54·10−5 | ±1.55·10−6 |
| 313.1 | 15.12 | 17.77 | 0.45 | 2.16·10−5 | ±1.54·10−6 |
| 313.1 | 20.10 | 19.10 | 0.30 | 2.58·10−5 | ±1.48·10−6 |
| 313.1 | 25.00 | 19.99 | 0.23 | 2.52·10−5 | ±1.38·10−6 |
| 313.1 | 30.01 | 20.68 | 0.19 | 2.30·10−5 | ±1.30·10−6 |
| 333.1 | 10.07 | 6.68 | 1.64 | 4.17·10−6 | ±3.18·10−6 |
| 333.1 | 12.58 | 10.87 | 1.66 | 9.65·10−6 | ±2.15·10−6 |
| 333.1 | 15.10 | 13.82 | 0.89 | 2.04·10−5 | ±1.92·10−6 |
| 333.1 | 20.04 | 16.47 | 0.43 | 4.16·10−5 | ±1.87·10−6 |
| 333.1 | 25.06 | 17.90 | 0.30 | 5.32·10−5 | ±1.86·10−6 |
| 333.1 | 29.89 | 18.84 | 0.24 | 5.57·10−5 | ±1.76·10−6 |
| 353.2 | 10.14 | 5.14 | 1.01 | 9.13·10−6 | ±4.21·10−6 |
| 353.2 | 12.53 | 7.24 | 1.08 | 1.46·10−5 | ±3.16·10−6 |
| 353.2 | 15.02 | 9.72 | 1.02 | 1.96·10−5 | ±2.52·10−6 |
| 353.2 | 20.06 | 13.52 | 0.59 | 4.58·10−5 | ±2.42·10−6 |
| 353.1 | 25.05 | 15.61 | 0.38 | 7.83·10−5 | ±2.46·10−6 |
| 353.3 | 29.83 | 16.89 | 0.28 | 9.92·10−5 | ±2.52·10−6 |
| (K) | (MPa) | ) | (%) | ) | ) |
|---|---|---|---|---|---|
| 313.2 | 15.15 | 17.78 | 0.45 | 1.37·10−5 | ±1.42·10−6 |
| 313.2 | 20.13 | 19.11 | 0.29 | 2.10·10−5 | ±1.43·10−6 |
| 313.2 | 25.15 | 20.00 | 0.23 | 2.36·10−5 | ±1.40·10−6 |
| 313.2 | 30.16 | 20.69 | 0.19 | 3.02·10−5 | ±1.44·10−6 |
| 313.2 | 35.02 | 21.24 | 0.17 | 2.98·10−5 | ±1.39·10−6 |
| 313.2 | 40.06 | 21.73 | 0.15 | 2.88·10−5 | ±1.34·10−6 |
| 333.1 | 15.10 | 13.82 | 0.89 | 1.23·10−5 | ±1.76·10−6 |
| 333.1 | 20.12 | 16.49 | 0.43 | 2.70·10−5 | ±1.73·10−6 |
| 333.1 | 25.26 | 17.94 | 0.29 | 3.95·10−5 | ±1.77·10−6 |
| 333.1 | 30.16 | 18.88 | 0.23 | 4.74·10−5 | ±1.79·10−6 |
| 333.1 | 35.08 | 19.62 | 0.20 | 5.73·10−5 | ±1.86·10−6 |
| 333.1 | 40.19 | 20.25 | 0.17 | 6.20·10−5 | ±1.85·10−6 |
| 353.2 | 15.20 | 9.90 | 1.00 | 7.34·10−6 | ±2.21·10−6 |
| 353.2 | 20.19 | 13.60 | 0.58 | 2.73·10−5 | ±2.04·10−6 |
| 353.2 | 25.20 | 15.65 | 0.37 | 4.30·10−5 | ±2.05·10−6 |
| 353.3 | 30.22 | 16.98 | 0.28 | 6.39·10−5 | ±2.21·10−6 |
| 353.2 | 35.26 | 17.97 | 0.22 | 8.80·10−5 | ±2.44·10−6 |
| 353.2 | 40.16 | 18.73 | 0.19 | 1.22·10−4 | ±2.82·10−6 |
| Isotherms | (K) | (MPa) | Ref. | ||
|---|---|---|---|---|---|
| Cu(acac)2 | 8 | 83 | range: 308–353 | range: 8–40 | [overall] |
| 1 | 8 | 313 | 10–35 | [44] | |
| 3 | 15 | 308, 318, 328 | 10–30 | [40] | |
| 1 | 3 | 333 | 15–30 | [45] | |
| 1 | 13 | 313 | 8–30 | [46] | |
| 4 | 32 | 313, 323, 333, 343 | 14–30 | [47] | |
| 2 | 12 | 333, 353 | 15–40 | [this work] | |
| Cu(tmhd)2 | 6 | 62 | range: 313–373 | range: 10–35 | [overall] |
| 1 | 8 | 313 | 10–35 | [44] | |
| 1 | 4 | 333 | 10–18 | [45] | |
| 4 | 35 | 313, 323, 333, 343 | 12–30 | [47] | |
| 1 | 7 | 333 | 10–17 | [34] | |
| 4 | 8 | 313, 333, 353, 373 | 11–15 | [49] | |
| Pd(acac)2 | 3 | 39 | range: 313–353 | range: 10–30 | [overall] |
| 1 | 3 | 313 | 10–30 | [50] | |
| 1 | 3 | 333 | 15–30 | [45] | |
| 1 | 15 | 313 | 10–30 | [46] | |
| 3 | 18 | 313, 333, 353 | 10–30 | [this work] | |
| Pd(tmhd)2 | 3 | 18 | 323–343 | 15–40 | [35] |
| Pt(acac)2 | 3 | 30 | 313–353 | range: 10–40 | [overall] |
| 1 | 5 | 313 | 10–30 | [50] | |
| 1 | 7 | 313 | 10–29 | [46] | |
| 3 | 18 | 313, 333, 353 | 15–40 | [this work] | |
| Pt(cod)me2 | 3 | 74 | range: 313–353 | range: 9–32 | [overall] |
| 1 | 3 | 313 | 10–30 | [50] | |
| 3 | 54 | 313, 333, 353 | 9–30 | [45] | |
| 3 | 17 | 313, 333, 353 | 13–32 | [34] |
| Chrastil | (K) | |||
| Cu(acac)2 | −6.71 | 3.03 | −4176 | 0.892 |
| Cu(tmhd)2 | 3.08 | 4.82 | −7729 | 0.974 |
| Pd(acac)2 | −4.31 | 2.61 | −4348 | 0.858 |
| Pd(tmhd)2 | −5.28 | 3.42 | −3968 | 0.962 |
| Pt(acac)2 | −10.05 | 3.39 | −3277 | 0.853 |
| Pt(cod)me2 (a) | −0.54 | 2.84 | −4614 | 0.971 |
| KJ ext. | (K) | |||
| Cu(acac)2 | −0.88 | 0.22 | −4486 | 0.910 |
| Cu(tmhd)2 | 11.50 | 0.37 | −8088 | 0.945 |
| Pd(acac)2 | 0.49 | 0.23 | −4779 | 0.928 |
| Pd(tmhd)2 | 0.89 | 0.21 | −4008 | 0.949 |
| Pt(acac)2 | −4.14 | 0.21 | −3233 | 0.803 |
| Pt(cod)me2 (a) | 4.63 | 0.21 | −4832 | 0.982 |
| Bartle ext. | (K) | |||
| Cu(acac)2 | 13.75 | 0.35 | −6461 | 0.951 |
| Cu(tmhd)2 | 28.45 | 0.47 | −10016 | 0.979 |
| Pd(acac)2 | 15.85 | 0.34 | −6911 | 0.956 |
| Pd(tmhd)2 | 15.38 | 0.36 | −5956 | 0.983 |
| Pt(acac)2 | 10.89 | 0.36 | −5390 | 0.952 |
| Pt(cod)me2 | 20.88 | 0.35 | −7400 | 0.969 |
| MST orig. (b) | ||||
| Cu(acac)2 | 1649 | 109.5 | – | 0.951 |
| Cu(tmhd)2 | 2668 | 152.5 | – | 0.974 |
| Pd(acac)2 | 2421 | 129.4 | – | 0.956 |
| Pd(tmhd)2 | 2789 | 135.2 | – | 0.921 |
| Pt(acac)2 | 1919 | 146.6 | – | 0.875 |
| Pt(cod)me2 | – | – | – | – |
| MST mod. | (K) | |||
| Cu(acac)2 | −8325 | 111.5 | 11.72 | 0.954 |
| Cu(tmhd)2 | −12413 | 155.8 | 25.86 | 0.976 |
| Pd(acac)2 | −8755 | 114.8 | 13.55 | 0.968 |
| Pd(tmhd)2 | −8135 | 119.7 | 13.89 | 0.987 |
| Pt(acac)2 | −7400 | 118.1 | 8.97 | 0.943 |
| Pt(cod)me2 | −9273 | 117.4 | 18.56 | 0.975 |
| (%) | Ref. | ||||||
|---|---|---|---|---|---|---|---|
| Chrastil | KJ Ext. | Bartle Ext. | MST Orig. | MST Mod. | |||
| Cu(acac)2 | 83 | 14.3 | 13.1 | 15.7 | 15.0 | 14.8 | [overall] |
| 8 | 13.4 | 12.2 | 14.9 | 11.4 | 13.9 | [44] | |
| 15 | 18.0 | 13.0 | 21.0 | 23.4 | 20.5 | [40] | |
| 3 | 12.5 | 9.3 | 9.2 | 6.4 | 8.4 | [45] | |
| 13 | 22.4 | 18.9 | 21.8 | 21.0 | 20.8 | [46] | |
| 32 | 8.5 | 8.2 | 9.8 | 11.3 | 9.6 | [47] | |
| 12 | 17.8 | 21.9 | 20.4 | 12.3 | 16.9 | [this work] | |
| Cu(tmhd)2 | 62 | 15.6 | 26.6 | 19.3 | 21.2 | 20.5 | [overall] |
| 8 | 44.1 | 57.1 | 45.8 | 60.6 | 51.6 | [44] | |
| 4 | 20.4 | 60.8 | 44.7 | 47.2 | 44.6 | [45] | |
| 35 | 9.7 | 16.5 | 11.9 | 10.8 | 11.0 | [47] | |
| 7 | 11.3 | 24.6 | 13.9 | 16.7 | 15.1 | [34] | |
| 8 | 14.2 | 24.5 | 16.7 | 18.0 | 24.0 | [49] | |
| Pd(acac)2 | 39 | 26.6 | 20.3 | 23.7 | 28.6 | 21.1 | [overall] |
| 3 | 33.0 | 29.5 | 25.6 | 12.5 | 24.7 | [50] | |
| 3 | 16.1 | 10.0 | 14.7 | 30.8 | 9.8 | [45] | |
| 15 | 33.1 | 24.5 | 28.7 | 26.3 | 25.7 | [46] | |
| 18 | 21.8 | 16.9 | 20.7 | 32.9 | 18.6 | [this work] | |
| Pd(tmhd)2 | 18 | 8.0 | 9.0 | 8.5 | 24.4 | 7.7 | [35] |
| Pt(acac)2 | 30 | 18.7 | 21.2 | 16.5 | 35.4 | 18.6 | [overall] |
| 5 | 12.8 | 13.6 | 12.3 | 33.2 | 12.4 | [50] | |
| 7 | 17.2 | 18.3 | 14.3 | 36.6 | 14.5 | [46] | |
| 18 | 20.9 | 24.5 | 18.6 | 35.5 | 21.8 | [this work] | |
| Pt(cod)me2 | 74 | 8.7 (c) | 8.9 (c) | 17.9 | – | 15.8 | [overall] |
| 3 | 10.5 (c) | 20.1 (c) | 71.9 | – | 65.3 | [50] | |
| 54 | 6.6 (c) | 7.7 (c) | 15.7 | – | 13.7 | [45] | |
| 17 | 14.4 (c) | 11.4 (c) | 15.4 | – | 13.7 | [34] | |
| (Chrastil) ) | (Bartle Ext.) ) | ) | |
|---|---|---|---|
| Cu(acac)2 | 34.7 | 53.7 | −19.0 |
| Cu(tmhd)2 | 64.3 | 83.3 | −19.0 |
| Pd(acac)2 | 36.1 | 57.5 | −21.4 |
| Pd(tmhd)2 | 33.0 | 49.5 | −16.5 |
| Pt(acac)2 | 27.2 | 44.8 | −17.6 |
| Pt(cod)me2 | 38.4 | 61.5 | −23.1 |
| CAS | ) | Purity (%) | Supplier | |
|---|---|---|---|---|
| Cu(acac)2 | 13395-16-9 | 261.78 | 98 | abcr GmbH (d) |
| Pd(acac)2 | 14024-61-4 | 304.64 | 99 | abcr GmbH (d) |
| Pt(acac)2 | 15170-57-7 | 393.29 | 98 | abcr GmbH (d) |
| CO2 | 124-38-9 | 44.01 | 99.995 | Air Liquide (e) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crone, M.; Türk, M. Solubility of Metal Precursors in Supercritical CO2: Measurements and Correlations. Molecules 2025, 30, 1660. https://doi.org/10.3390/molecules30081660
Crone M, Türk M. Solubility of Metal Precursors in Supercritical CO2: Measurements and Correlations. Molecules. 2025; 30(8):1660. https://doi.org/10.3390/molecules30081660
Chicago/Turabian StyleCrone, Marlene, and Michael Türk. 2025. "Solubility of Metal Precursors in Supercritical CO2: Measurements and Correlations" Molecules 30, no. 8: 1660. https://doi.org/10.3390/molecules30081660
APA StyleCrone, M., & Türk, M. (2025). Solubility of Metal Precursors in Supercritical CO2: Measurements and Correlations. Molecules, 30(8), 1660. https://doi.org/10.3390/molecules30081660