Anisotropic and Coherent Control of Radical Pairs by Optimized RF Fields
Abstract
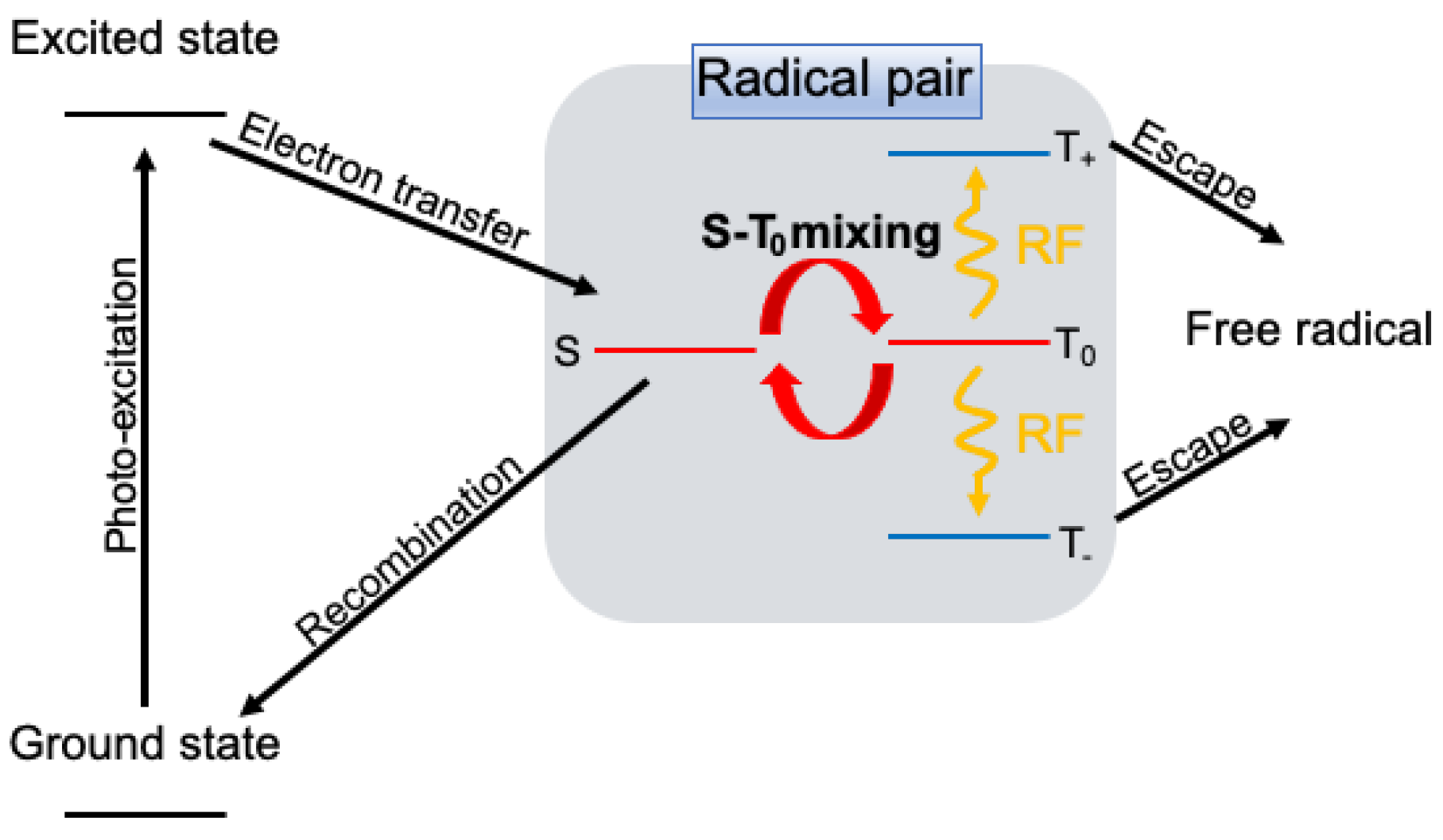
:1. Introduction
- (1)
- Smooth waveforms can be obtained because waveforms can be computed with very high time resolution. In contrast, the waveforms computed in GRAPE are optimized for relatively coarse time steps.
- (2)
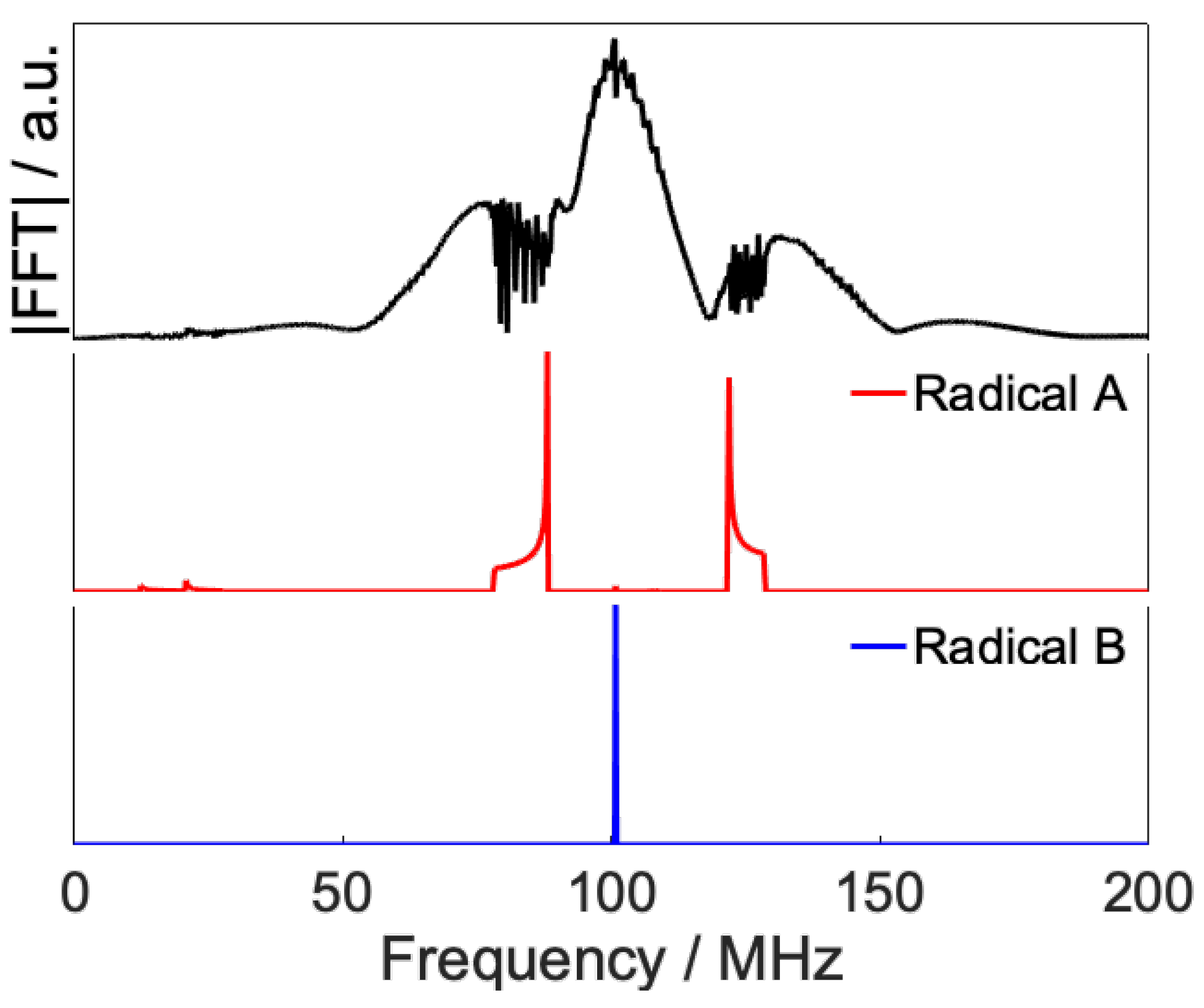
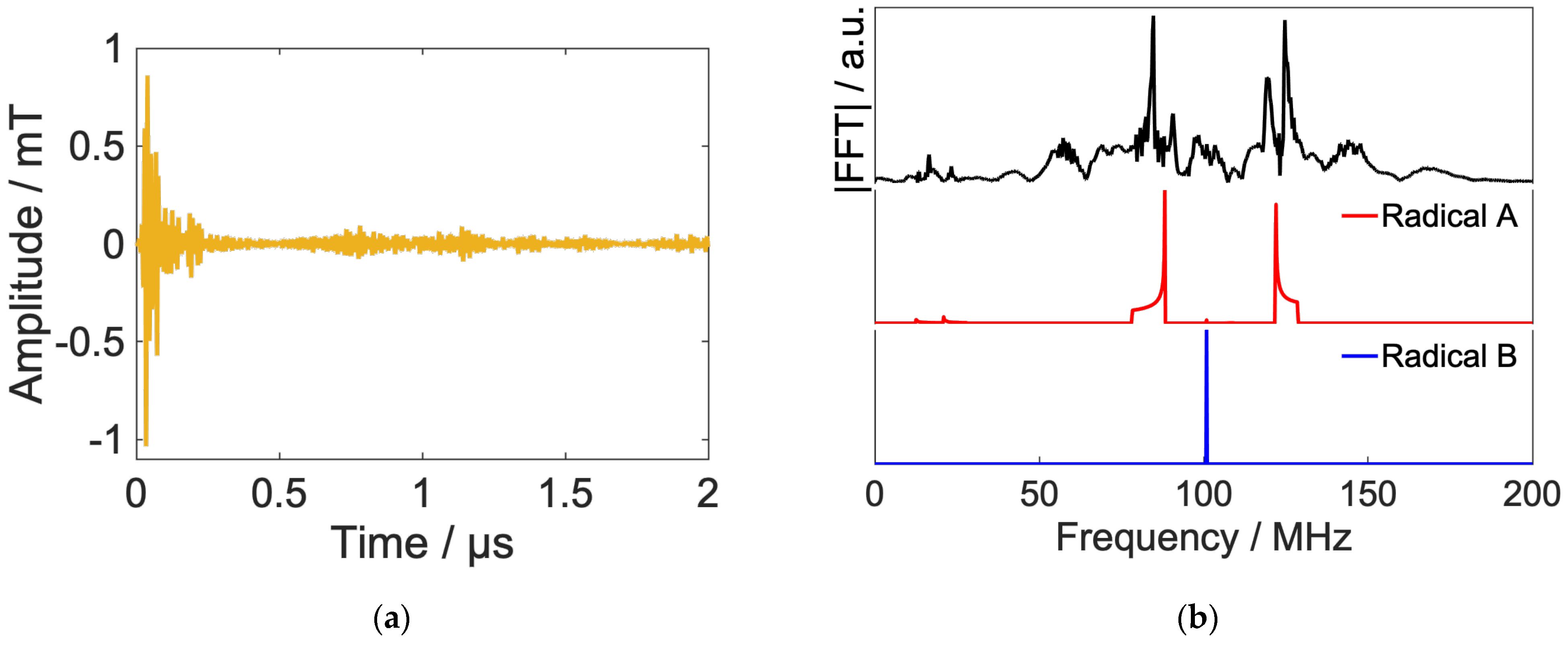
- Sub-ensemble systems can be easily selected by resonance frequency in inhomogeneous RP systems.
- (3)
- The calculation can incorporate strategies for the time evolution of the quantum system with respect to its path.
- (4)
- Calculations in a rotational coordinate system are easy because there is no computational burden due to the multidimensionality of radio waves (microwaves).
2. Theory
2.1. Local Optimization Theory
2.2. Weighting Parameters
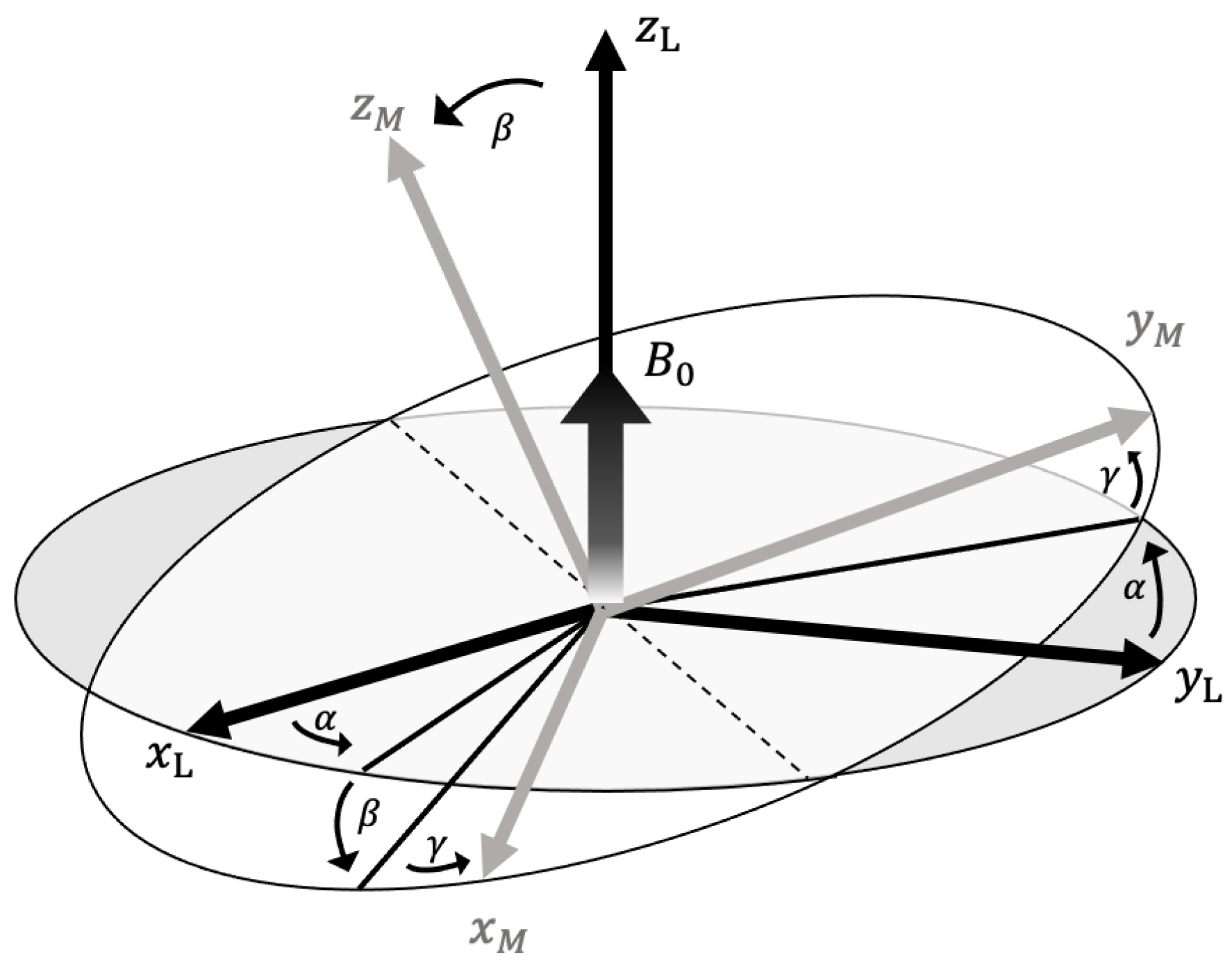
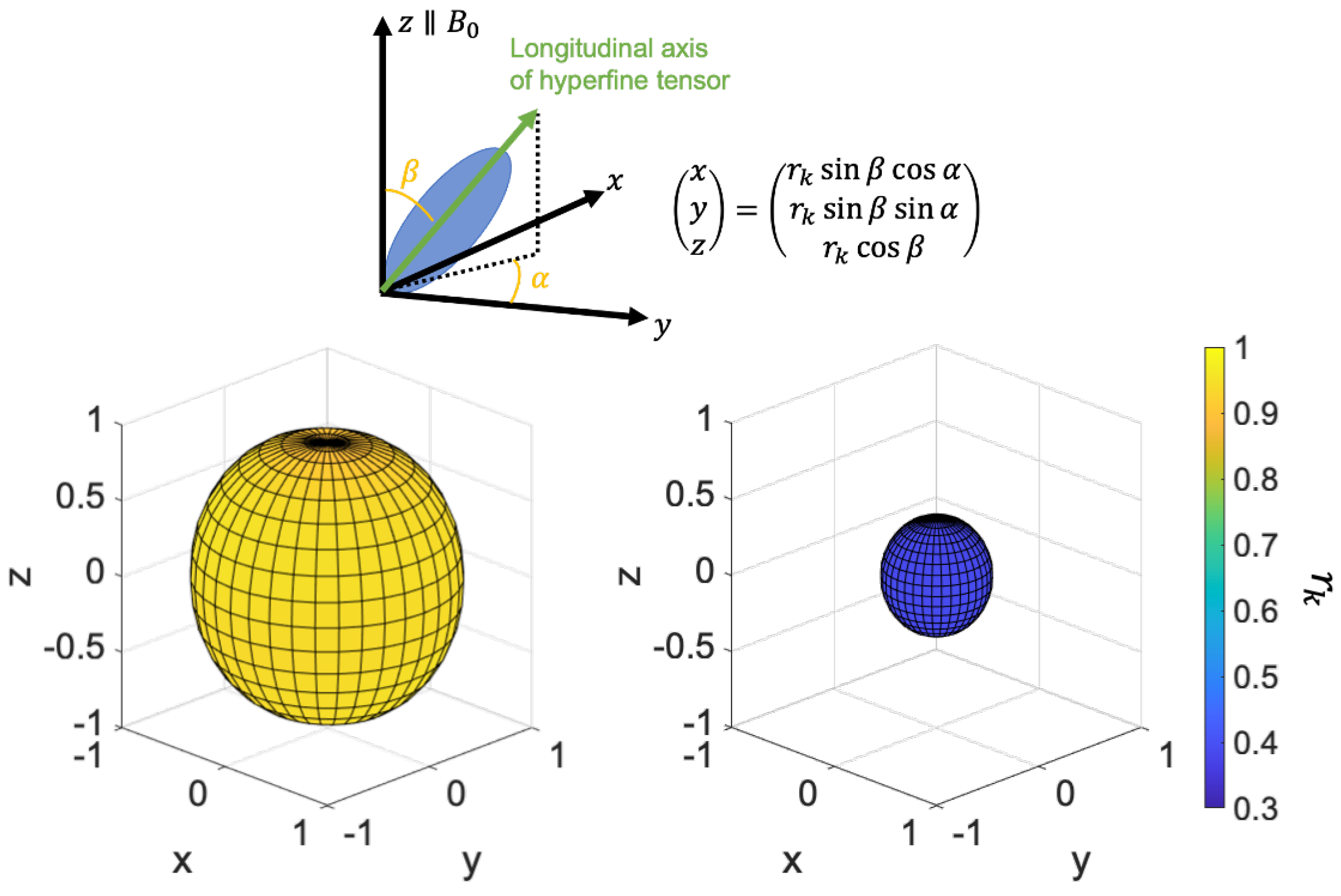
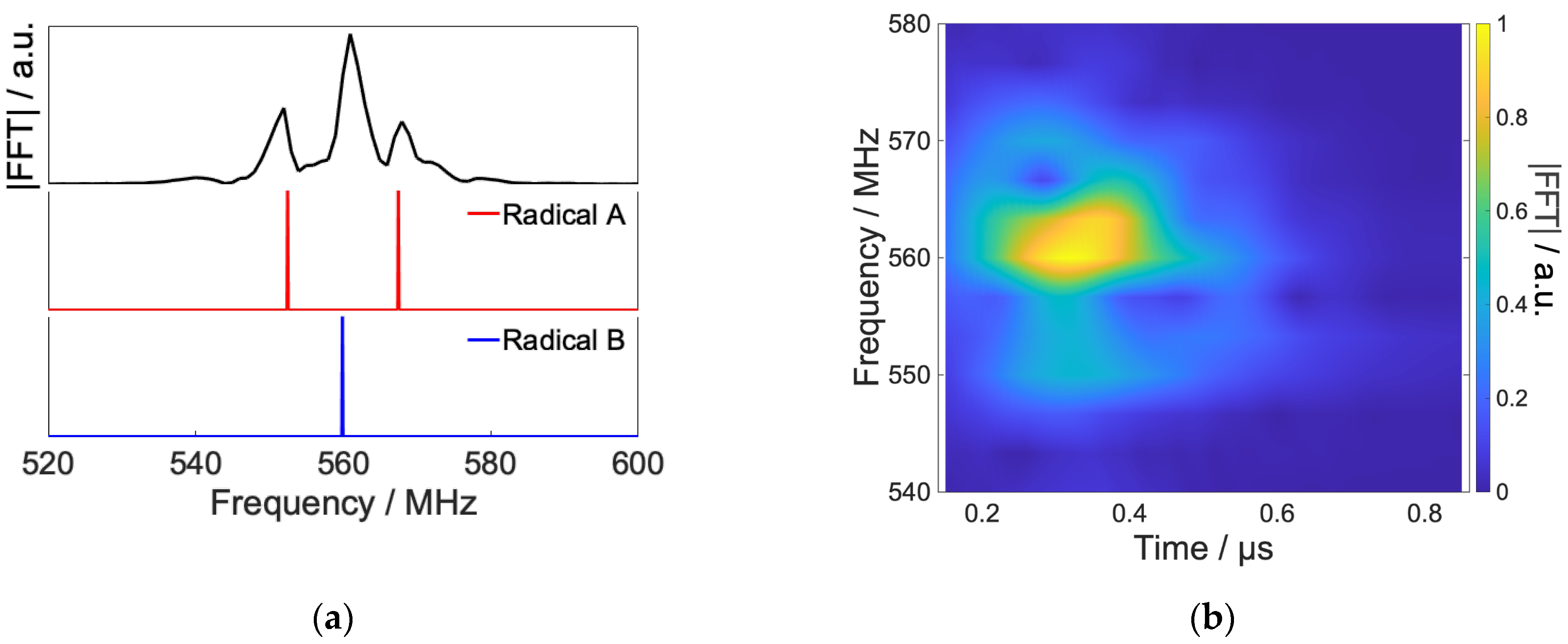
2.3. Anisotropic Sub-Ensemble Control
- The eigenstates of were calculated.
- The two eigenstates with the largest and characteristics were chosen, where the state and indicate electron spin state with α nuclear spin and with β nuclear spin, respectively.
- The sum of the projection operators onto these two eigenstates was determined to be the target, .
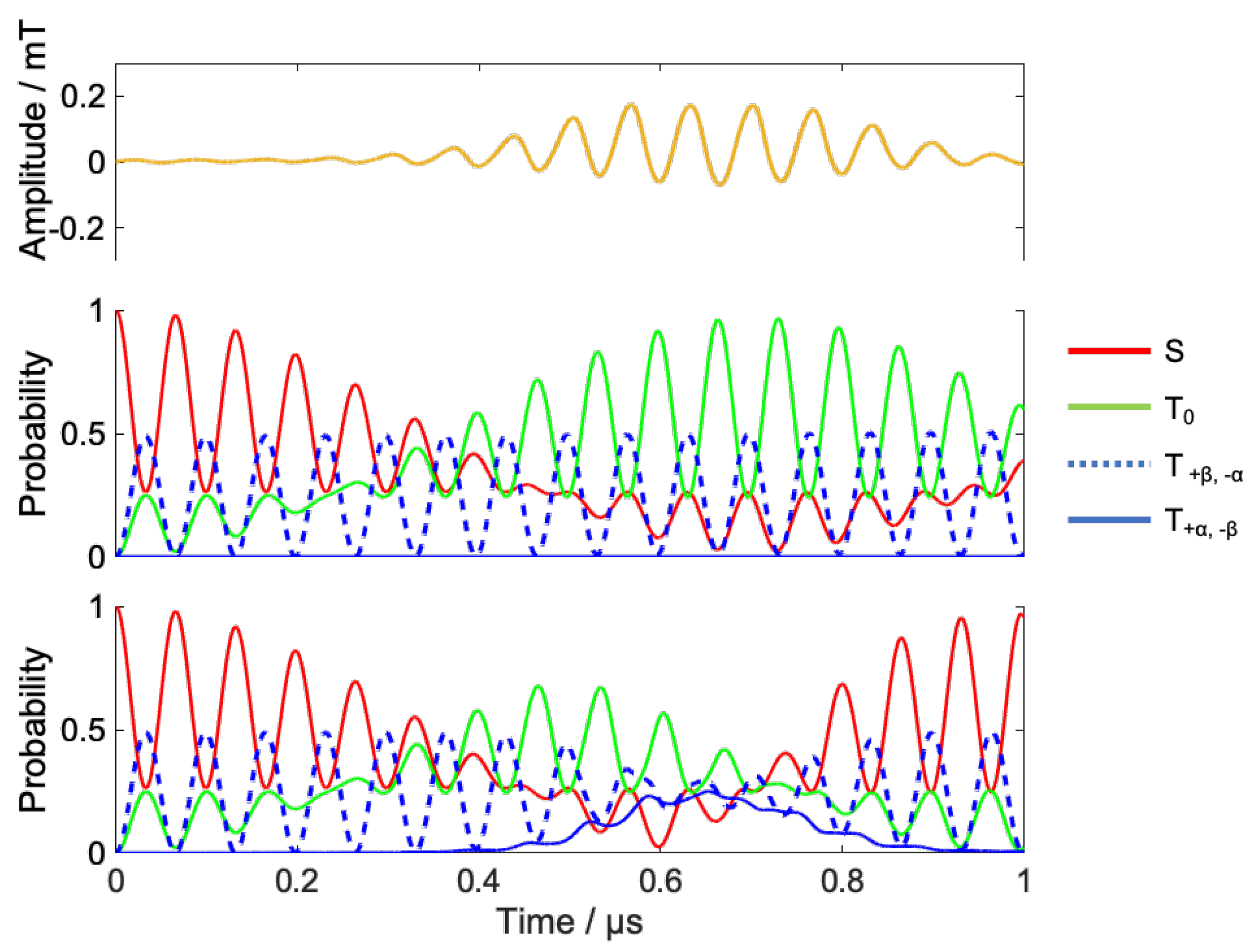
2.4. Coherent Pathway Control
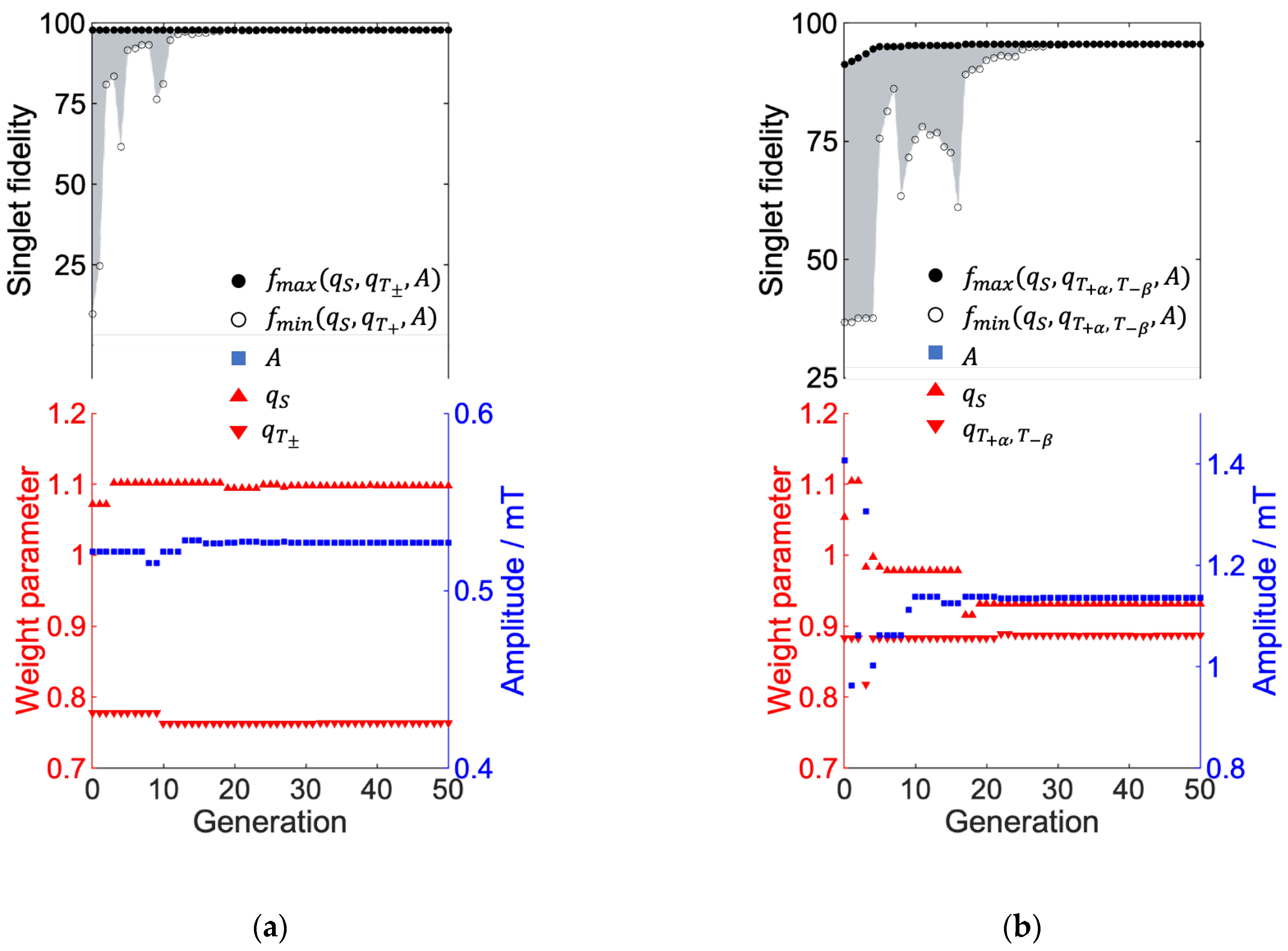
2.5. Parameter Global Optimization
3. Results and Discussion
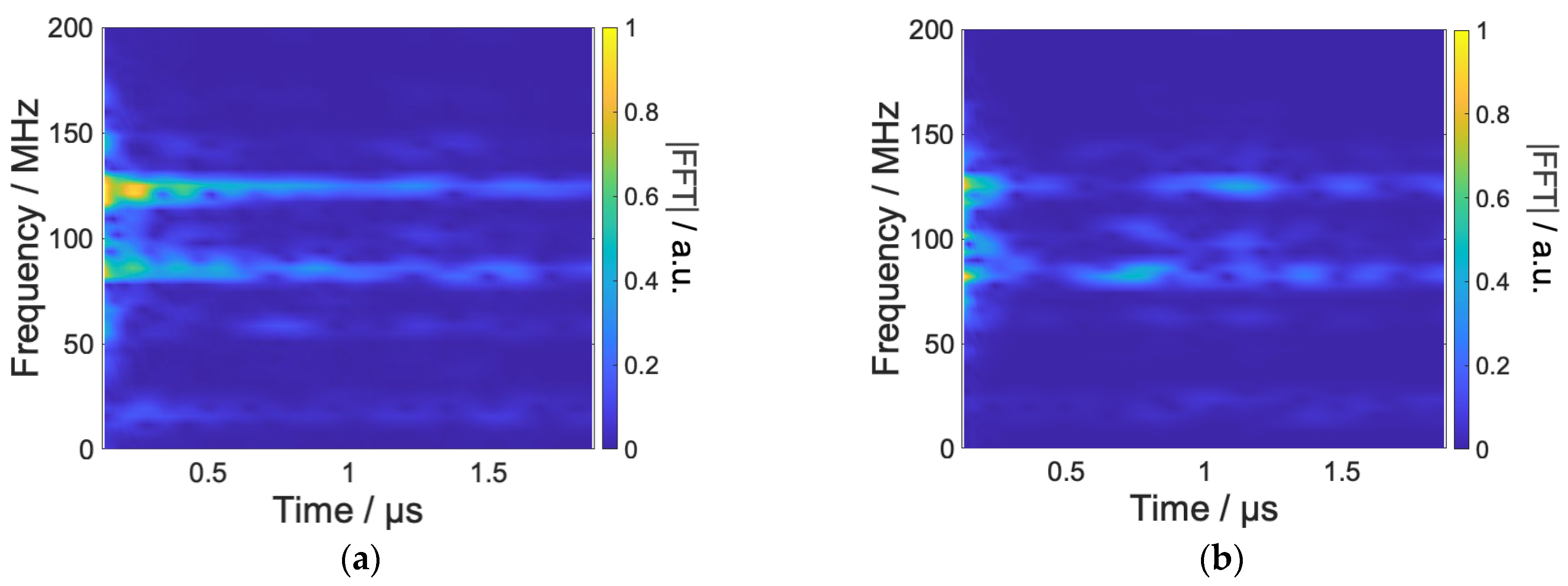
3.1. Anisotropic Reaction Control
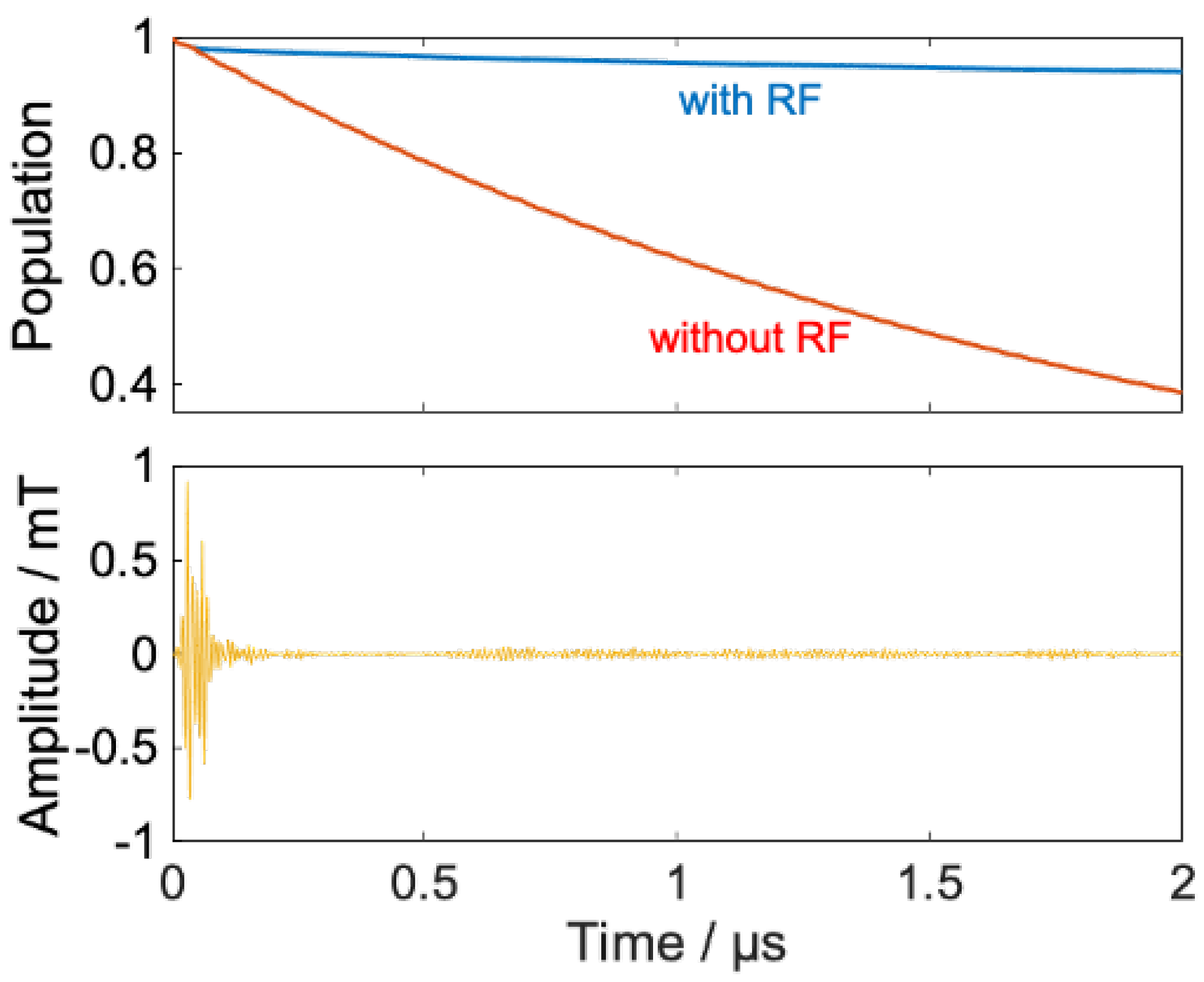
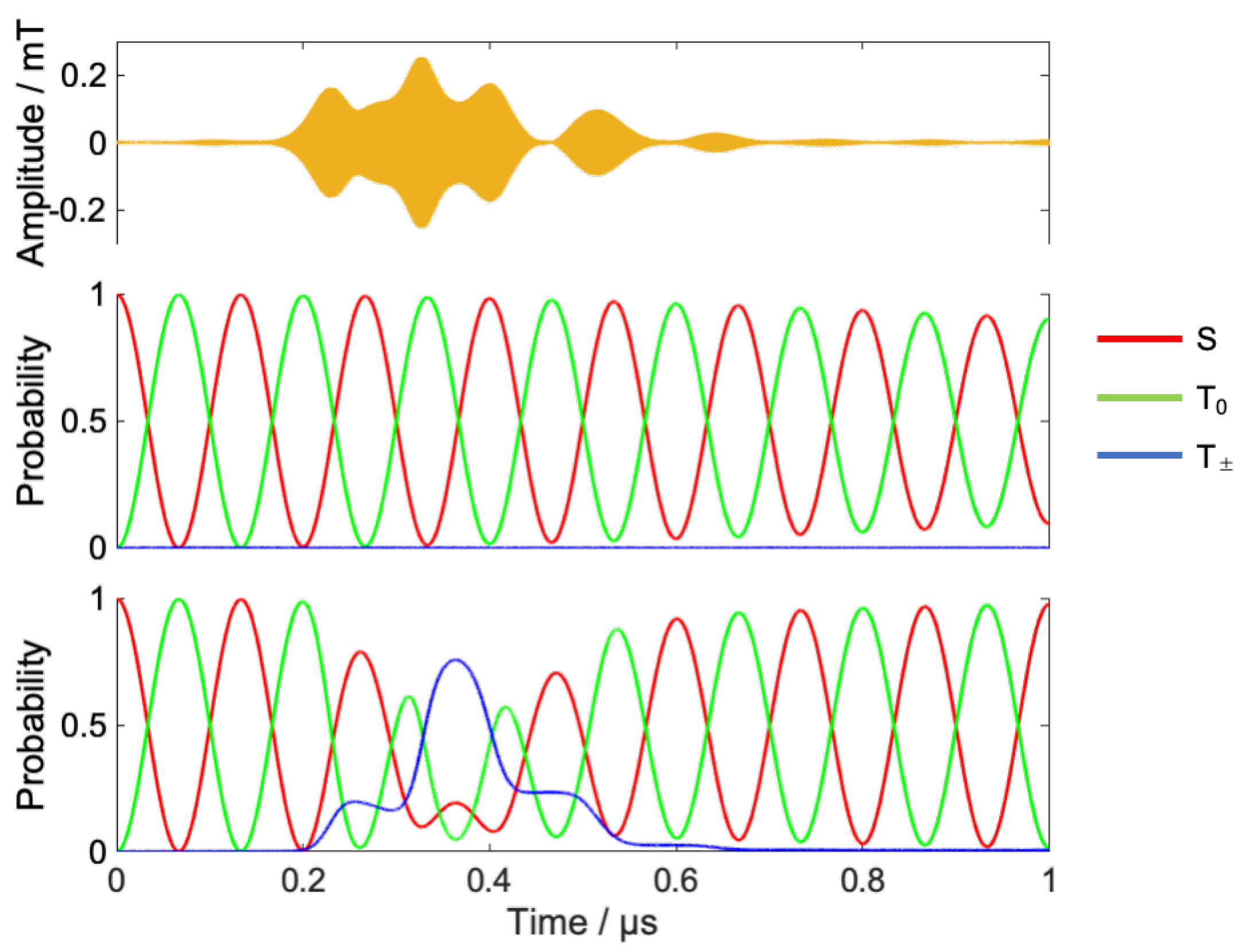
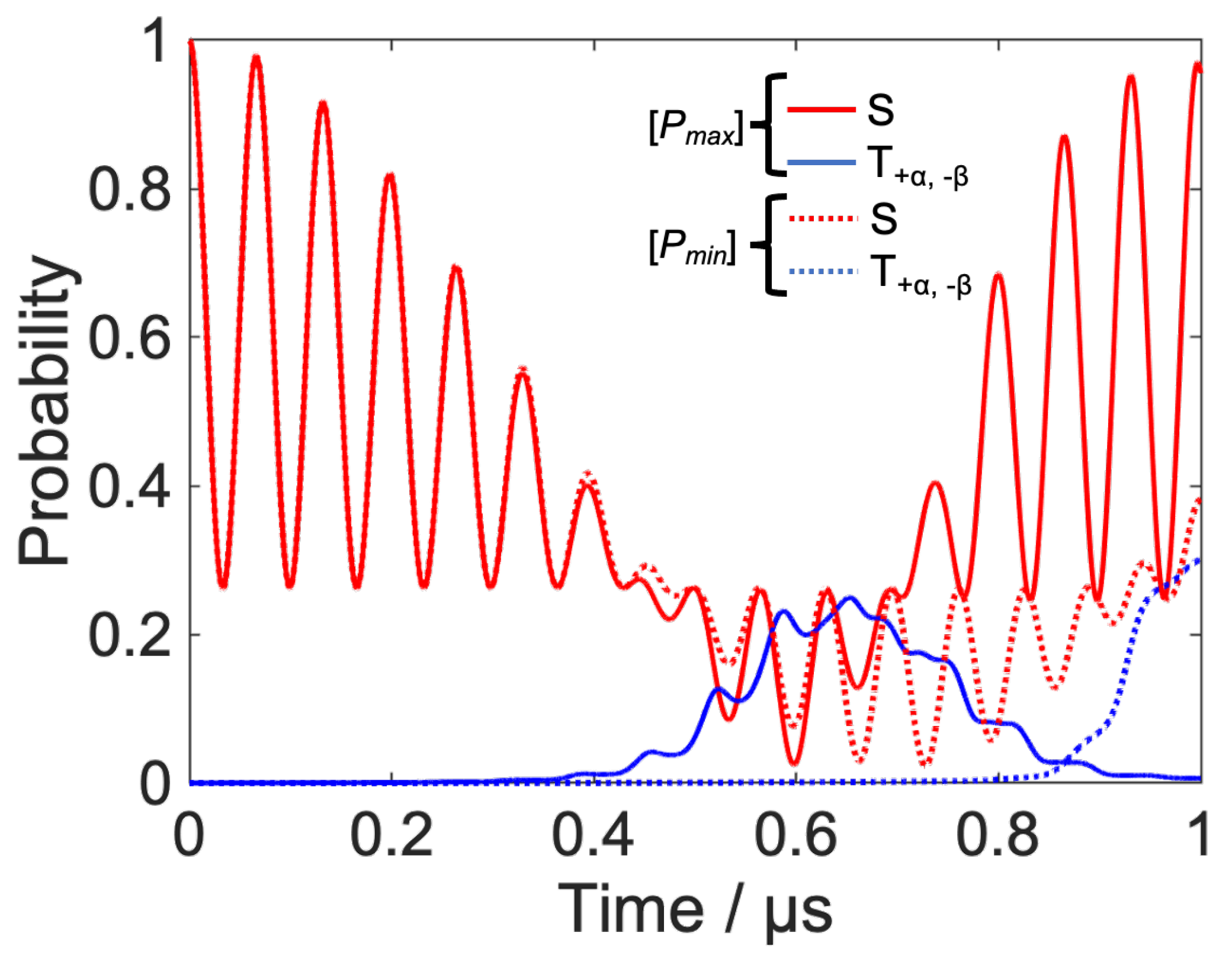
3.2. Coherent Pathway Control
- S-T0 mixing increases the population of T0 states;
- The RF provides a transition from the T0 state to the T± state;
- The transition from T± to T0 is again triggered by the RF, timed to maximize the singlet at the target time.
3.3. Parameter Optimization
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Nelson, J.N.; Zhang, J.; Zhou, J.; Rugg, B.K.; Krzyaniak, M.D.; Wasielewski, M.R. Effect of Electron–Nuclear Hyperfine Interactions on Multiple-Quantum Coherences in Photogenerated Covalent Radical (Qubit) Pairs. J. Phys. Chem. A 2018, 122, 9392–9402. [Google Scholar] [CrossRef] [PubMed]
- Rugg, B.K.; Krzyaniak, M.D.; Phelan, B.T.; Ratner, M.A.; Young, R.M.; Wasielewski, M.R. Photodriven Quantum Teleportation of an Electron Spin State in a Covalent Donor–Acceptor–Radical System. Nat. Chem. 2019, 11, 981–986. [Google Scholar] [CrossRef]
- Wasielewski, M.R.; Forbes, M.D.E.; Frank, N.L.; Kowalski, K.; Scholes, G.D.; Yuen-Zhou, J.; Baldo, M.A.; Freedman, D.E.; Goldsmith, R.H.; Goodson, T.; et al. Exploiting Chemistry and Molecular Systems for Quantum Information Science. Nat. Rev. Chem. 2020, 4, 490–504. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J.N.; Zhang, J.; Zhou, J.; Rugg, B.K.; Krzyaniak, M.D.; Wasielewski, M.R. CNOT Gate Operation on a Photogenerated Molecular Electron Spin-Qubit Pair. J. Chem. Phys. 2020, 152, 014503. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Pažėra, G.J.; Young, R.M.; Krzyaniak, M.D.; Wasielewski, M.R. Quantum Gate Operations on a Spectrally Addressable Photogenerated Molecular Electron Spin-Qubit Pair. J. Am. Chem. Soc. 2023, 145, 6585–6593. [Google Scholar] [CrossRef] [PubMed]
- Angerhofer, A.; Bittl, R. Radicals and Radical Pairs in Photosynthesis. Photochem. Photobiol. 1996, 63, 11–38. [Google Scholar] [CrossRef]
- Levanon, H.; Möbius, K. Advanced EPR spectroscopy on electron transfer processes in photosynthesis and biomimetic model systems. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 495–540. [Google Scholar] [CrossRef]
- Nugent, J.H.A.; Purton, S.; Evans, M.C.W. Oxygenic Photosynthesis in Algae and Cyanobacteria: Electron Transfer in Photosystems I and II. In Photosynthesis in Algae; Larkum, A.W.D., Douglas, S.E., Raven, J.A., Eds.; Advances in Photosynthesis and Respiration; Springer: Dordrecht, The Netherlands, 2003; Volume 14, pp. 133–156. ISBN 978-94-010-3772-3. [Google Scholar]
- Thurnauer, M.C.; Poluektov, O.G.; Kothe, G. Time-Resolved High-Frequency and Multifrequency EPR Studies of Spin-Correlated Radical Pairs in Photosynthetic Reaction Center Proteins. In Very High Frequency (VHF) ESR/EPR; Grinberg, O.Y., Berliner, L.J., Eds.; Biological Magnetic Resonance; Springer: Boston, MA, USA, 2004; Volume 22, pp. 165–206. ISBN 978-1-4419-3442-0. [Google Scholar]
- Giovani, B.; Byrdin, M.; Ahmad, M.; Brettel, K. Light-Induced Electron Transfer in a Cryptochrome Blue-Light Photoreceptor. Nat. Struct. Mol. Biol. 2003, 10, 489–490. [Google Scholar] [CrossRef]
- Langenbacher, T.; Immeln, D.; Dick, B.; Kottke, T. Microsecond Light-Induced Proton Transfer to Flavin in the Blue Light Sensor Plant Cryptochrome. J. Am. Chem. Soc. 2009, 131, 14274–14280. [Google Scholar] [CrossRef]
- Berndt, A.; Kottke, T.; Breitkreuz, H.; Dvorsky, R.; Hennig, S.; Alexander, M.; Wolf, E. A Novel Photoreaction Mechanism for the Circadian Blue Light Photoreceptor Drosophila Cryptochrome. J. Biol. Chem. 2007, 282, 13011–13021. [Google Scholar] [CrossRef] [Green Version]
- Song, S.-H.; Öztürk, N.; Denaro, T.R.; Arat, N.Ö.; Kao, Y.-T.; Zhu, H.; Zhong, D.; Reppert, S.M.; Sancar, A. Formation and Function of Flavin Anion Radical in Cryptochrome 1 Blue-Light Photoreceptor of Monarch Butterfly. J. Biol. Chem. 2007, 282, 17608–17612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kao, Y.-T.; Tan, C.; Song, S.-H.; Öztürk, N.; Li, J.; Wang, L.; Sancar, A.; Zhong, D. Ultrafast Dynamics and Anionic Active States of the Flavin Cofactor in Cryptochrome and Photolyase. J. Am. Chem. Soc. 2008, 130, 7695–7701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, J.; Jarocha, L.E.; Zollitsch, T.; Konowalczyk, M.; Henbest, K.B.; Richert, S.; Golesworthy, M.J.; Schmidt, J.; Déjean, V.; Sowood, D.J.C.; et al. Magnetic Sensitivity of Cryptochrome 4 from a Migratory Songbird. Nature 2021, 594, 535–540. [Google Scholar] [CrossRef] [PubMed]
- Mouritsen, H. Long-Distance Navigation and Magnetoreception in Migratory Animals. Nature 2018, 558, 50–59. [Google Scholar] [CrossRef]
- Hore, P.J.; Mouritsen, H. The Radical-Pair Mechanism of Magnetoreception. Annu. Rev. Biophys. 2016, 45, 299–344. [Google Scholar] [CrossRef]
- Ritz, T.; Adem, S.; Schulten, K. A Model for Photoreceptor-Based Magnetoreception in Birds. Biophys. J. 2000, 78, 707–718. [Google Scholar] [CrossRef] [Green Version]
- Liedvogel, M.; Maeda, K.; Henbest, K.; Schleicher, E.; Simon, T.; Timmel, C.R.; Hore, P.J.; Mouritsen, H. Chemical Magnetoreception: Bird Cryptochrome 1a Is Excited by Blue Light and Forms Long-Lived Radical-Pairs. PLoS ONE 2007, 2, e1106. [Google Scholar] [CrossRef]
- Ritz, T.; Wiltschko, R.; Hore, P.J.; Rodgers, C.T.; Stapput, K.; Thalau, P.; Timmel, C.R.; Wiltschko, W. Magnetic Compass of Birds Is Based on a Molecule with Optimal Directional Sensitivity. Biophys. J. 2009, 96, 3451–3457. [Google Scholar] [CrossRef] [Green Version]
- Engels, S.; Schneider, N.-L.; Lefeldt, N.; Hein, C.M.; Zapka, M.; Michalik, A.; Elbers, D.; Kittel, A.; Hore, P.J.; Mouritsen, H. Anthropogenic Electromagnetic Noise Disrupts Magnetic Compass Orientation in a Migratory Bird. Nature 2014, 509, 353–356. [Google Scholar] [CrossRef]
- Steiner, U.E.; Ulrich, T. Magnetic Field Effects in Chemical Kinetics and Related Phenomena. Chem. Rev. 1989, 89, 51–147. [Google Scholar] [CrossRef] [Green Version]
- Wasielewski, M.R.; Bock, C.H.; Bowman, M.K.; Norris, J.R. Controlling the Duration of Photosynthetic Charge Separation with Microwave Radiation. Nature 1983, 303, 520–522. [Google Scholar] [CrossRef]
- Lersch, W.; Lendzian, F.; Lang, E.; Feick, R.; Möbius, K.; Michel-Beyerle, M.E. High-Power RYDMR with a Loop-Gap Resonator. J. Magn. Reson. 1989, 82, 143–149. [Google Scholar] [CrossRef]
- Enjo, K.; Maeda, K.; Murai, H.; Azumi, T.; Tanimoto, Y. Effect of Polymethylene-Chain Dynamics on the Lifetime of a Charge-Separated Biradical Studied by RYDMR Spectroscopy. J. Phys. Chem. B 1997, 101, 10661–10665. [Google Scholar] [CrossRef]
- Woodward, J.R.; Timmel, C.R.; Hore, P.J.; Mclauchlan, K.A. Low Field RYDMR: Effects of Orthogonal Static and Oscillating Magnetic Fields on Radical Recombination Reactions. Mol. Phys. 2002, 100, 1181–1186. [Google Scholar] [CrossRef]
- Rodgers, C.T.; Wedge, C.J.; Norman, S.A.; Kukura, P.; Nelson, K.; Baker, N.; Maeda, K.; Henbest, K.B.; Hore, P.J.; Timmel, C.R. Radiofrequency Polarization Effects in Zero-Field Electron Paramagnetic Resonance. Phys. Chem. Chem. Phys. 2009, 11, 6569. [Google Scholar] [CrossRef]
- Wedge, C.J.; Lau, J.C.S.; Ferguson, K.-A.; Norman, S.A.; Hore, P.J.; Timmel, C.R. Spin-Locking in Low-Frequency Reaction Yield Detected Magnetic Resonance. Phys. Chem. Chem. Phys. 2013, 15, 16043. [Google Scholar] [CrossRef] [Green Version]
- Maeda, K.; Storey, J.G.; Liddell, P.A.; Gust, D.; Hore, P.J.; Wedge, C.J.; Timmel, C.R. Probing a Chemical Compass: Novel Variants of Low-Frequency Reaction Yield Detected Magnetic Resonance. Phys. Chem. Chem. Phys. 2015, 17, 3550–3559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khaneja, N.; Reiss, T.; Kehlet, C.; Schulte-Herbrüggen, T.; Glaser, S.J. Optimal Control of Coupled Spin Dynamics: Design of NMR Pulse Sequences by Gradient Ascent Algorithms. J. Magn. Reson. 2005, 172, 296–305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugawara, M. General Formulation of Locally Designed Coherent Control Theory for Quantum System. J. Chem. Phys. 2003, 118, 6784–6800. [Google Scholar] [CrossRef]
- Masuzawa, K.; Sato, M.; Sugawara, M.; Maeda, K. Quantum Control of Radical Pair Reactions by Local Optimization Theory. J. Chem. Phys. 2020, 152, 014301. [Google Scholar] [CrossRef]
- Haberkorn, R. Density Matrix Description of Spin-Selective Radical Pair Reactions. Mol. Phys. 1976, 32, 1491–1493. [Google Scholar] [CrossRef]
- Ivanov, K.L.; Petrova, M.V.; Lukzen, N.N.; Maeda, K. Consistent Treatment of Spin-Selective Recombination of a Radical Pair Confirms the Haberkorn Approach. J. Phys. Chem. A 2010, 114, 9447–9455. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.A.; Hore, P.J. Spin-Selective Reactions of Radical Pairs Act as Quantum Measurements. Chem. Phys. Lett. 2010, 488, 90–93. [Google Scholar] [CrossRef] [Green Version]
- Sugawara, M. Tracking of Wave Packet Dynamics by Locally Designed Control Field. Chem. Phys. Lett. 2003, 378, 603–608. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Pub. Co.: Reading, MA, USA, 1989; ISBN 978-0-201-15767-3. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef] [Green Version]
- Conn, A.R.; Gould, N.; Toint, P.L. A Globally Convergent Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds. Math. Comp. 1997, 66, 261–289. [Google Scholar] [CrossRef]
- Mims, D.; Herpich, J.; Lukzen, N.N.; Steiner, U.E.; Lambert, C. Readout of Spin Quantum Beats in a Charge-Separated Radical Pair by Pump-Push Spectroscopy. Science 2021, 374, 1470–1474. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tateno, A.; Masuzawa, K.; Nagashima, H.; Maeda, K. Anisotropic and Coherent Control of Radical Pairs by Optimized RF Fields. Int. J. Mol. Sci. 2023, 24, 9700. https://doi.org/10.3390/ijms24119700
Tateno A, Masuzawa K, Nagashima H, Maeda K. Anisotropic and Coherent Control of Radical Pairs by Optimized RF Fields. International Journal of Molecular Sciences. 2023; 24(11):9700. https://doi.org/10.3390/ijms24119700
Chicago/Turabian StyleTateno, Akihiro, Kenta Masuzawa, Hiroki Nagashima, and Kiminori Maeda. 2023. "Anisotropic and Coherent Control of Radical Pairs by Optimized RF Fields" International Journal of Molecular Sciences 24, no. 11: 9700. https://doi.org/10.3390/ijms24119700




