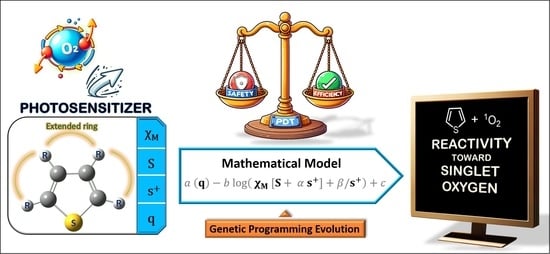
Thiophene Stability in Photodynamic Therapy: A Mathematical Model Approach
Abstract
:1. Introduction
2. Results and Discussion
2.1. Mechanism and Theory Level
2.2. The Role of Mulliken Electronegativity
2.3. Reactivity Prediction Model
2.4. Conceptual Interpretation of the Model
2.5. Fitting the Model to the Experimental Data
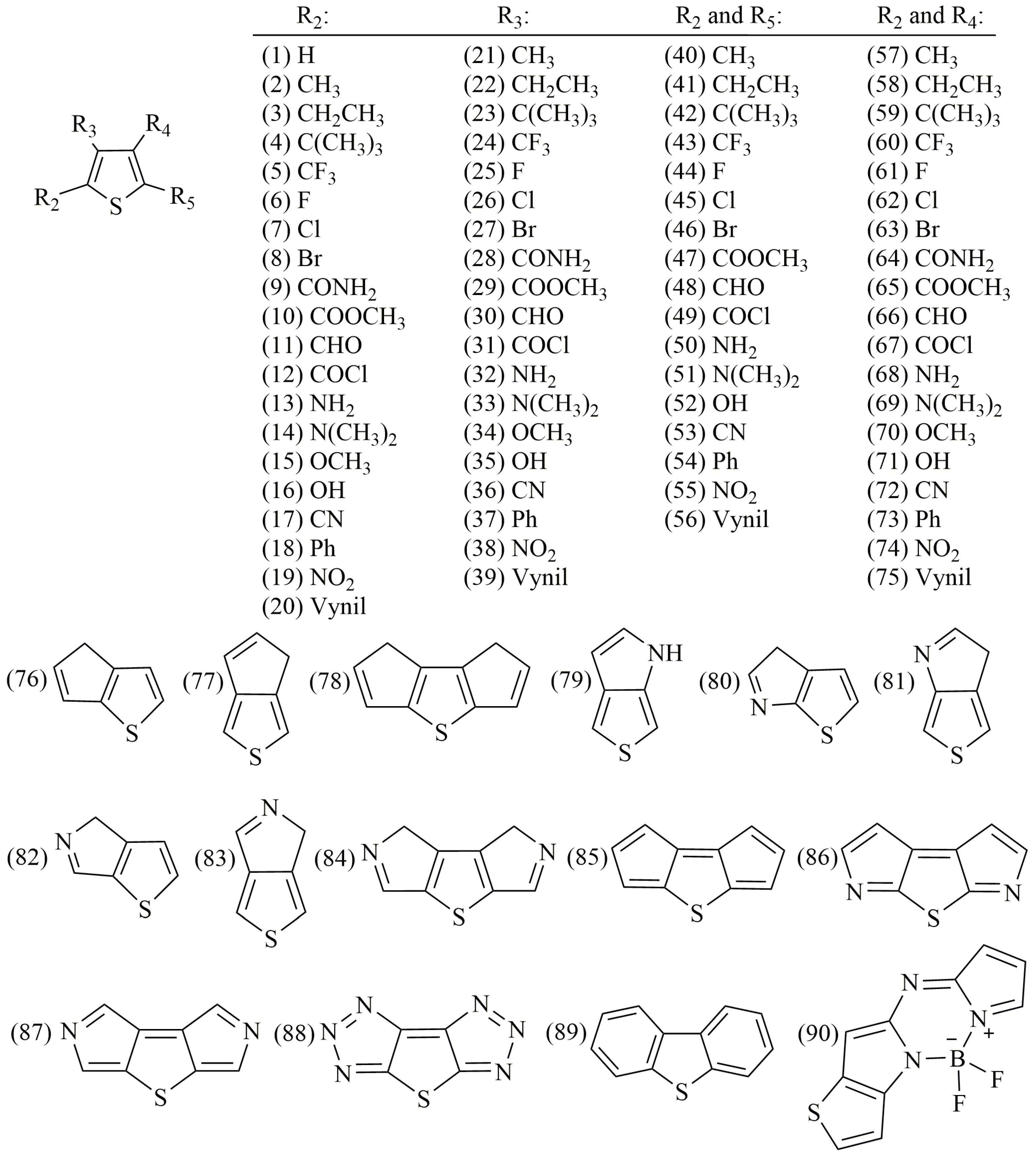
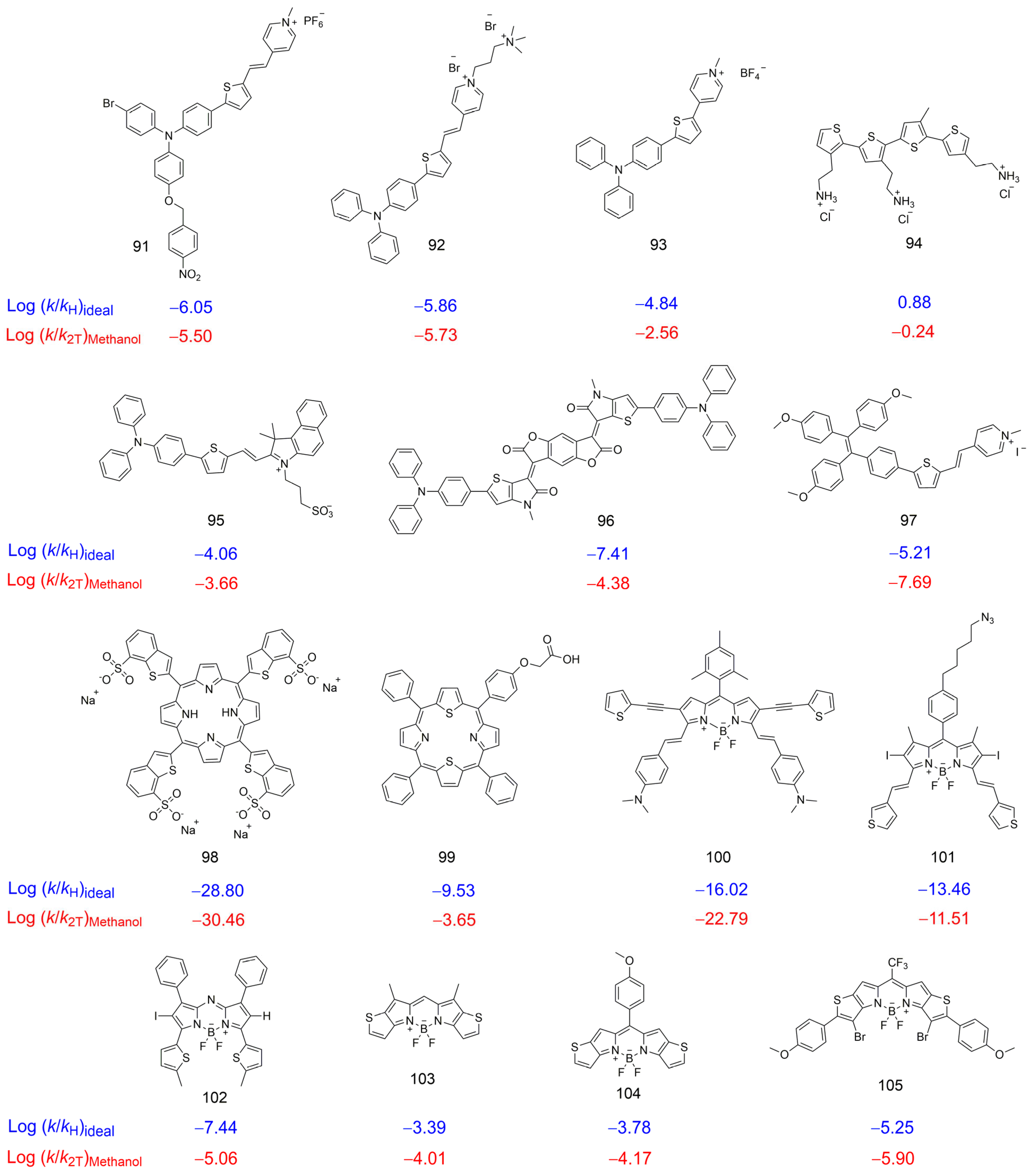
2.6. Evaluating the Reactivity of Some Thiophene-Based Photosensitizers
2.7. Script-Like Tool Description
3. Materials and Methods
3.1. Choice of Theoretical Level
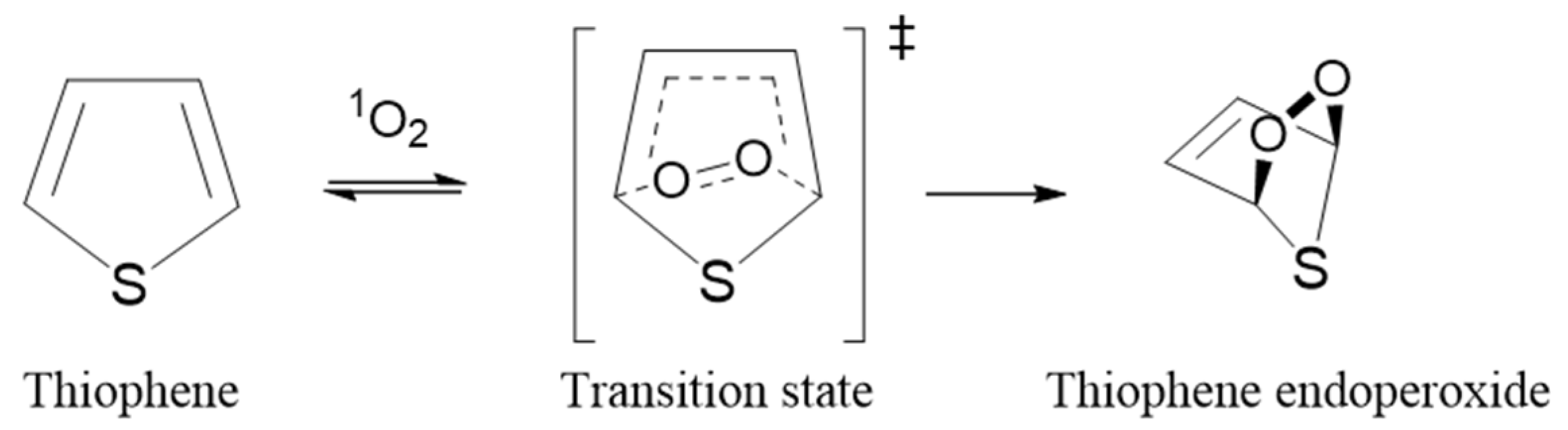
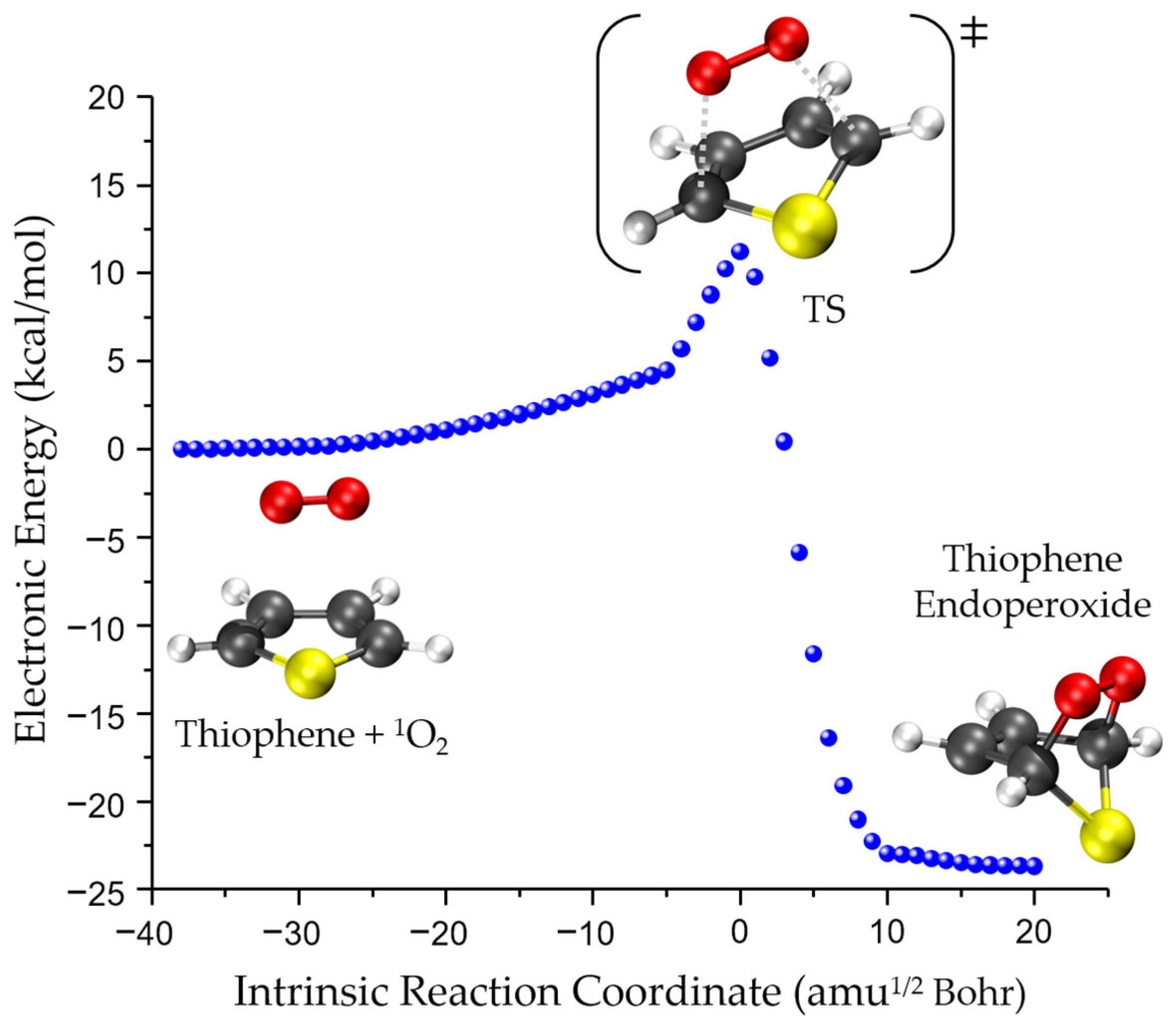
3.2. Kinetics of Singlet-Oxygen Oxidation of Thiophene Derivatives
3.3. Development of a Reactivity Prediction Model Using Conceptual DFT
3.3.1. Conceptual DFT Quantities:
3.3.2. Model Construction
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunaydin, G.; Gedik, M.E.; Ayan, S. Photodynamic Therapy for the Treatment and Diagnosis of Cancer–A Review of the Current Clinical Status. Front. Chem. 2021, 9, 608. [Google Scholar] [CrossRef] [PubMed]
- Juarranz, Á.; Gilaberte, Y.; González, S. Photodynamic therapy (PDT) in oncology. Cancers 2020, 12, 3341. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Sadler, P.J. How promising is phototherapy for cancer? Br. J. Cancer 2020, 123, 871–873. [Google Scholar] [CrossRef] [PubMed]
- Kessel, D. Photodynamic Therapy: Critical PDT Theory. Photochem. Photobiol. 2023, 99, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Sharma, D.; Singh, S.; Kumar, P.; Jain, G.K.; Aggarwal, G.; Almalki, W.H.; Kesharwani, P. Mechanisms of photodynamic therapy. In Nanomaterials for Photodynamic Therapy; Woodhead Publishing: Cambridge, UK, 2023; pp. 41–54. [Google Scholar] [CrossRef]
- Correia, J.H.; Rodrigues, J.A.; Pimenta, S.; Dong, T.; Yang, Z. Photodynamic therapy review: Principles, photosensitizers, applications, and future directions. Pharmaceutics 2021, 13, 1332. [Google Scholar] [CrossRef] [PubMed]
- Sai, D.L.; Lee, J.; Nguyen, D.L.; Kim, Y.P. Tailoring photosensitive ROS for advanced photodynamic therapy. Exp. Mol. Med. 2021, 53, 495–504. [Google Scholar] [CrossRef] [PubMed]
- Maharjan, P.S.; Bhattarai, H.K. Singlet Oxygen, Photodynamic Therapy, and Mechanisms of Cancer Cell Death. J. Oncol. 2022, 2022, 7211485. [Google Scholar] [CrossRef]
- Pham, T.C.; Nguyen, V.N.; Choi, Y.; Lee, S.; Yoon, J. Recent Strategies to Develop Innovative Photosensitizers for Enhanced Photodynamic Therapy. Chem. Rev. 2021, 121, 13454–13619. [Google Scholar] [CrossRef]
- Tavakkoli Yaraki, M.; Liu, B.; Tan, Y.N. Emerging Strategies in Enhancing Singlet Oxygen Generation of Nano-Photosensitizers Toward Advanced Phototherapy. Nano-Micro Lett. 2022, 14, 123. [Google Scholar] [CrossRef]
- Pang, E.; Zhao, S.; Wang, B.; Niu, G.; Song, X.; Lan, M. Strategies to construct efficient singlet oxygen-generating photosensitizers. Coord. Chem. Rev. 2022, 472, 214780. [Google Scholar] [CrossRef]
- Cakmak, Y.; Kolemen, S.; Duman, S.; Dede, Y.; Dolen, Y.; Kilic, B.; Kostereli, Z.; Yildirim, L.T.; Dogan, A.L.; Guc, D.; et al. Designing excited states: Theory-guided access to efficient photosensitizers for photodynamic action. Angew. Chem. Int. Ed. 2011, 50, 11937–11941. [Google Scholar] [CrossRef]
- Gao, J.; Yang, H.; Lu, Y.; Shi, Q.; Xu, S.; Wu, W.; Hu, F.; Liu, B. Anthracene-Bridged Photosensitizers for Effective and Safe Photodynamic Therapy. Chem. Mater. 2023, 35, 1229–1237. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Z.; Shen, C.; Pan, T.; Xie, L.; Xie, M.; Huang, L.; Jiang, Y.; Zhou, J.; Zuo, W.; et al. Hypoxia degradable AIE photosensitizer with high efficiency of photodynamic therapy and improved biological safety. Dye. Pigment. 2022, 200, 110122. [Google Scholar] [CrossRef]
- Huang, H.; Xie, W.; Wan, Q.; Mao, L.; Hu, D.; Sun, H.; Zhang, X.; Wei, Y. A Self-Degradable Conjugated Polymer for Photodynamic Therapy with Reliable Postoperative Safety. Adv. Sci. 2022, 9, 2104101. [Google Scholar] [CrossRef] [PubMed]
- Yuan, B.; Wu, H.; Wang, H.; Tang, B.; Xu, J.; Zhang, X. A Self-Degradable Supramolecular Photosensitizer with High Photodynamic Therapeutic Efficiency and Improved Safety. Angew. Chem. 2021, 133, 716–720. [Google Scholar] [CrossRef]
- Akimoto, J.; Fukami, S.; Kohno, M. Efficacy and safety of photodynamic therapy using talaporfin sodium and a semiconductor laser in patients with malignant meningeal tumors. Photodiagnosis Photodyn. Ther. 2023, 41, 103418. [Google Scholar] [CrossRef]
- Li, H.; Long, G.; Tian, J. Efficacy and safety of photodynamic therapy for non–muscle-invasive bladder cancer: A systematic review and meta-analysis. Front. Oncol. 2023, 13, 1255632. [Google Scholar] [CrossRef] [PubMed]
- Tan, G.; Xu, J.; Yu, Q.; Yang, Z.; Zhang, H. The safety and efficiency of photodynamic therapy for the treatment of osteosarcoma: A systematic review of in vitro experiment and animal model reports. Photodiagnosis Photodyn. Ther. 2022, 40, 103093. [Google Scholar] [CrossRef]
- Liu, Q.; Tian, J.; Tian, Y.; Sun, Q.; Sun, D.; Liu, D.; Wang, F.; Xu, H.; Ying, G.; Wang, J.; et al. Thiophene donor for NIR-II fluorescence imaging-guided photothermal/photodynamic/chemo combination therapy. Acta Biomater. 2021, 127, 287–297. [Google Scholar] [CrossRef]
- Wang, D.; Su, H.; Kwok, R.T.K.; Hu, X.; Zou, H.; Luo, Q.; Lee, M.M.S.; Xu, W.; Lam, J.W.Y.; Tang, B.Z. Rational design of a water-soluble NIR AIEgen, and its application in ultrafast wash-free cellular imaging and photodynamic cancer cell ablation. Chem. Sci. 2018, 9, 3685–3693. [Google Scholar] [CrossRef]
- Khatoon, S.S.; Chen, Y.; Zhao, H.; Lv, F.; Liu, L.; Wang, S. In situ self-assembly of conjugated polyelectrolytes for cancer targeted imaging and photodynamic therapy. Biomater. Sci. 2020, 8, 2156–2163. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, W.; Yang, L.; Ma, B.; Kong, Q.; Li, G.; Wang, Y.; Tang, B.Z. Multifunctional Two-Photon AIE Luminogens for Highly Mitochondria-Specific Bioimaging and Efficient Photodynamic Therapy. ACS Appl. Mater. Interfaces 2019, 11, 20715–20724. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Ergene, C.; Lee, J.Y.; Shirley, D.J.; Carone, B.R.; Caputo, G.A.; Palermo, E.F. Sequence and Dispersity Are Determinants of Photodynamic Antibacterial Activity Exerted by Peptidomimetic Oligo(thiophene)s. ACS Appl. Mater. Interfaces 2019, 11, 1896–1906. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; He, B.; Zhang, Z.; Li, Y.; Kang, M.; Wang, Y.; Li, K.; Wang, D.; Tang, B.Z. Aggregation-Induced Emission Luminogens Married to 2D Black Phosphorus Nanosheets for Highly Efficient Multimodal Theranostics. Adv. Mater. 2020, 32, 2003382. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Zhao, L.; Zhang, Q.; Chang, M.; Li, C.; Zhang, H.; Lu, Y.; Chen, Y. An Acceptor–Donor–Acceptor Structured Small Molecule for Effective NIR Triggered Dual Phototherapy of Cancer. Adv. Funct. Mater. 2020, 30, 1910301. [Google Scholar] [CrossRef]
- Zhu, W.; Kang, M.; Wu, Q.; Zhang, Z.; Wu, Y.; Li, C.; Li, K.; Wang, L.; Wang, D.; Tang, B.Z. Zwitterionic AIEgens: Rational Molecular Design for NIR-II Fluorescence Imaging-Guided Synergistic Phototherapy. Adv. Funct. Mater. 2021, 31, 2007026. [Google Scholar] [CrossRef]
- Chen, J.; Wen, K.; Chen, H.; Jiang, S.; Wu, X.; Lv, L.; Peng, A.; Zhang, S.; Huang, H. Achieving High-Performance Photothermal and Photodynamic Effects upon Combining D–A Structure and Nonplanar Conformation. Small 2020, 16, 2000909. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhang, Y.; Li, J.; An, J.; Li, C.; Bai, S.; Sharma, A.; Deng, G.; Kim, J.S.; Sun, Y. NIR-II emissive multifunctional AIEgen with single laser-activated synergistic photodynamic/photothermal therapy of cancers and pathogens. Biomaterials 2020, 259, 120315. [Google Scholar] [CrossRef]
- Awuah, S.G.; Polreis, J.; Biradar, V.; You, Y. Singlet oxygen generation by novel NIR BODIPY dyes. Org. Lett. 2011, 13, 3884–3887. [Google Scholar] [CrossRef]
- Tanaka, K.; Yamane, H.; Yoshii, R.; Chujo, Y. Efficient light absorbers based on thiophene-fused boron dipyrromethene (BODIPY) dyes. Bioorganic Med. Chem. 2013, 21, 2715–2719. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Q.; Chen, H.; Zhou, Z.; Guo, Z.; Shen, Z. Thienopyrrole-expanded BODIPY as a potential NIR photosensitizer for photodynamic therapy. Chem. Commun. 2013, 49, 3940–3942. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Burghart, A.; Derecskei-Kovacs, A.; Burgess, K. 4,4-Difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY) dyes modified for extended conjugation and restricted bond rotations. J. Org. Chem. 2000, 65, 2900–2906. [Google Scholar] [CrossRef] [PubMed]
- Dingyuan, Y.; Tan, Y.; Sun, Y.; Huang, W.; Zhu, D.; Yan, D.; Wang, D.; Tang, B.Z. Thiophene π-bridge based NIR-II AIEgens for biomedical applications. Luminescence 2023, 39, e4606. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Q.; Qiu, W.; Lyu, Y.; Zhu, Z.; Zhao, X.; Zhu, W.H. AIE-active luminogens as highly efficient free-radical ROS photogenerator for image-guided photodynamic therapy. Chem. Sci. 2022, 13, 3599–3608. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.J.; Li, W.; Xiang, Q.; Tan, Y.; Xing, X.; Wu, C.; Dong, H.; Zhang, X. Engineering Metal-Organic Framework Hybrid AIEgens with Tumor-Activated Accumulation and Emission for the Image-Guided GSH Depletion ROS Therapy. ACS Appl. Mater. Interfaces 2022, 14, 29599–29612. [Google Scholar] [CrossRef] [PubMed]
- Satyanarayan, M.N.; Trivedi, D.R.; Mohan, M.; Pangannaya, S. Aggregation-induced emission in thiophene derivatives. ISSS J. Micro Smart Syst. 2022, 11, 217–233. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, W.; Kang, M.; Wen, H.; Guo, H.; Zhang, P.; Xi, L.; Li, K.; Wang, L.; Wang, D.; et al. An All-Round Athlete on the Track of Phototheranostics: Subtly Regulating the Balance between Radiative and Nonradiative Decays for Multimodal Imaging-Guided Synergistic Therapy. Adv. Mater. 2020, 32, 2003210. [Google Scholar] [CrossRef] [PubMed]
- Xiong, W.; Wang, L.; Chen, X.; Tang, H.; Cao, D.; Zhang, G.; Chen, W. Pyridinium-substituted tetraphenylethylene salt-based photosensitizers by varying counter anions: A highly efficient photodynamic therapy for cancer cell ablation and bacterial inactivation. J. Mater. Chem. B 2020, 8, 5234–5244. [Google Scholar] [CrossRef]
- Zhao, N.; Li, P.; Zhuang, J.; Liu, Y.; Xiao, Y.; Qin, R.; Li, N. Aggregation-Induced Emission Luminogens with the Capability of Wide Color Tuning, Mitochondrial and Bacterial Imaging, and Photodynamic Anticancer and Antibacterial Therapy. ACS Appl. Mater. Interfaces 2019, 11, 11227–11237. [Google Scholar] [CrossRef]
- Xu, W.; Lee, M.M.S.; Zhang, Z.; Sung, H.H.Y.; Williams, I.D.; Kwok, R.T.K.; Lam, J.W.Y.; Wang, D.; Tang, B.Z. Facile synthesis of AIEgens with wide color tunability for cellular imaging and therapy. Chem. Sci. 2019, 10, 3494–3501. [Google Scholar] [CrossRef]
- Wang, D.; Lee, M.M.S.; Xu, W.; Kwok, R.T.K.; Lam, J.W.Y.; Tang, B.Z. Theranostics based on AIEgens. Theranostics 2018, 8, 4925–4956. [Google Scholar] [CrossRef] [PubMed]
- Yıldız Gül, E.; Erdem, M.; Kazan, H.H.; Tanrıverdi Eçik, E. Thiophene BODIPY-substituted cyclotriphosphazene-derived photosensitizers for photodynamic therapy applications. New J. Chem. 2023, 47, 17469–17480. [Google Scholar] [CrossRef]
- Cai, Y.; Liang, P.; Tang, Q.; Yang, X.; Si, W.; Huang, W.; Zhang, Q.; Dong, X. Diketopyrrolopyrrole-Triphenylamine Organic Nanoparticles as Multifunctional Reagents for Photoacoustic Imaging-Guided Photodynamic/Photothermal Synergistic Tumor Therapy. ACS Nano 2017, 11, 1054–1063. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Ge, J.; Escudero, D.; Wang, Z.; Zhao, J.; Jacquemin, D. Molecular structure-intersystem crossing relationship of heavy-atom-free bodipy triplet photosensitizers. J. Org. Chem. 2015, 80, 5958–5963. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Su, H.; Kwok, R.T.K.; Shan, G.; Leung, A.C.S.; Lee, M.M.S.; Sung, H.H.Y.; Williams, I.D.; Lam, J.W.Y.; Tang, B.Z. Facile Synthesis of Red/NIR AIE Luminogens with Simple Structures, Bright Emissions, and High Photostabilities, and Their Applications for Specific Imaging of Lipid Droplets and Image-Guided Photodynamic Therapy. Adv. Funct. Mater. 2017, 27, 1704039. [Google Scholar] [CrossRef]
- Rangasamy, S.; Ju, H.; Um, S.; Oh, D.C.; Song, J.M. Mitochondria and DNA Targeting of 5,10,15,20-Tetrakis(7-sulfonatobenzo[b]thiophene) Porphyrin-Induced Photodynamic Therapy via Intrinsic and Extrinsic Apoptotic Cell Death. J. Med. Chem. 2015, 58, 6864–6874. [Google Scholar] [CrossRef] [PubMed]
- Qi, S.; Kwon, N.; Yim, Y.; Nguyen, V.N.; Yoon, J. Fine-tuning the electronic structure of heavy-atom-free BODIPY photosensitizers for fluorescence imaging and mitochondria-targeted photodynamic therapy. Chem. Sci. 2020, 11, 6479–6484. [Google Scholar] [CrossRef]
- DeRosa, M.C.; Crutchley, R.J. Photosensitized singlet oxygen and its applications. Coord. Chem. Rev. 2002, 233–234, 351–371. [Google Scholar] [CrossRef]
- Moan, J. Effect of bleaching of porphyrin sensitizers during photodynamic therapy. Cancer Lett. 1986, 33, 45–53. [Google Scholar] [CrossRef]
- Bonnett, R.; Martínez, G. Photobleaching of sensitisers used in photodynamic therapy. Tetrahedron 2001, 57, 9513–9547. [Google Scholar] [CrossRef]
- Van Tilborg, W.J.M. Singlet-oxygen oxidation of thiophenes. Recl. Trav. Chim. Pays-Bas 1976, 95, 140–143. [Google Scholar] [CrossRef]
- Shi, Q.; Wu, J. Review on Sulfur Compounds in Petroleum and Its Products: State-of-the-Art and Perspectives. Energy Fuels 2021, 35, 14445–14461. [Google Scholar] [CrossRef]
- Betiha, M.A.; Rabie, A.M.; Ahmed, H.S.; Abdelrahman, A.A.; El-Shahat, M.F. Oxidative desulfurization using graphene and its composites for fuel containing thiophene and its derivatives: An update review. Egypt. J. Pet. 2018, 27, 715–730. [Google Scholar] [CrossRef]
- Pham, T.C.; Cho, M.; Nguyen, V.N.; Van Nguyen, T.K.; Kim, G.; Min, S.; Kim, M.R.; Yoon, J.; Lee, S. Regulating 1O2 generation from heavy-atom-free triplet photosensitizers based on thiophene-fused BODIPY. Dye. Pigment. 2023, 219, 111617. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, K.; Jiang, L.; Xiao, J.; Wang, B.; Zeng, L.; Song, X.; Lan, M. Polythiophene-Based Carbon Dots for Imaging-Guided Photodynamic Therapy. ACS Appl. Nano Mater. 2021, 4, 10528–10533. [Google Scholar] [CrossRef]
- Fuse, S.; Takizawa, M.; Sato, S.; Okazaki, S.; Nakamura, H. Elucidating the mode of action for thiophene-based organic D-π-A sensitizers for use in photodynamic therapy. Bioorganic Med. Chem. 2019, 27, 315–321. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A.; Neese, F. Density functional theory. Photosynth. Res. 2009, 102, 443–453. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- O’Neill, M.; Poli, R.; Langdon, W.B.; McPhee, N.F. A Field Guide to Genetic Programming. Genet. Program. Evolvable Mach. 2009, 10, 229–230. [Google Scholar] [CrossRef]
- Eyeing, H. The activated complex and the absolute rate of chemical reactions. Chem. Rev. 1935, 17, 65–77. [Google Scholar] [CrossRef]
- Mortimer, R.G.; Eyring, H. Elementary transition state theory of the Soret and Dufour effects. Proc. Natl. Acad. Sci. USA 1980, 77, 1728–1731. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Chattaraj, P.K. Conceptual density functional theory based electronic structure principles. Chem. Sci. 2021, 12, 6264–6279. [Google Scholar] [CrossRef] [PubMed]
- Jorner, K.; Brinck, T.; Norrby, P.O.; Buttar, D. Machine learning meets mechanistic modelling for accurate prediction of experimental activation energies. Chem. Sci. 2021, 12, 1163–1175. [Google Scholar] [CrossRef] [PubMed]
- Mhadeshwar, A.B.; Wang, H.; Vlachos, D.G. Thermodynamic Consistency in Microkinetic Development of Surface Reaction Mechanisms. J. Phys. Chem. B 2003, 107, 12721–12733. [Google Scholar] [CrossRef]
- Durant, J.L. Evaluation of transition state properties by density functional theory. Chem. Phys. Lett. 1996, 256, 595–602. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Li, Y.; Fang, D.C. DFT calculations on kinetic data for some [4 + 2] reactions in solution. Phys. Chem. Chem. Phys. 2014, 16, 15224–15230. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Fanelli, M.G.; Cook, J.M.; Bai, F.; Parish, C.A. Mechanisms for the reaction of thiophene and methylthiophene with singlet and triplet molecular oxygen. J. Phys. Chem. A 2012, 116, 4934–4946. [Google Scholar] [CrossRef]
- Skold, C.N.; Schlessinger, R.H. The reaction of singlet oxygen with a simple thiophene. Tetrahedron Lett. 1970, 11, 791–794. [Google Scholar] [CrossRef]
- Taft, R.W. Concerning the electron-withdrawing power and the electronegativity of groups. J. Chem. Phys. 1957, 26, 93–96. [Google Scholar] [CrossRef]
- Alcázar, J.J.; Misad Saide, A.C.; Campodónico, P.R. Reliable and accurate prediction of basic pKa values in nitrogen compounds: The pKa shift in supramolecular systems as a case study. J. Cheminform. 2023, 15, 90. [Google Scholar] [CrossRef]
- You, Y.; Gibson, S.L.; Hilf, R.; Davies, S.R.; Oseroff, A.R.; Roy, I.; Ohulchanskyy, T.Y.; Bergey, E.J.; Detty, M.R. Water soluble, core-modified porphyrins. 3. Synthesis, photophysical properties, and in vitro studies of photosensitization, uptake, and localization with carboxylic acid-substituted derivatives. J. Med. Chem. 2003, 46, 3734–3747. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Zhou, J.; Ji, X.; Lin, G.; Xu, S.; Dong, X.; Zhao, W. Discovery of a Monoiodo Aza-BODIPY Near-Infrared Photosensitizer: In vitro and in vivo Evaluation for Photodynamic Therapy. J. Med. Chem. 2020, 63, 9950–9964. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Lam, J.W.Y.; Tang, B.Z. Aggregation-induced emission. Chem. Soc. Rev. 2011, 40, 5361–5388. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. J. Chem. Phys. 1992, 96, 2155–2160. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06 functionals and 12 other functionals. Theor. Chem. Acc. 2008, 119, 525. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Lin, Y.S.; De Li, G.; Mao, S.P.; Chai, J. Da Long-range corrected hybrid density functionals with improved dispersion corrections. J. Chem. Theory Comput. 2013, 9, 263–272. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A revised low-cost variant of the B97-D density functional method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Ratés, M.; Neese, F. Effect of the Solute Cavity on the Solvation Energy and its Derivatives within the Framework of the Gaussian Charge Scheme. J. Comput. Chem. 2020, 41, 922–939. [Google Scholar] [CrossRef] [PubMed]
- Sinnecker, S.; Rajendran, A.; Klamt, A.; Diedenhofen, M.; Neese, F. Calculation of solvent shifts on electronic g-tensors with the conductor-like screening model (COSMO) and its self-consistent generalization to real solvents (direct COSMO-RS). J. Phys. Chem. A 2006, 110, 2235–2245. [Google Scholar] [CrossRef] [PubMed]
- Ásgeirsson, V.; Birgisson, B.O.; Bjornsson, R.; Becker, U.; Neese, F.; Riplinger, C.; Jónsson, H. Nudged Elastic Band Method for Molecular Reactions Using Energy-Weighted Springs Combined with Eigenvector following. J. Chem. Theory Comput. 2021, 17, 4929–4945. [Google Scholar] [CrossRef] [PubMed]
- Ishida, K.; Morokuma, K.; Komornicki, A. The intrinsic reaction coordinate. An ab initio calculation for HNC→HCN and H−+CH4→CH4+H−. J. Chem. Phys. 1976, 66, 2153–2156. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A “chain-of-spheres” algorithm for the Hartree-Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Hughes, T.B.; Flynn, N.; Le Dang, N.; Swamidass, S.J. Modeling the Bioactivation and Subsequent Reactivity of Drugs. Chem. Res. Toxicol. 2021, 34, 584–600. [Google Scholar] [CrossRef] [PubMed]
- Melen, R.L. Frontiers in molecular p-block chemistry: From structure to reactivity. Science 2019, 363, 479–484. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Su, N.Q.; Yang, W. Describing Chemical Reactivity with Frontier Molecular Orbitalets. JACS Au 2022, 2, 1383–1394. [Google Scholar] [CrossRef] [PubMed]
- Ertl, P.; Gerebtzoff, G.; Lewis, R.; Muenkler, H.; Schneider, N.; Sirockin, F.; Stiefl, N.; Tosco, P. Chemical Reactivity Prediction: Current Methods and Different Application Areas. Mol. Inform. 2022, 41, 2100277. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.B.; Le Dang, N.; Miller, G.P.; Swamidass, S.J. Modeling reactivity to biological macromolecules with a deep multitask network. ACS Cent. Sci. 2016, 2, 529–537. [Google Scholar] [CrossRef] [PubMed]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
- Suresh, C.H.; Remya, G.S.; Anjalikrishna, P.K. Molecular electrostatic potential analysis: A powerful tool to interpret and predict chemical reactivity. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1601. [Google Scholar] [CrossRef]
- Barrera, Y.; Anderson, J.S.M. Predicting reactivity with a general-purpose reactivity indicator. Chem. React. Approaches Appl. 2023, 2, 159–180. [Google Scholar] [CrossRef]
- Srivastava, R. Chemical reactivity theory (CRT) study of small drug-like biologically active molecules. J. Biomol. Struct. Dyn. 2021, 39, 943–952. [Google Scholar] [CrossRef]
- Lee, B.; Yoo, J.; Kang, K. Predicting the chemical reactivity of organic materials using a machine-learning approach. Chem. Sci. 2020, 11, 7813–7822. [Google Scholar] [CrossRef] [PubMed]
- Ehresmann, B.; Martin, B.; Horn, A.H.C.; Clark, T. Local molecular properties and their use in predicting reactivity. J. Mol. Model. 2003, 9, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Mulliken, R.S. A new electroaffinity scale; Together with data on valence states and on valence ionization potentials and electron affinities. J. Chem. Phys. 1934, 2, 782–793. [Google Scholar] [CrossRef]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 1977, 68, 3801–3807. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Yang, W.; Parr, R.G. Hardness, softness, and the fukui function in the electronic theory of metals and catalysis. Proc. Natl. Acad. Sci. USA 1985, 82, 6723–6726. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Roy, R.K.; Krishnamurti, S.; Geerlings, P.; Pal, S. Local softness and hardness based reactivity descriptors for predicting intra- and intermolecular reactivity sequences: Carbonyl compounds. J. Phys. Chem. A 1998, 102, 3746–3755. [Google Scholar] [CrossRef]
- Oláh, J.; Van Alsenoy, C.; Sannigrahi, A.B. Condensed Fukui functions derived from stockholder charges: Assessment of their performance as local reactivity descriptors. J. Phys. Chem. A 2002, 106, 3885–3890. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.; Chattaraj, P.K.; Liu, S. A comparative study to predict regioselectivity, electrophilicity and nucleophilicity with Fukui function and Hirshfeld charge. Theor. Chem. Acc. 2019, 138, 124. [Google Scholar] [CrossRef]




| Level of Theory | r2 |
|---|---|
| B97-3C | 0.8184 |
| B3LYP-D3BJ/def2-TZVP | 0.9437 |
| M06-2X/def2-TZVP | 0.5021 |
| M06-2X-D3(0)/def2-TZVP | 0.7573 |
| ωB97X-D3/TZVP | 0.9420 |
| ωB97X-D3/def2-TZVP | 0.9838 |
| ωB97X-D3/ma-def2-TZVP | 0.9109 |
| ID | )Methanola,b Experimental | )Methanola,c Theoretical |
|---|---|---|
| 2 | 0.08 | 0.21 |
| 3 | 0.00 | 0.40 |
| 8 | −0.70 | −0.73 |
| 21 | −0.30 | −0.59 |
| 40 | 1.81 | 1.43 |
| 42 | 1.67 | 1.63 |
| 54 | −0.05 | −0.04 |
| 59 | 0.90 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcázar, J.J. Thiophene Stability in Photodynamic Therapy: A Mathematical Model Approach. Int. J. Mol. Sci. 2024, 25, 2528. https://doi.org/10.3390/ijms25052528
Alcázar JJ. Thiophene Stability in Photodynamic Therapy: A Mathematical Model Approach. International Journal of Molecular Sciences. 2024; 25(5):2528. https://doi.org/10.3390/ijms25052528
Chicago/Turabian StyleAlcázar, Jackson J. 2024. "Thiophene Stability in Photodynamic Therapy: A Mathematical Model Approach" International Journal of Molecular Sciences 25, no. 5: 2528. https://doi.org/10.3390/ijms25052528
APA StyleAlcázar, J. J. (2024). Thiophene Stability in Photodynamic Therapy: A Mathematical Model Approach. International Journal of Molecular Sciences, 25(5), 2528. https://doi.org/10.3390/ijms25052528