Multivariate Analysis Techniques and Tolerance Indices for Detecting Bread Wheat Genotypes of Drought Tolerance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Description
2.2. Yield and Yield Components Parameters
2.3. Statistical Analyses
- (1)
- Expected mean squares-based heritability (h2ems) =
- (2)
- Genotype mean-based heritability (h2gm) =
- (3)
- Plot mean-heritability (h2pm) =
- (4)
- Cullis heritability (h2cullis) =
- (5)
- Piepho heritability (h2piepho) =
- -
- Genotypic coefficient of variation (CVgen) = ) × 100
- -
- Coefficient of determination of GEN:ENV effects (R2) =
- -
- Residual coefficient of variation (CVres) = ) × 100
- -
- Genotype–environment correlation (rgen-env) =
- -
- CV ratio =
3. Results
3.1. Deviance Analysis and Genetic Parameters
3.2. AMMI Analysis
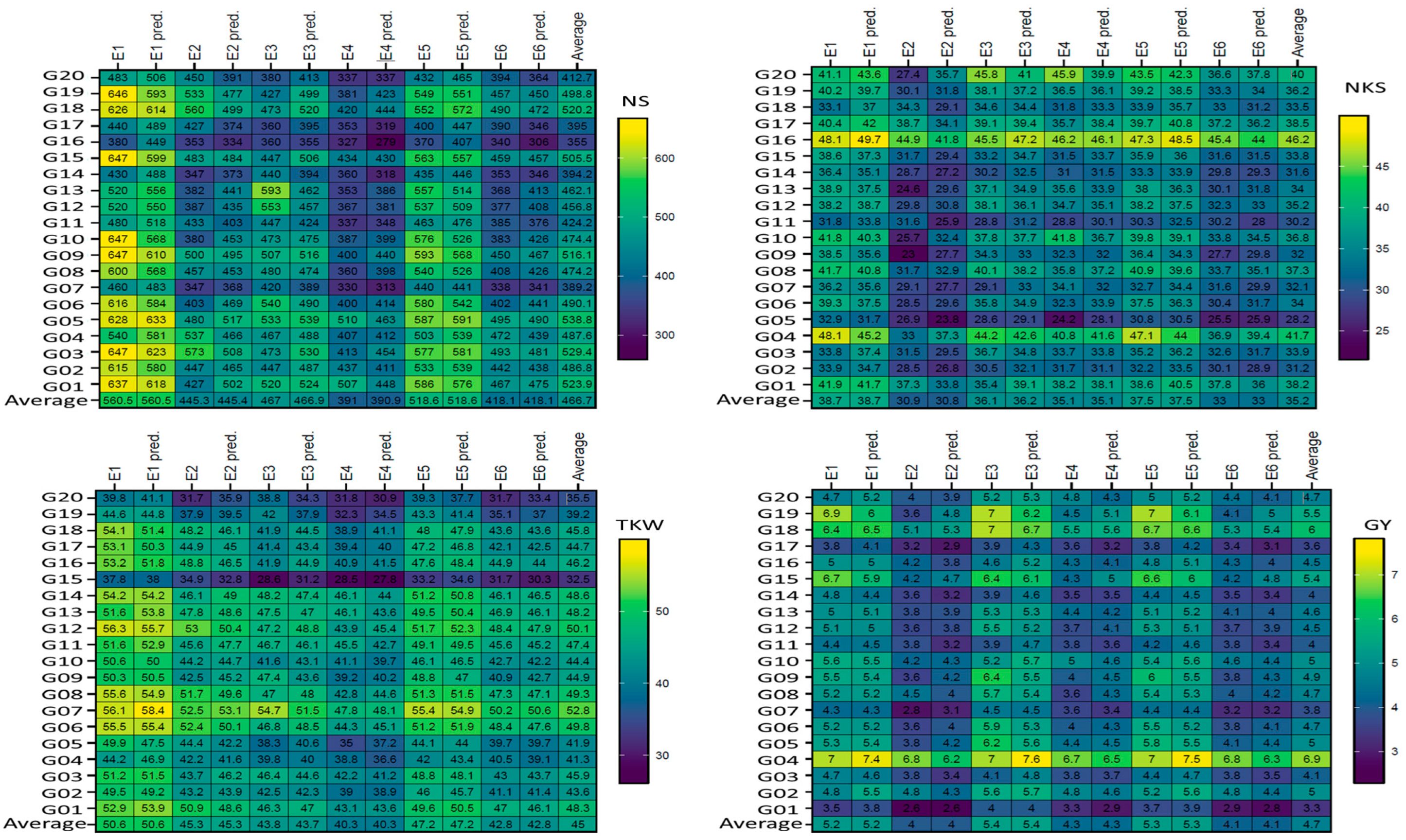
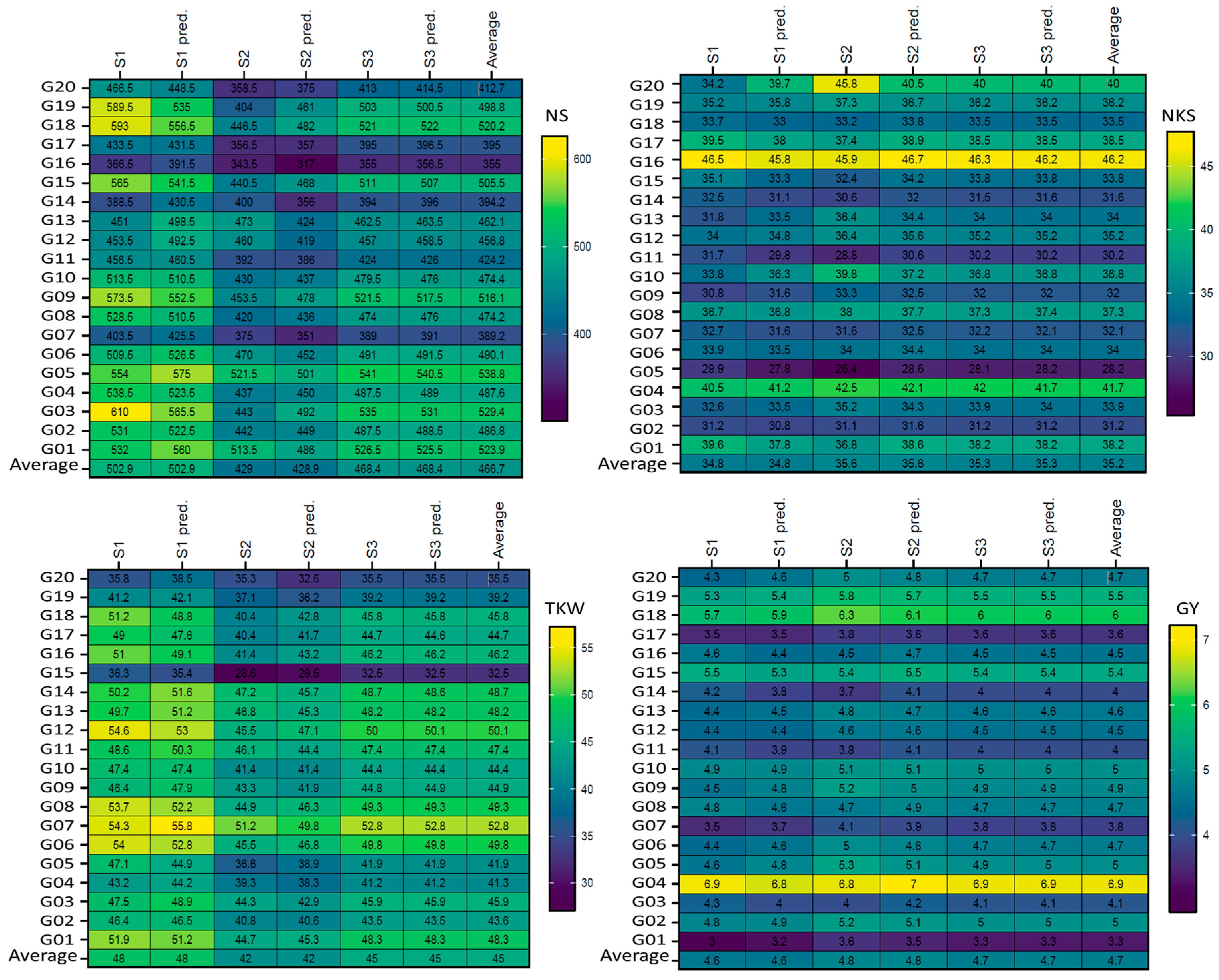
3.3. Mean Performance of Genotypes as Absolute and Predicted Values
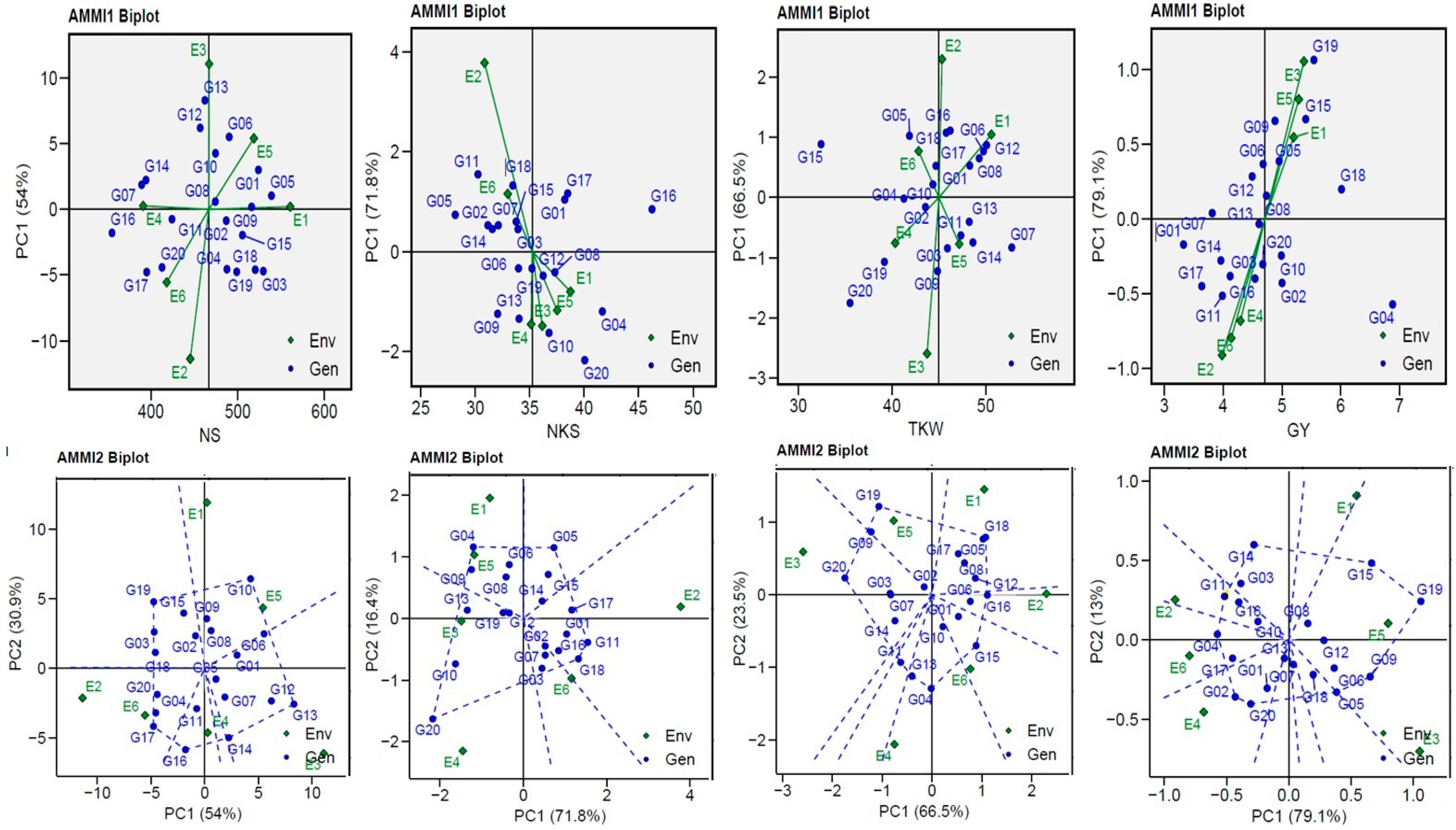
3.4. AMMI Biplot
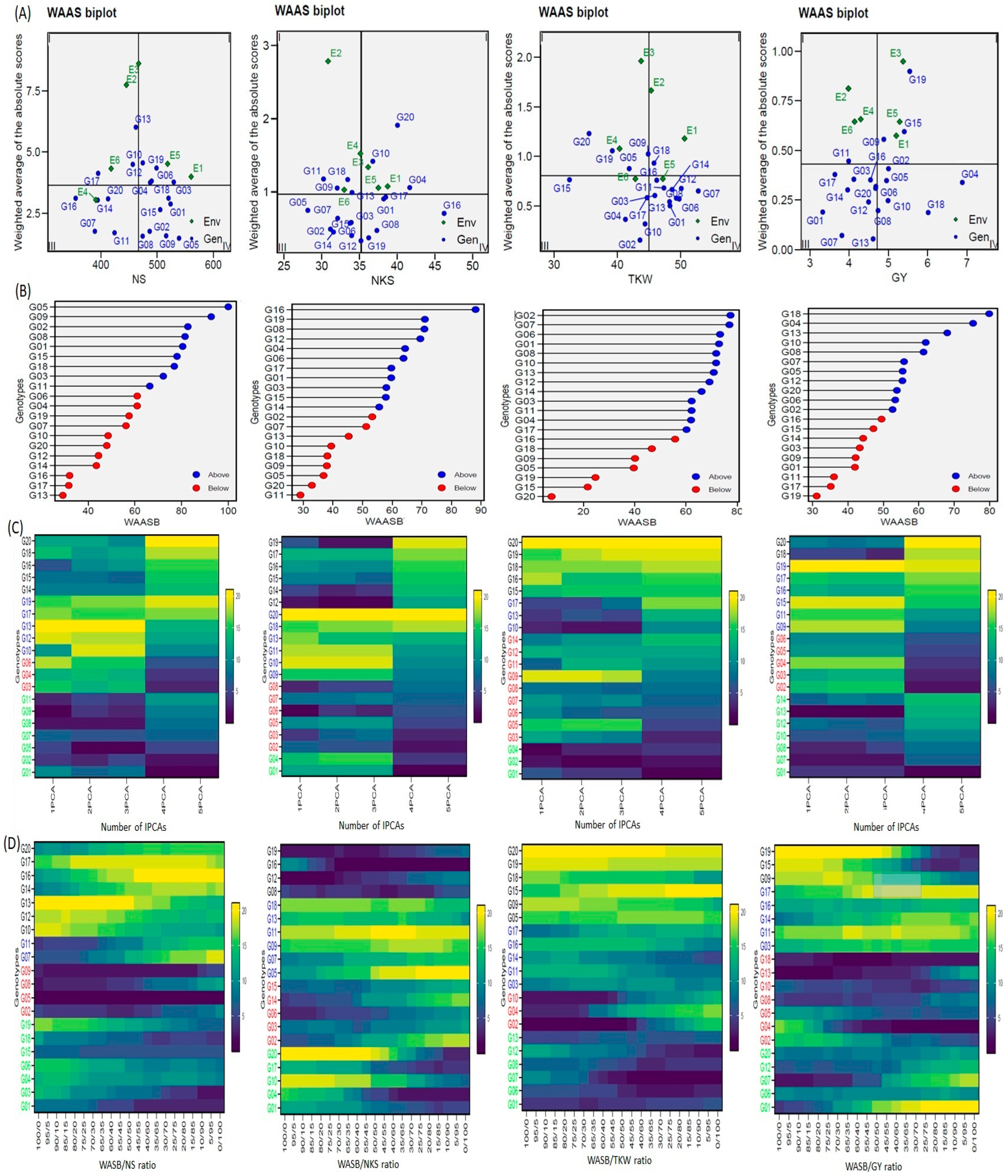
3.5. WAAS Biplot (WAASB)
3.6. Drought-Stress-Tolerance Indices in GY Trait
3.6.1. Indices’ Values and Correlation between GY and Stress-Tolerance Indices
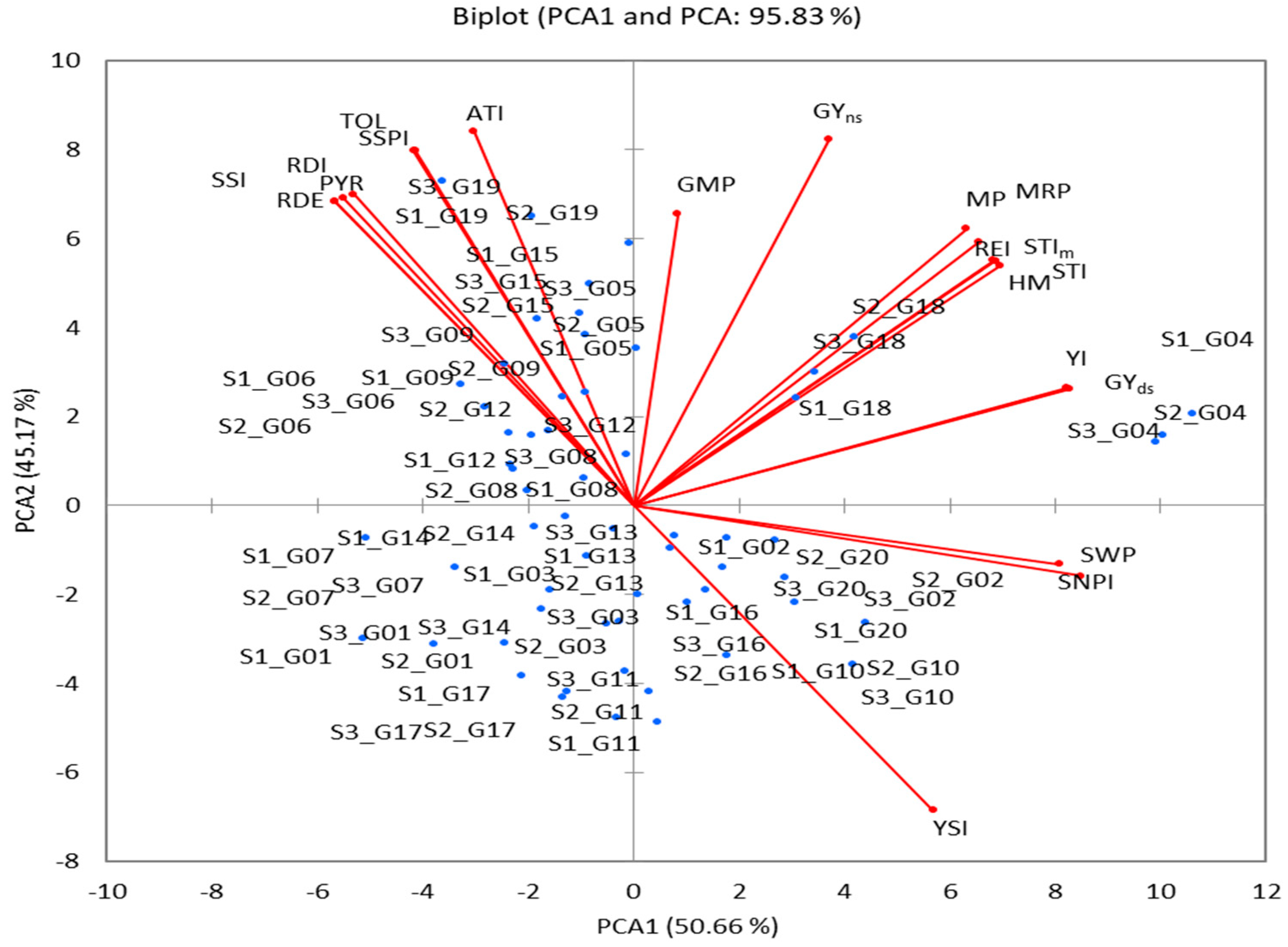
3.6.2. PCA and Biplot Analysis
3.6.3. Hierarchical Clustering and Linear Discriminant Analyses
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farhad, M.; Kumar, U.; Tomar, V.; Bhati, P.K.; Krishnan, N.J.; Barek, V.; Brestic, M.; Hossain, A. Heat stress in wheat: A global challenge to feed billions in the current era of the changing climate. Front. Sustain. Food Syst. 2023, 7, 1203721. [Google Scholar] [CrossRef]
- Bank, T.W. Population Growth (Annual%). 2019. Available online: https://data.worldbank.org/indicator/SP.POP.GROW (accessed on 5 September 2020).
- Yale University. World Population: 2020 Overview. YaleGlobal Online. 2020. Available online: https://archive-yaleglobal.yale.edu/content/world-population-2020-overview (accessed on 6 September 2020).
- Romdhane, W.B.; Al-Ashkar, I.; Ibrahim, A.; Sallam, M.; Al-Doss, A.; Hassairi, A. Aeluropus littoralis stress-associated protein promotes water deficit resilience in engineered durum wheat. Heliyon 2024, 10, e30933. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Al-Doss, A.; Ullah, N. Accelerating Crop Improvement through Speed Breeding. In Climate-Resilient Agriculture, Vol 1: Crop Responses and Agroecological Perspectives; Springer: Cham, Switzerland, 2023; pp. 821–847. [Google Scholar]
- McElrone, A.J.; Choat, B.; Gambetta, G.A.; Brodersen, C.R. Water uptake and transport in vascular plants. Nat. Educ. Knowl. 2013, 4, 6. [Google Scholar]
- Al-Ashkar, I.; Al-Suhaibani, N.; Abdella, K.; Sallam, M.; Alotaibi, M.; Seleiman, M.F. Combining Genetic and Multidimensional Analyses to Identify Interpretive Traits Related to Water Shortage Tolerance as an Indirect Selection Tool for Detecting Genotypes of Drought Tolerance in Wheat Breeding. Plants 2021, 10, 931. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Sallam, M.; Almutairi, K.F.; Shady, M.; Ibrahim, A.; Alghamdi, S.S. Detection of High-Performance Wheat Genotypes and Genetic Stability to Determine Complex Interplay between Genotypes and Environments. Agronomy 2023, 13, 585. [Google Scholar] [CrossRef]
- Xu, Z.H.; Lai, X.J.; Ren, Y.; Yang, H.M.; Wang, H.B.; Wang, C.S.; Xia, J.Q.; Wang, Z.L.; Yang, Z.Y.; Geng, H.W.; et al. Impact of Drought Stress on Yield-Related Agronomic Traits of Different Genotypes in Spring Wheat. Agronomy 2023, 13, 2968. [Google Scholar] [CrossRef]
- Sallam, M.; Ghazy, A.; Al-Doss, A.; Al-Ashkar, I. Combining Genetic and Phenotypic Analyses for Detecting Bread Wheat Genotypes of Drought Tolerance through Multivariate Analysis Techniques. Life 2024, 14, 183. [Google Scholar] [CrossRef]
- Barakat, M.; El-Hendawy, S.; Al-Suhaibani, N.; Elshafei, A.; Al-Doss, A.; Al-Ashkar, I.; Ahmed, E.; Al-Gaadi, K. The genetic basis of spectral reflectance indices in drought-stressed wheat. Acta Physiol. Plant. 2016, 38, 227. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Sallam, M.; Ghazy, A.; Ibrahim, A.; Alotaibi, M.; Ullah, N.; Al-Doss, A. Agro-Physiological Indices and Multidimensional Analyses for Detecting Heat Tolerance in Wheat Genotypes. Agronomy 2023, 13, 154. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Majeed, A.; Attia, K.A.; Javaid, R.A.; Siddique, F.; Farooq, M.S.; Uzair, M.; Yang, S.H.; Abushady, A.M. Country-wide, multi-location trials of Green Super Rice lines for yield performance and stability analysis using genetic and stability parameters. Sci. Rep. 2024, 14, 9416. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Sallam, M.; Ibrahim, A.; Ghazy, A.; Al-Suhaibani, N.; Ben Romdhane, W.; Al-Doss, A. Identification of Wheat Ideotype under Multiple Abiotic Stresses and Complex Environmental Interplays by Multivariate Analysis Techniques. Plants 2023, 12, 3540. [Google Scholar] [CrossRef]
- Raman, A.; Verulkar, S.; Mandal, N.; Variar, M.; Shukla, V.; Dwivedi, J.; Singh, B.; Singh, O.; Swain, P.; Mall, A.; et al. Drought yield index to select high yielding rice lines under different drought stress severities. Rice 2012, 5, 31. [Google Scholar] [CrossRef] [PubMed]
- Qaseem, M.F.; Qureshi, R.; Muqaddasi, Q.H.; Shaheen, H.; Kousar, R.; Roder, M.S. Genome-wide association mapping in bread wheat subjected to independent and combined high temperature and drought stress. PLoS ONE 2018, 13, e0199121. [Google Scholar] [CrossRef] [PubMed]
- Hamidou, F.; Halilou, O.; Vadez, V. Assessment of Groundnut under Combined Heat and Drought Stress. J. Agron. Crop Sci. 2013, 199, 1–11. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Alotaibi, M.; Refay, Y.; Ghazy, A.; Zakri, A.; Al-Doss, A. Selection criteria for high-yielding and early-flowering bread wheat hybrids under heat stress. PLoS ONE 2020, 15, e0236351. [Google Scholar] [CrossRef] [PubMed]
- Singamsetti, A.; Shahi, J.; Zaidi, P.; Seetharam, K.; Vinayan, M.; Kumar, M.; Singla, S.; Shikha, K.; Madankar, K. Genotype× environment interaction and selection of maize (Zea mays L.) hybrids across moisture regimes. Field Crops Res. 2021, 270, 108224. [Google Scholar] [CrossRef]
- Al-Ashkar, I.; Sallam, M.; Al-Suhaibani, N.; Ibrahim, A.; Alsadon, A.; Al-Doss, A. Multiple Stresses of Wheat in the Detection of Traits and Genotypes of High-Performance and Stability for a Complex Interplay of Environment and Genotypes. Agronomy 2022, 12, 2252. [Google Scholar] [CrossRef]
- Olivoto, T.; Lúcio, A.D.; da Silva, J.A.; Marchioro, V.S.; de Souza, V.Q.; Jost, E. Mean performance and stability in multi-environment trials I: Combining features of AMMI and BLUP techniques. Agron. J. 2019, 111, 2949–2960. [Google Scholar] [CrossRef]
- Olivoto, T.; Nardino, M.; Meira, D.; Meier, C.; Follmann, D.N.; de Souza, V.Q.; Konflanz, V.A.; Baretta, D. Multi-trait selection for mean performance and stability in maize. Agron. J. 2021, 113, 3968–3974. [Google Scholar] [CrossRef]
- Meier, C.; Meira, D.; Marchioro, V.S.; Olivoto, T.; Klein, L.A.; Souza, V.Q.d. Selection gain and interrelations between agronomic traits in wheat F 5 genotypes. Rev. Ceres 2019, 66, 271–278. [Google Scholar] [CrossRef]
- Pour-Aboughadareh, A.; Sanjani, S.; Nikkhah-Chamanabad, H.; Mehrvar, M.R.; Asadi, A.; Amini, A. Identification of salt-tolerant barley genotypes using multiple-traits index and yield performance at the early growth and maturity stages. Bull. Natl. Res. Cent. 2021, 45, 117. [Google Scholar] [CrossRef]
- Lamba, K.; Kumar, M.; Singh, V.; Chaudhary, L.; Sharma, R.; Yashveer, S.; Dalal, M.S. Heat stress tolerance indices for identification of the heat tolerant wheat genotypes. Sci. Rep. 2023, 13, 10842. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Kumar, H.; Gupta, V.; Kumar, A.; Singh, C.M.; Kumar, M.; Singh, A.K.; Panwar, G.S.; Kumar, S.; Singh, A.K. Capturing agro-morphological variability for tolerance to terminal heat and combined heat–drought stress in landraces and elite cultivar collection of wheat. Front. Plant Sci. 2023, 14, 1136455. [Google Scholar] [CrossRef]
- Pour-Aboughadareh, A.; Yousefian, M.; Moradkhani, H.; Moghaddam Vahed, M.; Poczai, P.; Siddique, K.H. iPASTIC: An online toolkit to estimate plant abiotic stress indices. Appl. Plant Sci. 2019, 7, e11278. [Google Scholar] [CrossRef] [PubMed]
- Al-Ashkar, I.; Alderfasi, A.; El-Hendawy, S.; Al-Suhaibani, N.; El-Kafafi, S.; Seleiman, M.F. Detecting Salt Tolerance in Doubled Haploid Wheat Lines. Agronomy 2019, 9, 211. [Google Scholar] [CrossRef]
- El-Hennawy, M.; Abdalla, A.; Al-Ashkar, I. Production of doubled haploid wheat lines (Triticum aestivum L.) using anther culture technique. Ann. Agric. Sci. 2011, 56, 63–72. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Sampaio Filho, J.S.; Olivoto, T.; Campos, M.S.; de Oliveira, E.J. Multi-trait selection in multi-environments for performance and stability in cassava genotypes. Front. Plant Sci. 2023, 14, 1282221. [Google Scholar] [CrossRef] [PubMed]
- Vargas, M.; Crossa, J. The AMMI Analysis and Graphing the Biplot; Biometrics Statistics Unit, CIMMYT: Hyderabad, India, 2000. [Google Scholar]
- Han, B.; Ma, X.; Cui, D.; Wang, Y.; Geng, L.; Cao, G.; Zhang, H.; Han, L. Comprehensive Evaluation and Analysis of the Mechanism of Cold Tolerance Based on the Transcriptome of Weedy Rice Seedlings. Rice 2020, 13, 12. [Google Scholar] [CrossRef]
- Bennani, S.; Nsarellah, N.; Jlibene, M.; Tadesse, W.; Birouk, A.; Ouabbou, H. Efficiency of drought tolerance indices under different stress severities for bread wheat selection. Aust. J. Crop Sci. 2017, 11, 395–405. [Google Scholar] [CrossRef]
- Olivoto, T.; Lúcio, A.D. metan: An R package for multi-environment trial analysis. Methods Ecol. Evol. 2020, 11, 783–789. [Google Scholar] [CrossRef]
- Fu, J.; Bowden, R.L.; Jagadish, S.V.K.; Prasad, P.V.V. Genetic variation for terminal heat stress tolerance in winter wheat. Front. Plant Sci. 2023, 14, 1132108. [Google Scholar] [CrossRef] [PubMed]
- Boliko, M.C. FAO and the Situation of Food Security and Nutrition in the World. J. Nutr. Sci. Vitaminol. 2019, 65, S4–S8. [Google Scholar] [CrossRef] [PubMed]
- Cattivelli, L.; Rizza, F.; Badeck, F.W.; Mazzucotelli, E.; Mastrangelo, A.M.; Francia, E.; Mare, C.; Tondelli, A.; Stanca, A.M. Drought tolerance improvement in crop plants: An integrated view from breeding to genomics. Field Crops Res. 2008, 105, 1–14. [Google Scholar] [CrossRef]
- Farshadfar, E.; Mohammadi, R.; Farshadfar, M.; Dabiri, S. Relationships and repeatability of drought tolerance indices in wheat-rye disomic addition lines. Aust. J. Crop Sci. 2013, 7, 130–138. [Google Scholar]
- Olivoto, T.; Lúcio, A.D.; da Silva, J.A.; Sari, B.G.; Diel, M.I. Mean performance and stability in multi-environment trials II: Selection based on multiple traits. Agron. J. 2019, 111, 2961–2969. [Google Scholar] [CrossRef]
- Szareski, V.J.; Carvalho, I.R.; Kehl, K.; Levien, A.M.; Nardino, M.; Dellagostin, S.M.; Demari, G.H.; Lautenchleger, F.; Villela, F.A.; Pedó, T.; et al. Adaptability and stability of wheat genotypes according to the phenotypic index of seed vigor. Pesqui. Agropecu. Bras. 2018, 53, 727–735. [Google Scholar] [CrossRef]
- Popović, V.; Ljubičić, N.; Kostić, M.; Radulović, M.; Blagojević, D.; Ugrenović, V.; Popović, D.; Ivošević, B. Genotype× environment interaction for wheat yield traits suitable for selection in different seed priming conditions. Plants 2020, 9, 1804. [Google Scholar] [CrossRef] [PubMed]
- Mebratu, A.; Wegary, D.; Mohammed, W.; Teklewold, A.; Tarekegne, A. Genotype× environment interaction of quality protein maize hybrids under contrasting management conditions in Eastern and Southern Africa. Crop Sci. 2019, 59, 1576–1589. [Google Scholar] [CrossRef]
- Senguttuvel, P.; Sravanraju, N.; Jaldhani, V.; Divya, B.; Beulah, P.; Nagaraju, P.; Manasa, Y.; Prasad, A.S.H.; Brajendra, P.; Gireesh, C.; et al. Evaluation of genotype by environment interaction and adaptability in lowland irrigated rice hybrids for grain yield under high temperature. Sci. Rep. 2021, 11, 15825. [Google Scholar] [CrossRef]
- Balla, K.; Karsai, I.; Bonis, P.; Kiss, T.; Berki, Z.; Horvath, A.; Mayer, M.; Bencze, S.; Veisz, O. Heat stress responses in a large set of winter wheat cultivars (Triticum aestivum L.) depend on the timing and duration of stress. PLoS ONE 2019, 14, e0222639. [Google Scholar] [CrossRef]
- Olivoto, T.; Diel, M.I.; Schmidt, D.; Lucio, A.D. MGIDI: A powerful tool to analyze plant multivariate data. Plant Methods 2022, 18, 121. [Google Scholar] [CrossRef]
- Zeng, L.; Shannon, M.C.; Grieve, C.M. Evaluation of salt tolerance in rice genotypes by multiple agronomic parameters. Euphytica 2002, 127, 235–245. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Hou, S.; Men, Y.; Han, Y. The Integration of Genome-Wide Association Study and Homology Analysis to Explore the Genomic Regions and Candidate Genes for Panicle-Related Traits in Foxtail Millet. Int. J. Mol. Sci. 2022, 23, 14735. [Google Scholar] [CrossRef] [PubMed]
- Ebdon, J.; Gauch, H., Jr. Additive main effect and multiplicative interaction analysis of national turfgrass performance trials: I. Interpretation of genotype× environment interaction. Crop Sci. 2002, 42, 489–496. [Google Scholar]
- Olivoto, T.; Nardino, M. MGIDI: Toward an effective multivariate selection in biological experiments. Bioinformatics 2021, 37, 1383–1389. [Google Scholar] [CrossRef]
- Aberkane, H.; Amri, A.; Belkadi, B.; Filali-Maltouf, A.; Valkoun, J.; Kehel, Z. Contribution of Wild Relatives to Durum Wheat (subsp.) Yield Stability across Contrasted Environments. Agronomy 2021, 11, 1992. [Google Scholar] [CrossRef]
- Shabani, A.; Zebarjadi, A.; Mostafaei, A.; Saeidi, M.; Poordad, S.S. Evaluation of drought stress tolerance in promising lines of chickpea (Cicer arietinum L.) using drought resistance indices. Environ. Stress. Crop Sci. 2018, 11, 289–299. [Google Scholar]
- Erdemcı, İ. Investigation of genotype× environment interaction in chickpea genotypes using AMMI and GGE biplot analysis. Turk. J. Field Crops 2018, 23, 20–26. [Google Scholar] [CrossRef]
- Kamrani, M.; Hoseini, Y.; Ebadollahi, A. Evaluation for heat stress tolerance in durum wheat genotypes using stress tolerance indices. Arch. Agron. Soil Sci. 2018, 64, 38–45. [Google Scholar] [CrossRef]
- Basavaraj, P.; Muralidhara, B.; Manoj, C.; Anantha, M.; Rathod, S.; Raju, C.D.; Senguttuvel, P.; Madhav, M.; Srinivasaprasad, M.; Prakasam, V.; et al. Identification and molecular characterization of high-yielding, blast resistant lines derived from Oryza rufipogon Griff. in the background of ‘Samba Mahsuri’rice. Genet. Resour. 2021, 68, 1905–1921. [Google Scholar] [CrossRef]
- Talebi, R.; Fayaz, F.; Naji, A.M. Effective selection criteria for assessing drought stress tolerance in durum wheat (Triticum durum Desf.). Gen. Appl. Plant Physiol. 2009, 35, 64–74. [Google Scholar]
- Al-Ashkar, I.; Ibrahim, A.; Ghazy, A.; Attia, K.; Al-Ghamdi, A.A.; Al-Dosary, M.A. Assessing the correlations and selection criteria between different traits in wheat salt-tolerant genotypes. Saudi J. Biol. Sci. 2021, 28, 5414–5427. [Google Scholar] [CrossRef] [PubMed]
- Mohi-Ud-Din, M.; Hossain, M.A.; Rohman, M.M.; Uddin, M.N.; Haque, M.S.; Dessoky, E.S.; Alqurashi, M.; Aloufi, S. Assessment of Genetic Diversity of Bread Wheat Genotypes for Drought Tolerance Using Canopy Reflectance-Based Phenotyping and SSR Marker-Based Genotyping. Sustainability 2022, 14, 9818. [Google Scholar] [CrossRef]
- El-Rawy, M.A.; Hassan, M.I. Assessment of genetic diversity in durum and bread wheat genotypes based on drought tolerance and SSR markers. Plant Breed. 2021, 9, 89–103. [Google Scholar] [CrossRef]
- Jha, U.C.; Basu, P.; Singh, D. Genetic variation and diversity analysis of chickpea genotypes based on quantitative traits under high temperature stress. Int. J. Bio-Resour. 2015, 6, 700–706. [Google Scholar] [CrossRef]
- De Leon, T.B.; Linscombe, S.; Gregorio, G.; Subudhi, P.K. Genetic variation in Southern USA rice genotypes for seedling salinity tolerance. Front. Plant Sci. 2015, 6, 374. [Google Scholar] [CrossRef]

| Environment Code | Treatments | Planting Dates | Season |
|---|---|---|---|
| ENV1 | Non-stress (80% field capacity) | 15 November | 2018/19 |
| ENV2 | Drought stress (33% field capacity) | 15 November | 2018/19 |
| ENV3 | Non-stress (80% field capacity) | 17 November | 2019/20 |
| ENV4 | Drought stress (33% field capacity) | 17 November | 2019/20 |
| ENV5 | Non-stress (80% field capacity) | 17 November | 2020/21 |
| ENV6 | Drought stress (33% field capacity) | 17 November | 2020/21 |
| Traits | NS | NKS | TKW | GY | |
|---|---|---|---|---|---|
| GEN | x2 | 56.10 | 88.3 | 166.0 | 105 |
| p-value | 6.8 × 10−14 | 5.72 × 10−21 | 4.90 × 10−38 | 1.10 × 10−24 | |
| GEN:ENV | x2 | 226 | 121 | 55.50 | 212 |
| p-value | 3.56 × 10−51 | 3.01 × 10−28 | 9.57 × 10−14 | 6.36 × 10−48 | |
| REML | Estimated variance components | ||||
| 2600 (53.90%) | 17.10 (64.50%) | 24.6 (81.60%) | 0.662 (72.60%) | ||
| 1740 (36.00%) | 5.87 (22.10%) | 2.45 (8.13%) | 0.191 (21.00%) | ||
| 486 (10.10%) | 3.54 (13.30%) | 3.1 (10.30%) | 0.0588 (6.44%) | ||
| 4826 | 26.51 | 30.15 | 0.912 | ||
| Heritability | h2ems | 0.54 | 0.64 | 0.82 | 0.73 |
| h2pm | 0.60 | 0.74 | 0.90 | 0.77 | |
| h2gm | 0.89 | 0.94 | 0.98 | 0.95 | |
| h2piepho | 0.97 | 0.98 | 0.98 | 0.98 | |
| h2cullis | 0.99 | 0.97 | 0.98 | 0.87 | |
| R2 GEN:ENV | 0.36 | 0.22 | 0.08 | 0.21 | |
| AS | 0.94 | 0.97 | 0.99 | 0.97 | |
| rgen-env | 0.78 | 0.62 | 0.44 | 0.77 | |
| CVgen% | 10.90 | 11.70 | 11.00 | 17.30 | |
| CVres% | 4.72 | 5.34 | 3.91 | 5.15 | |
| CV ratio | 2.32 | 2.20 | 2.82 | 3.36 | |
| SE | 4.70 | 0.30 | 0.33 | 0.06 | |
| SD | 89.15 | 5.70 | 6.28 | 1.10 | |
| CV | 19.13 | 16.21 | 13.96 | 23.38 | |
| NS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Source | df | SS | MS | F-Value | Total Variation Explained (%) | GEN × ENV Variation Explained (%) | ||
| Proportion | Accumulated | Proportion | Accumulated | |||||
| ENV | 5 | 1203005 | 240601.00 | 404.00 *** | 35.35 | 35.35 | ||
| REP(ENV) | 12 | 7148 | 595.67 | 1.23 ns | 0.21 | 35.56 | ||
| GEN | 19 | 998385 | 52546.58 | 108.00 *** | 29.34 | 64.9 | ||
| GEN:ENV | 95 | 541786 | 5703.01 | 11.70 *** | 15.92 | 80.82 | ||
| IPCA [1] | 23 | 292555 | 12719.78 | 26.20 ** | 8.60 | 89.42 | 54.00 | 54.00 |
| IPCA [2] | 21 | 167517 | 7977.00 | 16.40 ** | 4.92 | 94.34 | 30.90 | 84.90 |
| IPCA [3] | 19 | 81076 | 4267.16 | 8.79 ** | 2.40 | 96.74 | 15.01 | 100.00 |
| Residuals | 228 | 110708 | 485.56 | 3.26 | 100 | |||
| Total | 454 | 3402818 | ||||||
| NKS | ||||||||
| Source | df | SS | MS | F-Value | Total variation explained (%) | GEN × ENV variation explained (%) | ||
| Proportion | Accumulated | Proportion | Accumulated | |||||
| ENV | 5 | 2562.89 | 512.58 | 87.9 *** | 18.69 | 18.69 | ||
| REP(ENV) | 12 | 69.96 | 5.83 | 1.65 ns | 0.51 | 19.20 | ||
| GEN | 19 | 6256.53 | 329.29 | 93.1 *** | 45.69 | 64.89 | ||
| GEN:ENV | 95 | 2009.98 | 21.16 | 5.98 *** | 14.67 | 79.56 | ||
| IPCA [1] | 23 | 1443.84 | 62.78 | 17.7 ** | 10.51 | 90.07 | 71.8 | 71.8 |
| IPCA [2] | 21 | 329.92 | 15.71 | 4.44 ** | 2.41 | 92.48 | 16.4 | 88.2 |
| IPCA [3] | 19 | 234.41 | 12.34 | 3.49 ** | 1.71 | 94.19 | 11.8 | 100 |
| Residuals | 228 | 806.67 | 3.54 | 5.80 | 100.00 | |||
| Total | 454 | 13716.01 | ||||||
| TKW | ||||||||
| Source | df | SS | MS | F-Value | Total variation explained (%) | GEN × ENV variation explained (%) | ||
| Proportion | Accumulated | Proportion | Accumulated | |||||
| ENV | 5 | 3849.45 | 769.89 | 313.13 *** | 25.33 | 25.33 | ||
| REP(ENV) | 12 | 29.50 | 2.46 | 0.79 ns | 0.19 | 25.52 | ||
| GEN | 19 | 8600.69 | 452.67 | 146.10 *** | 56.58 | 82.10 | ||
| GEN:ENV | 95 | 992.31 | 10.45 | 3.37 *** | 6.53 | 88.63 | ||
| IPCA [1] | 23 | 659.85 | 28.69 | 9.26 ** | 4.34 | 92.97 | 66.5 | 66.5 |
| IPCA [2] | 21 | 232.98 | 11.09 | 3.58 ** | 1.53 | 94.50 | 23.5 | 90.0 |
| IPCA [3] | 19 | 99.49 | 5.24 | 1.69 * | 0.66 | 95.17 | 10.0 | 100.0 |
| Residuals | 228 | 4.65 | 100.00 | |||||
| Total | 454 | |||||||
| GY | ||||||||
| Source | df | SS | MS | F-Value | Total variation explained (%) | GEN × ENV variation explained (%) | ||
| Proportion | Accumulated | Proportion | Accumulated | |||||
| ENV | 5 | 123.00 | 24.60 | 349.00 *** | 24.80 | 24.80 | ||
| REP(ENV) | 12 | 0.85 | 0.07 | 1.20 ns | 0.17 | 24.97 | ||
| GEN | 19 | 239.00 | 12.60 | 214.00 *** | 48.19 | 73.15 | ||
| GEN:ENV | 95 | 60.10 | 0.63 | 10.80 *** | 12.12 | 85.27 | ||
| IPCA [1] | 23 | 47.50 | 2.07 | 35.20 *** | 9.58 | 94.85 | 79.10 | 79.10 |
| IPCA [2] | 21 | 7.82 | 0.37 | 6.34 *** | 1.58 | 96.42 | 13.00 | 92.10 |
| IPCA [3] | 19 | 4.76 | 0.25 | 4.26 *** | 0.96 | 97.30 | 7.90 | 100.00 |
| Residuals | 228 | 13.4 | 0.059 | 2.70 | 100.00 | |||
| Total | 454 | 496 | ||||||
| Variables | GYns | GYds | TOL | STI | STIm | SSPI | SSI | YI | YSI | RDI | MP | GMP | HM | MRP | REI | PYR | SWPI | RDC | ATI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GYds | 0.671 | ||||||||||||||||||
| TOL | 0.583 | −0.212 | |||||||||||||||||
| STI | 0.875 | 0.929 | 0.136 | ||||||||||||||||
| STIm | 0.875 | 0.929 | 0.136 | 1.000 | |||||||||||||||
| SSPI | 0.586 | −0.207 | 1.000 | 0.139 | 0.139 | ||||||||||||||
| SSI | 0.409 | −0.387 | 0.963 | −0.050 | −0.050 | 0.964 | |||||||||||||
| YI | 0.664 | 0.988 | −0.207 | 0.930 | 0.930 | −0.205 | −0.386 | ||||||||||||
| YSI | −0.388 | 0.411 | −0.962 | 0.065 | 0.065 | −0.960 | −0.991 | 0.402 | |||||||||||
| RDI | 0.417 | −0.376 | 0.960 | −0.022 | −0.022 | 0.956 | 0.958 | −0.357 | −0.981 | ||||||||||
| MP | 0.930 | 0.897 | 0.243 | 0.983 | 0.983 | 0.247 | 0.052 | 0.887 | −0.028 | 0.062 | |||||||||
| GMP | 0.660 | 0.283 | 0.559 | 0.475 | 0.475 | 0.562 | 0.451 | 0.269 | −0.431 | 0.443 | 0.534 | ||||||||
| HM | 0.879 | 0.943 | 0.125 | 0.988 | 0.988 | 0.130 | −0.061 | 0.932 | 0.087 | −0.057 | 0.992 | 0.474 | |||||||
| MRP | 0.905 | 0.908 | 0.198 | 0.990 | 0.990 | 0.200 | 0.001 | 0.908 | 0.010 | 0.038 | 0.991 | 0.492 | 0.989 | ||||||
| REI | 0.873 | 0.924 | 0.138 | 0.998 | 0.998 | 0.139 | −0.050 | 0.924 | 0.060 | −0.012 | 0.979 | 0.467 | 0.984 | 0.992 | |||||
| PYR | 0.388 | −0.411 | 0.962 | −0.065 | −0.065 | 0.960 | 0.991 | −0.402 | −1.000 | 0.981 | 0.028 | 0.431 | −0.087 | −0.010 | −0.060 | ||||
| SWPI | 0.270 | 0.892 | −0.622 | 0.669 | 0.669 | −0.618 | −0.756 | 0.880 | 0.777 | −0.745 | 0.604 | −0.023 | 0.693 | 0.631 | 0.664 | −0.777 | |||
| RDC | 0.388 | −0.411 | 0.962 | −0.065 | −0.065 | 0.960 | 0.991 | −0.402 | −1.000 | 0.981 | 0.028 | 0.431 | −0.087 | −0.010 | −0.060 | 1.000 | −0.777 | ||
| ATI | 0.684 | −0.075 | 0.983 | 0.266 | 0.266 | 0.983 | 0.902 | −0.070 | −0.902 | 0.913 | 0.371 | 0.612 | 0.258 | 0.330 | 0.269 | 0.902 | −0.499 | 0.902 | |
| SNPI | 0.266 | 0.839 | −0.568 | 0.652 | 0.652 | −0.566 | −0.701 | 0.837 | 0.715 | −0.643 | 0.576 | −0.008 | 0.648 | 0.605 | 0.646 | −0.715 | 0.929 | −0.715 | −0.465 |
| PCA1 | PCA2 | PCA3 | ||
|---|---|---|---|---|
| Eigenvalue | 10.132 | 9.034 | 0.514 | |
| Variability (%) | 50.662 | 45.168 | 2.570 | |
| Cumulative % | 50.662 | 95.831 | 98.400 | |
| Variables | Eigenvectors: | Squared cosines | ||
| PCA1 | PCA2 | PCA1 | PCA2 | |
| GYns | 0.135 | 0.299 | 0.183 | 0.809 |
| GYds | 0.300 | 0.095 | 0.913 | 0.082 |
| TOL | −0.152 | 0.290 | 0.233 | 0.759 |
| STI | 0.249 | 0.200 | 0.629 | 0.361 |
| STIm | 0.249 | 0.200 | 0.629 | 0.361 |
| SSPI | −0.151 | 0.290 | 0.230 | 0.760 |
| SSI | −0.200 | 0.251 | 0.407 | 0.571 |
| YI | 0.298 | 0.096 | 0.900 | 0.083 |
| YSI | 0.206 | −0.249 | 0.431 | 0.558 |
| RDI | −0.193 | 0.254 | 0.377 | 0.583 |
| MP | 0.229 | 0.226 | 0.533 | 0.461 |
| GMP | 0.030 | 0.238 | 0.009 | 0.513 |
| HM | 0.252 | 0.196 | 0.646 | 0.345 |
| MRP | 0.238 | 0.215 | 0.572 | 0.417 |
| REI | 0.248 | 0.200 | 0.622 | 0.362 |
| PYR | −0.206 | 0.249 | 0.431 | 0.558 |
| SWPI | 0.308 | −0.058 | 0.964 | 0.030 |
| RDC | −0.206 | 0.249 | 0.431 | 0.558 |
| ATI | −0.110 | 0.305 | 0.123 | 0.843 |
| SNPI | 0.293 | −0.048 | 0.871 | 0.020 |
| Genotypes | Classification | Cross-Validation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior | Posterior | Membership Probabilities | Posterior | Membership Probabilities | |||||||||
| Pr (HS) | Pr (HT) | Pr (M) | Pr (S) | Pr (T) | HS | HT | M | S | T | ||||
| G01 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| G02 | M | M | 0.000 | 0.000 | 0.999 | 0.001 | 0.000 | M | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| G03 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 0.998 | 0.000 | 0.000 | 0.002 | 0.000 |
| G04 | HT | HT | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | HT | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| G05 | T | T | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | S | 0.000 | 0.000 | 0.000 | 1.000 | 0.000 |
| G06 | S | S | 0.000 | 0.000 | 0.009 | 0.991 | 0.000 | S | 0.000 | 0.000 | 0.014 | 0.986 | 0.000 |
| G07 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 0.999 | 0.000 | 0.000 | 0.001 | 0.000 |
| G08 | M | S | 0.000 | 0.000 | 0.489 | 0.511 | 0.000 | S | 0.000 | 0.000 | 0.005 | 0.995 | 0.000 |
| G09 | S | S | 0.000 | 0.000 | 0.010 | 0.990 | 0.000 | S | 0.000 | 0.000 | 0.029 | 0.971 | 0.000 |
| G10 | M | M | 0.000 | 0.000 | 0.839 | 0.161 | 0.000 | M | 0.000 | 0.000 | 0.608 | 0.392 | 0.000 |
| G11 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| G12 | S | S | 0.000 | 0.000 | 0.007 | 0.993 | 0.000 | S | 0.000 | 0.000 | 0.013 | 0.987 | 0.000 |
| G13 | S | S | 0.000 | 0.000 | 0.404 | 0.596 | 0.000 | M | 0.000 | 0.000 | 0.759 | 0.241 | 0.000 |
| G14 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| G15 | M | M | 0.000 | 0.000 | 0.965 | 0.035 | 0.000 | S | 0.000 | 0.000 | 0.312 | 0.688 | 0.000 |
| G16 | S | S | 0.001 | 0.000 | 0.001 | 0.998 | 0.000 | S | 0.007 | 0.000 | 0.001 | 0.992 | 0.000 |
| G17 | HS | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | HS | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| G18 | HT | HT | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | M | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| G19 | T | T | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 | S | 0.000 | 0.000 | 0.001 | 0.999 | 0.000 |
| G20 | S | S | 0.000 | 0.000 | 0.092 | 0.908 | 0.000 | S | 0.000 | 0.000 | 0.242 | 0.758 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ashkar, I. Multivariate Analysis Techniques and Tolerance Indices for Detecting Bread Wheat Genotypes of Drought Tolerance. Diversity 2024, 16, 489. https://doi.org/10.3390/d16080489
Al-Ashkar I. Multivariate Analysis Techniques and Tolerance Indices for Detecting Bread Wheat Genotypes of Drought Tolerance. Diversity. 2024; 16(8):489. https://doi.org/10.3390/d16080489
Chicago/Turabian StyleAl-Ashkar, Ibrahim. 2024. "Multivariate Analysis Techniques and Tolerance Indices for Detecting Bread Wheat Genotypes of Drought Tolerance" Diversity 16, no. 8: 489. https://doi.org/10.3390/d16080489
APA StyleAl-Ashkar, I. (2024). Multivariate Analysis Techniques and Tolerance Indices for Detecting Bread Wheat Genotypes of Drought Tolerance. Diversity, 16(8), 489. https://doi.org/10.3390/d16080489






