Injectability of Partially Hydrolyzed Polyacrylamide Solutions Improved by Anionic-Nonionic Surfactant in Medium and Low Permeability Reservoirs

Abstract

Injectability of the polymer solution is a very important factor that determines the effectiveness of polymer flooding for enhanced oil recovery. Here, the medium and low permeability oil reservoir was taken as a research object, and effects of relative molecular weight, concentration and core permeability on the flow and injection performance of a partially hydrolyzed polyacrylamide (HPAM) solution with and without anionic-nonionic surfactant (ANS) were studied by indoor outcrop core physical model experiments. It was found that the influence of HPAM concentration on the flow performance was related to the core permeability. When the core permeability was lower than 59 mD, the resistance factor and residual resistance factor of HPAM increased with increasing the concentration. High molecular weight and low core permeability were not conducive to the injectability of HPAM solutions. The addition of ANS was beneficial in enhancing the injectability of HPAM solution by reducing the critical value of injectability of HPAM solution, which was elucidated by the Hall curve derivative method. In the presence of ANS, the flow pressure gradient and the residual resistance factor of the HPAM solution decreased. It is believed that the injectability of HPAM solution improved by ANS in the medium and low permeability reservoirs can be attributed to decrease in fluid viscosity and competitive adsorption on the surface of porous media. The study provides a new idea and theoretical basis for improving the injectability of an HPAM solution and the application of polymer flooding and a polymer/surfactant binary flooding system in medium and low permeability reservoirs.

1. Introduction

After decades of research and field testing, polymer flooding has developed into a very mature oil displacement technology in tertiary oil recovery [1,2]. In this technology, a macromolecular polymer solution is used as an oil displacement agent. A certain amount of polymer is added into the injected water to increase the viscosity of the displacing phase. The mobility ratio of the displacing phase and the displaced phase is improved, and the oil recovery efficiency is increased by enlarging the swept volume [3,4,5]. It has been verified that polymer flooding can further improve oil recovery up to 20% of original oil in place (OOIP) over the waterflooding under suitable conditions [6,7,8].

The premise of successful application of polymer flooding in the oil reservoir depends on the injectability of the polymer solution. At present, polymer flooding is mainly used in conventional oil reservoirs, and is rarely used in medium and low permeability ones. This is mainly because the entanglement of polymer macromolecular chains can cause plugging near the wellbore during injection [9,10]. During the injection process of the polymer fluid, due to the adsorption of the polymer and the entrapment of the porous medium, part of the polymer molecular segment stays in the pore structure of the formation. The adsorption is a result of interaction between polymer chains and rock surfaces such as Van der Waals attraction, hydrogen bonding and electrostatic interaction [11]. The entrapment is caused by the trapping of large polymer molecules in small pore throats [12]. The two effects result in reduction of the flow cross-section of the pore, or even blockage, which reduces the formation permeability. Meanwhile, increase in the displacement fluid viscosity also increases the flow resistance in the low permeability part of the oil layer [13]. Due to the long-term exploitation of the oilfield, the permeability of the bottom-hole oil layer decreases, resulting in a rapid increase in the injection pressure during the polymer displacement process. With the gradual increase of the polymer injection volume, the injection capacity in the polymer injection well declines, which is manifested as excessive injection pressure, insufficient injection volume, and more frequent acidizing and plugging removal measures [14,15]. Therefore, how to effectively improve the injectability of polymers in oil reservoirs, especially in medium and low permeability reservoirs, is of great significance for the application of polymer flooding.

Researchers have done much work on the improvement of polymer injectivity [16]. It was postulated that a low molecular weight polymer could be selected with no injectivity issues, but a higher dosage of polymer was used to meet a viscosity requirement which negatively increases economic cost [17]. Partially hydrolyzed polyacrylamide (HPAM) is a commonly used chemical agent in polymer flooding [18]. It has been reported that HPAM shows sensitivity to mechanical degradation due to irreversible scission of molecular backbones when the polymer chains rupture when the strain rate beyond a critical point [19]. Ghosh et al. [20] reported that shear degradation and filtration could be used as preprocessing tools for successful injection of HPAM into carbonate reservoirs. Al Shakry et al. [21] thought that the mechanical degradation during HPAM reinjection is closely related to parameters such as characteristics of the porous media, flow rate, geometry, and polymer exposure time to the porous media. Al Hashmi et al. [22] have investigated mechanical degradation during the flow of high molecular weight HAPM through stainless capillaries with different lengths and found that the degradation of HPAM starts to increase above 15,000 s⁻¹ due to the effect of shear in the capillaries. Sorbie et al. [23] proposed a kinetic model for HPAM degradation which was used to obtain the radial viscosity profile of the degrading polymer. However, the consequences of shear degradation near the wellbore on polymer injectivity needs to be verified by field-scale trials [24,25]. In summary, previous studies have mainly focused on enhancing the injectability of polymers through polymer degradation, while other means of enhancing the injectability of polymers are lacking.

At present, parameters such as injection pressure, viscosity retention rate, plugging ability, and the residual resistance factor are usually used to evaluate the injection ability of polymers during chemical flooding [26]. Among them, the empirical value of the residual resistance factor is the most used parameter to evaluate the injection capacity of the polymers [27]. When the residual resistance factor exceeds 10, it is considered that the polymer injection pressure is high, and the injection ability is poor. The critical point of residual resistance factor is determined based on the experience of the actual field polymer injection difficulty [28]. This empirical method lacks theoretical basis and has the shortcomings of chance and large errors. Moreover, it cannot be guaranteed that the empirical value is applicable to all reservoirs. The Hall curve was originally proposed for single-phase flow, steady-state and radial flow of Newtonian liquids. The method was proposed by Hall in 1963 [29], and the approximate analytical method was proposed by Bull et al. in 1990 [30] when the Hall curve method was introduced into the effect evaluation of tertiary oil recovery. The principle is that the injection well injects different fluids, and the Hall curve diagram presents different straight-line segments. The slope of each line segment was obtained by using curve piecewise regression. The slope term reflects the seepage resistance in each injection stage, and its variation range reflects the effectiveness of polymer injection [31].

In order to clarify the influencing factors of HPAM injectability and improve its injectability, we took the medium and low permeability oil reservoir as an example and studied the molecular weight, concentration, core permeability and anionic-nonionic surfactant (ANS) on HPAM fluidity and injectability through indoor outcrop core physical modeling experiments. Based on the Hall curve derivative method, the dominant factors affecting the injectability of HPAM in medium and low permeability reservoirs were identified. The mechanism of ANS improving the injectability of HPAM solution is discussed in detail. The study provides reference for the application of polymer flooding and polymer/surfactant binary flooding system in medium and low permeability reservoirs.

2. Materials and Methods

2.1. Materials

Six long square cross section sandstone outcrop cores (Figure 1) were obtained from an medium and low permeability oil reservoir block. Basic parameters including length, diameter, permeability (k) and porosity (φ) are presented in

Table 1. Petrophysical properties of core samples.

Sample No.	Length, cm	Section Size, cm	k, ×10−3 μm2	φ, %
# 1	29.87	4.49 × 4.35	33	17.3
# 2	29.80	4.35 × 4.49	47	17.5
# 3	29.83	4.53 × 4.42	59	17.9
# 4	30.08	4.53 × 4.47	74	18.1
# 5	30.12	4.48 × 4.51	96	19.1
# 6	29.31	4.52 × 4.43	110	19.9

^# is the symbol representing the core number.

. Test methods for k and φ are shown in Section 2.2.

HPAM solutions with two kinds of relative molecular weights were selected as injected fluid. The relative molecular weights of HPAMs are 8.0 × 10⁶ (low relative molecular weight HPAM, LW-HPAM) and 1.2 × 10⁷ (high relative molecular weight HPAM, HW-HPAM), respectively. The surfactant used in the experiments was anionic-nonionic surfactant (ANS), and the surface tension was 33.4 mN·m⁻¹ in pure water at 25 °C. HPAMs and ANS samples were all supplied by China Petrochemical Corporation and used as received. The viscosity was measured using a Brookfield DV-II+Pro Rotational Viscometer (USA). Synthetic formation water was prepared to have a salinity of 19,847 mg·L⁻¹. The compositions of the formation water are listed in

Table 2. Compositions of simulated formation water.

Compositions (mg·L−1)						Total Salinity (mg·L−1)
Na+, K+	Ca2+	Mg2+	SO42–	Cl−	HCO3–
6.786	756	27	4	11,347	927	19,847

.

2.2. Fluid Flow Tests

The outcrop core was placed in a core holder and evacuated, then the water-phase permeability and porosity of the core were determined by saturating water. The pore volume of the core was determined by dividing the weight difference between water saturated and dry core by the water density. The porosity was calculated as the ratio of the pore volume to the core volume. The water-phase permeability of the core was measured by conducting simulated formation water flow through the core at different flow rates according to Darcy’s Law.

Flow tests were carried out inside a temperature control box at 85 °C. For each test, the process was conducted as follows. First, the cores were injected with the simulated formation water until the pressure drop across the core was stable. Then, in the same way, polymer solution was injected and then extended brine injection. In the entire flow process, the injection rate of all fluids was set to be 0.3 mL/min. The pressure drop across the core during the injection process was monitored using a digital pressure gauge to determine the flow resistance. All the tests were conducted horizontally. After each test, the polymer retained in the core was flushed with isopropanol, and then the isopropanol was flushed with simulated formation water to restore the initial permeability of the core as much as possible. The experimental set-up is shown in Figure 2. The synthetic formation water, polymer solution and isopropanol were packed in different intermediate containers.

The resistance factor (RF) and the residual resistance factor (RRF) were estimated to study permeability reduction. RF is defined as the ratio of the polymer solution mobility to the water mobility before polymer injection. RRF is defined as the ratio of the extended water mobility after polymer injection to the water mobility before polymer injection. RF and RRF are calculated as follows:

$$\mathrm{RF}=\frac{\Delta \mathrm{P} \mathrm{of} \mathrm{polymer} \mathrm{flow} }{\Delta \mathrm{P} \mathrm{of} \mathrm{initial} \mathrm{formation} \mathrm{water} \mathrm{flow}}$$

(1)

$$\mathrm{RRF}=\frac{\Delta \mathrm{P} \mathrm{of} \mathrm{extended} \mathrm{formation} \mathrm{water} \mathrm{flow} }{\Delta \mathrm{P} \mathrm{of} \mathrm{initial} \mathrm{formation} \mathrm{water} \mathrm{flow}}$$

(2)

where ΔP is the stable pressure drop across the core in the flow of the liquid. RRF describes the rock resistance to the flow of water injected subsequent to the polymer solution, and provides a quantitative indication of permeability reduction, which is useful to control water fingering during to the water injection after the polymer flooding.

2.3. Hall Derivative Method

The Hall curve is established based on the Newtonian fluid theory of percolation. When the waterflooding is carried out to a certain extent, the water injection amount and the injection pressure reach a stable state, and the flow of the injected water is a stable seepage state. According to seepage mechanics, the relationship between injection volume and bottom hole pressure is explained by the expression formula of formation pressure of plane radial flow [32].

(1)

Based on the flow tests and data in (Section 2.2), we used the following formula to calculate the Hall integral corresponding to the ith data point:

$${\mathrm{I}}_{\mathrm{h},i}={\displaystyle \sum _{i=2}^n(\Delta t_i·\frac{{\mathrm{P}}_{i-1}+{\mathrm{P}}_i}{2})}$$

(3)

where, I_h,i is the Hall integral at the ith data point (I ≥ 2); MPa·min, Δt_i is the time interval between the i−1th data point and the ith data point, min; P_i−1 is the injection pressure at the i−1th data point, MPa; P_i is the injection pressure at the i-th data point, MPa; and n is the total number of data points.

(2)

Based on the calculation result of step (1), drawing the curve of the Hall integral versus the cumulative injection amount, the Hall curve was obtained.

(3)

We used the following formula to calculate the Hall derivative:

$$f{(\mathrm{I}}_{\mathrm{h},i})=\frac{{\mathrm{I}}_{h,i}-{\mathrm{I}}_{h,i-1}}{{\mathrm{Q}}_i-{\mathrm{Q}}_{i-1}}$$

(4)

where, f(I_h,i) is the Hall derivative at the i-th data point (I ≥ 2), MPa·min·mL⁻¹; I_h,i−1 is the Hall integral at the i1th data point, MPa·min; Q_i is the cumulative injection volume at the ith data point, mL; and Q_i−1 is the cumulative injection volume at the i1th data point, mL.

(4)

Based on the calculation result of step (3), a curve of Hall derivative versus cumulative injection amount was drawn, then the Hall derivative curve was obtained.

The relationship curves of the Hall derivative with the permeability of the core under different polymer concentrations were drawn. According to the mutation position of the Hall derivative in the polymer flooding stage, the inflection point was determined. The RRF value corresponding to the permeability at the inflection point was considered as the critical point (c_RFF) of the polymer injection ability. If the RRF value of the polymer was higher than the critical point, this indicates that the polymer solution is difficult to inject into the reservoir. Conversely, the polymer solution can be injected smoothly.

3. Results and Discussion

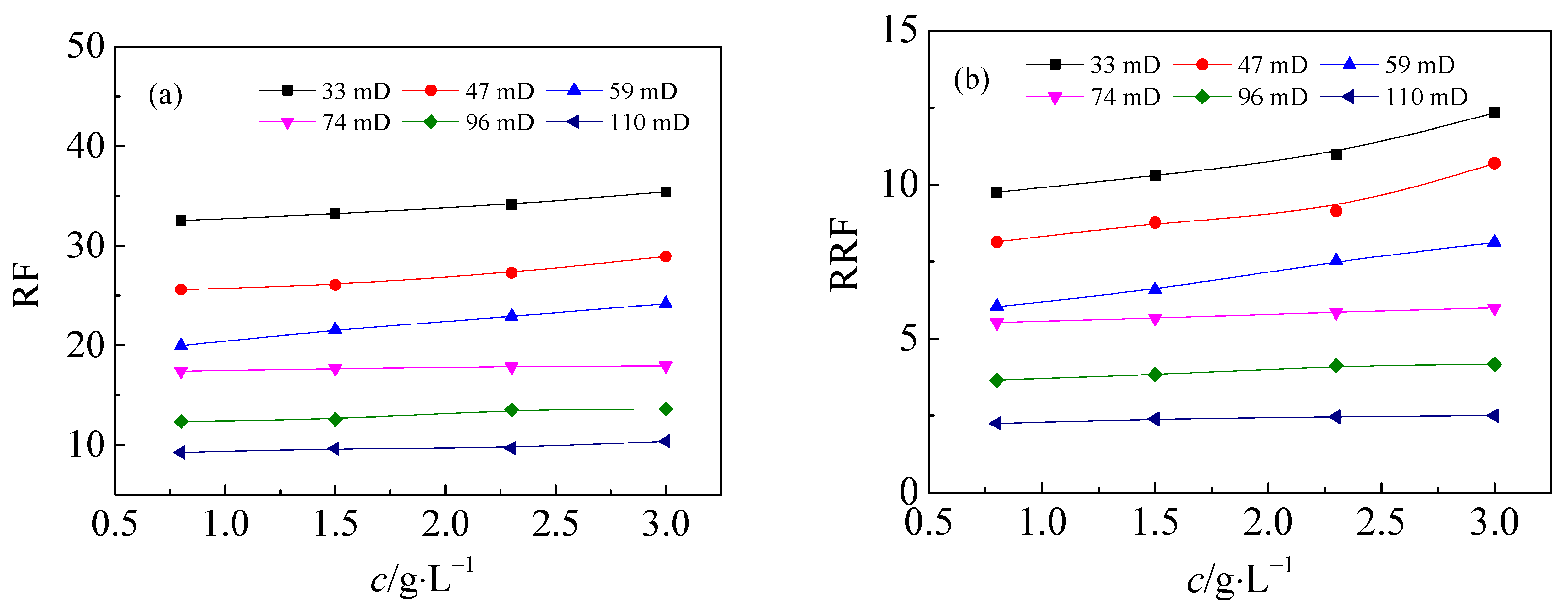
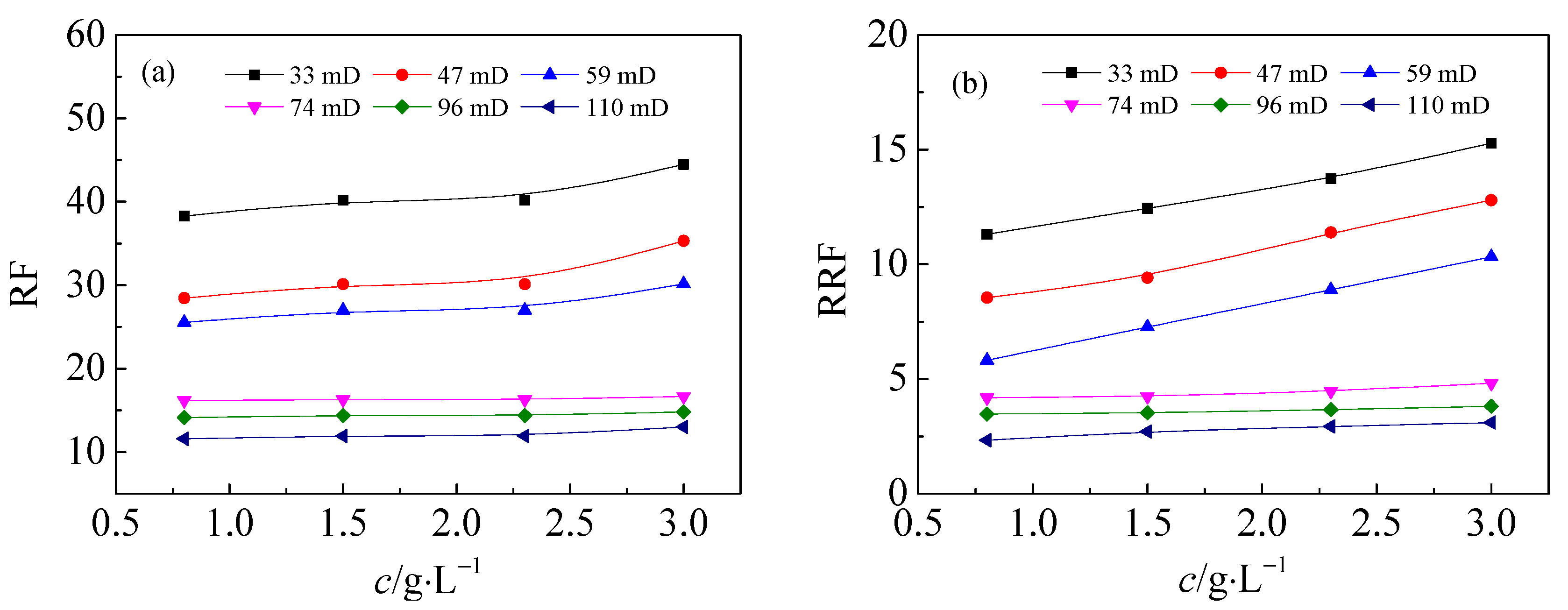
3.1. Flow Performance of HPAM Solutions in Medium and Low Permeability Cores

The application of a polymer in tertiary oil recovery operations is mainly determined the ability to control mobility. However, high temperature and high salinity of the reservoir always results in ineffective polymer ability. Polymer adsorption in the oil reservoir is desirable to some extent, since it reduces the area open to flow and reduces the effective permeability, thus improving the mobility ratio and increasing oil production [33]. Polymer adsorption may occur when polymer molecules interact with the solid surface, adhering to grain surfaces by physical forces such as van der Waals forces. Polymer adsorption can be measured dynamically by injecting the polymer solution in a core.

The pressure gradient changes of different concentrations of LW-HPAM flowing in the medium and low permeability cores are shown in Figure 3. When injecting the LW-HPAM solution, the pressure gradient rises rapidly. When injected to a certain PV, the pressure gradient tends to be stable, and a pressure plateau appears. During extended water flow, the pressure gradient decreases rapidly and gradually reaches stability. The stable pressure gradient during extended water flow is higher than that during initial water flow. The pressure gradient gradually increases with increasing the injection of polymer solutions, indicating that the permeability is reduced by injecting polymers. Moreover, as the core permeability decreases, the stable pressure gradient of LW-HPAM increases during the flow process. The concentration of LW-HPAM has little effect on the pressure gradient.

The mobility of HW-HPAM in medium and low permeability cores is similar to that of LW-HPAM, as shown in Figure 4. The difference is that the stable pressure gradient of HW-HPAM is larger than that of LW-HPAM.

The resistance factor and residual resistance factor of HPAM (LW-HPAM and HW-HPAM) ae shown in Figure 5 and Figure 6. With the decrease of core permeability, both of the resistance factor and residual resistance factor of HPAM significantly increased. The influence of HPAM concentration on the resistance factor and residual resistance factor is related to the core permeability. When the core permeability was higher than 59 mD, the HPAM concentration had little effect on the resistance factor and residual resistance factor. When the core permeability was lower than 59 mD, the resistance factor and residual resistance factor of HPAM increased with increasing the concentration. Moreover, the resistance factor and residual resistance factor of HW-HPAM are higher than those of LW-HPAM.

Generally, the resistance of polymers flowing in porous media mainly comes from two effects: interception and adsorption. The resistance factor reflects the permeability reduction of porous media induced by both of polymer interception and adsorption, and the residual resistance factor reflects the permeability reduction of porous media induced by polymer adsorption. Consequently, the resistance factor is always higher than the residual resistance factor for polymer flow. Macromolecular polymers are always intercepted by pore constrictions when the size of molecular aggregates is larger than the pore constrictions. This has a considerable effect on permeability reduction owing to the blockage of pore throats. A polymer with a higher molecular weight (HW-HPAM) forms larger size aggregates. Therefore, HW-HPAM is more easily intercepted by the pore throat, especially in small size pores (low permeability reservoirs).

Polymer adsorption can be described by the average thickness of the adsorbed layer on the sand grains, as given in the following Equation [34,35]:

$$e=r·(1-\frac{1}{{\mathrm{RFF}}^{1/4}})$$

(5)

where e is the average hydrodynamic adsorbed layer thickness (μm), RRF is the residual resistance factor at the steady stage, and r is the average pore radius (μm) for formation water flow, which can be calculated by the following Equation [36]:

$$r=(\frac{8k}{\phi }{)}^{1/2}$$

(6)

where k is the water-phase permeability of porous media (μm²), and φ is the porosity (%).

The above results indicate that the capacity of HPAM with higher molecular weight is stronger in permeability reduction. The permeability reduction is due to a decrease in free volume for flow and is mainly caused by adsorption or interception of polymers. The main component of the core used in the experiments is quartz (silicon dioxide, SiO₂); much hydroxyl is formed on the surface of SiO₂ in the aqueous solution. Hydrogen bonding and van der Waals forces occur between HPAM molecules and sandstone [37,38]. Therefore, a certain amount of HPAM adsorbs to the pore wall of the core. Moreover, benefiting from the longer molecular length and higher molecular weight of HW-HPAM, the adsorbed layer thickness is larger than that of LW-HPAM, which is confirmed by e values in

Table 3. Flow test summary and adsorption parameters of 3.0 g·L⁻¹ HPAM with and without 3.0 g·L⁻¹ ANS in the core with a permeability of 33 mD.

System	RF	RFF	r (μm)	e (μm)
LW-HPAM	35	12.4	1.24	0.58
HW-HPAM	46	16.1	1.24	0.62
LW-HPAM/ANS	34	11.2	1.24	0.56
HW-HPAM/ANS	44	14.7	1.24	0.60

. This indicates that the adsorption capacity of HW-HPAM is stronger than that of LW-HPAM.

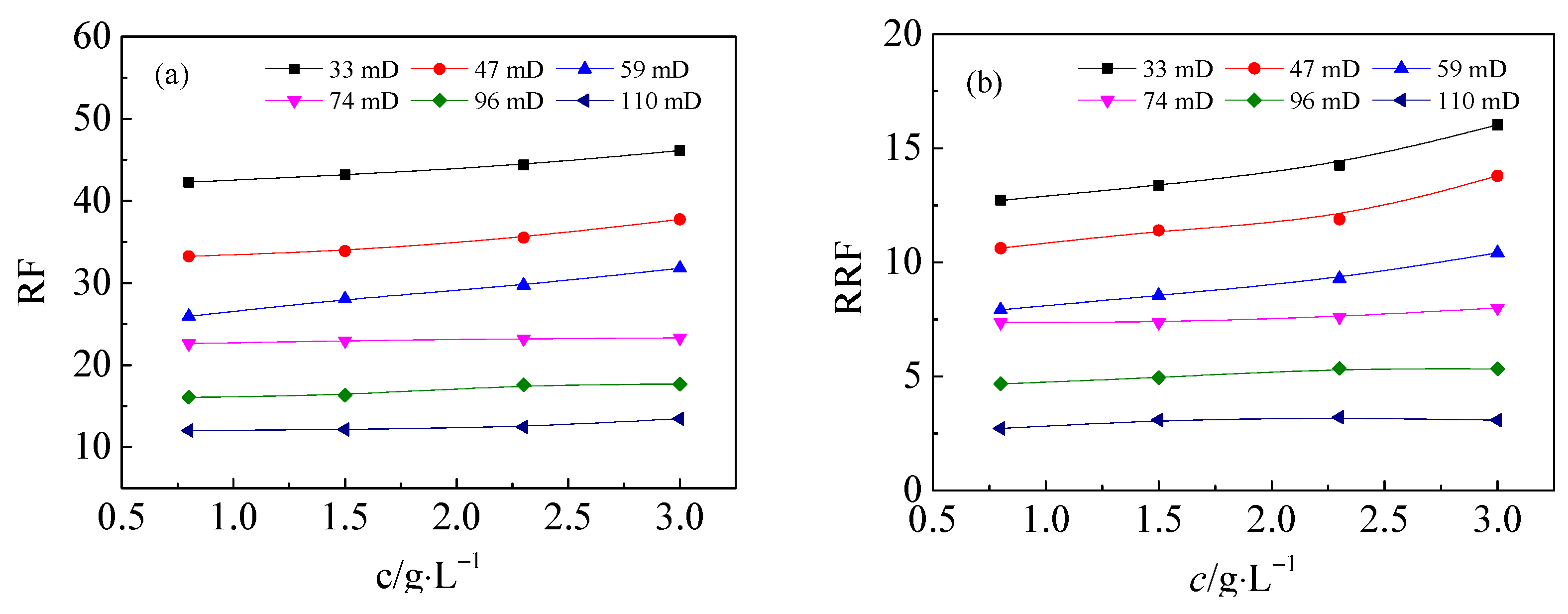
3.2. Effect of ANS on the Flow Performance of HPAM Solutions in Medium and Low Permeability Cores

The composite system of a water-soluble polymer and a surfactant has attracted much attention in practical applications. The coexistence of surfactants and polymers often results in unique properties and functions that are often superior to either pure component system [39]. Therefore, it is extremely important to study the interaction between polymers and surfactants. Especially in oilfield development, polymer/surfactant binary composite flooding has an excellent recovery effect [40]. As an oil displacement method, the polymer/surfactant binary composite system can maximize the viscoelasticity of the polymer and control the fluidity. The low interfacial tension properties of surfactants allow the displacing fluid to reach residual oil in rock crevices. Therefore, the polymer/surfactant binary composite flooding system can not only expand the swept volume of the oil displacement agent but also improve oil washing efficiency [41]. Anionic-nonionic surfactants have the advantages of both nonionic and anionic surfactants. They are more and more popular due to their mildness, safety, easy biodegradation and multifunctionality [42]. In this study, the anionic-nonionic surfactant ANS was selected as an influencing agent to combine with HPAM.

In the presence of 3.0 g·L⁻¹ ANS, the pressure gradient changes of different concentrations of LW-HPAM and HW-HPAM flowing in the medium and low permeability cores are shown in Figure 7 and Figure 8, respectively. The variation of the pressure gradient of HPAM/ANS with the number of injected PVs was similar to that of HPAM. The difference is that the stable pressure gradient of LW-HPAM/ANS was lower than that of LW-HPAM, and the stable pressure gradient of HW-HPAM/ANS was lower than that of HW-HPAM. Correspondingly, the resistance factor and residual resistance factor of LW-HPAM/ANS and HW-HPAM/ANS were lower than those of LW-HPAM and HW-HPAM, as shown in Figure 9 and Figure 10. The resistance factor and residual resistance factor of HW-HPAM/ANS were still higher than those of LW-HPAM/ANS. For example, in the core with a permeability of 33 mD, the resistance factor and residual resistance factor of HPAM with and without ANS are as shown in Table 3. In the presence of ANS, the adsorption capacity of the LW-HPAM and HW-HPAM on the core pore wall was weakened, as shown in Table 3. This is mainly due to the preferential adsorption of ANS on the rock surface relative to HPAM. The lower resistance factor of the HPAM/ANS composite system indicates that the aggregates formed by the combination of HPAM and ANS does not increase in size. Hence, no more molecular aggregates were captured by the pore throats.

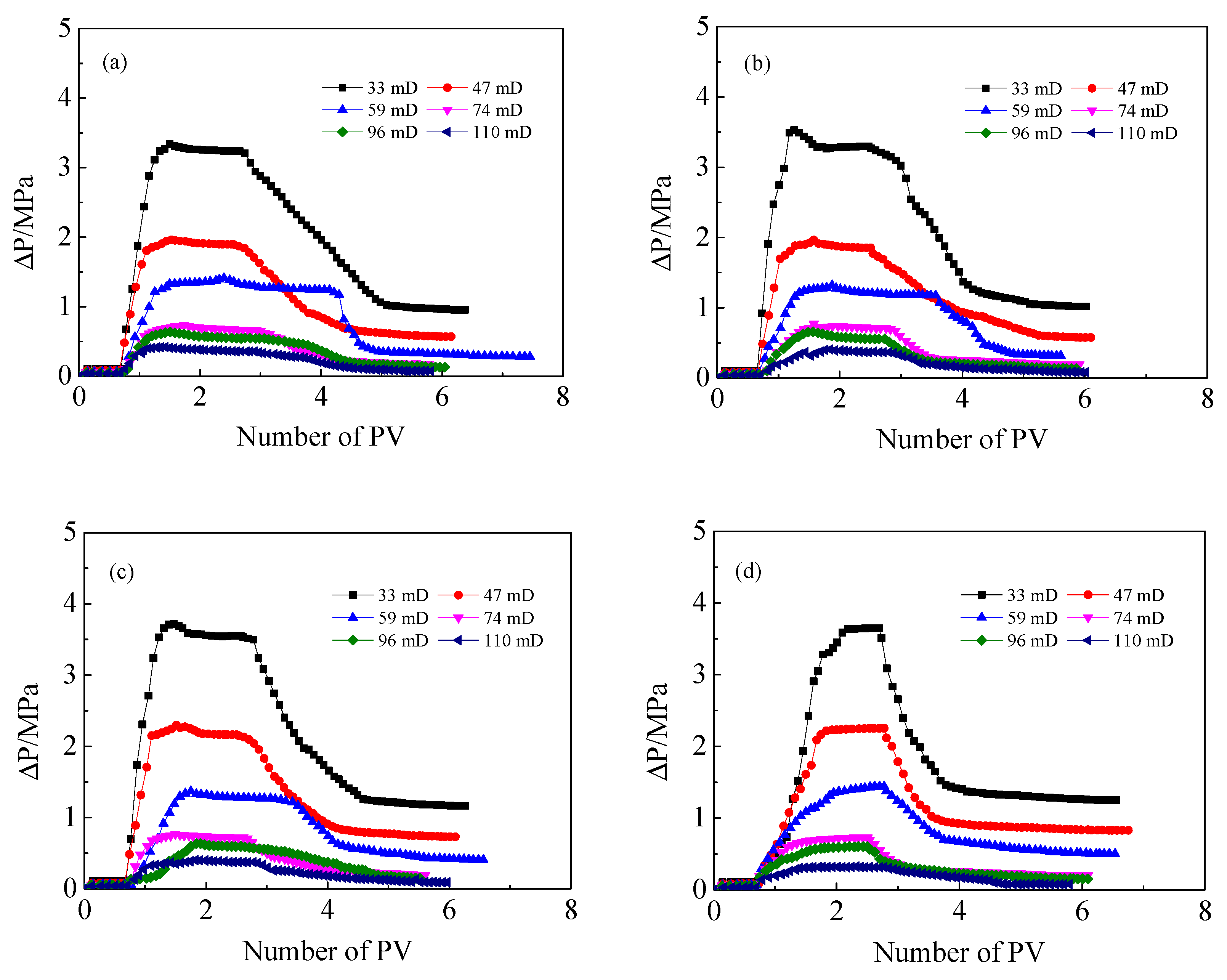
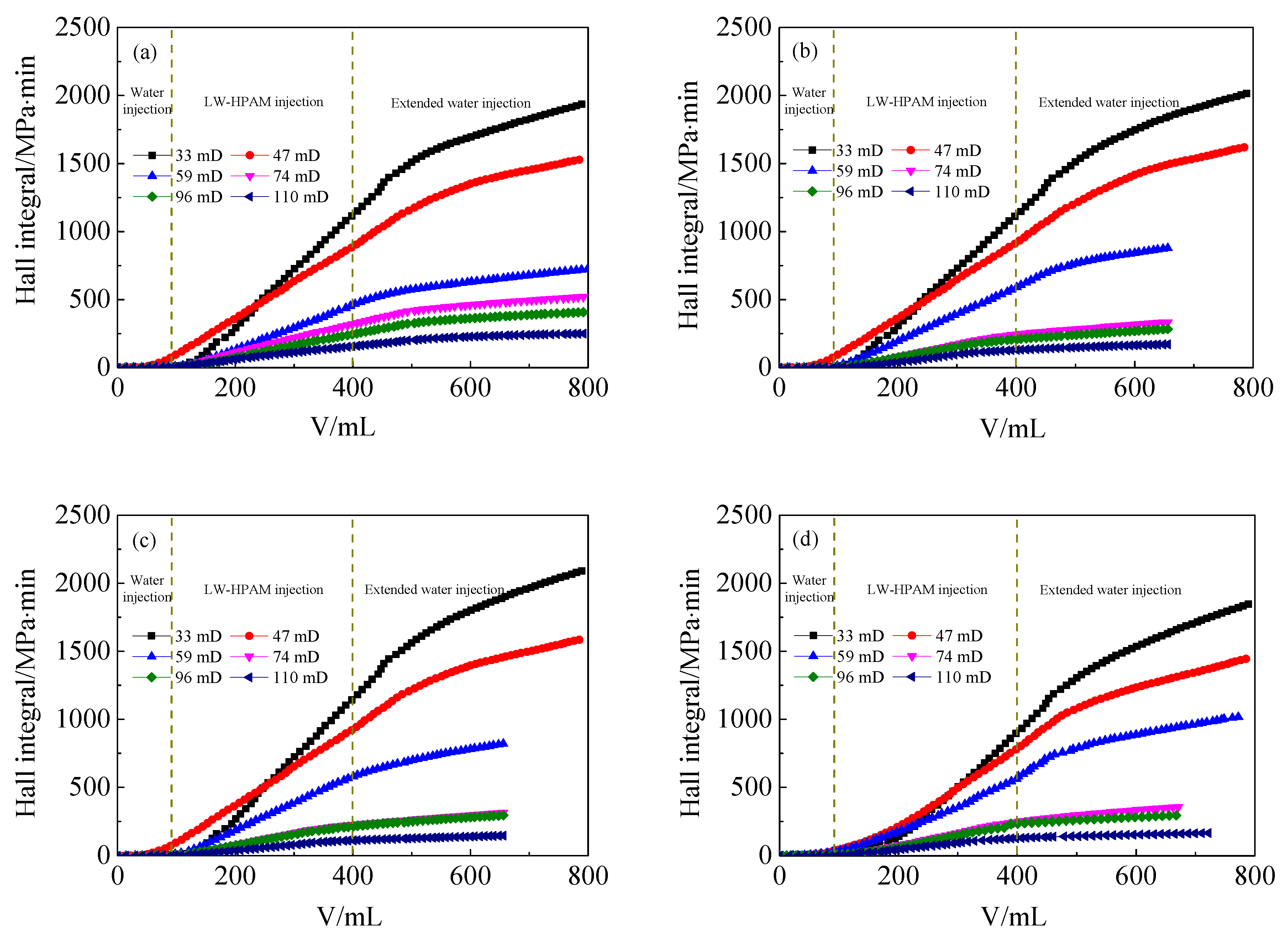
3.3. Injection Performance of HPAM Solutions in Medium and Low Permeability Cores

When different fluids were injected into the formation, the slope of the Hall curve was different in different injection stages, and the slope of each stage reflected the mobility of the injected fluid in the formation at that stage. Based on the Hall curve Formula (3) and the experimental data of the polymer injection tests, the Hall curves of HPAM with different concentrations in different permeability cores were obtained, as shown in Figure 11 and Figure 12. During the polymer injection stage, the slope of the Hall curve was greatest.

As shown in Figure 13, the Hall derivative of HPAM decreased with the increase in permeability, indicating that when the same amount of HPAM was injected, the higher the permeability, the lower the required displacement pressure. Moreover, for different concentrations of polymers, the Hall derivatives varied in magnitude with permeability, and an inflection point occurred at a certain value. Taking LW-HPAM with a concentration of 3.0 g·L⁻¹ as an example, when the permeability was less than 65 mD, the Hall derivative had a steep decline. When the permeability was greater than 65 mD, the Hall derivative has a gentle decline. This means that when the core permeability was lower than 65 mD, a larger injection pressure was required for LW-HPAM injection. When the core permeability was higher than 65 mD, a smaller injection pressure was required for LW-HPAM injection. The lower limit of permeability for this molecular weight polymer to match was 65 mD. This concentration of LW-HPAM was easier to inject in reservoirs with permeability greater than 65 mD. The critical point (c_RFF) of LW-HPAM injection ability is shown in Figure 14. The higher the polymer concentration, the larger the critical point for the residual resistance factor. This means that increasing the LW-HPAM concentration reduces its injectability in medium and low permeability reservoirs. For HW-HPAM, a similar phenomenon occurs with the variation of core permeability and concentration. The difference is that the critical point of HM-HPAM is higher than that of LM-HPAM at the same condition. The higher the relative molecular mass of the polymer and the longer the molecular chain, the easier it is for the polymer molecules to entangle together in the aqueous solution. At a constant core permeability and polymer concentration, as the polymer molecular weight increases, the hydrodynamic size of the polymer solution increases, and the injection pressure of the system increases gradually. When the polymer flows in the core, there is also a critical value of molecular weight. Polymers with larger molecular weight than the critical value are difficult to inject. This critical value is the upper limit of the molecular weight of the polymer that can pass through a core of this permeability. Previous studies have shown that when the ratio of the pore radius of the rock to the mean square radius of gyration of the polymer molecules in the solution is greater than 5, the phenomenon of blocking the rock pores due to the excessive polymer molecules generally does not occur [43]. A high molecular weight polymer increases the system viscosity and expands the sweep coefficient, but also reduce its injectability in medium and low permeability reservoirs. Therefore, these two contradictory aspects need to be comprehensively considered when selecting polymers for enhanced oil recovery.

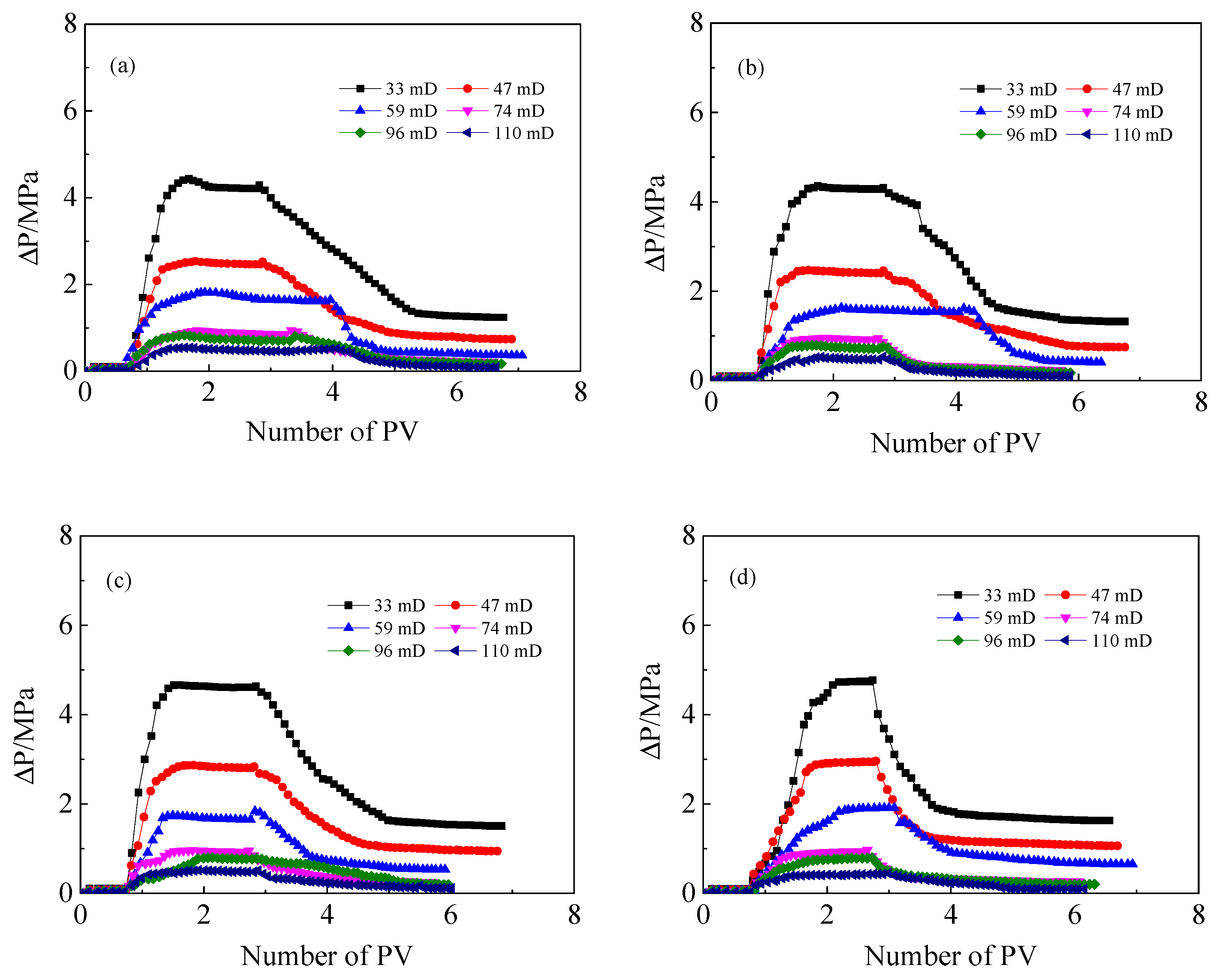
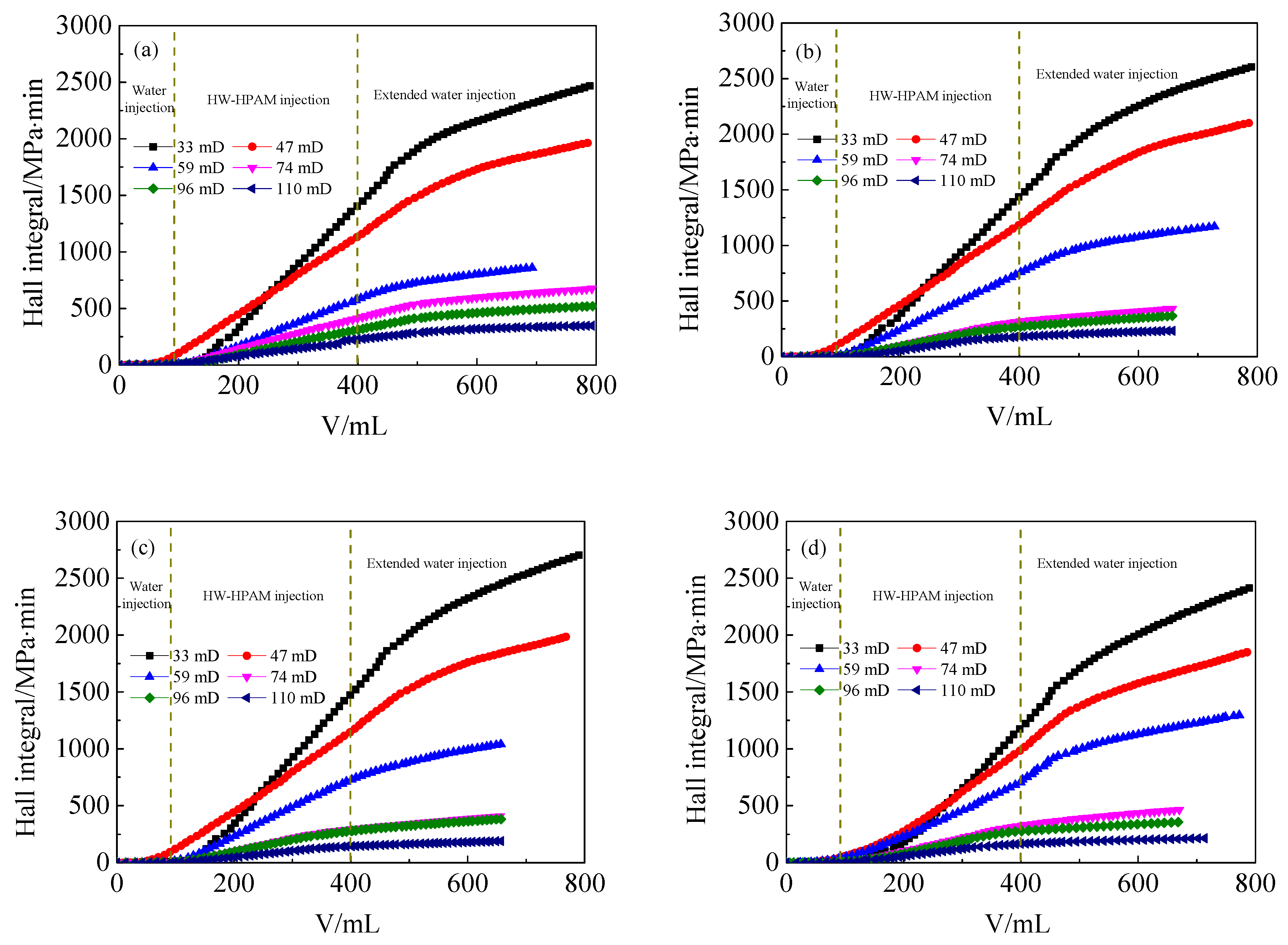
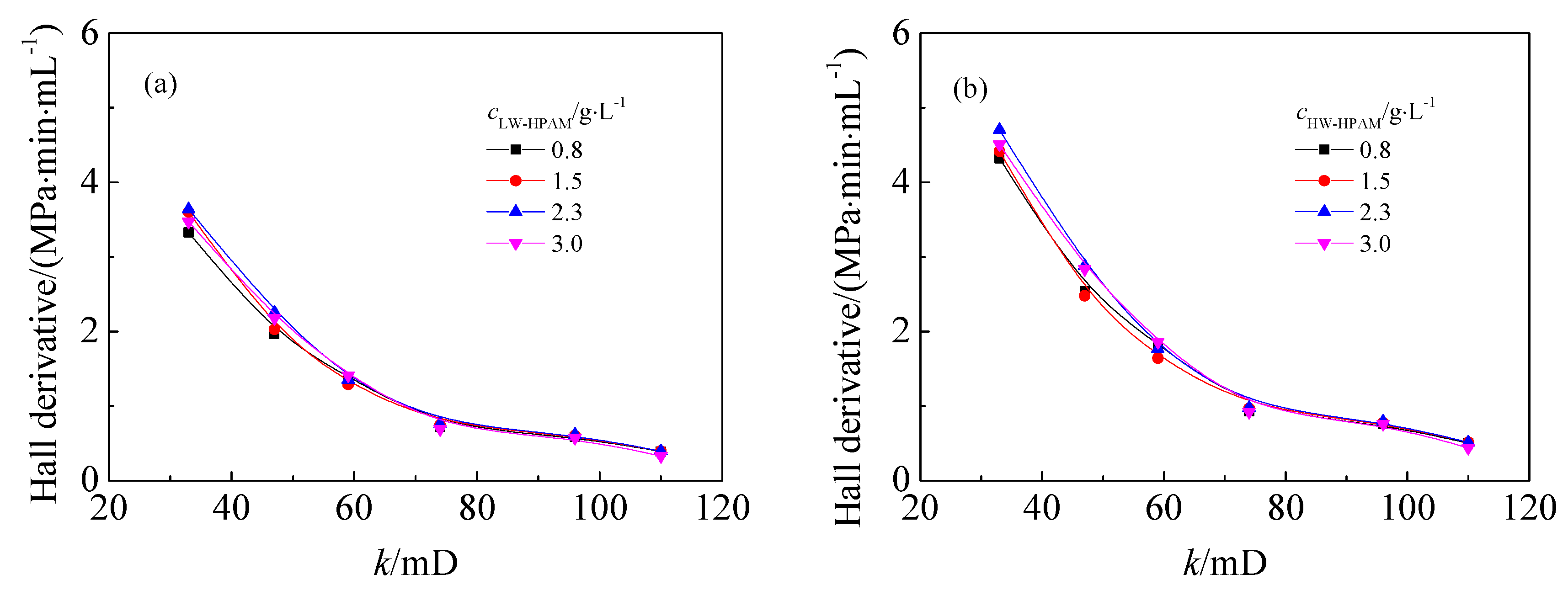
3.4. Effect of ANS on the Injection Performance of HPAM Solutions in Medium and Low Permeability Cores

In the presence of 3.0 g·L⁻¹ ANS, the Hall curves of LW-HPAM and HW-HPAM with different concentrations in different permeability cores were obtained, as shown in Figure 15 and Figure 16. Similar to the Hall curve of a single HPAM, during the HPAM/ANS composite system flow phase, the slope of the Hall curve was higher than that in initial water injection and extended water injection. Variations of the Hall derivative at different permeability cores under flow of polymer/surfactant composite system are shown in Figure 17. The Hall derivative of HPAM/ANS decreased with increasing core permeability.

Taking 3.0 g·L⁻¹ LW-HPAM/3.0 g·L⁻¹ ANS as an example, the permeability inflection point was 63 mD. This indicates that the LW-HPAM/ANS composite was easy to inject in reservoirs with permeability lower than 63 mD. When the permeability exceeded 63 mD, a higher injection pressure is required, meaning that the LW-HPAM/ANS composite system is difficult to inject. For the 3.0 g·L⁻¹ HW-HPAM/3.0 g·L⁻¹ ANS composite, the permeability inflection point was 65 mD.

The critical point of HPAM/ANS injection ability is shown in Figure 14. The higher the polymer concentration in HPAM/ANS composite, the larger the critical point for the residual resistance factor. Increasing the polymer concentration reduces the injectability of HPAM/ANS composite in medium and low permeability reservoirs. More importantly, the critical point for the residual resistance factor of HPAM/ANS composite was lower than that of HPAM, either LW-HPAM or HW-HPAM. This indicates that ANS can enhance the injectability of HPAM in medium and low permeability reservoirs.

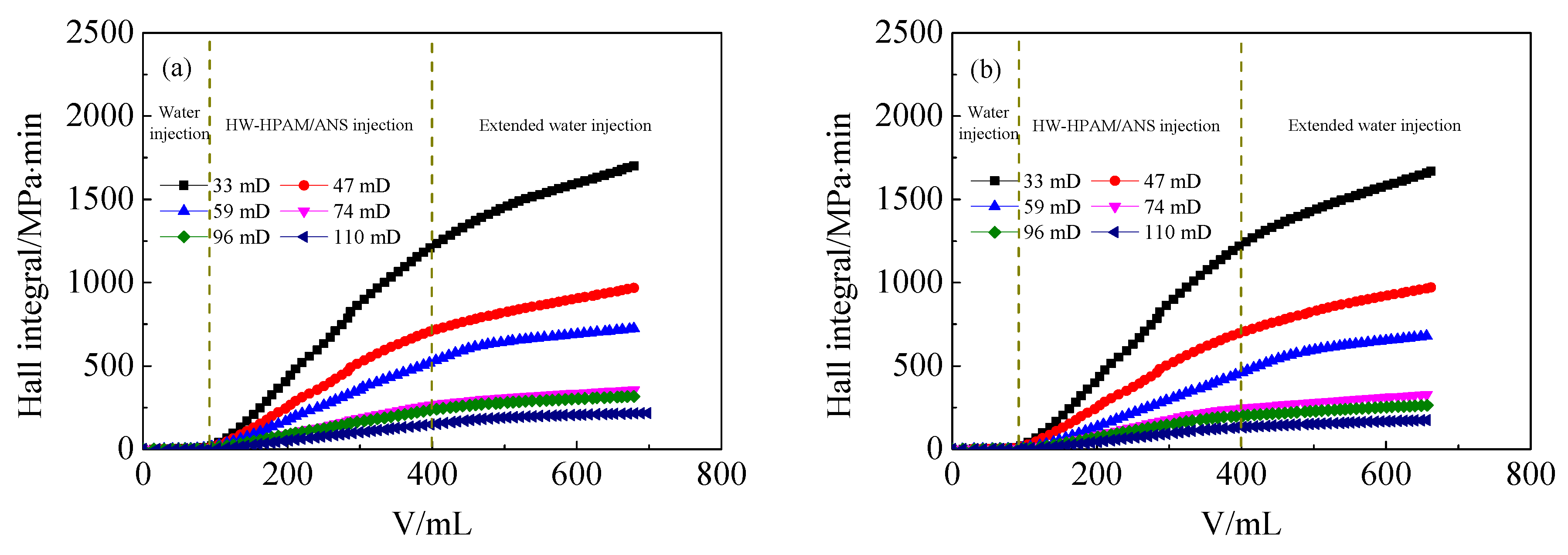
3.5. Mechanism of Improving HPAM Injectability by Anionic-Nonionic Surfactant

A higher viscosity of the polymer solution leads to a higher injection pressure during the injection process. In addition, the retention (capture and adsorption) of polymer macromolecules in the porous media further increases the injection pressure. The above experimental results show that ANS can effectively improve the injectability of polymers. Here, the mechanism of ANS reducing HPAM injection pressure and improving injectability are discussed.

The viscosity of HPAM solutions increases with increasing the concentration, as shown in Figure 18. High concentration enhances the entanglement and aggregation of macromolecule chains. Viscosity increases significantly with increasing degree of entanglement. The curve slope of HW-HPAM is higher than that of LW-HPAM. The dependence of the viscosity with respect to the concentration is more pronounced in HW-HPAM compared to LW-HPAM. This indicates that the thickening ability of HW-HPAM solution is stronger than that of LW-HPAM solution. The molecular weight of HW-HPAM is about 1.5 times higher than that of LW-HPAM, and the molecular length of HW-HPAM is longer as a consequence. In concentrated polymer solutions, the viscosity is highly dependent upon the molecular weight. The viscosity increases with increasing the molecular weight. In the concentration range (0.8~3.0 g·L⁻¹), some molecular aggregates are formed in solutions. The viscosity of HPAM solutions is greatly influenced by these molecular aggregates. The hydrodynamic length of HW-HPAM molecular aggregate is higher than that of LW-HPAM. Therefore, HPAM with high higher molecular weight and longer hydrodynamic length of molecular aggregates has a higher viscosity and is easier to be captured by narrow pore throat of porous media. After adding ANS, the viscosity of both LW-HPAM and HW-HPAM showed a decreasing trend, as shown in Figure 18. It was thought that the ANS interacts strongly with the HPAM at higher concentrations, destroying the aggregated structure of the HPAM in solution, reducing its hydrodynamic size, and thereby reducing the viscosity of the aqueous solution. When the free anionic-nonionic surfactant concentration reaches the critical micelle concentration, the oxygen-containing groups destroy the molecular association structure of the polymer and reduce the structural viscosity of the system [44]. Consequently, from the perspective of reducing the viscosity of HPAM fluid, ANS can reduce the injection pressure of HPAM.

Another important property of surfactants is the adsorption on the rock surface. It is believed that the hydrophobicity generated by the adsorption of surfactants on the rock surface has a great effect on reducing the injection pressure. This is because the hydrophobicity of the surfactant reduces the water attached to the rock surface and pores, and reduces the pressure generated by the attached water on the rock surface. Moreover, this also plays the role of reducing the blocking force of the capillary wall and expanding the diameter of the capillary, which is beneficial for dredging the channel for fluid flow, especially in medium and low permeability reservoirs [45].

After the polyacrylamide is hydrolyzed, the molecule is partially negatively charged. Due to the positively charged adsorption sites on the surface of the clay part of the rock, HPAM molecules gradually adsorb on the rock surface by electrostatic interaction. However, due to the large size of HPAM molecules, the diffusion rate to the solid-liquid interface (rock surface) is low. When ANS is added to the HPAM solution, ANS molecules diffuse to the rock surface faster because of its small molecular size, and preferentially occupy the positive charge adsorption sites on the rock surface. Due to the limited positive charge of the clay on the rock surface, the adsorbed surfactants prevent the HPAM molecules from approaching the clay surface. Hence, when the HPAM/ANS composite system is injected into the oil layer, the adsorption of the HPAM molecules on the rock surface is reduced due to the competitive adsorption of the ANS. Additionally, due to the small attraction force between ANS and HPAM, the adsorption amount of HPAM on the rock decreases, the flow radius of the rock pores in the entire oil layer increases, and the injection pressure decreases. Therefore, for the composite system, in order to reduce the adsorption and retention of the polymer in the oil layer, the surfactant used should not only be able to preferentially adsorb on the rock surface, but also not have a strong mutual attraction with the polymer.

4. Conclusions

In this study, flow tests in medium and low permeability cores were carried out in the laboratory to study the injection performance of HPAM solutions. By comparing and analyzing the dynamic changes of resistance factor and residual resistance factor with and without ANS, the relationship between HPAM injectability and its molecular weight, solution concentration and core permeability were clarified based on the Hall curve derivative method. This study provides the following conclusions:

(1)

During the flow process, the HPAM concentration has little effect on the pressure gradient. As the core permeability decreases, the stable pressure gradient of HPAM increases. The capacity of HPAM with higher molecular weight in permeability reduction is stronger with higher residual resistance factor.

(2)

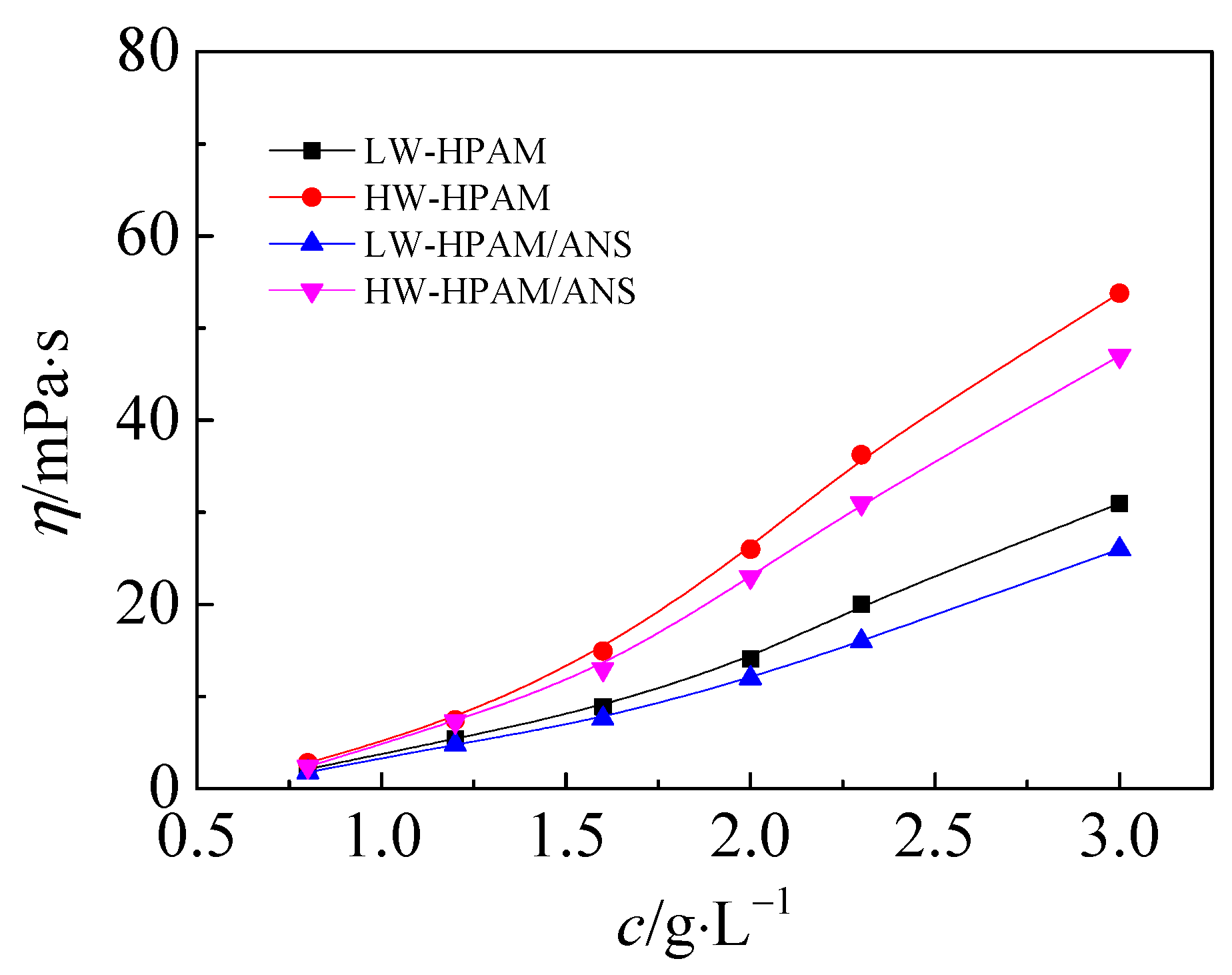
In medium and low permeability reservoirs, higher molecular weight increases the viscosity of HPAM solution, but also reduces its injectability. Therefore, the sweep coefficient and injectability need to be comprehensively considered when selecting HPAM type for enhanced oil recovery.

(3)

In the presence of ANS, the residual resistance factor and the injection critical point of HPAM decrease, either for LW-HPAM or HW-HPAM. This confirms that ANS can reduce HPAM injection pressure and enhance the injectability of HPAM in medium and low permeability reservoirs.

(4)

For interaction of ANS and HPAM, on the one side, ANS decreases the viscosity of the HPAM aqueous solution while, on the other side, the adsorption capacity of HPAM on the core pore wall is weakened due to the preferential adsorption of ANS on the rock surface. Consequently, the adsorption and retention of the HPAM in the in medium and low permeability reservoirs are reduced.