Numerical Study of the Magnetic Field Effect on Ferromagnetic Fluid Flow and Heat Transfer in a Square Porous Cavity
Abstract
:1. Introduction
2. Problem Definition
3. Mathematical Modeling
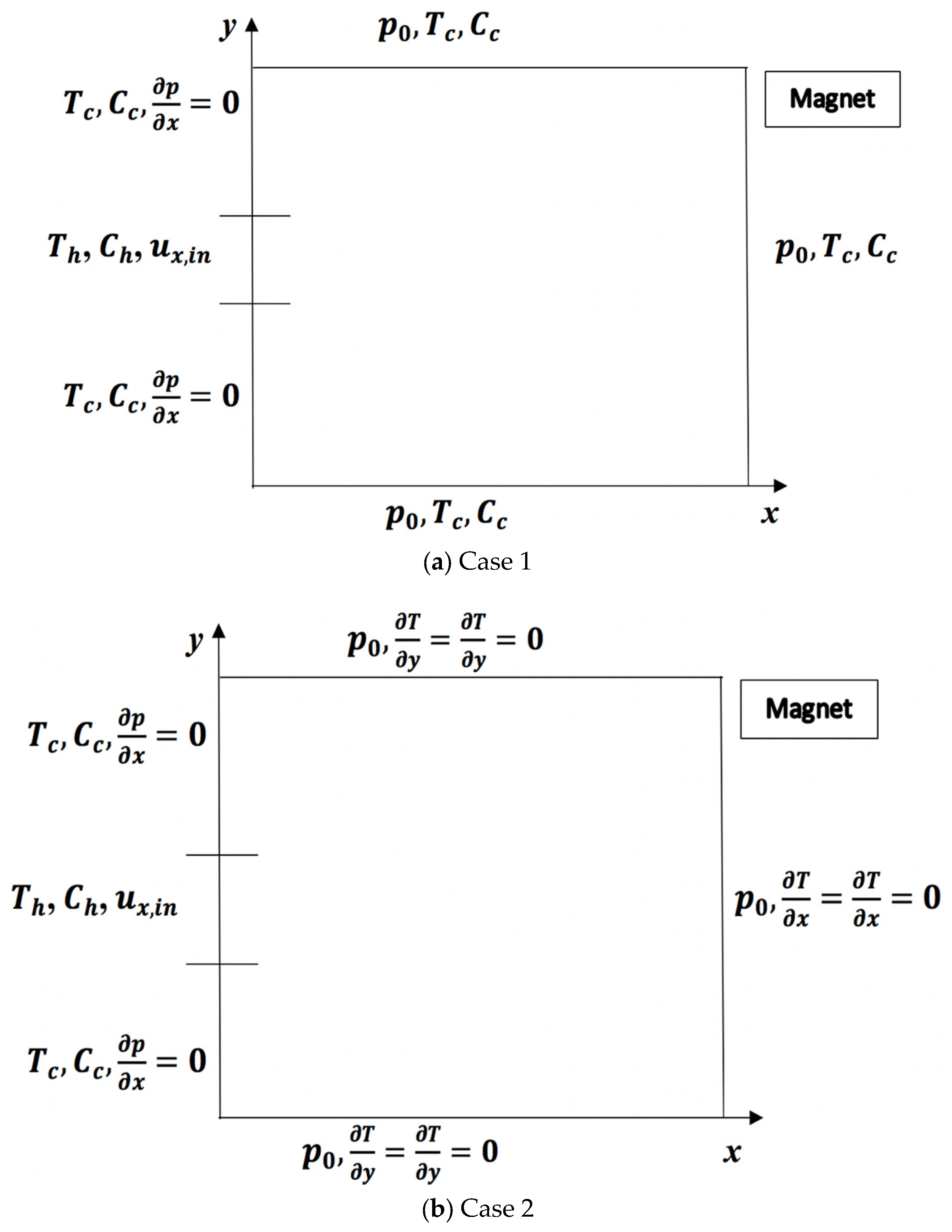
- at , , , , ,
- at inlet , , ;
- at , , , , ;
- at , , , , ;
- at , , , , ;
- at , , , , ,
- at inlet , , .
- at , , , , .
- at , , , , .
- at , , , , .
4. Numerical Method
- -
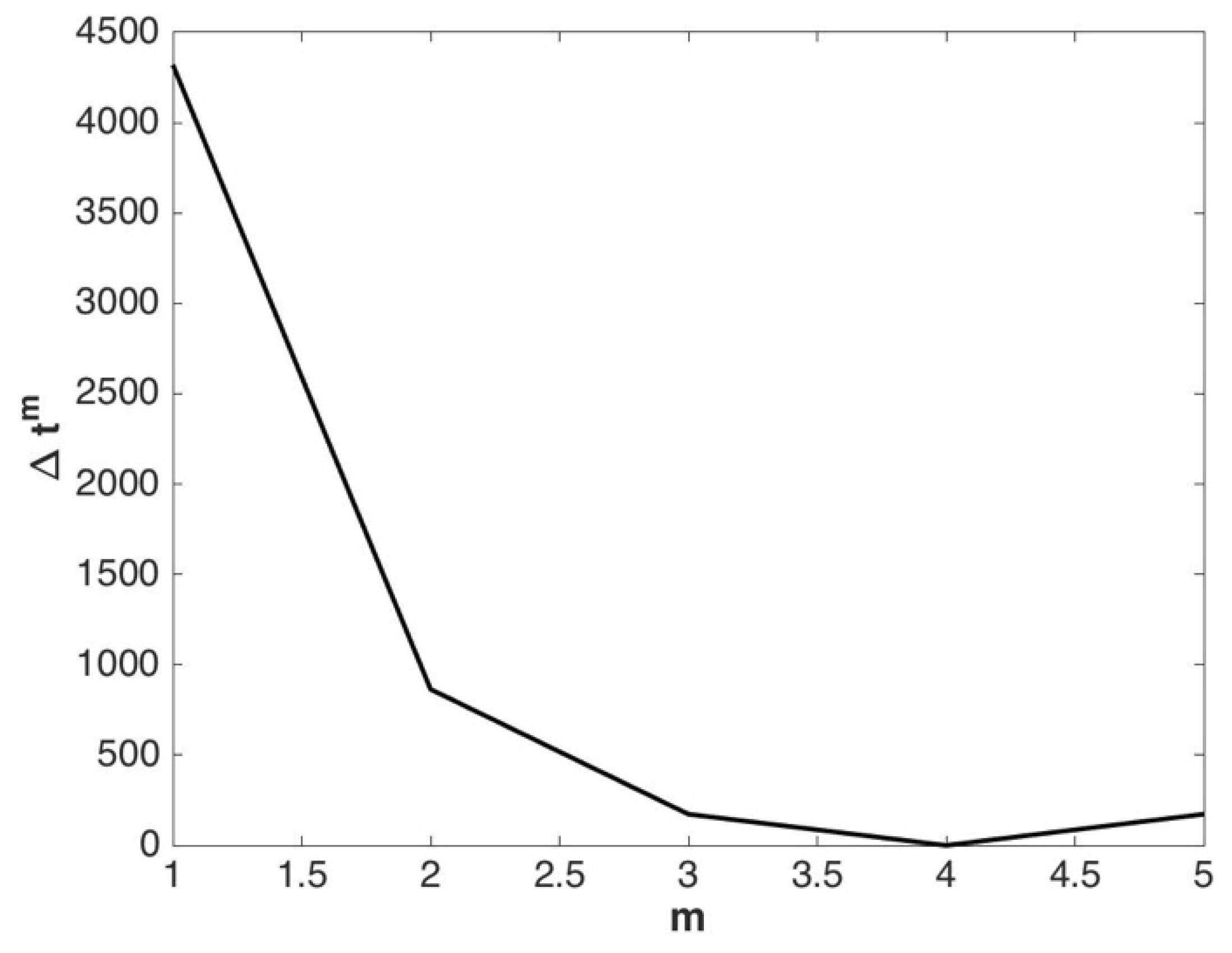
- The total time interval, [0, T], is divided into a number of time steps, namely, , with a time-step of length .
- -
- For temperature and concentration, each interval, , was divided into a number of subintervals, i.e., .
- -
- The Courant–Friedrichs–Lewy stability condition (CFL < 1) is used to accomplish the time step-size adaptation.
- -
- The time-step size of the pressure was taken to be larger than the time-step sizes of temperature and concentration.
- -
- Calculating the pressure implicitly by coupling the continuity and momentum equations.
- -
- Compute the velocity explicitly.
- -
- Solve energy and concentration equations implicitly.
- -
- Update porosity, permeability, and density.
- -
- The pressure time-step, is taken as an initial time step for both temperature and concentration equations.
- -
- After that, the conditions and are examined. If one of them is satisfied, the temperature/concentration time-step is divided into smaller steps.
- -
- Therefore, the conditions and are recalculated based on the new time steps and so on, until satisfying the conditions and .
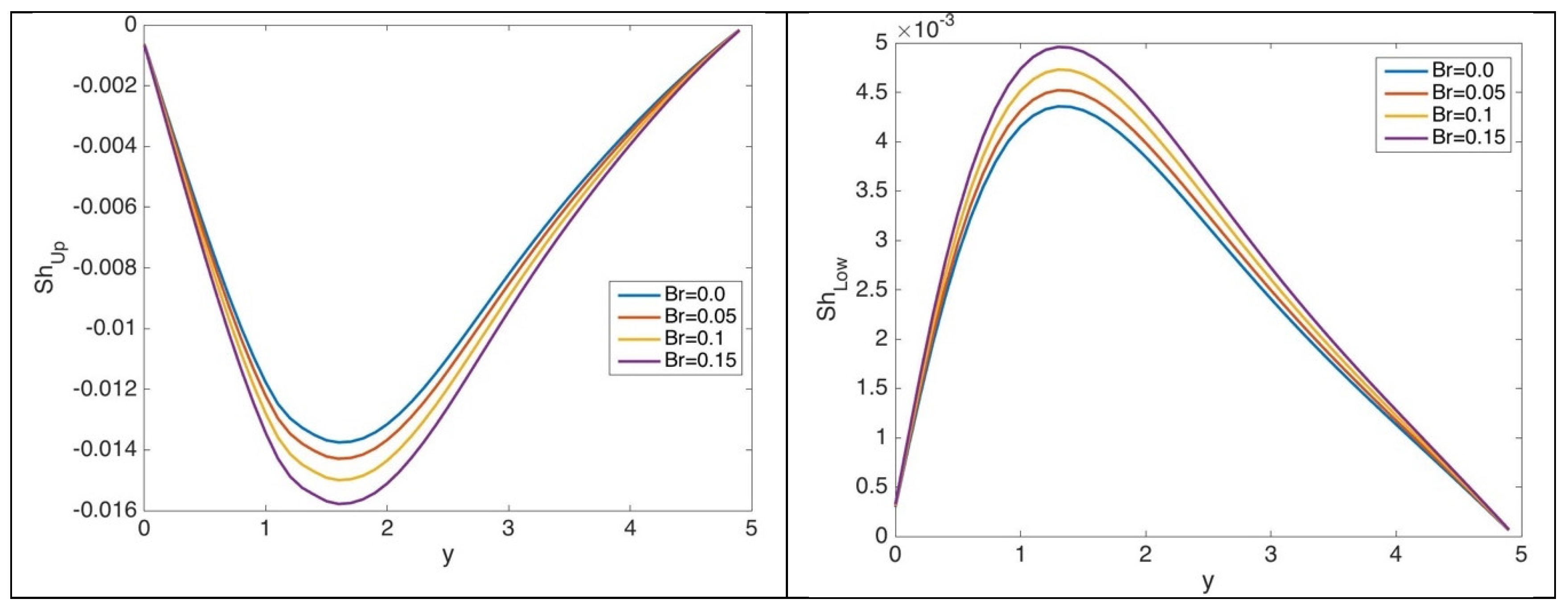
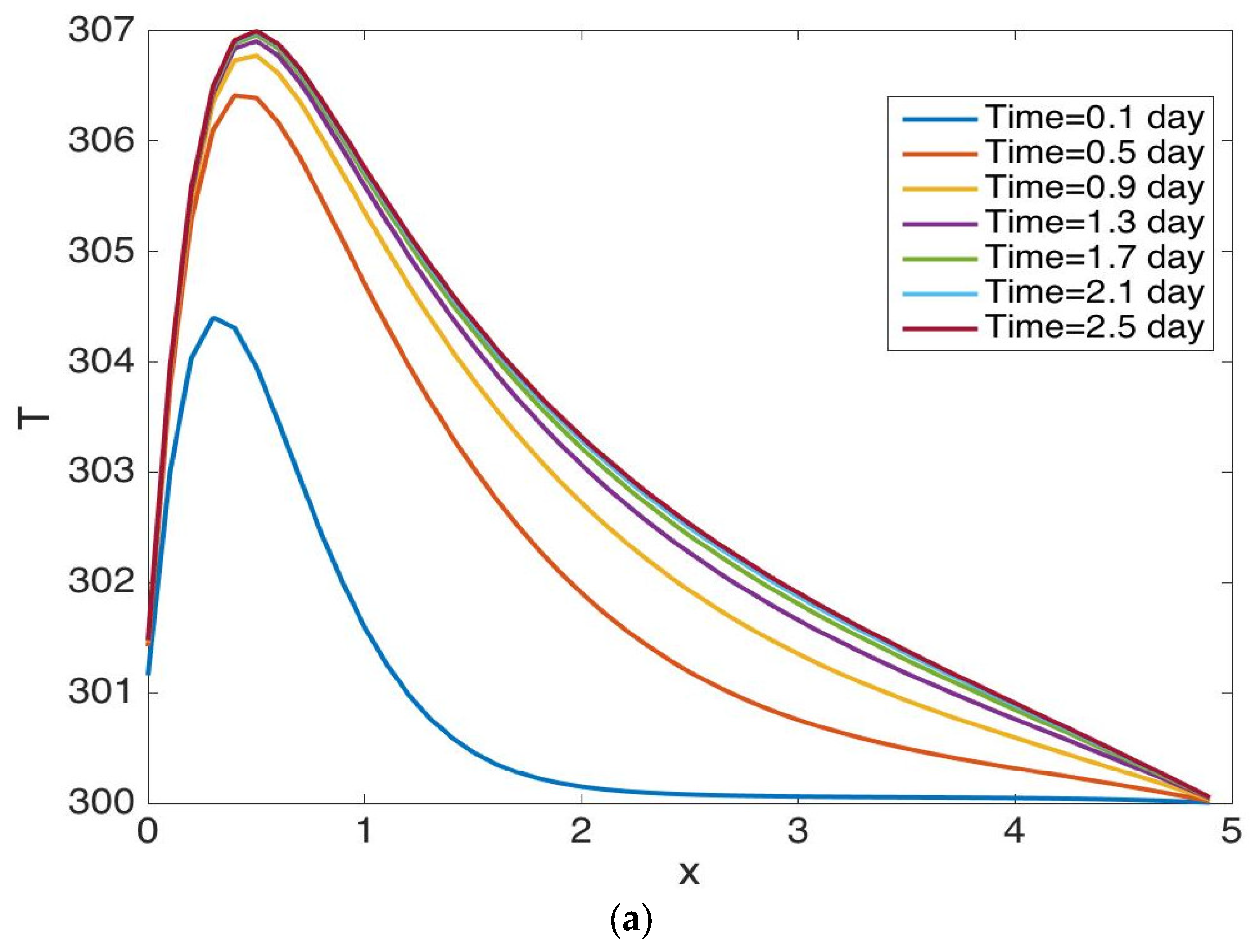
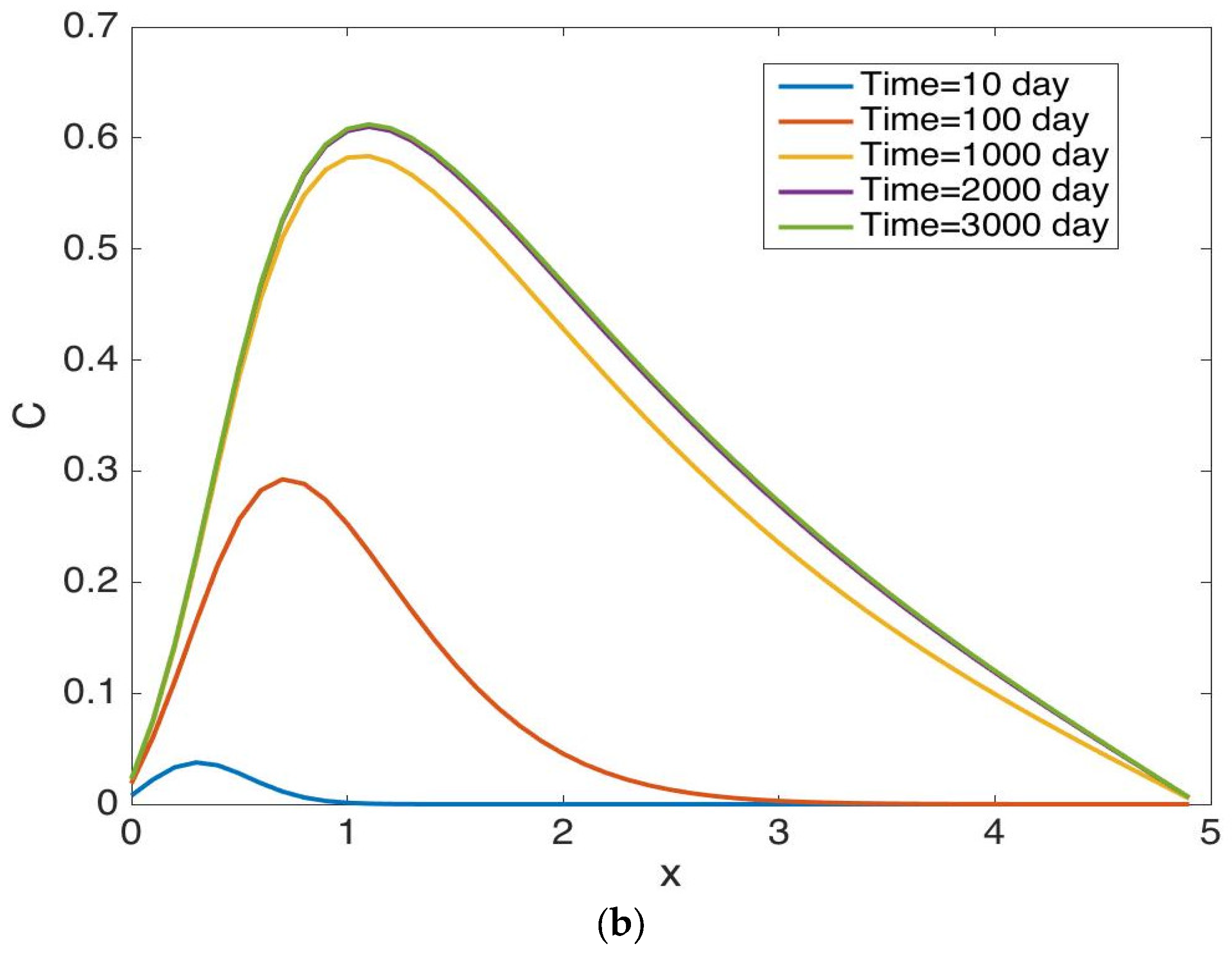
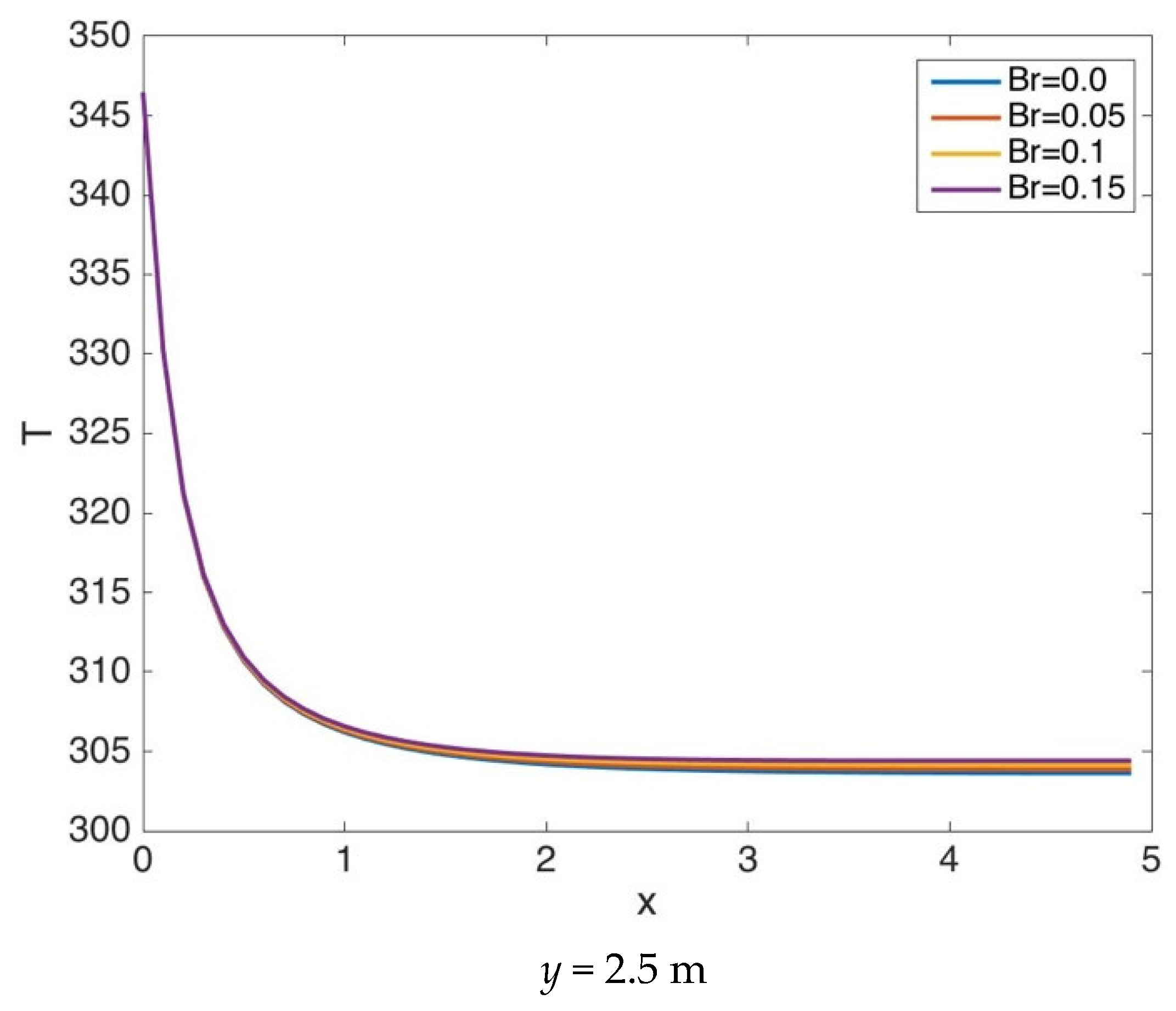
5. Results and Discussion
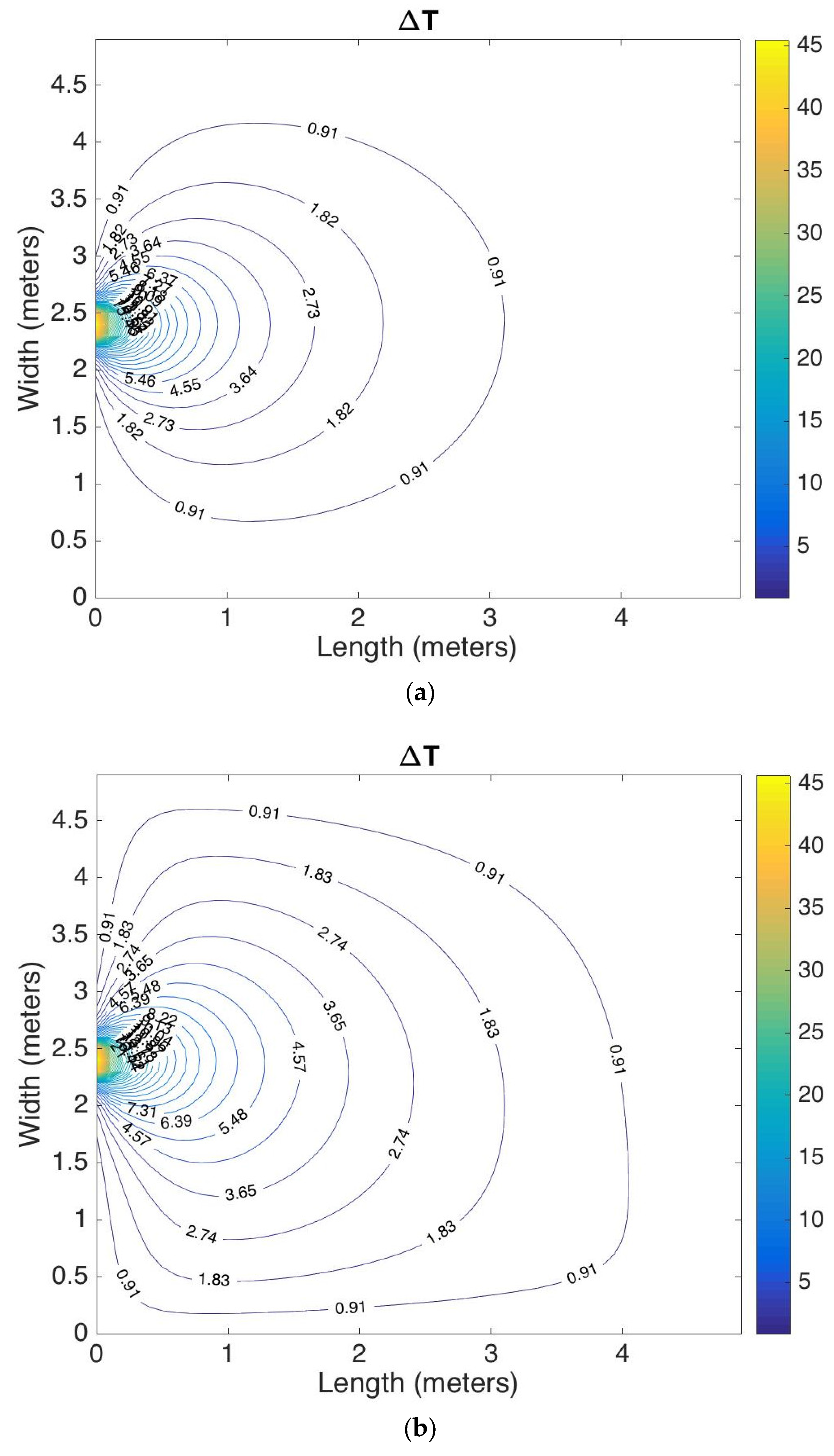
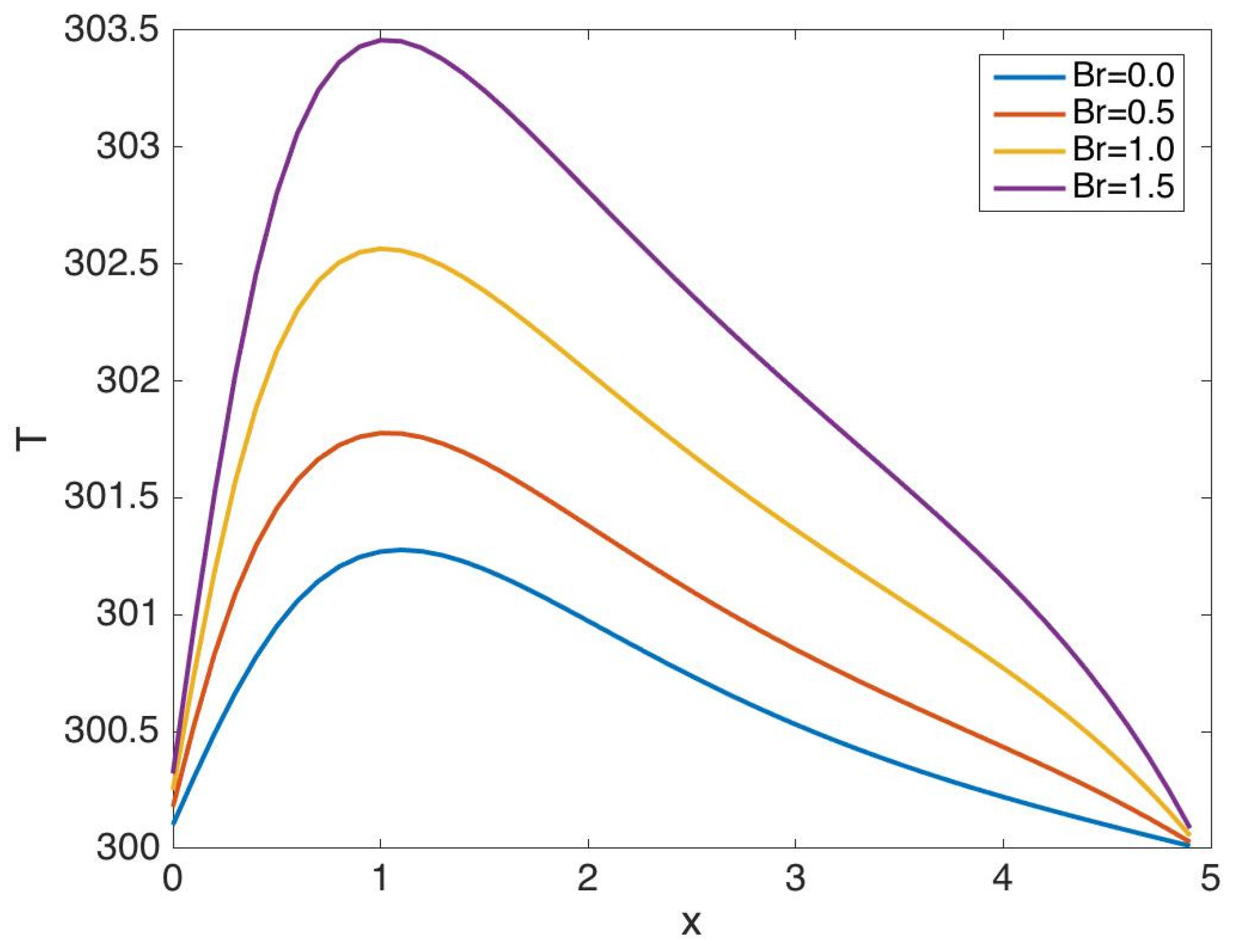
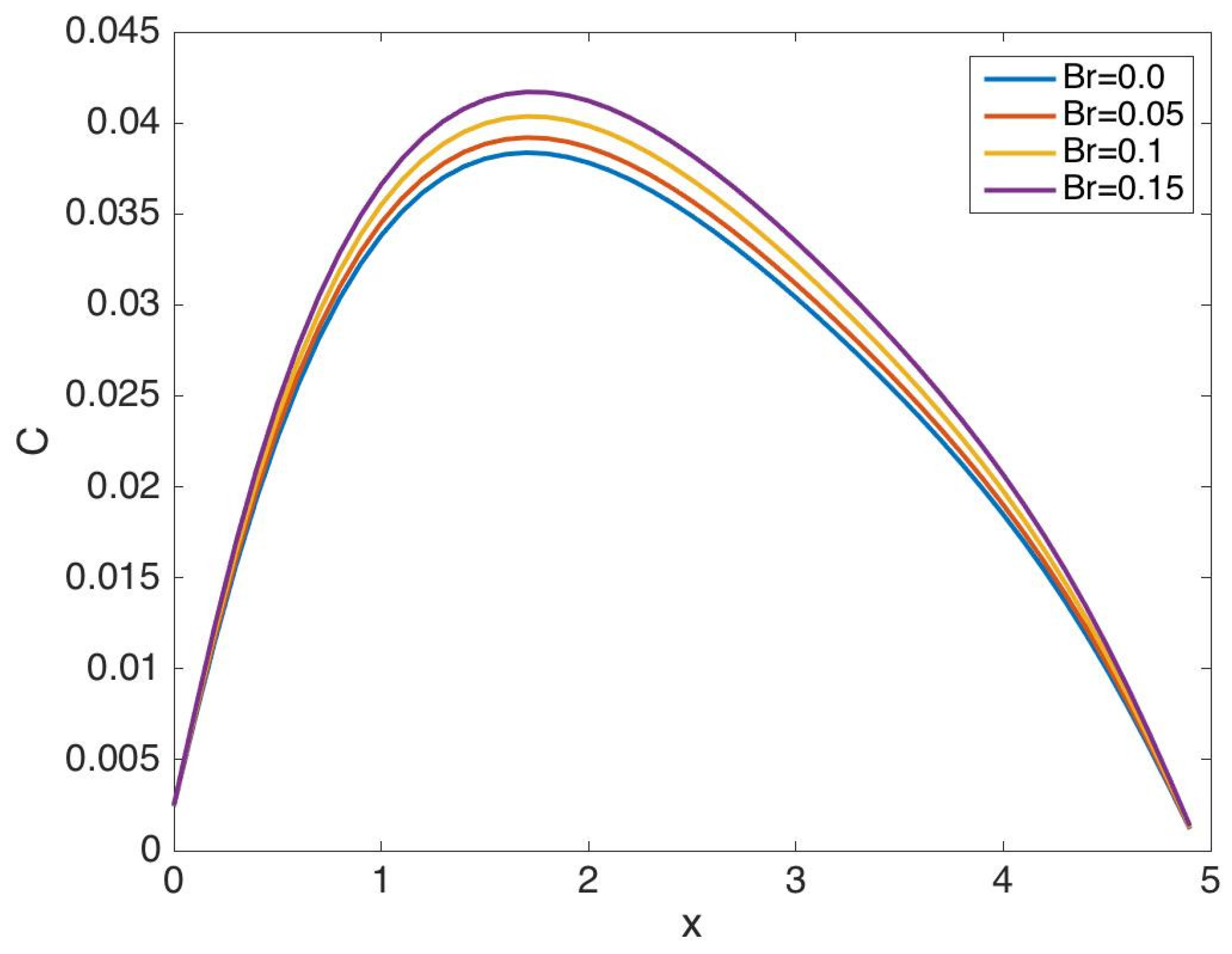
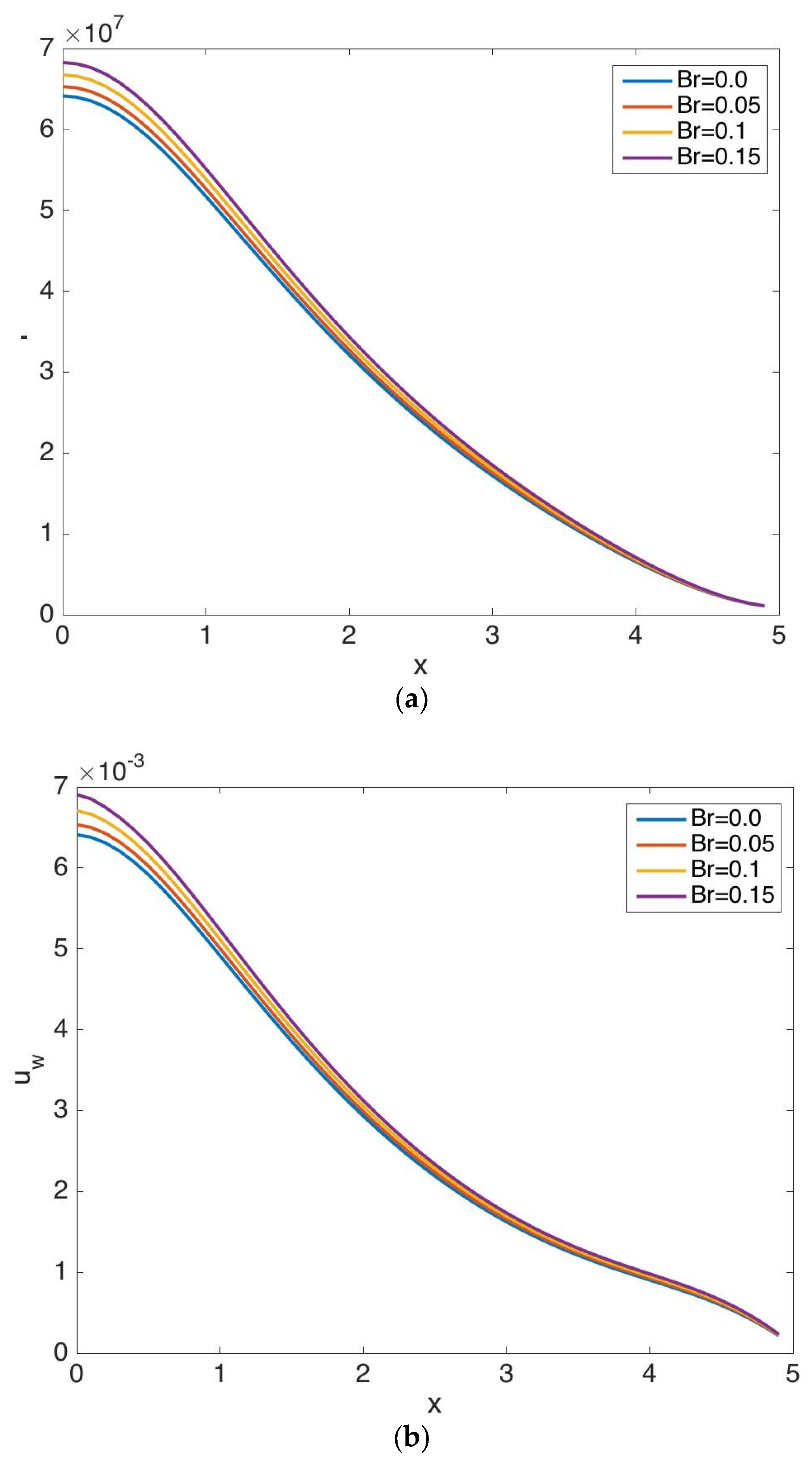
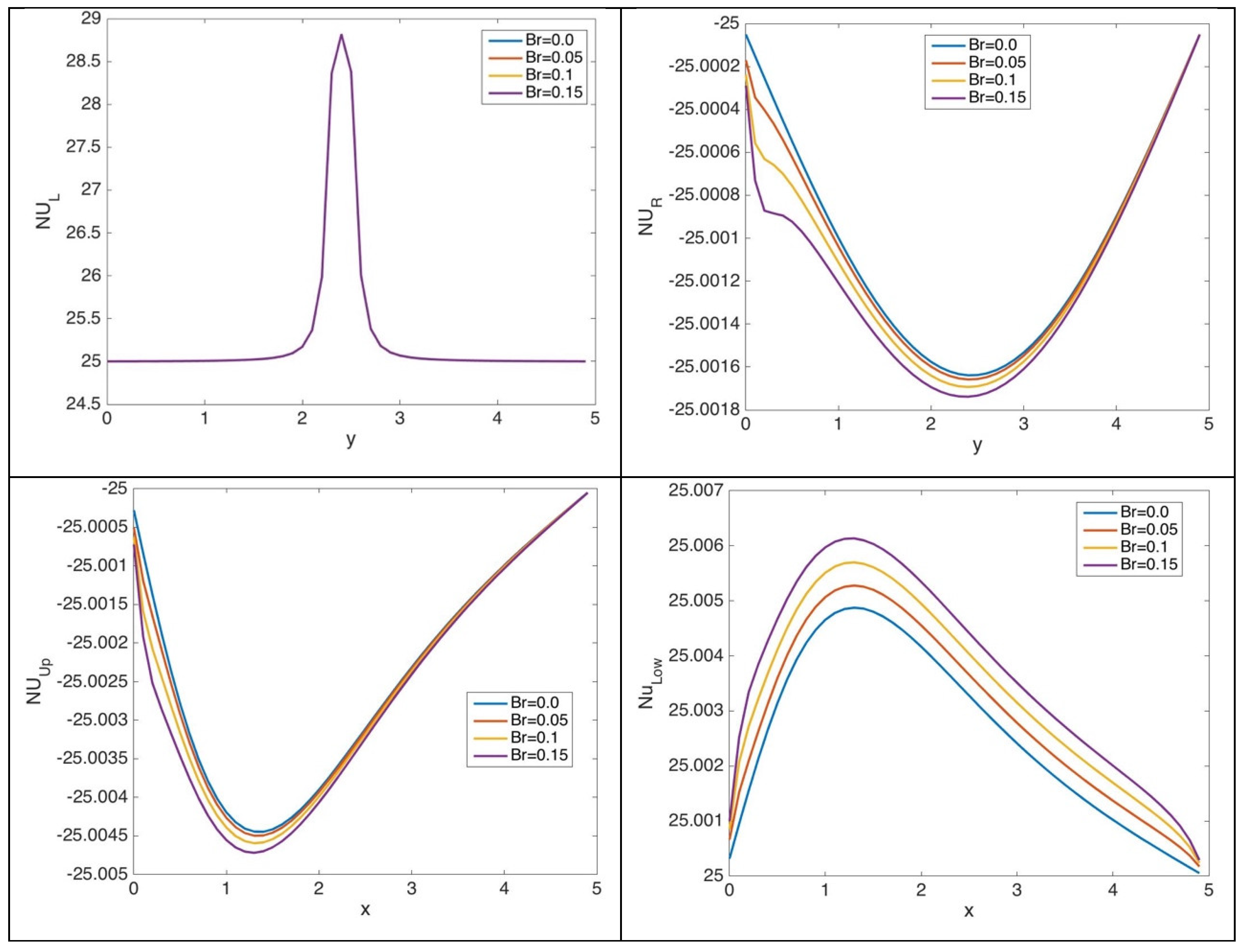
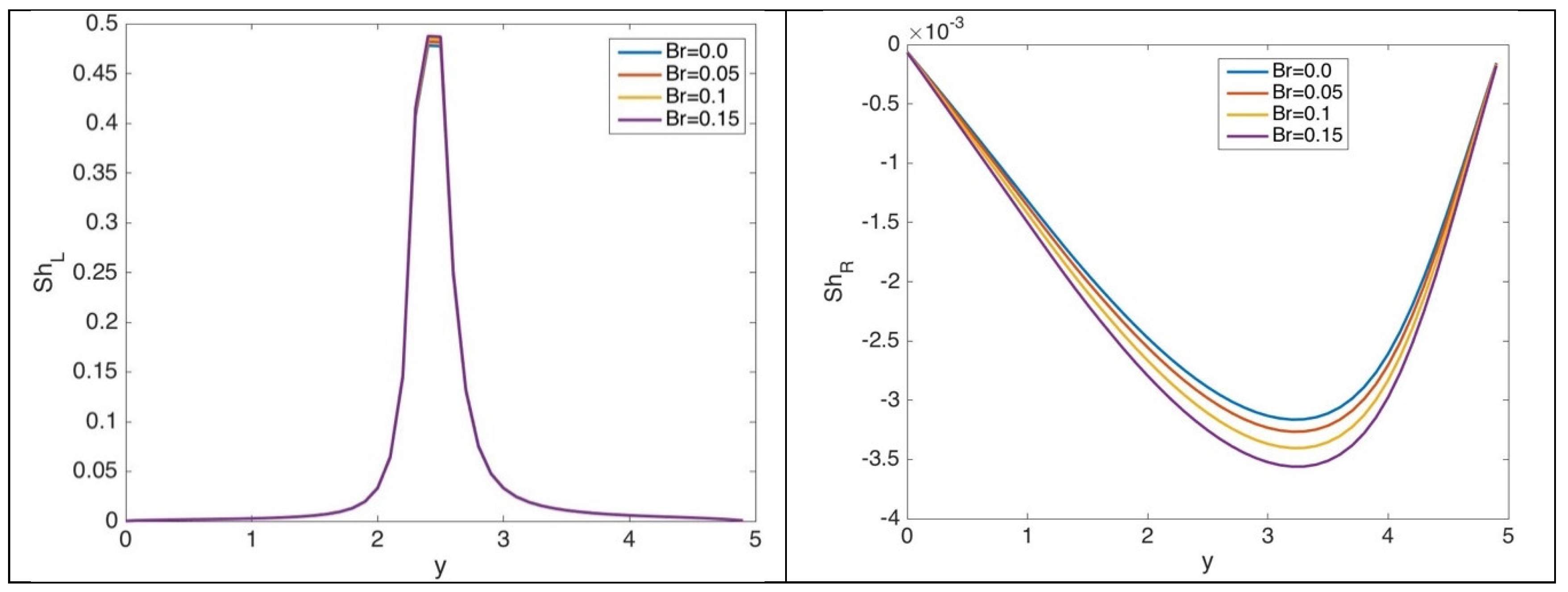
5.1. Results for Case 1
5.2. Results for Case 2
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | [m] | half of width of the magnet, |
| [A m−1] | constants depend on the type of the ferromagnetic material, | |
| b | [m] | half of height of the magnet, |
| [Tesla] | residual magnetization, | |
| [m m−3] | ferrofluid concentration, | |
| [m m−3] | ferrofluid initial concentration, | |
| [ | heat capacity, | |
| D | [m2 s−1] | diffusion coefficient, |
| [N] | external magnetic force, | |
| [m s−2] | gravitation acceleration, | |
| h | [ | thermal conductivity, |
| H | [A m−1] | magnetic field strength, |
| K | [m2] | permeability of the porous medium, |
| L | [m] | distance between the poles of the magnet, |
| Nu | [-] | Nusselt number, |
| [K] | temperature, | |
| [K] | reference temperature, | |
| [Pa] | fluid pressure, | |
| [kg s−1] | external mass flow rate, | |
| [ | rate of change of particle volume of a source/sink term, | |
| [ | heat source term, | |
| [ | fluid velocity vector, | |
| [m] | Cartesian coordinates, | |
| [K−1] | thermal expansion coefficient, | |
| solutal expansion coefficient, | ||
| [s] | time step for the loop k, | |
| [s] | time step for the loop l, | |
| [s] | time step for the loop m, | |
| [-] | porosity of porous media, | |
| [ | density of fluid mixture, | |
| [ | density of pure water component, | |
| [ | density of ferro-particles component, | |
| [ | density of solid phase, | |
| [m s−2] | viscosity of water-magnetic-particles mixture, | |
| [m s−2] | viscosity of water, | |
| [N A−2] | magnetic permeability. |
References
- Scherer, C.; Figueiredo Neto, A.M. Ferrofluids: Properties and applications. Braz. J. Phys. 2005, 35, 718–727. [Google Scholar] [CrossRef]
- Borglin, S.E.; Moridis, G.J.; Oldenburg, C.M. Experimental studies of the flow of ferrofluid in porous media. Transp. Porous Media 2000, 41, 61–80. [Google Scholar] [CrossRef]
- Huh, C.; Nizamidin, N.; Pope, G.A.; Milner, T.E.; Wang, B. Hydrophobic Paramagnetic Nanoparticles as Intelligent Crude Oil Tracers. U.S. Patent Application No. 14/765,426, 15 January 2014. [Google Scholar]
- Oldenburg, C.M.; Borglin, S.E.; Moridis, G.J. Numerical simulation of ferrofluid flow for subsurface environmental engineering applications. Transp. Porous Media 2000, 38, 319–344. [Google Scholar] [CrossRef]
- Zahn, M. Magnetic fluid and nanoparticle applications to nanotechnology. J. Nanopart. Res. 2001, 3, 73–78. [Google Scholar] [CrossRef]
- Chegenizadeh, N.; Saeedi, A.; Quan, X. Application of nanotechnology for enhancing oil recovery—A review. Petroleum 2016, 2, 324–333. [Google Scholar]
- El-Amin, M.F.; Salama, A.; Sun, S. Numerical and dimensional analysis of nanoparticles transport with two-phase flow in porous media. J. Pet. Sci. Eng. 2015, 128, 53–64. [Google Scholar] [CrossRef]
- El-Amin, M.F.; Salama, A.; Sun, S. Modeling and simulation of nanoparticles transport in a two-phase flow in porous media. In Proceedings of the SPE International Oilfield Nanotechnology Conference, Noordwijk, The Netherlands, 12–14 June 2012. SPE-154972-MS. [Google Scholar]
- Suleimanov, B.A.; Ismailov, F.S.; Veliyev, E.F. Nanofluid for enhanced oil recovery. J. Pet. Sci. Eng. 2011, 78, 431–437. [Google Scholar] [CrossRef]
- Ryoo, S.; Rahmani, A.; Yoon, K.Y.; Prodanovi, M.; Kots-mar, C.; Milner, T.E.; Johnston, K.P.; Bryant, S.L.; Huh, C. Theoretical and experimental investigation of the motion of multiphase fluids containing paramagnetic nanoparticles in porous media. J. Pet. Sci. Eng. 2012, 81, 129–144. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I. Mixed convection in a lid-driven square cavity filled by a nanofluid: Buongiorno’s mathematical model. App. Math. Comput. 2015, 266, 792–808. [Google Scholar] [CrossRef]
- Ghalambaz, M.M.; Sheremet, F.; Mikhail, A.; Pop, I. Triple-diffusive natural convection in a square porous cavity. Transp. Porous Media 2016, 111, 59–79. [Google Scholar] [CrossRef]
- Carvalho, P.H.S.; de Lemos, M.J.S. Passive laminar heat transfer across porous cavities using thermal non-equilibrium model. Numer. Heat Transf. 2014, 66, 1173–1194. [Google Scholar] [CrossRef]
- Javed, T.; Mehmood, Z.; Abbas, Z. Natural convection in square cavity filled with ferrofluid saturated porous medium in the presence of uniform magnetic field. Phys. B Condens. Matter 2017, 506, 122–132. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Xu, Z. Mathematical modeling and computer simulations of nanofluid flow with applications to cooling and lubrication. Fluids 2016, 1, 16. [Google Scholar] [CrossRef]
- Bhallamudi, S.M.; Panday, S.; Huyakorn, P.S. Sub-timing in fluid flow and transport simulations. Adv. Water Res. 2003, 26, 477–489. [Google Scholar] [Green Version]
- Martinez, V. A numerical technique for applying time splitting methods in shallow water equations. Comput. Fluids 2018, 169, 285–295. [Google Scholar] [CrossRef]
- Zhang, T.; Qian, Y. The time viscosity-splitting method for the Boussinesq problem. J. Math. Anal. Appl. 2017, 445, 186–211. [Google Scholar] [CrossRef]
- Caliari, M.; Zuccher, S. Reliability of the time-splitting Fourier method for singular-solutions in quantum fluids. Comput. Phys. Commun. 2018, 222, 46–58. [Google Scholar] [CrossRef]
- El-Amin, M.F.; Kou, J.; Sun, S. Discrete-fracture-model of multi-scale time-splitting two-phase flow including nanoparticles transport in fractured porous media. J. Comput. Appl. Math. 2018, 333, 327–349. [Google Scholar] [CrossRef]
- El-Amin, M.F.; Kou, J.; Salama, A.; Sun, S. An iterative implicit scheme for nanoparticles transport with two-phase flow in porous media. Procedia Comput. Sci. 2016, 80, 1344–1353. [Google Scholar] [CrossRef]
- El-Amin, M.F.; Kou, J.; Sun, S.; Salama, A. Adaptive time-splitting scheme for two-phase flow in heterogeneous porous media. Adv. Geo-Energy Res. 2017, 1, 182–189. [Google Scholar] [CrossRef]
- El-Amin, M.F.; Kou, J.; Salama, A.; Sun, S. Multiscale adaptive time-splitting technique for nonisothermal two-phase flow and nanoparticles transport in heterogeneous porous media. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 8–10 May 2017. SPE-186047-MS. [Google Scholar]
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt, Rinehart and Winston: New York, NY, USA, 1976; ISBN 0-03-083993-9. [Google Scholar]
- Herbert, A.W.; Jackson, C.P.; Lever, D.A. Coupled groundwater flow and solute transport with fluid density strongly dependent upon concentration. Water Resour. Res. 1988, 24, 1781–1795. [Google Scholar] [CrossRef]
- El-Amin, M.F. Double dispersion effects on natural convection heat and mass transfer in non-Darcy porous medium. Appl. Math Comput. 2004, 156, 1–17. [Google Scholar] [CrossRef]


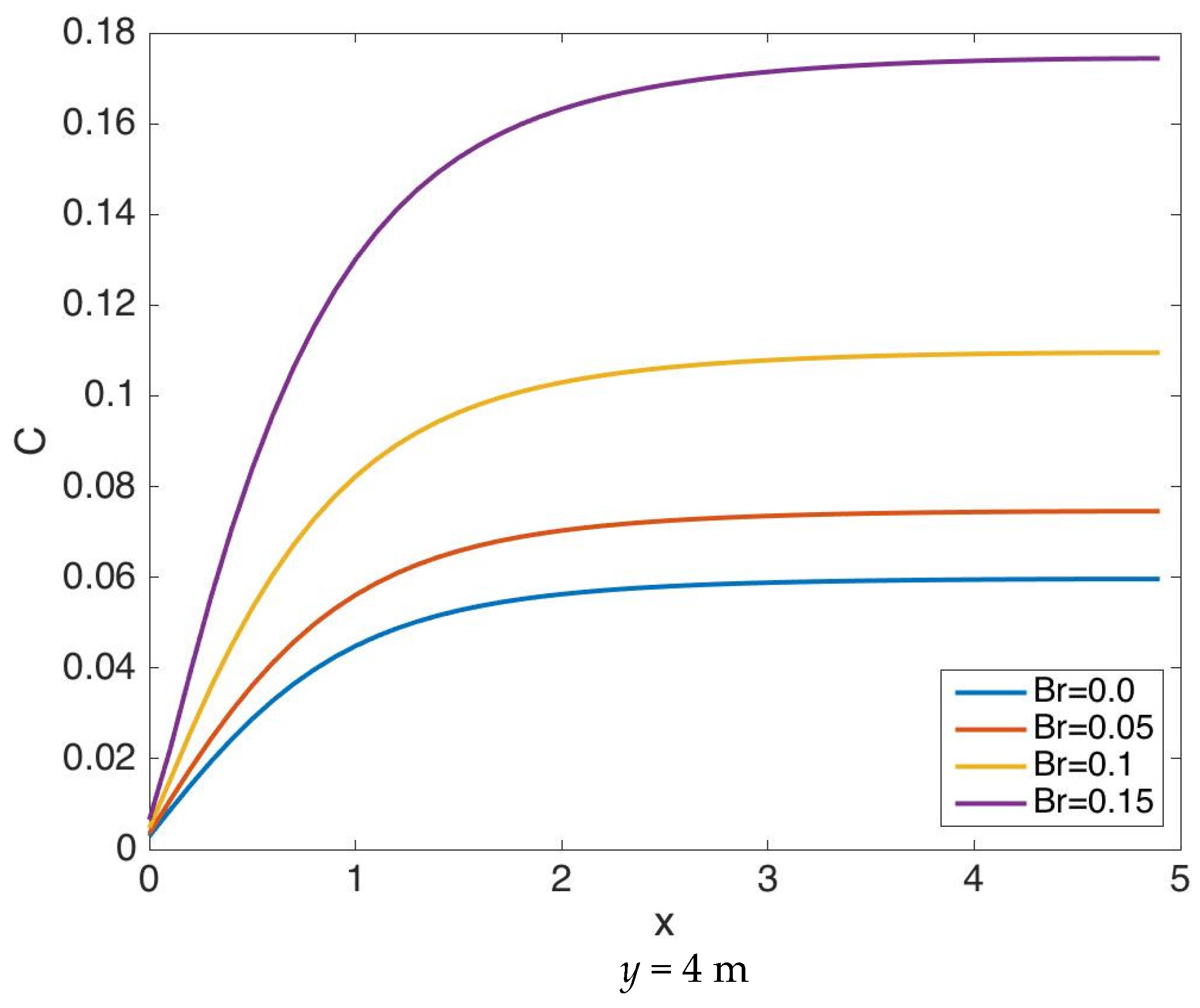
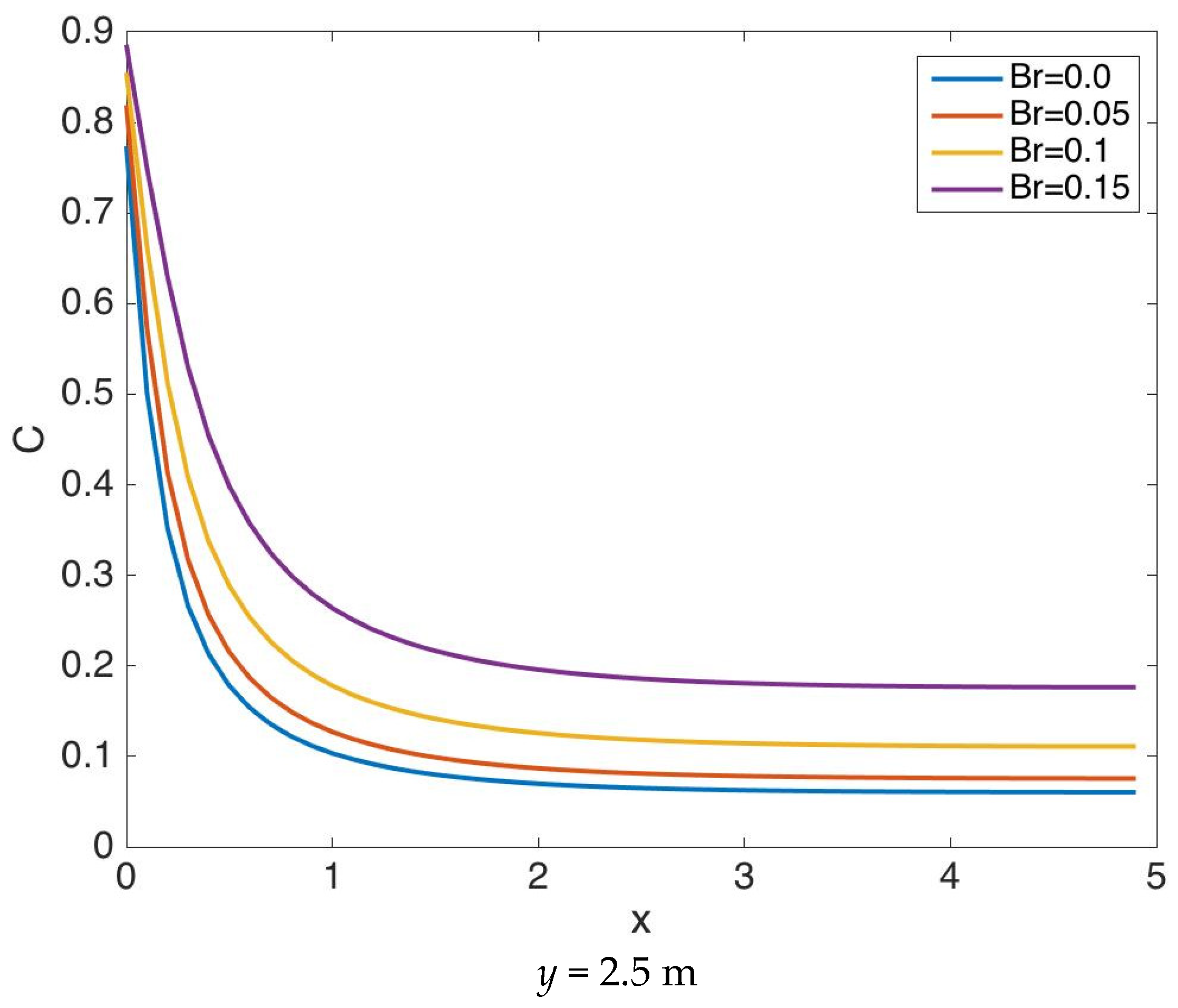
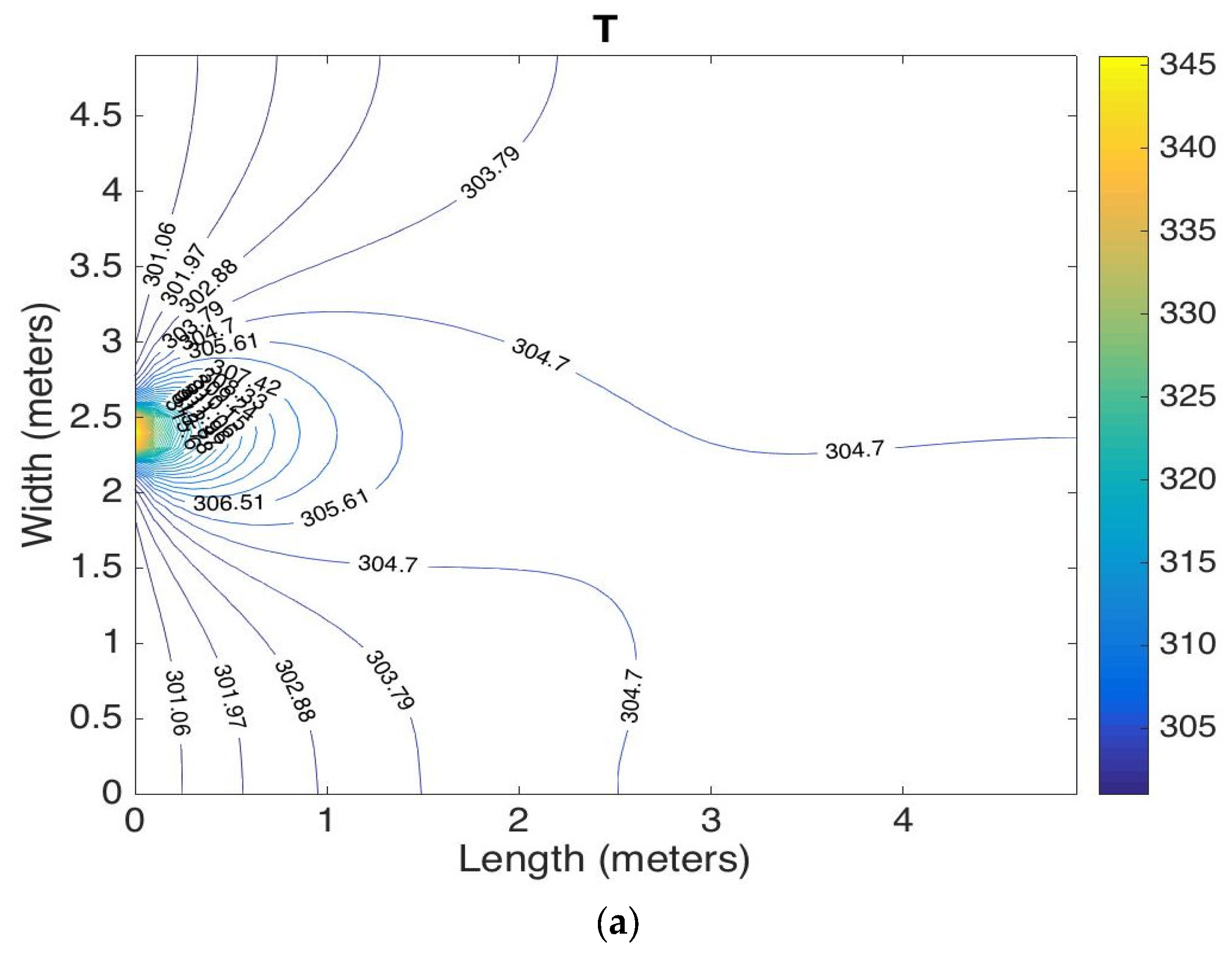

| Parameter | Description | Value | Units |
|---|---|---|---|
| Constant | 104–105 | m A−1 | |
| Constant | 10−6–10−5 | m A−1 | |
| a, b | Half of width/height of the magnet | 0.02 | m |
| Br | Residual magnetization | 0:0.2 | Tesla |
| Initial concentration | 0 | - | |
| Inlet concentration | 1 | - | |
| Heat capacity | 800 | J/Kg K | |
| D | Diffusion coefficient | 5 | /S |
| Thermal conductivity of the solid | 0.718 | W/(/K) | |
| Thermal conductivity of the ferrofluid | 0.6 | W/(/K) | |
| Gravity acceleration | 9.81 | ||
| K | Permeability | 100 | md |
| Lp | Distance between poles | 2.4 | m |
| Lin | Inlet width | 0.3 | m |
| L | Cavity side length | 5 | m |
| md | Millidarcy | 9.86923 | m2 |
| Initial pressure | 1 | ||
| Initial temperature | 300 | K | |
| Inlet temperature | 360 | K | |
| Inlet velocity | /s | ||
| Thermal expansion coefficient | 0.005 | ||
| Solute expansion coefficient | 0.001 | ||
| Porosity | 0.3 | - | |
| Water viscosity | 0.001 | Pa.s | |
| Magnetic permeability | 1 | N·A−2 | |
| Solid media density | 2500 | kg/ | |
| Pure water density | 1000 | kg/ | |
| Particles density | 8933 | kg/ |
| k | ||
|---|---|---|
| 50 | 5.0317 × 10−11 | 0.0198 |
| 100 | 6.9070 × 10−11 | 0.0099 |
| 300 | 3.0481 × 10−12 | 0.0033 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Amin, M.F.; Khaled, U.; Beroual, A. Numerical Study of the Magnetic Field Effect on Ferromagnetic Fluid Flow and Heat Transfer in a Square Porous Cavity. Energies 2018, 11, 3235. https://doi.org/10.3390/en11113235
El-Amin MF, Khaled U, Beroual A. Numerical Study of the Magnetic Field Effect on Ferromagnetic Fluid Flow and Heat Transfer in a Square Porous Cavity. Energies. 2018; 11(11):3235. https://doi.org/10.3390/en11113235
Chicago/Turabian StyleEl-Amin, Mohamed F., Usama Khaled, and Abderrahmane Beroual. 2018. "Numerical Study of the Magnetic Field Effect on Ferromagnetic Fluid Flow and Heat Transfer in a Square Porous Cavity" Energies 11, no. 11: 3235. https://doi.org/10.3390/en11113235





