Numerical Simulation and Validation of Thermoeletric Generator Based Self-Cooling System with Airflow
Abstract
1. Introduction
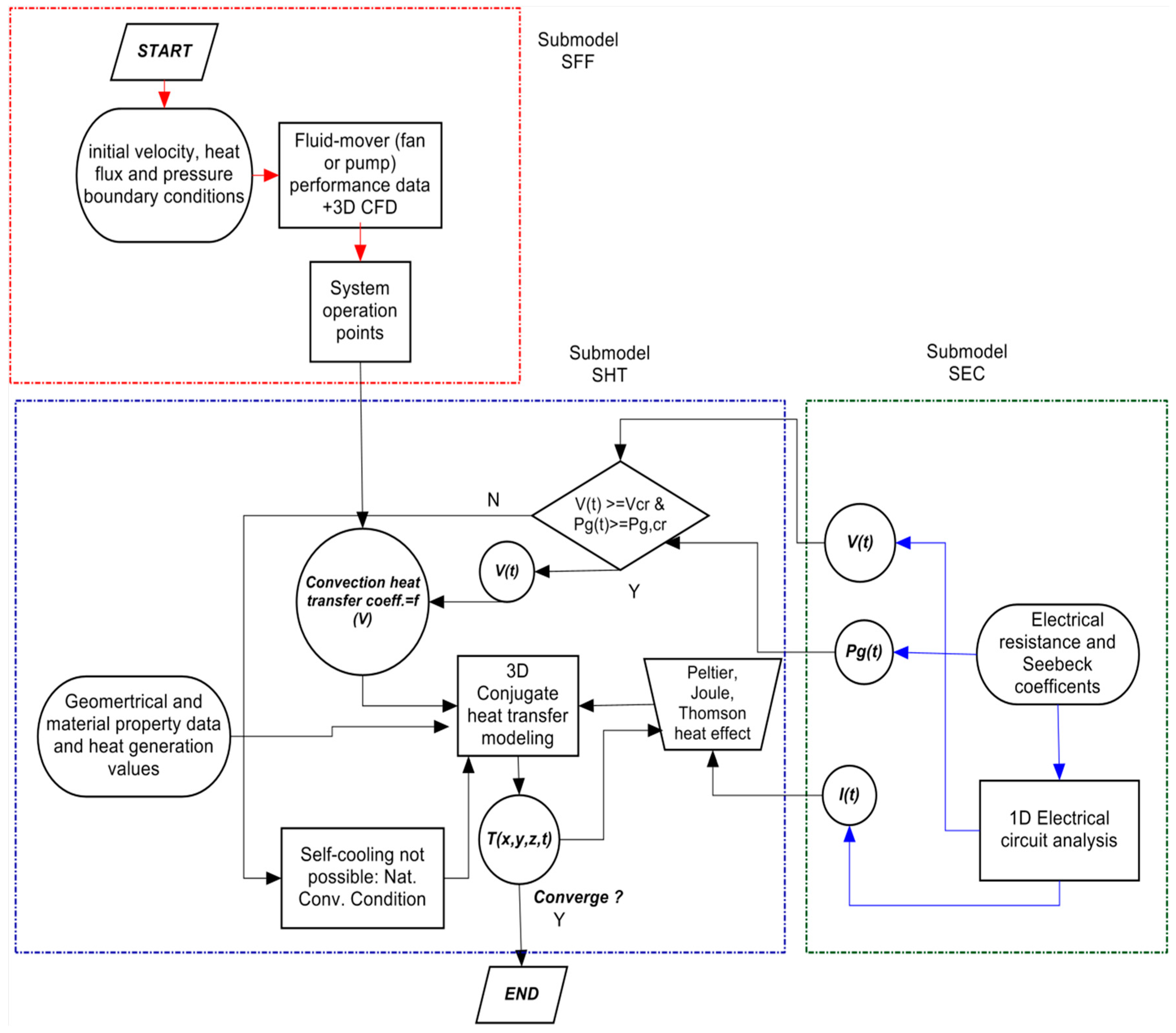
2. Numerical Methodology
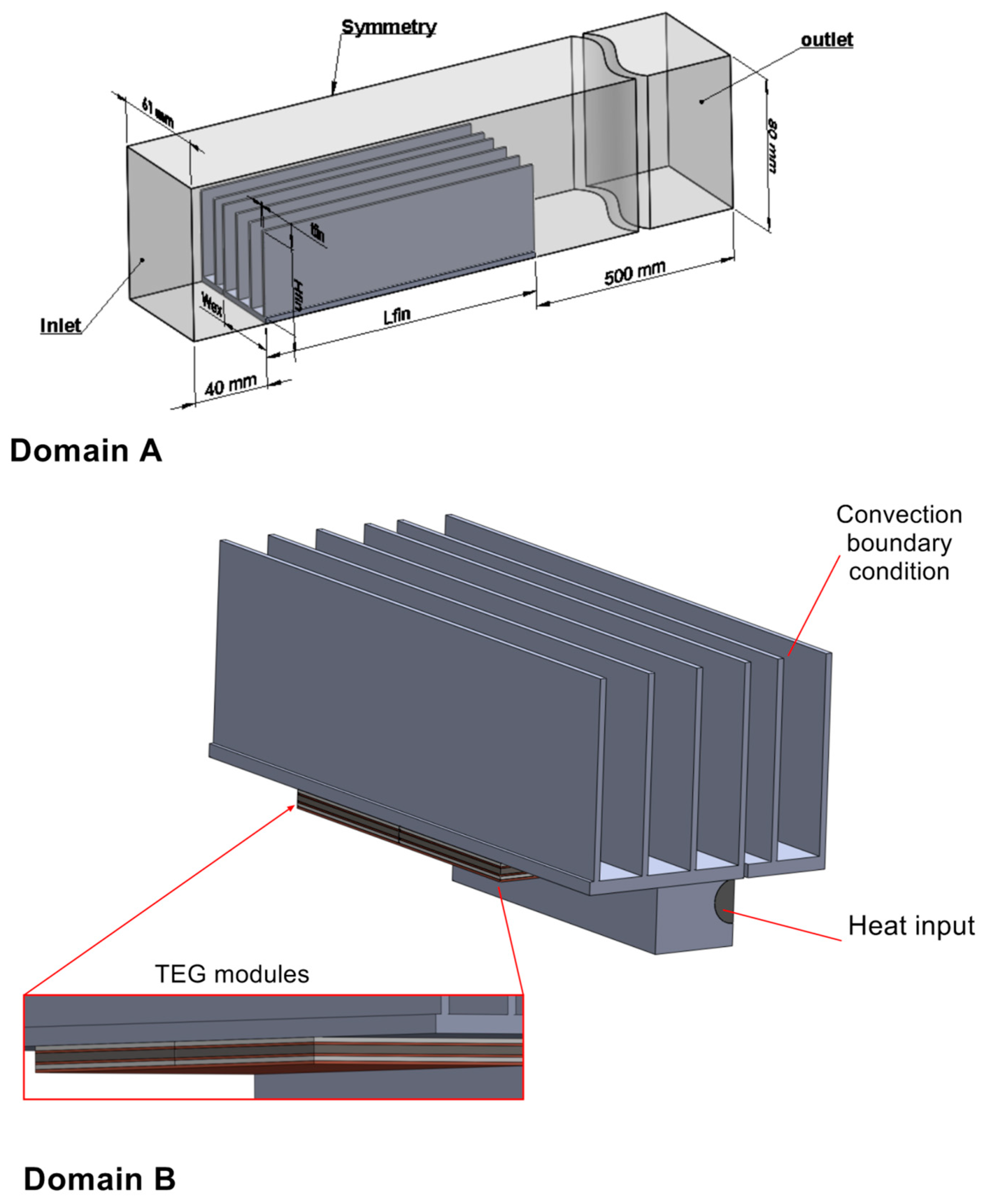
3. Numerical Model
User Defined Functions Based Modeling in FVM Model
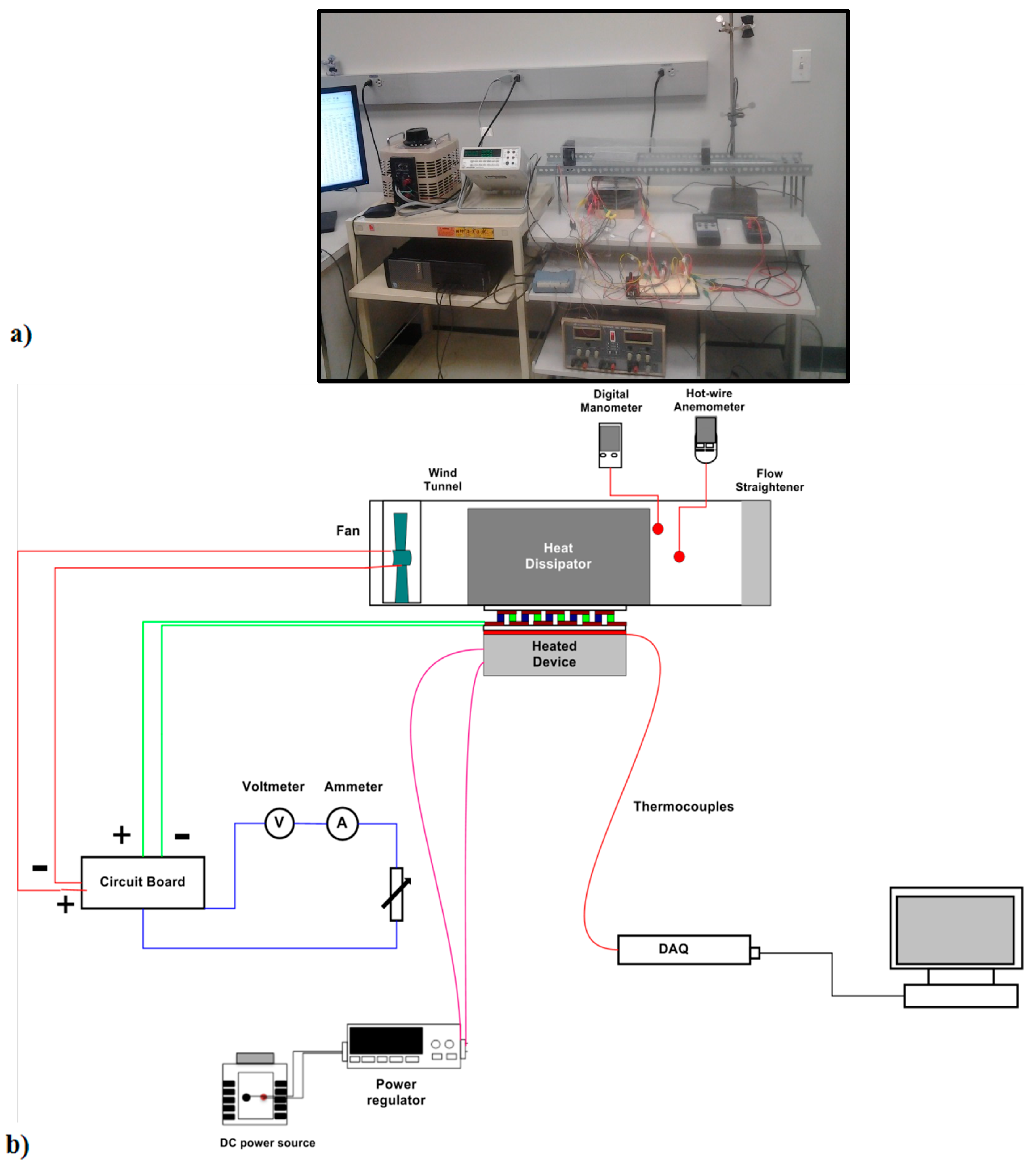
4. Experimental Data
5. Results and Discussion
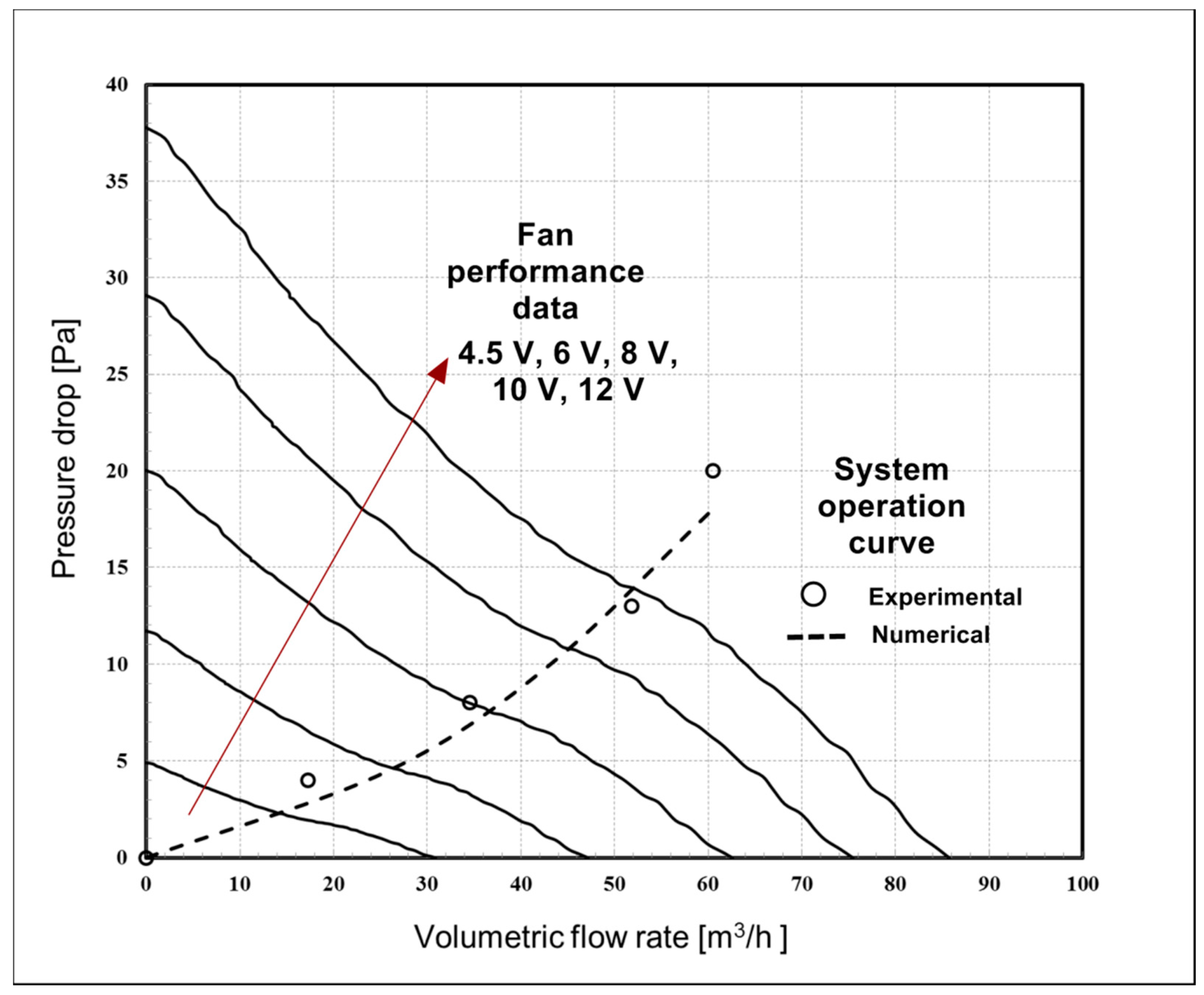
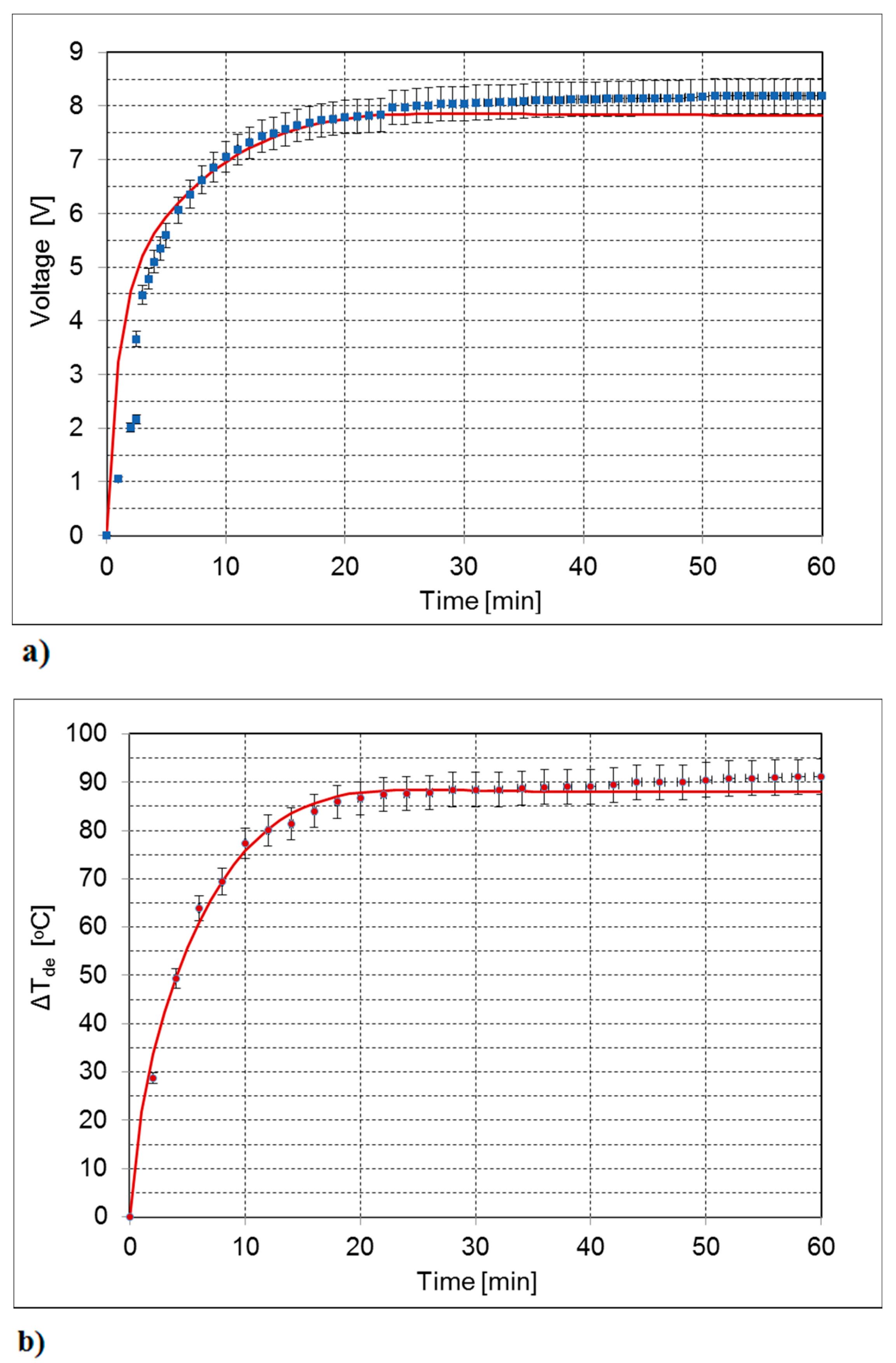
5.1. Validation of the Numerical Model
5.2. Parametric Study using FVM Model
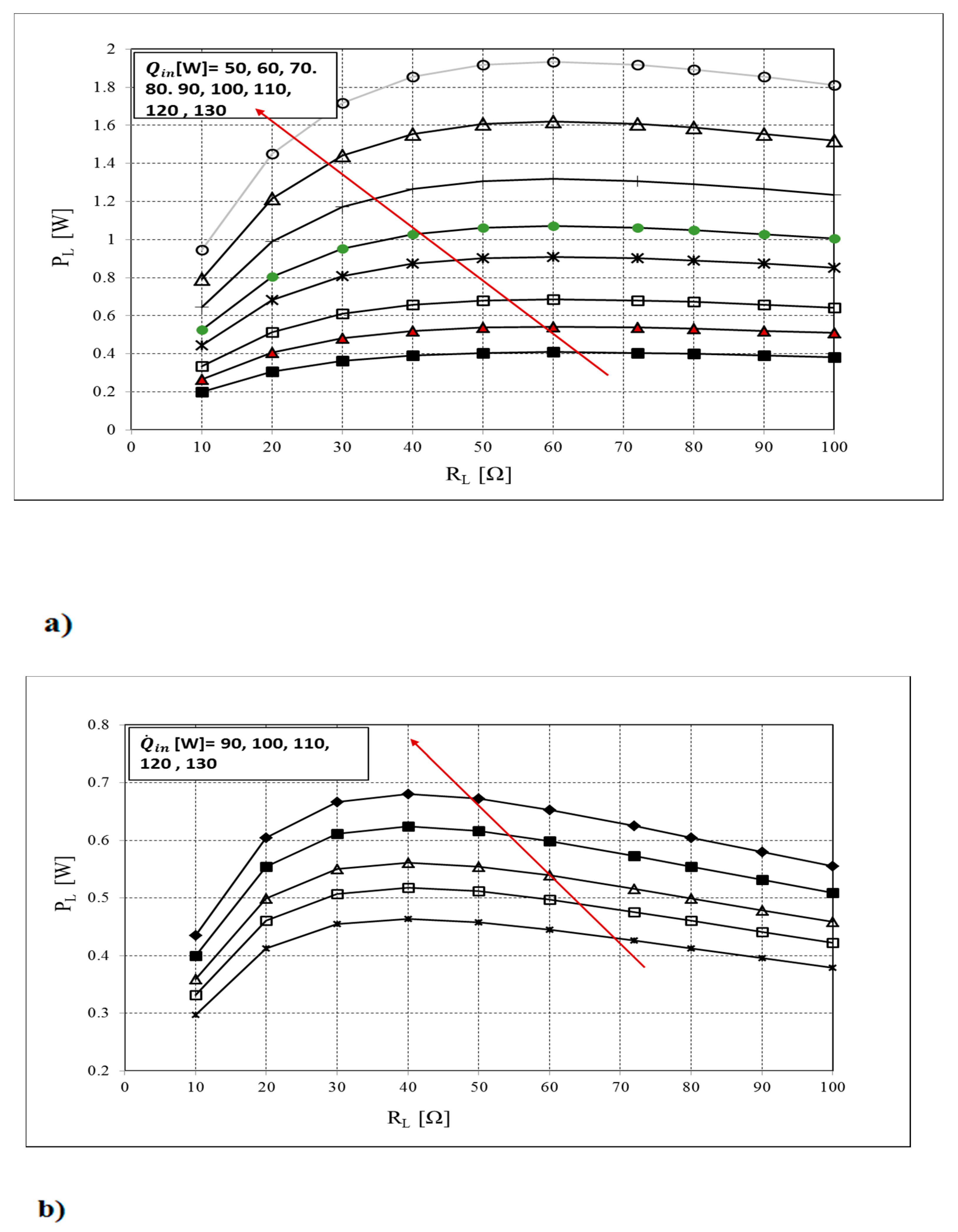
5.2.1. Effect of Load Resistance
5.2.2. Effect of Fin Height
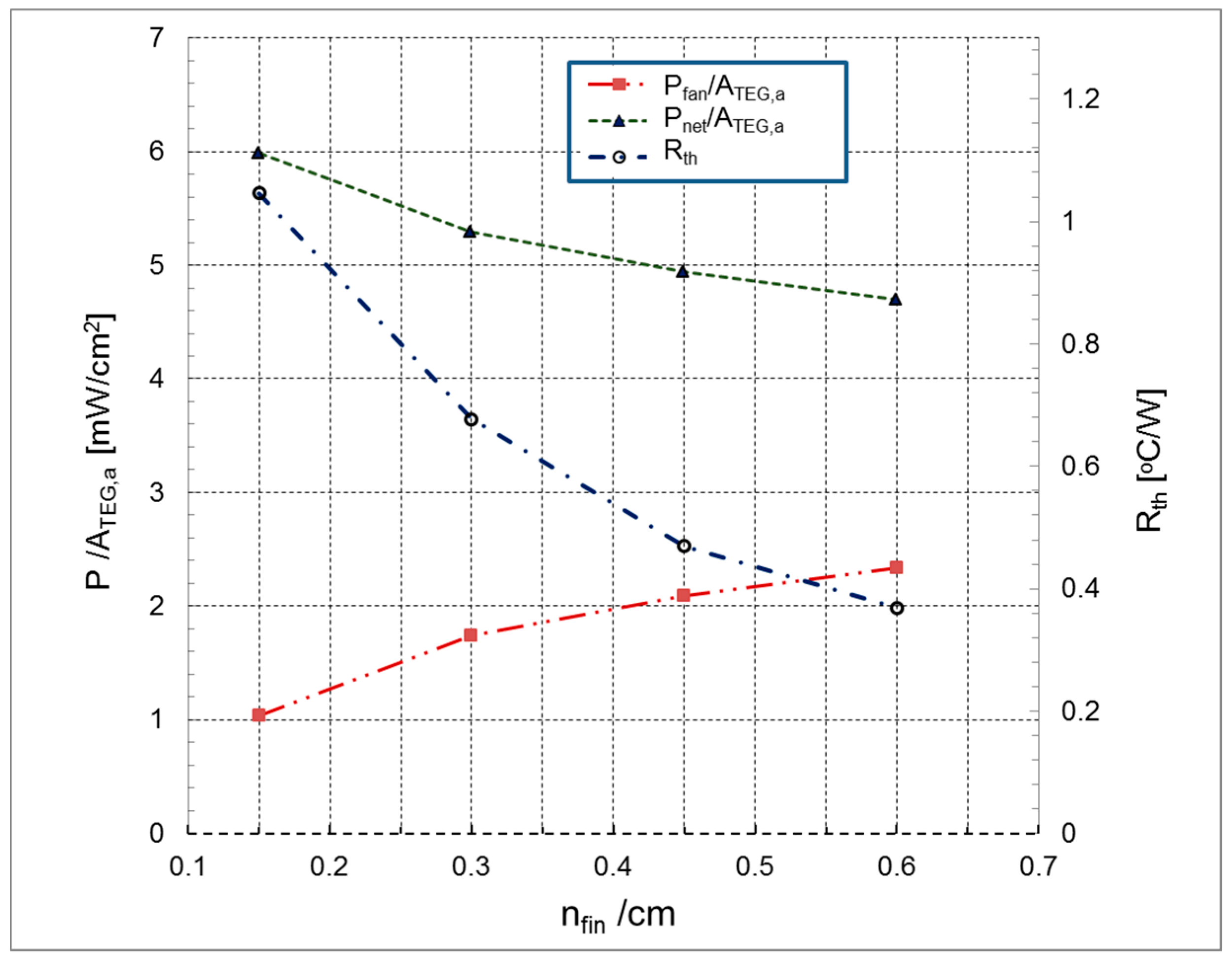
5.2.3. Effect of Fin Density
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | area (m2) | volume flow rate (m3/s) | |
| Cp | specific heat (J/kg K) | ||
| h | heat transfer coefficient (W/m2 K) | Greek symbols | |
| I | electric current ( A) | α | seebeck coefficient (V/K) |
| L | length (m) | ρf | fluid density (kg/m3) |
| m | number of modules in an array | τ | Thermal diffusivity (m2/s) |
| Np | number of semiconductor pairs | ||
| P | electrical power (W) | Subscripts | |
| Δp | pressure drop (Pa) | cer | ceramic |
| heat flux (W/m2) | cu | copper | |
| heat input to device (W) | fb | fin base | |
| T | temperature (°C) | fin | parallel-plate fins |
| fluid velocity (m/s) | h | hot side | |
| μf | dynamic viscosity (N.s/m2) | mod | module |
| Rel | electrical resistance (Ω) | P-N | P and N semiconductor pairs |
| Rth | thermal resistance (°C/W) | p | P elements in TEG module |
| S | source term of energy equation | n | N elements in TEG module |
| V | voltage (V) | s | spreader |
References
- Date, A.; Date, A.; Dixon, C.; Akbarzadeh, A. Progress of thermoelectric power generation systems: Prospect for small to medium scale power generation. Renew. Sustain. Energy Rev. 2014, 33, 371–381. [Google Scholar] [CrossRef]
- Gou, X.; Xiao, H.; Yang, S. Modeling, experimental study and optimization on low-temperature waste heat thermoelectric generator system. Appl. Energy 2010, 87, 3131–3136. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Deng, Y.; Su, C. An energy-harvesting system using thermoelectric power generation for automotive application. Int. J. Electr. Power Energy Syst. 2015, 67, 510–516. [Google Scholar] [CrossRef]
- Khattab, N.M.; El Shenawy, E. Optimal operation of thermoelectric cooler driven by solar thermoelectric generator. Energy Convers. Manag. 2006, 47, 407–426. [Google Scholar] [CrossRef]
- Zhu, N.; Matsuura, T.; Suzuki, R.; Tsuchiya, T. Development of a Small Solar Power Generation System based on Thermoelectric Generator. Energy Procedia 2014, 52, 651–658. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Deng, Y.; Gao, H.; Lin, Z.; Zhu, W.; Ye, H. A novel self-powered wireless temperature sensor based on thermoelectric generators. Energy Convers. Manag. 2014, 80, 110–116. [Google Scholar] [CrossRef]
- Champier, D.; Bédécarrats, J.; Kousksou, T.; Rivaletto, M.; Strub, F.; Pignolet, P. Study of a TE (thermoelectric) generator incorporated in a multifunction wood stove. Energy 2011, 36, 1518–1526. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.; Zhang, K.; Xu, M.; Xu, Y.; Su, C. Experiments and simulations on heat exchangers in thermoelectric generator for automotive application. Appl. Therm. Eng. 2014, 71, 364–370. [Google Scholar] [CrossRef]
- Deng, Y.; Zhu, W.; Wang, Y.; Shi, Y. Enhanced performance of solar-driven photovoltaic–thermoelectric hybrid system in an integrated design. Sol. Energy 2013, 88, 182–191. [Google Scholar] [CrossRef]
- He, W.; Su, Y.; Wang, Y.; Riffat, S.; Ji, J. A study on incorporation of thermoelectric modules with evacuated-tube heat-pipe solar collectors. Renew. Energy 2012, 37, 142–149. [Google Scholar] [CrossRef]
- Kim, K.J.; Cottone, F.; Goyal, S.; Punch, J. Energy scavenging for energy efficiency in networks and applications. Bell Labs Tech. J. 2010, 15, 7–29. [Google Scholar]
- Kiflemariam, R.; Lin, C.-X. Numerical simulation of integrated liquid cooling and thermoelectric generation for self-cooling of electronic devices. Int. J. Therm. Sci. 2015, 94, 193–203. [Google Scholar] [CrossRef]
- Kiflemariam, R.; Lin, C.-X.; Moosavi, R. Numerical simulation, parametric study and optimization of thermoelectric generators for self-cooling of devices. In Proceedings of the 11th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Kiflemariam, R.; Lin, C.-X. Numerical Simulation and Parametric Study of Heat-Driven Self-Cooling of Electronic Devices. J. Therm. Sci. Eng. Appl. 2015, 7, 011008. [Google Scholar] [CrossRef]
- Martínez, A.; Astrain, D.; Rodríguez, A. Experimental and analytical study on thermoelectric self cooling of devices. Energy 2011, 36, 5250–5260. [Google Scholar] [CrossRef]
- Yazawa, K.; Solbrekken, G.; Bar-Cohen, A. Thermoelectric-powered convective cooling of microprocessors. IEEE Trans. Adv. Packag. 2005, 28, 231–239. [Google Scholar] [CrossRef]
- Solbrekken, G.; Yazawa, K.; Bar-Cohen, A. Heat driven cooling of portable electronics using thermoelectric technology. IEEE Trans. Adv. Packag. 2008, 31, 429–437. [Google Scholar] [CrossRef]
- Gould, C.; Shammas, N.; Grainger, S.; Taylor, I. Thermoelectric cooling of microelectronic circuits and waste heat electrical power generation in a desktop personal computer. Mater. Sci. Eng. B 2011, 176, 316–325. [Google Scholar] [CrossRef]
- Martinez, A.; Astrain, D.; Rodriguez, A. Dynamic model for simulation of thermoelectric self cooling applications. Energy 2013, 55, 1114–1126. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Fluent Theory and User Guide, Release 14; Ganonsburg: Pennsylvania, PA, USA, 2011. [Google Scholar]
- Chen, L.; Gong, J.; Sun, F.; Wu, C. Effect of heat transfer on the performance of thermoelectric generators. Int. J. Therm. Sci. 2002, 41, 95–99. [Google Scholar] [CrossRef]
- Zebarjadi, M. Heat Management in Thermoelectric Power Generators. Sci. Rep. 2016, 6, 20951. [Google Scholar] [CrossRef]
- Shukla, K.N. Thermal math modeling and analysis of an electronic assembly. J. Electron. Packag. 2001, 123, 372–378. [Google Scholar] [CrossRef]
- Jónsson, H.; Moshfegh, B. Modeling of the thermal and hydraulic performance of plate fin, strip fin, and pin fin heat sinks-influence of flow bypass. IEEE Trans. Compon. Packag. Technol. 2001, 24, 142–149. [Google Scholar] [CrossRef]
- Saini, M.; Webb, R.L. Heat rejection limits of air cooled plane fin heat sinks for computer cooling. InITherm 2002. In Proceedings of the Eighth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (Cat. No. 02CH37258), San Diego, CA, USA, 30 May–1 June 2002. [Google Scholar] [CrossRef]
- Shukla, K. Hydrodynamics of diffusive processes. Appl. Mech. Rev. 2001, 54, 391–404. [Google Scholar] [CrossRef]
- Ko, T.; Ting, K. Optimal Reynolds number for the fully developed laminar forced convection in a helical coiled tube. Energy 2006, 31, 2142–2152. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Lorenzini, G.; Shariatzadeh, O.J.; Biserni, C. Evolution in the Design of V-Shaped Highly Conductive Pathways Embedded in a Heat-Generating Piece. J. Heat Transf. 2015, 137, 061001. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Moulod, M.; Joneydi Shariatzadeh, O.; Nourazar, S.S. Essential reformulations for optimization of highly conductive inserts embedded into a rectangular chip exposed to a uniform heat flux. J. Mech. Eng. Sci. 2014, 228, 2337–2346. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Maleki, H.; Lorenzini, G.; Nourazar, S.S. Effects of Cu and Ag nano-particles on flow and heat transfer from permeable surfaces. Adv. Powder Technol. 2014, 26, 193–199. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Pouzesh, A.; Poozesh, S. Controlling the heat flux distribution by changing the thickness of heated wall. J. Basic Appl. Sci. 2012, 2, 7270–7275. [Google Scholar]
- Hajmohammadi, M.; Nourazar, S.; Campo, A.; Poozesh, S. Optimal discrete distribution of heat flux elements for in-tube laminar forced convection. Int. J. Heat Fluid Flow 2013, 40, 89–96. [Google Scholar] [CrossRef]
- Najafi, H.; Najafi, B.; Hoseinpoori, P. Energy and cost optimization of a plate and fin heat exchanger using genetic algorithm. Appl. Therm. Eng. 2011, 31, 1839–1847. [Google Scholar] [CrossRef]
- Memon, S.; Tahir, K.N. Experimental and analytical simulation analyses on the electrical performance of thermoelectric generator modules for direct and concentrated Quartz-Halogen heat varvesting. Energies 2018, 11, 3315. [Google Scholar] [CrossRef]
- Junior, O.H.A.; Calderon, N.H.; De Souza, S.S. Characterization of a thermoelectric generator (TEG) system for waste heat recovery. Energies 2018, 11, 1555. [Google Scholar] [CrossRef]
- Kim, Y.; Yoon, G.; Chao, B.J.; Park, S.H. Multi-layer mettalization structure development for highly efficient polycrystalline SnSe thermoelectric devices. Energies 2017, 7, 1116. [Google Scholar]
- Lee, G.; Choi, G.; Kim, C.S.; Kim, Y.J.; Choi, H.; Kim, S.; Kim, H.S.; Lee, W.B.; Cho, B.J. Material Optimization for a High Power Thermoelectric Generator in Wearable Applications. Appl. Sci. 2017, 7, 1015. [Google Scholar] [CrossRef]
- Nesarajah, M.; Frey, G. Optimized Design of thermoelectric energy harvesting systems for waste heat recovery. Energies 2017, 7, 634. [Google Scholar] [CrossRef]
- Fan Performance Data. 2014. Available online: www.sunon.com (accessed on 9 September 2019).
- Chen, M.; Snyder, G.J. Analytical and numerical parameter extraction for compact modeling of thermoelectric coolers. Int. J. Heat Mass Transf. 2013, 60, 689–699. [Google Scholar] [CrossRef]
- James, F.; William, A. Material Science and Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Rowe, D.M. Thermoelectrics Handbook: Macro to Nano; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]







| Physical Properties | Symbol | Units | Aluminum | Copper | Ceramic |
|---|---|---|---|---|---|
| Thermal conductivity | k | W/(m.K) | 237 | 398 | 25.12 |
| Electrical resistivity | R | Ω m |
| Dimensions: 40 mm × 40 mm × 3.8 mm Maximum working temperature = 210 °C |  | |||
| Based on hot side temperature of 160 °C and cold side of 50 °C | ||||
| Open circuit Voltage (Voc) | Matched Voltage | Matched Power | Electrical Resistance (Ω) | Thermal Resistance (°C/W) |
| 12.1 (V) | 6 (V) | 3.6 (W) | 10 | 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-X.; Kiflemariam, R. Numerical Simulation and Validation of Thermoeletric Generator Based Self-Cooling System with Airflow. Energies 2019, 12, 4052. https://doi.org/10.3390/en12214052
Lin C-X, Kiflemariam R. Numerical Simulation and Validation of Thermoeletric Generator Based Self-Cooling System with Airflow. Energies. 2019; 12(21):4052. https://doi.org/10.3390/en12214052
Chicago/Turabian StyleLin, Cheng-Xian, and Robel Kiflemariam. 2019. "Numerical Simulation and Validation of Thermoeletric Generator Based Self-Cooling System with Airflow" Energies 12, no. 21: 4052. https://doi.org/10.3390/en12214052
APA StyleLin, C.-X., & Kiflemariam, R. (2019). Numerical Simulation and Validation of Thermoeletric Generator Based Self-Cooling System with Airflow. Energies, 12(21), 4052. https://doi.org/10.3390/en12214052




