Annual Variation in Energy Consumption of an Electric Vehicle Used for Commuting
Abstract
:1. Introduction
2. Simulation Tool for an Electric Vehicle
2.1. Modeling of the Electric Vehicle
2.1.1. Modeling of the Traction and Battery Subsystems
2.1.2. Modeling of the Comfort Subsystem
2.2. Validation of the EV Simulation Tool
3. Annual Variation in Energy Consumption for an Urban Driving Cycle
3.1. Case Study
3.2. Generation of a Reference Driving Cycle
3.3. Annual Variation in Energy Consumption for an Urban Driving Cycle
4. Annual Variation in EV Energy Consumption Considering Different Commuting Trips
4.1. Studied Driving Cycles
4.2. Annual Variation in Energy Consumption
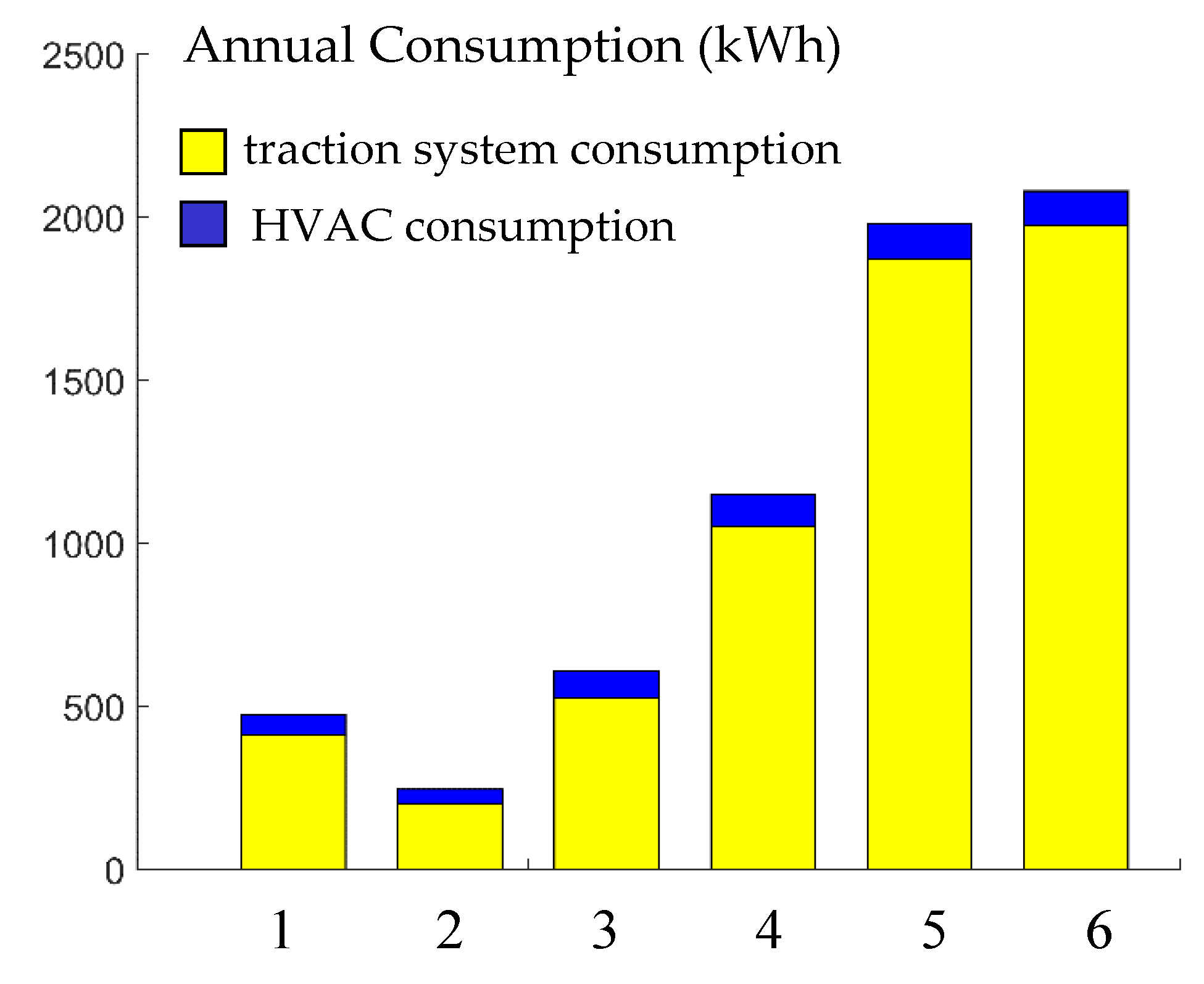
4.2.1. Effect of the HVAC and Traction Subsystems on Consumption
4.2.2. Annual Consumption of the Electric Vehicle
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Van Mierlo, J.; Messagie, M.; Rangaraju, S. Comparative environmental assessment of alternative fueled vehicles using a life cycle assessment. Transp. Res. Procedia 2017, 25, 3435–3445. [Google Scholar] [CrossRef]
- Tucki, K.; Orynycz, O.; Świć, A.; Mitoraj-Wojtanek, M. The Development of Electromobility in Poland and EU States as a Tool for Management of CO2 Emissions. Energies 2019, 12, 2942. [Google Scholar] [CrossRef] [Green Version]
- Global EV Outlook 2020, Entering the Decade of Electric Drive? International Energy Agency Report; International Energy Agency: Paris, France, 2020.
- C40 Cities Organization. Fossil Fuel Free Streets Declaration. Available online: https://www.c40.org/other/green-and-healthy-streets (accessed on 20 July 2020).
- Bouscayrol, A.; Castex, E.; Desreveaux, A.; Ferla, O.; Frotey, J.; German, R.; Lhomme, W.; Sergent, J.F. Campus of University with Mobility based on Innovation and carbon Neutral. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion, Belfort, France, 11–14 December 2017. [Google Scholar]
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar] [CrossRef]
- Giansoldati, M.; Danielis, R.; Rotaris, L.; Scorrano, M. The role of driving range in consumers’ purchasing decision for electric cars in Italy. Energy 2018, 165, 267–274. [Google Scholar] [CrossRef]
- Higueras-Castillo, E.; Molinillo, S.; Coca-Stefaniak, J.A.; Liébana-Cabanillas, F. Perceived Value and Customer Adoption of Electric and Hybrid Vehicles. Sustainability 2019, 11, 4956. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Lee, J.; Lee, C. Does Driving Range of Electric Vehicles Influence Electric Vehicle Adoption? Sustainability 2017, 9, 1783. [Google Scholar] [CrossRef] [Green Version]
- Rauh, N.; Franke, T.; Krems, J.F. User experience with electric vehicles while driving in a critical range situation—a qualitative approach. IET Intell. Transp. Syst. 2015, 9, 734–739. [Google Scholar] [CrossRef] [Green Version]
- Eisel, M.; Nastjuk, I.; Kolbe, L.M. Understanding the influence of in-vehicle information systems on range stress—Insights from an electric vehicle field experiment. Transp. Res. Part F Traffic Psychol. Behav. 2016, 43, 199–211. [Google Scholar] [CrossRef]
- Varga, B.O.; Sagoian, A.; Mariasiu, F. Prediction of Electric Vehicle Range: A Comprehensive Review of Current Issues and Challenge. Energies 2019, 12, 946. [Google Scholar] [CrossRef] [Green Version]
- Yi, Z.; Bauer, P.H. Effects of environmental factors on electric vehicle energy consumption: A sensitivity analysis. IET Electr. Syst. Transp. 2017, 7, 3–13. [Google Scholar] [CrossRef]
- Kambly, K.; Bradley, T.H. Geographical and temporal differences in electric vehicle range due to cabin conditioning energy consumption. J. Power Sources 2015, 275, 468–475. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J.J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the United States. Environ. Sci. Technol. 2015, 49, 3974–3980. [Google Scholar] [CrossRef] [PubMed]
- Horrein, L.; Bouscayrol, A.; Lhomme, W.; Depature, C. Impact of Heating System on the Range of an Electric Vehicle. IEEE Trans. Veh. Technol. 2017, 66, 4668–4677. [Google Scholar] [CrossRef]
- Lindgren, J.; Lund, P.D. Effect of extreme temperatures on battery charging and performance of electric vehicles. J. Power Sources 2016, 328, 37–45. [Google Scholar] [CrossRef]
- German, R.; Shili, S.; Desreveaux, A.; Sari, A.; Venet, P.; Bouscayrol, A. Dynamical Coupling of a Battery Electro-Thermal Model and the Traction Model of an EV for Driving Range Simulation. IEEE Trans. Veh. Technol. 2020, 69, 328–337. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperature. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Desreveaux, A.; Bouscayrol, A.; Trigui, R.; Castex, E.; Klein, J. Impact of the Traffic Stops on the Energy Consumption of Electric Vehicles. In Proceedings of the 32nd Electric Vehicle Symposium, Lyon, France, 19–22 May 2019. [Google Scholar]
- Fernández, R.A.; Caraballo, S.C.; López, F.C. A probabilistic approach for determining the influence of urban traffic management policies on energy consumption and greenhouse gas emissions from a battery electric vehicle. J. Clean. Prod. 2019, 236, 117604. [Google Scholar] [CrossRef]
- Desreveaux, A.; Bouscayrol, A.; Trigui, R.; Castex, E.; Klein, J. Impact of the Velocity Profile on the Energy Consumption of Electric Vehicle. IEEE Trans. Veh. Technol. 2019, 68, 11420–11426. [Google Scholar] [CrossRef]
- Fiori, C.; Arcidiacono, V.; Fontaras, G.; Makridis, M.; Mattas, K.; Marzano, V.; Thiel, C.; Ciuffo, B. The effect of electrified mobility on the relationship between traffic conditions and energy consumption. Transp. Res. Part D Transp. Environ. 2019, 67, 275–290. [Google Scholar] [CrossRef]
- Neubauer, J.; Wood, E. Thru-life impacts of driver aggression, climate, cabin thermal management, and battery thermal management on battery electric vehicle utility. J. Power Sources 2014, 259, 262–275. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Yamamoto, T.; Morikawa, T. Modeling the multilevel structure and mixed effects of the factors influencing the energy consumption of electric vehicles. Appl. Energy 2016, 183, 1351–1360. [Google Scholar] [CrossRef]
- De Cauwer, C.; Verbeke, W.; Coosemans, T.; Faid, S.; Van Mierlo, J. A data-driven method for energy consumption prediction and energy-efficient routing of electric vehicles in real-world conditions. Energies 2017, 10, 608. [Google Scholar] [CrossRef] [Green Version]
- Chan, C.C.; Bouscayrol, A.; Chen, K. Electric, hybrid, and fuel-cell vehicles: Architectures and modeling. IEEE Trans. Veh. Technol. 2010, 59, 589–598. [Google Scholar] [CrossRef]
- Baouche, F.; Billot, R.; Trigui, R.; El Faouzi, N.E. Efficient Allocation of Electric Vehicles Charging Stations: Optimization Model and Application to a Dense Urban Network. IEEE Intell. Trans. Syst. Mag. 2014, 6, 33–43. [Google Scholar] [CrossRef]
- Joud, L.; Da Silva, R.; Chrenko, D.; Kéromnès, A.; Le Moyne, L. Smart Energy Management for Series Hybrid Electric Vehicles Based on Driver Habits Recognition and Prediction. Energies 2020, 13, 2954. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, J.; Liu, B.; Zhou, N.; Li, S. Optimal Energy Management of Plug-In Hybrid Electric Vehicles Concerning the Entire Lifespan of Lithium-Ion Batteries. Energies 2020, 13, 2543. [Google Scholar] [CrossRef]
- Renault, Z. Available online: http://www.renault.fr/vehicules/vehicules-electriques/zoe (accessed on 20 July 2020).
- Mayet, C.; Horrein, L.; Bouscayrol, A.; Delarue, P.; Verhille, J.N.; Chattot, E.; Lemaire-Semail, B. Comparison of Different Models and Simulation Approaches for the Energetic Study of a Subway. IEEE Trans. Veh. Technol. 2014, 63, 556–565. [Google Scholar] [CrossRef]
- Bouscayrol, A.; Hautier, J.P.; Lemaire-Semail, B. Graphic Formalisms for the Control of Multi-Physical Energetic Systems. Systemic Design Methodologies for Electrical Energy, Tome 1, Analysis, Synthesis and Management; Roboam, X., Ed.; ISTE: London, UK; Willey: Hoboken, NJ, USA, 2012; Chapter 3; ISBN 9781848213883. [Google Scholar]
- EMR Website. Available online: https://www.emrwebsite.org/ (accessed on 20 July 2020).
- Martínez-García, M.; Zhang, Y.; Gordon, T. Modeling Lane Keeping by a Hybrid Open-Closed-Loop Pulse Control Scheme. IEEE Trans. Ind. Inf. 2016, 12, 2256–2265. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Stockar, S.; Canova, M. Energy-Optimal Control of an Automotive Air Conditioning System for Ancillary Load Reduction. IEEE Trans. Control Syst. Technol. 2016, 24, 67–80. [Google Scholar] [CrossRef]
- Weather Data in Lille in 2018. Available online: https://www.meteofrance.fr (accessed on 20 July 2020).
- OpenStreetMap API. Available online: https://api.openstreetmap.org (accessed on 20 July 2020).













| Elements | Characteristics |
|---|---|
| Battery | Li–ion NMC–22 kWh |
| Electric Machine | Synchronous machine 65 kW |
| Weight | 1468 kg |
| Daily Trips | Road Type | Average Velocity (km/h) | Distance (km) | Duration (min) |
|---|---|---|---|---|
| 1 | Urban | 28 | 7 | 15 |
| 2 | Urban | 34 | 4 | 7 |
| 3 | Extra-urban | 42 | 9 | 13 |
| 4 | Extra-urban | 49 | 16 | 20 |
| 5 | Highway | 69 | 27 | 23 |
| 6 | Highway | 89 | 20 | 13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desreveaux, A.; Bouscayrol, A.; Castex, E.; Trigui, R.; Hittinger, E.; Sirbu, G.-M. Annual Variation in Energy Consumption of an Electric Vehicle Used for Commuting. Energies 2020, 13, 4639. https://doi.org/10.3390/en13184639
Desreveaux A, Bouscayrol A, Castex E, Trigui R, Hittinger E, Sirbu G-M. Annual Variation in Energy Consumption of an Electric Vehicle Used for Commuting. Energies. 2020; 13(18):4639. https://doi.org/10.3390/en13184639
Chicago/Turabian StyleDesreveaux, Anatole, Alain Bouscayrol, Elodie Castex, Rochdi Trigui, Eric Hittinger, and Gabriel-Mihai Sirbu. 2020. "Annual Variation in Energy Consumption of an Electric Vehicle Used for Commuting" Energies 13, no. 18: 4639. https://doi.org/10.3390/en13184639





